2019广东省考行测技巧:从时间入手解决相遇追及问题
2019年公务员招聘考试行测数学运算必考题型速解技巧全解:16.时钟问题

16.时钟问题时钟问题是研究钟面上时针和分针关系的问题。
一般类型包括时针和分针重合、成一直线或直角问题,实际上相当于时针和分针的追及问题或相遇问题。
时钟问题可以细分为表针问题和快慢问题。
(1)表针问题常见的表针问题有:求某一时刻时针与分针的夹角角度,计算两针重合、两针垂直、两针成直线时的时刻等类型。
表针问题是在公考中经常出现的题目,也是考生需要熟练掌握的题型之一。
【例题1】每天钟表的分针追上时针每次间隔()分钟?A.55.45B.60C.64D.65.45【例题解析】本题最简便的思路是这样的。
分针每12小时追上时针共11次,由于分钟与时针都是匀速的,这样次间隔时间为12小11时,即约等于65.45分钟。
答案为D【思路点拨】本题是考察表针问题中的基本关系,分针追及时针的所用时间。
考生若是仔细阅读我们总结出的注意要点,就可以直接得出答案。
【例题2】小明晚上八点多开始做作业,此时钟表的分针与时针正好在一条直线上,当分针与时针第一次重合的时候,小明刚好做完作业。
请问小明做作业一共用了( )分钟?A.32.73B.35.71C. 38D.41.54【例题解析】方法一:设8点x 分,分针与时针在一条直线上,则有x+30=5×8+12x (分针每走12分钟,时针走一格),解得:x=11120,设8点y 分时第一次重合,y=5×8+12y ,y=11480 y-x=11360≈32.73分 方法二:由上题我们可知,由于时针、分针都是匀速转动,所以每12小时重合11次,每次需用1112小时,因为匀速从两针成一条直线到相重合,就应该是1112÷2=116小时=32.73分钟。
故应选择A 选项。
【思路点拨】对待表针问题,考生不要急于直接做题。
充分理解题意后,可以像“方法二”一样,快速解答本题。
【例题3】(2006年国考一卷第45题)从12时到13时,钟的时针与分针可成直角的机会有( )。
追及和相遇问题解题技巧
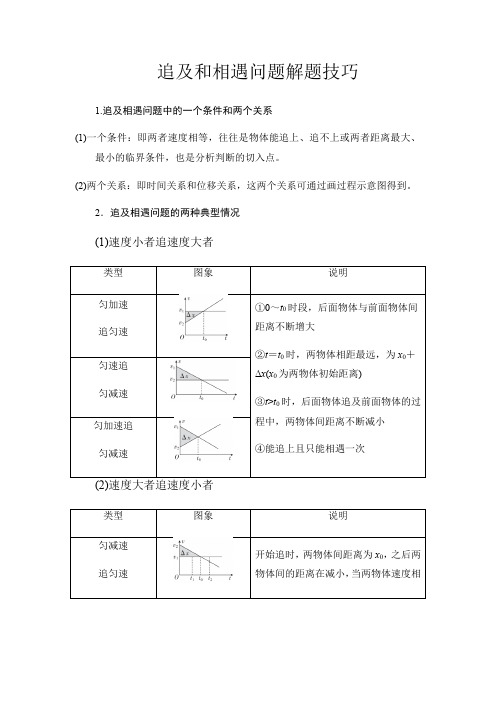
追及和相遇问题解题技巧1.追及相遇问题中的一个条件和两个关系(1)一个条件:即两者速度相等,往往是物体能追上、追不上或两者距离最大、最小的临界条件,也是分析判断的切入点。
(2)两个关系:即时间关系和位移关系,这两个关系可通过画过程示意图得到。
2.追及相遇问题的两种典型情况(1)速度小者追速度大者这一时刻一辆自行车以v=6 m/s的速度匀速驶来,从旁边超过汽车。
试求:自(1)汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?(2)什么时候汽车能追上自行车?此时汽车的速度是多少?(1)追上前汽车和自行车相距最远的条件是什么?提示:汽车和自行车速度相等。
(2)追上时汽车和自行车的位移关系是什么?提示:位移相等。
尝试解答(1)2_s__6_m__(2)4_s__12_m/s(1)解法一:(物理分析法)如图甲所示,汽车与自行车的速度相等时相距最远,设此时经过的时间为t1,汽车和自行车间的距离为Δx,则有v自=at1所以t1=v自a=2 sΔx=v自t1-12at21=6 m。
解法二:(相对运动法)以自行车为参考系,则从开始到相距最远的这段时间内,汽车相对这个参考系的各个物理量为初速度v0=v汽初-v自=0-6 m/s=-6 m/s末速度v t=v汽车-v自=0加速度a′=a-a自=3 m/s2-0=3 m/s2所以汽车和自行车相距最远时经历的时间为t1=v t-v0a′=2 s最大距离Δx=v2t-v202a′=-6 m负号表示汽车在后。
注意:利用相对运动的方法解题,要抓住三个关键:①选取哪个物体为研究对象;②选取哪个物体为参考系;③规定哪个方向为正方向。
解法三:(极值法)设汽车在追上自行车之前经过时间t1汽车和自行车相距为Δx,则Δx=v自t1-12at21代入已知数据得Δx=6t1-3 2t21由二次函数求极值的条件知:t1=2 s时,Δx有最大值6 m。
所以经过t1=2 s后,汽车和自行车相距最远,为Δx=6 m。
国家公务员考试行测多次相遇题型总结

国家公务员考试行测多次相遇题型总结在国家公务员考试行测中,多次相遇题型是一个比较常见的考点。
这种题型要求考生在给定的条件下,通过分析、推理和判断,找出多次相遇的规律,进而解决问题。
为了帮助考生更好地掌握这种题型,本文将对其进行总结和解析。
一、基本概念多次相遇题型通常涉及两个或多个对象在同一路径上多次相遇的情况。
例如,甲和乙两人在一条路上多次相遇,每次相遇的时间间隔和地点都有规律可循。
二、解题思路1、确定研究对象:首先要明确题目中涉及的对象,以及它们之间的相互关系。
2、分析相遇条件:多次相遇的情况通常有一定的规律可循。
通过分析题目的条件,找出每次相遇的时间、地点等规律。
3、建立数学模型:根据题目所给条件,建立适当的数学模型,以便更好地解决问题。
4、推导结论:根据建立的数学模型,进行计算和推理,得出结论。
三、常见题型及解析1、追及问题:两个对象在同一路径上运动,一个对象比另一个对象速度快,最终追上另一个对象。
这类问题通常涉及到速度、时间和距离之间的关系。
例题:甲和乙两辆车在同一条路上行驶,甲车速度是乙车速度的2倍。
两车从同一地点出发,当甲车追上乙车时,乙车已经行驶了10公里。
问甲车追上乙车需要多少时间?解析:设乙车的速度为x,甲车的速度为2x。
根据题意,当甲车追上乙车时,乙车已经行驶了10公里。
因此,甲车行驶的距离为10公里加上乙车行驶的距离。
根据速度、时间和距离之间的关系,可以列出方程:(10 + 10) / (2x - x) = 10 / x。
解得x = 1公里/小时。
因此,甲车的速度为2公里/小时,甲车追上乙车需要10小时。
2、相遇问题:两个对象在同一路径上运动,它们的运动方向相反,最终相遇。
这类问题通常涉及到速度、时间和距离之间的关系。
例题:甲和乙两辆车在同一条路上行驶,它们的速度相同。
两车从同一地点出发,当它们相遇时,它们各自行驶了10公里。
问它们相遇需要多少时间?解析:设它们相遇需要t小时。
行测数量关系:多次相遇 简单解决

行测数量关系:多次相遇简单解决为大家提供行测数量关系:多次相遇简单解决,一起来看看吧!希望大家能顺利解决多次相遇的问题!行测数量关系:多次相遇简单解决相信大家在备考行测时经常会遇到行程问题,而行程问题往往思路不够清晰、对应情景比较复杂,如经常看到有多者相遇、追及的情景,甚至还会出现多次相遇。
今天,就带大家一起来看一下,多次相遇题型的奥秘,帮你迅速解决难题!一、什么叫多次相遇:所谓多次相遇,即在题干中出现两个主体,在运动中不断地相遇的题型。
我们都知道,如果在直线异地相遇的情景中,两者同时相对出发,会相遇一次,那如果想要出现多次相遇,则需要两者“到达对方出发点后立即返回,在两地间往返运动”,这就是直线异地多次相遇的题型特征。
二、解题思路想要分析直线异地多次相遇的解题思路,需要借助行程图,我们一起来看看每次相遇时的具体情况。
对于直线异地多次相遇,我们掌握了对应的路程、时间和速度的比例关系,就等于掌握了解题的核心思路,只要灵活套用这个比例,我们就一定能把多次相遇问题,变得相对简单!行测数量关系:行程问题之相遇型牛吃草牛吃草问题是行测当中经常会考到的题型,在2020省考中还出现了一道牛吃草问题的变形题,难倒了很多考生。
但是其实牛吃草问题已经是相对来说比较固定的模型了,解题方法和思路也是比较固定的,如果能将这些解题思路和公式熟练掌握,牛吃草问题也就迎刃而解了;反之,如果不能掌握相应的解题方法的话,这一个相对来说比较容易的知识点就会变成公考路上的拦路虎。
今天就带大家一起来探究下相遇型牛吃草问题的解题思路。
一、题型特征相遇型牛吃草问题的典型题型特征:1、题目呈排比句式2、原始量受两个因素影响,且相遇型牛吃草的两个因素对原始量都是消耗二、模型求解方法原始草量M=(牛吃草的速度﹢草生长的速度)×时间(其中:M为原始草量,N为牛的数量,x为草枯萎的速度,t 为时间)三、例题剖析例题1.由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少。
国考行测数量关系——直线型相遇追及问题

国考行测数量关系——直线型相遇追及问题【答题妙招】相遇问题:相遇距离=(大速度+小速度)×相遇时间追及问题:追及距离=(大速度-小速度)×追及时间【例1】公路上有三辆同向行驶的汽车,其中甲车的时速为63公里,乙、丙两车的时速均为60公里,但由于水箱故障,丙车每连续行驶30分钟后必须停车2分钟。
早上10点,三车到达同一位置,问1小时后,甲、丙两车最多相距多少公里()A.5B.7C.9D.11【答案】B。
在这1个小时中,丙车最多休息4分钟,也即丙在一个小时内最少行程为56公里。
而甲车持续行驶,可达63公里。
因此两车最多相距7公里。
【例2】甲、乙两人分别从A.B两地同时出发,相向而行,乙的速度是甲的2/3,两人相遇后继续前进,甲到达B地,乙到达A地立即返回,已知两人第二次相遇的地点距离第一次相遇的地点是3000米,求A.B两地的距离是()米。
A.6000B.6500C.7000D.7500【答案】D 。
解法一:如图所示,设甲第一次走的路程为S 1,乙第一次走的路程为S 2。
可以看出,从第一次相遇到第二次相遇,甲走的路程为2S 2+3000,乙走的路程为2S 1-3000。
由路程与速度成正比可列方程:S 1:S 2=(2S 2+3000):(2S 1-3000)=2:3,解得S 1=4500,S 2=3000。
因此A.B 两地相距4500+3000=7500米。
因此答案选择D 选项。
解法二:设总路程为S ,分析题意可知,甲速:乙速=3:2,所以第一次相遇时,甲乙总路程为1个全程,乙的路程应为总路程的S 52;第二次相遇时,甲乙总路程为3个全程,甲的路程为S 54S S 59+=。
所以第一次相遇点距离第二次相遇点为3000S 52S 52S 54==-,S=7500米。
因此答案选择D 选项。
【例3】往返A 市和B 市的长途汽车以同样的发车间隔从两个城市分别发车,以每小时40公里的速度前往目标城市。
2019广东省考行测数学运算题:利用比例法快速求解行程题目

2019广东省考行测数学运算题:利用比例法快速求解行程题目在我们广东公务员考试中有一种高频题目,那就是行程问题。
行程问题就是利用公式S=vt来进行求解,往往各位同学在求解过程中会比较头疼,而且就算学习了对应的理论模型后,去求解行程题目依旧会觉得比较耗时和麻烦,那么,现在我们就一起来探讨下如何快速利用比例法进行求解行程题目。
比例法的核心是份数思想,例如男生20人,女生30人,男女生人数比为2:3,也就看成男生有2份,女生有3份,一份对应的人数就是10人。
而对于行程问题利用的更多是正反比来求解:路程一定的时候,速度和时间成反比;速度(时间)一定的时候,路程和时间(速度)成正比。
例如甲乙两人速度为2:3,经过相同的时间,两人走的路程比值也为2:3,正比关系;甲乙两人速度为2:3,走过相同的路程,所用时间比为3:2,为反比关系。
接下来我们通过题目来看看如何快速利用比例求解题目:【例1】甲乙两人相距若干千米,已知甲每分钟走60米,乙每分钟走50米。
如果两人先对而行,3分钟相遇;如果两人同时同向而行,甲在以后面。
那么甲几分钟可以追上乙?A 27B 30C 33D 35【答案】C。
解析:这题主要考察的点是相遇追及的模型,我们知道相遇是用速度和来计算,追及是用速度差来计算,这题里面追及和相遇的距离都是一样的。
在路程相同的情况下,就可以利用速度和时间成反比来进行求解了:相遇和追及的速度比为(60+50):(60-50)=11:1,也就可得到相遇和追及的时间比为1:11,相遇时间为3分钟,故追及时间为33分钟,答案选C。
【例2】甲以每小时6千米的速度步行从A地前往B地,在甲出发90分钟时,乙发现甲落下了重要物品,立刻骑自行车以每小时12千米的速度追甲,终于在上午11点追上了甲。
问甲出发时间是上午几点?A 7B 8C 9D 10【答案】B。
解析:这题涉及的考点为追及模型,可以利用基本公式进行求解,但使用比例法更加快速。
行程问题、相遇问题和追及问题的解题技巧[1]
行程问题.相遇问题和追及问题的解题技能一.行程问题.相遇问题和追及问题的焦点公式:行程问题最焦点的公式“速度=旅程÷时光”.由此可以演化成相遇问题和追及问题.个中:相遇时光=相遇距离÷速度和,追实时光=追及距离÷速度差.速度和=快速+慢速速度差=快速-慢速二.相遇距离.追及距离.速度和(差)及相遇(追及)时光的肯定第一:相遇时光和追实时光是指甲乙在完成相遇(追及)义务时配合走的时光.第二:在甲乙同时走时,它们之间的距离才是相遇距离(追及距离)分为:相遇距离——甲与乙在雷同时光内走的距离之和;S=S1+S2甲︳→S1→∣←S2←︳乙A C B追及距离——甲与乙在雷同时光内走的距离之差甲︳→S1←∣乙→ S2 ︳A B C在雷同时光内S甲=AC, S乙=BC距离差AB=S甲- S乙第三:在甲乙同时走之前,不管是甲乙谁先走,走的偏向若何?走的距离是若干?都不影响相遇时光和追实时光,只是引起相遇距离和追及距离的变更,具体变更都应视情形从开端相距的距离中加减.简略的有以下几种情形:三.例题:(一)相遇问题(1)A.B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B 地开出,每小时走80千米.若两车从A.B两地同时开出,相向而行,T小时相遇,则可列方程为T =1000/(120+80).甲︳→ S1 →∣← S2 ←︳乙A C B解析一:①此题为相遇问题;②甲乙配合走的时光为T小时;③甲乙在同时走时相距1000千米,也就是说甲乙相遇的距离为1000千米;④应用公式:相遇时光=相遇距离÷速度和依据等量关系列等式T =1000/(120+80)解析二:甲乙相距的距离是由甲乙在雷同的时光内配合走完的.相距的距离=甲车走的距离+乙车走的距离依据等量关系列等式1000=120*T+80*T(2)A.B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B 地开出,每小时走80千米.若甲车先从A地向B开出30分钟后,甲乙两车再相向而行,T小时相遇,则可列方程为1000-120*30/60=(120+80)*T甲︳→ S1 →∣→︳←︳乙A C D B解析一:①此题为相遇问题;②甲乙配合走的时光为T小时;③因为甲车先向乙走30分钟,使甲乙间的现实距离变短,甲乙在同时走时现实相距(1000-120*30/60)千米,也就是说甲乙相遇的距离实为940千米;④应用公式:相遇时光=相遇距离÷速度和依据等量关系列等式 T=(1000-120*30/60)/(120+80)解析二:甲车先走20分钟到C点,这时甲乙两车现实相距距离CB为(1000-120*30/60)千米,CB间的距离是由甲乙在雷同的时光内配合走完的.相遇距离=(开端两车相距的距离-甲车先走的距离),相遇距离=(甲车的速度+乙车的速度)*T(1000-120*30/60)=(120+80)*T(3)A.B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B 地开出,每小时走80千米.若乙车先从B地向A开出20分钟后,甲乙两车再相向而行,T小时相遇,则可列方程为1000-120*20/60=(120+80)*T甲︳→∣相遇←乙︳→乙先走←︳乙A DC B解析一:①此题为相遇问题;②甲乙配合走的时光为T小时;③甲乙在同时走时相距AC(1000-120*20/60)千米,也就是说甲乙相遇的距离实为960千米;④应用公式:相遇时光=相遇距离÷速度和依据等量关系列等式 T=(1000-120*20/60)/(120+80)(4)A.B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B 地开出,每小时走80千米.若甲车先从A地背向B开出10分钟后到C(或乙车先从B地背向A开出10分钟后到D),甲乙两车再相向而行,T小时相遇,则可列方程为T=(1000+120*10/60)/(120+80)︳←︳甲乙︳︳C A B D解析一:①此题为相遇问题;②甲乙配合走的时光为T小时;③因为甲车先背向乙走了10分钟,使甲乙间的现实距离变长,甲乙在同时向相而行时现实相距(1000+120*10/60)千米,也就是说甲乙相遇的距离实为1020千米;④应用公式:相遇时光=相遇距离÷速度和依据等量关系列等式T=(1000+120*10/60)/(120+80)解析二:乙车先背向甲而行同甲(5)A.B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B 地开出,每小时走80千米.若甲车先从A背向乙走10分钟到C,乙车也从B背向甲走30分钟到D后,甲乙两车再相向而行,T小时相遇,则可列方程为T=(1000+120*10/60+80*30/60)/(120+80)C A B D解析一:①此题为相遇问题;②甲乙配合走的时光为T小时;③因为甲乙两车先分离背向而行走了10分钟和30分钟,使甲乙间的现实距离变长,甲乙在同时走时现实相距(1000+120*10/60+80*30/60)千米,也就是说甲乙相遇的距离实为CD=1060千米;④应用公式:相遇时光=相遇距离÷速度和依据等量关系列等式T=(1000+120*10/60+80*30/60)/(120+80)归纳总结:不管甲乙两车在同时走之前谁先行(或同时行),只如果相向而行,就会造成现实相遇距离变短,在肯定相遇距离时,需用原始相距距离减去某车先行距离;只如果相背而行,就会造成现实相遇距离变长,在肯定相遇距离时,需用原始相距距离加上某车先行距离;(二)追及问题(1)A.B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B 地开出,每小时走80千米.若甲乙两车同时开出,同向而行,甲(快车)在乙(慢车)后面,T小时后快车追上乙车,可列方程为T=1000/(120-80)解析一:甲︳→ S1 ∣乙→︳A B C①此题为追及问题;②甲乙配合走的时光为T小时;③在甲乙同时走时相距1000千米,也就是说甲乙追及的距离为1000千米;④应用公式:追实时光=追及距离÷速度差.依据等量关系列等式T=1000/(120-80)解析二:①甲乙在同时动身前相距1000千米为甲追上乙多走的距离,应肯定为追及距离②甲每小时比乙多走了(120-80)千米,③求追实时光,现实上是求1000千米中有T个(120-80)(2)若甲乙两车同时从A地动身,甲车的速度为每小时行120千米,乙车的速度为每小时走80千米.乙(慢车)在(甲)快车后面,同向而行,T小时后甲与乙相距900千米,则可列方程为T=900/(120-80)解析一:①此题为追及问题;②甲乙配合走的时光为T小时;③因为甲乙速度不合,造成甲乙经T小时后相距900千米,也就是说甲乙追及的距离为900千米;④应用公式:追实时光=追及距离÷速度差.依据等量关系列等式T=900/(120-80)(3)若甲乙两车在长方形的跑道上同时从A地同向而行,甲车的速度为每小时行120千米,乙车的速度为每小时走80千米.已知长方形跑道的周长为500千米,T小时后甲与乙相遇,则可列方程为T=500/(120-80)解析一:①此题为追及问题;②甲乙配合走的时光为T小时;③因为甲乙速度不合,只有甲经T小时多走一圈后才干追上乙,也就是说甲乙追及的距离为长方形的周长500千米;④应用公式:追实时光=追及距离÷速度差.依据等量关系列等式T=500/(120-80)Array(4)甲乙同时从A地以40千米/小时速度同向动身,15分钟后,甲车因油量缺少以90千米/小时需返回到A地加油,乙车持续原速前行,甲车在A地加油用了10分钟,随后甲车又以90千米/小时速度用了T小时追上乙车,可列方程为:甲乙︳→ S1 ∣乙→S2︳A B C解析一:①此题为追及问题;②甲追乙配合走的时光为T小时;③因为甲乙同业15分钟产生距离AB=40*(15/60),甲在返回A地所用时光40*(15/60)/90小时和加油时光(10/60)小时乙车在依旧前行,前行的距离为BC=40*【40*(15/60)/90+10/60】千米;则甲车追乙车现实距离为AC=40*(15/60)+40*【40*(15/60)/90+10/60】④甲乙两车的速度差为(90-40)千米/小时⑤应用公式:追实时光=追及距离÷速度差.依据等量关系列等式T={40*(15/60)+40*【40*(15/60)/90+10/60】}/(90-40)归纳总结:解追及问题的症结也在于肯定追实时光和追及距离,具体同相遇问题.。
行程问题相遇问题和追及问题的解题技巧
行程问题、相遇问题和追及问题的解题技巧一、行程问题、相遇问题和追及问题的核心公式:。
由此可以演= 行程问题最核心的公式“速度路程÷时间”???变为相遇问题和追及问题。
其中:相遇时间=相遇距离÷速度和,追及距离÷速度差。
追及时间= +慢速速度和=快速-慢速速度差=快速二、相遇距离、追及距离、速度和(差)及相遇(追及)时间的确定相遇时间和追及时间是指甲乙在完成相遇(追及)任第一:务时共同走的时间。
第二:在甲乙同时走时,它们之间的距离才是相遇距离(追及距离)分为:相遇距离——甲与乙在相同时间内走的距离?之和;S=S1+S2 甲︳→S1 →∣←S2 ←︳乙BC A?之差追及距离——甲与乙在相同时间内走的距离︳S1 ←∣乙→S2 甲︳→C A B在相同时间内S甲=AC ,S乙=BC 距离差AB =S甲- S乙第三:在甲乙同时走之前,不管是甲乙谁先走,走的方向如何?走的距离是多少?都不影响相遇时间和追及时间,只是引起相遇距离和追及距离的变化,具体变化都应视情况从开始相距的距离中加减。
简单的有以下几种情况:三、例题:(一)相遇问题(1)A、B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B地开出,每小时走80千米。
若两车从A、B两地同时开出,相向而行,T小时相遇,则可列方程为?T??=1000/(120+80)??。
甲︳→S1 →∣←S2 ←︳乙BC A解析一:①此题为相遇问题;②甲乙共同走的时间为T小时;③甲乙在同时走时相距1000千米,也就是说甲乙相遇的距离为1000千米;④利用公式:相遇时间=相遇距离÷速度和根据等量关系列等式T??=1000/(120+80)?解析二:甲乙相距的距离是由甲乙在相同的时间内共同走完的。
相距的距离=甲车走的距离+乙车走的距离根据等量关系列等式1000=120*T+80*T(2)A、B两地相距1000千米,甲车从A地开出,每小时行120千米,乙车从B地开出,每小时走80千米。
相遇追及问题解题技巧
相遇追及问题是数学中常见的运动问题类型,通常涉及两个物体或人以不同的速度出发,然后在某个时间点相遇的情况。
以下是解决相遇追及问题的一些常见技巧:
确定问题中的已知量和未知量:首先,要仔细阅读问题,确定已知量和未知量。
已知量可能包括两个物体的初始位置、速度,相遇的时间点等。
未知量通常是问题要求求解的内容,如相遇的距离、时间等。
建立关系式:根据已知量和问题要求的未知量,建立起物体之间的关系式。
可以使用时间、距离和速度之间的关系来表达。
常见的关系式有:距离= 速度× 时间。
运用代数解决方程:根据建立的关系式,将问题转化为一个方程或一组方程。
运用代数的方法解决方程,求解未知量。
常用的代数技巧包括消元法、代入法和等式配凑等。
注意单位和量纲:在运算过程中,要特别注意物理量的单位和量纲的一致性。
确保所有的速度、时间和距离都采用相同的单位进行计算。
图形辅助:对于一些复杂的相遇追及问题,可以绘制图表或示意图来帮助理解和解决问题。
图形辅助可以更直观地表示物体之间的运动情况,有助于找到问题的解答路径。
反证法:有时,反证法也可以用于相遇追及问题的求解。
假设未知量的某个值,然后通过推理和计算来验证是否符合已知条件,从而确定正确的解。
以上是解决相遇追及问题的一些常见技巧。
在实际应用中,根据问题的具体情况选择合适的方法,结合数学思维和分析能力,可以高效地解决相遇追及问题。
国考行测相遇追及问题
国考行测相遇追及问题
最近几年,国家公务员考试、各地方省考大受欢迎,很多考生在考试前不知道如何复习。
尤其是数量关系部分,更是大家公认的难度较大的一部分,今天我们就来说一说数量关系中一个常考考点——相遇追及。
其实相遇追及最主要的知识点就是掌握两个公式,一个关于相遇,一个关于追及。
掌握这两个公式,问题就不难解决。
【例题1】:甲乙两人同时从相距30千米的两地出发,相向而行,甲每小时走3.5千米,乙每小时走2.5千米,问甲乙两人经过几小时相遇?
A.4
B.5
C.6
D.7
【解析】B:通过分析题干我们可以得到这是一个相遇问题,我们可以借助相遇的公式路程和=速度和×时间,来解题。
此题我们已知路程和还有速度,将其代入公式得
,解得t=5小时,所以经过5小时相遇,故选B。
【例题2】:一只猎豹锁定了距离自己200米远的一只羚羊,以30米/秒的速度发起进攻,同时羚羊意识到危险以20米/秒的速度迅速逃命,问猎豹捕捉到羚羊时,羚羊跑了多远?
A.400米
B.500米
C.600米
D.700米
综上,是相遇追及问题的解题方法,如果想要灵活运用这个方法还要勤加练习,做一些难度高些的题目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019广东省考行测技巧:从时间入手解决相遇追及问题
相遇问题和追及问题在公考中十分常见,常规思路都是从速度入手解决。但
如果题干中给出的条件都是时间相关的,那么直接从时间入手也是一种不错的思
路。比如:
例题1.甲、乙二人分别从A、B两地同时出发,如果两人同向而行,甲30
分钟追上乙;如果两人相向而行,6分钟可相遇,可知乙每分钟走50米,则AB
两地相距多少米?
A.750米 B.800米 C.850米 D.900米
解析:由题意可知,①甲走30分钟-乙走30分钟=全程;②甲走6分钟+乙
走6分钟=全程;我们知道乙的速度,不知道甲的速度,所以我们要寻找乙与全程
之间的关系,②*5-①得,乙走60分钟=4倍全程,所以乙走15分钟=全程,
所以AB之间的距离为50*15=750(米),选A。
如果题目所求值为时间,从时间入手就更加方便了,例如:
例题2.老林和小陈绕着周长为720米的小花园匀速散步,小陈比老林速度
快。若两人同时从某一起点同时出发,则每隔18分钟相遇一次;若两人同时从某
一起点相反方向出发,则每隔6分钟相遇一次。由此可知,小陈绕你小花园散步
一圈需要( )分钟。
A.6 B.9 C.15 D.18
解析:由题意可知,①陈走18分钟-林走18分钟=1圈;②陈走6分钟+林
走6分钟=1圈;题目求的是陈走一圈需要的时间,所以我们只关注陈走一圈的时
间,那么①+②*3可得,陈走36分钟=4圈,所以陈走一圈需要9分钟,选B。
哪怕是更加复杂的题目,从时间入手也是一种很好的选择。
例题3.清晨,爷爷、爸爸和小磊在同一条笔直跑道上朝同一方向匀速晨跑。
现在爷爷在前,爸爸在中,小磊在后,且三人之间的间距正好相等。12分钟后
小磊追上了爸爸,又过了6分钟后小磊追上了爷爷,则再过( )分钟,爸爸可追上
爷爷。
A.12 B.15 C.18 D.36
解析:由题意可知,①磊跑12分钟-爸跑12分钟=1间距;②磊跑18分钟-
爷跑18分钟=2间距;题目求的是爸爸追上爷爷花费的时间,我们要消除掉磊磊
的因素,②-①*1.5得,爸跑18分钟-爷跑18分钟=0.5间距,所以爸跑36分
钟-爷跑36分钟=1间距。也就是说爸爸要花36分钟追上爷爷。因为已经过去
了18分钟,所以爸爸再花18分钟可以追上爷爷。
综上所述,在题干本身就是给出时间条件的相遇和追及问题中,我们直接从
时间入手,也可以快速的求解。
