第三章 空域滤波:原理及
空间滤波的基本原理与各式滤波器

Chapter 3強度轉換與空間濾波空間濾波的基本原理與各式濾波器Chapter 3強度轉換與空間濾波(S ti l filt i )遮罩mask空間濾波(Spatial filtering)將濾波遮罩在影像中移動,在每一點(x,y)計算濾波係數及遮罩所涵蓋的影像區域的像素乘積和mask 濾波器filter 核心kernel template 模板template 窗windowmaskimage++++++−−+−−−−=y x f w y x f w y x f w y x f w y x g )1,1()1,1(...),()0,0(...),1()0,1()1,1()1,1(),(∑∑−=−=++=aa s bbs t y s x f t s w y x g ),(),(),(Chapter 3強度轉換與空間濾波相關性(correlation)迴旋積(convolution)相關性¾迴旋積Chapter 3強度轉換與空間濾波相關性迴旋積相關性∑++=a bt s x t s w y x f y x w ,,),(),(o ∑−=−=a s bt y f )()(•y x f y x w ),(),(迴旋積∑∑−=−=−−=a a s bbt t y s x f t s w ),(),(Chapter 3強度轉換與空間濾波Chapter 3強度轉換與空間濾波z w z w z w R mn mn +++= (221)1h (-1,-1)h (-1,0)h (-1,1)-1z w mni k k =∑=1h (0,1)h (0,0)h (0,1)h (1,-1)h (1,0)h (1,1)zw T =產生空間濾波器遮罩h (x ,y )1.平均濾波器z w z w z w R +++=...對於3*3的遮罩2.101 and 101 1),(,,-y ,,-x y x h ===z w kk =∑9992211 2.高斯濾波器101and 101 2222−=−==+x ex h y x σzw Tk ==1,,,,,),(y yChapter 3強度轉換與空間濾波平滑空間濾波器Smoothing spatial filters•∑a bGeneral form用於模糊化跟減少雜訊•以濾波器所定義的平均值取代原灰階值•對於銳利的邊緣也有模糊的負效果∑∑−=−=++=aba s bt t s w t y s x f t s w y x g ),(),(),(Box filterWeighted average∑−=−=a s bt ),(1(所有係數都相等)g g (每個像素有不同的重要性)∑==919i izRChapter 3強度轉換與空間濾波3使用方形濾波器的結果N=3N9N=5N=9N 15N35N=15N=35Chapter 3強度轉換與空間濾波Threshing with a threshold value equal to 影像平均遮罩的大小建立了會被融入背景的物體的相對大小,可用於標示較大較亮的物體Threshing with a threshold value equal to 25% of the highest intensity in the blurredimage, the small objects are eliminated.After averaging, the small objectsblend with backgroundChapter 3強度轉換與空間濾波排序統計濾波器(Order-statistics filters)非線性的濾波器,其響應建立在由濾波器所包圍的影像區域中所含的像素順序上•中值濾波器Median filterM di filt•將像素值用該鄰近區域像素的“中間值"代替•適用於胡椒鹽式雜訊(salt and pepper noise)M filt Mi filt•Max filter, Min filter平均濾波中間值濾波Chapter 3強度轉換與空間濾波•中值濾波器1818191919202021155將九宮格中的灰階值重新排序1819182021中值19155202121 20192120191819182021 191920212119202116018 17192220192019212019 19202116018 1719222019胡椒鹽式雜訊Chapter 3強度轉換與空間濾波•中值濾波器—水彩畫特效Chapter 3強度轉換與空間濾波S li銳化空間濾波器(Sharpening spatial filters)突顯影像中細微的部分或增強模糊的細節,藉由微分來達成Scan line •微分運算子的響應強度正比於所在影像處的不連續程度•微分增強邊緣和不連續處fderivative order -First −∂()()x fx f xderivative order -Second 12∂+=∂()()()x f x f x f xf2112−−++=∂Chapter 3強度轉換與空間濾波銳化空間濾波器(Sharpening spatial filters)微分運算子的響應強度正比於運算子在其運用點處影像強度不連續的程度一階導數first derivative•在常數強度區域中為零•在強度步階斜面起始處不為零•沿著斜面不為零二次導數Second-order derivatives•在常數強度區域中為零•在強度步階或斜面起始處以及尾端不為零沿著有常數斜率的斜面為零•Chapter 3強度轉換與空間濾波二次導數濾波器圖3.37(a)用來實現(3.6-6) 式的濾波器遮罩;Laplacian22∂(b)實現此式之延伸所用的遮罩,其中包括對角項;(c)和(d) 兩個實際上常見之拉普拉斯的其它實現。
《非线性空域滤波器》课件

非线性空域滤波器的优势
非线性空域滤波器相比于传统线性滤波器具有更好的图像处理效果和性能。 它能够更有效地去除图像噪声、增强图像细节,提高图像质量。
总结:非线性空域滤波器的应用前景
非线性空域滤波器在图像处理领域有着广泛的应用前景。随着计算机技术的发展,非线性滤波器也将不断进步 和创新,为图像处理提供更好的解决方案。
参考资料
为了更好地理解和学习非线性空域滤波器,以下是一些推荐的参考资料: • 相关论文 • 专业书籍 • 学术文献
《非线性空域滤波器》PPT课 件
欢迎来到《非线性空域滤波器》PPT课件。本课程将带您深入了解非线性空域 滤波器的原理、应用和操作步骤。
什么是非线性空域滤波器?
非线性空域滤波器是一种用于图像处理的滤波器,它不仅可以改善图像的质 量,还可以实现模糊图像复原、噪声去除和图像增强等功能。
非线性空域滤波器的原理
非线性空域滤波器基于图像的局部特征进行处理,通过对图像的像素进行重 新排列和操作,来实现去除噪声、增强细节等效果。
应用:模糊图像的复原
非线性空域滤波器可以根据图像的模糊程度和特点,选择合适的滤波算法进 行图像复原,使得模糊的图像重新变得清晰和可辨认。
操作步骤:如何进行非线性滤 波
进行非线性滤波的步骤包括图像预处理、选择合适的滤波算法和参数设置、 滤波处理和结果评估等。正确的操作步骤
空间滤波机理

空间滤波机理空间滤波是一种图像处理方法,通过对图像中的像素进行加权平均或者运算,以减小图像中的噪声、平滑图像、边缘检测等目的。
空间滤波的机理涉及图像中像素的邻域关系与像素权重的计算。
空间滤波的机理主要包括以下几个方面:1. 邻域关系:空间滤波通过对像素的邻域进行处理,利用像素周围的信息进行滤波操作。
一般来说,邻域的大小是一个关键因素,常见的邻域形状有矩形、圆形等。
邻域大小的选择会影响到滤波效果,邻域过小可能会导致平滑不彻底,邻域过大可能会导致模糊效果。
2. 权重计算:在空间滤波中,对于每个像素,都需要给予其周围像素一个权重系数。
一般来说,邻域内的像素越接近中心像素,其权重越高。
根据权重系数的不同计算方法,空间滤波可以分为均值滤波、中值滤波、自适应滤波等多种方法。
3. 均值滤波:均值滤波是一种简单的空间滤波方法,它以邻域内像素的平均灰度值作为当前像素的灰度值。
这种方法适用于去除高斯噪声等均值为零的噪声。
4. 中值滤波:中值滤波是一种非线性空间滤波方法,它将中心像素的值替换为邻域内像素值的中值。
中值滤波对于椒盐噪声等离群点噪声有较好的抑制效果。
5. 自适应滤波:自适应滤波是一种根据邻域内像素之间的差异性动态调整权重的滤波方法。
这种方法可以根据图像中的边缘信息来保护边缘,并对平滑区域进行较大程度的平滑。
空间滤波的机理可以通过数学模型来进行描述和分析,其中包括邻域模板的建立、权重系数的计算公式等等。
在具体应用中,可以根据具体问题选择合适的滤波方法和参数,以达到更好的滤波效果。
空间滤波是图像处理中非常基础和常用的方法,掌握其机理对于图像处理的应用和算法设计具有重要意义。
第三章空域图像增强1

生成图象叠加效果 对于两个图象f(x,y)和h(x,y)的均值有: g(x,y) = 1/2f(x,y) + 1/2h(x,y) 会得到二次暴光的效果。推广这个公式为: g(x,y) = αf(x,y) + βh(x,y) 其中α+β= 1 我们可以得到各种图象合成的效果,也可以 用于两张图片的衔接
(3)
第3章
补(COMPLEMENT,也常称反或 非):记为NOT q(也可写为 q )
3.3 直方图修正
直方图是多种空间域处理技术的基础。直方图操作 能有效地用于图像增强。 1.灰度直方图 灰度直方图是灰度值的函数,它描述了图像中各灰 度值的像素个数。 通常用横坐标表示像素的灰度级别,纵坐标表示对 应的灰度级出现的频率(像素的个数)。频率的计算 公式为: p(r)=nr nr是图像中灰度为r的像素数 。
t C log(1 | s |)
第3章
3、阶梯量化
将图像灰度分阶段量化成较少的级数
获得数据量压缩的效果
第3章
4、阈值切分
增强图只剩下2个灰度级,对比度最大但细节全丢
失了
第3章
灰度变换可以选择不同的灰度变换函数,如正 比函数和指数函数等 。常用的灰度变换函数主 要有:
1.线性灰度变换。 2.分段线性灰度变换。 3.非线性灰度变换。
空域平滑滤波和锐化滤波
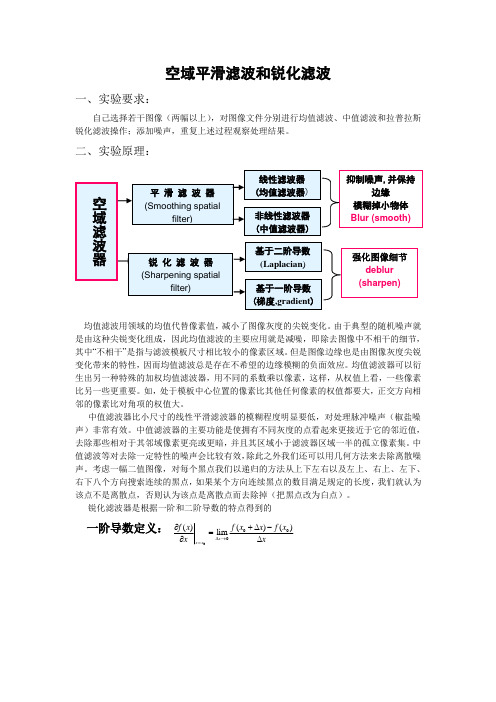
空域平滑滤波和锐化滤波 一、实验要求: 自己选择若干图像(两幅以上),对图像文件分别进行均值滤波、中值滤波和拉普拉斯锐化滤波操作;添加噪声,重复上述过程观察处理结果。
二、实验原理:
均值滤波用领域的均值代替像素值,减小了图像灰度的尖锐变化。由于典型的随机噪声就是由这种尖锐变化组成,因此均值滤波的主要应用就是减噪,即除去图像中不相干的细节,其中“不相干”是指与滤波模板尺寸相比较小的像素区域。但是图像边缘也是由图像灰度尖锐变化带来的特性,因而均值滤波总是存在不希望的边缘模糊的负面效应。均值滤波器可以衍生出另一种特殊的加权均值滤波器,用不同的系数乘以像素,这样,从权值上看,一些像素比另一些更重要。如,处于模板中心位置的像素比其他任何像素的权值都要大,正交方向相邻的像素比对角项的权值大。 中值滤波器比小尺寸的线性平滑滤波器的模糊程度明显要低,对处理脉冲噪声(椒盐噪声)非常有效。中值滤波器的主要功能是使拥有不同灰度的点看起来更接近于它的邻近值,去除那些相对于其邻域像素更亮或更暗,并且其区域小于滤波器区域一半的孤立像素集。中值滤波等对去除一定特性的噪声会比较有效,除此之外我们还可以用几何方法来去除离散噪声。考虑一幅二值图像,对每个黑点我们以递归的方法从上下左右以及左上、右上、左下、右下八个方向搜索连续的黑点,如果某个方向连续黑点的数目满足规定的长度,我们就认为该点不是离散点,否则认为该点是离散点而去除掉(把黑点改为白点)。 锐化滤波器是根据一阶和二阶导数的特点得到的
一阶导数定义:
? 锐 化 滤 波 器
(Sharpening spatial filter) 基于二阶导数 (Laplacian) 基于一阶导数 (梯度,gradient)
强化图像细节 deblur (sharpen)
空域滤波器
(Spatial filter平 滑 滤 波 器 (Smoothing spatial filter)
线性滤波器 (均值滤波器) 非线性滤波器 (中值滤波器) 抑制噪声,并保持边缘 模糊掉小物体 Blur (smooth)
空间滤波的实验原理是

空间滤波的实验原理是空间滤波是一种图像处理技术,用于图像降噪、锐化等应用领域。
其实验原理可以从以下几个方面解释。
1. 图像表示:图像是由一个个像素点组成的二维矩阵,其中每个像素点包含亮度信息。
在进行空间滤波前,需要将图像进行灰度化操作,将彩色图像转化为黑白图像。
2. 滤波器:空间滤波的核心是滤波器,也称为卷积核。
它是一个小矩阵,用于对图像的每个像素点进行操作。
滤波器中的数值称为权重,决定了每个像素点受到滤波器的影响程度。
滤波器的大小决定了影响像素点的范围,常见的滤波器有3x3、5x5等。
3. 滤波原理:空间滤波的原理基于图像中局部像素之间的相关性。
通过将每个像素与其周围像素加权求和,可以对图像进行平滑或锐化处理。
具体操作是将滤波器沿图像的每个位置进行平移,将滤波器与图像的对应位置进行元素乘积,再将乘积结果相加得到输出图像的像素值。
4. 常用滤波器:- 均值滤波器:滤波器中的权重均为1,用于平滑图像、去除噪声。
计算每个像素周围邻居像素的平均值,并将结果作为输出图像的像素值。
- 中值滤波器:滤波器中的权重根据周围像素的亮度进行排序,将中间值作为输出图像的像素值。
适用于去除椒盐噪声等。
- Sobel滤波器:用于边缘检测,通过计算每个像素点在X和Y方向上的亮度梯度,来检测图像中的边缘。
5. 实验步骤:- 载入图像:选择一个需要处理的图像,载入到图像处理软件中。
- 灰度化:将图像转化为黑白图像,每个像素点只包含亮度信息。
- 选择滤波器:根据需求选择合适的滤波器,比如均值滤波器、中值滤波器、Sobel滤波器等。
- 滤波处理:将滤波器沿图像的每个位置进行平移,与图像对应位置的像素进行乘积累加,得到输出图像的像素点。
- 保存结果:将处理后的图像保存,用于后续分析或展示。
6. 实验效果评估:根据实际需求,可以使用定量或定性的方法评估实验效果。
常见的评估指标包括峰值信噪比(PSNR)、结构相似性指数(SSIM)等。
空间滤波系统的基本原理
空间滤波系统的基本原理
空间滤波系统的基本原理是根据空间域中的像素点与其周围像素点的灰度值关系,对图像进行滤波处理,以改善图像的质量或提取感兴趣的图像特征。
空间滤波系统通常包括以下步骤:
1. 图像采样:将连续的图像转换为离散的像素点表示。
2. 图像卷积:对每个像素点,用其周围像素点的灰度值与一组滤波器进行卷积运算。
滤波器通常是一组权重矩阵,用于对像素点进行加权平均或加权求和。
3. 灰度变换:对卷积结果进行灰度变换操作,以调整图像的对比度或亮度等特征。
4. 图像重建:根据卷积和灰度变换的结果,重建图像并进行显示或进一步处理。
空间滤波系统的关键是设计和选择合适的滤波器。
常用的滤波器有平滑滤波器、边缘检测滤波器和锐化滤波器等。
平滑滤波器用于去除图像中的噪声,边缘检测滤波器用于检测图像中的边缘,锐化滤波器用于增强图像的细节。
空间滤波系统的性能可以通过滤波器的大小、权重矩阵以及滤波器的数量等参数进行调整。
不同的滤波器参数可以产生不同的滤波效果,以满足不同的应用需求。
阵列信号处理基础教程
授课教师:廖桂生
西安电子科技大学雷达信号处理实验室
课程目的
掌握空间传播波携带信号的获取与处理的基 本理论和方法,特别是空间多维信号算法,熟悉 参数估计和自适应波束形成的常用算法。
课程要求
期间:含上机实践 期末:论文、考试
西安电子科技大学雷达信号处理实验室
参考文献
1. Prabhakar S.naidu,Sensor Array Signal Processing 2. 王永良.空间谱估计理论与算法,清华大学出版社 3. Monzingo.R.and Miller T. Introduction to adaptive array.
西安电子科技大学雷达信号处理实验室
代入波动方程:k
2 x
s(r
,
t
)
若约束条件:
k
2 x
k
2 y
k
2 y
s(r,
t
)
kz2s(r
,
t
)
kz2
2
c2
2
c2
s(r,t)
即
kk
k
2 x
k
2 y
kz2
c
则:(*)式表示的信号是波动方程的解,称为“单色”
或“单频”解。
c
为传播速度,2
频率 f 之外无其它频率分量,那么该信号由其整个
持续期内的时间间隔为1/ 2 f 的信号采样值完全确
定,从而使模拟信号可以由无限个离散的点信号来 表示(拟合)。
空间采样:与时间采样类似,采样频率必须足够高才 不会引起空间模糊(即空间混叠),但由于受到实 际条件的限制,空间采样的点数不可能无限,这相 当于时域加窗,所以会出现旁瓣泄漏。
第3章之间衔接-空域与频域
2
数字图像是离散的,所以要用差分表示, p5 点 的梯度可以表示为:
∂f 表示 ⎯⎯ → p 6 − p 5 ⎯ ∂x ∂f 表示 ⎯⎯ → p8 − p 5 ⎯ ∂y
但一般选取:
∂f = ( p9 + 2 p6 + p3 ) − ( p7 + 2 p4 + p1 ) ∂x ∂f = ( p7 + 2 p8 + p9 ) − ( p1 + 2 p2 + p3 ) ∂y
图3-1. 像素邻域
像素连通 连通性是决定图像中目标的边界和不同区域 用到的重要概念。 考虑连通性时,首先是边缘或区域的二值图像。 4连通:如果q属于N4(p),则p和q是4连通。 8连通:如果q属于N8(p),则p和q是4连通。
距离-Distance 数字图像中两个像素坐标(i,j) 和 (h,k)之间的距离有不同的定义: (1) 欧氏距离(Euclidean distance):
g ( X , Y ) = T ∗ f ( X , Y ) = ∑∑ T (i, j ) f ( X − i, Y − j )
i =0 j =0 m −1 m −1
[例子]卷积模板运算 模板 1 0 0 1 1 2 2 1 图像 1 1 1 1 3 4 3 1 3 4 3 4 4 3 3 4 2 2 3 * 结果 5 4 2 * 7 7 7 * 6 7 7 * * * * *
《数字图像处理》
Digital Image Processing
图像处理: • 空域处理 • 频域(或变换域)处理
0. 空域与频域(或变换域)概念
• 空域处理⎯模板运算: 直接对采集得到的图像处理,即直接对像素灰度处理。 如3×3模板:
第三章+空域增强
个值d的象素组成以(x,y)为 中心的正方形
D8距离为1的象素就是(x,y)
的8-邻接象素
象素间的距离
明可夫斯基距离
点p和q之间的明可夫斯基距离(范数为k的距 离)定义为
DM ,k ( p, q) x s y t
k
1 k k
通常被称为Lk范数,或范数为k的距离。 k=1,k=2, k 分别是欧式距离,城区距离和棋 盘距离。
像素位置依次重合;
② 将模版系数与模版对应像素相乘; ③ 将所有乘积相加; ④ 将和(模板的输出响应)赋给图中对应模版
中心位置的像素。
模板运算
Y Y
s4
y
s3 s0 s7
x
s2 s1 s8
X
k4 k3 k2
s5 s6
k5 k0 k1
k6 k7 k8
y
R
x
X
R k0 s0 k1s1 k8 s8
在空间域中与相邻数据基本不相关(相互独立); 在变换域中表现为很高的空间频率分量。
为了消除图象中的这些孤立噪声点,应当设法修正这些象 元的灰度值,使它们与相邻象元的灰度取值相近或一致。
平滑滤波
方法:选择一定的平滑模板,通过卷积处理在
图象的空间域计算完成。
平滑模板:是具有低通滤波形式的数据阵列,
锐化滤波
一阶的差分运算在计算机处理时,表达形式可 以灵活地拓广。
G[ f (i, j )] f (i, j ) f (i 1, j ) f (i, j ) f (i, j 1)
G[ f (i, j )] f (i, j ) f (i 1, j 1) f (i 1, j ) f (i, j 1)
