路面不平度数学模型

合集下载

关于路面不平度重构的研究

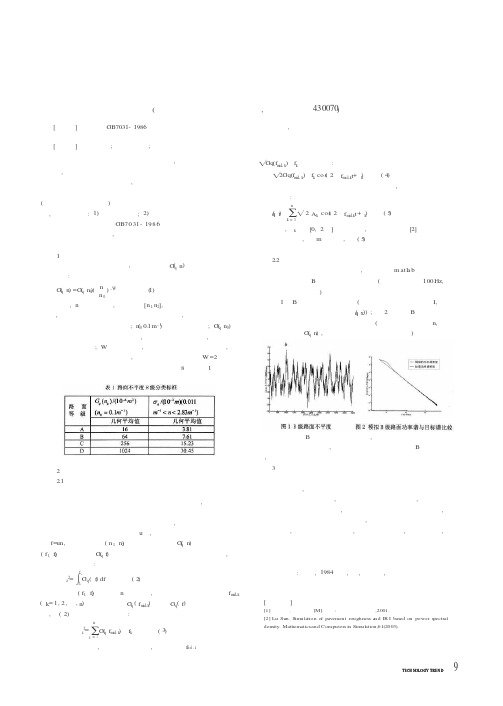
T NOLO GY TR N D[摘要]通过对GB7031-1986建议的公路路面功率谱密度的拟合表达式进行研究,可以得出采用谐波叠加法进行模拟得到的路面不平度所对应的功率谱密度可以很好地逼近目标谱的结论。

[关键词]谐波叠加;路面不平度;仿真在进行汽车动力响应分析和平顺性研究中,时域路面模型日益受到重视,因为路面输人模型能否准确的反映实际研究的路面对分析研究的准确性有着根本的影响。

所以,建立合理的路面输人模型是进行汽车平顺性和操稳性研究需首先解决的问题之一。

对于时域内的路面激励(也即路面不平度或高程)可以利用路面不平度数据和汽车行驶速度获得,获得方法有:1)试验测试方法;2)将给定的路面功率谱密度变换为路面不平度。

本文通过对GB7031-1986建议的公路路面功率谱密度的拟合表达式进行研究后,采用谐波叠加法进行模拟得到的路面不平度所对应的功率谱密度可以很好地逼近目标谱。

1路面不平度的功率谱密度的描述根据国际标准化组织文件,功率谱密度G q (n )可以用下式作为拟合表达式:G q (n )=G q (n 0)(n n 0)-W(1)式中,n 为空间频率,其带宽为[n 1,n 2],分别为有效频带的上限和下限,带宽的确定应保证汽车在一平均速度行驶时,不平度引起的振动要包括汽车振动的主要固有频率;n 0(0.1m -1)为参考空间频率;G q (n 0)为参考空间频率下的路面功率谱密度,称为路面不平度系数,数据取决于公路的路面等级;W 为频率指数,为双对数坐标上斜线的频率,它决定路面功率谱密度的频率结构,分级路面铺的频率指数W =2。

国际标准化组织提出了把路面的不平度分为8级。

表1列举出了部分等级路面的功率谱密度值及几何平均值。

表1路面不平度8级分类标准2谐波叠加算法模拟路面不平度2.1谐波叠加法模型的建立谐波叠加法是将随机激励表示成大量具有随机相位的正弦或余弦之和。

本文采用余弦谐波叠加法生成路面不平度仿真数据,其主要思想就是将路面不平度表示成大量具有随机相位的余弦级数之和。

白噪声路面不平度时域模型的建立与仿真

10.16638/ki.1671-7988.2019.03.026白噪声路面不平度时域模型的建立与仿真赵斌，董浩，黄波，张建（成都大学机械工程学院，四川成都610106）摘要：为合理模拟路面时域模型，通过路面不平度空间功率谱密度分析路面频域模型，并由路面频域模型推导路面时域模型的滤波白噪声数值模拟方法。

提出了采用滤波白噪声方法模拟路面时域模型时，改变仿真车速的同时调整不同的路面不平度系数，对30km/h、60km/h车速下B、C级路面的时域模型进行了仿真，仿真结果准确，可作为进一步的汽车动力学分析的路面输入，具有研究价值。

关键词：路面不平度；白噪声；时域中图分类号：U467.1 文献标识码：A 文章编号：1671-7988(2019)03-89-03Establishment and simulation of time domain model for Band-Limited WhiteNoise pavement roughnessZhao Bin, Dong Hao, Huang Bo, Zhang Jian( School of mechanical engineering, Chengdu University, Sichuan Chengdu 610106 )Abstract: In order to reasonably simulate the time domain model of road surface, the frequency domain model of road surface is analyzed by the spatial power spectral density of pavement roughness, and the numerical simulation method of filtering white noise is deduced from the road surface frequency domain model. This paper presents a method to simulate the time-domain model of road surface by filtering white noise, and to adjust the different roughness coefficients The simulation results of the time domain model of the B-and C-class pavement under the speed of 30km/h and 60km/h are accurate, which can be used as the road input for further analysis of vehicle dynamics, which has research value. Keywords: pavement roughness; Band-Limited White Noise; time domainCLC NO.: U467.1 Document Code: A Article ID: 1671-7988(2019)03-89-031 路面不平度功率谱密度统计描述1984年国际标准化组织在文件ISO/TC108/SC2N67中提出了《路面不平度表示方法草案》，我国也参照制定了《机械振动—道路路面谱测量数据报告》（GB703—2005）。

路面时域波形的数学模型与再现研究

、
ｐｒｏｍａｃｆｔｅａｔｍｏｉｙａｃ．Ｔｈｖｒｉｅｏｏｄｒｕｈｌｓｋｓｔｅｒｄｒｏｍａｃｎａｉｕａｅｅｆｒｎｅｏｈｕｏｂｌｄｎｍｉｓｅｅｏｅｓｚｆｒａｏｇｒｓｍａｅｉｅｐｆｒｎｅａｄｍｎｐｌｔｅｈｅ
ｈｍａｓｕｃｎｕｎｒｏｒｅａｄｍａｅｉｌｅｏｒｅＳ．ｈｅｔｒａｓｕｃ．ｏｔｅｍｏｅ’ ｃｕａｙｏｔｒｄｌａｃｒｃｆｈｅｐｖｍｅｔｌｙｎｉｐａｎｔ＂ｅｏｔｅｒｓａｃｎＳａｅｎｐａｓａｍｏｎ１ｎｈｅｅｒｈｏＯｌａｔｍｏｉｙａｉｓＴｉａｅｎｔｄｃｓｔｕｏｂｌｅｄｎｍｃ．ｈｓｐｐｒｉｒｕｅｈｅｅｐｅｓｏｏｒａｕｈｅｓａｄｔｅｍｅｏｏｍａｅｔａｍｏｅｂｕｏｘｒｓｉｎｆｏｄｒｇｎｓｎｈｏｈｔｄｆｔｍａｉｌｄｌｏｔｈｃａｐｖｍｅｔｔｅｗａｅｂｓｄｏａｅｎｉｖａｅｎＡＲｄ１ｔｅｅｅｏｅｓｆａｅｏｃｎｔｕｔｇｔｅｓｎａｄｐｖｍｅｔｔｅｗａｅｍｍｏｅ．ｎｄｖｌｐｔｏｗｒｆｒｏｓｒｃｉｔｄｒａｅｎｉｖｈｈｔｅｎｈａｍａｃｒｉｇｔｃｏｄＡＲｄｅ．ｄｓｍｕａｅｅｅｙｌｖｌａｅｅｔｘｄｉｎｏｍｏ１ａｉｌｔｖｒｅｅｖｎｐｍｎｅＧＢ７３ —－７Ｔｅｒｓｌｉｄｃｔｓｔａ：ｈｓｍｏｅ￣１ｉｆｎ０１８．ｈｕｔｎｉａｔｔｉｄｌＥ１ｅｅｈ３

路面病害预测的数学模型

路面病害预测的数学模型作者：王佳秋来源：《科学导报·学术》2019年第43期摘;;要：本文建立的是路面凹凸变化的数学模型，随着我国的经济建设高度快速发展，城市路面和高速公路的路面损毁严重，尤其是北方严寒地带。

实时提取道路统计数字，根据数字的统计规律建立数学模型，预测路面病害，从而及时修补和保养。

关键词：路面凹凸;数学模型;高程1;引言时间序列分析是统计学科的一个重要分支内容，在数字信号处理、管理科学、预测等方面得到了广泛应用。

在实际路面测量中，只能测到路面不平度的有限数据，利用时间序列分析的主要任务就是根据观测数据的特点为数据建立尽可能合理的统计模型，然后利用模型的统计特性去解释数据的统计规律，以达到控制或预报的目的。

本文研究的是路面测量的数据采集，用数据验证时间序列的变化模型，由此可预测道路路面病害。

通过论述了路面凹凸变形的时序建模方法、实际检验和模型应用，获得道路实测数据的时序模型，为路面病害程度做预测。

通过长时间研究实践证明，所采用的时序道路建模具有可操作性。

2;;时间序列数学模型时间序列方法是定量预测方法之一。

主要包括一般统计分析（如自相关分析，谱分析等），统计模型的建立与推断，以及关于时间序列的最优预测、控制与滤波等内容。

经典的统计分析都假定数据序列具有独立性，而时间序列分析则侧重研究数据序列的互相依赖关系。

后者实际上是对离散指标的随机过程的数据进行的统计分析。

例如，记录了某路段的不同时段的路面高程，建立探究数据所包含的动态依存关系，所以又可看作是随机过程统计的一个组成部分的数学模型，可以对未来时段路面的高程变化进行判断，并借以对路面凹凸变化的未来进行预报。

时间序列趋势分析目的：有些时间序列具有非常显著的趋势，我们分析的目的就是要找到序列中的这种趋势，并利用这种趋势对序列的發展作出合理的预测。

通过数据分析，线性拟合的使用场合为长期趋势呈现出线形特征的场合。

参数估计方法为最小二乘估计。

基于Simulink的路面不平度时域模型仿真研究.

．
ｗａｅａｉｇｍｏｅｏｌｅｅａｅｔｅｔ — ｏｉｏｄｒｕｈｅｓｉｅｍｓｏｉｅｅｏｄｃｎｉｉｎｎｅｉｌｐｅｓＴｅｅｐｒｍｅｔｌｒｓＩｓｖｄｄｎｄｌｃｕｄｇｎｒｔｈｉｍｅｄｍａｎｒａｇｎｓｎｔｒｆｄｆｒｎｔｒａｏｄｔｓａｄｖｈｃｅｓｅｄｈｘｅｉｎａｅｕｔｏｏ
．
【要】摘时域路面不平度建模对轮椅振动分析具有重要意义。对Ｇ／０１２０ＢＴ７３— ０５中提出的路面功率谱密度表达式及等分方法应用线性滤波法与谐波叠加法分别重构路面不平度模型，用周期图谱估计法验证仿真结果。结果表明线性滤波法与谐波叠加法均能在谱一致准则使下生成不同路面与车速下的时域路面不平度，为人与轮椅系统分析研究提供了数据支持【关键词】轮椅；时域路面不平度；线性滤波法；谐波叠加法
科技信息
０高校讲ｌＯｋ
ＳＩＮＥ＆ＴＣＮＬＧＦＲＴＯＣＥＣＥＨＯＯＹＩＯＭＡＩＮＮ
２１年０２
第７期
基于Ｓｕｎ的路面不平度时域模型仿真研究ｉｌｋｍｉ
陈龙何草丰（重庆邮电大学自动化学院中国重庆４０６）００５
【ｂｔｃ］ｈａｕｈｅｏｅｉｃｃｌｏｈｅｈｉｖｒｉａｓ．ｏｔｘｒｓｏｅｏｏｅｓｅｒｄｃｓｆａ０ＡｓａｔＴｅｒｄｒｇｎｓｍｄｌｓｒｉｅｌａｉａｏａｌｉＦｒｈｅｐｅｓｎｏｔａｐｗｒＤｃｕａａｉｃｔｎｒｏｏｓｕａｔｗｃｒｂｔｎｎｙｓｅｉｆｒｓａｃｏｌｒｖｄａｅｓｐｏｔｔｈｅｓｎａｄｗｈｅｃａｒｓｓｅａｙｉｔｄｅｅｅｌｔａｈｅｅｈｃｕｄｐｏｉｅｄｔｕｐｒｏｔｅｐｒｏｎｅｌｈｉｙｔｍｓａｌｓｓｓｕｉｓｒｎ

路面输入及其模型

4.1.2 傅里叶分析
前面讨论的概率密度、均值、方差等是用来在幅值领域里描写随机过程的。而相关函数则是在时域里研究问题。除此之外，还需要在频域里研究随机过程，这就要用到傅里叶分析手段。
傅立叶的两个最主要的贡献——
• “周期信号都可表示为谐波关系的正弦信号的加权和” ——傅里叶的第一个主要论点 • “非周期信号都可用正弦信号的加权积分表示” ——傅里叶的第二个主要论点
∫
t 0 + T1
t0
f ( t ). dt
周期函数的频谱
• 周期信号的谱线只出现在基波频率的整数倍的频率处。直观看出：各分量的大小，各分量的频移。
Cn
ϕ n (ω )
ω1
nω 1
ω1
nω 1
周期函数的复指数级数形式傅里叶级数
三角函数式 f1 (t ) = a0 + ∑ (an cos nω1t + bn sin nω1t )
随机过程
2 随机过程的数字特征
随机过程既是一个随机变量系，显然就可以用描述随机变量系的办法来描述随机过程。例如，可以用一维二维乃至n维的分布函数或概率密度来描述。在实际应用中，要确定随机过程的分布函数族十分困难，甚至不可能。因而，有必要像随机变量一样，引入描述随机过程的数字特征。
n =1 ∞
由欧拉公式得其中
e jnω1t − e− jnω1t sin nω1t = 2j
e jnω1t + e− jnω1t cos nω1t = 2j
f (t ) =
n = −∞
∑
∞
F ( n ω 1 ) e jn ω 1t
F ( 0) = a 0
1 F(nω1) = (an − jbn ) 2

路面输入及其模型

路面不平给予汽车系统的激励是一种随机过程，汽车的振动也是随机的，即在同一条路面上测量其振动幅值与频率，各次试验结果都不同，而且在试验之前无法预测其试验结果，其振幅、速度、加速度均为非确定函数。随机振动服从概率统计规律，只能应用概率统计理论来进行描述。
4.1 路面不平的统计描述 4.1.1 随机过程 4.1.2 傅里叶分析 4.1.3 功率谱密度
∫
∞
−∞
x(t ) dt < ∞
即绝对可积
如能满足，则其傅里叶变换存在。
随机信号是时域无限信号，不具备可积分条件，因此不能直接进行傅里叶变换。随机信号的频率、幅值、相位都是随机的，因此从理论上讲，一般不作幅值谱和相位谱分析，而是用具有统计特性的功率谱密度(power spectral density)来作谱分析。自功率谱密度函数(Auto-power spectral density function) 互功率谱密度函数(cross-power spectral density function) 相干函数(coherence function)与频率响应函数 (frequency response function)
n =1 ∞
由欧拉公式得其中
e jnω1t − e− jnω1t sin nω1t = 2j
e jnω1t + e− jnω1t cos nω1t = 2j
f (t ) =
n = −∞
∑
∞
F ( n ω 1 ) e jn ω 1t
F ( 0) = a 0
1 F(nω1) = (an − jbn ) 2
4.1.2 傅里叶分析
前面讨论的概率密度、均值、方差等是用来在幅值领域里描写随机过程的。而相关函数则是在时域里研究问题。除此之外，还需要在频域里研究随机过程，这就要用到傅里叶分析手段。

路面不平度构造以及功率谱密度生成检测

路面不平度构造以及功率谱密度生成检测一构造C级路面不平度构造，采用谐波叠加法（又称为三角级数法），常见空间频率范围为：0.011<n<2.83,车速为30km/h, 采用Parseval 公式和相关定理，谐波叠加，生成C级路面不平度时域信号。

程序如下：n1=0.011;nh=2.83;n0=0.1;G0=256*10^(-6);N=2000;v=30/3.6;L=1000; %区间数车速距离fl=n1*v;fh=nh*v; %时间频域fk=fl+(fh-fl)/(2*N):(fh-fl)/N:fh-(fh-fl)/(2*N); %中心频率faik=2*pi*rand(1,N); %相位角ak=zeros(1,N); %系数for i=1:Nak(i)=sqrt(2*G0*n0^2*v*(fh-fl)/N/(fl+(i-1)*(fh-fl)/N)/(fl+i*(fh-fl)/N ));endt=0:1/fh/2:L/v; %时间采样频率为最高时间频率的两倍Lt=length(t);qk=zeros(N,Lt);for i=1:Nqk(i,:)=ak(i)*sin(2*pi*fk(i)*t+faik(i));endqt=zeros(Lt,1);qt(:,1)=sum(qk)';plot(t,qt(:,1)),grid ontitle('c级路面时域不平度q（t）')xlabel('时间t/s')ylabel('位移q/m')GC=sqrt(sum(qt.^2)/length(qt)) %路面不平度均方值L=0:0.05/2.83:1000;Ll=length(L);qll=zeros(N,Ll);nk=0.011+(2.83-0.011)/(2*N):(2.83-0.011)/N:2.83-(2.83-0.011)/(2*N);for i=1:Nqll(i,:)=ak(i)*sin(2*pi*nk(i)*L+faik(i)); endql=zeros(Ll,1);ql(:,1)=sum(qll)';figure(2);plot(L,ql(:,1)),grid onGC =0.0143路面功率谱密度：figure(3)ns=10*nh;% 空间采样频率[pxx,m]=psd(qt,512,ns);% 512为快速傅里叶变换点数loglog(m,pxx)grid on ;hold on ;n=0.011:0.001:2.83;y1=128e-6./n.^2 ;y2=512e-6./n.^2 ;loglog(n,y1) ;grid on ;loglog(n,y2) ;grid on;xlabel('空间频率/(1/m)')ylabel('路面公路车谱密度G(n)/[m^2/(1/m)]')二构造F级路面不平度，常见空间频率范围为：0.011<n<2.83,车速为100km/h。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

路面不平度数学模型
目录
1. 功率谱分析模型
1. 1.1 三角级数法
2. 1.2 过滤泊松模型
3. 1.3 线性滤波白噪声法
4. 1.4 域功率谱采样的数值模拟方法
2. 时间序列分析模型
1. 2.1 ARMA模型
2. 2.2 AR模型
3. 小波分析模型
4. 分形分析模型
总结和研究展望
展开
1. 功率谱分析模型
1. 1.1 三角级数法
2. 1.2 过滤泊松模型
3. 1.3 线性滤波白噪声法
4. 1.4 域功率谱采样的数值模拟方法
2. 时间序列分析模型
1. 2.1 ARMA模型
2. 2.2 AR模型
3. 小波分析模型
4. 分形分析模型
总结和研究展望
展开

编辑本段
1. 功率谱分析模型
由于信号处理领域中功率谱理论的研究已经非常成熟，因此在道路不平度
模型中，功率谱分析模型也就是最早进行研究的了。对于不同等级的路面，
主要区别表现在粗糙度的不同。通常我们采用谱密度函数来表达不同粗糙
度的路面，以给出车辆系统的输入激励。对于路面不平度的研究，各国学
者提出了不同形式的功率谱密度表达式模型。

1.1 三角级数法
理论上讲，任意一条路面轨迹均可由一系列离散的正弦波叠加而成。假如
已知路面频域模型，那么每个正弦波的振幅可由相应频率的频率谱密度获
得，相位差由随机数发生器产生。从理论上讲，任意一条路面轨迹均可由
一系列离散的正弦波叠加而成。假如已知路面频域模型，那么每个正弦波
的振幅可由相应频率的频率谱密度获得，相位差由随机数发生器产生。三
角级数法尤其适用于实测道路谱的时域模拟，该算法数学基础严密，使用
路面范围广。这对于在非标道路和非等级公路上行驶汽车的平顺性研究具
有重要意义，但此模型涉及大量三角函数运算，计算很费时。一般采用FFT
算法提高其计算效率。

1.2 过滤泊松模型
该模型在频率大于一定值后。能较好地逼近目标谱密度，在频率为零附近
效果较差。它的最大缺点是参数的求取缺乏严密的算法，需要试凑，因此
很不方便。

1.3 线性滤波白噪声法
基于线性滤波的白噪声激励模拟是目前较普遍的方法。基本思想是将路面
高程的随机波动抽象为满足一定条件的白噪声，然后经一假设系统进行适
当变换而拟合出路面随机不平度的时域模型。线性滤波法具有计算量小、
速度快的优点，但算法繁琐、模拟精度差。

1.4 域功率谱采样的数值模拟方法
利用对已知功率谱进行采样的数值模拟方法对公路路面的功率谱密度进行
研究。获得了分布在一定频率范围内的离散功率谱密度数据。通计算、分
析获得路面不平度的离散傅立叶变换，对离散傅立叶变换的数据按照一定
规则补齐后再进行傅立叶逆变换，进而得到路面不平度值。

编辑本段
2. 时间序列分析模型
时间序列分析是统计学科的一个重要分支内容。在信号处理、经济管理、
市场价格预测等方面得到了广泛应用。在实际路面测量中，只能测到路面
不平度的有限数据，利用时间序列分析的主要任务就是根据观测数据的特
点为数据建立尽可能合理的统计模型，然后利用模型的统计特性去解释数
据的统计规律，以达到控制或预报的目的。在时间序列分析中，有两类简
单而又常用的模型：AR( 自回归) 模型和ARMA模型。

2.1 ARMA模型
从总体精度来看，ARMA模型优于AR模型，它能够很好的逼近目标谱。在阶
次很低时，ARMA模型在低频段效果较差，阶次增加后,在整个模拟范围内都
达到极好的效果。ARMA模型阶次的选择应综合考虑运算量，总体模拟精度
两个因素来确定，但对于ARMA模型的最优阶次的选取尚无成熟理论，需要
进一步的研究。

2.2 AR模型
用时间序列分析的方法对路面的实际测量值进行分析计算建立一个自回归
(AR)模型，并以此为基础进行路面的模拟，自相关函数以及谱密度分析。
与AR模型相对应的功率谱是连续谱，分辨率可以无限提高。可以很好的解
决以采用FFT为基础的功率谱分析时产生的数据泄漏。还可利用AR模型对
二维路面进行模拟，其方法是一维模型的直接推广，经过仿真证明了该模
型的可行性。
基于快速Fourier 变换技术的AR (Auto －Regressive) 模型和ARMA
(Auto－Regressive and Moving Average)模型对于路面谱的拟合具有较好
的效果。该方法70年代开始用于随机过程的模拟，并在80年代得到了较
系统的发展，它是一种比谐波叠加法更有效的数字模拟方法，而且数字信
号处理理论为它提供了严密的数学基础。但是在实际的计算中，AR模型和
ARMA模型并不能保证生成的随机路面是绝对稳定的。要达到稳定需满足其
路面不平度的拟合方程的系数特征方程的全部复数根都位于单位圆内的条
件。这在车辆行驶的实际过程中难以保证，这就使得AR模型和ARMA 模型
在路面模拟的应用中受到限制。

编辑本段
3. 小波分析模型
前面讨论到的路面不平度模型都是基于FFT的统计分析，由于Fourier分
析使用的是一种全局变换，不能获得信号的局部特征; 而且对于非平稳信
号的分析。要么完全在时域，要么完全在频域无法表述信号的时频局域性
质。小波变换是一种时频分析方法。其基本原理是以小波函数(t-b/a)为基
函数。
对车辆的振动响应与路面不平度的关系进行分析，结果表明将小波变换引
入路面激励和汽车振动响应分析中，可以清楚地了解信号的时频特性，识
别车辆振动响应与路面不平度的关系，从而可以通过路面特性分析车辆平
顺性能或由振动响应推断路面激励。

编辑本段
4. 分形分析模型
近十几年来，分形理论已在表面不平度的研究领域获得成功的应用。从一
般意义上说，分形维数是用来衡量一个几何集或自然物体不规则程度的数，
分维值D越高反映的道路表面越平坦。在计算出分维值后，可以利用W2M
函数、布朗函数、中点位移随机算法等方法来模拟路面不平度，作为汽车
平顺性研究的输入激励。分形测量属于对测度的相似性测量，是一种相对
性的描述参数，它无法唯一表达道路表面不平程度，也就是说分形维数与
功率谱不存在对应关系。将分形维数与尺度系数联系起来可提出表观分形
维数，表观分形维数结合分形维数的相似测量和尺度系数的绝对测量。其
表观分形维数数值越大,道路表面不平度越大。

编辑本段
总结和研究展望
1.分形和小波理论还在不断的发展和完善，其各个分支都发展很快。因此，
应该密切关注这些新动向，以使分形和小波理论在路面不平度的研究中得
到深入的应用。
2.虽然现在已经使用了分形和小波理论对路面不平度进行分析，但都处于
初级阶段，对于这两种理论在对路面不平度特性的描述以及使用方法还有
待进一步的研究。例如，利用分形维数描述路面的二维特性，寻找分维数
与土壤本构之间的关系等。
3.率谱密度与路面高程并非一对一的映射，因此从频域模型所得的道路高
度的时程函数只能看成是满足给定路面谱的全部可能的路面高程中的一个
样本函数，为从已知的路面谱获得路面激励时域模型——随机路面高程，
通用的方法是将路面高程定性为平稳的Gaussian 随机过程。因此对于平稳
Gaussian 随机过程的数值模拟，各种路谱(包括标准的和实测的，确定性
的和随机的)建模、模型建库及封装、道路激励的可视化、以及与汽车虚拟
仿真系统的链接等都是有待深入研究的内容。