(遵义专版)2018年中考数学总复习第一篇第7章圆第1节圆的有关概念及性质(精练)课件
2018年中考数学备考资料圆及有关概念公式定理-文档资料

2018中考数学备考资料圆及有关概念公式定理2018中考复习最忌心浮气躁,急于求成。
指导复习的教师,应给学生一种乐观、镇定、自信的精神面貌。
要扎扎实实地复习,一步一步地前进,下文为大家准备了2018中考数学备考资料。
我们学习的圆是轴对称图形,其对称轴是任意一条通过圆心的直线,所以是无数条对称轴。
圆及有关概念1 到定点的距离等于定长的点的集合叫做圆(circle).这个定点叫做圆的圆心。
2 连接圆心和圆上的任意一点的线段叫做半径(radius)。
3 通过圆心并且两端都在圆上的线段叫做直径(diameter)。
4 连接圆上任意两点的线段叫做弦(chord). 最长的弦是直径。
5 圆上任意两点间的部分叫做圆弧,简称弧(arc).大于半圆的弧称为优弧,优弧是用三个字母表示。
小于半圆的弧称为劣弧,劣弧用两个字母表示。
半圆既不是优弧,也不是劣弧。
优弧是大于180度的弧,劣弧是小于180度的弧6 由两条半径和一段弧围成的图形叫做扇形(sector)。
7 由弦和它所对的一段弧围成的图形叫做弓形。
8 顶点在圆心上的角叫做圆心角(central angle)。
9 顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。
10 圆周长度与圆的直径长度的比值叫做圆周率。
它是一个超越数,通常用表示,=3.1415926535。
在实际应用中,一般取3.14。
11 圆周角等于弧所对的圆心角的一半。
字母表示圆半径r或R(在环形圆中外环半径表示的字母); 弧直径扇形弧长周长面积S。
圆的表示方法要求很严格,需要用到相应的知识要求。
这就是我们为大家准备的2018中考数学备考资料的内容,希望符合大家的实际需要。
(遵义专版)2018年中考数学总复习 第一篇 教材知识梳理篇 第7章 圆 第3节 与圆有关的计算(精练)试题

第三节 与圆有关的计算1.(2017宿迁中考)若将半径为12 cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( D )A .2 cmB .3 cmC .4 cmD .6 cm2.(2017临沂中考)如图,AB 是⊙O 的直径,BT 是⊙O 的切线,若∠ATB=45°,AB =2,则阴影部分的面积是( C )A .2B .32-14π C .1 D .12+14π3.(2017达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( A )A .22 B .32C . 2D . 3 4.(2017莱芜中考)将半径为3 cm 的圆形纸片沿AB 折叠后,圆弧恰好能经过圆心O ,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( A )A .2 2 cmB . 2 cmC .10 cmD .32cm(第4题图)(第5题图)5.(2017深圳中考)如图,在扇形AOB 中,∠AOB =90°,正方形CDEF 的顶点C 是AB ︵的中点,点D 在OB 上,点E 在OB 的延长线上,当正方形CDEF 的边长为22时,阴影部分的面积为( A )A .2π-4B .4π-8C .2π-8D .4π-46.(桂林中考)如图,在Rt △AOB 中,∠AOB =90°,OA =3,OB =2,将Rt △AOB 绕点O 顺时针旋转90°后得Rt △FOE ,将线段EF 绕点E 逆时针旋转90°后得线段ED ,分别以O ,E 为圆心,OA ,ED 长为半径画弧AF 和弧DF ,连接AD ,则图中阴影部分面积是( D )A .πB .5π4C .3+πD .8-π(第6题图)(第7题图)7.(2017乌鲁木齐中考)用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影部分面积为__π-2.8.(2017黄冈中考)已知:如图,圆锥的底面直径是10 cm ,高为12 cm ,则它的侧面展开图的面积是__65π__cm 2.(第8题图)(第9题图)9.(2017日照中考)如图,四边形ABCD 中,AB =CD ,AD ∥BC ,以点B 为圆心,BA 为半径的圆弧与BC 交于点E ,四边形AECD 是平行四边形,AB =6,则扇形(图中阴影部分)的面积是__6π__.10.(襄阳中考)如图,AB 是半圆O 的直径,点C ,D 是半圆O 的三等分点,若弦CD =2,则图中阴影部分的面积为__23π__.(第10题图)(第11题图)11.(2017河南中考)如图,在扇形AOB 中,∠AOB =90°,以点A 为圆心,OA 的长为半径作OC ︵交AB ︵于点C ,若OA =2,则阴影部分的面积为3.12.(2017济宁中考)如图,正六边形A 1B 1C 1D 1E 1F 1的边长为1,它的六条对角线又围成一个正六边形A 2B 2C 2D 2E 2F 2,如此继续下去,则正六边形A 4B 4C 4D 4E 4F 4的面积是18. 13.(2017广州中考)如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是5,则圆锥的母线l =.(第13题图)(第14题图)14.(2017达州中考)如图,矩形ABCD 中,E 是BC 上一点,连接AE ,将矩形沿AE 翻折,使点B 落在CD 边F 处,连接AF ,在AF 上取点O ,以O 为圆心,OF 长为半径作⊙O 与AD 相切于点P.若AB =6,BC =33,则下列结论:①F 是CD 的中点;②⊙O 的半径是2;③AE =92CE ;④S 阴影=32.其中正确结论的序号是__①②④__.15.(2017永州中考)如图,在平面直角坐标系中,点A 的坐标(-2,0),△ABO 是直角三角形,∠AOB =60°.现将Rt △ABO 绕原点O 按顺时针方向旋转到Rt △A ′B ′O 的位置,则此时边OB 扫过的面积为__14π__.(第15题图)(第16题图)16.(2017遵义红花岗一模)如图,将含60°角的直角三角板ABC 绕顶点A 顺时针旋转45°后得到△AB′C′,点B 经过的路径为BB′︵.若∠BAC=60°,AC =1,则图中阴影部分的面积是__π2__.17.(2017玉林中考)如图,在⊙O 中,AB 是直径,点D 是⊙O 上一点,且∠BOD=60°,过点D 作⊙O 的切线CD 交AB 的延长线于点C ,E 为AD ︵的中点,连接DE ,EB ,交于点F.(1)求证:四边形BCDE 是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O 的半径r. 解:(1)连接EO. ∵∠BOD =60°, ∴∠AOD =120°, ∴BD ︵=12AD ︵.∵E 为AD ︵的中点,∴AE ︵=DE ︵=BD ︵,∴∠EOD =60°. 又OE =OD , ∴∠EDO =60°, ∴DE ∥AB ,即DE∥BC. ∵CD 是⊙O 的切线,∴OD ⊥CD.由垂径定理得OD⊥EB, ∴BE ∥CD ,∴四边形BCDE 是平行四边形; (2)∵S △DEF =S △BOF ,∴S 阴影=S 扇形OBD ,即60°×π×r2360°=6π,∴r =6.18.(昆明中考)如图,AB 是⊙O 的直径,∠BAC =90°,四边形EBOC 是平行四边形,EB 交⊙O 于点D ,连接CD 并延长交AB 的延长线于点F.(1)求证:CF 是⊙O 的切线;(2)若∠F=30°,EB =4,求图中阴影部分的面积.(结果保留根号和π) 解:(1)连接OD.∵四边形OBEC 是平行四边形, ∴OC ∥BE ,∴∠AOC =∠OBE,∠COD =∠ODB. ∵OB =OD , ∴∠OBD =∠ODB, ∴∠DOC =∠AOC. 在△COD 和△COA 中, ⎩⎪⎨⎪⎧OC =OC ,∠COD =∠COA,OD =OA , ∴△COD ≌△COA , ∴∠CDO =∠CAO=90°, ∴CF ⊥OD , ∴CF 是⊙O 的切线;(2)∵∠F=30°,∠BAC =90°, ∴∠ACF =60°. 由(1)知△COD≌△COA, ∴S △AOC =S △DOC ,∴∠ACO =∠DCO=12∠ACF=30°,∴∠AOC =∠DOC=60°.∵四边形EBOC 是平行四边形,EB =4, ∴OC =EB =4. 在Rt △AOC 中,∵∠ACO =30°,∴AO =2,AC =2 3. ∴S 阴影=2S △AOC -S 扇形OAD =2×12×2×23-120π·22360=43-43π.。
2018年中考数学必考知识点圆-文档资料

2018中考数学必考知识点-圆2018中考数学必考知识点-圆1圆的重要性质;2直线与圆、圆与圆的位置关系;③3与圆有关的角的定理;4与圆有关的比例线段定理。
一、圆的基本性质1.圆的定义(两种)2.有关概念:弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。
3.“三点定圆”定理4.垂径定理及其推论5.“等对等”定理及其推论5.与圆有关的角:⑴圆心角定义(等对等定理)⑵圆周角定义(圆周角定理,与圆心角的关系)⑶弦切角定义(弦切角定理)二、直线和圆的位置关系1.三种位置及判定与性质:2.切线的性质(重点)3.切线的判定定理(重点)。
圆的切线的判定有⑴…⑵…4.切线长定理三、圆换圆的位置关系1.五种位置关系及判定与性质:(重点:相切)2.相切(交)两圆连心线的性质定理3.两圆的公切线:⑴定义⑵性质四、与圆有关的比例线段1.相交弦定理2.切割线定理五、与和正多边形1.圆的内接、外切多边形(三角形、四边形)2.三角形的外接圆、内切圆及性质3.圆的外切四边形、内接四边形的性质4.正多边形及计算中心角:内角的一半: (右图)(解Rt△OAM可求出相关元素,、等)六、一组计算公式1.圆周长公式2.圆面积公式3.扇形面积公式4.弧长公式5.弓形面积的计算方法6.圆柱、圆锥的侧面展开图及相关计算七、点的轨迹六条基本轨迹八、有关作图1.作三角形的外接圆、内切圆2.平分已知弧3.作已知两线段的比例中项4.等分圆周:4、8;6、3等分九、基本图形十、重要辅助线1.作半径2.见弦往往作弦心距3.见直径往往作直径上的圆周角4.切点圆心莫忘连5.两圆相切公切线(连心线)6.两圆相交公共弦。
初三《圆》章节知识点总结

《圆》章节知识点复习一、圆的概念集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部:可以看作是到定点的距离大于定长的点的集合;3、圆的内部:可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内;2、点在圆上⇒d r=⇒点B在圆上;3、点在圆外⇒d r>⇒点A在圆外;三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点;2、直线与圆相切⇒d r=⇒有一个交点;3、直线与圆相交⇒d r<⇒有两个交点;A四、圆与圆的位置关系外离(图1)⇒ 无交点 ⇒ d R r >+; 外切(图2)⇒ 有一个交点 ⇒ d R r =+; 相交(图3)⇒ 有两个交点 ⇒ R r d R r -<<+; 内切(图4)⇒ 有一个交点 ⇒ d R r =-; 内含(图5)⇒ 无交点 ⇒ d R r <-;图1五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。
(遵义专版)中考数学总复习 第7章 圆 第1节 圆的有关概念及性质(精练)试题
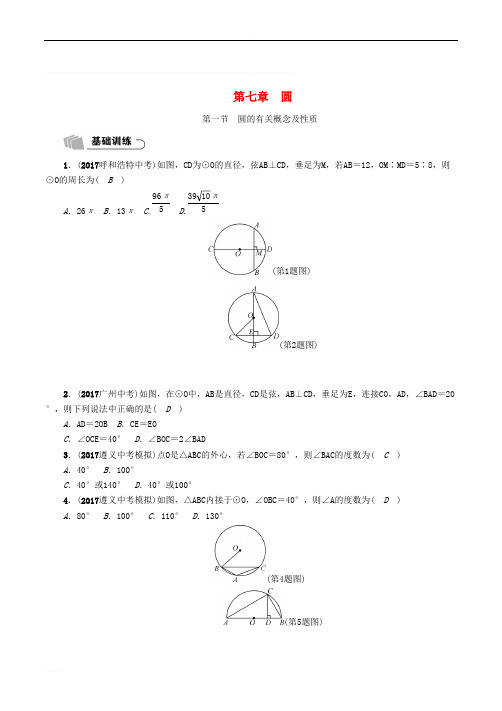
第七章 圆第一节 圆的有关概念及性质1.(2017呼和浩特中考)如图,CD 为⊙O的直径,弦AB⊥CD,垂足为M ,若AB =12,OM∶MD=5∶8,则⊙O的周长为( B )A .26πB .13πC .D .96π53910π5(第1题图) (第2题图)2.(2017广州中考)如图,在⊙O中,AB 是直径,CD 是弦,AB⊥CD,垂足为E ,连接CO ,AD ,∠BAD=20°,则下列说法中正确的是( D )A .AD =2OB B .CE =EOC .∠OCE=40°D .∠BOC=2∠BAD3.(2017遵义中考模拟)点O 是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( C )A .40°B .100°C .40°或140°D .40°或100°4.(2017遵义中考模拟)如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( D )A .80°B .100°C .110°D .130°(第4题图) (第5题图)5.(2017遵义中考模拟)如图是以△ABC的边AB 为直径的半圆O ,点C 恰好在半圆上,过C 作CD⊥AB交AB于D.已知cos ∠ACD=,BC =4,则AC 的长为( D )35A .1 B . C .3 D .2031636.(2017新疆建设兵团中考)如图,⊙O的半径OD 垂直于弦AB ,垂足为点C ,连接AO 并延长交⊙O于点E ,连接BE ,CE.若AB =8,CD =2,则△BCE的面积为( A )A .12B .15C .16D .18(第6题图) (第7题图)7.(2017金华中考)如图,在半径为13 cm 的圆形铁片上切下一块高为8 cm 的弓形铁片,则弓形弦AB 的长为( C )A .10 cmB .16 cmC .24 cmD .26 cm8.(2017台州中考)如图,已知等腰直角三角形ABC ,点P 是斜边BC 上一点(不与B ,C 重合),PE 是△ABP的外接圆⊙O的直径.(1)求证:△APE是等腰直角三角形;(2)若⊙O的直径为2,求PC 2+PB 2的值.解:(1)∵AB=AC ,∠BAC=90°,∴∠C=∠ABC=45°,∴∠AEP=∠ABP=45°.∵PE是直径,∴∠PAE=90°,∴∠APE=∠AEP=45°,∴AP=AE ,∴△PAE是等腰直角三角形;(2)作PM⊥AC于M ,PN⊥AB于N ,则四边形PMAN 是矩形,∴PM=AN.∵△PCM,△PNB都是等腰直角三角形,∴PC=PM ,PB =PN ,22∴PC 2+PB 2=2(PM 2+PN 2)=2(AN 2+PN 2)=2PA 2=PE 2=22=4.(也可以证明△ACP≌△ABE,△PBE是直角三角形)9.(2017潍坊中考)点A ,C 为半径是3的圆周上两点,点B 为的中点,以线段BA ,BC 为邻边作菱形ABCAC ︵ D ,顶点D 恰在该圆直径的三等分点上,则该菱形的边长为( D )A .或2B .或25253C .或2D .或2626310.(2017毕节中考)如图,AB 是⊙O的直径,CD 是⊙O的弦,∠ACD=30°,则∠BAD为( C )A .30° B .50° C .60° D .70°(第10题图) (第11题图)11.(2017泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( D )A .180°-2αB .2αC .90°+αD .90°-α12.(2017临沂中考)如图,∠BAC的平分线交△ABC的外接圆于点D ,∠ABC的平分线交AD 于点E ,(1)求证:DE =DB ;(2)若∠BAC=90°,BD =4,求△ABC外接圆的半径.解:(1)∵AD平分∠BAC,BE 平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD.∵∠DBC=∠CAD,∴∠DBC=∠BAE.∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB ;(2)连接CD.∵∠BAD=∠CAD,∴=,BD ︵ CD ︵ ∴CD=BD =4.∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,BD2+CD22∴△ABC外接圆的半径=×4=2.122213.(2017枣庄中考)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC 于点D ,点O 在AB 上,以点O 为圆心,OA 为半径的圆恰好经过点D ,分别交AC ,AB 于点E ,F.(1)试判断直线BC 与⊙O的位置关系,并说明理由;(2)若BD =2,BF =2,求阴影部分的面积.(结果保留π)3解:(1)BC 与⊙O相切.理由如下:连接OD.∵AD是∠BAC的平分线,∴∠BAD=∠CAD.又∵OD=OA ,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.又∵BC过半径OD 的外端点D ,∴BC与⊙O相切;(2)设OF =OD =x ,则OB =OF +BF =x +2,根据勾股定理得:OB 2=OD 2+BD 2,即(x +2)2=x 2+12,解得x =2,即OD =OF =2,∴OB=2+2=4.∵Rt △ODB中,OD =OB ,12∴∠B=30°,∴∠DOB=60°,∴S 扇形DOF ==,60π×43602π3S 阴影=S △ODB -S 扇形DOF =×2×2-=2-.1232π332π3∴阴影部分的面积为2-.32π314.(2017葫芦岛中考)如图,△ABC内接于⊙O,AC 是直径,BC =BA ,在∠ACB的内部作∠ACF=30°,且CF =CA ,过点F 作FH⊥AC于点H ,连接BF.(1)若CF 交⊙O于点G ,⊙O的半径是4,求AG 的长;(2)请判断直线BF 与⊙O的位置关系,并说明理由.解:(1)连接BO.∵AC是直径,∴∠CBA=90°.∵BC=BA ,OC =OA ,∴OB⊥AC.∵FH⊥AC,∴OB∥FH.在Rt △CFH中,∵∠FCH=30°,∴FH=CF.12∵CA=CF ,∴FH=AC =OC =OA =OB ,12∴四边形BOHF 是平行四边形.∵∠FHO=90°,∴四边形BOHF 是矩形,∴BF=OH.在Rt △ABC中,∵AC=8,∴AB=BC =4.2∵CF=AC =8,∴CH=4,BF =OH =4-4.33∵BF∥AC,∴===.BG AG BF AC 43-483-12∵BG+AG =4,2∴AG=4-4;62(2)结论:BF 是⊙O的切线.理由:由(1)可知四边形BOHF 是矩形,∴∠OBF=90°,∴OB⊥BF,∴BF是⊙O的切线.15.(2017西宁中考)如图,在△ABC中,AB =AC ,以AB 为直径作⊙O交BC 于点D ,过点D 作⊙O的切线DE 交AC 于点E ,交AB 延长线于点F.(1)求证:DE⊥AC;(2)若AB =10,AE =8,求BF 的长.解:(1)连接OD ,AD.∵DE切⊙O于点D ,∴OD⊥DE.∵AB是直径,∴∠ADB=90°.又∵AB=AC ,∴D是BC 的中点.又∵O是AB 的中点,∴OD∥AC,∴DE⊥AC;(2)∵AB=10,∴OB=OD =5.由(1)得OD∥AC,∴△ODF∽△AEF,∴==,OD AE OF AF BF +OBBF +AB ∴=,58BF +5BF +10解得BF =.10316.(2016遵义六中一模)如图,在△ABC中,BA =BC ,以AB 为直径的⊙O分别交AC ,BC 于点D ,E ,BC 的延长线与⊙O的切线AF 交于点F.(1)求证:∠ABC=2∠CAF;(2)若AC =2,CE∶EB=1∶4,求CE 的长.10解:(1)连接BD.∵AB为⊙O的直径,∴∠ADB=90°,∴∠DAB+∠ABD=90°.∵AF是⊙O的切线,∴∠FAB=90°.即∠DAB+∠CAF=90°,∴∠CAF=∠ABD.∵BA=BC ,∠ADB=90°,∴∠ABC=2∠ABD,∴∠ABC=2∠CAF;(2)连接AE.∵AB是直径,∴∠AEB=90°,设CE =x.∵CE∶EB=1∶4,∴EB=4x ,BA =BC =5x ,AE =3x.在Rt △ACE中,AC 2=CE 2+AE 2,即(2)2=x 2+(3x)2,10∴x=2,∴CE=2.17.(2017遵义一中二模)如图,AB 是半圆O 的直径,C ,D 是半圆O 上的两点,且OD∥BC,OD 与AC 交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB =4,AC =3,求DE 的长.解:(1)∵OD∥BC,∴∠DOA=∠B=70°.又∵OA=OD ,∴∠DAO=∠ADO=55°.∵AB是直径,∴∠ACB=90°,∴∠CAB=90°-70°=20°,∴∠CAD=55°-20°=35°;(2)在Rt △ACB中,BC ==.AB2-AC27∵圆心O 是直径AB 的中点,OD∥BC,∴OE=BC =.1272又OD =AB =2,12∴DE =OD -OE =2-.72。
遵义专版2018年中考数学总复习第一篇教材知识梳理篇第7章圆第3节与圆有关的计算精讲试题201801082145
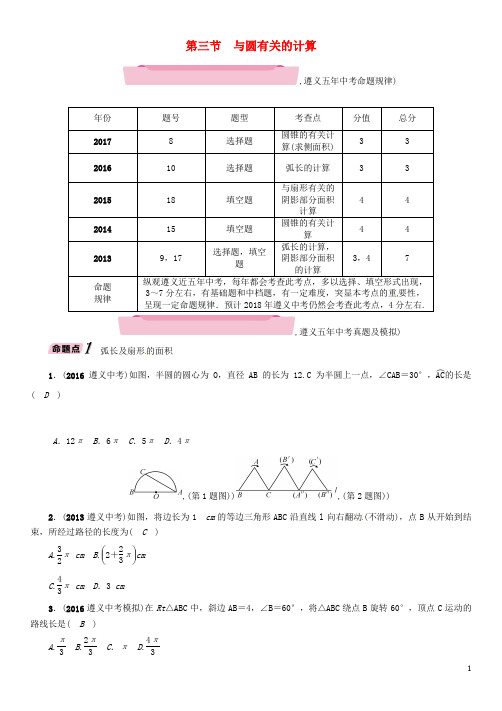
第三节 与圆有关的计算,遵义五年中考命题规律)分左右,有基础题和中档题,有一定难度,突显本考点的重要性,,遵义五年中考真题及模拟)弧长及扇形的面积1.(2016遵义中考)如图,半圆的圆心为O ,直径AB 的长为12.C 为半圆上一点,∠CAB =30°,AC ︵的长是( D )A .12πB .6πC .5πD .4π,(第1题图)),(第2题图))2.(2013遵义中考)如图,将边长为1 cm 的等边三角形ABC 沿直线l 向右翻动(不滑动),点B 从开始到结束,所经过路径的长度为( C )A .32π cm B .⎝ ⎛⎭⎪⎫2+23πcm C .43π cm D .3 cm3.(2016遵义中考模拟)在Rt △ABC 中,斜边AB =4,∠B =60°,将△ABC 绕点B 旋转60°,顶点C 运动的路线长是( B )A .π3B .2π3 C .π D .4π3与扇形有关的阴影面积计算4.(2015遵义中考)如图,在圆心角为90°的扇形OAB 中,半径OA =2 cm ,C 为AB ︵的中点,D ,E 分别是OA ,OB 的中点,则图中阴影部分的面积为__⎝ ⎛⎭⎪⎫12π+2-12__ cm 2.,(第4题图)) ,(第5题图))5.(2013遵义中考)如图,在Rt △ABC 中,∠ACB =90°,AC =BC =1,E 为BC 边上的一点,以点A 为圆心,AE 长为半径的圆弧交AB 于点D ,交AC 的延长线于点F ,且图中两个阴影部分的面积相等,则AF 的长为π__.(结果保留根号)圆锥的有关计算6.(2016遵义六中一模)如图,在正方形ABCD 中,以点A 为顶点作等边△AEF,交边BC 于点E ,交边DC 于点F.又以点A 为圆心,AE 长为半径作EF ︵.若△AEF 的边长为2,则阴影部分的面积约是__0.64__.(结果精确到0.01),中考考点清单)圆的弧长及扇形面积公式如果圆的半径是R ,弧所对的圆心角度数是n ,那么圆锥的侧面积与全面积圆锥简介是圆锥的母线,其长为侧面展开后所得扇形的③续表正多边形与圆【方法点拨】1.牢记圆的有关计算公式,并灵活处理好公式之间的转换,当出现求不规则图形的面积时,注意利用割补法与等面积变换转化为规则图形,再利用规则图形的公式求解.2.圆锥的侧面问题转化为平面问题,如最短路线问题.,中考重难点突破)弧长与扇形面积【例1】(1)(2017遵义六中一模)如图,在扇形OAB 中,∠AOB =60°,扇形半径为r ,点C 在AB ︵上,CD ⊥OA ,垂足为D ,当△OCD 的面积最大时,AC ︵的长为________;[例1(1)题图][例1(2)题图](2)(2017青岛中考)如图,直线AB 与CD 分别与⊙O 相切于B ,D 两点,且AB⊥CD,垂足为P ,连接BD.若BD =4,则阴影部分的面积为________.【解析】(1)在Rt △OCD 中由勾股定理可用圆的半径及OD 表达出DC ,进而表示出△OCD 的面积,把这个式子两边平方后,等号右边可以配方成二次函数的顶点式形式;根据二次函数的性质确定出当△OCD 面积最大时的OD 的值,在Rt △OCD 中,求出∠OCD 的余弦值,从而可求出∠OCD 的值;最后根据弧长计算公式l =n πr180求出弧AC的长即可;(2)连接OB ,OD ,根据切线的性质和垂直得出∠OBP=∠P=∠ODP=90°,求出四边形BODP 是正方形,根据正方形的性质得出∠BOD=90°,求出扇形BOD 和△BOD 的面积,即可得出答案.【答案】(1)14πr ;(2)2π-41.(2017武威中考)如图,AB 是⊙O 的直径,弦C D⊥AB,∠CDB =30°,CD =23,则阴影部分的面积为( D )A .2πB .πC .π3D .2π3,(第1题图)) ,(第2题图))2.(2016汇川升学模拟)如图,在△ABC 中,∠C =90°,AC =BC ,斜边AB =2,O 是AB 的中点,以O 为圆心,线段OC 的长为半径画圆心角为90°的扇形OEF ,弧EF 经过点C ,则图中阴影部分的面积为__π4-12__.3.(2017汇川五模)如图,半圆O 的直径AE =4,点B ,C ,D 均在半圆上,若AB =BC ,CD =DE ,连接OB ,OD ,则图中阴影部分的面积为__π__.,(第3题图)) ,(第4题图))4.如图,半圆O 的直径AB =2,弦CD∥AB,∠COD =90°,则图中阴影部分面积为__π4__.圆锥的侧面积与全面积【例2】一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为________ .(结果保留π)【解析】几何体的上半部分是圆锥,用扇形的面积计算公式即可求解,下面的部分是圆,中间的部分是圆柱,展开图是矩形,用矩形的面积计算公式求解,最后计算各部分的和即可.【答案】68π5.如图,从一张腰长为60 cm ,顶角为120°的等腰三角形铁皮OAB 中剪出一个最大的扇形 OCD ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( D )A .10 cmB .15 cmC .10 3 cmD .20 2 cm正多边形和圆【例3】(2016遵义六中一模)如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是________ .【解析】延长AB和过CD的直线交于E点,可以直接计算△ABC的面积,也可以通过计算△ACE和△BCE的面积差来解决问题.【答案】2 36.(2016遵义航中一模)正六边形的边心距为3,则该正六边形的边长是( B)A. 3 B.2 C.3 D.2 3教后反思:_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________。
中考数学第一编教材知识梳理篇第七章圆第一节圆的有关概念及性质课件
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
Байду номын сангаас
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
2017年中考数学命题研究(河北专版)
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考总复习:圆的有关概念、性质与圆有关的位置关系--知识讲解(基础)
中考总复习:圆的有关概念、性质与圆有关的位置关系—知识讲解(基础)责编:常春芳【考纲要求】1. 圆的基本性质和位置关系是中考考查的重点,但圆中复杂证明及两圆位置关系中证明会有下降趋势,不会有太复杂的大题出现;2.中考试题中将更侧重于具体问题中考查圆的定义及点与圆的位置关系,对应用、创新、开放探究型题目,会根据当前的政治形势、新闻背景和实际生活去命题,进一步体现数学来源于生活,又应用于生活.【知识网络】【考点梳理】考点一、圆的有关概念及性质1.圆的有关概念圆、圆心、半径、等圆;弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧;三角形的外接圆、三角形的内切圆、三角形的外心、三角形的内心、圆心角、圆周角.要点诠释:等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.2.圆的对称性圆是轴对称图形,任何一条直径所在直线都是它的对称轴,圆有无数条对称轴;圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性.3.圆的确定不在同一直线上的三个点确定一个圆.要点诠释:圆心确定圆的位置,半径确定圆的大小.4.垂直于弦的直径垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.要点诠释:在图中(1)直径CD ,(2)CD ⊥AB ,(3)AM =MB ,(4)C C A B =,(5)AD BD =.若上述5个条件有2个成立,则另外3个也成立.因此,垂径定理也称“五二三定理”.即知二推三. 注意:(1)(3)作条件时,应限制AB 不能为直径.5.圆心角、弧、弦之间的关系定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量也相等. 6.圆周角圆周角定理 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半. 推论1 在同圆或等圆中,相等的圆周角所对的弧也相等.推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径. 要点诠释:圆周角性质的前提是在同圆或等圆中.考点二、与圆有关的位置关系 1.点和圆的位置关系设⊙O 的半径为r ,点P 到圆心的距离OP =d ,则有:点P 在圆外⇔d >r ; 点P 在圆上⇔d =r ; 点P 在圆内⇔d <r . 要点诠释:圆的确定:①过一点的圆有无数个,如图所示.②过两点A 、B 的圆有无数个,如图所示.③经过在同一直线上的三点不能作圆.④不在同一直线上的三点确定一个圆.如图所示.2.直线和圆的位置关系(1)切线的判定切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.(会过圆上一点画圆的切线)(2)切线的性质切线的性质定理圆的切线垂直于过切点的半径.(3)切线长和切线长定理切线长经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.切线长定理从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.要点诠释:直线l是⊙O的切线,必须符合两个条件:①直线l经过⊙O上的一点A;②OA⊥l.3.圆和圆的位置关系(1)基本概念两圆相离、相切、外离、外切、相交、内切、内含的定义.(2)请看下表:要点诠释:①相切包括内切和外切,相离包括外离和内含.其中相切和相交是重点. ②同心圆是内含的特殊情况.③圆与圆的位置关系可以从两个圆的相对运动来理解. ④“R-r ”时,要特别注意,R >r .【典型例题】类型一、圆的性质及垂径定理的应用【高清课堂:圆的有关概念、性质及与圆有关的位置关系 ID:412074 经典例题1】1.已知:如图所示,在⊙O 中,弦AB 的中点为C ,过点C 的半径为OD .(1)若AB =OC =1,求CD 的长; (2)若半径OD =R ,∠AOB =120°,求CD 的长.【思路点拨】如图所示,一般的,若∠AOB =2n °,OD ⊥AB 于C ,OA =R ,OC =h ,则AB =2R ·sin n °=2n ·tan n °=CD =R -h ;AD 的长180n Rπ=. 【答案与解析】解:∵半径OD 经过弦AB 的中点C , ∴半径OD ⊥AB .(1)∵AB=AC=BC∵OC=1,由勾股定理得OA=2.∴CD=OD-OC=OA-OC=1,即CD=1.(2)∵OD⊥AB,OA=OB,∴∠AOD=∠BOD.∴∠AOB=120°,∴∠AOC=60°.∵OC=OA·cos∠AOC=OA·cos60°=12 R,∴1122CD OD OC R R R =-=-=.【总结升华】圆的半径、弦长的一半、弦心距三条线段组成一个直角三角形,其中一个锐角为弦所对圆心角的一半,可充分利用它们的关系解决有关垂径定理的计算问题.举一反三:【变式】在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到A点时,乙已跟随冲到B点(如图所示),此时甲是自己直接射门好还是迅速将球回传给乙,让乙射门好呢?(不考虑其他因素)【答案】解:过M、N、B三点作圆,显然A点在圆外,设MA交圆于C,则∠MAN<∠MCN.而∠MCN=∠MBN,∴∠MAN<∠MBN.因此在B点射门较好.即甲应迅速将球回传给乙,让乙射门.2.(2015•大庆模拟)已知AB是⊙O的直径,C是圆周上的动点,P是弧AC的中点.(1)如图1,求证:OP∥BC;(2)如图2,PC交AB于D,当△ODC是等腰三角形时,求∠A的度数.【思路点拨】(1)连结AC,延长PO交AC于H,如图1,由P是弧AC的中点,根据垂径定理得PH⊥AC,再根据圆周角定理,由AB是⊙O的直径得∠ACB=90°,然后根据OP∥BC;(2)如图2,根据圆心角、弧、弦的关系,以及三角形内角和等推论证来求得∠A的度数.【答案与解析】(1)证明:连结AC,延长PO交AC于H,如图1,∵P是弧AB的中点,∴PH⊥AC,∵AB是⊙O的直径,∴∠ACB=90°,∴BC⊥AC,∴OP∥BC;(2)解:如图2,∵P是弧AC的中点,∴PA=PC,∴∠PAC=∠PCA,∵OA=OC,∴∠OAC=∠OCA,∴∠PAO=∠PCO,当DO=DC,设∠DCO=x,则∠DOC=x,∠PAO=x,∴∠OPC=∠OCP=x,∠PDO=2x,∵∠OPA=∠PAO=x,∴∠POD=2x,在△POD中,x+2x+2x=180°,解得x=36°,即∠PAO=36°,当CO=CD,设∠DCO=x,则∠OPC=x,∠PAO=x,∴∠POD=2x,∴∠ODC=∠POD+∠OPC=3x,∵CD=CO,∴∠DOC=∠ODC=3x,在△POC中,x+x+5x=180°,解得x=()°,即∠PAO=()°.综上所述,∠A的度数为36°或()°.【总结升华】本题考查了圆周角定理及其推论同时考查了等腰三角形的性质、垂径定理和三角形内角和定理.举一反三:【变式】(2015•温州模拟)如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.(1)求BE的长;(2)求△ACD外接圆的半径.【答案】解:(1)∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),∴∠AED=90°(直径所对的圆周角为直角),又AD是△ABC的角平分线(已知),∴∠CAD=∠EAD(角平分线定义),∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴AC=AE(全等三角形的对应边相等);∵△ABC为直角三角形,且AC=5,CB=12,∴根据勾股定理得:AB==13,∴BE=13﹣AC=13﹣5=8;(2)由(1)得到∠AED=90°,则有∠BED=90°,设CD=DE=x,则DB=BC﹣CD=12﹣x,EB=AB﹣AE=AB﹣AC=13﹣5=8,在Rt△BED中,根据勾股定理得:BD2=BE2+ED2,即(12﹣x)2=x2+82,解得:x=,∴CD=,又AC=5,△ACD为直角三角形,∴根据勾股定理得:AD==,根据AD是△ACD外接圆直径,∴△ACD外接圆的半径为:×=.类型二、圆的切线判定与性质的应用3.如图所示,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC与⊙O相切.【思路点拨】AC与⊙O有无公共点在已知条件中没有说明,因此只能过点O向AC作垂线段OE,长等于⊙O的半径,则垂足E必在⊙O上,从而AC与⊙O相切.【答案与解析】证明:连接OD,作OE⊥AC,垂足为E,连结OA.∵AB与⊙O相切于点D,∴OD⊥AB.∵AB=AC,OB=OC,∴∠1=∠2,∴OE=OD.∵OD为⊙O半径,∴AC与⊙O相切.【总结升华】如果已知直线经过圆上一点,那么连半径,证垂直;如果已知直线与圆是否有公共点在条件中并没有给出,那么作垂直,证半径.举一反三:【变式】如图所示,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c.求△ABC的内切圆的半径.【答案】解:设△ABC的内切圆与三边的切点分别为D、E、F,根据切线长定理可得:AE =AF ,BF =BD ,CD =CE ,而AE+CE =b ,CD+BD =a ,AF+BF =c , 可求2a b cCE +-=. 连接OE 、OD ,易证OE =CE .即直角三角形的内切圆半径2a b cr +-=.4.如图所示,已知:△ABC 内接于⊙O ,点D 在OC 的延长线上,1sin 2B =,∠D =30°. (1)求证:AD 是⊙O 的切线; (2)若AC =6,求AD 的长.【思路点拨】(1)连接OA ,根据圆周角定理求出∠O 的度数,根据三角形的内角和定理求出∠OAD ,根据切线的判定推出即可;(2)得出等边三角形AOC ,求出OA ,根据勾股定理求出AD 的长即可. 【答案与解析】(1)证明:连接OA ,∵1sin 2B =,∴∠B =30°. ∵∠AOC =2∠B ,∴∠AOC =60°. ∵∠D =30°,∴∠OAD =180°-∠D -∠AOD =90°. ∴AD 是⊙O 的切线.(2)解:∵OA =OC ,∠AOC =60°,∴△AOC是等边三角形,∴OA=AC=6.∵∠OAD=90°,∠D=30°,∴AD=【总结升华】证明直线是圆的切线的方法:①有半径,证垂直;②有垂直,证半径.举一反三:【变式】如图所示,半径OA⊥OB,P是OB延长线上一点,PA交⊙O于D,过D作⊙O的切线交PO于C 点,求证:PC=CD.【答案】证明:连接OD.∵CE切⊙O于D,∴OD⊥CE.∴∠2+∠3=90°.∵OA⊥OB,∴∠P+∠A=90°.∵OD=OA,∴∠3=∠A..∴∠P=∠2.又∵∠1=∠2,∴∠P=∠1.∴PC=CD.类型三、切线的性质与等腰三角形、勾股定理综合运用5.已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC 的平分线交AC于点D,求∠CDP的度数.【思路点拨】连接OC,根据题意,可知OC⊥PC,∠CPD+∠DPA+∠A+∠ACO=90°,可推出∠DPA+∠A=45°,即∠CDP=45°.【答案与解析】解:连接OC,∵OC=OA,,PD平分∠APC,∴∠CPD=∠DPA,∠A=∠ACO,∵PC为⊙O的切线,∴OC⊥PC,∵∠CPD+∠DPA+∠A+∠ACO=90°,∴∠DPA+∠A=45°,即∠CDP=45°.【总结升华】本题主要考查切线的性质、等边三角形的性质、角平分线的性质、外角的性质,解题的关键在于做好辅助线构建直角三角形,求证∠CPD+∠DPA+∠A+∠ACO=90°,即可求出∠CDP=45°.【高清课堂:圆的有关概念、性质及与圆有关的位置关系 ID:412074 经典例题3】6.如图所示,AB是⊙O的直径,AF是⊙O的弦,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF于点D,交AB的延长线于点C.(1)求证:CD是⊙O的切线;(2)若DE=4,sinC=35,求AE的长.【思路点拨】构造半径、半弦、弦心距的直角三角形.【答案与解析】解:(1)证明:连接OE,BF,交于点G,则BF⊥AF,BF∥CD.∵OA=OE,∴∠OAE=∠OEA.∵∠OAE=∠FAE,∴∠OEA=∠FAE.∴OE∥AF,∵AF⊥DE,∴OE⊥CD.∴CD为⊙O的切线.(2)解:∵ BF∥DE,OE∥AF,∠D=90°,∴四边形DEGF为矩形.∴BF=2GF=2DE=8.∵BF∥CD,∴∠C=∠ABF.可求得OA=OB=5,OG=3.∴DF=EG=2,AF=AB·sinC=6.∴AD=8,AE=【总结升华】(1)通过挖掘图形的性质,将分散的条件sinC=35,DE=4,集中到一个直角三角形中,使问题最终得到解决;(2)本题第(2)问还可以适当改变后进行变式训练,如改为:若DF=2,sinC=35,求AE的长;(3)第(2)问还可以过O作OM⊥AF于M后得OM=DE=4,sin∠AOM=sinC=35加以解决.。
矿产
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
(完整版)初三数学圆知识点复习专题经典
A
D
E
O
C
B
线长是这点到割
( 4 )割线定理 :从圆外一点引圆的两条割线, 这一点到每条割线与圆的交点的两条线段长的积相等
(如上图) 。
即:在⊙ O 中,∵ PB 、 PE 是割线
∴PC PB PD PE
例 1. 如图 1,正方形 ABCD的边长为 1,以 BC为直径。在正方形内作半圆 于 E,求 DE: AE的值。
六、圆心角定理
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。
此定理也称 1
推 3 定理,即上述四个结论中, 只要知道其中的 1 个相等,则可以推出其它的 3 个结论,
即:① AOB DOE ;② AB DE ; ③ OC OF ;④ 弧 BA 弧 BD
O A
C
E F D
∴C D
推论 2 :半圆或直径所对的圆周角是直角;圆周角是直角所对的弧
C
是半圆,所对的弦是直径。
即:在⊙ O 中,∵ AB 是直径
或∵ C 90
B
A
O
∴ C 90
∴AB 是直径
推论 3 :若三角形一边上的中线等于这边的一半,那么这个三角形是
C
直角三角形。
即:在△ ABC 中,∵ OC OA OB
B
A
推论 1:( 1 )平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2 )弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3 )平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共 4 个定理,简称 2 推 3 定理:此定理中共 5 个结论中,只要知道其中 2 个即可推出其它 3 个结
