最新高考数学二轮复习立体几何专题训练习题(含答案解析)
2024届高考数学总复习《立体几何》复习题及答案

则t (2,0,﹣c),设平面 PAB 的法向量为 (x,y,z),
则t
,即
t⺁ t
,
取 x=c,则 (c,c,2), 由(Ⅱ)知平面 A1BE 的法向量为 (1,﹣1,﹣2).
所以|cos< , >|
,
解得 c
<2,
故在棱 CC1 上存在一点 P,使得平面 PAB 与平面 A1BE 所成二面角为 60°,P 点的坐标
为(0,0, ).
第3页共3页
∴ (﹣2,2,0),
(2,0,1), (0,2,﹣1).
第2页共3页
设平面 A1BE 的法向量为 (x,y,z),则
令 x=1,则 (1,﹣1,﹣2).
所以 cos< , >
.
,即
t
⺁ ⺁
所以直线 AB 与平面 A1BE 所成角的正弦值为 . (Ⅲ)解:假设在棱 CC1 上存在一点 P,使得平面 PAB 与平面 A1BE 所成二面角为 60°, 设 P(0,0,c),0≤c≤2.
【解答】(Ⅰ)证明:取 AB 的中点 F,连接 DF,交 A1B 于点 M,可知 M 为 DF 中点, 连接 EM,易知四边形 C1DME 为平行四边形, 所以 C1D∥EM. 又 C1D⊄平面平面 A1BE,EM⊂平面 A1BE, 所以 C1D∥平面 A1BE. (Ⅱ)解:如图建立空间直角坐标系 C﹣xyz,则 A(2,0,0),B(0,2,0),E(0,0, 1),A1(2,0,2).
,即 t t
⺁,
第1页共3页
取 z=1 可得 (0,1,1),
∴cos< , >
.
∴二面角 M﹣CB﹣P 的余弦值为 .
2.如图,在三棱柱 ABC﹣A1B1C1 中,AA1⊥平面 ABC,AA1=AC=BC=2,∠ACB=90°, D,E 分别是 A1B1,CC1 的中点 (Ⅰ)求证:C1D∥平面 A1BE; (Ⅱ)求直线 AB 与平面 A1BE 所成角的正弦值; (Ⅲ)在棱 CC1 上是否存在一点 P,使得平面 PAB 与平面 A1BE 所成二面角为 60°?若 存在,求出 P 点的坐标;若不存在,请说明理由.
高考数学二轮复习立体几何多选题练习题及解析

高考数学二轮复习立体几何多选题练习题及解析一、立体几何多选题1.如图①,矩形ABCD 的边2BC =,设AB x =,0x >,三角形BCM 为等边三角形,沿BC 将三角形BCM 折起,构成四棱锥M ABCD -如图②,则下列说法正确的有( )A .若T 为BC 中点,则在线段MC 上存在点P ,使得//PD 平面MATB .当)3,2x ∈时,则在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCDC .若使点M 在平面ABCD 内的射影落在线段AD 上,则此时该四棱锥的体积最大值为1 D .若1x =,且当点M 在平面ABCD 内的射影点H 落在线段AD 上时,三棱锥M HAB -6322++【答案】BCD 【分析】对于A ,延长AT 与DC 的延长线交于点N ,此时,DP 与MN 必有交点; 对于B ,取AD 的中点H ,表示出2223MH MT HT x --,验证当)3,2x ∈时,无解即可; 对于C ,利用体积公式21233V x x =⨯⨯-,借助基本不等式求最值即可; 对于D ,要求外接球半径与内切球半径,找外接圆的圆心,又内接圆半径为2323r =++【详解】对于A ,如图,延长AT 与DC 的延长线交于点N ,则面ATM ⋂面()MDC N MN =.此时,DP 与MN 必有交点,则DP 与面ATM 相交,故A 错误; 对于B ,取AD 的中点H ,连接MH ,则MH AD ⊥.若面MAD ⊥面ABCD ,则有2223MH MT HT x =-=- 当)3,2x ∈时,无解,所以在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD故B 正确;对于C ,由题可知,此时面MAD ⊥面ABCD ,由B 可知,(3x ∈,所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭当且仅当223x x =-,即6x =时等号成立.故C 正确; 对于D ,由题可知,此时面MAD ⊥面ABCD ,且2MH =因为AHB ,MHB 都是直角三角形,所以M ABH -底面外接圆的圆心是中点,所以1R =,由等体积法,可求得内接圆半径为2323r =++,故61322R r +=,故D 正确.故选:BCD . 【点睛】本题从多个角度深度考查了立体几何的相关内容,注意辅助线的作法,以及求内接圆半径的公式、基本不等式、构造函数等核心思想.2.已知三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,其长度分别为a ,b ,c .点A 在底面BCD 内的射影为O ,点A ,B ,C ,D 所对面的面积分别为A S ,B S ,C S ,D S .在下列所给的命题中,正确的有( ) A .2A BCO D S SS ⋅=; B .3333A B C D S S S S <++;C .若三条侧棱与底面所成的角分别为1α,1β,1γ,则222111sin sin sin 1αβγ++=;D .若点M 是面BCD 内一个动点,且AM 与三条侧棱所成的角分别为2α,2β,2γ,则22cos α+2222cos cos 1βγ+=.【答案】ACD 【分析】由Rt O OA '与Rt O AD '相似,得边长关系,进而判断A 正确;当M 与O 重合时,注意线面角与线线角的关系,即可得C 正确;构造长方体,建立直角坐标系,代入夹角公式计算可得D 正确;代入特殊值,可得B 错误. 【详解】由三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,则将三棱锥A BCD -补成长方体ABFC DGHE -,连接DO 并延长交BC 于O ', 则AO BC ⊥.对A :由Rt O OA '与Rt O AD '相似,则2O A O O O D '''=⨯ 又12A S BC O D '=⋅,12BCOS BC O O '=⋅, 22221124D S BC O A BC O A ⎛⎫''=⋅=⋅ ⎪⎝⎭所以2A BCOD S SS ⋅=,故A 正确.对B :当1a b c ===时,33318B C D S S S ===,则33338B C D S S S ++=,而332333322288A S ⎛⎫=⨯⨯=> ⎪ ⎪⎝⎭,此时3333A B C D S S S S >++,故B 不正确. 对D :分别以AB ,AC ,AD 为x ,y ,z 轴,建立空间直角坐标系. 设(),,M x y z ,则(),,AM x y z =,222AM x y z =++,(),0,0AB a =,()0,,0AC b =,()0,0,AD c =所以222222222cos cos cos AM AB AM AC AM AD AM ABAM ACAM ADαβγ⎛⎫⎛⎫⎛⎫⋅⋅⋅++=++ ⎪ ⎪ ⎪ ⎪⎪⎪⋅⋅⋅⎝⎭⎝⎭⎝⎭2222221x y z AMAMAM=++=,所以D 正确.对C :当M 与O 重合时,AO ⊥面BCD ,由D 有222222cos cos cos 1αβγ++=,由各侧棱与底面所成角与侧棱与所AO 成角互为余角,可得C 正确. 故选:ACD.【点睛】关键点睛:本题考查空间线面角、线线角、面积关系的问题,计算角的问题关键是建立空间直角坐标系,写出点的坐标,利用数量积的公式代入计算,解决这道题目还要结合线面角与线线角的关系判断.3.已知四面体ABCD 的所有棱长均为2,则下列结论正确的是( ) A .异面直线AC 与BD 所成角为60︒B .点A 到平面BCD 的距离为3C .四面体ABCDD .动点P 在平面BCD 上,且AP 与AC 所成角为60︒,则点P 的轨迹是椭圆 【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ,通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误;在四面体ABCD 中,过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心,因为所有棱长均为2,AF ==即点A 到平面BCD 的距离为3,故B 正确;设O 为正四面体的中心则OF 为内切球的半径,OA 我外接球的半径, 因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△,所以4AF OF =,即2=6OF AO =,所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确;建系如图:,A C ⎛⎛⎫⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ,则,,0,,333AP x y AC →→⎛⎛=-=- ⎝⎭⎝⎭,因为cos 60AP AC AP AC →→→→⋅=,所以241392y +=,83y +,平方化简可得:22400399y x y ----,可知点P 的轨迹为双曲线,故D 错误. 故选:BC .【点睛】方法点睛:立体几何中动点轨迹的求解问题,解决此类问题可采用空间向量法,利用空间向量法表示出已知的角度或距离的等量关系,从而得到轨迹方程.4.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +的最小值为1705【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos AA AC AAC ''==∠=-, 所以217042222()105AC '=+-⨯⨯⨯-=. 故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.5.M ,N 分别为菱形ABCD 的边BC ,CD 的中点,将菱形沿对角线AC 折起,使点D 不在平面ABC 内,则在翻折过程中,下列结论正确的有( )A .MN ∥平面ABDB .异面直线AC 与MN 所成的角为定值C .在二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径先变小后变大D .若存在某个位置,使得直线AD 与直线BC 垂直,则ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭【答案】ABD 【分析】利用线面平行的判定即可判断选项A ;利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ;借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D. 【详解】对于选项A:因为M ,N 分别为菱形ABCD 的边BC ,CD 的中点,所以MN 为BCD ∆的中位线,所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ,所以MN ∥平面ABD ,故选项A 正确;对于选项B :取AC 的中点O ,连接,DO BO ,作图如下:则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知,AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90,故选项B 正确;对于选项C:借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,球心离开平面ABC ,但是球心在底面的投影仍然是ABC ∆外接圆圆心,故二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径不可能先变小后变大, 故选项C 错误;对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角,H 在线段BC 上;若ABC ∠为直角,H 与B 重合;若ABC ∠为钝角,H 在线段BC 的延长线上;若存在某个位置,使得直线AD 与直线BC 垂直,因为AH BC ⊥,所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角,H 与B 重合,所以CB BD ⊥,在CBD ∆中,因为CB CD =, 所以CB BD ⊥不可能成立,即ABC ∠为直角不可能成立;若ABC ∠为钝角,H 在线段BC 的延长线上,则在原平面图菱形ABCD 中,DCB ∠为锐角,由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小,,所以DCB ∠为锐角,CB HD ⊥,故点H 在线段BC 与H 在线段BC 的延长线上矛盾,因此ABC ∠不可能为钝角;综上可知,ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭.故选项D 正确;故选:ABD 【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题;考查空间想象能力和逻辑推理能力;借助极限状态和反证法思想的运用是求解本题的关键;属于综合型强、难度大型试题.6.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点 B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=,E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点, 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.7.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点P 在线段B 1C 上运动,则( )A .直线BD 1⊥平面A 1C 1DB .三棱锥P ﹣A 1C 1D 的体积为定值C .异面直线AP 与A 1D 所成角的取值范用是[45°,90°]D .直线C 1P 与平面A 1C 1D所成角的正弦值的最大值为3【答案】ABD【分析】 在A 中,推导出A 1C 1⊥BD 1,DC 1⊥BD 1,从而直线BD 1⊥平面A 1C 1D ;在B 中,由B 1C ∥平面 A 1C 1D ,得到P 到平面A 1C 1D 的距离为定值,再由△A 1C 1D 的面积是定值,从而三棱锥P ﹣A 1C 1D 的体积为定值;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°];在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出直线C 1P 与平面A 1C 1D. 【详解】解:在A 中,∵A 1C 1⊥B 1D 1,A 1C 1⊥BB 1,B 1D 1∩BB 1=B 1,∴A 1C 1⊥平面BB 1D 1,∴A 1C 1⊥BD 1,同理,DC 1⊥BD 1,∵A 1C 1∩DC 1=C 1,∴直线BD 1⊥平面A 1C 1D ,故A 正确;在B 中,∵A 1D ∥B 1C ,A 1D ⊂平面A 1C 1D ,B 1C ⊄平面A 1C 1D ,∴B 1C ∥平面 A 1C 1D ,∵点P 在线段B 1C 上运动,∴P 到平面A 1C 1D 的距离为定值,又△A 1C 1D 的面积是定值,∴三棱锥P ﹣A 1C 1D 的体积为定值,故B 正确;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°],故C 错误;在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1,P (a ,1,a ),则D (0,0,0),A 1(1,0,1),C 1(0,1,1),1DA =(1,0,1),1DC =(0,1,1),1C P =(a ,0,a ﹣1),设平面A 1C 1D 的法向量(),,n x y z =, 则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x =1,得1,1,1n ,∴直线C 1P 与平面A 1C 1D 所成角的正弦值为: 11||||||C P n C Pn ⋅⋅=∴当a =12时,直线C 1P 与平面A 1C 1D ,故D 正确. 故选:ABD .【点睛】求直线与平面所成的角的一般步骤:(1)、①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解;(2)、用空间向量坐标公式求解.8.如图所示,在棱长为1的正方体1111ABCD A B C D 中,过对角线1BD 的一个平面交棱1AA 于点E ,交棱1CC 于点F ,得四边形1BFD E ,在以下结论中,正确的是( )A .四边形1BFD E 有可能是梯形B .四边形1BFD E 在底面ABCD 内的投影一定是正方形C .四边形1BFDE 有可能垂直于平面11BB D DD .四边形1BFDE 面积的最小值为62 【答案】BCD【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形;1BFD E 在底面ABCD 内的投影是四边形ABCD ;当与两条棱上的交点是中点时,四边形1BFD E 垂直于面11BB D D ;当E ,F 分别是两条棱的中点时,四边形1BFD E 6【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E ,如图所示,因为平面11//ABB A 平面11DCC D ,且平面1BFD E平面11ABB A BE =. 平面1BFD E 平面1111,//DCC D D F BE D F =,因此,同理1//D E BF ,故四边形1BFD E 为平行四边形,因此A 错误;对于选项B ,四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ,因此B 正确; 对于选项C ,当点E F 、分别为11,AA CC 的中点时,EF ⊥平面11BB D D ,又EF ⊂平面1BFD E ,则平面1BFD E ⊥平面11BB D D ,因此C 正确;对于选项D ,当F 点到线段1BD 的距离最小时,此时平行四边形1BFD E 的面积最小,此时点E F 、分别为11,AA CC 的中点,此时最小值为162322⨯⨯=,因此D 正确. 故选:BCD【点睛】关键点睛:解题的关键是理解想象出要画的平面是怎么样的平面,有哪些特殊的性质,考虑全面即可正确解题.。
2023年高考数学总复习《立体几何》附答案解析

所以 z1=0,
,故可取
, ,,
于是 < , >
,
设所成锐二面角为θ,所以 sinθ
,
所以平面 PAD 和平面 PBE 所成锐二面角的正弦值为 .
第3页共3页
第1页共3页
∴CF CC1 AA1 , ∵∠BAC=90°,
∴CD
,
在 Rt△FCD 中,tan∠FDC 맨
,
故直线 DF 与平面 ABC 所成角的正切值为 .
2.如图所示,四棱锥 P﹣ABCD 的底面 ABCD 是边长为 1 的菱形,∠BCD=60°,E 是 CD 的中点,PA⊥底面 ABCD,PA=2. (1)证明:平面 PBE⊥平面 PAB; (2)求平面 PAD 和平面 PBE 所成二面角(锐角)的正弦值.
【解答】(1)证明:如图所示,连接 BD,由 ABCD 是菱形且∠BCD=60°, 知△ABC 是等边三角形. ∵E 是 CD 的中点, ∴BE⊥CD,又 AB∥CD, ∴AB⊥BE,∴BE⊥平面 PAB, 又 BE⊂平面 PBE, ∴平面 PBE⊥平面 PAB. (2)解:在平面 ABCD 内,过点 A 作 AB 的垂线,如图所示,以 A 为原点建立空间直角
【解答】(1)证明:连接 DG、FG, 由直三棱柱的性质知,BB1∥CC1,且 BB1=CC1, ∵B1E=2EB,C1F=2FC, ∴EB∥FC,且 EB=FC, ∴四边形 BCFE 为平行四边形, ∴EF∥BC,EF=BC, ∵BD=2DA,CG=2GA, ∴GD∥BC,且 GD BC, ∴EF∥GD,且 GD EF, ∴四边形 DEFG 为梯形,即 D、E、F、G 四点共面, ∴点 G 在平面 EFD 内. (2)解:由直三棱柱的性质知,CC1⊥平面 ABC, ∵F 为 CC1 上一点, ∴点 F 在平面 ABC 上的投影为点 C, 连接 CD,则∠FDC 即为直线 DF 与平面 ABC 所成角. ∵点 D 在棱 AB 上,且 BD=2DA, ∴AD AB , ∵C1F=2FC,
高考数学(理)二轮复习:立体几何(含答案)
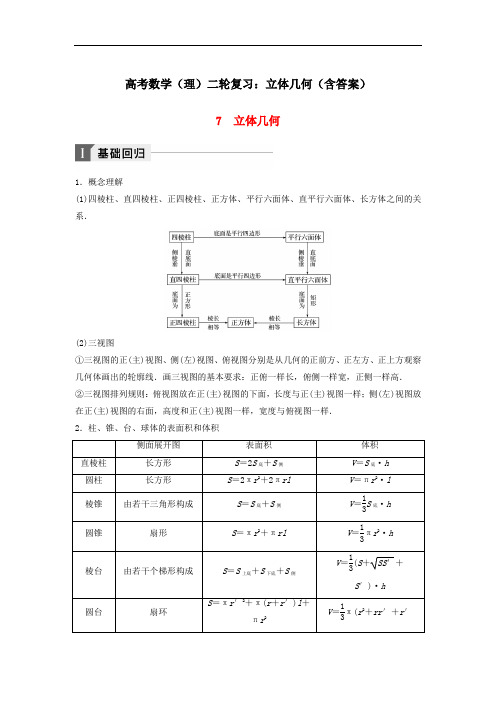
高考数学(理)二轮复习:立体几何(含答案)7 立体几何1.概念理解(1)四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系.(2)三视图①三视图的正(主)视图、侧(左)视图、俯视图分别是从几何的正前方、正左方、正上方观察几何体画出的轮廓线.画三视图的基本要求:正俯一样长,俯侧一样宽,正侧一样高. ②三视图排列规则:俯视图放在正(主)视图的下面,长度与正(主)视图一样;侧(左)视图放在正(主)视图的右面,高度和正(主)视图一样,宽度与俯视图一样. 2.柱、锥、台、球体的表面积和体积侧面展开图 表面积 体积直棱柱 长方形 S =2S 底+S 侧 V =S 底·h 圆柱 长方形 S =2πr 2+2πrl V =πr 2·l 棱锥 由若干三角形构成S =S 底+S 侧 V =13S 底·h 圆锥扇形S =πr 2+πrlV =13πr 2·h 棱台 由若干个梯形构成 S =S 上底+S 下底+S 侧 V =13(S +SS ′+S ′)·h圆台 扇环 S =πr ′2+π(r +r ′)l +πr 2V =13π(r 2+rr ′+r ′2)·h 球 S =4πr 2 S =43πr 33.平行、垂直关系的转化示意图 (1)(2)两个结论 ①⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒a ∥b ,②⎭⎪⎬⎪⎫a ∥b a ⊥α⇒b ⊥α.4.用空间向量证明平行垂直设直线l 的方向向量为a =(a 1,b 1,c 1),平面α,β的法向量分别为μ=(a 2,b 2,c 2),v =(a 3,b 3,c 3).则有: (1)线面平行l ∥α⇔a ⊥μ⇔a ·μ=0⇔a 1a 2+b 1b 2+c 1c 2=0.(2)线面垂直l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 2,b 1=kb 2,c 1=kc 2.(3)面面平行α∥β⇔μ∥v ⇔μ=λv ⇔a 2=λa 3,b 2=λb 3,c 2=λc 3.(4)面面垂直α⊥β⇔μ⊥v ⇔μ·v =0⇔a 2a 3+b 2b 3+c 2c 3=0.5.用向量求空间角(1)直线l 1,l 2的夹角θ有cos θ=|cos 〈l 1,l 2〉|(其中l 1,l 2分别是直线l 1,l 2的方向向量).(2)直线l 与平面α的夹角θ有sin θ=|cos 〈l ,n 〉|(其中l 是直线l 的方向向量,n是平面α的法向量).(3)平面α,β的夹角θ有cos θ=|cos 〈n 1,n 2〉|,则α—l —β二面角的平面角为θ或π-θ(其中n 1,n 2分别是平面α,β的法向量).1.混淆“点A 在直线a 上”与“直线a 在平面α内”的数学符号关系,应表示为A ∈a ,a ⊂α.2.在由三视图还原为空间几何体的实际形状时,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线为虚线.在还原空间几何体实际形状时一般是以正(主)视图和俯视图为主.3.易混淆几何体的表面积与侧面积的区别,几何体的表面积是几何体的侧面积与所有底面面积之和,不能漏掉几何体的底面积;求锥体体积时,易漏掉体积公式中的系数13.4.不清楚空间线面平行与垂直关系中的判定定理和性质定理,忽视判定定理和性质定理中的条件,导致判断出错.如由α⊥β,α∩β=l ,m ⊥l ,易误得出m ⊥β的结论,就是因为忽视面面垂直的性质定理中m ⊂α的限制条件.5.注意图形的翻折与展开前后变与不变的量以及位置关系.对照前后图形,弄清楚变与不变的元素后,再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系. 6.几种角的范围两条异面直线所成的角0°<α≤90°; 直线与平面所成的角0°≤α≤90°; 二面角0°≤α≤180°;两条相交直线所成的角(夹角)0°<α≤90°; 直线的倾斜角0°≤α<180°; 两个向量的夹角0°≤α≤180°; 锐角0°<α<90°.7.空间向量求角时易忽视向量的夹角与所求角之间的关系,如求解二面角时,不能根据几何体判断二面角的范围,忽视向量的方向,误以为两个法向量的夹角就是所求的二面角,导致出错.1.(2017·重庆外国语学校月考)一个几何体的三视图如图所示,则这个几何体的体积是( )A.π3B.π4 C.π2 D .π答案 D解析 由三视图可知,该几何体为球的34,其半径为1,则体积V =34×43×π×13=π.2.直三棱柱ABC —A 1B 1C 1的直观图及三视图如图所示,D 为AC 的中点,则下列命题是假命题的是( )A .AB 1∥平面BDC 1 B .A 1C ⊥平面BDC 1 C .直三棱柱的体积V =4D .直三棱柱的外接球的表面积为43π 答案 D解析 由三视图可知,直三棱柱ABC —A 1B 1C 1的侧面B 1C 1CB 是边长为2的正方形,底面ABC 是等腰直角三角形,AB ⊥BC ,AB =BC =2. 连接B 1C 交BC 1于点O ,连接OD .在△CAB 1中,O ,D 分别是B 1C ,AC 的中点,∴OD ∥AB 1,又OD ⊂平面BDC 1,AB 1⊄平面BDC 1, ∴AB 1∥平面BDC 1.故A 正确;在直三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC , ∴AA 1⊥BD .又AB =BC =2,D 为AC 的中点, ∴BD ⊥AC ,又AA 1∩AC =A ,AA 1,AC ⊂平面AA 1C 1C , ∴BD ⊥平面AA 1C 1C . ∴BD ⊥A 1C .又A 1B 1⊥B 1C 1,A 1B 1⊥B 1B , ∴A 1B 1⊥平面B 1C 1CB , ∴A 1B 1⊥BC 1.∵BC 1⊥B 1C ,且A 1B 1∩B 1C =B 1, ∴BC 1⊥平面A 1B 1C . ∴BC 1⊥A 1C ,又BD ∩BC 1=B ,BD ,BC 1⊂平面BDC 1, ∴A 1C ⊥平面BDC 1.故B 正确;V =S △ABC ×C 1C =12×2×2×2=4,故C 正确;此直三棱柱的外接球的半径为3,其表面积为12π,D 错.故选D. 3.已知直线l ,m 和平面α,则下列结论正确的是( ) A .若l ∥m ,m ⊂α,则l ∥α B .若l ⊥α,m ⊂α,则l ⊥m C .若l ⊥m ,l ⊥α,则m ∥α D .若l ∥α,m ⊂α,则l ∥m 答案 B解析 若l ∥m ,m ⊂α,则l ∥α或l ⊂α,故A 错误;若l ⊥α,m ⊂α,则l ⊥m ,B 正确;若l ⊥m ,l ⊥α,则m ⊂α或m ∥α,故C 错误;若l ∥α,m ⊂α,则l ∥m 或l ,m 异面,故选B.4.已知互相垂直的平面α,β交于直线l .若直线m ,n 满足m ∥α,n ⊥β,则( ) A .m ∥l B .m ∥n C .n ⊥l D .m ⊥n 答案 C解析 由题意知,α∩β=l ,∴l ⊂β,∵n ⊥β,∴n ⊥l .故选C.5.已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,l ⊄α,l ⊄β,则( )A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l 答案 D解析 假设α∥β,由m ⊥平面α,n ⊥平面β,得m ∥n ,这与已知m ,n 为异面直线矛盾,那么α与β相交,设交线为l 1,则l 1⊥m ,l 1⊥n ,在直线m 上任取一点作n 1平行于n ,那么l 1和l 都垂直于直线m 与n 1所确定的平面,所以l 1∥l .6.如图,正方体AC 1的棱长为1,过点A 作平面A 1BD 的垂线,垂足为点H ,以下四个命题:①点H 是△A 1BD 的垂心;②AH 垂直于平面CB 1D 1;③直线AH 和BB 1所成角为45°;④AH 的延长线经过点C 1,其中假命题的个数为( ) A .0 B .1 C .2 D .3 答案 B解析 ∵AB =AA 1=AD ,BA 1=BD =A 1D , ∴三棱锥A -BA 1D 为正三棱锥, ∴点H 是△A 1BD 的垂心,故①正确;∵平面A 1BD 与平面B 1CD 1平行,AH ⊥平面A 1BD , ∴AH ⊥平面CB 1D 1,故②正确; ∵AA 1∥BB 1,∴∠A 1AH 就是直线AH 和BB 1所成的角, 在直角三角形AHA 1中,∵AA 1=1,A 1H =23×32×2=63,∴sin ∠A 1AH =63≠22,故③错误; 根据正方体的对称性得到AH 的延长线经过C 1, 故④正确,故选B.7.将正方体的纸盒展开如图,直线AB ,CD 在原正方体的位置关系是( )A.平行 B.垂直C.相交成60°角D.异面且成60°角答案 D解析如图,直线AB,CD异面.因为CE∥AB,所以∠ECD即为直线AB,CD所成的角,因为△CDE为等边三角形,故∠ECD=60°.8.长方体的顶点都在同一球面上,其同一顶点处的三条棱长分别为3,4,5,则该球面的表面积为( )A.25π B.50πC.75π D.12523π答案 B解析设球的半径为R,由题意可得(2R)2=32+42+52=50,∴4R2=50,球的表面积为S=4πR2=50π.9.如图,三棱锥A-BCD的棱长全相等,点E为AD的中点,则直线CE与BD所成角的余弦值为( )A.36B.32C.336D.12答案 A解析 方法一 取AB 中点G ,连接EG ,CG . ∵E 为AD 中点,∴EG ∥BD .∴∠GEC 为CE 与BD 所成的角.设AB =1, 则EG =12BD =12,CE =CG =32, ∴cos ∠GEC =EG 2+EC 2-GC 22×EG ×EC=⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫322-⎝ ⎛⎭⎪⎫3222×12×32=36. 方法二 设AB =1,则CE →·BD →=(AE →-AC →)·(AD →-AB →)=⎝ ⎛⎭⎪⎫12AD →-AC →·(AD →-AB →)=12AD →2-12AD →·AB →-AC →·AD →+AC →·AB →=12-12cos 60°-cos 60°+cos 60°=14. ∴cos 〈CE →,BD →〉=CE →·BD →|CE →||BD →|=1432=36,故选A.10.已知正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等,则AB 1与侧面ACC 1A 1所成角的正弦值等于( ) A.64 B.104 C.22D.32答案 A解析 如图所示建立空间直角坐标系,设正三棱柱的棱长为2,则O (0,0,0),B (3,0,0),A (0,-1,0),B 1(3,0,2),则AB →1=(3,1,2),则BO →=(-3,0,0)为侧面ACC 1A 1的法向量,故sin θ=|AB →1·BO →||AB →1||BO →|=64.11.如图,在空间四边形ABCD 中,点M ∈AB ,点N ∈AD ,若AM MB =ANND,则直线MN 与平面BDC 的位置关系是________.答案 平行解析 由AM MB =AN ND,得MN ∥BD . 而BD ⊂平面BDC ,MN ⊄平面BDC , 所以MN ∥平面BDC .12.已知长方体ABCD —A ′B ′C ′D ′,E ,F ,G ,H 分别是棱AD ,BB ′,B ′C ′,DD ′的中点,从中任取两点确定的直线中,与平面AB ′D ′平行的有________条.答案 6解析 如图,连接EG ,EH ,FG ,∵EH 綊FG , ∴EFGH 四点共面,由EG ∥AB ′,EH ∥AD ′,EG ∩EH =E ,AB ′∩AD ′=A ,可得平面EFGH 与平面AB ′D ′平行, ∴符合条件的共有6条.13.点P 在正方形ABCD 所在平面外,PA ⊥平面ABCD ,PA =AB ,则PB 与AC 所成角的大小是________.答案π3解析 以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴建立空间直角坐标系,设正方形ABCD 的边长为1,则A (0,0,0),P (0,0,1),B (1,0,0),C (1,1,0),PB →=(1,0,-1),AC →=(1,1,0),因此 cos 〈PB →,AC →〉=1+0×1+0×()-112+02+()-12·12+12+02=12, 因此PB 和AC 所成的角为60°,即π3.14.设m ,n 是不同的直线,α,β,γ是不同的平面,有以下四个命题:①⎩⎪⎨⎪⎧ α∥β,α∥γ⇒β∥γ;②⎩⎪⎨⎪⎧α⊥β,m ∥α⇒m ⊥β;③⎩⎪⎨⎪⎧m ⊥α,m ∥β⇒α⊥β;④⎩⎪⎨⎪⎧m ∥n ,n ⊂α⇒m ∥α.其中,正确的命题是________.(填序号) 答案 ①③解析 ①中平行于同一平面的两平面平行是正确的;②中m ,β可能平行,相交或直线在平面内;③中由面面垂直的判定定理可知结论正确;④中m ,α可能平行或线在面内. 15.如图(1),在边长为4的菱形ABCD 中,∠DAB =60°,点E ,F 分别是边CD ,CB 的中点,AC ∩EF =O ,沿EF 将△CEF 翻折到△PEF ,连接PA ,PB ,PD ,得到如图(2)所示的五棱锥P -ABFED ,且PB =10.(1)求证:BD ⊥PA ;(2)求四棱锥P -BFED 的体积.(1)证明 ∵点E ,F 分别是边CD ,CB 的中点, ∴BD ∥EF .∵菱形ABCD 的对角线互相垂直, ∴BD ⊥AC . ∴EF ⊥AC . ∴EF ⊥AO ,EF ⊥PO .∵AO ⊂平面POA ,PO ⊂平面POA ,AO ∩PO =O ,∴EF ⊥平面POA ,∴BD ⊥平面POA ,又PA ⊂平面POA ,∴BD ⊥PA .(2)解 设AO ∩BD =H .连接BO ,∵∠DAB =60°,∴△ABD 为等边三角形,∴BD =4,BH =2,HA =23,HO =PO =3,在Rt △BHO 中,BO =BH 2+HO 2=7,在△PBO 中,BO 2+PO 2=10=PB 2,∴PO ⊥BO .∵PO ⊥EF ,EF ∩BO =O ,EF ⊂平面BFED , BO ⊂平面BFED ,∴OP ⊥平面BFED ,梯形BFED 的面积S =12(EF +BD )·HO =33, ∴四棱锥P -BFED 的体积V =13S ·PO =13×33×3=3.16.如图,四棱锥S -ABCD 的底面是正方形,SD ⊥平面ABCD ,SD =AD =a ,点E 是SD 上的点,且DE =λa (0<λ≤1).(1)求证:对任意的λ∈(0,1],都有AC ⊥BE ;(2)若二面角C -AE -D 的大小为60°,求λ的值.(1)证明 如图,建立空间直角坐标系Dxyz ,则A (a,0,0),B (a ,a,0),C (0,a,0),D (0,0,0),E (0,0,λa ).∴AC →=(-a ,a,0),BE →=(-a ,-a ,λa ),∴AC →·BE →=0对任意λ∈(0,1]都成立,即对任意的λ∈(0,1],都有AC ⊥BE .(2)解 显然n =(0,1,0)是平面ADE 的一个法向量,设平面ACE 的法向量为m =(x ,y ,z ),∵AC →=(-a ,a,0),AE →=(-a,0,λa ),∴⎩⎪⎨⎪⎧ m ·AC →=0,m ·AE →=0,即⎩⎪⎨⎪⎧ -ax +ay =0,-ax +λaz =0,∴⎩⎪⎨⎪⎧ x -y =0,x -λz =0,取z =1,则x =y =λ,∴m =(λ,λ,1),∵二面角C -AE -D 的大小为60°,∴cos 〈n ,m 〉=n ·m ||n ||m =λ1+2λ2=12, ∵λ∈(0,1],∴λ=22. 亲爱的读者:春去燕归来,新桃换旧符。
2024年高考数学总复习立体几何测试卷及答案解析

2024年高考数学总复习立体几何测试卷及答案(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.下列说法正确的是()A.空间中,两不重合的平面若有公共点,则这些点一定在一条直线上B.空间中,三角形、四边形都一定是平面图形C.空间中,正方体、长方体、四面体都是四棱柱D.用一平面去截棱锥,底面与截面之间的部分所形成的多面体叫棱台答案A解析空间四边形不是平面图形,故B错;四面体不是四棱柱,故C错;平行于底面的平面去截棱锥,底面和截面之间的部分所形成的多面体才叫棱台,故D错;根据公理2可知A正确,故选A.2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是() A.α∩β=n,m⊂α,m∥β⇒m∥nB.α⊥β,α∩β=m,m⊥n⇒n⊥βC.m⊥n,m⊂α,n⊂β⇒α⊥βD.m∥α,n⊂α⇒m∥n答案A解析对于A,根据线面平行的性质定理可得A选项正确;对于B,当α⊥β,α∩β=m时,若n⊥m,n⊂α,则n⊥β,但题目中无条件n⊂α,故B不一定成立;对于C,若m⊥n,m ⊂α,n⊂β,则α与β相交或平行,故C错误;对于D,若m∥α,n⊂α,则m与n平行或异面,则D错误,故选A.3.如图,在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且DF→=αAB→+βAC→,则()A.α=12,β=-1B.α=-12,β=1C .α=1,β=-12D .α=-1,β=12答案A解析根据向量加法的多边形法则以及已知可得,DF →=DC →+CB →+BF →=12C 1C →+CB →+12BA →1=12A 1A →+AB →-AC →+12BA →+12AA →1=12AB →-AC →,∴α=12,β=-1,故选A.4.平行六面体ABCD -A 1B 1C 1D 1中,AB →=(1,2,0),AD →=(2,1,0),CC →1=(0,1,5),则对角线AC 1的边长为()A .42B .43C .52D .12答案C解析因为AC →1=AA →1+A 1B 1→+B 1C 1→=CC →1+AB →+AD →=(0,1,5)+(1,2,0)+(2,1,0)=(3,4,5),所以|AC →1|=32+42+52=52,故选C.5.(2019·凉山诊断)如图,在四棱柱ABCD -A 1B 1C 1D 1中,E ,F 分别是AB 1,BC 1的中点,下列结论中,正确的是()A .EF ⊥BB 1B .EF ⊥平面BCC 1B 1C .EF ∥平面D 1BC D .EF ∥平面ACC 1A 1答案D解析连接B 1C 交BC 1于F ,由于四边形BCC 1B 1是平行四边形,对角线互相平分,故F 是B 1C 的中点.因为E 是AB 1的中点,所以EF 是△B 1AC 的中位线,故EF ∥AC ,所以EF ∥平面ACC 1A 1.故选D.6.(2019·湖北黄冈中学、华师附中等八校联考)《九章算术》中“开立圆术”曰:“置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径”.“开立圆术”相当于给出了已知球的体积V ,求球的直径d 的公式d =13169V ⎛⎫⎪⎝⎭.若球的半径为r =1,根据“开立圆术”的方法计算该球的体积为()A.43πB.916C.94D.92答案D 解析根据公式d =13169V ⎛⎫⎪⎝⎭得,2=13169V ⎛⎫ ⎪⎝⎭,解得V =92.故选D.7.已知棱长为2的正方体ABCD -A 1B 1C 1D 1,球O 与该正方体的各个面相切,则平面ACB 1截此球所得的截面的面积为()A.8π3B.5π3C.4π3D.2π3答案D 解析因为球与各面相切,所以直径为2,且AC ,AB 1,CB 1的中点在所求的切面圆上,所以所求截面为此三点构成的边长为2的正三角形的外接圆,由正弦定理知,R =63,所以截面的面积S =2π3,故选D.8.已知向量n =(2,0,1)为平面α的法向量,点A (-1,2,1)在α内,则P (1,2,-2)到α的距离为()A.55B.5C .25D.510答案A解析∵PA →=(-2,0,3),∴点P 到平面α的距离为d =|PA ,→·n ||n |=|-4+3|5=55.∴P (1,2,-2)到α的距离为55.故选A.9.正方体ABCD -A 1B 1C 1D 1中,点P 在A 1C 上运动(包括端点),则BP 与AD 1所成角的取值范围是()A.π4,π3 B.π4,π2C.π6,π2 D.π6,π3答案D解析以点D 为原点,DA ,DC ,DD 1分别为x ,y ,z 轴建立空间直角坐标系,设正方体棱长为1,设点P 坐标为(x ,1-x ,x )(0≤x ≤1),则BP →=(x -1,-x ,x ),BC 1→=(-1,0,1),设BP →,BC 1→的夹角为α,所以cos α=BP ,→·BC 1→|BP →||BC 1→|=1(x -1)2+2x 2×2=x =13时,cos α取得最大值32,α=π6.当x =1时,cos α取得最小值12,α=π3.因为BC 1∥AD 1.故选D.10.(2019·淄博期中)在直三棱柱ABC -A 1B 1C 1中,CA =CB =4,AB =27,CC 1=25,E ,F 分别为AC ,CC 1的中点,则直线EF 与平面AA 1B 1B 所成的角是()A .30°B .45°C .60°D .90°答案A 解析连接AC 1,则EF ∥AC 1,直线EF 与平面AA 1B 1B 所成的角,就是直线EF 与平面AA 1B 1B 所成的角,AC 1与平面AA 1B 1B 所成的角;作C 1D ⊥A 1B 1于D ,连接AD ,因为直三棱柱ABC -A 1B 1C 1中,CA =CB =4,所以底面是等腰三角形,则C 1D ⊥平面AA 1B 1B ,可知∠C 1AD 就是直线EF 与平面AA 1B 1B 所成的角,CA =CB =4,AB =27,CC 1=25,可得C 1D =42-(7)2=3,AD =(7)2+(25)2=33,所以tan ∠C 1AD =C 1D AD =33,所以∠C 1AD =30°.故选A.11.(2019·陕西汉中中学月考)点A ,B ,C ,D ,E 是半径为5的球面上五点,A ,B ,C ,D 四点组成边长为42的正方形,则四棱锥E -ABCD 体积的最大值为()A.2563B .256 C.643D .64答案A解析正方形ABCD 对角线长为(42)2+(42)2=8.则球心到正方形中心的距离d =52-42=3.则E 到正方形ABCD 的最大距离为h =d +5=8.则V E -ABCD =13×42×42×8=2563.故选A.12.(2019·四省联考诊断)如图所示,四边形ABCD 为边长为2的菱形,∠B =60°,点E ,F 分别在边BC ,AB 上运动(不含端点),且EF ∥AC ,沿EF 把平面BEF 折起,使平面BEF ⊥底面ECDAF ,当五棱锥B -ECDAF 的体积最大时,EF 的长为()A .1 B.263C.3D.2答案B解析由EF ∥AC 可知△BEF 为等边三角形,设EF =x ,等边△BEF 的高为32x ,面积为34x 2,所以五边形ECDAF 的面积为2×34×22-34x 2=23-34x 2,故五棱锥的体积为13×23-34x 2×32x =x -18x 3(0<x <2).令f ′(x )=x -18x 3′=1-38x 2=0,解得x =263,且当0<x <263时,f (x )单调递增,当263x <2时,f (x )单调递减,故在x =263时取得极大值也即最大值.故选B.二、填空题(本大题共4小题,每小题5分,共20分)13.设m ,n 为空间两条不同的直线,α,β为空间两个不同的平面,给出下列命题:①若m ∥α,m ∥β,则α∥β;②若m ⊥α,m ∥β,则α⊥β;③若m ∥α,m ∥n ,则n ∥α;④若m ⊥α,α∥β,则m ⊥β.其中正确的命题序号是________.答案②④解析对于①,若m ∥α,m ∥β,则α与β可能相交,故①错误;对于②,若m ⊥α,m ∥β,根据线面垂直和线面平行的性质定理以及面面垂直的判定定理得到α⊥β,故②正确;对于③,若m ∥α,m ∥n ,则n 可能在α内,故③错误,对于④,若m ⊥α,α∥β,则根据线面垂直的性质定理以及面面平行的性质定理得到m ⊥β,故④正确.故答案为②④.14.如图,在三棱柱A 1B 1C 1-ABC 中,已知D ,E ,F 分别为AB ,AC ,AA 1的中点,设三棱锥A -FED 的体积为V 1,三棱柱A 1B 1C 1-ABC 的体积为V 2,则V 1∶V 2的值为________.答案124解析设三棱柱的高为h ,∵F 是AA 1的中点,则三棱锥F -ADE 的高为h2,∵D ,E 分别是AB ,AC 的中点,∴S △ADE =14S △ABC ,∵V 1=13S △ADE ·h2,V 2=S △ABC ·h ,∴V 1V 2=16S △ADE ·h S △ABC ·h =124.15.如图,直三棱柱ABC -A 1B 1C 1的六个顶点都在半径为1的半球面上,AB =AC ,侧面BCC 1B 1是半球底面圆的内接正方形,则侧面ABB 1A 1的面积为________.答案2解析由题意知,球心在正方形的中心上,球的半径为1,则正方形的边长为 2.∵三棱柱ABC —A 1B 1C 1为直三棱柱,∴平面ABC ⊥平面BCC 1B 1,∴BC 为截面圆的直径,∴∠BAC =90°.∵AB =AC ,∴AB =1,∴侧面ABB 1A 1的面积为2×1=2.16.(2019·陕西四校联考)直三棱柱ABC-A1B1C1的底面是直角三角形,侧棱长等于底面三角形的斜边长,若其外接球的体积为32π3,则该三棱柱体积的最大值为____________.答案42解析设三棱柱底面直角三角形的直角边为a,b,则棱柱的高h=a2+b2,设外接球的半径为r,则43πr3=32π3,解得r=2,∵上、下底面三角形斜边的中点连线的中点是该三棱柱的外接球的球心,∴2h=2r=4.∴h =22,∴a2+b2=h2=8≥2ab,∴ab≤4.当且仅当a=b=2时“=”成立.∴三棱柱的体积V=Sh=12abh=2ab≤42.三、解答题(本大题共70分)17.(10分)如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC与BD交于点O,PC⊥底面ABCD,点E为侧棱PB的中点.求证:(1)PD∥平面ACE;(2)平面PAC⊥平面PBD.证明(1)连接OE.因为O为正方形ABCD对角线的交点,所以O为BD的中点.因为E为PB的中点,所以PD∥OE.又因为OE⊂平面ACE,PD⊄平面ACE,所以PD∥平面ACE.(2)在四棱锥P-ABCD中,因为PC ⊥底面ABCD ,BD ⊂底面ABCD ,所以BD ⊥PC .因为O 为正方形ABCD 对角线的交点,所以BD ⊥AC .又PC ,AC ⊂平面PAC ,PC ∩AC =C ,所以BD ⊥平面PAC .因为BD ⊂平面PBD ,所以平面PAC ⊥平面PBD .18.(12分)(2019·广州执信中学测试)如图,在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,AB ∥DC ,△PAD 是等边三角形,已知BD =2AD =8,AB =2DC =45.(1)设M 是PC 上的一点,证明:平面MBD ⊥平面PAD ;(2)求四棱锥P -ABCD 的体积.(1)证明在△ABD 中,由于AD =4,BD =8,AB =45,所以AD 2+BD 2=AB 2.故AD ⊥BD .又平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,BD ⊂平面ABCD ,所以BD ⊥平面PAD ,又BD ⊂平面MBD ,故平面MBD ⊥平面PAD .(2)解如图,过P 作PO ⊥AD 交AD 于O ,由于平面PAD ⊥平面ABCD ,所以PO ⊥平面ABCD .因此PO 为四棱锥P -ABCD 的高,又△PAD 是边长为4的等边三角形.因此PO =32×4=2 3.在四边形ABCD 中,AB ∥DC ,AB =2DC ,所以四边形ABCD 是梯形,在Rt △ADB 中,斜边AB 边上的高为4×845=855,此即为梯形ABCD 的高,所以四边形ABCD 的面积为S =25+452×855=24.故V P -ABCD =13×24×23=16 3.19.(12分)(2019·化州模拟)如图所示,在四棱锥E -ABCD 中,ED ⊥平面ABCD ,AB ∥CD ,AB ⊥AD ,AB =AD =12CD =2.(1)求证:BC ⊥BE ;(2)当几何体ABCE 的体积等于43时,求四棱锥E -ABCD 的侧面积.(1)证明连接BD ,取CD 的中点F ,连接BF ,则直角梯形ABCD 中,BF ⊥CD ,BF =CF=DF ,∴∠CBD =90°,即BC ⊥BD .∵DE ⊥平面ABCD ,BC ⊂平面ABCD ,∴BC ⊥DE ,又BD ∩DE =D ,∴BC ⊥平面BDE .由BE ⊂平面BDE 得,BC ⊥BE .(2)解∵V ABCE =V E -ABC =13×DE ×S △ABC=13×DE ×12×AB ×AD =23DE =43,∴DE =2,∴EA =DE 2+AD 2=22,BE =DE 2+BD 2=23,又AB =2,∴BE 2=AB 2+AE 2,∴AB ⊥AE ,∴四棱锥E -ABCD 的侧面积为12×DE ×AD +12×AE ×AB +12×BC ×BE +12×DE ×CD =6+22+2 6.20.(12分)(2019·青岛调研)如图,在长方形ABCD 中,AB =π,AD =2,E ,F 为线段AB 的三等分点,G ,H 为线段DC 的三等分点.将长方形ABCD 卷成以AD 为母线的圆柱W 的半个侧面,AB ,CD 分别为圆柱W 上、下底面的直径.(1)证明:平面ADHF ⊥平面BCHF ;(2)求二面角A -BH -D 的余弦值.(1)证明因为H 在下底面圆周上,且CD 为下底面半圆的直径,所以DH ⊥CH ,又因为DH ⊥FH ,且CH ∩FH =H ,所以DH ⊥平面BCHF .又因为DH ⊂平面ADHF ,所以平面ADHF ⊥平面BCHF .(2)解以H 为坐标原点,分别以HD ,HC ,HF 所在直线为x ,y ,z 轴建立空间直角坐标系.设下底面半径为r ,由题意得πr =π,所以r =1,CD =2.因为G ,H 为DC 的三等分点,所以∠HDC =30°,所以在Rt △DHC 中,HD =3,HC =1,所以A (3,0,2),B (0,1,2),D (3,0,0),设平面ABH 的法向量为n =(x ,y ,z ),因为n ·HA →=(x ,y ,z )·(3,0,2)=0,n ·HB →=(x ,y ,z )·(0,1,2)=0,+2z =0,2z =0,所以平面ABH 的法向量n =(-2,-23,3).设平面BHD 的法向量m =(x ,y ,z ).因为m ·HD →=(x ,y ,z )·(3,0,0)=0,m ·HB →=(x ,y ,z )·(0,1,2)=0,=0,+2z=0,所以平面BHD的法向量m=(0,-2,1),由图形可知,二面角A—BH—D的平面角为锐角,设为θ,所以二面角A-BH-D的余弦值为cosθ=|m·n||m||n|=28519.21.(12分)(2019·成都七中诊断)如图,在多面体ABCDE中,AC和BD交于一点,除EC以外的其余各棱长均为2.(1)作平面CDE与平面ABE的交线l,并写出作法及理由;(2)求证:平面BDE⊥平面ACE;(3)若多面体的体积为2,求直线DE与平面BCE所成角的正弦值.(1)解过点E作AB(或CD)的平行线,即为所求直线l.∵AC和BD交于一点,∴A,B,C,D四点共面.又∵四边形ABCD边长均相等,∴四边形ABCD为菱形,从而AB∥DC.又AB⊄平面CDE,且CD⊂平面CDE,∴AB∥平面CDE.∵AB⊂平面ABE,且平面ABE∩平面CDE=l,∴AB∥l.(2)证明取AE的中点O,连接OB,OD.∵AB=BE,DA=DE,∴OB⊥AE,OD⊥AE.又OB∩OD=O,∴AE⊥平面OBD,∵BD⊂平面OBD,故AE⊥BD.又四边形ABCD为菱形,∴AC⊥BD.又AE∩AC=A,∴BD⊥平面ACE.又BD⊂平面BDE,∴平面BDE ⊥平面ACE .(3)解由V E -ABCD =2V E -ABD =2V D -ABE =2,即V D -ABE =1.设三棱锥D -ABE 的高为h ,h =1,解得h = 3.又∵DO= 3.∴DO ⊥平面ABE .以点O 为坐标原点,OB ,OE ,OD 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则A (0,-1,0),B (3,0,0),D (0,0,3),E (0,1,0).∴BC →=AD →=(0,1,3),BE →=(-3,1,0).设平面BCE 的一个法向量为n =(x ,y ,z ),+3z =0,-y =0得,平面BCE 的一个法向量为n =(1,3,-1).又DE →=(0,1,-3),于是cos 〈DE →,n 〉=235·2=155.故直线DE 与平面BCE 所成角的正弦值为155.22.(12分)如图,△ABC 的外接圆⊙O 的半径为5,CD ⊥⊙O 所在的平面,BE ∥CD ,CD =4,BC=2,且BE =1,tan ∠AEB =2 5.(1)求证:平面ADC⊥平面BCDE;(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为27若存在,确定点M的位置,若不存在,请说明理由.(1)证明∵CD⊥平面ABC,BE∥CD,∴BE⊥平面ABC,∴BE⊥AB.∵BE=1,tan∠AEB=25,∴AE=21,从而AB=AE2-BE2=2 5.∵⊙O的半径为5,∴AB是直径,∴AC⊥BC,又∵CD⊥平面ABC,BC⊂平面ABC,∴CD⊥BC,故BC⊥平面ACD.∵BC⊂平面BCDE,∴平面ADC⊥平面BCDE.(2)解方法一假设点M存在,过点M作MN⊥CD于N,连接AN,作MF⊥CB于F,连接AF.∵平面ADC⊥平面BCDE,平面ADC∩平面BCDE=DC,MN⊂平面BCDE,∴MN⊥平面ACD,∴∠MAN为MA与平面ACD所成的角.设MN=x,计算易得,DN=32x,MF=4-32x,故AM=AF2+MF2=AC2+CF2+MF2=sin∠MAN=MNAM==2 7,解得x=-83(舍去),x=43,故MN=23CB,从而满足条件的点M存在,且DM=23DE.方法二以点C为坐标原点,CA,CB,CD所在直线分别为x轴,y轴,z轴,建立如图所示空间直角坐标系,则A (4,0,0),B (0,2,0),D (0,0,4),E (0,2,1),C (0,0,0),则DE →=(0,2,-3).易知平面ACD 的法向量为BC →=(0,-2,0),假设M 点存在,设M (a ,b ,c ),则DM →=(a ,b ,c -4),再设DM →=λDE →,λ∈(0,1],=0,=2λ,-4=-3λ=0,=2λ,=4-3λ,即M (0,2λ,4-3λ),从而AM →=(-4,2λ,4-3λ).设直线AM 与平面ACD 所成的角为θ,则sin θ=|cos 〈AM →,BC →〉|=|2λ×(-2)|216+4λ2+(4-3λ)2=27,解得λ=-43或λ=23,其中λ=-43应舍去,而λ=23∈(0,1],故满足条件的点M 存在,且点M ,43,。
2024届高考数学总复习《立体几何》复习题附答案解析

则 G 是 OF 靠近 O 的三等分点,则 OG ,OP ,
∴PG
,
又 th
t th Mi L
,
∴h t
th
th
.
第1页共3页
2.如图甲,平面四边形 ABCD 中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD =2,现将四边形 ABCD 沿 BD 折起,使得平面 ABD⊥平面 BDC(如图乙),设点 E,F 分别是棱 AC,AD 的中点. (1)求证:DC⊥平面 ABC; (2)求三棱锥 A﹣BEF 的体积.
∴EF∥DC,且 EF DC,
由已知可得∠DBC=30°,求得 EF DC ,BC , 又 DC⊥平面 ABC,∴EF⊥平面 ABC,
t
h
,
∴VA﹣BEF=VF﹣ABE
t th
.
第2页共3页
第3页共3页
【解答】证明:(1)连接 DE,交 BF 于点 O,连接 PO, 由题意知四边形 BEFD 为菱形,故 ED⊥BF, 可得 PD=PE=DE,∴△PDE 是正三角形,则 ED⊥PO, 又 BF∩PO=O,∴ED⊥平面 PBF, 又 ED⊂平面 BEFD,∴平面 PBF⊥平面 BEFD; 解:(2)如图,作 PG⊥BF 于 G,则 PG⊥平面 BEFD, 四面体 PEFD 为正四面体,且棱长为 2,
【解答】证明:(1)图甲中,∵AB=BD 且∠A=45°, ∴∠ADB=45°,∠ABD=90°,即 AB⊥BD. 图乙中,∵平面 ABD⊥平面 BDC,且平面 ABD∩平面 BDC=BD, ∴AB⊥底面 BDC,得 AB⊥CD. 又∠DCB=90°,∴DC⊥BC,且 AB∩BC=B, ∴DC⊥平面 ABC; 解:(2)∵点 E,F 分别是棱 AC,AD 的中点,
2024届高考数学总复习:立体几何及答案解析

1.如图,在矩形 ABCD 中,将△ACD 沿对角线 AC 折起,使点 D 到达点 E 的位置,且 AE ⊥BE. (1)求证:平面 ABE⊥平面 ABC;
(2)若 EB ,三棱锥 B﹣AEC 的体积为 ,求二面角 E﹣AC﹣B 的余弦值.
【解答】解:(1)证明:由翻折可得 AE⊥EC, ∵AE⊥BE,BE∩CE=E,∴AE⊥平面 BEC, 又 BC⊂平面 BEC,∴AE⊥BC, ∵BC⊥AB,AE∩AB=A,∴CB⊥平面 ABE, ∵CB⊂平面 ABC,∴平面 ABE⊥平面 ABC.
∴AQ∥平面 CPB1;
解:(2)如图,过点 A 作 AH⊥BC 于点 H,
∵三棱柱 ABC﹣A1B1C1 为直三棱柱,∴AH⊥平面 CBB1C1,
∵BC=BA ㌳,AC
,
∴կ
կ
,
即 AH կ
㌳
㌳ ㌳,
㌳ 则点 P 到平面 BCB1 的距离为 ㌳ .
又կ
ͳ,CP=PB1=4,∴△CPB1 的面积为 ㌳,
立空间直角坐标系,
∵EO⊥平面 ABC,∴平面 ABC 的一个法向量为 (0,0,1),
在直角三角形 AEB 中,AE⊥BE,EO⊥AB,AE=3,AB=4,EB ,
∴AO h,BO ,EO
,
∴E(0,0, ),A(ꥐ h,0,0),C( ,3,0),
第1页共3页
则 կ (4,3,0),
h
( , , ),
(2)设 BC=a,则 AE=a,∵AE⊥BE,∴S△ABE
,
由(1)知 CB⊥平面 ABE,
∵EB ,三棱锥 B﹣AEC 的体积为 ,
∴ ꥐկ
կꥐ
կ
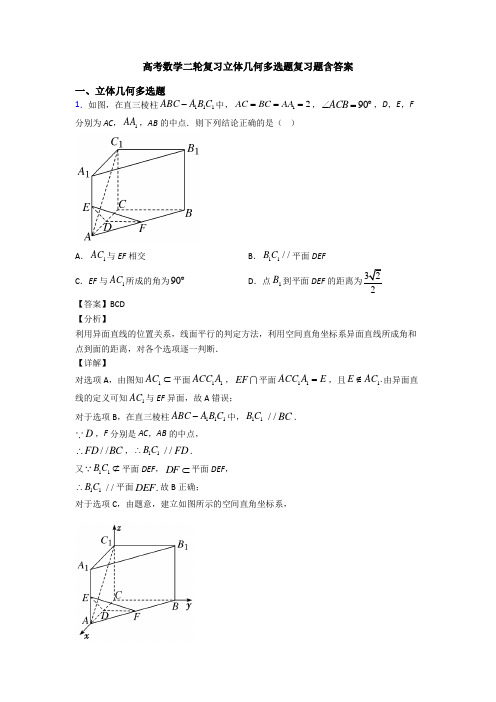
高考数学二轮复习立体几何多选题复习题含答案
高考数学二轮复习立体几何多选题复习题含答案一、立体几何多选题1.如图,在直三棱柱111ABC A B C -中,12AC BC AA ===,90ACB ∠=︒,D ,E ,F分别为AC ,1AA ,AB 的中点.则下列结论正确的是( )A .1AC 与EF 相交B .11//BC 平面DEF C .EF 与1AC 所成的角为90︒D .点1B 到平面DEF 的距离为322【答案】BCD 【分析】利用异面直线的位置关系,线面平行的判定方法,利用空间直角坐标系异面直线所成角和点到面的距离,对各个选项逐一判断. 【详解】对选项A ,由图知1AC ⊂平面11ACC A ,EF 平面11ACC A E =,且1.E AC ∉由异面直线的定义可知1AC 与EF 异面,故A 错误;对于选项B ,在直三棱柱111ABC A B C -中,11B C //BC .D ,F 分别是AC ,AB 的中点, //∴FD BC ,11B C ∴ //FD .又11B C ⊄平面DEF ,DF ⊂平面DEF ,11B C ∴ //平面.DEF 故B 正确;对于选项C ,由题意,建立如图所示的空间直角坐标系,则(0C ,0,0),(2A ,0,0),(0B ,2,0),1(2A ,0,2),1(0B ,2,2),1(0C ,0,2),(1D ,0,0),(2E ,0,1),(1F ,1,0).(1EF ∴=-,1,1)-,1(2AC =-,0,2). 1·2020EF AC =+-=,1EF AC ∴⊥,1EF AC ∴⊥. EF 与1AC 所成的角为90︒,故C 正确;对于选项D ,设向量(n x =,y ,)z 是平面DEF 的一个法向量. (1DE =,0,1),(0DF =,1,0), ∴由n DE n DF ⎧⊥⎨⊥⎩,,,即·0·0n DE n DF ⎧=⎨=⎩,,,得00.x z y +=⎧⎨=⎩,取1x =,则1z =-,(1n ∴=,0,1)-, 设点1B 到平面DEF 的距离为d . 又1(1DB =-,2,2),1·102DB n d n-+∴===, ∴点1B 到平面DEF 的距离为2,故D 正确.故选:BCD 【点睛】本题主要考查异面直线的位置关系,线面平行的判定,异面直线所成角以及点到面的距离,还考查思维能力及综合分析能力,属难题.2.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -所得截面面积为3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.3.如图,在边长为4的正方形ABCD 中,点E 、F 分别在边AB 、BC 上(不含端点)且BE BF =,将AED ,DCF 分别沿DE ,DF 折起,使A 、C 两点重合于点1A ,则下列结论正确的有( ).A .1A D EF ⊥B .当12BE BF BC ==时,三棱锥1A F DE -6π C .当14BE BF BC ==时,三棱锥1A F DE -217 D .当14BE BF BC ==时,点1A 到平面DEF 的距离为177【答案】ACD 【分析】A 选项:证明1A D ⊥面1A EF ,得1A D EF ⊥;B 选项:当122BE BF BC ===时,三棱锥1A EFD -的三条侧棱111,,A D A E A F 两两相互垂直,利用分隔补形法求三棱锥1A EFD -的外接球体积; C 选项:利用等体积法求三棱锥1A EFD -的体积; D 选项:利用等体积法求出点1A 到平面DEF 的距离. 【详解】 A 选项:正方形ABCD,AD AE DC FC ∴⊥⊥由折叠的性质可知:1111,A D A E A D A F ⊥⊥ 又111A E A F A ⋂=1A D ∴⊥面1A EF又EF ⊂面1A EF ,1A D EF ∴⊥;故A 正确.B 选项:当122BE BF BC ===时,112,A E A F EF ===在1A EF 中,22211A E A F EF +=,则11A E A F ⊥由A 选项可知,1111,A D A E A D A F ⊥⊥∴三棱锥1A EFD -的三条侧棱111,,A D A E A F 两两相互垂直,把三棱锥1A EFD -=, 三棱锥1A EFD -,体积为334433R ππ==,故B 错误C 选项:当114BE BF BC ===时,113,A E A F EF ===在1A EF中,22222211111338cos 22339A E A F EF EA F A E A F+-+-∠===⋅⨯⨯,1sin 9EA F ∠=则111111sin 332292A EFSA E A F EA F =⋅⋅∠=⨯⨯⨯=111111433A EFD D A EF A EF V V SA D --∴==⋅⋅==故C 正确;D 选项:设点1A 到平面EFD 的距离为h ,则在EFD △中,2222225524cos 225525DE DF EF EDF DE DF +-+-∠===⋅⨯⨯, 7sin 25EDF ∠=则1177sin 5522252EFDSDE DF EDF =⋅⋅∠=⨯⨯⨯=11173323A EFD DEFV Sh h -∴=⋅⋅=⨯⨯=即7h =故D 正确; 故选:ACD 【点睛】方法点睛:求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.4.如图,正方体1111ABCD A B C D -的棱长为3,点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动,且满足直线//BM 平面1D EF ,则( )A .过1D ,E ,F 的平面截正方体所得截面为等腰梯形B .三棱锥1D EFM -的体积为定值C .动点M 10D .过B ,E ,M 的平面截正方体所得截面面积的最小值为10【答案】BCD 【分析】由题做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,进而计算即可排除A 选项;根据//BM平面1D EF ,由等体积转化法得1111D EFM M D EF B D EF D BEFV V V V ----===即可得B 选项正确;取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知M 的轨迹为线段HI 10,故C 选项正确;过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,易知过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而得当H 位于点I 时,截面面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅= 【详解】解:对于A 选项,如图,取BF 中点G ,连接1A G ,由点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=,故四边形11A D EG 为平行四边形,故11//AGD E ,由于在11A B G △,F 为1B G 中点,当N 为11A B 中点时,有11////NF A G D E ,故过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,此时22133532D N ⎛⎫=+= ⎪⎝⎭,223110EF =+=,故梯形1D EFN 不是等腰梯形,故A 选项错误;对于B 选项,三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积,由于//BM平面1D EF ,故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积,三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积,而三棱锥1D BEF -的体积为定值,故B 选项正确; 对于C 选项,取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知1////HB AG NF ,1//BI D F ,由于1,HI BI I NFD F F ==,故平面//BHI 平面1D EF ,故M 的轨迹为线段HI ,其长度为10,故C 选项正确;对于D 选项,过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,则过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,易知当H 位于点I 时,平行四边形BPOE 边BP 最小,且为AB ,此时截面平行四边形BPOE 的面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅=,故D 选项正确; 故选:BCD【点睛】本题解题的关键在于根据题意,依次做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而讨论AD选项,通过//BM平面1D EF ,并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确,通过构造面面平行得M 的轨迹为线段HI ,进而讨论C 选项,考查回归转化思想和空间思维能力,是中档题.5.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( ) A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE 所成的角的正切为155【答案】ABD 【分析】对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tan DF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且ECED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,222222113122152tan 511122DE CE DFDBF BFBC CE ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∠=====⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,所以DB 与平面ABCE 所成的角的正切为15,故D 正确; 故选:ABD 【点睛】关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.6.如图,点E 为正方形ABCD 边CD 上异于点C ,D 的动点,将ADE 沿AE 翻折成SAE △,在翻折过程中,下列说法正确的是( )A .存在点E 和某一翻折位置,使得SB SE ⊥ B .存在点E 和某一翻折位置,使得//AE 平面SBCC .存在点E 和某一翻折位置,使得直线SB 与平面ABC 所成的角为45°D .存在点E 和某一翻折位置,使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项:当SE CE ⊥时,⊥SE SB ,A 正确,//AE 平面SBC ,则//AE CB ,这与已知矛盾,故B 错误,取二面角D AE B --的平面角为α,取4=AD ,计算得到2cos 3α=,C 正确,取二面角D AE B --的平面角为60︒,计算得到5tan θ=,故D 正确,得到答案. 【详解】当SE CE ⊥时,SE AB ⊥,SE SA ⊥,故SE ⊥平面SAB ,故⊥SE SB ,A 正确; 若//AE 平面SBC ,因AE ⊂平面ABC ,平面ABC 平面SBC BC =,则//AE CB ,这与已知矛盾,故B 错误;如图所示:DF AE ⊥交BC 于F ,交AE 于G ,S 在平面ABCE 的投影O 在GF 上, 连接BO ,故SBO ∠为直线SB 与平面ABC 所成的角,取二面角D AE B --的平面角为α,取4=AD ,3DE =,故5AE DF ==,1CE BF ==,125DG =,12cos 5OG α=,故只需满足12sin 5SO OB α==, 在OFB △中,根据余弦定理:2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得2cos 3α=,故C 正确; 过O 作OMAB ⊥交AB 于M ,则SMO ∠为二面角S AB C --的平面角,取二面角D AE B --的平面角为60︒,故只需满足22DG GO OM ==,设OAG OAM θ∠=∠=,84ππθ<<,则22DAG πθ∠=-,tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭,化简得到2tan tan 21θθ=,解得5tan θ=,验证满足,故D 正确; 故选:ACD .【点睛】本题考查了线线垂直,线面平行,线面夹角,二面角,意在考查学生的计算能力,推断能力和空间想象能力.7.(多选题)在四面体P ABC -中,以上说法正确的有( )A .若1233AD AC AB =+,则可知3BC BD = B .若Q 为△ABC 的重心,则111333PQ PA PB PC =++C .若0PA BC =,0PC AB =,则0PB AC =D .若四面体P ABC -各棱长都为2,M N ,分别为,PA BC 的中点,则1MN = 【答案】ABC 【分析】作出四面体P ABC -直观图,在每个三角形中利用向量的线性运算可得. 【详解】对于A ,1233AD AC AB =+,32AD AC AB ∴=+,22AD AB AC AD ∴-=- , 2BD DC ∴=,3BD BD DC BC ∴=+=即3BD BC ∴=,故A 正确;对于B ,Q 为△ABC 的重心,则0QA QB QC ++=,33PQ QA QB QC PQ ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++=即111333PQ PA PB PC ∴=++,故B 正确;对于C ,若0PA BC =,0PC AB =,则0PA BC PC AB +=,()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+= 0CA BC PC AC ∴+=,0AC CB PC AC ∴+=()0AC PC CB ∴+=,0AC PB ∴=,故C 正确;对于D ,111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+22211122222222222222222=++-⨯⨯⨯-⨯⨯⨯+⨯⨯⨯=2MN ∴=,故D 错误.故选:ABC 【点睛】用已知向量表示某一向量的三个关键点(1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键. (2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.8.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且2EF =.则下列结论正确的是( )A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图,研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO =11221334212A BEF BEF V S AO -∆∴=⨯=⨯⨯=A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB , 由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中,221cos 45222FT EF =⨯=⨯=12HG FT ∴== 选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=22AR = 由余弦定理得13cos 6AD R ∠= 故选:AC 【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.9.已知棱长为1的正方体1111ABCD A B C D -,过对角线1BD 作平面α交棱1AA 于点E ,交棱1CC 于点F ,以下结论正确的是( ) A .四边形1BFD E 不一定是平行四边形 B .平面α分正方体所得两部分的体积相等 C .平面α与平面1DBB 不可能垂直 D .四边形1BFD E 面积的最大值为2 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E 、F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积最大,且最大值为2,可判断D 正确. 【详解】 如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误; 对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥, 又1BD BB B ⋂=,所以AC ⊥平面1BB D , 当E 、F 分别为棱11,AA CC 的中点时, 有//AC EF ,则EF ⊥平面1BB D , 又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD , 当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值, 此时1212S D E BE =⋅=,故D 正确; 故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.10.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点P 在线段B 1C 上运动,则( )A .直线BD 1⊥平面A 1C 1DB .三棱锥P ﹣A 1C 1D 的体积为定值C .异面直线AP 与A 1D 所成角的取值范用是[45°,90°] D .直线C 1P 与平面A 1C 1D 6【答案】ABD 【分析】在A 中,推导出A 1C 1⊥BD 1,DC 1⊥BD 1,从而直线BD 1⊥平面A 1C 1D ;在B 中,由B 1C ∥平面 A 1C 1D ,得到P 到平面A 1C 1D 的距离为定值,再由△A 1C 1D 的面积是定值,从而三棱锥P ﹣A 1C 1D 的体积为定值;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°];在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为63. 【详解】解:在A 中,∵A 1C 1⊥B 1D 1,A 1C 1⊥BB 1,B 1D 1∩BB 1=B 1, ∴A 1C 1⊥平面BB 1D 1,∴A 1C 1⊥BD 1,同理,DC 1⊥BD 1, ∵A 1C 1∩DC 1=C 1,∴直线BD 1⊥平面A 1C 1D ,故A 正确; 在B 中,∵A 1D ∥B 1C ,A 1D ⊂平面A 1C 1D ,B 1C ⊄平面A 1C 1D , ∴B 1C ∥平面 A 1C 1D ,∵点P 在线段B 1C 上运动,∴P 到平面A 1C 1D 的距离为定值,又△A 1C 1D 的面积是定值,∴三棱锥P ﹣A 1C 1D 的体积为定值,故B 正确; 在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°],故C 错误;在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1,P (a ,1,a ),则D (0,0,0),A 1(1,0,1),C 1(0,1,1),1DA =(1,0,1),1DC =(0,1,1),1C P =(a ,0,a ﹣1), 设平面A 1C 1D 的法向量(),,n x y z =,则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x =1,得1,1,1n,∴直线C 1P 与平面A 1C 1D 所成角的正弦值为:11||||||C P n C P n ⋅⋅=22(1)3a a +-⋅=21132()22a ⋅-+, ∴当a =12时,直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为63,故D 正确. 故选:ABD .【点睛】求直线与平面所成的角的一般步骤:(1)、①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解; (2)、用空间向量坐标公式求解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
