初中几何八大经典模型大盘点
初中几何九大模型汇总

初中几何九大模型汇总
初中几何常见模型解析
黄金屋教育中考研究中心出品
1.打造精细课堂实现个性教育
在初中几何中,有一些常见的几何模型,掌握它们的特点和解题方法对于学生来说非常重要。
2.手拉手模型-全等
1)等边三角形
条件:三角形均为等边三角形,且对应边相等,角度相等。
结论:三角形全等。
2)等腰直角三角形
条件:三角形均为等腰直角三角形,且对应边相等,角度相等。
结论:三角形全等。
3)任意等腰三角形
条件:三角形均为等腰三角形,且对应边相等,角度相等。
结论:三角形全等。
3.手拉手模型-相似
1)一般情况
条件:两个三角形对应角度相等,且对应边成比例。
结论:两个三角形相似。
2)特殊情况
条件:两个三角形对应角度相等,且对应边成比例,其中一条边是公共边。
结论:两个三角形相似,且公共边上的线段成比例。
4.对角互补模型
1)全等型-90°
条件:四边形对角线互相垂直,其中一个角度为90度。
结论:对角线上的线段互补。
2)全等型-120°
条件:四边形对角线互相垂直,其中一个角度为120度。
结论:对角线上的线段互补。
初中8大几何模型——一线三等角模型、三垂直模型

初中8大几何模型——一线三等角模型、三垂直模型
初中8大几何模型——一线三等角模型、三垂直模型,九年级同学必须掌握的几何技巧,中考满分秘籍精选内容!
目录
“一线三等角”,一条直线上有三个相等的角,一般就会存在相似三角形,当对应边也相等时,就会有全等三角形,即:“一线三等角,全等相似两边找”。
学会用“一线三等角”基本模型,解决全等三角形、相似三角形中的相关问题。
难点在于“一线三等角”基本模型的提炼、构造和运用。
三垂直模型的构造方法:
一般情况下,碰到斜着放置的直角,要想到在直角顶点所在的直线上构造三垂直模型,可能是全等型,也可能是相似型。
666咨询资料。
初中化学几何模型大全(精心整理)

初中化学几何模型大全(精心整理)初中化学几何模型大全(精心整理)
初中化学中的几何模型是帮助我们理解分子结构和化学反应的重要工具。
下面是一些常见的初中化学几何模型:
1. 线性分子模型
线性分子模型是由两个原子通过共价键相连接的分子。
这些原子在同一直线上排列,形成一条直线。
2. 非线性分子模型
非线性分子模型是由三个或三个以上的原子通过共价键相连接的分子。
这些原子在空间中呈现出曲线或多边形的形状。
3. 三角形平面分子模型
三角形平面分子模型是由三个原子通过共价键相连接的分子。
这些原子在同一平面上排列,形成一个三角形。
4. 四面体分子模型
四面体分子模型是由四个原子通过共价键相连接的分子。
这些
原子在空间中排列成一个四面体的形状。
5. 正四面体分子模型
正四面体分子模型是由四个原子通过共价键相连接的分子。
这
些原子在空间中排列成一个具有四个相等边长和四个相等面角的正
四面体。
6. 八面体分子模型
八面体分子模型是由六个原子通过共价键相连接的分子。
这些
原子在空间中排列成一个八面体的形状。
7. 正八面体分子模型
正八面体分子模型是由六个原子通过共价键相连接的分子。
这
些原子在空间中排列成一个具有六个相等边长和六个相等面角的正
八面体。
这些是初中化学中常见的几何模型。
通过了解和学习这些模型,我们可以更好地理解分子及其属性,以及化学反应的机制。
初中数学几何模型总结

初中数学几何模型总结几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
初中几何46种模型大全

初中几何46种模型大全篇一:初中几何46种模型大全引言几何是初中数学的重要分支,其知识点涵盖了平面几何、立体几何、向量等多个方面。
在学习几何时,掌握各种几何模型是非常重要的,这些模型可以帮助我们理解和解决几何问题,提高解题能力。
本文将介绍初中几何中的46种常见的模型,包括它们的名称、定义、性质和应用。
正文1. 正方形模型正方形模型是几何中最基本的模型之一,它是一种边长相等的矩形。
正方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
正方形模型的性质有:- 正方形的四条边相等;- 正方形的对角线相等;- 正方形的面积等于其边长的平方。
2. 长方形模型长方形模型是有两个相等的长和两个不相等的宽的英雄。
长方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和小于斜边的平方。
长方形模型的性质有:- 长方形的两条对角线相等;- 长方形的宽比长大,长比宽大;- 长方形的长和宽相等。
3. 平行线模型平行线模型是相互平行的直线。
平行线模型的定义如下:- 两直线平行,当且仅当它们的对应角相等且且它们的方向相同。
平行线模型的性质有:- 平行线之间有且仅有一个交点;- 平行线上的点的横坐标相等;- 平行线的方向相同。
4. 菱形模型菱形模型是具有四个相等的直角边的矩形。
菱形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方,且任意两条边的长度小于第三条边的长度。
菱形模型的性质有:- 菱形的四条边相等;- 菱形的对角线相等;- 菱形的面积等于其四条边长度的平方和。
5. 等腰三角形模型等腰三角形模型是有一个相等的腰部的两个三角形。
等腰三角形模型的定义如下:- 在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
等腰三角形模型的性质有:- 等腰三角形的两条直角边相等;- 等腰三角形的底角相等;- 等腰三角形的顶角平分线相等。
6. 等边三角形模型等边三角形模型是具有三个相等的边长的三角形。
(完整版)初中数学——最全:初中数学几何模型.docx
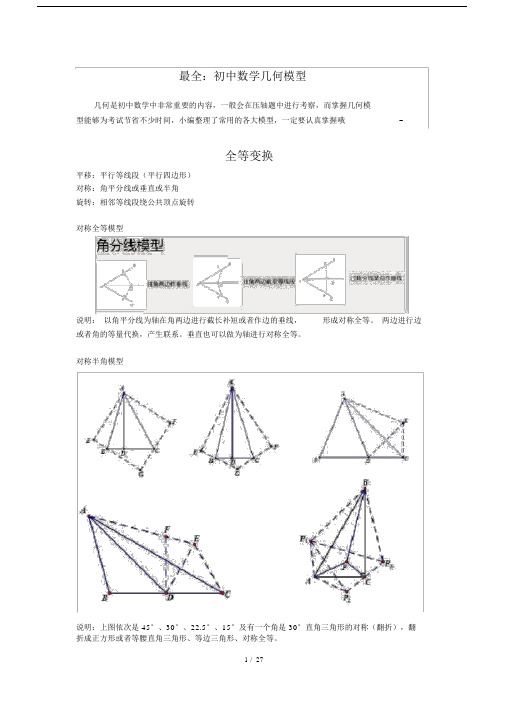
最全:初中数学几何模型几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,小编整理了常用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是 45°、30°、22.5°、15°及有一个角是 30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2 角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇 60 度旋 60 度,造等边三角形;遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等;遇中点旋180 度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
初中所有几何模型

初中所有几何模型
初中几何中常见的模型包括但不限于以下几种:
1. 手拉手模型:这种模型通常涉及到两个三角形,其中一个三角形的顶点与另一个三角形的对应顶点相连。
根据角度和边的关系,可以证明这两个三角形是相似的或全等的。
2. 倍长中线模型:如果一个中线长度超过另一边的一半,则可以通过倍长中线来构造新的三角形,从而利用中线性质进行证明。
3. 平行线模型:通过平行线的性质,可以证明一些角的关系,或者利用平行线的传递性来证明一些线段的比例关系。
4. 角平分线模型:利用角平分线的性质,可以证明一些角或者线段的比例关系。
5. 直角三角形模型:通过直角三角形的性质,可以证明一些角或者线段的关系。
6. 对角线模型:利用对角线的性质,可以证明一些线段的比例关系,或者通过构造新的三角形来证明一些结论。
7. 旋转模型:通过旋转图形,可以证明一些结论或者找到一些新的等量关系。
8. 相似三角形模型:通过相似三角形的性质,可以证明一些角或者线段的比例关系。
9. 特殊四边形模型:对于一些特殊的四边形,如平行四边形、矩形、菱形等,可以利用它们的性质来证明一些结论。
以上是一些常见的初中几何模型,它们都是基于几何的基本性质和定理构建的。
掌握这些模型可以帮助学生在解决几何问题时更加高效和准确。
初中数学几何模型大全

几何模型大全---第一部分一、全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转模型一:对称全等模型以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
模型二:对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
模型三:旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题(一)旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
(二)自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称(三)共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
(三)中点旋转模型说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何八大经典模型大盘点
1.初中几何八大经典模型(一)中点模型
2.初中几何八大经典模型(二)角分线模型
3.初中几何八大经典模型(三)相似基本模型
4.初中几何八大经典模型(四)一线三等角模型
5.初中几何八大经典模型(五)三垂直模型
6.初中几何八大经典模型(六)手拉手模型
7.初中几何八大经典模型(七)旋转模型
8.初中几何八大经典模型(八)“将军饮马”模型
由于内容比较多,一次无法完全发完,我从每个章节选取3个图片给大家做一个简单的分享,需要打印完整版内容看到最后提示吧!。
