SPSS 时间系列分析
spss时间序列分析案例
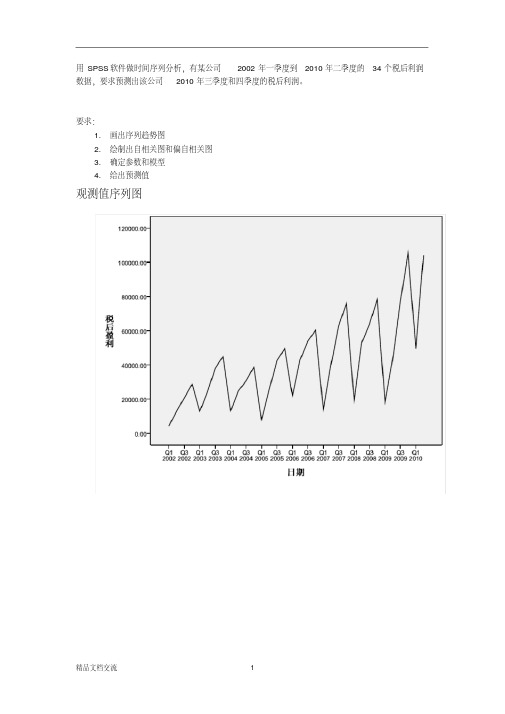
用SPSS软件做时间序列分析，有某公司2002年一季度到2010年二季度的34个税后利润数据，要求预测出该公司2010年三季度和四季度的税后利润。
要求：1.画出序列趋势图2.绘制出自相关图和偏自相关图3.确定参数和模型4.给出预测值观测值序列图2税后盈利自相关图序列:税后盈利滞后自相关标准误差aBox-Ljung 统计量值df Sig.b1 .306 .164 3.482 1 .0622 .198 .162 4.987 2 .0833 .185 .159 6.340 3 .0964 .542 .157 18.342 4 .0015 .084 .154 18.641 5 .0026 .067 .151 18.836 6 .0047 .094 .149 19.239 7 .0078 .458 .146 29.093 8 .0009 .041 .143 29.176 9 .00110 .016 .140 29.189 10 .00111 .012 .137 29.197 11 .00212 .236 .134 32.308 12 .00113 -.092 .131 32.806 13 .00214 -.094 .128 33.345 14 .00315 -.079 .125 33.745 15 .00416 .106 .121 34.510 16 .005a. 假定的基础过程是独立性（白噪音）。
b. 基于渐近卡方近似。
偏自相关序列:税后盈利滞后偏自相关标准误差1 .306 .1712 .115 .1713 .107 .1714 .503 .1715 -.279 .1716 -.010 .1717 .046 .1718 .268 .1719 -.130 .17110 -.054 .17111 -.053 .17112 -.081 .17113 -.040 .17114 -.051 .17115 -.027 .17116 -.062 .1713、确定参数和模型时间序列建模程序模型描述模型类型模型 ID 税后利润模型_1 ARIMA(0,1,0)(0,1,0) 模型摘要模型统计量模型预测变量数模型拟合统计量Ljung-Box Q(18)离群值数平稳的 R 方统计量DF Sig.税后利润-模型_1 0 5.502E-17 17.688 18 .476 04、给出预测值2010年第三季度139621.02万元2010年第四季度170144.55万元剔除季节成分后，平滑处理及剔除循环波动因素的序列图SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列自相关图序列:SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列滞后自相关标准误差aBox-Ljung 统计量值df Sig.b1 .728 .164 19.633 1 .0002 .450 .162 27.383 2 .0003 .310 .159 31.169 3 .0004 .207 .157 32.911 4 .0005 .219 .154 34.941 5 .0006 .241 .151 37.484 6 .0007 .243 .149 40.168 7 .0008 .226 .146 42.571 8 .0009 .183 .143 44.213 9 .00010 .162 .140 45.551 10 .00011 .093 .137 46.012 11 .00012 .006 .134 46.015 12 .00013 -.047 .131 46.145 13 .00014 -.021 .128 46.172 14 .00015 -.022 .125 46.204 15 .00016 -.036 .121 46.294 16 .000a. 假定的基础过程是独立性（白噪音）。
实验·6-时间序列分析的spss应用
实验·6-时间序列分析的spss 应用实验6 时间序列分析的spss应用6.1 实验目的学会运用SPSS统计软件创建时间数列，熟练掌握长期趋势线性模型拟合和季节变动测定的SPSS方法与技能。
6.2 相关知识（略）6.3 实验内容6.3.1 用SPSS统计软件创建时间序列的创建6.3.2用SPSS统计软件处理长期趋势线性模型的拟合（最小二乘法、指数平滑法）及预测。
6.3.3掌握测定季节变动规律的SPSS测定方法。
6.4实验要求6.4.1准备实验数据6.4.2用SPSS统计软件创建彩电出口数量的时间序列6.4.3用最小二乘法测定长期趋势，拟合线性趋势方程，并进行趋势预测。
6.4.4测定彩电出口数量的季节变动规律。
6.4.5用指数平滑法预测2014和2015年的彩电出口数量。
6.5 实验步骤6.5.1 实验数据为了研究某国彩电出口的情况，某研究机构收集了从2003-2013年某国彩电出口的月度数据，如表6-1所示。
表6-1 我国 2003-2013年的我国彩电出口的月度数据（单位：万台）1月2月3月4月5月6月7月8月9月10月11月12月2003年12.53 13.73 24.45 28.75 32.45 31.11 25.94 32.98 43.49 42.94 63.29 77.28 2004年30.01 39.63 29.77 42.74 32.25 31.94 32.27 32.59 32.92 30.98 47.44 52.82 2005年24.08 16.42 31.24 29.33 31.88 30.09 28.08 32.99 44.99 47.57 50.36 75.19 2006年39.02 25.81 43.38 37.34 39.22 39.87 51.10 50.99 55.16 62.78 57.75 72.20图6-3 定义日期变量后的结果（部分图）３．创建时间序列（用移动平均法）选择“转换-创建时间序列”，打开“创建时间序列”对话框，将“出口量”变量移入右侧的“变量-新名称”框中，在“函数”下拉框中选择“中心移动平均”，在“跨度”中输入5表示五项移动平均，然后点击“更改”按钮，设置情况如下图6-4所示：图6-4 创建时间序列对话框设置完毕，单击“确定”按钮，则会在原数据文件中增加一个变量，名称为“出口量_1”的五项移动平均序列。
第十四章 SPSS的时间序列分析
第十四章SPSS 的时间序列分析14.9 季节调整法一、时间序列的趋势分解：长期趋势(Trend ): 现象在较长时期内持续发展变化的一种趋向或状态由影响时间序列的基本因素作用形成是时间序列中最基本的构成要素可分为上升趋势、下降趋势、水平趋势或分为：线性趋势和非线性趋势。
周期变动(Periodicity) ：这种因素的影响使现象呈现出以若干年为一周期、涨落相间、扩张与紧缩、波峰与波谷相交替的波动。
不同于长期趋势T 表现为单一方向的持续变动，P 表现为波浪式的涨落交替的变动。
季节变动(Seasonal Fluctuation ) ：是一种使现象以一定时期（如一年、一月、一周等）为一周期呈现较有规律的上升、下降交替运动的影响因素通常表现为现象在一年内随着自然季节的更替而发生的较有规律的增减变化，有旺季和淡季之分是一种周期性的变化周期长度小于一年形成原因：有自然因素，也有人为因素不规则变动(Irregular Variations) ：包括随机变动和突然变动。
随机变动――现象受到各种偶然因素影响而呈现出方向不定、时起时伏、时大时小的变动。
突然变动――战争、自然灾害或其它社会因素等意外事件引起的变动。
影响作用无法相互抵消，影响幅度很大。
一般只讨论有随机波动而不含突然异常变动的情况。
二、时间序列的分解模型Y= T×S×P×I 在加法模型中各种影响因素是相互独立的，均为与Y 同计量单位的绝对量。
季节变动和循环变动的数值在各自的周期时间范围内总和为零；不规则变动的数值从长时间来看，其总和也应为零。
加法模型中，各因素的分解是根据减法进行（如：Y。
【IBM-SPSS课件】时间序列分析
▪ 圖23-10所示給出了模型擬合的八個擬合優度指 標，以及這些指標的均值、最小值、最大值及 百分位數。其中平穩的R方值為0.418。
▪ 圖23-11所示為模型的擬合統計量和Ljung-BoxQ 統計量。平穩的R方值為0.418 。Ljung-BoxQ統 計量值為 18.537，顯著水準為0.293。
▪ 例23.2：利用1992年初～2002年底共11年彩電 出口量（單位：“臺”）的月度數據，見例23.2
sav.
▪ 操作步驟如下：
▪ （1）單擊“數據”|“定義日期”命令，彈出圖 23-2所示的對話框，打開“定義日期”，在“ 個案為”選項中選擇“年份、月份”，然後在 “第一個個案為”中的“年”和“月份”輸入 數據開始的具體的年份1992和月份1，單擊“確 定”按鈕，完成時間變數的定義。
▪ 時間序列預處理的主要方法：
▪ 對缺失數據的處理和對數據的變換處理。主要包括 序列的平穩化處理和序列的平滑處理等。SPSS提 供了8種平穩處理的方法：差分、季節差分、中心 移動平均、先前移動平均、運行中位數、累計求和 、滯後、提前。
▪ 例23.1：描述了中國某城市女士服裝從1993年到 2002十年的出口總額及外匯儲備情況，資料庫見 例23.1.sav。研究如何創建時間序列數據。
▪ 1．操作步驟
▪ （1）單擊“數據”|“定義日期”命令，彈出圖 23-2所示的對話框，在“個案為”選項中選擇 “年份、月份”，然後在“第一個個案為”中 的“年”和“月份”輸入數據開始的具體的年 份1993和月份1，單擊“確定”，完成時間變數 的定義。
▪ （2）單擊“轉換”|“創建時間序列”命令，彈 出圖23-3所示的對話框，將sum變數選入“變數 -新名稱”列表中。在函數子菜單中選擇“季節 差分”選項。
实验八-spss11中的时间序列分析
实验八spss11中的时间序列分析一、实验目的了解spss11中时间序列分析的简单方法二、实验原理介绍1.SPSS中时间序列分析简要介绍依时间顺序排列起来的一系列观测值称为时间序列，跟大部分的统计不同，这类资料的先后顺序是不能忽视的，更关键的是观测值之间不独立。
因此，这类数据不能用普通的统计方法解决。
时间序列分析（Time series）是专门用于分析这种时间序列资料的统计模型。
它考虑的不是变量之间的因果关系，而是重点考察变量在时间方面的发展变化规律，并为之建立数学模型。
时间序列分析的方法可以分为两大类：Time domain和Frequency domain。
前者将时间序列看成是过去一些点的函数，或者认为序列具有时间系统变化的趋势，它可以用不多的参数来加以描述，或者说可以通过差分、周期等还原成随机序列。
后者则认为时间序列是由数个正弦波成分叠加而成，当序列的确来自一些周期函数集合时，该方法特别有用。
不同的专业领域习惯用不同的方法：经济学习惯用Time domain，而电力工程专家则对Frequency domain更感兴趣。
下面讲述的都是Time domain由于时间序列模型的复杂性，它在spss中横跨了数据整理、统计分析和绘图三大部分，具体来说是：✧预处理模块：包括用于填充序列缺失值的Transform | replace Missing Values过程，建立时间变量的Data | Define dates过程和将序列平稳化的Transform | Create TimeSeries过程。
✧图形化观察/分析：时间序列在分析中高度依赖图形。
Spss为其提供了特有的观察工具：序列图（Sequence Chart）、自相关/偏自相关图（Autocorrelation Function，ACF & Autocorrelation Function，PACF）、交叉相关图（Crosscorrelation Function，CCF）、周期图（Periodogram）和谱密度图（Spectral Chart）。
spss时间序列模型要点
《统计软件实验报告》SPSS软件的上机实践应用时间序列分析数学与统计学学院一、实验内容：时间序列是指一个依时间顺序做成的观察资料的集合。
时间序列分析过程中最常用的方法是：指数平滑、自回归、综合移动平均及季节分解。
本次实验研究就业理论中的就业人口总量问题。
但人口经济的理论和实践表明，就业总量往往受到许多因素的制约，这些因素之间有着错综复杂的联系，因此，运用结构性的因果模型分析和预测就业总量往往是比较困难的。
时间序列分析中的自回归求积分移动平均法 (ARIMA )则是一个较好的选择。
对于时间序列的短期预测来说，随机时序ARIMA 是一种精度较高的模型。
我们已辽宁省历年( 1969-2005)从业人员人数为数据基础建立一个就业总量的预测时间序列模型，通过SPSS建立模型并用此模型来预测就业总量的未来发展趋势。
二、实验目的：1.准确理解时间序列分析的方法原理2.学会实用SPSS建立时间序列变量3.学会使用SPSS绘制时间序列图以反应时间序列的直观特征。
4.掌握时间序列模型的平稳化方法。
5.掌握时间序列模型的定阶方法。
6.学会使用SPSS建立时间序列模型与短期预测。
7.培养运用时间序列分析方法解决身边实际问题的能力。
三、实验分析：总体分析：先对数据进行必要的预处理和观察，直到它变成稳态后再用SPSS对数据进行分析。
数据的预处理阶段，将它分为三个步骤：首先，对有缺失值的数据进行修补，其次将数据资料定义为相应的时间序列，最后对时间序列数据的平稳性进行计算观察。
数据分析和建模阶段：根据时间序列的特征和分析的要求，选择恰当的模型进行数据建模和分析。
四、实验步骤：SPSS的数据准备包括数据文件的建立、时间定义和数据期间的指定。
SPSS的时间定义功能用来将数据编辑窗口中的一个或多个变量指定为时间序列变量，并给它们赋予相应的时间标志，具体操作步骤是:1.选择菜单：Date f Define Dates出现窗口:单击【ok（确认）】按钮，此时完成时间的定义，SPSS将在当前数据编辑窗口中自动生成标志时间的变量。
基于SPSS的时间系列预测分析
福建农林渔牧业总产值的分析与预测图2-1 ARMA模型建模步骤3数据的采集、整理和分析3.1 数据的采集本文选取1978 年—2007 年福建农业经济产值时间序列数据，资料如下表3-1 所示：表3-1 福建省1978年—2007 农业经济产值时间序列数据(单位：亿)年份农业产值年份农业产值年份农业产值1978 36.33 1988 182.00 1998 973.371979 43.11 1989 209.92 1999 1010.821980 45.49 1990 227.12 2000 1037.271981 56.11 1991 253.51 2001 1061.611982 63.73 1992 295.24 2002 1125.291983 68.08 1993 386.34 2003 1170.541984 80.66 1994 574.05 2004 1315.101985 99.05 1995 738.63 2005 1373.011986 107.07 1996 850.67 2006 1449.781987 132.97 1997 925.56 2007 1692.16数据来源：福建经济与社会统计年鉴3.2 数据的分析处理利用17.0SPSS软件绘制原始数据的时间序列图，如图3-1所示：图3-1 原始数据时间序列图从图3-1可以看出福建省农林渔业总产值呈增长趋势，特别是在1993年以后，呈现出强劲的增长势头。
1992—2007年福建农林渔牧业总产值平均每年增长84.46亿元，平均年增长率为29.28%，呈现加快增长趋势。
从整个时间来看，福建农林渔牧业总产值时间序列呈现出指数增长的趋势，并且具有很强的非平稳性。
3.3 对数据进行零均值化和平稳化处理对含有指数趋势的时间序列，通常可以通过取对数将指数趋势转化为线性趋势，然后再对其进行差分来消除线性趋势[4]。
绘制取对数后的时间序列图3-2所示：图3-2：取对数后的时间序列图取对数后的序列图显示出了线性趋势，对该序列进行取差分运算，先进行一阶差分，绘制一阶差分后的时间序列图，如图3-3所示：图3-3 一阶差分时间序列从图3-3可以看到，一阶差分后，数据图前期波动较大，后期波动较小，且具有一定的非平稳性。
【生物数学】时间序列分析及SPSS实现
一、横截面数据与时间序列数据
• 而时间序列的最大特点是观测值并不独立。时间 序列的一个目的是用变量过去的观测值来预测同 一变量的未来值。
• 即时间序列的因变量为变量未来的可能值，而用 来预测的自变量中就包含该变量的一系列历史观 测值。
• 当然时间序列的自变量也可能包含随着时间度量 的独立变量。
例1 某企业从1990年1月到2002年12月到销售数据 （单位：百万元）。该数据共有按时间顺序的月销售 记录156个，数据如下(tssales.sav)。
SPSS操作：时间序列数据绘图
• 早期的SPSS版本，绘制时间序列图可以选择“Graphs→Sequence()”， 对本例选择sales为变量，months为时间轴标签即可。
• 对于SPSS较新的版本，例如SPSS23.0，要选择“分析→时间序列预测→ 序列图”，然后选择sales为变量，months为时间轴标签即可。
SPSS操作：时间序列附加数据的产生
• 当然，根据数据记录的背景不同和不同的需要，我们 也可以选择“Days”、“Weeks” 等其他形式的时间变 量。
• 作为时间序列数据的一个基本要求，其数据都是等间 隔记录的，比如每天或每月记录一个数据。
• 在金融时间序列(比如股票价格)，每周的记录时间只 有5天(周一至周五)，此时我们也把它当成是等间隔 记录的，此时记录的时间间隔是“每个工作日”。
• Yt = aXt+a(1-a)Xt -1+a(1-a)2Xt -2+ … +a(1-a)t-1X1 (3) • 其中0<a<1为权重指数。a 越大，表示在加权时给予 当前观测值的权重越大，相应地，给予过去观测值的 权重就越小。
• 这里的系数为几何级数。因此称之为“几何平滑”比 使人不解的“指数平滑”似乎更有道理。