spss(时间序列分析)精讲
时间序列分析教案

时间序列分析教案
ARIMA模型基础:平稳性和可逆性问题
v ARMA(p,q)模型有意义则要求时间序列满足平稳性和可逆
性的条件.
v 这意味着序列均值不随着时间增加或减少,序列的方差不随时
间变化等。
v 一个实际的时间序列是否满足这些条件是无法在数学上验证的
,但模型可以近似地从后面要介绍的时间序列的自相关函数和
•注:spss中ARIMA 建模方法会自动进行差分和平滑处理,但不处理异常值。
PPT文档演模板
时间序列分析教案
时间序列模型: SARIMA 模型
v 在对含有季节、趋势和循环等成分的时间序列进行ARIMA模型 的拟合研究和预测时,模型需要增加4个参数,增加后可记为 ARIMA(p,d,q)(P,D,Q)s。(在有已知的固定周期s时,如果 是每年的月数据则s=12,其它周期依此类推,如每月的周数据 s=4等)
v 如果不仅满足于分解现有的时间序列,想要对未来进行预测,就 需要建立模型。这里先介绍比较简单的指数平滑(exponential smoothing)。
v 指数平滑只能用于纯粹时间序列的情况,而不能用于含有独立变 量时间序列的因果关系的研究。
v 指数平滑的原理为:当利用过去观测值的加权平均来预测未来的 观测值时(这个过程称为平滑),离得越近的观测值要给以更多 的权。
v 一般的ARIMA模型有多个参数,没有季节成分的可以记为ARIMA(p,d,q) ,如果没有必要利用差分来消除趋势或循环成分时,差分阶数d=0,模型为 ARIMA(p,0,q),即ARMA(p, q)。
v 在有已知的固定周期s时,模型多了4个参数,可记为 ARIMA(p,d,q)(P,D,Q)s。(如果是每年的月数据则s=12,其它周期依 此类推,如每月的周数据s=4等)
spss教程第四章---时间序列分析
第四章时间序列分析由于反映社会经济现象的大多数数据是按照时间顺序记录的,所以时间序列分析是研究社会经济现象的指标随时间变化的统计规律性的统计方法。
.为了研究事物在不同时间的发展状况,就要分析其随时间的推移的发展趋势,预测事物在未来时间的数量变化。
因此学习时间序列分析方法是非常必要的。
本章主要内容:1. 时间序列的线图,自相关图和偏自关系图;2. SPSS 软件的时间序列的分析方法−季节变动分析。
§4.1 实验准备工作§4.1.1 根据时间数据定义时间序列对于一组示定义时间的时间序列数据,可以通过数据窗口的Date菜单操作,得到相应时间的时间序列。
定义时间序列的具体操作方法是:将数据按时间顺序排列,然后单击Date →Define Dates打开Define Dates对话框,如图4.1所示。
从左框中选择合适的时间表示方法,并且在右边时间框内定义起始点后点击OK,可以在数据库中增加时间数列。
图4.1 产生时间序列对话框§4.1.2 绘制时间序列线图和自相关图一、线图线图用来反映时间序列随时间的推移的变化趋势和变化规律。
下面通过例题说明线图的制作。
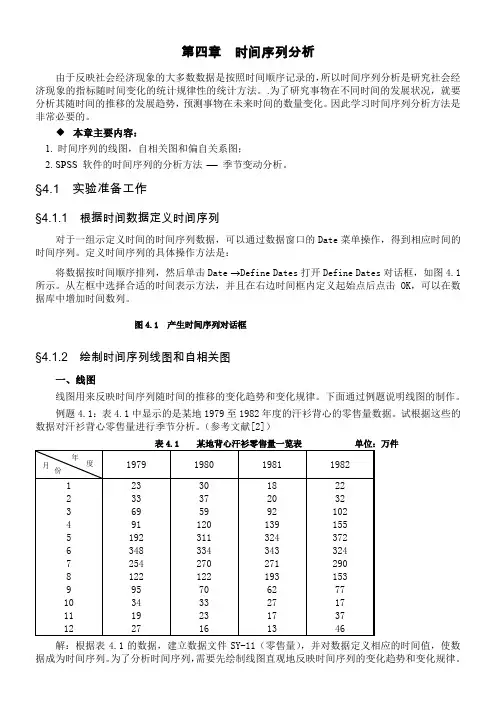
例题4.1:表4.1中显示的是某地1979至1982年度的汗衫背心的零售量数据。
试根据这些的数据对汗衫背心零售量进行季节分析。
(参考文献[2])表4.1 某地背心汗衫零售量一览表单位:万件解:根据表4.1的数据,建立数据文件SY-11(零售量),并对数据定义相应的时间值,使数据成为时间序列。
为了分析时间序列,需要先绘制线图直观地反映时间序列的变化趋势和变化规律。
具体操作如下:1. 在数据编辑窗口单击Graphs→Line,打开Line Charts对话框如图4.2.。
从中选择Simple单线图,从Date in Chart Are 栏中选择Values of individual cases,即输出的线图中横坐标显示变量中按照时间顺序排列的个体序列号,纵坐标显示时间序列的变量数据。
(整理)时间序列分析讲义__第01章_差分方程.

第一章 差分方程差分方程是连续时间情形下微分方程的特例。
差分方程及其求解是时间序列方法的基础,也是分析时间序列动态属性的基本方法。
经济时间序列或者金融时间序列方法主要处理具有随机项的差分方程的求解问题,因此,确定性差分方程理论是我们首先需要了解的重要内容。
§1.1 一阶差分方程假设利用变量t y 表示随着时间变量t 变化的某种事件的属性或者结构,则t y 便是在时间t 可以观测到的数据。
假设t y 受到前期取值1-t y 和其他外生变量t w 的影响,并满足下述方程:t t t w y y ++=-110φφ (1.1)在上述方程当中,由于t y 仅线性地依赖前一个时间间隔自身的取值1-t y ,因此称具有这种结构的方程为一阶线性差分方程。
如果变量t w 是确定性变量,则此方程是确定性差分方程;如果变量t w 是随机变量,则此方程是随机差分方程。
在下面的分析中,我们假设t w 是确定性变量。
例1.1 货币需求函数 假设实际货币余额、实际收入、银行储蓄利率和商业票据利率的对数变量分别表示为t m 、t I 、bt r 和ct r ,则可以估计出美国货币需求函数为:ct bt t t t r r I m m 019.0045.019.072.027.01--++=-上述方程便是关于t m 的一阶线性差分方程。
可以通过此方程的求解和结构分析,判断其他外生变量变化对货币需求的动态影响。
1.1.1 差分方程求解:递归替代法差分方程求解就是将方程变量表示为外生变量及其初值的函数形式,可以通过以前的数据计算出方程变量的当前值。
由于方程结构对于每一个时间点都是成立的,因此可以将(1.1)表示为多个方程:0=t :01100w y y ++=-φφ 1=t :10101w y y ++=φφt t =:t t t w y y ++=-110φφ依次进行叠代可以得到:1011211010110101)()1()(w w y w w y y ++++=++++=--φφφφφφφφ0111122113121102)1(w w w y y φφφφφφφ++++++=-i ti i t t i it w y y ∑∑=-=++=011110φφφφ (1.2)上述表达式(1.2)便是差分方程(1.1)的解,可以通过代入方程进行验证。
SPSS时间序列分析-spss操作步骤讲述

Time Serises Modeler 对话框Variables选项卡
返回
专家建模标准模型选项卡
返回
判断异常值选项卡
指数平滑标准模型选项卡
返回
ARIMA Criteria Model选项卡
返回
侦查异常值的选项卡
返回
自变量转换选项卡
Байду номын сангаас
返回
时间序列模型Statistics选项卡
返回
Time Serises Modler Plots选项卡
第17章
时间序列分析
Time Series
返回
目 录
各种时间序列分析过程 修补缺失值与创建时间序列
序列图
操作 实例
季节分解法
操作 实例
频谱分析法
频谱分析操作 实例
建立时间序列模型
操作 实例
互相关
操作 实例
应用时间序列模型
操作
自相关
操作 实例
习题17及参考答案
结束
返回
各种时间序列分析过程
返回
修补缺失值过程与对话框
返回
时间序列习题参考答案(5)
三、自相关分析
返回
时间序列习题参考答案(6)
表中显示的是自相关计算结果,从左向右,依次列出的是:滞后数、自相关系数 值值、标准误差、Box-ljung统计量(值、自由度、原假设成立的概率值)。由于原假 设(假设基本过程是独立的,也即假定时间序列所反映的随机过程是白噪声)成立的 概率值都小于0.05,所以全部自相关均有显著性意义。
返回
时间序列习题参考答案(17)
六、数据转换
返回
时间序列习题参考答案(18)
返回
spss(时间序列分析)

• 横截面数据也常称为变量的一个简单随机样本,也即假设每个数据 都是来自于总体分布的一个取值,且它们之间是相互独立的(独立 同分布)。
• 而时间序列的最大特点是观测值并不独立。时间序列的一个目的
是用变量过去的观测值来预测同一变量的未来值。 • 下面看一个时间序列的数据例子。 • 例1. 某企业从1990年1月到2002年12月的月销售数据(单位:百
三、指数平滑模型
• 时间序列分析的一个简单和常用的预测模型叫做指数平滑
(exponential smoothing)模型。
• 指数平滑只能用于纯粹时间序列的情况,而不能用于含有独立变量 时间序列的因果关系的研究。
• 指数平滑的原理为:利用过去观测值的加权平均来预测未来的 观测值(这个过程称为平滑),且离现在越近的观测值要给以越重
Seanal adjusted series SA
Seas factors SF
YEAR
图3 销售数据的季节因素分离
第十七页,共70页。
120
可以看出,逐月的销
100 售额大致沿一个指数
80 曲线呈增长趋势。
60
↘
40
20
0
-20 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002
3. saf_1:季节因素(seasonal factor) ,记为{SFt }; 4. stc_1:去掉季节及随机扰动后的趋势及循环因素(trend-
cycle series),记为{TCt }。
第十五页,共70页。
• 这些分解出来的序列或成分与原有时间序列 之间有如下的简单和差关系:
SPSS随机时间序列分析技巧教材

SPSS随机时间序列分析技巧教材SPSS(Statistical Package for the Social Sciences)是一款用于统计分析和数据挖掘的软件工具。
它提供了丰富的功能和功能,可以用于各种统计分析任务。
其中一个强大的功能是随机时间序列分析,它可以帮助用户了解和解释时间序列数据的模式和趋势。
本文将介绍一些SPSS中常用的随机时间序列分析技巧。
1. 数据导入:首先,将时间序列数据导入SPSS中。
确保数据以适当的格式存储,并正确地标识时间变量。
SPSS支持多种数据格式,如CSV、Excel等。
2. 数据检查:在进行时间序列分析之前,需要对数据进行一些基本的检查。
可以使用SPSS中的描述性统计量来检查数据的一般概况,比如数据的均值、方差、最大值和最小值等。
如果数据存在缺失值、异常值或离群值,需要进行适当的数据清洗。
3. 时间序列图:时间序列图可以帮助用户直观地了解数据的模式和趋势。
SPSS提供了绘制时间序列图的功能,用户可以选择不同的图形类型,如折线图、散点图等。
通过观察时间序列图,用户可以判断数据是否存在趋势、季节性或周期性等特征。
4. 时间序列分解:时间序列分解是将时间序列数据分解为趋势、周期和随机成分的过程。
SPSS提供了用于时间序列分解的函数和工具,用户可以根据需要选择不同的分解方法,如移动平均法、指数平滑法等。
分解后的时间序列可以帮助用户更好地理解数据的结构和组成。
5. 自相关分析:自相关分析是研究时间序列数据自身相关性的一种方法。
SPSS提供了自相关分析的功能,用户可以计算自相关系数,并绘制自相关图。
自相关分析可以帮助用户判断时间序列数据是否具有持续性,即当前的值是否与以前的值相关。
6. 平稳性检验:平稳性是时间序列分析的一个重要概念,它指的是时间序列数据的均值和方差在时间上保持稳定。
SPSS提供了多种平稳性检验方法,如ADF检验、KPSS检验等。
通过进行平稳性检验,用户可以判断时间序列数据是否适合进行随机时间序列分析。
spss时间序列分析教程
3.3时间序列分析3.3.1时间序列概述1.基本概念(1)一般概念:系统中某一变量的观测值按时间顺序(时间间隔相同)排列成一个数值序列,展示研究对象在一定时期内的变动过程,从中寻找和分析事物的变化特征、发展趋势和规律。
它是系统中某一变量受其它各种因素影响的总结果。
(2)研究实质:通过处理预测目标本身的时间序列数据,获得事物随时间过程的演变特性与规律,进而预测事物的未来发展。
它不研究事物之间相互依存的因果关系。
(3)假设基础:惯性原则。
即在一定条件下,被预测事物的过去变化趋势会延续到未来。
暗示着历史数据存在着某些信息,利用它们可以解释与预测时间序列的现在和未来。
近大远小原理(时间越近的数据影响力越大)和无季节性、无趋势性、线性、常数方差等。
(4)研究意义:许多经济、金融、商业等方面的数据都是时间序列数据。
时间序列的预测和评估技术相对完善,其预测情景相对明确。
尤其关注预测目标可用数据的数量和质量,即时间序列的长度和预测的频率。
2.变动特点(1)趋势性:某个变量随着时间进展或自变量变化,呈现一种比较缓慢而长期的持续上升、下降、停留的同性质变动趋向,但变动幅度可能不等。
(2)周期性:某因素由于外部影响随着自然季节的交替出现高峰与低谷的规律。
(3)随机性:个别为随机变动,整体呈统计规律。
(4)综合性:实际变化情况一般是几种变动的叠加或组合。
预测时一般设法过滤除去不规则变动,突出反映趋势性和周期性变动。
3.特征识别认识时间序列所具有的变动特征,以便在系统预测时选择采用不同的方法。
(1)随机性:均匀分布、无规则分布,可能符合某统计分布。
(用因变量的散点图和直方图及其包含的正态分布检验随机性,大多数服从正态分布。
)(2)平稳性:样本序列的自相关函数在某一固定水平线附近摆动,即方差和数学期望稳定为常数。
样本序列的自相关函数只是时间间隔的函数,与时间起点无关。
其具有对称性,能反映平稳序列的周期性变化。
特征识别利用自相关函数ACF:ρk=γk/γ0其中γk是y t的k阶自协方差,且ρ0=1、-1<ρk<1。
时间序列季节性分析spss
时间序列季节性分析spss表1 为某公司连续144个⽉的⽉度销售量记录,变量为sales。
试⽤专家模型、ARIMA模型和季节性分解模型分析此数据。
选定样本期间为1978年9⽉⾄1990年5⽉。
按时间顺序分别设为1⾄141。
⼀、画出趋势图,粗略判断⼀下数据的变动特点。
具体操作为:依次单击菜单“Analyz e→Forecasting→Sequence Chart”,打开“Sequence Chart”对话框,在打开的对话框中将sales选⼊“Variables”列表框,时间变量date选⼊“Time Axis Labels”,单击“OK”按钮,则⽣成如图2 所⽰的sales序列。
图1 “Sequence Chart”对话框从趋势图可以明显看出,时间序列的特点为:呈线性趋势、有季节性变动,但季节波动随着趋势增加⽽加⼤。
⼆、模型的估计(⼀)、季节性分解模型根据时间序列特点,我们选择带线性趋势的季节性乘法模型作为预测模型。
1、定义⽇期具体操作为:依次单击菜单“Data→Define Date”,打开“Define Date”对话框,在“Cases Are”列表框选择“Years,months”的⽇期格式,在对话框的右侧定义数据的起始年份、⽉份。
定义完毕后,单击“OK”按钮,在数据集中⽣成⽇期变量。
图3 “Define Date”对话框2、季节分解具体操作为:“Analyze→Forecasting→Seasonal Decomposition”打开“Seasonal Decomposition”对话框,将待分析的序列变量名选⼊“Variable”列表框。
在“Model Type”选择组中选择“Multiplicative”模型;在“Moving Average Weight”选择组中选择“Endpoints weighted by 0.5”。
单击“OK”按钮,执⾏季节分解操作。
图4 “Seasonal Decomposition”对话框3、画出序列图①原始序列和校正了季节因⼦作⽤的序列图图5为sales 序列和校正了季节因⼦作⽤的序列图。
第十一章SPSS的时间序列分析
3.1 AR(自回归)模型
一般地,如果和p个过去值有关则是p阶自回归模型, 记为AR(p),表达式为: xt 0 1 xt 1 2 xt 2 p xt p t
(B) xt t
或者
其中, (B) 1 1 B 2 B 2 p B p
1 - 12
第三节 时间序列的图形化观察
4、互相关图(CCF) 对两个互相对应的时间序列进行相关性分 析,检验一个序列与另一个序列的滞后 序列之间的相关性 Analyze>Forecasting>Cross Correlations 举例: GDP与通信业务收入,0阶滞后相关性最显 著
1 - 13
3.2 MA模型
(Moving Average Model)
3.3 ARMA模型
(Auto Regression Moving Average model)
3.4 ARIMA模型
( Autoregressive Integrated Moving Average Model )
1 - 22
3.1 AR(自回归)模型
1 - 15
第六节 ARIMA模型
ARIMA模型全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA),是由博克 思(Box)和詹金斯(Jenkins)于70年代初提出的著名时间序列 预测方法,所以又称为box-jenkins模型、博克思-詹金斯法。
第十一章 SPSS的时间序列分析
1-1
第一节 时间序列分析概述
一、相关概念 时间序列:有序的数列:y1,y2,y3,…yt 理解: 1、有先后顺序且时间间隔均匀的数列; 2、随机变量族或随机过程的一个“实现” ,即在每一个固定时间点t上,现象yt看 作是一个随机变量, y1,y2,y3,…yt是一系 列随机变量所表现的一个结果。
课题_第11章 SPSS在时间序列预测中的应用 SPSS19.0软件使用教程
第11章SPSS在时间序列预测中的应用SPSS19.0软件使用教程在进入SPSS后,具体工作流程如下:1.将数据输入SPSS,并存盘以防断电。
2.进行必要的预分析(分布图、均数标准差的描述等),以确定应采用的检验方法。
3.按题目要求进行统计分析。
4.保存和导出分析结果。
下面就按这几步依次讲解。
§1.1 数据的输入和保存1.1.1 SPSS的界面当打开SPSS后,展现在我们面前的界面如下:请将鼠标在上图中的各处停留,很快就会弹出相应部位的名称。
请注意窗口顶部显示为“SPSS for Windows Data Editor”,表明现在所看到的是SPSS的数据管理窗口。
这是一个典型的Windows软件界面,有菜单栏、工具栏。
特别的,工具栏下方的是数据栏,数据栏下方则是数据管理窗口的主界面。
该界面和EXCEL极为相似,由若干行和列组成,每行对应了一条记录,每列则对应了一个变量。
由于现在我们没有输入任何数据,所以行、列的标号都是灰色的。
请注意第一行第一列的单元格边框为深色,表明该数据单元格为当前单元格。
对Windows操作界面不熟悉的朋友可参见SAS入门第一课中的相关内容。
对数据表界面操作不熟悉的朋友可先学习一下EXCEL的操作(因为它的帮助是中文的)。
有的SPSS系统打开时会出现一个导航对话框,请单击右下方的Cancer按钮,即可进入上面的主界面。
1.1.2 定义变量该资料是定量资料,设计为成组设计,因此我们需要建立两个变量,一个变量代表血磷值,习惯上取名为X,另一个变量代表观察对象是健康人还是克山病人,习惯上取名为GROUP。
对数据的统计分析格式不太熟悉的朋友请先学习统计软件第一课。
选择菜单Data==>Define Variable。
系统弹出定义变量对话框如下:该变量定义对话框在SPSS 10.0版中已被取消,这里的操作只适合9.0~7.0版的用户。
对话框最上方为变量名,现在显示为“VAR00001”,这是系统的默认变量名;往下是变量情况描述,可以看到系统默认该变量为数值型,长度为8,有两位小数位,尚无缺失值,显示对齐方式为右对齐;第三部分为四个设置更改按钮,分别可以设定变量类型、标签、缺失值和列显示格式;第四部分实际上是用来定义变量属于数值变量、有序分类变量还是无序分类变量,现在系统默认新变量为数值变量;最下方则依次是确定、取消和帮助按钮。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
击“OK‖即可得到分解结果。
• 1.
上述SPSS对时间序列做分解的结果自动储存在原有数据
文件中新增的几个变量中,它们分别是:
err_1:误差(error)项,也即原序列的随机扰动成分,记 为{ERt };
2.
3. 4.
sas_1:季节调整后的序列(seasonal adjusted series) , 记为{SAt };
第二节
一、成分的分离
时间序列的分解
• 从图1可以看出,该销售数据序列由三部分组成:指数向上 的趋势(trend)、周期性变化的季节成分(seasonal component) 和无法用趋势和季节模式解释的随机干扰 (disturbance)。
• 一般的时间序列还可能有循环或波动成分(Cyclic, or fluctuations)。 • 循环模式和有规律的季节模式不同,其周期长短不一定固定。 比如经济危机周期,金融危机周期等等。
• 若记时刻 t 的观测值为 Xt • 时刻 t 的指数平滑记为 Yt 。
• 指数平滑的数学模型为
Yt = aXt+a(1-a)Xt -1+a(1-a)2Xt -2+ „ +a(1-a)t-1X1,
(1)
其中0<a<1为权重指数。a 越大,表示在加 权时给予当前观测值的权重越大,相应地, 给予过去观测值的权重就越小。
二、时间序列分析的目的
• 在例1中,我们希望能够从这些历史销售数据出发,找出其
中的一些规律,并且建立可以对未来的销售额进行预测的时 间序列模型,这一统计过程就是时间序列分析。 • 事实上,时间序列分析也是一种回归。 • 回归分析的目的是建立应变量和自变量之间关系的模型;并
且可以用自变量来对应变量进行预测。
3.
在“Trend Component‖下选择“Exponential‖(因为本 例中的趋势近似一条指数曲线),在“Seasonal Component‖下选择“Additive‖,点击“Continue‖返 回一级窗口。
4.
点击“Parameters‖来进行参数选择和估计。在弹出的二
级窗口中的“General‖、“Trend‖和“Seasonal‖下方 都选择“Grid Search‖,表示留给程序自己去搜索(估计), 其下的搜索范围(―Start‖和“Stop‖)和搜索步长(―By‖)可 不作修改。这三个参数中的第一项,也即权重指数 a , 一般可作人为选择。选好参数后,点击“Continue‖返回 一级窗口。 5.
YEAR
图5 分离季节和趋势后的扰动序列
(返回27页)
二、带季节与趋势的指数平滑
• 如果我们不仅仅满足于分解现有的时间序列,而且想利用该 分解对未来进行更好的预测,就可以建立带季节成分和趋势 的指数平滑模型。 • 作这样的指数平滑,必须事先估计出季节成分和趋势,其估 计结果就是这两条曲线的函数关系式(参数),也即时间指标 t 的两个确定的(非随机的)函数。 • 分别记季节因素和趋势(及循环)的估计为 SFt 和 TCt ,而剩 ︿ 余的扰动(自然也是估计)记为 ERt 。 • 带季节和趋势的指数平滑就是先计算扰动序列的指数平滑, 然后再加上估计(预测)的季节和趋势成分,作为最终的指数 平滑数据。
saf_1:季节因素(seasonal factor) ,记为{SFt }; stc_1:去掉季节及随机扰动后的趋势及循环因素(trendcycle series),记为{TCt }。
• 这些分解出来的序列或成分与原有时间序列 之间有如下的简单和差关系: Xt = SFt + SAt ,
Xt = SFt + TCt + ERt .
120
100
80
60
40
SALES
20
YEAR
90 19
91 19
图1 销售数据的时间序列图
92 19
93 19
94 19
95 19
96 19
97 19
98 19
99 19
00 20
01 20
02 20
(返回27页)
03 20
• 从图1可以看出:该企业销售额总的趋势是增长的;但增长
并不是单调上升的,有涨有落。
Time Series => Exponential Smoothing‖选项,在弹出的 窗口中把变量“sales‖选入“Variables‖空格。
• —— 点击右下方“Parameter‖按钮,在新弹出窗口改变权
重指数a 的取值;点击“Continue‖返回。
• —— 点击“Save‖按钮,在新窗口选择“Predict through‖, 并在下方“Year‖后输入“2003‖,表示将预测2003年的销 售额;点击“Continue‖返回一级窗口,点“OK‖即可。 • 指数平滑的结果储存在原数据文件后新增的两个变量中,它 们分别是指数平滑数据Yt 以及Yt 与 Xt 之间的误差。 • 图2即为Xt 与 Yt 叠合在一起的共同的时间序列图。
• 更进一步,这种升降不是杂乱无章的,和季节或月份的周期 有关系。
• 当然,除了增长的趋势和季节影响之外,还有些无规律的随 机因素的作用。
• 这些都说明了这个数据前后之间不是独立而是相关的。 • 上述图形是选择SPSS菜单中的“Graphs => Sequences‖ 选项,在窗口中把“sales‖作为画图变量“Variables‖,而 把“year‖作为横坐标“Time Axis Labels‖而得到的。在 成图后我们还把时间标值的间隔和格式做了修改。
6.
点击“Save‖按钮作预测选择后,此操作同上一节的简单 指数平滑。
再在一级窗口点击“OK‖,即可得到所需要的结果了。
-20
图3 销售数据的季节因素分离
00 20 99 19
01 20
02 20
120
100
80
可以看出,逐月的销 售额大致沿一个指数 曲线呈增长趋势ies TC Error series ER
40
20
0
-20
YEAR
90 19
91 19
92 19
图4 销售数据的趋势与扰动分离
︿
︿
• 1.
我们不介绍上述指数平滑背后的数学,而直接来看它的
SPSS操作,该操作要分步来完成。
选择菜单中的“Analyze => Time Series => Exponential Smoothing‖选项,在弹出的窗口中把变量
“sales‖选入“Variables‖空格。
2. 在该窗口的“Model‖下选择“Custom‖,并点击其下的 “Custom‖按钮进入二级窗口(进行模型选择)。
• 一般地来讲,一个时间序列可能有趋势、季节、循环这三个
成分中的某些或全部再加上随机成分组成。
• 时间序列的分解就是要把一个时间序列中可能包含的各种成 分分解开来,以便于有针对性的进一步分析讨论。
• 就例1中的时间序列的分解,通过SPSS软件,可以很轻而
易举地得到该序列的趋势、季节和误差成分。 • SPSS操作 —— 选择菜单中的“Analyze => Time Series => Seasonal Decomposition‖选项,把变量“sales‖选入 “Variables‖空格,再在“Model‖下选择“Additive‖,点
• 下面看一个时间序列的数据例子。 • 例1. 某企业从1990年1月到2002年12月的月销售数据(单位: 百万元)储存于SPSS数据文件tssales.sav中。 • 在该数据文件中,除了销售额变量“sales‖以外,还有三个
时间变量“year‖、“month‖和“date‖。事实上这三个变
量是我们后期通过SPSS操作自动加上去的。
•
从图2可以看出一下几点:
1.
2.
指数平滑曲线比原有观测值曲线来得平整光滑些,其波动 没有原来那么强了,这也是平滑一词的来意。
不考虑最初几个指数平滑值,当 t < N 时,指数平滑数据
Yt与原有观测值 Xt 之间的误差较小;可见用指数平滑作为 原有观测值的一种估计效果还是较好的。
3. 但是当 t >N 时,指数平滑曲线很快得呈一条直线状,没 有体现出原有观测值的上升趋势和周期性规律。可见用这 一指数平滑作为原销售数据的预测效果不理想。 • 上述第三点的原因是我们在做指数平滑时没有考虑原数据 的任何趋势或周期规律,我们在下一节再对此做弥补。
• 模型(1)还可改写为
Yt = a Xt + (1-a)Yt -1 ,
t = 2, 3, „
(2)
• 容易看出,经过这样的改写,模型(2)不仅可 以用来计算时间 t≤N 的指数平滑,还可对将 来时刻进行预测,即用 Yt 预测 Xt ,其中t >N 。见图2,其中取a = 0.4。
XSMO O TH
• 而在时间序列分析中,应变量为变量未来的可能值,而用来 预测的自变量中就包含该变量的一系列历史观测值。 • 时间序列的自变量也可能包含随着时间度量的独立变量。
三、指数平滑模型
• 时间序列分析的一个简单和常用的预测模型叫做指数平滑 (exponential smoothing)模型。
• 指数平滑只能用于纯粹时间序列的情况,而不能用于含有独 立变量时间序列的因果关系的研究。 • 指数平滑的原理为:利用过去观测值的加权平均来预测未来 的观测值(这个过程称为平滑),且离现在越近的观测值要给 以越重的权。 • 而“指数”意味着:按历史观测值记录时间离现在的距离远 近,其上的权数按指数速度递减。 • 这一距离通常用数据间隔位置差,也称步数(lag)来表示。
• 选择SPSS菜单中的“Data => Define Dates‖选项,在弹
出窗口的“Cases Are‖下方选择“Years, months‖,再在
