初中生必须掌握的五种经典几何模型
初中所有几何模型

初中所有几何模型一、圆锥体圆锥体是一种几何模型,它的形状像一个圆锥。
我记得,在初中的几何课上,老师曾经给我们讲解过圆锥体的性质和特点。
圆锥体有一个底面和一个顶点,顶点在底面的正上方,并且与底面的中心相连。
底面是一个圆,它的半径决定了圆锥体的大小。
圆锥体的侧面是由顶点和底面上各点相连形成的直线段组成的。
在我的记忆中,我曾经亲手制作过一个小型的圆锥体模型。
当时,我用纸张做底面,然后将它卷成一个锥形,最后用胶水固定住。
这个小小的圆锥体模型让我更加深入地理解了它的结构和性质。
圆锥体在生活中有许多应用。
例如,冰淇淋蛋筒就是一个圆锥体的形状。
当我们吃冰淇淋时,可以想象蛋筒就像一个圆锥体,顶部是尖的,底部是扁平的。
这种设计使得冰淇淋更容易放入蛋筒中,并且更加美味可口。
在建筑设计中,圆锥体也被广泛应用。
例如,教堂的尖顶就是圆锥体的形状。
这种设计不仅美观,而且能够提供更好的结构稳定性。
总的来说,圆锥体是一个有趣而又实用的几何模型。
通过了解它的性质和特点,我们可以更好地理解和应用它在生活中的各种形式。
二、长方体长方体是一种常见的几何模型,它的形状像一个长方形的盒子。
在初中的几何课上,我们学习了长方体的性质和特点。
长方体有六个面,每个面都是一个矩形。
它有一个底面和一个顶面,以及四个侧面。
底面和顶面是相似的,但是侧面是矩形而不是长方形。
我还记得,在一个数学实验课上,我们用纸板制作了一个小型的长方体模型。
我们按照老师给出的尺寸,剪下了六个矩形的纸板,然后用胶水将它们粘在一起。
最后,我们得到了一个完整的长方体模型。
长方体在生活中有许多应用。
例如,书包就是一个长方体的形状。
它有一个底部用来放书和文具,四个侧面可以用来放置其他物品。
这种设计使得书包更加方便携带和使用。
在建筑设计中,长方体也被广泛应用。
例如,大楼的建筑常常采用长方体的形状。
这种设计不仅美观,而且能够提供更好的空间利用率。
总的来说,长方体是一个常见而又实用的几何模型。
初中数学——最全:初中数学几何模型

最全:初中数学几何模型几何是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,小编整理了常用的各大模型,一定要认真掌握哦~全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形;遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等;遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
初中数学九大几何模型
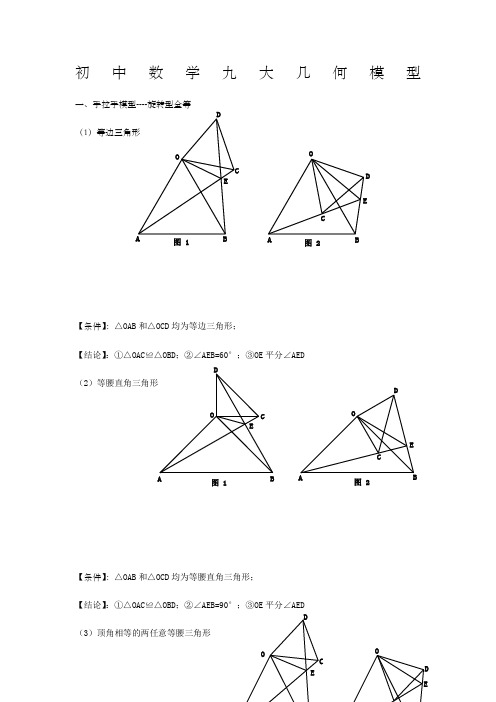
初中数学九大几何模型一、手拉手模型----旋转型全等 (1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形OB C DE图 1OABCD E图 2OABCDE图 1OACDE图 2OCDEOD E【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ;OAB COBCDEOB CDEOA CD③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ;③2△OCD △OCE OC 21S S =-(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=AOBCDE 图 1A OBCDEM N图 2A OBCDEF图 3A O BCDEMN 图 4证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
中考数学几何模型大汇总

中考数学几何模型大汇总下面是中考几何模型的大汇总:1、平面直角坐标系模型平面直角坐标系模型中,我们可以使用坐标系来描述平面上图形和点的位置关系。
这个模型常用于图形的平移、旋转、对称等问题。
2、矩形模型矩形模型用于讨论四边形的性质、面积、周长等问题。
在这个模型中,我们将四边形近似为一个矩形,从而使问题更易解决。
3、三角形模型三角形模型是中考中最常见的模型之一、它可以用于计算三角形的面积、周长,讨论三角形的性质。
在这个模型中,我们通常使用海伦公式、正弦定理、余弦定理等方法来求解。
4、圆形模型圆形模型用于讨论圆、弧、扇形等问题。
在这个模型中,我们通常使用圆的周长、面积公式,以及角度与弧长的关系来进行计算。
5、球体模型球体模型用于讨论球体的体积、表面积以及球冠、球缺等问题。
在这个模型中,我们通常使用球的体积、表面积公式,以及球冠、球缺的体积和表面积公式来求解。
6、棱锥模型棱锥模型用于讨论棱锥的体积、表面积、正棱锥、锥台等问题。
在这个模型中,我们通常使用棱锥的体积、表面积公式,以及正棱锥、锥台的体积和表面积公式来求解。
7、棱柱模型棱柱模型用于讨论棱柱的体积、表面积、正棱柱、柱台等问题。
在这个模型中,我们通常使用棱柱的体积、表面积公式,以及正棱柱、柱台的体积和表面积公式来求解。
8、立体几何模型立体几何模型用于讨论正方体、长方体、正六面体等立体图形的体积、表面积、对角线等问题。
在这个模型中,我们通常使用立体图形的体积、表面积公式,以及对角线长的求法来计算。
总之,几何模型是中考数学中重要的一环,通过利用这些模型,我们可以更好地理解几何知识,更好地应对考试。
初中几何五大模型,学会轻松搞定初中几何,考试不再愁

初中几何五大模型,学会轻松搞定初中几何,考试不再愁初二的同学(即将初二的同学)注意了:到了初二,几何学可以说是初二数学中最重要的一大板块了。
对于整个的初中数学,甚至中考数学而言,也是至关重要的一部分!因此学好几何,就显得尤为重要了!在之前,我们就曾经分享过一篇关于几何辅助线的文章:今天,我们接着为大家分享几何中常见常考的五大模型。
希望对您的日常学习已经各种考试有所帮助!一:共角定理(鸟头定理)即在两个三角形中,它们有一个角相等(或互补),则他们就是共角三角形。
它们的面积之比,就是对应角(相等角或互补角)两夹边的乘积之比。
(这一定理不建议记,符合这种定理的直接应用,不符合的,还不如直接推导的思路)1.等底等高的两个三角形面积相等:2.两个三角形(底)高相等,面积之比等于高(底)之比:3.在一组平行线之间的等积变形,如图:AB平行于CD,则S△ACD=S△BCD;反之,如果S△ACD=S△BCD,则可知直线AB平行于CD。
三:梯形蝴蝶定理1.S2=S4(因为S△ABC=S△DBC,所以S△ABC-S△OBC=S△DBC-S△OBC),S1:S3=a:b2.S1:S3:S2 :S4=a:b:ab:ab3.梯形S的对应数为(a b)在任意四边形中,同样也有蝴蝶定理,如下图:1.S1:S2=S4:S3或者S1×S3=S4×S2;2.AO:OC=(S1 S2):(S4 S3)四:相似三角形定理1.相似三角形:形状相同,大小不相等的两个三角形相似2.寻找相似模型的大前提是平行线:平行于三角形一边的直线和其它两边或两边延长线相交,所构成的三角形与原三角形相似。
3.相似三角形性质:①相似三角形的一切对应线段(对应高,对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型,沙漏模型这两大类,注意这两大类都含有 BC平行DE这样一组平行线!第四定理练习:在等腰直角三角形ABC中,D是BC上的一点,BD:BC=2:5,而四边形ADEF是正方形,如果S△ABC=98,求S正方形ADEF?五:燕尾定理性质:1.S△ABG:S△ACG=S△BGE:S△CGE=BE=CE2.S△BGA:S△BGC=S△GAF:S△GCF=AF:CF3.S△AGC:S△BGC=S△AGD:S△BGD=AD:BD(这就是燕尾模型)。
初中数学必背几何模型
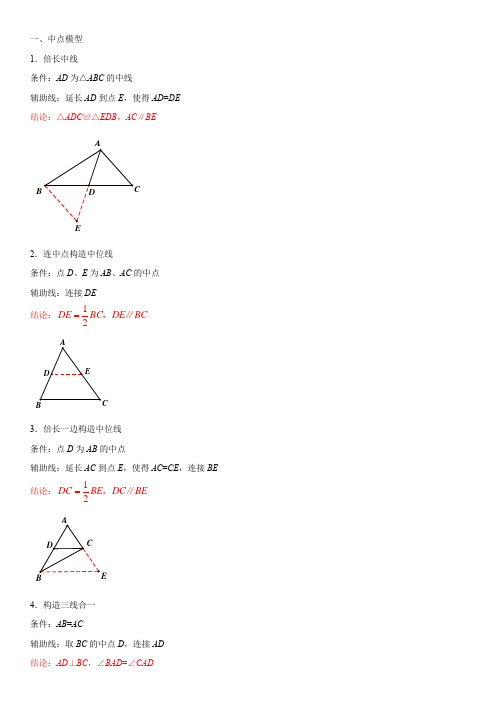
一、中点模型1.倍长中线条件:AD 为△ABC 的中线辅助线:延长AD 到点E ,使得AD =DE结论:△ADC ≌△EDB ,AC ∥BE2.连中点构造中位线条件:点D 、E 为AB 、AC 的中点辅助线:连接DE 结论:12DE BC DE BC =,∥3.倍长一边构造中位线条件:点D 为AB 的中点辅助线:延长AC 到点E ,使得AC =CE ,连接BE 结论:12DC BE DC BE =,∥4.构造三线合一条件:AB =AC辅助线:取BC 的中点D ,连接AD结论:AD ⊥BC ,∠BAD =∠CADB5.构造斜边中线条件:∠ABC =90°辅助线:取AC 的中点D ,连接BD 结论:12BD AC AD CD ===二、角平分线模型6.往角两边作垂线条件:AD 平分∠BAC辅助线:过点D 作AB 、AC 的垂线,垂足分别为E 、F结论:△ADE ≌△ADF7.在角的两边截取等长线段条件:AD 平分∠BAC辅助线:在AB 、AC 上取点E 、F ,满足AE =AF ,连接DE 、DF 结论:△ADE ≌△ADF8.过角平分线上一点作垂线条件:AD 平分∠BAC辅助线:过点D 作EF ⊥AD ,交AB 、AC 于点E 、FD CBB CCC结论:△ADE ≌△ADF三、双角平分线模型9.内内模型条件:BD 、CD 平分∠ABC 、∠ACB 结论:1902D A ∠=︒+∠10.内外模型条件:BD 、CD 平分∠ABC 、∠ACE 结论:12D A ∠=∠11.外外模型条件:BD 、CD 平分∠CBE 、∠BCF 结论:1902D A ∠=︒-∠四、平行线模型12.猪蹄模型CA BCC ED条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D =∠BED13.铅笔头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D +∠BED =360°14.鸟头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠D +∠BED =∠B15.平行线+角平分线模型条件:AB ∥CD ,CE 平分∠ACD结论:AC =AE五、等积模型16.等底等高条件:AD ∥BCFAFBC结论:ABC DBC S S =,ADB ADC S S =17.等高模型条件:B 、C 、D 共线结论:::ABD ADC S S BD CD =18.等底模型条件:AE 、DE 为△ABC 、△DBC 边BC 上的高结论:::ABC DBC S S AE DE =六、对称半角模型19.对称半角模型-含45°角的三角形条件:∠BAC =45°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等腰直角三角形20.对称半角模型-含30°角的三角形B CB C DED条件:∠BAC =30°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等边三角形七、旋转半角模型21.旋转半角模型-等腰直角三角形条件:AB =AC ,∠BAC =90°,∠MAN =45°辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ACM ' 结论:ANM ANM '≌,222BM CN MN +=22.旋转半角模型-等边三角形条件:△ABC 是等边三角形,BD =CD ,∠BDC =120°, ∠MDN =60°辅助线:将△BDM 绕点D 顺时针旋转120°,得到△DCM ' 结论:NDM NDM '≌,BM CN MN +=23.旋转半角模型-正方形条件:正方形ABCD ,∠MAN =45°,FEAM'M CAB辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ADM ' 结论:NAM NAM '≌,BM DN MN +=八、自旋转模型24.自旋转模型-等边三角形条件:△ABC 是等边三角形,点P 为其内任意一点辅助线:将△BAP 绕点B 顺时针旋转60°,得到△BCP ' 结论:△BPP '是等边三角形25.自旋转模型-等腰直角三角形条件:△ABC 中,∠BAC =90°,AB =AC ,点P 为△ABC 内任 意一点辅助线:将△BAP 绕点A 逆时针旋转90°,得到△ACP ' 结论:△APP '是等腰直角三角形26.自旋转模型-等腰三角形条件:△ABC 中,AB =AC ,点P 为△ABC 内任意一点,∠BAC =α 辅助线:将△BAP 绕点A 逆时针旋转α,得到△ACP ' 结论:△APP '是等腰三角形M'DNCBAB九、手拉手模型29.手拉手模型-等边三角形条件:△ABC和△CDE都是等边三角形结论:△ACE≌△BCD27.手拉手模型-等腰直角三角形条件:△ABC和△CDE都是等腰直角三角形结论:△ACE≌△BCD,AE⊥BDEE28.手拉手模型-等腰三角形条件:△ABC 和△CDE 都是等腰三角形,CA =CB , CD =CE ,且∠ACB =∠DCE结论:△ACE ≌△BCD30.手拉手模型-正方形条件:四边形ABCD 和AEFH 都是正方形结论:△ABE ≌△ADH ,BE ⊥DH十、最短路程模型31.直线同侧两线段之和最小(将军饮马)条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作点A 关于直线l 的对称点A ',连接A 'B 结论:点P 为A 'B 和l 交点时,AP +BP 最小C32.直线异侧两线段之差最小条件:点A 、B 在直线l 异侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小33.直线同侧两线段之差最小条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小34.过桥模型(将军饮马)条件:A 、B 为定点,l 1∥l 2,MN 为定长线段且MN ⊥l 1 辅助线:将点A 向上平移MN 的长度得到A ',连接A 'B 结论:点N 为A 'B 与l 1交点时,AM +MN +BN 最小35.四边形周长最小(将军饮马)条件:A 、B 为定点,M 、N 为角两边上的动点辅助线:作点A 、B 关于角两边的对称点A '、B ',连接 lAlAll 1l 2A'B'结论:M、N为A'B'与角两边交点时,四边形ABMN的周长最小B'36.三角形周长最小(将军饮马)条件:A为定点,B、C为角两边上的动点辅助线:作点A关于角两边的对称点A'、A",连接A'A"结论:B、C为A'A"与角两边交点时,△ABC的周长最小37.旋转类最短路程模型条件:线段OA=a,OB=b(a>b),OB绕点O在平面内旋转结论:点B与点N重合时,AB最小;点B与点M重合时,AB最大十一、基本相似模型38.A字型条件:BC∥DE结论:△ABC∽△ADE条件:∠ABC =∠ADE结论:△ABC ∽△ADE39.8字型条件:AB ∥CD结论:△AOB ∽△DOC条件:∠BAO =∠DCO结论:△AOB ∽△COD40.母子型条件:△ABC 中,∠ACB =90°,CD ⊥AB结论:△ABC ∽△ACD ∽△CBD41.一线三等角模型条件:∠B =∠D =∠ACE结论:△ABC ∽△CDECBCC A42.手拉手相似模型条件:△ABC ∽△ADE结论:△ACE ∽△ABD十二、对角互补模型43.对角互补模型-90°全等型条件:∠AOB =∠DCE =90°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OEOC ,212OECD S OC 四边形CB ACE AB D CDD44.对角互补模型-120°全等型条件:∠AOB =120°,∠DCE =60°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OE =OC ,24OECD S =四边形45.对角互补模型-任意角全等型条件:∠AOB =2α,∠DCE =180°-2α,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,2cos OD OE OC α+=⋅, 2sin cos OEC OCD S S OC αα+=⋅46.邻边相等的对角互补模型条件:四边形ABCD 中,AB =AD ,∠ABC +∠ADC =180°D BAN E OB辅助线:延长CD 到E ,使得DE =BC ,连接AE结论:△ABC ≌△ADE ,CA 平分∠BCD十三、隐圆模型47.动点定长模型条件:AB =AC =AP ,点P 为动点结论:点B 、C 、P 三点共圆,点A 为圆心,AB 为半径48.直角圆周角模型条件:点C 为动点,∠ACB =90°结论:点A 、B 、C 三点共圆,线段AB 的中点为圆心,线段 AB 为直径49.定弦定长模型条件:点P 为动点,固定线段AB 所对的动角∠APB 为定值 结论:点A 、B 、P 三点共圆,线段AB 和BP 的中垂线的交点 为圆心BA50.四点共圆模型①条件:点A 、C 为动点,∠BAD +∠BCD =180°结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°,BD 为直径51.四点共圆模型②条件:线段AB 为固定长度,点D 为动点,∠C =∠D结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°,AB为直径。
有哪些初中几何的常见模型

有哪些初中几何的常见模型
1,倍长中线模型
2,截长补短模型
3,一线三垂直模型
4,将军饮马模型
常见的还有手拉手模型、半角模型、奔驰模型、十字架模型、胡不归模型等等
想学好几何模型,不仅要知道为什么,还要知道为什么。
只有明确了原理,很多模型才能举一反三,一些新问题才能指明解决问题的方向。
比如一般的马饮模型的原理就是轴对称和三角形的两边之和大于第三边。
掌握原理后,你就可以轻松掌握一般马饮水的几个变形问题了。
此外,胡不归模型也是一般饮马的变形。
把握两种模式的区别和联系,可以快速学习胡不归模式。
郭老师,初中数学老师,从教15年。
开放式公益教学课程:郭数学公益课系列。
教初中数学各年级各章节考点和解题方法。
欢迎关注郭数学,免费学习。
初中几何46种模型大全

初中几何46种模型大全篇一:初中几何46种模型大全引言几何是初中数学的重要分支,其知识点涵盖了平面几何、立体几何、向量等多个方面。
在学习几何时,掌握各种几何模型是非常重要的,这些模型可以帮助我们理解和解决几何问题,提高解题能力。
本文将介绍初中几何中的46种常见的模型,包括它们的名称、定义、性质和应用。
正文1. 正方形模型正方形模型是几何中最基本的模型之一,它是一种边长相等的矩形。
正方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
正方形模型的性质有:- 正方形的四条边相等;- 正方形的对角线相等;- 正方形的面积等于其边长的平方。
2. 长方形模型长方形模型是有两个相等的长和两个不相等的宽的英雄。
长方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和小于斜边的平方。
长方形模型的性质有:- 长方形的两条对角线相等;- 长方形的宽比长大,长比宽大;- 长方形的长和宽相等。
3. 平行线模型平行线模型是相互平行的直线。
平行线模型的定义如下:- 两直线平行,当且仅当它们的对应角相等且且它们的方向相同。
平行线模型的性质有:- 平行线之间有且仅有一个交点;- 平行线上的点的横坐标相等;- 平行线的方向相同。
4. 菱形模型菱形模型是具有四个相等的直角边的矩形。
菱形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方,且任意两条边的长度小于第三条边的长度。
菱形模型的性质有:- 菱形的四条边相等;- 菱形的对角线相等;- 菱形的面积等于其四条边长度的平方和。
5. 等腰三角形模型等腰三角形模型是有一个相等的腰部的两个三角形。
等腰三角形模型的定义如下:- 在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
等腰三角形模型的性质有:- 等腰三角形的两条直角边相等;- 等腰三角形的底角相等;- 等腰三角形的顶角平分线相等。
6. 等边三角形模型等边三角形模型是具有三个相等的边长的三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中生必须掌握的五种经典几何模型(一)手拉手模型
模型教学产生于教育理论发展的新时代,在新课标的背景下慢慢成熟起来,模型可以让孩子更快的代入到几何之中,形成自己的兴趣。
也是近来来学习初中几何中不可或缺的一部分。
下面我先给大家介绍第一种经典几何模型---手拉手模型,这也是历年数学中考常考的几何压轴题型之一。
例1、在直线ABC的同一侧作两个等边三角形△ABD和△BCE,连接AE与CD,证明:
(1)△ABE≌△DBC (2)AE=DC
(3)AE与DC的夹角为60 (4)△AGB≌△DFB
(5)△EGB≌△CFB (6)BH平分∠AHC
(7)GF∥AC
解析:(1)∵△ABD和△BCE是等边三角形,
∴AB=DB,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠ABC=∠CBE+∠ABC,
即∠DBC=∠ABE,
在△ABE和△DBC中,
易证明△ABE≌△DBC(SAS)
(2) ∵△ABE≌△DBC(SAS)∴AE=CD;
(3) ∵△ABE≌△DBC,∴∠AEB=∠DCB.
又∵∠HFE=∠BFC(对顶角相等)
△HFE和△BFC中,
∠EHF=180-∠AEB-∠HFE;
∠CBF=180-∠DCB -∠BFC,
∴∠EHF=∠CBF=60∴AE与DC的夹角为60。
(4)AB=BD,BG=BF, ∠ABG=∠DBF=60
∴△AGB≌△DFB
(5)EB=EC,BG=BF, ∠EBG=∠CBF=60
∴△EGB≌△CFB
(6)过B作BM垂直AE于M,BN垂直CD于N。
证明△ABM ≌△DBM,则BM=BN
∴BH平分∠AHC
(7)∵△AGB≌△DFB∴BG=BF, 又∠GBF=60,∴GBF为等边三角形
∴∠GFB=EBC=60, ∴GF∥AC。
