翔宇教育集团课时设计活页纸
高一数学教案:函数的应用_2
教学内容
备课札记
例3某地1990年底人口为500万人,人均住房面积为6m2。如果该地区的人口年平均增长率为0.190。为了使2010年底人均住房面积增加到7m2,平均每年新增住房面积为多少m2?(精确到1万m2)
例4、如图是由5对滚筒组成的一台冷轧机,送进去的钢板厚度为2 .1mm,经过各对滚筒逐步减薄后输出,生产出厚度为0.2mm的带钢。;
(1)如果在每对滚筒上减薄的百分比不变,试求出该百分比。
(2)如果每对滚筒提供的减薄百分比为25%,那么从2.1mm的钢板到不厚于0 .2mm的带钢输出。至少需要多少对滚筒?
[小结]
1、复利公式y=N(1+p)x的应用非常广泛,不单可以计算货币金额,还可以计算工业产值、农业产量、人口数量等。P>0为递增增长率,p<0表示递减或折旧率。
教学过程
教学内容
备课札记
[作业]
1、5000元存款,储蓄一年后,从利息中取出100元,其余的钱加到本金里再储蓄一年,第二年的利率比第一年高1%,利息比第一年多70元,求第一年利率。
2、某新产品成本价a元,由于不断进行技术革新,每年成本价降低10%,x年后的成本价为()
A、a(1-10%)x+1B、a(1-10%)x
翔宇教育集团课时设计活页纸
主备人:顾云飞
总课题
函数的应用
总课时
30
第8课时
课题
函数的应用举例(二)
课型
新授
教学目标
1、学会用的模型来解决有关增长率的问题。
2、增强学生的分析问题、解决问题的能力
教学重点
解决有关增长率的问题
教学难点
如何从实际情境中抽象出函数问题
教学过程
高一数学教案:指数与对数函数_4

1 x 1 x
(3) f(x)=lg( x 2 2 +x)-lg 2
例 2.在同一坐标系中分别作出下列函数的图象 (1)y=lgx, y=lg(-x), y=-lgx (2)y= log 2 ( x 1) +2 (3)y= lg x (4)y=lg x
翔宇教育集团课时设计活页纸
教学过程
翔宇教育集团课时设计活页纸
翔宇教育集团课时设计活页纸
主备人:仲坚
总 课 题 课 题 教学目标 教学重点 教学难点 教学过程 函数 总课时 课 型
对数函数(三)
第 32 课时 新授
1.进一步理解和掌握对数函数的性质 2.会判断与对数函数有关的复合函数的奇偶性、会求有关的反函数 3.掌握对数函数的图象变换 函数奇偶性的判断以及函数图象的变换 对数函数的图象变换
练习 (1)y= lg x 的(2)y=log2 x 3 的对称轴是 (3)y=loga 2 x 1 对称轴方程为
10x 例 3.已知 f(x)= x ,求 f-1(x)函数的表达式及其定义域、值域 10 1
巩固新课 小结 (1)判断奇偶性 (3) 图象变换 (4) 求反函数 作业 另附
教学内容
备课札记
一、复习旧课 1. 对数函数的图象及其性质 2. 与对数函数有关的复合函数的定义域、值域、单调区间 的求法 3. 函数图象的变换规律 (1) 平移 (2) 对称
二、新授 例 1.判断下列函数的奇偶性 (1) f(x)=log2(x+1)+log2(x-1) (2) f(x)=log2
翔宇教育集团课时设计活页纸
教学过程
教学内容
备课札记
高一数学教案:映射与定义域值域_3

4.新课讲解:
x3( x >0)
例4.已知ƒ(x)= 3 (x = 0)
0 (x = 0)
求ƒ(3),ƒ(- 1),ƒ[ƒ(- 3)]
教学过程
教学内容
备课札记
例5.根据图象写出解析式
思考题(可选讲):
如图,在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动。设P运动的路程为x,△APB的面积为y,求:
教学过程
教学内容
备课札记
例3.画出函数
x x≤0
y=| x |=
-x x < 0
的图象
引深:画出函数
y = |2 X – 1| + | X + 2 |
的图象
注意说明下面两点:
①函数的图象不一定是一条或几条无限长的平滑曲线,也可以是一些点,一些线段,一段曲线等;
②表示函数的式子也可以不止一个(见例2和例3),对于这类分几个式子表示的函数,应注意不要把它误认为是“概念,运动变化观点下的定义与映射观点下的定义;
函数的三个要素:对应法则、定义域、值域;
函数的三种表示法:解析法、列表法、图象法;
讲解作业中出现的问题
2.新课讲解
例1.某种茶杯每个5元,买x个茶杯的钱数(元)
y = 5 x ,x∈{1,2,3,4}
画出这个函数的图象
例2.国内投寄信函(外埠),假设每封信函不超过20g付邮资80分,超过20g而不超过40g付邮资160分,依此类推,每封x g(0 <x≤100)的信函应付邮资为(单位:分)
(1)y与x之间的函数关系式
(2)画出y =ƒ (x)的图象
高一数学教案:指数与对数函数_3

例 4.求下列函数的单调区间 (1) y=log 2 (x2-3x+2) (2) y=(log 1 x)2+ log 1 x
3 3
三巩固新课 P89 练习 3 小结 (1)求定义域 (2)比较大小 (3)求值域 (4)求单调区间 作业 另附
翔宇教育集团课时设计活页纸教 Nhomakorabea过程教学内容
备课札记
翔宇教育集团课时设计活页纸
教学内容
备课札记
一、复习旧课 1.对数函数的概念 2.对数函数的图象及性质 当 a>1 时 3 求下列函数的定义域 (1) y=
当 0<a<1 时
1 log 1 (2 x)
2
(2)y=
x2 4 lg( x 2 2 x 3)
二、新授 例 1. 比较下列各组中两个值的大小 (1) log23.4, log28.5 (2) log0.31.8 log0.32.7 (3) loga5.1 loga5.9 (a>0,a≠1) (4) log67 log76 (5) log3л log20.8
(3)y=loga(x2-4x+7) (a>0,a≠1) (4)y=log 1
2
3 2x x 2
分析 (1) 你知道 y=log2t (t>0)的值域吗? 设 y=log2t,t=x+3, t 的范围怎样? (2)设 t=3-x2 则 t 的范围怎样? (3)设 t=x2-4x+7 则 t 的范围怎样? (4)设 u= 3 2x x 则 u 的范围怎样?
例 2.比较下列各组中各数的大小 (1)0.32, log20.3 , 20.3 (2)log0.20.4, (3)log23,
高一数学教案:函数复习_1

教学内容
备课札记
一、基本知识点:
1、函数概念,定义域、值域、单调性、奇偶性、反函数的概念。
2、几种所学初等函数的图象、性质。
3、几种图象的变Βιβλιοθήκη 原则。二、典型例题分析:例1、求下列函数的定义域
(1) (2)
例2、已知f(x)= ,求函数y=f[f(x)]的定义域。
例3、求下列函数的值域
(1)y=|x-3|-|x+1| (2)y=x -2x+5
翔宇教育集团课时设计活页纸
主备人:胡定芳
总课题
函数复习
总课时
第时
课题
单元复习(1)
课型
复习
教学目标
1、进一步理解函数的有关概念及其性质。
2、会求某些函数的定义域、值域、单调区间、反函数以及
函数奇偶性的判定。能根据图象变换原则画出某些函数的图象
教学重点
函数概念的理解及性质的应用。
教学难点
函数知识的综合应用。
(3)y= (4)y=
(5)y= +x (6)y=2+
教学过程
教学内容
备课札记
例4、画出下列函数的图象:(根据图象可考察函数的性质)
(1)y= (2)y=x -4|x|+1 (3)y=
(4)y= (5)y=2 (6)y=|2 -2|
例5、已知f(x)=( ) 在(0,+∞)上是增函数,求m的取值范围。
例6、求函数y=a 的值域和单调区间
高一数学:等差数列 教学设计1
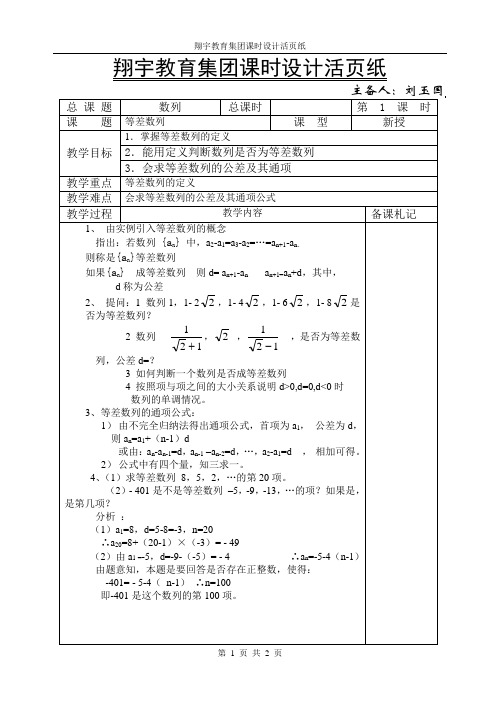
1 2 1
, 2 ,
1 2 1
,是否为等差数
列,公差 d=? 3 如何判断一个数列是否成等差数列 4 按照项与项之间的大小关系说明 d>0,d=0,d<0 时 数列的单调情况。 3、等差数列的通项公式: 1) 由不完全归纳法得出通项公式,首项为 a1, 公差为 d, 则 an=a1+(n-1)d 或由:an-an-1=d,an-1 –an-2=d,…,a2-a1=d , 相加可得。 2) 公式中有四个量,知三求一。 4、 (1)求等差数列 8,5,2,…的第 20 项。 (2)- 401 是不是等差数列 –5,-9,-13,…的项?如果是, 是第几项? 分析 : (1)a1=8,d=5-8=-3,n=20 ∴a20=8+(20-1)×(-3)= - 49 (2)由 a1 =-5,d=-9-(-5)= - 4 ∴an=-5-4(n-1) 由题意知,本题是要回答是否存在正整数,使得: -401= - 5-4( n-1) ∴n=100 即-401 是这个数列的第 100 项。
翔宇教育集团课时设计活页纸
翔宇教育集团课时设计活页纸
主备人:刘玉国
总 课 题 课 题 教学目标 教学重点 教学难点 教学过程 数列
等差数列 1.掌握等差数列的定义
总课时 课 型
第
1 课 新授
时
2.பைடு நூலகம்用定义判断数列是否为等差数列 3.会求等差数列的公差及其通项
等差数列的定义 会求等差数列的公差及其通项公式 教学内容
第 1 页 共 2 页
翔宇教育集团课时设计活页纸
教学过程
教学内容
备课札记
5、在等差数列 {an}中,已知,a5=10,a12=31,求首项 a1 与公 差 d, 分析:由题意知: a1+4d=10 解之得:a1= - 2,d=3。 a1+11d+31
集合与简易逻辑复习
例题 7:已知 p 是 s 的充分不必要条件,s 是 q 的必要不充分
条件同时又是 r 的充分不必要条件,q 是 r 的必要不充分条件, 问:(1)r 是 p 的什么条件,p 是 q 的什么条件?(2)p,q,r,s 中, 有几对是互为充要条件?
例题 5:写出下列命题的否定和否命题,并判断其真假:
矩形的对角线相等; (2)弦心距相等则弦长相等; 2 (3)若 b 4ac 0 ,则方程 ax2 bx c 0 有实数解; (4)若 x,y 都是偶数,则 x+y 与 xy 都是偶数
例题 6:写出下列命题的逆命题、否命题和逆否命题,并判断
1 A .求证: 1 a
第 4 页 共 4 页
选题人:仲坚
3 3 3 3 3 3 3 3
)
A. a b B. a b C. a b 且 a b D. 3 a 3 b 或 3 a 3 b 6、若甲为乙的必要条件,丙为乙的充分条件,但不为乙的必要条件,那么丙是甲的( ) A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分又非必要条件 7 、 设全集 U={(x,y)|x ∈ R,y ∈ R} ,集合 M={(x,y)|y ≠ x} , N={(x,y)|y ≠ -x} ,则集合 P={(x,y)|y2=x2}等于( ) A. ( CU M ) ∩ ( CU N ) B. ( CU M ) ∪N C. ( CU M ) ∪ ( CU N ) D. M∪ ( CU N ) 8、若命题 p:a2<0,q:2a+1 是奇数, (a∈N).则复合命题 p 且 q,p 或 q,┐p,┐q 中真 命题的个数是( ) A.1 B.2 C.3 D.4 9、下列说法:①若一个命题的否命题是真命题,则这个命题不一定是真命题;②若一个 命题的逆否命题是真命题,则这个命题是真命题;③若一个命题的逆命题是真命题,则这 个命题不一定是真命题;④若一个命题的逆命题和否命题都是真命题,则这个命题一定是 真命题;其中正确的说法是( ) A.①② B.①③④ C.②③④ D.①②③ 二、填空题: 10、在 100 个学生中,有篮球爱好者 60 人,排球爱好者 65 人,则既爱好篮球又爱好排球 的人数的最小值_____;最大值______.
高一数学教案:函数的应用_1
翔宇教育集团课时设计活页纸
顾云飞
[作业]
1,某商场购进一批单价为16元的日用品,销售一段时间后,为了获得更多的利润,商场决定提高销售价格。
经实验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件。
假定每月销售件数y(件)是价格x(元/件)的一次函数。
(1)试求y与x 之间的关系式。
(2)在商品不积压,且不考虑其他因素的条件下,问:
销售价格定为多少时,才能使每月获得最大利润?每月的利润是多
少?
2、如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b)在AB、AD、CB、CD上分别截取AE、AH、CF、CG都等于x ,当x 取什么值时,四边形EFGH的面积最大,求出这个最大值。
D G C。
人教九下《孔乙己》教学设计(陈连书)
人教九下《孔乙己》教学设计(陈连书)翔宇教育集团课时设计活页纸总课题第三单元小说之林总课时3 第1课时课题孔乙己课型新授教学目标1、认识封建科举制度的罪恶,教育学生珍惜现在的学习生活2、学习通过人物的外貌、语言、动作表现人物性格的写作方法3、理解孔乙己这一形象所揭示的社会意义。
教学重点目标2、3教学难点目标1、3教学过程教学内容备课札记教师活动内容、方式学生活动方式背景:本文写于1918年冬天,发表于1919年4月的《新青年》杂志,后来收入短篇小说集《呐喊》。
在当时的文化教育领域,虽然在1906年就废止了封建科举制度,但封建复古逆流仍然很猖獗。
封建教育仍然是社会教育的核心内容。
鲁迅先生针对现状,写了二十多年前的社会现实,启发人们将其与当时现状进行对照,懂得批判与取舍。
一、布置预习作业1、自读课文,整理生字词2、用不同符号画出文中外貌、语言、动作描写的句子,并思考其对于刻画人物的作用3、尝试归纳孔乙己人物形象的特点二、导入新课鲁迅一生写了33篇小说,最喜欢的是《孔乙己》,巴金先生也说,孔乙己写得多么好,日本一位作家也说,孔乙己是最完美的艺术典型,凡读过《孔乙己》的人,无不在心中留下孔乙己这个深受封建科举制度毒害,又遭到冷酷现实凉薄的苦人儿的形象。
鲁迅先生怎样运用鬼斧神工之笔来精心塑造这个形象呢?请让我们一起来学习这篇课文——《孔乙己》。
三、感知课文(了解情节结构)1、检查生字词自学情况阔绰(chuò)羼(chàn)绽出(zhàn)间或(jiàn)拭(shì)蘸(zhàn)打折(shé)附和(hè)不屑置辩(xiè)颓唐(tuí)2、教者范读课文,要求学生用一句话归纳小说的情节3、指名回答教师活动内容、方式学生活动方式备课札记4、引导学生理清小说的结构提示:按照小说情节的开端、发展、高潮、结局划分课文结构。
高一数学-正弦函数图象3 精品
四.课时小结:
y=Asin(ωx+φ)(A>0,ω>0,x∈R)的图象作法:(1)五点法(2)变换法(方法,顺序不唯一且方法具有一般性)
课外练习:P68 T4,5
翔宇教育集团数学专用作业纸
班级
高一()
姓名
学号
翔宇教育集Hale Waihona Puke 课时设计活页纸主备人:杨德玉
总课题
函数y=Asin(ωx+φ)的图象
总课时
第3课时
课题
函数y=Asin(ωx+φ)的图象3
课型
新授
教学目标
1.会用“五点法”和变换法作函数y=Asin(ωx+φ)
2.有关振幅,周期,频率,相位,初相的求法
3.化归思想的渗透及观察概括能力
教学重点
函数y=Asin(ωx+φ)的图象作法及相关概念
2.P66 T1(8)(9)(10)
备用题:
1.把函数y=3cos(x+ )的图象向()可得y=-3sinx的图象
A左移 B右移 C左移 D右移
2.函数y=3sin(2x+ )的图象可由y=sinx的图象作怎样的变换而得?
3.若函数y=f(x)图象上每一点纵坐标不变,横坐标伸长到原来的2倍,然后再将整个图象左移 个单位且下移1个单位可得y= sinx的图象。则f(x)=
课题
一.填空题
1.把曲线y=3sin(2x+ )向左平移 ,再把所得图象各点横坐标缩为原来的 ,并将所得图象上各点纵坐标变为原来的 倍得到的图象对应函数为
2.函数y=4cos 的对称中心坐标为,对称轴方程为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 4 页
翔宇教育集团课时设计活页纸
主备人:周松声
总 课 题 棱锥 总课时 4 第1 课时
课 题 棱锥的概念和性质 课 型
新授课
教学目标
1.通过棱锥、正棱锥概念的教学,培养学生知识迁移能力及数学表达能力;
2.通过对正棱锥中相关元素的相互转化的研究,提高学生空间想象能力及
空间问题向平面转化的能力.
教学重点
正棱锥的性质
教学难点
棱锥的概念和性质的运用
教学过程 教学内容 备课札记
一.复习提问
1.什么叫做棱柱?若上底面缩成一点,其侧面棱有何变化?
2.这种几何体的本质有何特征?
二.新课讲解
(板书)棱锥
1.棱锥的有关概念。
(1)棱锥的定义。
有一个面是多边形,其余各面都是有一个公共顶点的三角形,这些
面围成的几何体叫做棱锥
(2)棱锥的几个概念。
这里,这个多边形叫做棱锥的底面,其余各面叫做棱锥的侧面;相邻
侧面的公共边叫做棱锥的侧棱,各侧面的公共顶点叫做棱锥的顶点,
顶点到底面的距离叫做棱锥的高。
(3)棱锥的表示方法。
棱锥用表示顶点和底面各顶点,或底面一条对角线端点的字母来表
示。
(4)棱锥的分类。
棱锥的底面可以是三角形,四边形,五边形…我们把这样的棱锥叫做
三棱锥,四棱锥,五棱锥…
2.棱锥的性质
一般棱锥的性质:
如果棱锥被平行于底面的平面所截,那么截面和底面相似,并且它
们的面积的比等于截得的棱锥的高与已知棱锥的高的平方的比。
3.正棱锥的概念和性质
正棱锥的定义:
如果一个棱锥底面是正多边形,并且顶点在底面内的射影是底面
的中心,这样的棱锥叫做正棱锥。
正棱锥的性质:
(1)各侧棱相等,各侧面都是全等的等腰三角形。各等腰三角形底
边上的高相等,它叫做正棱锥的斜高。
第 2 页 共 4 页
教学过程 教学内容 备课札记
(2)棱锥的高,斜高和斜高在底面内的射影组成一个三角形;棱锥的
高,侧棱和侧棱在底面内的射影也组成一个三角形
4.棱锥的体积
V
棱锥
=Sh31,其中S是棱锥的底面积,h是棱锥的高。
5.例题分析
例1 已知:正四棱锥S—ABCD中,底面边长为2,斜高为2.
求:(1)侧棱长;
(2)棱锥的高;
(3)侧棱与底面所成的角
(4)侧面与底面所成的角
例2.已知正三棱锥S-ABC的高SO=h,斜高SM=L,求经过SO的中
点且平行于底面 ⊿A′B′C′的面积
例3.如图 四棱锥P-ABCD的底面是一直角梯形,BA⊥AD,CDAD侧面PAD
底面ABCD
(1)求证:平面PCD平面PAD;
(2)若AB=2,CD=4,侧面PBC是边长为10的正三角形,求对角
线AC与侧面PCD所成角的正弦值。
三.小结
(1)棱锥的有关概念和性质;
(2)正棱锥的概念和性质。
第 3 页 共 4 页
翔宇教育集团数学专用作业纸
班级 高二( ) 姓名 学号 课题 棱锥(1)
1.满足下列哪一个条件的棱锥必是正棱锥 ( )
A . 侧面都是等腰三角形
B. 底面是正多边形
C. 底面是正多边形,且侧棱与底面所成的角相等
D. 对角面是全等的正三角形
2三棱锥P-ABC的侧棱与底面所成的角相等,O是P在底面上的射影,则下列判断不一定
正确的是 ( )
A. O是△ABC的中心 B. PA=PB=PC
C. OA=OB=OC D. O是△ABC的外心
3. 一棱锥的底面积是Q,经过这个棱锥的高的中点作一平行于底面的截面,那么这个截面的面
积是 ( )
A 21Q B 31Q C 41Q D 22Q
4. 三棱锥P-ABC的侧棱两两垂直,则P在底面上的射影是△ABC的 ( )
A 重心 B 外心 C 内心 D 垂心
5.一棱锥的各棱都相等,则这棱锥必不是 ( )
A 三棱锥 B 四棱锥 C五棱锥 D六棱锥
6。正三棱锥底面边长为3,侧棱长为6,则高为
7.正四棱锥的每一条棱均为a,则它的对角面的面积为
8.已知正四棱锥的底面边长是4cm,侧棱长是23cm,求它的斜高长以及它的侧面和底面
所成的二面角.
第 4 页 共 4 页
9. 如图,棱锥V-ABC的侧棱长都等于13cm,底面为等腰三角形ABC,AB=AC,
底边BC=6cm,BC上的高AD=9cm,求这三棱锥的高。
10 正四棱锥的棱长均为a ,(1)求侧面与底面所成角的余弦值;(2)求相邻
两个侧面所成二面角的余弦值;(3)求证 =2。
A
B
C
V
D
