模糊c-均值聚类算法
【计算机科学】_模糊c均值聚类算法_期刊发文热词逐年推荐_20140727
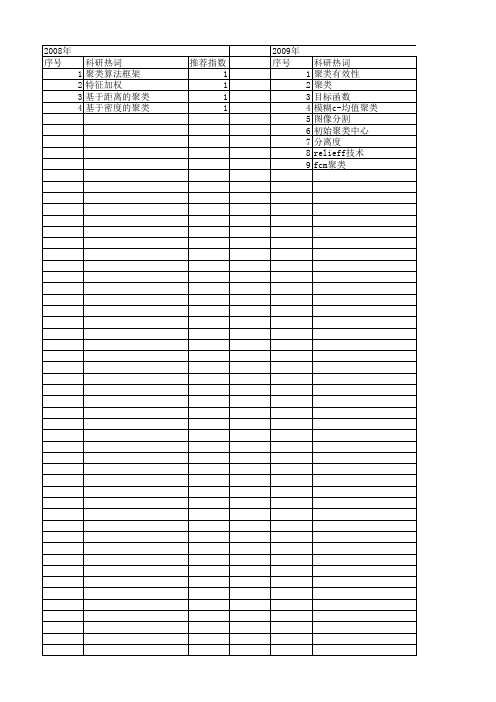
科研热词 聚类算法框架 特征加权 基于距离的聚类 基于密度的聚类
推荐指数 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9
科研热词 聚类有效性 聚类 目标函数 模糊c-均值聚类 图像分割 初始聚类中心 分离度 relieff技术 fcm聚类
推荐指数 1 1 1 1 1 1 1 1 1
2011年 序号
科研热词 1 阴影集 2 粗糙聚类 3 粗糙模糊聚类
推荐指数 2 2 2
2012年 序号 1 2 3构 粒子群优化 模糊聚类 模糊c均值聚类 支持向量机 图形处理器 可能性c均值
推荐指数 2 2 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9
2013年 科研热词 阴影集 粗糙集 模糊c均值 核空间 拉普拉斯映射 彩色图像分割 局部线性嵌入 pcm fcm 推荐指数 1 1 1 1 1 1 1 1 1
模糊C均值聚类

主 单
讲:周润景 教授 位:电子信息工程学院
目 录
模糊C均值聚类应用背景 模糊C均值算法 模糊C均值聚类的MATLAB实现 模糊C均值聚类结果分析
一.模糊C均值聚类应用背景
传统的聚类分析是一种硬划分(Crisp Partition),它把每个待辨识的对 象严格地划分到某类中,具有“非此即彼”的性质,因此这种类别划分的界限 是分明的。然而实际上大多数对象并没有严格的属性,它们在性质和类属方面 存在着中介性,具有“亦此亦彼”的性质,因此适合进行软划分。Zadeh提出 的模糊集理论为这种软划分提供了有力的分析工具,人们开始用模糊方法来处 理聚类问题,并称之为模糊聚类分析。模糊聚类得到了样本属于各个类别的不 确定性程度,表达了样本类属的中介性,建立起了样本对于类别的不确定性的
三.模糊C均值聚类的MATLAB实现
426.31 3105.29 2057.8 1507.13 1556.89 1954.51 343.07 3271.72 2036.94 2201.94 3196.22 935.53 2232.43 3077.87 1298.87 1580.1 1752.07 2463.04 1962.4 1594.97 1835.95 1495.18 1957.44 3498.02 1125.17 1594.39 2937.73 24.22 3447.31 2145.01 1269.07 1910.72 2701.97 1802.07 1725.81 1966.35 1817.36 1927.4 2328.79 1860.45 1782.88 1875.13]; [center,U,obj_fcn] = fcm(data,4); plot3(data(:,1),data(:,2),data(:,3),'o');
模糊c均值聚类算法python

模糊c均值聚类算法python以下是Python实现模糊c均值聚类算法的代码:pythonimport numpy as npimport randomclass FuzzyCMeans:def __init__(self, n_clusters=2, m=2, max_iter=100, tol=1e-4): self.n_clusters = n_clusters # 聚类数目self.m = m # 模糊因子self.max_iter = max_iter # 最大迭代次数self.tol = tol # 中心点变化停止阈值# 初始化隶属度矩阵def _init_membership_mat(self, X):n_samples = X.shape[0]self.membership_mat = np.random.rand(n_samples, self.n_clusters)self.membership_mat = self.membership_mat /np.sum(self.membership_mat, axis=1)[:, np.newaxis]# 更新聚类中心点def _update_centers(self, X):membership_mat_pow = np.power(self.membership_mat, self.m)self.centers = np.dot(X.T, membership_mat_pow) /np.sum(membership_mat_pow, axis=0)[:, np.newaxis]# 计算隶属度矩阵def _update_membership_mat(self, X):n_samples = X.shape[0]self.distances = np.zeros((n_samples, self.n_clusters))for j in range(self.n_clusters):self.distances[:, j] = np.linalg.norm(X-self.centers[j, :], axis=1) self.membership_mat = 1 / np.power(self.distances, 2/(self.m-1))self.membership_mat = self.membership_mat /np.sum(self.membership_mat, axis=1)[:, np.newaxis]# 判断是否满足停止迭代的条件def _check_stop_criteria(self):return np.sum(np.abs(self.centers - self.old_centers)) < self.tol # 聚类过程def fit(self, X):self._init_membership_mat(X)for i in range(self.max_iter):self.old_centers = self.centers.copy()self._update_centers(X)self._update_membership_mat(X)if self._check_stop_criteria():break# 预测样本所属的簇def predict(self, X):distances = np.zeros((X.shape[0], self.n_clusters))for j in range(self.n_clusters):distances[:, j] = np.linalg.norm(X-self.centers[j, :], axis=1) return np.argmin(distances, axis=1)使用方法:pythonfrom sklearn.datasets import make_blobsimport matplotlib.pyplot as pltX, y = make_blobs(n_samples=500, centers=3, random_state=42)fcm = FuzzyCMeans(n_clusters=3)fcm.fit(X)plt.scatter(X[:, 0], X[:, 1], c=fcm.predict(X))plt.show()。
模糊C均值聚类算法的C++实现代码

算法描述 模糊 C 均值聚类算法的步骤还是比较简单的,模糊 C 均值聚类(FCM),即众
所周知的模糊 ISODATA,是用隶属度确定每个数据点属于某个聚类的程度的一种 聚类算法。1973 年,Bezdek 提出了该算法,作为早期硬 C 均值聚类(HCM)方法 的一种改进。
研究背景
模糊 C 均值聚类算法的实现
聚类分析是多元统计分析的一种,也是无监督模式识别的一个重要分支,在 模式分类 图像处理和模糊规则处理等众多领域中获得最广泛的应用。它把一个 没有类别标记的样本按照某种准则划分为若干子集,使相似的样本尽可能归于一 类,而把不相似的样本划分到不同的类中。硬聚类把每个待识别的对象严格的划 分某类中,具有非此即彼的性质,而模糊聚类建立了样本对类别的不确定描述, 更能客观的反应客观世界,从而成为聚类分析的主流。
FCM 把 n 个向量 xi(i=1,2,…,n)分为 c 个模糊组,并求每组的聚类中心, 使得非相似性指标的价值函数达到最小。FCM 与 HCM 的主要区别在于 FCM 用模糊 划分,使得每个给定数据点用值在 0,1 间的隶属度来确定其属于各个组的程度。 与引入模糊划分相适应,隶属矩阵 U 允许有取值在 0,1 间的元素。不过,加上 归一化规定,一个数据集的隶属度的和总等于 1:
c
uij 1,j 1,..., n
i 1
(6.9)
那么,FCM 的价值函数(或目标函数)就是式(6.2)的一般化形式:
c
cn
J (U , c1,..., cc ) Ji
u
m ij
d
2 ij
模糊聚类算法的原理和实现方法

模糊聚类算法的原理和实现方法模糊聚类算法是一种数据分类和聚类方法,它在实际问题中有着广泛的应用。
本文将介绍模糊聚类算法的原理和实现方法,包括模糊C均值(FCM)算法和模糊神经网络(FNN)算法。
一、模糊聚类算法的原理模糊聚类算法是基于模糊理论的一种聚类方法,它的原理是通过对数据进行模糊分割,将每个数据点对应到多个聚类中心上,从而得到每个数据点属于各个聚类的置信度。
模糊聚类算法的原理可以用数学公式进行描述。
设有n个数据样本点X={x1, x2, ..., xn},以及m个聚类中心V={v1, v2, ..., vm}。
对于每个数据样本点xi,令uij为其属于第j个聚类中心的置信度,其中j=1,2,..., m,满足0≤uij≤1,且∑uij=1。
根据模糊理论,uij的取值表示了xi属于第j个聚类中心的隶属度。
为了达到聚类的目的,我们需要对聚类中心进行调整,使得目标函数最小化。
目标函数的定义如下:J = ∑∑(uij)^m * d(xi,vj)^2其中,m为模糊度参数,d(xi,vj)为数据点xi与聚类中心vj之间的距离,常用的距离度量方法有欧氏距离和曼哈顿距离。
通过不断调整聚类中心的位置,最小化目标函数J,即可得到模糊聚类的结果。
二、模糊C均值(FCM)算法的实现方法模糊C均值算法是模糊聚类算法中最经典的一种方法。
其具体实现过程如下:1. 初始化聚类中心:随机选取m个数据点作为初始聚类中心。
2. 计算隶属度矩阵:根据当前聚类中心,计算每个数据点属于各个聚类中心的隶属度。
3. 更新聚类中心:根据隶属度矩阵,更新聚类中心的位置。
4. 判断是否收敛:判断聚类中心的变化是否小于设定的阈值,如果是则停止迭代,否则返回第2步。
5. 输出聚类结果:将每个数据点分配到最终确定的聚类中心,得到最终的聚类结果。
三、模糊神经网络(FNN)算法的实现方法模糊神经网络算法是一种基于模糊理论和神经网络的聚类方法。
其实现过程和传统的神经网络类似,主要包括以下几个步骤:1. 网络结构设计:确定模糊神经网络的层数和每层神经元的个数。
基于模糊C均值的聚类分析

• U = initfcm(cluster_n, data_n); %初始 化模糊分割矩阵
%以下为主循环: • for i = 1:max_iter, • [U, center, obj_fcn(i)] =
stepfcm(data, U, cluster_n, expo); • if display, • fprintf('Iteration count = %d, obj.
基于模糊C均值的聚类分析
1 模糊c均值聚类(FCM)方法
模糊C均值聚类(FCM)方法是一种在已 知聚类数的情况下,利用隶属度函数和迭 代算法将有限的数据集分别聚类的方法。 其目标函数为:
式中, 为样本数; 为聚类数; 为第 个 样本相对于第 个聚类中心的隶属度; 为
第 个类别的聚类中心; 为样本到聚类 中心的欧式距离。聚类的结果使目标函 数 最小,因此,构造如下新的目标函 数:
(2)
这里 , =1,⋯ ,n,是等式的n个约束 式的拉格朗日乘子。对所有输入参量求 导,使式(1)达到最小的必要条件为:
(3)
(4)
由上述两个必要条件,模糊c均值聚类算 法是一个简单的迭代过程。在批处理方 式运行时,FCM采用下列步骤确定聚类中 心 和隶属矩阵 U:
步骤1 用值在0,1间的随机数初始 化隶属矩阵U,使其满足式(2)中的约束 条件。
1735.33; 2421.83; 2196.22; 535.62; 584.32; 2772.9; 2226.49; 1202.69;
2949.16 1692.62 1680.67 2802.88 172.78 2063.54 1449.58 1651.52 341.59 291.02
3244.44 1867.5 1575.78 3017.11 3084.49 3199.76 1641.58 1713.28 3076.62 3095.68
关于模糊C-均值(FCM)聚类算法的改进
隶 属度 。 = { 是 一个 n×c的模 糊分 割 矩 U t} x
阵, = V , , } A, 是一 个 S×c的矩 阵 。 m用 来控制 分 割 矩 阵 的模糊 程度 , m越 大 ,分 类 的 模 糊 程 度 越 高 , 。 时 , = m一 。 一 1 c 实 际 上 已不 能 提供 分 类 信 息 ; m = 1 /, 当 时 , ∈ [ , ] 算 法 退 化 为 HC 算 法 , 以 i x 01 , M 所 F M实质 上是 H M 的 自然 推广 。 氏距 离准则 C C 欧 适合 于类 内数 据点 为 超 球 型分 布 的情 况 , d 采 用不 同 的距 离定 义 , 可将 聚类 算 法 用 于 不 同分 布类 型数据 的聚类 问题 。
别、 分析 与 预 测 的 目的 。17 9 3年 D n u n提 出 了
J = ∑ 1
1 J= 1
l ∈[, 01 ]
式 中 为样 本 数 据 点 的数 目, 类 别 数 c为
目, 常 1< c<n m > 1为一 个标 量 ; , 通 ; d (, ) = l i一 _示数 据点 , 之 间 的欧 氏距 】 I x 心
1 引 言
模糊 聚 类 分 析 ( C F :
Bl a e m n和 Z d h等 人 在 16 l ae 9 6年 提 出 的 , 是 它 近些年 来发展 很 快 的一 种 分析 方 法 , 目的是 其 对 样本 进行合 理 分 配 , 而 达 到 对样 本 进 行 判 从
离 ; ={ , , } 的集合 , ∈R 为 A, cR 点 聚类 的中心 ; t 表示 数据 点 属 于类 中心 的 z
用 于求类 中心 的迭 代 问题 , 算 法 中没 有 考 虑 该
模糊C均值聚类算法的C 实现代码讲解
模糊C均值聚类算法的实现研究背景模糊聚类分析算法大致可分为三类1)分类数不定,根据不同要求对事物进行动态聚类,此类方法是基于模糊等价矩阵聚类的,称为模糊等价矩阵动态聚类分析法。
2)分类数给定,寻找出对事物的最佳分析方案,此类方法是基于目标函数聚类的,称为模糊C均值聚类。
3)在摄动有意义的情况下,根据模糊相似矩阵聚类,此类方法称为基于摄动的模糊聚类分析法聚类分析是多元统计分析的一种,也是无监督模式识别的一个重要分支,在模式分类图像处理和模糊规则处理等众多领域中获得最广泛的应用。
它把一个没有类别标记的样本按照某种准则划分为若干子集,使相似的样本尽可能归于一类,而把不相似的样本划分到不同的类中。
硬聚类把每个待识别的对象严格的划分某类中,具有非此即彼的性质,而模糊聚类建立了样本对类别的不确定描述,更能客观的反应客观世界,从而成为聚类分析的主流。
模糊聚类算法是一种基于函数最优方法的聚类算法,使用微积分计算技术求最优代价函数,在基于概率算法的聚类方法中将使用概率密度函数,为此要假定合适的模型,模糊聚类算法的向量可以同时属于多个聚类,从而摆脱上述问题。
我所学习的是模糊C均值聚类算法,要学习模糊C均值聚类算法要先了解虑属度的含义,隶属度函数是表示一个对象x隶属于集合A的程度的函数,通常记做μA(x),其自变量范围是所有可能属于集合A的对象(即集合A所在空间中的所有点),取值范围是[0,1],即0<=μA (x)<=1。
μA(x)=1表示x完全隶属于集合A,相当于传统集合概念上的x∈A。
一个定义在空间X={x}上的隶属度函数就定义了一个模糊集合A,或者叫定义在论域X={x}上的模糊子集~A。
对于有限个对象x1,x2,……,xn模糊集合~A可以表示为:}|)),({(~XxxxAiiiA∈=μ (6.1)有了模糊集合的概念,一个元素隶属于模糊集合就不是硬性的了,在聚类的问题中,可以把聚类生成的簇看成模糊集合,因此,每个样本点隶属于簇的隶属度就是[0,1]区间里面的值。
基于自适应近邻信息的模糊C_均值聚类算法
第 32 卷第 7 期2024 年 4 月Vol.32 No.7Apr. 2024光学精密工程Optics and Precision Engineering基于自适应近邻信息的模糊C均值聚类算法高云龙1,李建鹏2,郑兴莘1,邵桂芳1,祝青园1,曹超3*(1.厦门大学萨本栋微米纳米科学技术研究院,福建厦门 361102;2.厦门大学自动化系,福建厦门 361102;3.自然资源部第三海洋研究所,福建厦门 361005)摘要:传统的模糊C均值算法直接基于原始数据进行聚类,数据的内在结构可能会被噪声、异常值或其他因素破坏,因此聚类性能会受到影响。
为提升FCM算法的鲁棒性,提出了一种基于自适应近邻信息的模糊C均值聚类算法。
近邻信息指的是一种基于数据点之间相似度的度量,每个数据点都可以看作其他数据点的近邻,但是不同数据点之间的相似度是不同的。
将样本点的近邻信息G X和类中心点的近邻信息G V融入基础FCM模型中,为聚类过程提供更多的数据结构信息,用于指导聚类算法中的簇划分过程,以提升算法的稳定性,并提出了3个迭代算法求解本文提出的聚类模型。
与其他先进聚类算法对比,在部分基准数据集上聚类性能有10%以上的提升,同时还从参数敏感性、收敛性、消融实验等方面对算法进行评价。
实验结果可以充分显示本文提出的聚类算法的可行性与有效性。
关键词:模糊C均值聚类;自适应近邻;算法鲁棒性;迭代算法中图分类号:TP394.1;TH691.9 文献标识码:A doi:10.37188/OPE.20243207.1045Fuzzy C-means clustering algorithm based onadaptive neighbors informationGAO Yunlong1,LI Jianpeng2,ZHENG Xingshen1,SHAO Guifang1,ZHU Qingyuan1,CAO Chao3*(1.Pen-Tung Sah Institute of Micro-Nano Science and Technology, Xiamen University,Xiamen 361102, China;2.Department of Automation, Xiamen University, Xiamen 361102, China;3.Third Institute of Oceanography, Ministry of Natural Resources, Xiamen 361005, China)* Corresponding author, E-mail: caochao@Abstract: Traditional FCM algorithms cluster based on raw data, risking distortion from noise, outliers, or other disruptions, which can degrade clustering outcomes. To bolster FCM's resilience, this study intro⁃duces a fuzzy C-means clustering algorithm that leverages adaptive neighbor information. This concept hinges on the similarity between data points, treating each point as a potential neighbor to others, albeit with varying degrees of similarity. By integrating the neighbor information of sample points, labeled G X, and that of cluster centers, labeled G V, into the standard FCM framework, the algorithm gains additional insights into data structure. This aids in steering the clustering process and enhances the algorithm's robust⁃文章编号1004-924X(2024)07-1045-14收稿日期:2023-08-28;修订日期:2023-10-11.基金项目:国家自然科学基金资助项目(No.42076058,No.52075461);福建省自然科学基金资助项目(No.2020J01713,第 32 卷光学精密工程ness. Three iterative methods are presented to implement this enhanced clustering model. When com⁃pared to leading clustering techniques, our approach demonstrates over a 10% improvement in cluster⁃ing efficacy on select benchmark datasets. It undergoes thorough evaluation across different dimen⁃sions, including parameter sensitivity, convergence rate, and through ablation studies, confirming its practicality and efficiency.Key words: fuzzy C-means clustering; adaptive neighbors; algorithm robustness; iterative algorithm1 引言作为一种无监督方法,聚类的基本任务是将数据点划分为不相交的簇,使得同一簇内数据点之间的相似度最大化,而不同簇之间数据点的相似度最小化。
一种扩展的条件模糊C-均值聚类算法
e c le t l se ig pe f r nc . x el n u t rn ro ma e c
Ke o d : uz - a sF M) ls r g C n io a F z - a s F M) ls r g fz atinma i yw r s F zyC Men ( C c t n ; o dt n l u yC Men ( C c t n ;uz p rt tx ue i i z C ue i y io r
C m u r nier gad p la os o p t gnei A pi t n计算机工程与应用 eE n n ci
一
种扩展 的条件模糊 均值聚类算法
曾振 东
ZENG e d n Zh n o g
广东青年职业学院 , 广州 500 15 7
Gu n d n o t o  ̄i n l l g , a g h u 5 0 0 , i a a g o g Y u h V c o a l e Gu n z o 5 7 Ch n Co e 1
we k n d ti a e r p s sa xe d d c n i o a CM l se n lo i a e e , hsp p rp o o e n e tn e o dt n l i F cu tr g ag r h . h a i o ar n r t— i t m T ep r t n m ti a d p oo t i x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模糊c-均值聚类算法
模糊c-均值聚类算法
聚类算法是机器学习领域中的一种非监督学习算法,其目的是将数据集中的数据分成不同的类别。
聚类是一项重要的数据分析技术,对于数据挖掘、可视化和特征提取等领域都有着广泛的应用。
模糊c-均值聚类算法(FCM)是聚类算法中的一种方法,它允许一个数据点属于不同的类别的程度表示为一个0到1之间的值。
模糊c-均值聚类算法是基于c-均值聚类算法的一种改进,c-均值聚类算法是一种经典的划分聚类算法,它将样本集合非随机地分为c个类。
c-均值聚类算法的基本思想是通过计算一组质心(即类别的均值)来分离数据。
这个算法的主要问题是它仅适用于识别在分离超平面上紧密且凸形成团的类别,因此不能很好地处理重叠的类别。
对于数据集中的每个数据点,模糊c-均值聚类算法允许给出改数据点属于不同的类别的程度表示为一个概率值。
这是因为该算法使用的是一种模糊逻辑,即一种可以量化事物不确定性的逻辑,可以被用于处理数据模糊化的问题。
在模糊c-均值聚类算法中,样本之间的距离是通过一种模糊分割矩阵来表示的,该矩阵中每个元素表示一个样本属于一个类别的程度,可以使用分割矩阵计算每个样本属于每个类别的概率。
模糊c-均值聚类算法的优点是它可以自适应地划分数据,使得该算法
可以更好地处理数据的重叠和模糊性。
此外,模糊c-均值聚类算法也支持将数据点分配到多个类别中,这可以很好地解决当数据不仅仅具有单一特征时的问题。
同样,该算法还可以被用于图像分割和空间分析等领域。
在实际应用中,模糊c-均值聚类算法通常需要设置一些参数,例如类别数量c、模糊指数m和迭代次数k等。
这些参数的不同取值对算法的结果产生影响,因此需要通过实验和调参来调整这些参数。
总结来说,模糊c-均值聚类算法是一种非常强大的数据聚类算法,其能力在于用概率表示每个数据点属于不同类别的程度。
该算法处理数据重叠和模糊性方面表现良好,并且可以应用到数据挖掘、图像处理和空间分析等领域。
