中考数学压轴题必考破解瓜豆原理的三种必考题型

合集下载

2024年广东省中考数学二轮复习特色专题突破课件：项目15+种瓜得瓜,种豆得豆

M运动的路径长 = × 2π ×
= π.

探究3 算理的灵活运用及拓展

5. 如图，在反比例函数 = − 的图象上有一动点A，连接AO并延长交

图象的另一支于点B，第一象限内有一点C且AC = BC，当点A运动
时，点C始终在某一函数的图象上运动.若tan∠CAB = 2，则点C所在

接CG，则CG的最小值为

.
思路：
如图解，将线段EB绕E顺时针旋转60°至EM，连
接GM，过C作CN⊥GM于点N，过E作EP⊥CN于
点P，可得△BEF ≌ △MEG，所以点G在射线MG
上运动，CN的长度即CG长度的最小值.
2. 如图，已知点A是第一象限内的一个定点，若点P是以O为圆心，2
个单位长度为半径的圆上的一个动点，连接AP，以AP为边向AP右
侧作等边三角形APB.当点P在⊙O上运动一周时，点B运动的路径长
是
4π
.
思路：
如图解，由瓜豆原理易得点B的运动轨迹是
圆，易证△APO ≌ △ABO′，所以O′B =
OP = 2，点B的运动路径长为2 × 2π = 4π.
3. 如图，点P（3，4），⊙P的半径为2，A（2.8，0），B（5.6，0），
1.“瓜”在直线上运动，“豆”的运动轨迹也是直线.
2.“瓜”在圆上运动，“豆”的运动轨迹也是圆.
瓜豆原理必须要满足两个前提条件：
①主动点、从动点与某定点的连线夹角为定值；
②主动点、从动点到该定点的距离之比为定值.
确定了瓜豆原理后，利用相似（全等）解题，求最值.
2. （2023广州一模）如图，Rt△ABC中，AB = AC = 3，点O在AC上，

中考数学专题复习之三——捆绑旋转(瓜豆原理)

中考数学专题复习之三——捆绑旋转（瓜豆原理）初中数学有一类动态问题叫做主从联动，这类问题应该说是网红问题，原因是它在很多名校模考的时候经常出现，有的老师叫他瓜豆原理，也有的老师叫他捆绑旋转或旋转相似，这类问题在解答的时候需要有轨迹思想，就是先要明确主动点的轨迹，然后要搞清楚主动点和从动点的关系，进而确定从动点的轨迹来解决问题，但在解答问题时，要符合解不超纲的原则，所以最后解决问题还是用到了旋转相似的知识，也就是动态手拉手模型，下面整理一些练习集中训练一下这类问题，希望对你能有所帮助。

一、轨迹之圆篇：引例1：如图，P是⊙O上一个动点，A为定点，连接AP，Q为AP中点．考虑：当点P在⊙O上运动时，Q点轨迹是？AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，QM:PO=AQ:AP=1:2．即Q点运动轨迹应该是以A为位似中心，将⊙O按2:1缩小一半得到的⊙M。

引例2：如图，P是⊙O上一个动点，A为定点，连接AP，作AQ⊥AP且AQ=AP．考虑：当点P在⊙O上运动时，Q点轨迹是？【分析】Q点轨迹是一个圆，可理解为将AP绕点A逆时针旋转90°得AQ，故Q点轨迹与P点轨迹都是圆．考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；考虑AP=AQ，可得AM=AO，且可得半径MQ=PO，从而△APO ≌△AQM．即点Q的运动轨迹应该是将⊙O绕点A逆时针旋转90°的⊙M。

引例3：如图，△APQ Q点轨迹是？【分析】考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；考虑AP:AQ=2:1，可得Q点轨迹圆圆心M满足AO:AM=2:1，即可确定⊙M位置，△APO∽△AQM，且相似比为2：1．即点Q的运动轨迹应该是将⊙O绕点A逆时针旋转90°后，再以A为位似中心缩小一半得到的⊙M。

引例4：如图，P 是⊙O 上一个动点，A 为定点，连接AP ，以AP 为一边作等边△APQ ．考虑：当点P 在⊙O 上运动时，Q 点轨迹是？【分析】Q 点满足（1）∠PAQ=60°；（2）AP=AQ ，故Q 点轨迹是个圆。

初中数学中考压轴之瓜豆原理求线段最值问题

中考线段最值问题----瓜豆原理【问题引入】如下图1所示，Q为OP的中点，P为线段AB上的一个动点，Q为OP的中点，当P点在线段AB上运动时，Q点的运动轨迹是什么？【问题分析】如下图2，当P点为于A点时，此时Q点位于OA的中点Q1；当P点位于B点时，此时Q点位于OB的中点Q2；我们发现，△OQ1Q2△△OAB，随着Q点位置的不同，△OQ1Q2与△OAB 一直相似，其本质为动态相似！【模型建立】此类题中，题目或许先描述的是动点P，但最终问题问的是另一个动点Q，P和Q之间存在着某种联系，从P点出发探讨Q点运动轨迹即为本文要探讨的瓜豆原理。

1、两个概念：主动点：主动运动的点称为主动点，如上图1中的P点；从动点：由于主动点运动而“被迫”运动的点称为从动点，如上图1中的Q点；2、瓜豆原理成立的两个必要条件△主动点、从动点与定点连线的夹角为定值；△主动点、从动点到定点的距离之比是定值.举例如下：如下图3:，动点P在直线BC上运动，A为定点，Q为另一动点，且满足条件：①∠PAQ是定值；②AP：AQ是定值，则动点Q的轨迹与动点P的轨迹一致，即：P在直线BC上动，则Q在另一直线MN上动，且△BAC∽△MAN(动态相似)。

3、核心结论①从动点的运动轨迹与主动点运动轨迹一致，即如果主动点在直线上运动，则从动点也必然在直线上运动；如果主动点在圆上运动，则从动点也必然在圆上运动，故非常形象的称之为“瓜豆原理”。

②主动点的起点、终点、定点组成的三角形与从动点的起点、终点、定点组成的三角形相似(或全等)，如上图中△AMN∽△ABC。

③主动点运动轨迹与从动点的运动轨迹的夹角(锐角)等于主、从动点与定点连线的夹角。

如上图中∠PAQ=α。

【类型总结】---核心处理方法：Step1：找出主动点的起点和终点；Step2：找出题中所有的定点；Step3：验证两个必要条件，即：①主、从动点与定点连线的夹角为定值；②主、从动点到定点的距离之比是定值。

2022年九年级中考数学冲刺难点突破瓜豆原理与最值问题训练

瓜豆原理1.动点轨迹直线型最值问题【知识精讲】动点轨迹为一条直线时，利用“垂线段最短”求最值。

（1）当动点轨迹确定时可直接运用垂线段最短求最值（2）当动点轨迹不易确定是直线时，可通过以下三种方法进行确定①观察动点运动到特殊位置时，如中点，端点等位置时是否存在动点与定直线的端点连接后的角度不变，若存在该动点的轨迹为直线。

②当某动点到某条直线的距离不变时，该动点的轨迹为直线。

③当一个点的坐标以某个字母的代数式表示时，若可化为一次函数，则点的轨迹为直线。

如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q点轨迹是？【分析】当P点轨迹是直线时，Q点轨迹也是一条直线．可以这样理解：分别过A、Q向BC作垂线，垂足分别为M、N，在运动过程中，因为AP=2AQ，所以QN始终为AM的一半，即Q点到BC的距离是定值，故Q点轨迹是一条直线．【引例】如图，△APQ是等腰直角三角形，∠P AQ=90°且AP=AQ，当点P在直线BC上运动时，求Q点轨迹？【分析】当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q 点的起始位置和终点位置，连接即得Q点轨迹线段．【模型总结】必要条件：主动点、从动点与定点连线的夹角是定量（∠P AQ是定值）；主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．结论：P、Q两点轨迹所在直线的夹角等于∠P AQ（当∠P AQ≤90°时，∠P AQ等于MN与BC夹角）P 、Q 两点轨迹长度之比等于AP :AQ （由△ABC ∽△AMN ，可得AP :AQ =BC :MN ）【精典例题】1、如图，等腰Rt △ABC 中，斜边AB 的长为2，O 为AB 的中点，P 为AC 边上的动点，OQ ⊥OP 交BC 于点Q ，M 为PQ 的中点，当点P 从点A 运动到点C 时，点M 所经过的路线长为（）A B C ．1 D ．22、如图，矩形ABCD 中，4AB =，6BC =，点P 是矩形ABCD 内一动点，且∆∆=PAB PCD S S ，则PC PD +的最小值为_____．3、如图，在平面内，线段AB =6，P 为线段AB 上的动点，三角形纸片CDE 的边CD 所在的直线与线段AB 垂直相交于点P ，且满足PC =P A ．若点P 沿AB 方向从点A 运动到点B ，则点E 运动的路径长为______．4、如图，等边三角形ABC 的边长为4，点D 是直线AB 上一点．将线段CD 绕点D 顺时针旋转60°得到线段DE，连结BE．（1）若点D在AB边上（不与A，B重合）请依题意补全图并证明AD=BE；（2）连接AE，当AE的长最小时，求CD的长．2.动点轨迹圆或圆弧型最值问题动点的轨迹为定圆时，可利用：“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和，最小值为定点到圆心的距离与半径之差”的性质求解。

初中数学中考二轮专题专题6 动点最值之瓜豆模型(老师版)

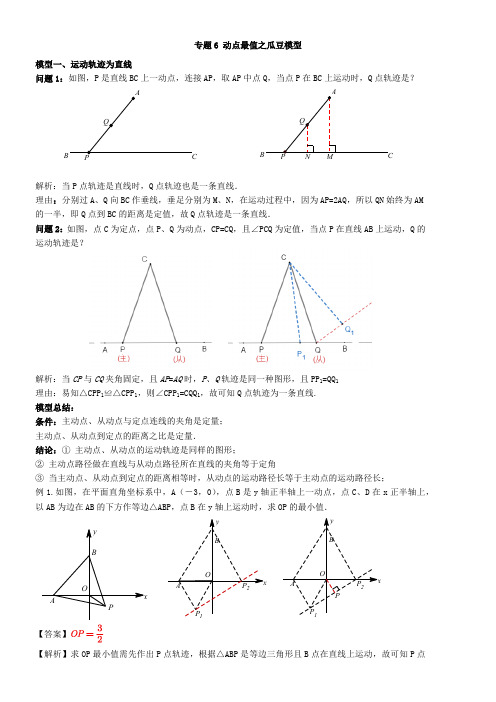
专题6 动点最值之瓜豆模型模型一、运动轨迹为直线问题1：如图，P 是直线BC 上一动点，连接AP ，取AP 中点Q ，当点P 在BC 上运动时，Q 点轨迹是？解析：当P 点轨迹是直线时，Q 点轨迹也是一条直线．理由：分别过A 、Q 向BC 作垂线，垂足分别为M 、N ，在运动过程中，因为AP=2AQ ，所以QN 始终为AM 的一半，即Q 点到BC 的距离是定值，故Q 点轨迹是一条直线．问题2：如图，点C 为定点，点P 、Q 为动点，CP=CQ ，且∠PCQ 为定值，当点P 在直线AB 上运动，Q 的运动轨迹是？解析：当CP 与CQ 夹角固定，且AP =AQ 时，P 、Q 轨迹是同一种图形，且PP 1=QQ 1理由：易知△CPP 1≌△CPP 1，则∠CPP 1=CQQ 1，故可知Q 点轨迹为一条直线.模型总结：条件：主动点、从动点与定点连线的夹角是定量；主动点、从动点到定点的距离之比是定量．结论：① 主动点、从动点的运动轨迹是同样的图形；② 主动点路径做在直线与从动点路径所在直线的夹角等于定角③ 当主动点、从动点到定点的距离相等时，从动点的运动路径长等于主动点的运动路径长；例1.如图，在平面直角坐标系中，A （－3，0），点B 是y 轴正半轴上一动点，点C 、D 在x 正半轴上，以AB 为边在AB 的下方作等边△ABP ，点B 在y 轴上运动时，求OP 的最小值．【解析】求OP 最小值需先作出P 点轨迹，根据△ABP 是等边三角形且B 点在直线上运动，故可知P 点轨迹也是直线．取两特殊时刻：（1）当点B 与点O 重合时，作出P 点位置P 1；（2）当点B 在x 轴上方且AB 与x 轴夹角为60°时，作出P 点位置P 2．连接P 1P 2，即为P 点轨迹．根据∠ABP ＝60°，可知：与y 轴夹角为60°，作OP ⊥，所得OP 长度即为最小值，OP 2＝OA ＝3，所以．例2.如图，已知点A 是第一象限内横坐标为的一个定点，AC ⊥x 轴于点M ，交直线y ＝－x 于点N ，若点P 是线段ON上的一个动点，∠APB ＝30°，BA ⊥PA ，则点P 在线段ON 上运动时，A 点不变，B 点随之运动．求当点P 从点O 运动到点N 时，点B 运动的路径长是________．【分析】∵∠PAB ＝90°，∠APB ＝30＝，故且P 点轨迹路径长之比也为，P 点轨迹长ON ，故B ．【变式训练1】如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE ＝1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG，求CG 的最小值是多少？【答案】【解析】同样是作等边三角形，区别于上一题求动点路径长，本题是求CG 最小值，可以将F 点看成是由点B 向点A 运动，由此作出G 点轨迹：考虑到F 点轨迹是线段，故G 点轨迹也是线段，取起点和终点即可确定线段位置，初始时刻G 点在位置，最终G 点在位置（不一定在CD 边），即为G 点运动轨迹．CG 最小值即当CG ⊥的时候取到，作CH ⊥于点H ，CH 即为所求的最小值．根据模型可知：与AB 夹角为60°，故⊥．过点E 作EF ⊥CH 于点F ，则HF ＝＝1，因此CG ．【变式训练2】如图，△ABC 是边长为6的等边三角形，点E 在AB 上，点D 为BC 的中点，△EDM 为等边三角形．若点E 从点B 运动到点A ，则M 点所经历的路径长为　6　．GABCDEF 22【解答】解：当点E在B时，M在AB的中点N处，当点E与A重合时，M的位置如图所示，所以点E从点B运动到点A，则M点所经历的路径为MN的长，∵△ABC是等边三角形，D是BC的中点，∴AD⊥BC，∠BAD＝30°，∵AB＝6，∴AD＝＝3，∵△EDM是等边三角形，∴AM＝AD＝3，∠DAM＝60°，∴∠NAM＝30°+60°＝90°，∵AN＝AB＝3，在Rt△NAM中，由勾股定理得：MN＝＝＝6，则M点所经历的路径长为6，故答案为：6．【变式训练3】如图，在矩形ABCD中，AB＝4，∠DCA＝30°，点F是对角线AC上的一个动点，连接DF，以DF 为斜边作∠DFE＝30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E 的运动路径长是．【解答】解：E的运动路径是线段EE'的长；∵AB＝4，∠DCA＝30°，∴BC＝，当F与A点重合时，在Rt△ADE'中，AD＝，∠DAE'＝30°，∠ADE'＝60°，∴DE'＝，∠CDE'＝30°，当F与C重合时，∠EDC＝60°，∴∠EDE'＝90°，∠DEE'＝30°，在Rt△DEE'中，EE'＝；故答案为．【变式训练4】如图，已知线段AB＝12，点C在线段AB上，且△ACD是边长为4的等边三角形，以CD为边的右侧作矩形CDEF，连接DF，点M是DF的中点，连接MB，则线段MB的最小值为 .【答案】6【解析】如图所示，∵∠FCB＝30º，∴F的路径是定射线DF，又∵点M是DF的中点，∴∵D点为定点，F点为主动点，M点为从动点，由瓜豆原理内容可知M点的路径亦是一条射线，取CD的中点N，连接NM并延长，则射线NM就是M点的路径，且NM∥CF，作BG⊥NM于点G，交CF于点H，则BG⊥CF，故BG＝BH＋HG＝BH＋CN＝4＋2＝6，∴线段BM的最小值即为BG，最小值为6.模型二、运动轨迹为圆问题1.如图，P是圆O上一个动点，A为定点，连接AP，Q为AP中点．当点P在圆O上运动时，Q点轨迹是？解析：Q点轨迹是一个圆理由：Q点始终为AP中点，连接AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，．问题2.如图，△APQ是直角三角形，∠PAQ=90°且AP=2AQ，当P在圆O运动时，Q点轨迹是？解析：Q点轨迹是一个圆理由：∵AP⊥AQ，∴Q点轨迹圆圆心M满足AM⊥AO；又∵AP：AQ=2：1，∴Q点轨迹圆圆心M满足AO：AM=2：1．即可确定圆M位置，任意时刻均有△APO∽△AQM，且相似比为2．模型总结：条件：两个定量主动点、从动点与定点连线的夹角是定量（∠PAQ是定值）；主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．结论：（1）主、从动点与定点连线的夹角等于两圆心与定点连线的夹角：∠PAQ=∠OAM；（2）主、从动点与定点的距离之比等于两圆心到定点的距离之比：AP:AQ=AO:AM，也等于两圆半径之比．例1.如图，点P（3，4），圆P半径为2，A（2.8，0），B（5.6，0），点M是圆P上的动点，点C是MB的中点，则AC的最小值是_______．Q1=2QM AQPO AP【答案】1.5【解析】由题意可知M 点为主动点，C 点为从动点，B 点为定点．∵C 是BM 中点，可知C 点轨迹为取BP 中点F ，以F 为圆心，FC 为半径作圆，即为点C 轨迹，如图所示：由题中数据可知OP ＝5，又∵点A 、F 分别是OB 、BP 的中点，∴AF 是△BPO 的中位线，∴AF ＝2.5，当M 运动到如图位置时，AC 的值最小，此时A 、C 、O 三点共线，∴AC ＝2.5－1＝1.5.例2.如图，A 是⊙B 上任意一点，点C 在⊙B 外，已知AB ＝2，BC ＝4，△ACD 是等边三角形，则的面积的最大值为（）A ．4B ．4C ．8D ．6【答案】A【详解】解：如图，以BC 为边向上作等边三角形BCM ，连接DM ，∵，∴，即在和中，，∴，∴，∴点D 的运动轨迹是以点M 为圆心，DM 长为半径的圆，要使面积最大，则求出点D 到线段BC 的最大距离，∵是边长为4的等边三角形，∴点M 到BC 的距离是∴点D 到BC 的最大距离是，∴的面积最大值是．故选：A ．例3.如图，正方形ABCD 中，O 是BC 边的中点，点E 是正方形内一动点，OE =2，连接DE ，将线段DE 绕点D 逆时针旋转90°得DF ，连接AE 、CF ．求线段OF 长的最小值．OABCDE FBCD △60DCA MCB ∠=∠=︒DCA ACM MCB ACM ∠-∠=∠-∠DCM ACB=∠∠DCM △ACB △DC AC DCM ACB MC BC =⎧⎪∠=∠⎨⎪=⎩()DCM ACB SAS ≅V V 2DM AB ==BCD △BCM V 2BCD △()14242⨯⨯=AB =【解析】E 是主动点，F 是从动点，D 是定点，E 点满足EO =2，故E 点轨迹是以O 为圆心，2为半径的圆．考虑DE ⊥DF 且DE =DF ，故作DM ⊥DO 且DM =DO ，F 点轨迹是以点M 为圆心，2为半径的圆．直接连接OM ，与圆M 交点即为F 点，此时OF 最小．可构造三垂直全等求线段长，再利用勾股定理求得OM ，减去MF 即可得到OF 的最小值．答案为【变式训练1】如图，在等腰Rt △ABC 中，AC ＝BC ＝，点P 在以斜边AB 为直径的半圆上，M 为PC 的中点，当半圆从点A 运动至点B 时，点M 运动的路径长为________．【答案】π【解析】当点AB 的中点时，M 为AB的中点，，设分别为AC 、BC 的中点，连接交CP 于点O，如图所示：∵，当点P 沿半圆从点A 运动至点B 时，点M 的运动路径是以O 为圆心，1为半径的半圆，如图蓝色半圆，∴点M的运动路径长为π.【变式训练2】如图，AB 为的直径，C 为上一点，其中，，P 为上的动点，连AP ，取AP 中点Q ，连CQ ，则线段CQ 的最大值为（）O e O e 6AB =120AOC ∠=︒O eA．B．C．D．【答案】D【详解】如图，连接OQ，作CH⊥AB于H．∵AQ＝QP，∴OQ⊥PA，∴∠AQO＝90°，∴点Q的运动轨迹为以AO为直径的⊙K，连接CK，当点Q在CK的延长线上时，CQ的值最大,∵∴∠COH＝60°在Rt△OCH中，∵∠COH＝60°，OC=AB=3，∴OH＝OC＝，CH，在Rt△CKH中，CKCQ的最大值为，故选：D．【变式训练3】如图，中，于点是半径为2的上一动点，连结，若是的中点，连结，则长的最大值为（）A．3B．C．4D．【答案】B【详解】解：如图，可知P在BA延长线与的交点时此时长的最大，证明如下：连接BP,∵,∴BD=DC,∵是的中点，∴DE//BP, ,32+2+32120AOC∠=︒121232==32ABCV,6,AB AC BC AD BC==⊥,4,D AD P=Ae PC E PC DE DE3.54.5Ae DE,6,AB AC BC AD BC==⊥E PC12DE BP=所以当BP 的长最大时，长的最大，由题意可知P 在BA 延长线与的交点时BP 的长最大此时长的最大，∵BC =6,AD =4,∴BD =DC =3,BA =5,∵的半径为2，即AP =2,∴BP =5+2=7,∴.故选：B.课后训练1.如图，在△ABC 中，∠ACB ＝90º，∠A ＝30º，BC ＝2，D 是AB 上一动点，以DC 为斜边向右侧作等腰Rt △DCE ，使∠CED ＝90º，连接BE ，则线段BE 的最小值为 .【解答】【解析】由题意可知C 为定点，DAB ，点E 为从动点，∵△DCE 是等腰直角三角形，∴∠DCE ＝45º，，E 的路径为一条线段，可以看成是由线段AB先绕着定点C 逆时针旋转45º，再以定点C 为位似中心，以为位似比缩小来的，如图，将BE的最小距离转化为点到线的最小距离（点B 的最短距离），，中，有∴线段BE 的最小值为3.如图，，点O 在线段上，，的半径为1，点P 是上一动点，以为一边作等边，则的最小值为_____．DE A e DE A e 13.52DE BP ==6AB =AB 2AO =O e O e BP BPQ V AQ【答案】【详解】解：如图，在上方以为一边作等边，连接，和都是等边三角形，，，即，在和中，，，，点在以点为圆心，长为半径的圆上，如图，设与交于点，过点作于点，则，则当点与点重合时，取得最小值，最小值为，，，是等边三角形，，，，在中，，即的最小值为，故答案为：．4.点A是双曲线在第一象限上的一个动点，连接AO并延长交另一交令一分支点B ，以AB 为斜边作等腰Rt△ABC ，点C 在第二象限，随着点A 的运动，点C 的位置也在不断变化，但始终在某函数图像上运动，则这个函数的解析式为.【答案】【解析】连接OC ，作CD ⊥轴于点D ，AE ⊥轴于点E ，如图所示：设点A 的坐标为，∵A 、B 两点是正比例函数图像与反比例函数图像的交点，∴点A 与点B 关于原点对称，∴OA ＝OB ，∵△ABC 为等腰直角三角形，∴OC ＝OA ，OC ⊥OA ，∴∠DOC ＋∠AOE ＝90º，∵∠DOC ＋∠DCO ＝90º，∴∠DCO ＝∠AOE ，1AB OB OBC V ,,OP CQ AC V OBC BPQ V ,,60OB CB BP BQ OBC PBQ ∴==∠=∠=︒OBC PBC PBQ PBC ∴∠-∠=∠-∠OBP CBQ ∠=∠OBP V CBQ △OB CB OBP CBQ BP BQ =⎧⎪∠=∠⎨⎪=⎩()OBP CBQ SAS ∴≅V V 1CQ OP ∴==∴Q C CQ AC C e D C CM AB ⊥M 1CD =Q D AQ AD 2,6AO AB ==Q 4OB AB AO ∴=-= V OBC CM AB ⊥14,22OC OB OM OB ∴====4CM AM AO OM ∴===+=Rt ACM △AC ==1AD AC CD =-=-AQ 11在△COD与△OAE中，，∴△COD≌△OAE（AAS），，，∴点C在反比例函数的图像上.7．如图，AB为⊙O的直径，C为⊙O上一点，其中AB＝2，∠AOC＝120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为____________．【详解】解：如图，连接OQ，作CH⊥AB于H．∵AQ=QP，∴OQ⊥PA，∴∠AQO=90°∴点Q的运动轨迹为以AO为直径的⊙K，连接CK当点Q在CK的延长线上时，CQ的值最大，在中，∵∠COH=60°，OC=1，∴OH=，在中，CQ8.如图，已知点M（0，4），N（4，0），开始时，△ABC的三个顶点A、B、C分别与点M、N、O重合，点A在y轴上从点M开始向点O滑动，到达点O结束运动，同时点B沿着x轴向右滑动，则在此运动过程中，点C的运动路径长　4　．【解答】解：过点C'作C'D⊥x轴，C'E⊥y轴∵点M（0，4），N（4，0），∴OM＝ON，∵∠CA'C'+45°＝∠EAB+∠MGB＝45°+∠MGB，∴∠EA'C'＝∠B'GB，∵∠B'GB+∠GB'B＝45°，∠GB'B+∠DB'C'＝45°，∴∠EA'C'＝∠DB'C'，又∵A'C'＝B'C'，∴Rt△A'C'E≌Rt△B'C'D（HL），∴EC'＝DC'，∴C'在第四象限的角平分线上，∴C的运动轨迹是线段AC，∴C的运动路径长为4；故答案为4；Rt OCHn1122OC=CH=Rt CKHn CK==9.如图，已知在扇形AOB中，OA＝3，∠AOB＝120º，C是在上的动点，以BC为边作正方形BCDE，当点C从点A移动至点B时，求点D运动的路径长？【解析】将圆O补充完整，延长BO交圆O于点F，取的中点H，连接FH、HB、BD，如图所示：由题意可得△FHB是等腰直角三角形，HF＝HB，∠FHB＝90º，∵∠FDB＝45FHB，∴点D在圆H上运动，轨迹如图中蓝色虚线，∴∠HFG＝∠HCF＝15CHB＝120º，∴∴点D。

中考专题：最值问题之瓜豆原理

中考专题 ----- 路径之瓜豆原理知识必备一、旋转及性质1.旋转的定义:一个图形绕点沿定方向旋转定的角度；2.旋转三要素:①旋转中心（绕哪个点转）；②旋转方向（顺时针或逆时针）；③旋转角度；3.旋转的性质:①旋转不改变图形的大小与形状，只改变图形的位置，即旋转前后图形全等;②对应点与旋转中心所连线段间的夹角等于旋转角.二、位似及性质1.位似的定义:若两个图形F和F的点之间可以建立一对应关系,并且满足:①每组对应点的连线所在的直线都经过同一点O；②每组对应点都在点O的同侧或异侧;③对每组对应点A 和OAA',有4 k（k为常数），则称图形F和F位似,k叫位似比；OA2.位似三要素:①位似中心（关于哪个点位似）；②位似方向（同侧或异侧）；③位似比（等于相似比）；3.位似的性质:成位似的两个图形必相似：把一个几何图形变换成与之位似的图形,叫做位似变换；利用位似变换可把一个图形放大或缩小，若位似比大于1，则通过位似变换把原图形放大；若位似比小于1.则通过位似变换把原图形缩小。

方法提炼一.旋转作图问题1：在平面内有两点A.B.请将点B绕点人按顺时针方向旋转40°.二、位似作图1问题2：如图:.已知线段AB，请以点A为位似中心1为位似比，在同侧将线段AB进行位似3变换。

「三、模型建立1 / 13(一)旋转变换问题3:(1)如图14-2-5,已知等腰Rt^APQ.其中A为定点，根据旋转作图的经验，请你说说: 点Q可以看作点P经过怎样的变换得到？(2)如图14-2-6.若改为等边AAPQ呢？⑶如图1-27.若改为任意等腰4APQ(其顶角为o)呢？问题4:在问题3中，若点P在一条定直线l上运动，其他条件不变如图14-2-8至图14-2-10 所示，请问：点Q的运动路径是什么？它可以看作点P的路径如何而来？问题5:在问题4中，若将“定直线1”改为“定。

0〃 .其他条件不变，结果如何?反思：这里是“圆生圆”；注意:点Q所在的轨迹圆圆心0’也是原来的圆心0定点A经过相应的旋转而来;2 / 13总结：这里仅牵扯到“旋转变换”不妨称P 为主动点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
中考数学压轴题必考破解瓜豆原理的三种必考题型
一.轨迹解析式
例 1：如图，△ ABO 为等腰直角三角形， A（－ 4， 0），直角顶点 B 在第二象限，点 C在
y
轴上移动，以 BC 为斜边作等腰直角△ BCD ，我们发现直角顶点 D 点随着 C 点的移动也在一条直线
上移动，这条直线的函数解析式是 ________________________

分析：我们先来看看当时的解法．显然，由于题目已经明确给出点 D 的轨迹是一条直线，那么，可以采
用特殊值法来考虑，选取两个特殊位置的点 C，确定相应的点 D 的坐标，两
点确定一条直线即可．
当然，本题要分两种情况，点 D 在 BC 上方，和点 D在 BC 下方．

解答：
2

我们发现，两种情况下，点 D 的确都在直线上运动，能用瓜豆原理来解释吗？
何为瓜豆原理？下面就具体来解释下瓜豆原理的由来：

D
的轨迹是一条直线呢？
反思：题目解完了，但你肯定会问，为何点
3

由此可见，在旋转放缩过程中，从动点和主动点的轨迹是一致的！即所谓 “种瓜得瓜，种豆得豆 ”
也！而本题若用一般方法求解，也不难，构造一线三直角全等可破．解答：

.
求经过的路径长

例 2：如图，正方形 ABCD 的边长为 2，动点 E 从点 A 出发，沿边 AB 向终点 B 运动，以
DE 为边作正方形 DEFG（点 D.E.F 、 G按顺时针方向排列）．求在点 E 的整个运动过程中，点 F
经过的路径长．
4

分析：
解答：
当点 E与A 点重合时，点
F 在点 B
处：

当点 E与 B 点重合时，点
F
的位置如下图所示，

点 F 运动的路径为 BF ；
5

三.求最值问题
例 3：如图，在直角坐标系中，已知点 A（4 ， 0），点 B 为 y 轴正半轴上一动点，连接 AB，
以 AB 为一边向下作等边△ ABC ，连接 OC ，则 OC 的最小值 _____________
.

分析：点 B为主动点，点 C为从动点，根据瓜豆原理， BA 绕点 A逆时针旋转 60°到 CA，主动点
B
的轨迹是 y轴的正半轴，则从动点 C的运动轨迹为 y轴正半轴绕点 A 逆时针旋转 60°后的射线，我们可
以用特殊位置来考虑．当 OC⊥点 C轨迹所在射线时， OC 最短．
当然，我们也可以构造手拉手模型，将 OC 边转化，详细过程请见方法 2．

解答：
方法

方法二
:
6