非平稳时间序列分析
非平稳时间序列建模步骤

非平稳时间序列建模步骤介绍非平稳时间序列是指其统计特性在时间上发生变化的序列。
在实际应用中,我们经常面临非平稳时间序列的建模问题,如股票价格、气温变化等。
本文将探讨非平稳时间序列建模的步骤和方法。
为什么要建立模型非平稳时间序列在其统计特性的变化中存在一定的规律性,因此建立模型可以帮助我们理解和预测序列的行为。
模型可以从数据中提取有用的信息,揭示序列的规律和动态特征。
步骤一:观察时间序列的特性在建立模型之前,我们首先需要观察时间序列的特性,包括趋势、周期性、季节性和随机性等。
这些特性是决定时间序列模型选择的重要因素。
步骤二:平稳化处理由于非平稳时间序列的统计特性随时间变化,不利于建模和分析。
因此,我们需要对时间序列进行平稳化处理。
常用的平稳化方法包括差分法和变换法。
2.1 差分法差分法是通过计算相邻两个观测值的差异来实现序列的平稳化。
一阶差分是指相邻观测值之间的差异,二阶差分是指一阶差分的差异,以此类推。
差分法可以有效地去除序列的趋势和季节性,使序列平稳。
2.2 变换法变换法是通过对时间序列进行数学变换,将非平稳序列转化为平稳序列。
常用的变换方法包括对数变换、平方根变换和 Box-Cox 变换等。
变换法可以改变序列的分布特性,使序列满足平稳性的要求。
步骤三:选择模型平稳化处理后,我们需要选择合适的模型进行建模。
常用的时间序列模型包括自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)、季节性自回归移动平均模型(SARIMA)和指数平滑模型等。
3.1 自回归移动平均模型(ARMA)ARMA 模型是描述时间序列随机变动的经典模型,其包括自回归和移动平均两个部分。
自回归部分考虑了序列的历史值对当前值的影响,移动平均部分考虑了序列的误差对当前值的影响。
ARMA 模型适用于没有趋势和季节性的平稳序列。
3.2 自回归积分移动平均模型(ARIMA)ARIMA 模型是在 ARMA 模型基础上引入了积分项,用于处理非平稳序列。
时间序列分析

趋 势
1000 500 0
1986 1988 1990 1992 1994 1996 1998 2000 2002 2004
季 节
4000 3000 2000 1000 0 1 3 5 7 9 11 13 15 17 19
5000 4000 3000 2000 1000 0 1 3 5 7 9 11 13 15 17 19
ˆ a bt Y t
ˆ —时间序列的预测值 Y t t —时间标号 a—趋势线在Y 轴上的截距 b—趋势线的斜率,表示时间 t 变动一个 单位时观察值的平均变动数量
线性模型法
(a 和 b 的求解方程)
1. 根据最小二乘法得到求解 a 和 b 的标准方程为
Y na b t 2 tY a t b t
t 1 m t m 1
Y
2m
t
, S3
t 2 m 1
Y
3m
t
2. 根据三和法求得
1 S3 S 2 m b S 2 S1 b 1 a S S 2 1 2 m b b 1 m 1 ab b 1 K S1 m b 1
季 节 与 趋 势
时间序列的分解模型
1. 乘法模型
Yi=Ti×Si×Ci×Ii
2. 加法模型
Yi=Ti+Si+Ci+Ii
4.2 趋势型序列的预测
4.2.1 线性趋势预测 4.2.2 非线性趋势预测
趋势序列及其预测方法
1. 趋势(trend)
持续向上或持续下降的状态或规律
2. 有线性趋势和非线性趋势 3. 方法主要有
运用小波分析对非平稳时间序列的灰色预测

函数 ,,就有可能观察到信号的局部特征以及 ( )
这 种局 部特性 随时 间的演 变 。 上 面介 绍 的是连 续 小波变 换 的定 义 ,连续 小 波 不利 于编 程计 算 ,必须 要通 过 离散 化 。本文 介 绍一种被称为a r s o 小波分解的方法把序列分解 Tu 成 不 同的小波 平面 , 一种无 抽取 离散 小波变 换 , 是 其 基本 思想 是通 过有 限滤 波器 的 内插近 似 ,将 输
列 的处 理 。
济等 领 域 。与任 何 一种预 测理 论相 同,灰色 预测
理论 也 存在 着一 定 的局 限性 ,尤其 是对 原始 非平
稳 时间序 列难 以取得满 意 的预测 效果 。 L 十 年来 , 为提 高 灰色 理论 的预 测精 度 ,科技 一作 者在 灰色 r
预测 模 型参 数 的优 化 以及 数据 拟合 函数 的选 抒两
入时 间序 列分解 为多个 细1 信号与一个近似信 号,则原始时间序列为各细节系数与逼近系数的 叠加 。
‘ Lj ∥I
:
C =
由最 / _ 乘法得 : i- x2
=
设{( } x )为时间序列,且 c() xk , 七 o = () 七
k=0l , , 2…Ⅳ一 , 0 To s , l贝 a ru 算法女。 : 口F 。
维普资讯
《 I技 术》2 0 机 ' U 0 7年第 2期
计算机技术应用
运用小波分析对非平稳 时间序 列 的灰色预测
李盘荣 马纲 侯 宁
( 无锡 市广播 电视 大学,江苏 无锡 2 4 2 ) l0 1
摘 要 :作者提 一种 于小波分析理论的狄色预测方法,以此方法将非 稳时间序列分解 N;,J 度u 以减少原 l F" I 】
基于小波分析的非平稳时间序列分解
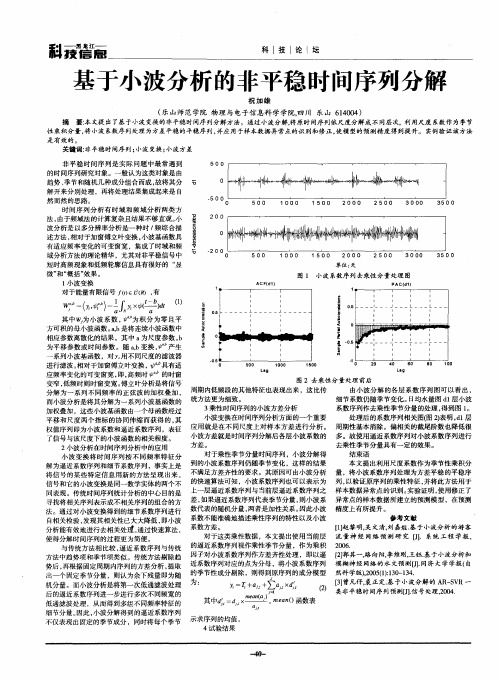
法, 由于频域法 的计算复杂且结果不够直观。 小 波分析是 以多分辨率分析是一种 时 / 频综 合描 述方法 , 相对于加窗傅立叶变换 , 小波基函数具 有适应频率变化 的可变窗宽 ,集成 了时域和频 域分析方法的理论精华 ,尤其对非平稳信号中 短时高频现象和低频轮廓 信息具有很好的 “ 显
微” “ 和 概括 ” 果 。 效
200
0
.
1 5 0 0
2 0 0 0
2 5 0 0
3 00 0
35 0 0
单位 : 天
图 1 小 波 系数 序 列 去 乘 性 分量 处理 图
科
科技 论 坛 ll j
基于小波 分析 的非平稳 时 问序列 分解
祝 加 雄
( 山 师 范 学院 物 理 与 电 子信 息科 学学 院 , 川 乐 山 6 40 ) 乐 四 10 4
摘 要: 文提 出了基于小波变换的非平稳时问序列分解方法 。通过小波分解, 时间序列依尺度分解成不同层次, 用尺度 系数作 为季节 本 将原 利 性 乘积分 量, 小波 系数序列处理为方差平稳的平稳序列, 将 并应 用于样本数据 异常点的-  ̄ 和修正 , / , y 1 , 使模型的预 测精度得 到提升 。实例验证该 方法 是有效的。 关键词: 非平稳时间序 列; 小波 变换 ; 小波方差 非 平稳时 间序列是实 际问题 中最 常遇到 的时间序列研究对象 。一般认为这类对象是 由 趋势 、 季节和随机几种成分组合而成 , 故将其分 解开来分别处理 ,再将处理结果集成起来是 自
然 而然 的思 路 。 时 间序列分析有 时域和频域 分析两类 方
L p
.
0
a0 5 D 0 ∞ p c ∞日 ∞ - OI 0 5 00
时间序列分析实验报告

《时间序列分析》课程实验报告一、上机练习(P124)1.拟合线性趋势程序:data xiti1;input x@@;t=_n_;cards;;proc gplot data=xiti1;plot x*t;symbol c=red v=star i=join;run;proc autoreg data=xiti1;model x=t;output predicted=xhat out=out;run;proc gplot data=out;plot x*t=1 xhat*t=2/overlay;symbol2c=green v=star i=join;run;运行结果:分析:上图为该序列的时序图,可以看出其具有明显的线性递增趋势,故使用线性模型进行拟合:x t=a+bt+I t,t=1,2,3,…,12分析:上图为拟合模型的参数估计值,其中a=,b=,它们的检验P值均小于,即小于显著性水平,拒绝原假设,故其参数均显著。
从而所拟合模型为:x t=+.分析:上图中绿色的线段为线性趋势拟合线,可以看出其与原数据基本吻合。
2.拟合非线性趋势程序:data xiti2;input x@@;t=_n_;cards;;proc gplot data=xiti2;plot x*t;symbol c=red v=star i=none;run;proc nlin method=gauss;model x=a*b**t;parameters a= b=;=b**t;=a*t*b**(t-1);output predicted=xh out=out;run;proc gplot data=out;plot x*t=1 xh*t=2/overlay;symbol2c=green v=none i=join;run;运行结果:分析:上图为该时间序列的时序图,可以很明显的看出其基本是呈指数函数趋势慢慢递增的,故我们可以选择指数型模型进行非线性拟合:x t=ab t+I t,t=1,2,3,…,12分析:由上图可得该拟合模型为:x t=*+I t分析:图中的红色星号为原序列值,绿色的曲线为拟合后的拟合曲线,可以看出原序列值与拟合值基本上是重合的,故该拟合效果是很好的。
非线性时间序列分析STAR模型及其在经济学中的应用

非线性时间序列分析的基本概念 和理论
时间序列是指按照时间顺序排列的一组数据。在经济学中,时间序列数据通 常反映了某一经济现象的历史演变过程,如股票价格、消费支出、生产产量等。 非线性时间序列是指时间序列数据之间存在非线性关系,这种关系往往比线性关 系更为复杂和真实。
STAR模型是一种非线性时间序列分析方法,它可以捕捉时间序列中的非线性 结构和变化。STAR模型基于自回归模型,通过引入平滑转换函数,允许模型在不 同时间点之间平滑转换,以适应时间序列数据的非线性特征。
3、数据预处理
在应用STAR模型之前,需要对时间序列数据进行预处理,如去噪、季节调整 等。这些预处理步骤可以帮助STAR模型更好地识别时间序列的非线性结构。
4、模型应用
一旦STAR模型被估计和识别后,可以将其应用于预测时间序列的未来走势。 此外,STAR模型还可以用于时间序列的分解,将时间序列分解为线性部分和非线 性部分,以便更深入地理解时间序列数据的特征。
非线性动力系统基础
非线性动力系统是指由非线性微分方程或动态方程描述的系统。这些系统具 有丰富的动态行为和复杂的相互作用,无法简单地通过线性系统进行描述。李雅 可夫斯基定理是非线性动力系统理论中的重要成果之一,它揭示了系统中混沌现 象的存在和重要性。此外,同步也是非线性动力系统中的一个重要概念,它描述 了两个或多个系统在某种条件下以相同的方式运动的现象。
非线性时间序列分析STAR模型及其 在经济学中的应用
目录
01 引言
03
非线性时间序列分析 STAR模型
02 非线性时间序列分析 的基本概念和理论
04 参考内容
引言
在经济学中,时间序列数据的应用越来越广泛,例如金融市场价格波动、消 费者行为模式、生产活动变化等。为了更好地理解和预测这些时间序列数据,非 线性时间序列分析方法逐渐受到重视。其中,STAR(Smooth Transition Autoregressive)模型是一种被广泛应用于非线性时间序列分析的方法。本次演 示将详细介绍非线性时间序列分析STAR模型及其在经济学中的应用。
应用时间序列分析(第6版)PPTch5
例5-7
• 已知ARIMA(1,1,1)模型为
• 已知:
•求
的95%置信区间。
【解】 • 展开原模型,得到等价模型 • 预测值的递推公式为
例5-7解
• 3期预测误差的方差为
• 广义自相关函数为
• Green函数为 • 3期预测值方差为 • 3期预测值的95%置信区间为
例5-6续
例4.9
差分平稳
• 一阶差分时序图
• ADF 检验
结论: 平稳非白噪声序列
• 白噪声检验
模型定阶
• 一阶差分后序列自相关图
• 一阶差分后序列偏自相关图
1阶差分后序列的自相关图显示拖尾特征,偏自相关图显示1阶截尾特征。所以考虑用 AR(1) 模型拟合1阶差分后序列。考虑到前面已经进行的1阶差分运算,实际上使用ARIMA(1,1,0) 模型拟合原序列。
无季节效应的非平稳序列分析
05
本章内容
01
Cramer分解定理
02
差分平稳
03
ARIMA模型
04
疏系数模型
Cramer分解定理
• Cramer分解定理
• Harald Cramer(1893-1985)。瑞典人,斯德哥尔 摩大学教授,著名的统计学家和保险精算学家。
• Cramer 分解定理是Wold分解定理的推广。Wold分 解定理是平稳序列的理论基础,Cramer分解定理是 非平稳序列的理论基础。
• 但应当注意的是,差分运算的阶数并不是越多越好。因为差分运算是一种 对信息的提取、加工过程,每次差分都会有信息的损失。
• 在实际应用中差分运算的阶数得适当,应当避免过度差分的现象 。
例5-4
• 假设序列如下
时间序列分析基于R_习题答案
第一章习题答案第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图Au{oeorr&lal. i orsCorrelation M 7 6 5 4 3 2 1 0 I ; 3 4 5 6 7 9 9 11.00000■Hi ■ K. B H,J B ik L L1■* J.1 jA1-.IM L L*rn^rp ■ i>i™iTwin H'iTiii M[lrp i,*nfr 'TirjlvTilT'1 iBrpO.7QOO0■ill. Ii ill ■ _.ill«L■ ill iL si ill .la11 ■ fall■ 1 ■ rpTirp Tp和阳申■丽轉■晒?|•卉(ft0.41212■强:料榊<牌■0.14343'■讯榊*-.07078■-.25758, WWHOHHfi■-.375761marks two 总t and&rd errors2.2(1)非平稳,时序图如下(2)- (3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图raa rka two standard errors2.3(1) 自相关系数为: 0.20230.013 0.042-0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070-0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062-0.139 -0.034 0.206 -0.010 0.080 0.118(2 )平稳序列 (3) 白噪声序列 2.4LB=4.83 , LB 统计量对应的分位点为 0.9634 , P 值为0.0363。
adf单位根检验法
adf单位根检验法
ADF (Augmented Dickey-Fuller) 单位根检验法是一种常用的时间序列分析方法,用于检验时间序列数据是否具有单位根(非平稳性)。
单位根表示数据具有随机漂移或趋势,而非平稳性的数据在进行统计分析时可能会导致误导性的结果。
ADF 单位根检验法基于 Dickey-Fuller 测试统计量,该测试统计量的原假设为时间序列存在单位根。
如果原假设不能被拒绝,则说明时间序列是非平稳的;反之,如果原假设被拒绝,则说明时间序列是平稳的。
ADF 单位根检验法的步骤如下:
1. 建立原假设(H0):时间序列具有单位根,即非平稳。
2. 构建回归模型:将时间序列作为因变量,加入滞后项和可能的趋势项作为自变量。
3. 估计回归模型:利用最小二乘法估计回归模型的参数。
4. 计算测试统计量:根据估计的回归模型,计算 ADF 测试统计量。
5. 判断显著性:与临界值比较 ADF 测试统计量,若大于临界值,则拒绝原假设,认为时间序列是平稳的;否则,接受原假设,认为时间序列是非平稳的。
通过ADF 单位根检验法可以判断时间序列数据是否平稳,进而决定是否需要进行差分或其他预处理方法来使数据平稳化。
在经济学、金融学等领域,ADF 单位根检验法被广泛应用于时间序列数据的建模
和分析中。
时间序列分析模型
时间序列分析模型时间序列分析是一种广泛应用于统计学和经济学领域的建模方法,用于研究随时间变化的数据。
它的目的是揭示和预测数据中隐含的模式和关系,以便更好地理解和解释现象,并做出相应的决策。
时间序列分析模型可以分为统计模型和机器学习模型两类。
一、统计模型1.平稳时间序列模型:平稳时间序列是指在统计学意义上均值和方差都是稳定的序列。
常用的平稳时间序列模型包括:自回归移动平均模型(ARMA)、自回归整合移动平均模型(ARIMA)和季节性自回归整合移动平均模型(SARIMA)等。
-自回归移动平均模型(ARMA)是根据时间序列数据的自相关和移动平均性质建立的模型。
它将序列的当前值作为过去值的线性组合来预测未来值。
ARMA(p,q)模型中,p表示自回归项的阶数,q表示移动平均项的阶数。
-自回归整合移动平均模型(ARIMA)在ARMA模型基础上引入差分操作,用于处理非平稳时间序列。
ARIMA(p,d,q)模型中,d表示差分的次数。
-季节性自回归整合移动平均模型(SARIMA)是ARIMA模型的扩展,在存在季节性变化的时间序列数据中应用。
SARIMA(p,d,q)(P,D,Q)s模型中,s表示季节周期。
2.非平稳时间序列模型:非平稳时间序列是指均值和/或方差随时间变化的序列。
常用的非平稳时间序列模型包括:趋势模型、季节性调整模型、自回归积分滑动平均模型(ARIMA)和季节性自回归积分滑动平均模型(SARIMA)等。
- 趋势模型用于描述数据中的趋势变化,例如线性趋势模型(y = ax + b)和指数趋势模型(y = ab^x)等。
-季节性调整模型用于调整季节性变化对数据的影响,常见的方法有季节指数调整和X-12-ARIMA方法。
-自回归积分滑动平均模型(ARIMA)和季节性自回归积分滑动平均模型(SARIMA)在非平稳时间序列中引入差分操作进行模型建立。
二、机器学习模型机器学习模型在时间序列分析中发挥了重要作用,主要应用于非线性和高维数据的建模和预测。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非平稳时间序列分析1、首先画出时序图如下:t从时序图中看出有明显的递增趋势,而该序列是一直递增,不随季节波动,所以认为该序列不存在季节特征。
故对原序列做一阶差分,画出一阶差分后的时序图如下:difx140 130 120 110 100 90 80 70 60 50 40 30 20 10 0 -10从中可以看到一阶差分后序列仍然带有明显的增长趋势,再做二阶差分:dif2x90 80 70 60 50 40 30 20 10 0 -10 -20 -30 -40 -50 -60 -70 -80 -90 -100 -110做完二阶差分可以看到,数据的趋势已经消除,接下来对二阶差分后的序列进行194519501945 19551960196519701975198019851990199520001950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000检验:AutocorrelationsLag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1 Std Error0 577.333 1.00000 | |********************| 01 -209.345 -.36261 | *******| . | 0.0712472 -52.915660 -.09166 | .**| . | 0.0800693 9.139195 0.01583 | . | . | 0.0806004 15.375892 0.02663 . |* . | 0.0806155 -59.441547 -.10296 .**| . | 0.0806606 -23.834489 -.04128 | . *| . | 0.0813247 100.285 0.17370 | . |*** | 0.0814318 -146.329 -.25346 | *****| . | 0.0832909 52.228658 0.09047 | . |**. | 0.08711810 21.008575 0.03639 | . |* . | 0.08759311 134.018 0.23213 | . |***** | 0.08767012 -181.531 -.31443 | ******| . | 0.09073613 23.268470 0.04030 | . |* . | 0.09610814 71.112195 0.12317 | . |** . | 0.09619415 -105.621 -.18295 | ****| . | 0.09699116 37.591996 0.06511 . |* . | 0.09872717 23.031506 0.03989 | . |* . | 0.09894518 45.654745 0.07908 | . |** . | 0.09902719 -101.320 -.17550 | ****| . | 0.09934720 127.607 0.22103 | . |**** | 0.10090821 -61.519663 -.10656 | . **| . | 0.10333722 35.825317 0.06205 | . |* . | 0.10389323 -93.627333 -.16217 | .***| . | 0.10408124 55.451208 0.09605 | . |** . |从其自相关图中可以看出二阶差分后的序列自相关系数很快衰减为零,且都在两倍标准差范围之内,所以认为平稳,白噪声检验结果:Autocorrelation Check for White NoiseTo Chi- Pr >Lag Square DF ChiSq------------------- Autocorrelations -------------------6 30.70 6 <.0001 -0.363 -0.092 0.016 0.027 -0.103 -0.04112 84.54 12 <.0001 0.174 -0.253 0.090 0.036 0.232 -0.31418 97.98 18 <.0001 0.040 0.123 -0.183 0.065 0.040 0.07924 126.99 24 <.0001 -0.175 0.221 -0.107 0.062 -0.162 0.096P 值都小于 0.05 ,认为不是白噪声。
接下来对模型进行定阶:Minimum Information CriterionLags MA 0 MA 1 MA 2 MA 3 MA 4 MA 5AR 06.356905 6.141831 6.1498386.175552 6.191564 6.203649 AR 1 6.236922 6.168121 6.151526.172674 6.186962 6.193905 AR 2 6.193215 6.180818 6.177337 6.197407 6.203224 6.207239 AR 36.19748 6.203081 6.2028376.221083 6.215313 6.188712 AR 4 6.220313 6.22949 6.227445 6.241883 6.162837 6.189358 AR 5 6.2221316.236739 6.2440256.264968 6.1859636.210425Error series model:AR(10)Minimum Table Value: BIC(0,1) = 6.141831BIC(0,1)取得最小值,所以选取 MA (1)模型,接下来 对模型进行拟合: 得到模型为:模型检验结果为:Conditional Least Squares EstimationStandard Approx Parameter Estimate Error t Value Pr > |t| Lag MU 0.402860.169002.38 0.0181 0 MA1,1 0.89063 0.0326627.27<.0001 1Forecasts for variable x 时间Forecast Std Error 95% Confidence Limits1997一季度 7759.2061 31.2276 7698.0011 7820.4112 1997二季度 7842.6135 40.3048 7763.6175 7921.6095 1997三季度 7926.4237 48.9444 7830.4945 8022.3530 1997四季度8010.636857.43567898.06518123.2085预测图:从 sas 的定阶结果来看, 检验结果显示都显著。
接下来利用此模型对1997 年的四个季度进行预测:t本题代码data aa; | in put x@@; | difx=dif(x); dif2x=dif(difx); |t=intnx( 'quarter' , '1jan1947'd,_n_- 1);format t year4. ; |cards ;227.8 231.7 236.1 246.3 252.6 259.9 266.8 268.1263.0259.5 261.2 258.9 269.6279.3 296.9 308.4 323.2 331.1337.9 373.7342.3 345.3 345.9 351.7 364.2 371.0 374.5 368.7 417.8368.4 368.7 373.4 381.9 394.8 403.1 411.4 420.5 444.4426.0 430.8 439.2 448.1 450.1 457.2 451.7 448.6 461.8 475.0 499.0 512.0 512.5 516.9 530.3 529.2532.2 527.3 531.8 542.4 553.2 566.3 579.0 586.9 594.1597.7 606.8 615.3628.2637.5 654.5 663.4 674.3679.9701.2 713.9 730.4 752.6 775.6 785.2 798.6 812.5 822.2828.2 844.7 861.2 886.5 910.8 926.0 943.6 966.3 979.9999.31144.41008.0 1020.3 1035.7 1053.8 1058.4 1104.2 1124.91158.8 1198.5 1231.8 1256.7 1297.0 1347.9 1379.4 1404.4 1449.71463.9 1496.8 1526.4 1563.2 1571.3 1608.3 1670.6 1725.3 1783.51814.0 1847.9 1899.0 1954.5 2026.4 2088.7 2120.4 2166.8 2293.72356.2 2437.0 2491.4 2552.9 2629.7 2687.5 2761.7 2756.1 2818.82941.5 3076.6 3105.4 3197.7 3222.8 3221.0 3270.3 3287.8 3323.83388.2 3501.0 3596.8 3700.3 3824.4 3911.3 3975.6 4022.7 4100.44158.7 4238.8 4306.2 4376.6 4399.4 4455.8 4508.5 4573.1 4655.54731.4 4845.2 4914.5 5013.7 5105.3 5217.1 5329.2 5423.9 5501.35557.0 5681.4 5767.8 5796.8 5813.6 5849.0 5904.5 5959.4 6016.66138.3 6212.2 6281.1 6390.5 6458.4 6512.3 6584.8 6684.5 6773.66876.3 6977.6 7062.2 7140.5 7202.4 7293.4 7344.3 7426.6 7537.57593.6 proc gplot ;plot x*t difx*t dif2x*t; |symbol c=black i =join v=star; run ;proc arima ;iden tify estimate var =x( 1,1) nlag =8 minic p=( 0: 5)q = 1;q=( 0: 5);forecast run ; lead =5 id =t interval =quarter out =results; |proc gplot data =results;plot x*t= 1 forecast*t= 2 l95*t= 3 u95*t= 3 / overlay symbol1 c=black i =none v =star; |symbol2 c=red i =join v=none ; |symbolc=gree n i =join v = none 丨=32;run ;2、首先画出时序图:xt从时序图中可以看出序列存在递增趋势,而且存在季节性特征,接下来对序列进行一阶差分,画出差分后的时序图:difx可以看到趋势已经消除,但季节性仍存在,对其进行检验:AutocorrelationsLag CovarianceCorrelation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1Std Error0 16681.747 1.00000 | |********************| 0 1 -3098.631 -.18575 |****||0.049568 2 49.867617 0.00299 | . | . | 0.051250 3 -4342.304 -.26030 | *****| | 0.051250 4 -1177.801 -.07060 | .*| . |0.054402 5 3921.886 0.23510 | |*****|0.054626 6 -258.497 -.01550 | . | . | 0.057058 7 3392.968 0.20339 | |**** | 0.057069 8 -1407.632 -.08438 | **| . | 0.058823 9 -4040.701 -.24222 | *****| | 0.059120 10 -1262.123 -.07566 | **| . | 0.061510 11 -1890.805 -.11335 | **| . |0.061738 12 10239.264 0.61380 | |************ | 0.062247 13 -2555.185 -.15317 | ***| | 0.075671 14 -784.895 -.04705 | . *| . | 0.076429 15 -4767.938 -.28582 | ******| | 0.076500 16 -1583.636 -.09493 | .**| . | 0.079080 174107.732 0.24624 | |***** | 0.079360 18-931.403-.05583| . *| .|0.081215800700600500400300200100-100-200-300-4001948 1950 1952 1954 1956 1958 1960 1962 19641966 1968 1970 1972 1974 1976 1978 1980 1982t19 3860.394 0.23141 ||***** | 0.081309 20 -2035.458 -.12202 | .**| .| 0.082912 21 -3762.045 -.22552 | *****| | 0.083352 22 -868.587 -.05207 |.*| . | 0.084838 23-1587.006 -.09513 | .**| . | 0.084916 249517.3080.57052| |***********|0.085178从自相关系数图中可以看到,在其延迟 12阶时,相关系数变大,说明序列存在明显季节性特征,对序列进行12步差分,时序图如下:dif12x500-400检验结果为:Lag Covariance Correlation -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1Std Error0 12557.531 1.00000 | |********************| 0 1 -1734.813 -.13815 | ***| | 0.050315 2 2375.783 0.18919 | |****| 0.051267 3 279.359 0.02225 | . | . | 0.053005 4 759.808 0.06051 |.|*. |0.053028 5 138.150 0.01100 | .| .| 0.053203 6 655.488 0.05220 | . |*. | 0.053209 7-1028.202-.08188| **| . |0.053338400-2003002001000 --100 -1954 1956 1958 1948 1950 1952 1960 1962 1964 1966 1968 1970 1972 1974 1976 1978 1980 1982-300 -8 533.734 0.04250 | . |*. | 0.0536559 -158.605 -.01263 | . | . | 0.05374110 -1606.237 -.12791 | ***| | 0.05374811 858.206 0.06834 . |*. 0.05451312 -5698.457 -.45379 *********| . 0.05473013 521.120 0.04150 . |* . 0.06354514 -509.219 -.04055 . *| . 0.06361415 -1020.660 -.08128 .**| . 0.06367916 -730.212 -.05815 . *| . 0.06394117 429.071 0.03417 . |* . 0.06407518 -825.235 -.06572 . *| . 0.06412119 592.947 0.04722 . |* . 0.06429220 -565.282 -.04502 . *| . 0.06437921 206.681 0.01646 . | . 0.06445922 -117.966 -.00939 . | . 0.06447023 774.691 0.06169 . |* . 0.06447324-929.421 -.07401 . *| .、/■.、r 0.064622平稳性检验显示该序列相关系数迅速衰减为0,且在两倍标准差之内,序列已经平稳,接下来进行白噪声检验:Autocorrelation Check for White NoiseTo Chi- Pr >Lag Square DF ChiSq---------- Autocorrelations----------6 24.69 6 0.0004 -0.138 0.189 0.022 0.061 0.011 0.05212 121.08 12 <.0001 -0.082 0.043 -0.013 -0.128 0.068 -0.45418 128.87 18 <.0001 0.041 -0.041 -0.081 -0.058 0.034 -0.06624 134.72 24 <.0001 0.047 -0.045 0.016 -0.009 0.062 -0.074p值均小于0.05,该序列不是白噪声。
