利用EXCE的规划求解进行求解威布尔分布参数共49页文档
用Excel求解数学规划

用Excel求解数学规划武汉大学水利水电学院万飚Excel是Microsoft Office办公软件中的一个组件,以其强大的电子表格处理功能备受广大用户的青睐。
由于Excel支持丰富的公式和函数,因而在一般财务计算、高级财务管理、财务分析、信息管理、管理决策、市场营销、工程管理,以及管理科学、经济学和统计学等领域都得到了广泛的应用。
一、关于规划求解“规划求解”是Microsoft Excel中的一个加载宏,借助它可以求解许多运筹学中的数学规划问题。
Excel的“规划求解”工具来自德克萨斯大学奥斯汀分校的Leon Lasdon和克里夫兰州立大学的Allan Waren共同开发的Generalized Reduced Gradient(GRG2)非线性最优化代码;线性规划和整数规划算法来自Frontline Systems公司的John Watson和Dan Fylstra 提供的有界变量单纯形法和分支定界法。
安装Office的时候,系统默认的安装方式不会安装该宏程序,需要用户自己选择安装。
安装方法为:从Excel菜单中选择“工具”→“加载宏”,打开如下对话框:选择其中的“规划求解”后单击“确定”按钮,会出现提示:“这项功能目前尚未安装,是否现在安装?”,选择“是”,系统要你插入Office的安装光盘,准备好后单击确定,很快就会安装完毕。
于是,你会发现在“工具”菜单下多出一个名为“规划求解”的子菜单,说明“规划求解”功能已经成功安装。
二、第一个线性规划问题例:求解以下线性规划问题:⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0,124 16 48232 21212121x x x x x x x x z max 步骤:1.将模型中的目标函数和约束条件的系数输入到单元格中;为了使我们在操作过程中看得更清楚,可以附带输入相应的标识符,并给表格加上边框。
如下图所示:2.在E4单元格(目标值)输入“=SUMPRODUCT($C$3:$D$3,C4:D4)”;其中,SUMPRODUCT 函数的功能是将数组间对应的元素相乘,并返回乘积之和,即SUMPRODUCT($C$3:$D$3,C4:D4)=C3×C4+D3×D4;$C$3:$D$3表示这几个单元格为绝对引用。
EXCEL规划求解解析

例1. 工厂生产计划优化问题
某工厂生产4种小型工具,由于该四种工具有 不同的大小、形状、重量和风格,所以它们所需要 的主要原料(钢材和橡胶)、制作时间、最大销售 量与利润均不相同。该厂每天可提供的钢材、橡胶 和工人劳动时间分别为600单位、1000单位与400小 时,详细的数据资料见下表。
应如何安排这四种工具的日产量,使得该厂的日利 润最大?
,求x2+3y的最大值。
完整的模型描述:
第二步 在“工具”菜单中选择“规划求解”。 第三步 在“规划求解参数”对话框进行选择如下图。
第四步 点击“选项”按钮,弹出“规划求解选项”对话框
第五步 单击“求解”,即可解决此题。
最后结果如下页图所示。
例2. 整数求解问题
完成下题的求解:
一般数值求解问题: 已知x,y取值满足
工具类型
表1 生产基本数据
12 3
4 可提供两
劳动时间(小时/件) 2 1 3 2 400小时
钢材(单位/件)
4 2 1 2 600单位
橡胶(单位/件)
6 2 1 2 1000单位
单位利润(元/件) 60 20 40 30
最大销售量(件) 100 200 50 100
解:依题意,设置四种工具的日产量分别为决策变量
2.如何加载“规划求解”
1) 在“工具”菜单上,单击“加载宏”
2) 在弹出的对话框中的“可用加载宏”列表框 中,选定待添加的加载宏“规划求解”选项旁 的复选框,然后单击“确定”.单击“确定” 后,“工具”菜单下就会出现一项“规划求解”
3. “规划求解”各参数设置
单击“规划求解”按钮,将会出现以下规划求Fra bibliotek解参数设置对话框
怎么利用EXCEL求解线性规划

利用线性回归方法求解生产计划方法一:1、建立数学模型:①设变量:设生产拉盖式书桌x台,普通式书桌y台,可得最大利润②确定目标函数及约束条件目标函数:y=max+115P90x约束条件:200x .....................⑴+y10≤20x .....................⑵4≤+y16128x .....................⑶+y1015≤220yx ..........................⑷,≥2、在Excel中求解线性规划①首先,如图1所示,在Excel工作表格输入目标函数的系数、约束方程的系数和右端常数项:图1②将目标方程和约束条件的对应公式输入各单元格中F2=MMULT(B6:C6,F6:F7);F3=MMULT(B3:C3,F6:F7);F2=MMULT(B4:C4,F6:F7);F2=MMULT(B5:C5,F6:F7);出现图2样式:图2线性规划问题的电子表格模型建好后,即可利用“线性规划”功能进行求解。
选择“工具”→“规划求解”出现“规划求解参数”窗口,如图3所示:图3在该对话框中,目标单元格选择F2,问题类型选择“最大值”,可变单元格选择F6:F7,点击“添加”按钮,弹出“添加约束条件”窗口,如图4所示:图4根据所建模型,共有4个约束条件,针对约束(1):2002010≤+y x ,左端“单元格所引用位置”选择F3,右端“约束值”选择D3,符号类 型选择“<=”,同理继续添加约束(2)(3)(4),完成后选择“确定”,回到“规划求解参数”对话框,如5图所示:图5④点击“选项”按钮,弹出“规划求解选项”对话框,选择“采用线性模型”和“假定非负”两项,如图6所示:图6⑤点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果: 运算结果报告:敏感性报告:极限报告:方法二:1、建立数学模型设生产拉盖式书桌x 台,普通式书桌y 台,总利润为Z 元 确定目标函数及约束条件 目标函数:y x Z 90115max += 约束条件:⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0,22010151281642002010..y x y x y x y x t s 2、在Excel 中规划求解在Excel 中建立线性规划模型,如图1所示:图11)在E2中输入“=B2*B6+C2*C6”如图2所示,同理 E3=B3*B6+C3*C6E4=B4*B6+C4*C6B7=B5*B6+C5*C6图22)单击“工具”菜单下的“规划求解”,在弹出的“规划求解参数”对话框输入各项参数:✓目标单元格选择B7✓问题类型选择“最大值”✓可变单元选择B6:C6✓约束条件选择B6:C6≥0;E2:E4≤D2:D4参数设置完毕,如图3:图33)点击“选项”,弹出“规划求解选项”对话框,选择“采用线性模型”、“假定非负”和“显示迭代结果”,说明要求求解的问题是线性模型且所求的变量必须为非负,如图4所示:图44)点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果:运算结果报告:敏感性报告:极限值报告:。
用Excel软件求解规划问题的方法

用Excel 软件求解规划的方法Microsoft Excel 软件是当今十分流行的功能强大操作方便的软件。
在Microsoft Excel 软件中,具有规划求解功能。
如图1,在工具菜单下,一般有“规划求解”项,若未有,则应先运行“加载宏”项目把其安装上。
图1 图21 一般线性规划的求解现在让我们以下面的模型为例,介绍如何利用Microsoft Excel 软件求解线性规划模型的操作方法。
首先,打开Microsoft Excel 的一个工作簿,把模型的约束系数矩阵置于A1至B4范围,约束常数置于D1至D4范围,而利润系数则置于A5至B5范围。
选择A7至B7范围作可变单元(即这两个格相当于变量X1与X2),并输入初值0。
然后,在单元格C1处输入“=A1*A7+B1*B7”,即第一个约束不等式的左边;同理,在单元格C2处输入“=A2*A7+B2*B7”,即第二个约束不等式的左边;对C3与C4也同样处理。
最后,以单元格C5作目标单元格,输入“=A5*A7+B5*B7”。
如图2。
接下来,按下主菜单的工具处,再在下拉菜单处选择“规划求解”,则弹出窗口如图3。
⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤≤≤0x 0,x x x x x x 4+x s.t. x +x =f max 21112121222700050122700075.182700025.56270000155.75.2图3 图4在“设置目标单元格”处输入“C5”,然后选“最大值”,再在“可变单元格”处输入“A7:B7”,在“约束”处按一下“添加”按钮,又弹出如图4的窗口。
在此,我们要添加5个约束:“C1 <= D1”、“C2 <= D2”、“C3 <= D3”、“C4 <= D4”、“A7:B7 >= 0”。
对第一个约束,在“单元格引用位置”处输入“C1”,在中间下拉框选择“<=”, 再在“约束值”处输入“D1”。
然后按“添加”按钮,再类似地添加其它约束。
Excel的规划求解

− 1
+ 1
3、规划求解一般步骤 1.加载宏 1.加载宏 2.在excel中将模型表示出来 2.在excel中将模型表示出来 3.设置单元格及目标值的确定 3.设置单元格及目标值的确定 4.选定可变单元格 4.选定可变单元格 5.添加约束条件 5.添加约束条件 6.求解 6.求解
5、规划求解结果
2、利用“规划求解”解整数规划问题 利用“规划求解”
仍然以上述线性规划问题为例,假定变量全为整数,则只 需添加一个约束条件即可:
此时的参数设定
计算结果: 计算结果:
整数规划问题的特例0 整数规划问题的特例0—1型问题 不难发现,在刚才的例子中,假定变量的取值非 不难发现,在刚才的例子中,假定变量的取值非0 型问题, 即1,则整数规划问题就转化为 ,则整数规划问题就转化为0—1型问题,在 型问题 excel规划求解中只需在约束条件中添加两个约束条 规划求解中只需在约束条件中添加两个约束条 件即可: 件即可:
Excel的规划求解 Excel的规划求解
一、Excel规划求解预备知识 Excel规划求解预备知识
1.加载“规划求解” 1.加载“规划求解”宏 加载
注:宏加载的越多,excel启动越慢,请根据实际情况酌情考虑 宏加载的越多, 启动越慢, 启动越慢
2、“规划求解”各参数解释和设置 、 规划求解”
2、“规划求解”各参数解释和设置 、 规划求解”
二、Excel规划求解 Excel规划求解 利用“规划求解” 利用“规划求解”解线性规划问题 利用“规划求解” 利用“规划求解”解整数规划问题 利用“规划求解”解运输问题 利用“规划求解” 利用“规划求解” 利用“规划求解”解目标规划问题 利用“规划求解” 利用“规划求解”解最短路问题 利用“规划求解” 利用“规划求解”解最大流问题 利用“规划求解”解数据包络分析(DEA)问 利用“规划求解”解数据包络分析 问 题 • 利用“规划求解”解其他运筹学问题(精确重 利用“规划求解” • • • • • • •
解答Excel之规划求解(说明)
解答Excel之规划求解
2006-09-30 23:38
一个工厂接了一批鼠标,键盘的订单,用现在的设备来生产,鼠标每个\1分钟,键盘第个\1.5分钟,1个鼠标的毛利是50元,1个键盘的毛利是75元,成本价鼠标为15元,键盘为20元,鼠标每日要生产最少200个,一天成本控制在10000元以下,每天10小时,这个工厂每天生产多少个鼠标?多少个键盘才能赚到最大的利润?
步骤1、首先在Excel表中输入如下内容:
其中“计划产量”中的值是自己随便输入的初始值。
最后3行是公式。
总时间:各自产量*各自单位时间;
总成本:各自产量*各自成本,然后相加求和;
总利润:各自产量*各自单位毛利,然后相加求和;
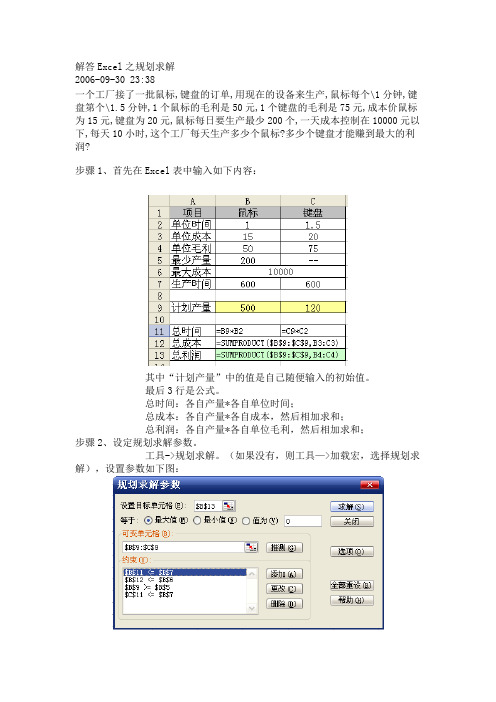
步骤2、设定规划求解参数。
工具->规划求解。
(如果没有,则工具—>加载宏,选择规划求解),设置参数如下图:
其中:“设置目标单元格”是所求的最大利润;
可变单元格是鼠标键盘的各自计划产量,即通过改变产量搭配,以实现在满足约束条件情况下得到最大利润;
几个约束条件的解释:
1)、鼠标、键盘的各自生产总时间不超过10小时(600分钟);
2)、总成本不超过最大成本10000;
3)、鼠标产量不小于200;
点击“选项”,在弹出窗口中勾选“采用线性模型”和“假定非负”,然后单击“确定”。
步骤3、设置完成后,点击“求解”,规划求解将计算出一个最佳解决方案(如果有)。
本题中,我求得的结果是:
计划产量:鼠标200,键盘350;
最大利润:36250。
Excel规划求解

3.4 规划求解
6)约束条件将出现在“约束”列表区:$C$4=6和 $D$4=3。若约束条件设置有误,可通过“更改” 或“删除”对约束条件进行改变。 7)所有参数设置好后,按“求解”,得到相应结果:
3.4 规划求解
3.4.2 解非线性方程组
多元一次线性方程比较容易,对初始值设定无严 格要求。若方程为非线性,则必须设置不同初始 值,才能保证解的可信性。
例:在Cd(ClO4)2和NaCN的水溶液中有如下平衡:
CdCNi2-i Cd 2 iCN H + +CN HCN H + +OH H 2 O
2-i CdCN i i 2 i Cd CN + H CN Ka HCN + KW H OH
3.4 规划求解
Excel步骤:
4)“设置目标单元格”输 入方程F1所在位置: $B$4,“等于”栏设置 目标值为0。“可变单元 格”编辑框输入未知数所 在单元格:$B$2:$D$2。
3.4 规划求解
Excel步骤:
5)单击“约束”选项区的“添加”按钮,出现添加 约束对话框,在“单元格引用位置”处输入方程 F2的位“添加”, 给出新的添加约束对话框,继续增“单元格引用 位置”处输入F3的位置:$D$4,选“=”,约束 值为3。单击“确定”,回到“规划求解参数”对 话框。
3.4 规划求解
CL是加入的NaCN总浓度,CM是加入的Cd(ClO4)2总 浓度,KW是水的离子积(=10-14)。 三个方程均为未知浓度的高次函数,用“规划求解” 步骤如下: 1)在B1:B3单元格输入Cd2+总浓度CM ,CN-的总 浓度CL,HCN的酸解离常数Ka。 2)D2:F2是要求解的未知浓度[CN]、[Cd2+]和[H+]所 在位置。
威布尔分布表达式

威布尔分布表达式
威布尔分布是一种概率分布,通常用于描述一些物理、化学或生物现象的寿命或失效时间。
其概率密度函数表示为:f(x) = (α/λ)×(x/λ)^(α-1)×exp(-(x/λ)^α),其中α和λ为分布的形状参数和尺度参数。
威布尔分布表达式的推导可以使用最大似然估计方法,通过样本数据对参数进行估计。
对于给定的n个样本数据x1,x2,...,xn,威布尔分布的似然函数为:L(α,λ) = ∏(i=1 to n)[(α/λ)×(xi/λ)^(α-1)×exp(-(xi/λ)^α)]。
通过对似然函数进行求导,并令其等于0,可以求得最大似然估计值:α = (n/Σ(xi/λ)^2)^(1/α),λ = (Σ(xi/λ)^α/n)^(1/α)。
这个估计方法可以通过计算机程序实现,方便地得到威布尔分布的参数估计值。
威布尔分布表达式的应用十分广泛,包括风力场和振动信号的分析、设备寿命的预测、信号传输的可靠性评估等。
其具有良好的数学性质,可以方便地进行推导和计算,因此被广泛应用于工程和科学领域。
- 1 -。
