计数型MSA分析表交叉表法
计数型MSA分析

102.00
总计
50.00 18.00 100 132.00 150 150.00
评 价 人 B 与 参 考 交 叉 表
#### 计算 期望值的计
B
算#### 计算Fra bibliotek期望值的计
总计
算 计算
期望值的计算
参考
0.00
1.00
45
2
2.88
6.12
3
100
45.12
95.88
48
102
48.00
102.00
0.00 43 0.12 8 1.88 51.00 2.00
C 1.00 7 8.88 92 139.12 99.00 148.00
47.00 18.00 103.00 132.00 150.00 150.00
总计 50.00 9.00 100.00 141.00 150.00 150.00
评 价 人 之 间 的 Kap pa 值
10 1 1 1 1 1 1 1 1 1
11 1 1 1 1 1 1 1 1 1
12 1 1 1 1 1 1 1 1 1
13 1 1 1 1 1 1 1 1 1
14 1 1 1 1 1 1 1 1 1
15 0 1 1 1 1 1 1 1 1
16 1 1 1 1 1 1 1 1 1
17 1 1 1 1 1 1 1 1 1
26 1 1 1 1 1 1 1 1 1
27 0 0 0 0 0 0 1 1 1
28 0 0 0 0 0 0 1 1 1
29 1 1 1 1 1 1 1 1 1
30 1 1 1 1 1 1 1 1 1
31 1 1 1 1 1 1 1 1 1
第十四章交叉表分析法(课件)
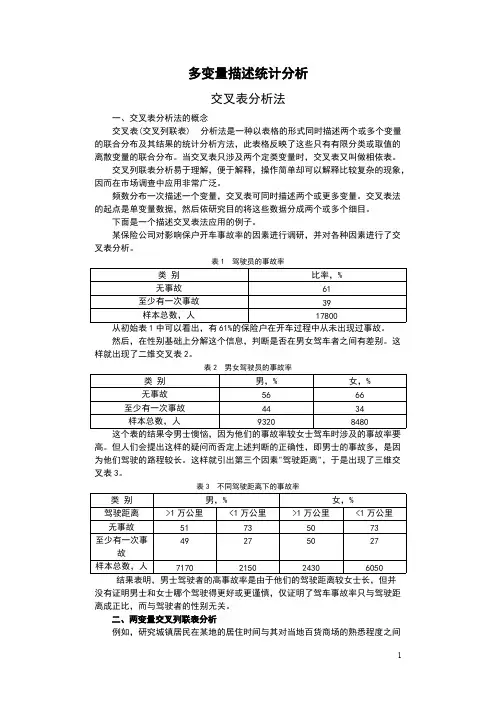
多变量描述统计分析交叉表分析法一、交叉表分析法的概念交叉表(交叉列联表) 分析法是一种以表格的形式同时描述两个或多个变量的联合分布及其结果的统计分析方法,此表格反映了这些只有有限分类或取值的离散变量的联合分布。
当交叉表只涉及两个定类变量时,交叉表又叫做相依表。
交叉列联表分析易于理解,便于解释,操作简单却可以解释比较复杂的现象,因而在市场调查中应用非常广泛。
频数分布一次描述一个变量,交叉表可同时描述两个或更多变量。
交叉表法的起点是单变量数据,然后依研究目的将这些数据分成两个或多个细目。
下面是一个描述交叉表法应用的例子。
某保险公司对影响保户开车事故率的因素进行调研,并对各种因素进行了交叉表分析。
表1 驾驶员的事故率类别比率,%无事故61至少有一次事故39样本总数,人17800从初始表1中可以看出,有61%的保险户在开车过程中从未出现过事故。
然后,在性别基础上分解这个信息,判断是否在男女驾车者之间有差别。
这样就出现了二维交叉表2。
表2 男女驾驶员的事故率类别男,%女,%无事故5666至少有一次事故4434样本总数,人93208480这个表的结果令男士懊恼,因为他们的事故率较女士驾车时涉及的事故率要高。
但人们会提出这样的疑问而否定上述判断的正确性,即男士的事故多,是因为他们驾驶的路程较长。
这样就引出第三个因素"驾驶距离",于是出现了三维交叉表3。
表3 不同驾驶距离下的事故率类别男,%女,%驾驶距离>1万公里<1万公里>1万公里<1万公里无事故51735073至少有一次事49275027故样本总数,人7170215024306050结果表明,男士驾驶者的高事故率是由于他们的驾驶距离较女士长,但并没有证明男士和女士哪个驾驶得更好或更谨慎,仅证明了驾车事故率只与驾驶距离成正比,而与驾驶者的性别无关。
二、两变量交叉列联表分析例如,研究城镇居民在某地的居住时间与其对当地百货商场的熟悉程度之间的关系,对“居住时间”和“熟悉程度”这两个变量进行交叉列联分析。
计数型MSA
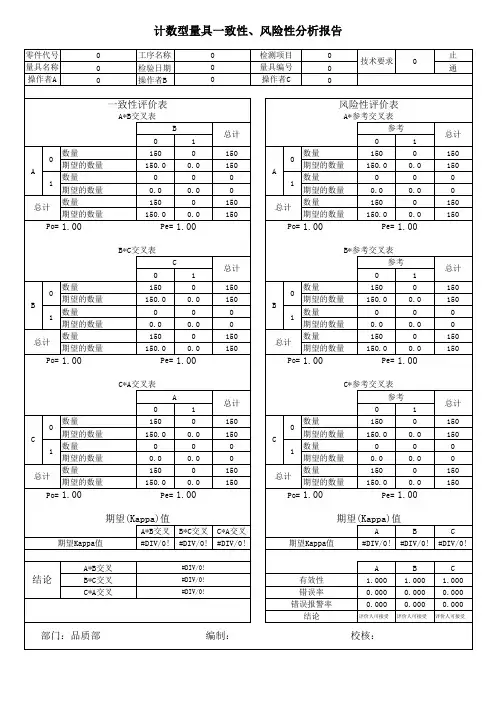
零件代号 量具名称 操作者A 0 0 0 工序名称 检验日期 操作者B 0 0 0 检测项目 量具编号 操作者C 0 0 0 技术要求 0 B 数量 期望的数量 A 数量 1 期望的数量 数量 总计 期望的数量 Po= 1.00 0 0 150 150.0 0 0.0 150 150.0 Pe= B*C交叉表 C 数量 期望的数量 B 数量 1 期望的数量 数量 总计 期望的数量 Po= 1.00 0 0 150 150.0 0 0.0 150 150.0 Pe= C*A交叉表 A 数量 期望的数量 C 数量 1 期望的数量 数量 总计 期望的数量 Po= 1.00 0 0 150 150.0 0 0.0 150 150.0 Pe= 1 0 0.0 0 0.0 0 0.0 总计 150 150 0 0 150 150 0 1 0 0.0 0 0.0 0 0.0 总计 150 150 0 0 150 150 0 1 0 0.0 0 0.0 0 0.0 总计 150 150 0 0 150 150 0
评价人可接受
B #DIV/0! B 1.000 0.000 0.000
评价人可接受
C #DIV/0! C 1.000 0.000 0.000
评价人可接受
结论
有效性 错误率 错误报警率 结论
部门:品质部
编制:
校核:
总计 150 150 0 0 150 150
1.00
1.00
C*参考交叉表 参考 数量 期望的数量 C 数量 1 期望的数量 数量 总计 期望的数量 Po= 1.00 0 150 150.0 0 0.0 150 150.0 Pe= 1 0 0.0 0 0.0 0 0.0
总计 150 150 0 0 150 150
计数型msa分析表
A*C 0.788
Good
Reproducib 0.776
REF
0.00
1.00 Total
Po:
45
5
50
16.0
34.0
50.0 Pe:
3
97
100
Prepared by Richard Li
0.94 0.56
0.91 0.56
0.90 0.55
0.95 0.56
Page 2 of 3
Total B*REF Crosstabu lation
Pe)/(1-Pe)
B*C 0.863
Good
A*REF Crosstabu lation
A
0.00 Count
Expected
1.00 Count
With
reference/
与基准一致
A
B
C
42
45
40
B
0.00
1.00 Total
Po:
44
6
50
15.7
34.3
50
Pe:
3
97
100
31.3
68.7
3
50
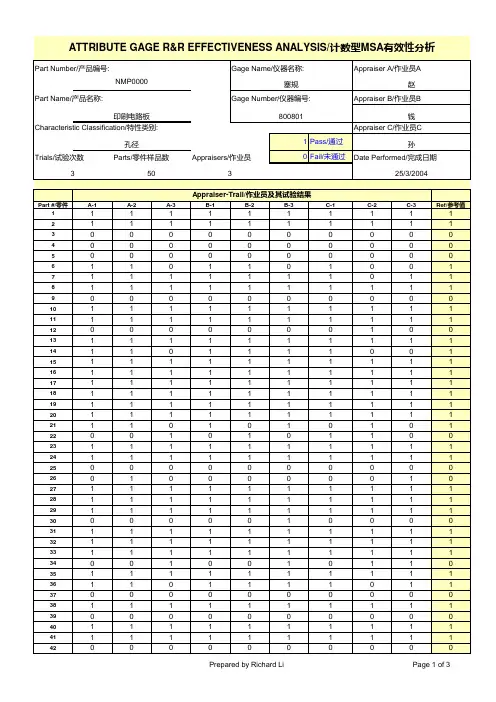
Gage Name/仪器名称:
Appraiser A/作业员A
塞规 Gage Number/仪器编号:
赵 Appraiser B/作业员B
Appraisers/作业员
800801
钱 Appraiser C/作业员C
1 Pass/通过
孙
0 Fail/未通过 Date Performed/完成日期
Total Po:
0.90
42
9
51
MSA第三版中KAPPA分析法精讲

Top Consulting
总计 7 33.0 92 66.0 99 99.0 50 50.0 100 100.0 150 150.0
A
1
总计
观测值 期望值 观测值 期望值 观测值 期望值
假设检验分析—交叉表方法
计算Kappa值 Kappa=(P0-Pe)/(n-Pe) 其中P0=对角线单元中观测值的总和; Pe=对角线单元中期望值的总和。 A与B的Kappa值 P0=44+97=141 Pe=15.7+68.7=84.4 Kappa=(141-84.4)/(150-84.4)=0.86
Top Consulting
风险分析法
数据收集 随机从过程中抽取50个零件样本,以获得覆盖过 程范围的零件。使用3名评价人,每位评价人 对每个零件评价3次,将评价结果记录在“计 数型研究数据表”中。1代表接受,0代表不接 受。参见附表。 评价的组织人员通过使用实验室设备等获得每个 零件的基准值,表中的“-”、“+”、“×”代 表零件处于I区、III区和II区。
50 39
系统有效得分与计数
50 39
64%
78%
64%
78%
89%
89%
结论:1 评价人自己在所有试验上都一致 2 评价人在所有试验上都与基准一致 3 所有评价人自己保持一致,两两间一致 4 所有评价人自己和两两间一致且与基准一致
Top Consulting
Top Consulting
A与B的交叉表
0 44 15.7 3 31.3 47 47.0
Top Consulting
计数型MSA分析表(最新)
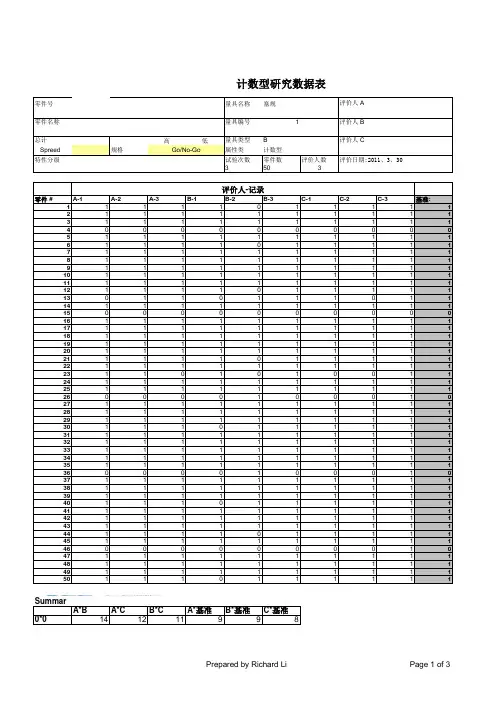
135.0
150
Po:
0.92
Pe:0.77源自Po:0.89Pe:
0.78
C
0.00
1.00 总计
Po:
0.95
12
5
17
1.7
15.3
17 Pe:
0.81
3
130
133
13.3 119.7
133
15
135
150
15.0 135.0
150
A*C
0.521 差
Reprodu 0.720
Prepared by Richard Li
基准
0.00
1.00 总计
Po:
0.93
9
6
15
1.5
13.5
15.0 Pe:
0.77
0
75
75
7.5
67.5
75.0
9
81
90
9.0
81.0
90.0
0.00 计算 期望的计
1.00 计算 期望的计 计算 期望的计
基准
0.00
1.00
总计 Po:
0.98
8
1
9
0.9
8.1
9.0 Pe:
0.82
1
80
A*基准 B*基准 C*基准
11
9
9
8
C-2 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1
C-3 1 1 1 0 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1
计数型MSA分析表
计数型MSA分析表
内容正确、语言规范[title]MSA分析表[Introduction]MSA(多因素分析)是一种统计分析技术,主要用于研究多个变量之间的关系。
MSA分析表是一张用于描述多因素分析的表格,包括因素、变量、分组、比较组等。
此表是帮助统计分析师和研究者更好地理解数据的有用工具。
[Main Body]
因素(factors):因素是一组相关变量,其有助于解释观察数据的数量和结构差异。
因素一般被划分为受试者特征(人口学因素)、设备设计(技术因素)和操作过程(程序因素)。
变量(variables):变量是一个可以被数字表示的量,用于评估结果的变化。
变量可以是定量的(如温度和比重)或者定性的(如看法和性格)。
分组(grouping):分组是把数据按照特定的方式组织起来的一种方法。
MSA可以采用两种分组方式,一种是随机分组,即样本是随机抽取;另一种是非随机分组,即样本是依据特定要求抽取。
MSA测量系统分析全套表格模板(全公式未加密)
1、2、3、4、5、线性GRR计数型Kappa分析MSA测量系统分析全套表格模板稳定性偏倚Excel原件可在本文档左侧回形针处取出再现性Kappa=(Po-Pe)/(1-Pe)A*参考 交叉表A01总计Po:0.95Pe:0.51B*参考 交叉表B01总计Po:0.97Pe:0.51C*参考 交叉表C01总计Po:0.96Pe:0.5130期望的数量26.4636.5463数量38487期望的数量数量60363一致性好6666Kappa 一致性好判定误发期望的数量638728 4.76%可接受2.30%可接受 4.76%可接受3.45%可接受可接受5.75%可接受01参考总计62063871501C0.90有效性判定重复性检查总数匹配数漏发A A B 评价人评价人%B 93.33%可接受判 定判定0.9383.33%2530 3.17%36.5450.4687数量638715090.00%可接受0.92A C 一致性好150期望的数量B 期望的数量36.9651.0488数量6387150期望的数量26.0435.9662数量38588期望的数量6387数量60248.7284150数量6387150期望的数量35.28数量28284总计01Kappa 判 定A*B 0.89一致性好C 3027A*C 0.93一致性好参考B*C 参考总计可接受期望的数量27.7238.280.90一致性好数量615Page 11 of 11。
MSA知识讲解及MSA分析
抽样的 随机性
与测量方法 相关的变异
与测量人员 相关的变异
稳定性
线性 偏倚性
分辨力
重复性 再现性
注:计数型数据测量系统分析方法主要有交叉表法、信号检查法。
分辨力(分辨率、可读性)
■别名:最小可读单位、测量解析度、最小刻度极限、探测的最小极限
分辨力老要求:公差的1/10
分套MSA知 识讲解及分析样
表
课程简介
一、基础知识回顾
扫盲
二、正题(实用知识)
“伪专家”
基础知识回顾
目录
1、理解MSA
◆什么是测量系统分析(MSA) ◆为什么要进行MSA ◆哪些地方要进行MSA ◆什么时候进行MSA
2、MSA类型简介
分辨力、重复性、再现性、线性、偏倚性、 稳定性、一致性
3、MSA五性案例及判定标准
测量室温的测量系统构成如下:
经测量,现在
的室温为 17.5℃
◆量具(仪器)——摄氏温度计 ◆标准——在一个标准大气压下,将纯净水的结冰点定义为0℃,沸点定义为 100℃,温差的1/100即为1℃; ◆操作(方法)——将温度计放置在相对固定的环境中,5min后,平视目测, 读取温度示值,估读至0.1℃。 ◆夹具——温度计挂钩+平整的墙面(用以限制温度计自由度的任何工具) ◆软件——无 ◆人员——我 ◆环境——风速、湿度、照度 ◆假设——假设上面提到的一些参数(时间、风速、湿度、照度等)均是准确 可靠的,温度计校验合格,操作方法合理,“我”具备测量技能,……
)
分辨力(分辨率、可读性)
重复性、再现性(GR&R)
重复性、再现性(GR&R)
线性、偏倚性
◆量具线性告诉你测量系统在预期测量范围内的准确性如何。
计数型测量系统的msa方法
计数型测量系统的msa方法嘿,咱今儿来聊聊计数型测量系统的 MSA 方法。
这玩意儿啊,就像是一把神奇的尺子,能帮咱衡量好多东西呢!你想啊,咱在工作中、生活里,是不是经常得判断这个行还是不行,合格还是不合格呀?这计数型测量系统就派上大用场啦!它能让咱更准确、更靠谱地做出这些判断。
那 MSA 方法呢,就是让这把尺子更精准的法宝。
它就好像是给尺子做了一次全面的体检和校准。
通过一系列的操作和分析,咱能知道这尺子准不准,误差有多大。
比如说,咱用这计数型测量系统去检测一批零件。
如果 MSA 方法没做好,那可能就会出现明明合格的零件被误判为不合格,或者不合格的零件反而被放过了的情况。
这可不得了哇,就好像医生误诊一样,会带来好多麻烦呢!那怎么做好MSA 方法呢?首先得有严谨的态度,不能马马虎虎的。
就跟咱做饭一样,调料放得恰到好处,做出来的菜才好吃。
然后呢,得按照正确的步骤一步一步来,不能跳步骤,也不能瞎糊弄。
咱可以想象一下,要是盖房子不按步骤来,那房子能结实吗?肯定不行呀!这 MSA 方法也是一样的道理。
在做的过程中,要仔细观察数据,就像侦探找线索一样。
看看有没有异常的地方,有没有不合理的情况。
一旦发现问题,就得赶紧解决,可不能拖着。
而且啊,这 MSA 方法还不是一锤子买卖,得定期检查、更新。
就像咱的车子要定期保养一样,这样才能保证它一直好用。
你说,要是咱不重视这计数型测量系统的 MSA 方法,那会咋样?那可就乱套啦!产品质量没法保证,工作效率也会下降,那损失可就大啦!咱可不能让这种事情发生呀!所以说呀,计数型测量系统的MSA 方法可太重要啦!咱得好好学,认真用,让它为咱的工作和生活保驾护航。
咱可不能小瞧了它,不然到时候吃亏的可是咱自己哟!这可不是开玩笑的呢!大家都要重视起来呀!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
零件
A-1A-2A-3B-1B-2B-3C-1C-2C-3Ref/参考值
1
1111111111
2
1111111111
3
0000000000
4
0000000000
5
0000000000
6
0000000000
7
1111111101
8
1111111111
9
0000000000
10
1111111111
11
1111111111
12
0000000000
13
1111111111
14
1110111101
15
1111111111
16
1111111111
17
1111111111
18
1111111111
19
1111111111
20
1111111111
21
0000000000
22
0000000000
23
1111111111
24
1111111111
25
0000000000
26
0000000000
27
1111111111
28
1111111111
29
1111111111
30
0000000000
31
1111111111
32
1111111111
33
1111111111
34
0111111011
35
1111111111
36
1111111101
37
0000000000
38
1111111111
39
0000000000
40
1111111111
41
1111111111
42
0000000000
43
1011111111
44
1111111111
45
0000000000
46
1111111111
47
1111111111
48
0000000000
49
0011111111
50
0000000000
Data Summary/数据总结
A*BA*CB*CA*RefB*RefC*Ref
0*0515151515151
1*0144000
0*1441414
1*1949194959895
Self agreement/自评 With reference/与基准一致特性类别:计数型MSA有效性分析作业员A:作业员B:产品编号:产品名称:仪器名称:完成日期:仪器编号:作业员C:作业员及其试验结果Prepared by Richard Li Page 1 of 2
特性类别:计数型MSA有效性分析作业员A:作业员B:产品编号:产品名称:仪器名称:完成日期:仪器编号:作业员C:
ABCABC
474946474946
A*B Crosstabulation
0.001.00TotalPo:0.97
A0.00Count51455
Expected Count19.135.955Pe:0.54
1.00Count19495
Expected Count32.962.195
TotalCount5298150
Expected Count52.098.0150
B*C Crosstabulation
0.001.00TotalPo:0.97
B0.00Count51152
Expected Count19.132.952Pe:0.54
1.00Count49498
Expected Count35.962.198
TotalCount5595150
Expected Count55.095.0150
A*C Crosstabulation
0.001.00TotalPo:0.95
A0.00Count51455
Expected Count20.234.855Pe:0.54
1.00Count49195
Expected Count34.860.295
TotalCount5595150
Expected Count55.095.0150
注:“1”表示合格;“0”表示不合格
作业员之间的一致性Kappa≥0.75合格ConcludeKappa=(Po-Pe)/(1-Pe)ABC作业员与基准的一致性Kappa0.940.990.94≥0.75合格ConcludeGoodGoodGood作业员的有效性ABC50505047494694%98%92%≥0.90合格GoodGoodGoodABC结论:此测量系统可接受ConcludeConclusion% AppraiserTotal InspectedMatchedRepeatability%0.0%4.0%漏发≤0.02合格误发≤0.05合格0.0%1.0%Acceptable0.0%4.0%AcceptableAcceptableA*B0.927GoodB*C0.927Good0.885GoodCCA*C
B
Acceptable
Conclusion
Acceptable
Acceptable
Prepared by Richard Li Page 2 of 2
