第8讲 三角函数的图象与性质
三角函数的图像和性质

高三数学总复习讲义——三角函数性质与图像一.基本初等函数图像:“五点法”和“两线一点法”如①sin y x=−−−−→图例变化为②sin()y A x ωϕ=+(A >0,ω>0)相应地,①的单调增区间2,222k k ππππ⎡⎤-++⎢⎥⎣⎦−−−→变为2222k x k πππωϕπ-+++≤≤的解集是②的增区间.注:⑴)sin(ϕω+=x y 或cos()y x ωϕ=+(0≠ω)的周期ωπ2=T ;⑵sin()y x ωϕ=+的对称轴方程是2x k ππ=+(Z k ∈),对称中心(,0)k π;cos()y x ωϕ=+的对称轴方程是x k π=(Z k ∈),对称中心1(,0)2k ππ+;)tan(ϕω+=x y 的对称中心(0,2πk ). 课前预习1.函数sin cos y x x =-的最小正周期是 . 2. 函数1π2sin()23y x =+的最小正周期T = . 3.函数sin2xy =的最小正周期是( ) (A)2π(B)π (C) 2π (D) 4π 4.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是( )(A)]3,0[π (B)]127,12[ππ (C) ]65,3[ππ (D)],65[ππ 5.函数22cos()()363y x x πππ=-≤≤的最小值是( )()2A - ()B ()1C - ()1D6.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象( )(A)向右平移6π个单位长度 (B)向右平移3π个单位长度 (C)向左平移6π个单位长度 (D)向左平移3π个单位长度7.将函数sin y x =的图象上各点的横坐标扩大为原来的2倍,纵坐标不变,再把所得图象上所有点向左平移3π个单位,所得图象的解析式是__________________.8. 函数sin y x x =在区间[0,2π]的最小值为______.10.已知f (x )=5sin x cos x -35cos 2x +325(x ∈R ) ⑴求f (x )的最小正周期; ⑵求f (x )单调区间;⑶求f (x )图象的对称轴,对称中心。
三角函数的图像与性质考点及经典例题讲解

三角函数的图象与性质考纲解读 1.结合y =sin x ,y =cos x ,y =tan x 的图象,进行简单的变换;2.利用y =sin x ,y =cos x ,y =tan x 在一个周期内的性质,求解简单的三角方程、不等式、周期性等.[基础梳理]1.用五点法作正弦函数和余弦函数的简图正弦函数y =sin x ,x ∈[0,2π]的图象上,五个关键点是:(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0).余弦函数y =cos x ,x ∈[0,2π]的图象上,五个关键点是:(0,1),⎝⎛⎭⎫π2,0,()π,-1,⎝⎛⎭⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )且x ≠k π+(1)周期函数:对于函数f (x ),如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有f (x +T )=f (x ),那么函数f (x )就叫作周期函数,非零常数T 叫作这个函数的周期.(2)最小正周期:如果在周期函数f (x )的所有周期中存在一个最小的正数,那么这个最小正数就叫作f (x )的最小正周期.[三基自测]1.函数y =12sin x ,x ∈[-π,π]的单调性是( )A .在[-π,0]上是增函数,在[0,π]上是减函数B .在⎣⎡⎦⎤-π2,π2上是增函数,在⎣⎡⎦⎤-π,-π2和⎣⎡⎦⎤π2,π上都是减函数 C .在[0,π]上是增函数,在[-π,0]上是减函数D .在⎣⎡⎦⎤π2,π和⎣⎡⎦⎤-π,-π2上是增函数,在⎣⎡⎦⎤-π2,π2上是减函数 答案:B2.函数y =tan 2x 的定义域是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π+π4,k ∈Z B.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2+π8,k ∈Z C.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π+π8,k ∈Z D.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2+π4,k ∈Z 答案:D3.f (x )=cos 2x 在x ∈⎣⎡⎦⎤0,π2上的值域为( ) A .[-1,1] B .[0,1] C .[-1,0] D .[0,π]答案:A4.(必修4·习题1.4B 组改编)函数y =-tan ⎝⎛⎭⎫2x -3π4的单调递减区间为 __________________. 答案:⎝⎛⎭⎫π8+k 2π,58π+k2π,k ∈Z 5.(2017·高考全国卷Ⅱ改编)函数f (x )=3cos x -34的最小正周期为__________.答案:2π[考点例题]考点一 有关三角函数的定义域、值域、最值|模型突破角度1 单调性法求三角函数的最值(值域)[例1] 已知函数f (x )=(cos x -sin x )·sin 2xcos x .(1)求函数f (x )的定义域及最小正周期; (2)当x ∈⎝⎛⎦⎤-π2,0时,求函数f (x )的最值. [解析] (1)由cos x ≠0,得x ≠k π+π2,k ∈Z ,所以函数f (x )的定义域为{x |x ≠k π+π2,k ∈Z }.因为f (x )=(cos x -sin x )·2sin x ·cos xcos x=2sin x cos x -2sin 2x =sin 2x -(1-cos 2x )=2sin ⎝⎛⎭⎫2x +π4-1, 所以函数f (x )的最小正周期为T =2π2=π.(2)因为-π2<x ≤0,所以-3π4<2x +π4≤π4.令-3π4<2x +π4<-π2,则-π2<x <-3π8;令-π2≤2x +π4≤π4,则-3π8≤x ≤0,所以函数f (x )在⎝⎛⎭⎫-π2,-3π8上单调递减,在⎣⎡⎦⎤-3π8,0上单调递增. 所以当x =-3π8时,函数f (x )取得最小值,所以f (x )min =-2-1.因为f (0)=2sin π4-1=0,f ⎝⎛⎭⎫-π2=2sin ⎝⎛⎭⎫-π+π4-1=-2,所以f (x )max =0. 所以函数f (x )的最大值为0,最小值为-2-1. [模型解法]角度2 换元法求三角函数的最值(值域)[例2] 已知x ∈⎣⎡⎦⎤π6,5π6,则函数f (x )=-cos 2x -sin x sin π6+cos 2x +1716的最小值为__________.[解析] 因为f (x )=-cos 2x -sin x sin π6+cos 2x +1716,所以f (x )=2sin 2x -12sin x +cos 2x +116=sin 2x -sin x 2+1716=⎝⎛⎭⎫sin x -142+1. 设t =sin x ,则y =⎝⎛⎭⎫t -142+1. 因为x ∈⎣⎡⎦⎤π6,5π6, 所以12≤t ≤1.又函数y =⎝⎛⎭⎫t -142+1在⎣⎡⎦⎤12,1上单调递增, 所以当t =12时,y =⎝⎛⎭⎫t -142+1取得最小值y min =⎝⎛⎭⎫12-142+1=1716, 即函数f (x )的最小值为1716.[答案]1716[模型解法][高考类题](2017·高考全国卷Ⅱ)函数f (x )=sin 2x +3cos x -34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0,π2的最大值是__________. 解析:依题意,f (x )=sin 2x +3cos x -34=-cos 2x +3cos x +14=-⎝⎛⎭⎫cos x -322+1,因为x ∈⎣⎡⎦⎤0,π2,所以cos x ∈[0,1],因此当cos x =32时,f (x )max =1. 答案:1考点二 三角函数的性质及应用|方法突破命题点1 三角函数的单调性[例3] (1)(2018·佛山模拟)已知x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,则f (x )的一个单调递减区间是( )A.⎝⎛⎭⎫π6,2π3B.⎝⎛⎭⎫π3,5π6 C.⎝⎛⎭⎫π2,πD.⎝⎛⎭⎫2π3,π(2)若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω等于( )A.23 B.32 C .2D .3(3)已知ω>0,函数f (x )=cos ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递增,则ω的取值范围是( ) A.⎣⎡⎦⎤12,54 B.⎣⎡⎦⎤12,74 C.⎣⎡⎦⎤34,94D.⎣⎡⎦⎤32,74[解析] (1)因为x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,所以sin ⎝⎛⎭⎫2×π3+φ=1,所以2×π3+φ=2k π+π2, 解得φ=2k π-π6,k ∈Z ,不妨取φ =-π6,此时f (x )=sin ⎝⎛⎭⎫2x -π6, 令2k π+π2<2x -π6<2k π+3π2可得k π+π3<x <k π+5π6,所以函数f (x )的单调递减区间为⎝⎛⎭⎫k π+π3,k π+5π6,k ∈Z ,结合选项可知当k =0时,函数的一个单调递减区间为⎝⎛⎭⎫π3,5π6. (2)∵f (x )=sin ωx (ω>0)过原点,∴当0≤ωx ≤π2,即0≤x ≤π2ω时,y =sin ωx 是增函数;当π2≤ωx ≤3π2,即π2ω≤x ≤3π2ω时,y =sin ωx 是减函数. 由f (x )=sin ωx (ω>0)在⎣⎡⎦⎤0,π3上单调递增, 在⎣⎡⎦⎤π3,π2上单调递减知,π2ω=π3,∴ω=32. (3)函数y =cos x 的单调递增区间为[-π+2k π,2k π],k ∈Z ,则⎩⎨⎧ωπ2+π4≥-π+2k π,k ∈Z ,ωπ+π4≤2k π,k ∈Z ,解得4k -52≤ω≤2k -14,k ∈Z ,又由4k -52-⎝⎛⎭⎫2k -14≤0,k ∈Z 且2k -14>0,k ∈Z ,得k =1,所以ω∈⎣⎡⎦⎤32,74.[答案] (1)B (2)B (3)D [方法提升]1.求三角函数单调区间的方法2.[母题变式]1.若本例(2)的条件改为函数f (x )=m sin ωx (其中ω>0,m >0)在区间⎣⎡⎦⎤-π2,2π3上单调递增,则ω的取值范围是__________.解析:因为ω>0,m >0, 由2k π-π2≤ωx ≤2k π+π2,k ∈Z ,得f (x )的增区间是⎣⎡⎦⎤2k πω-π2ω,2k πω+π2ω,k ∈Z . 因为f (x )在⎣⎡⎦⎤-π2,2π3上单调递增,所以⎣⎡⎦⎤-π2,2π3⊆⎣⎡⎦⎤-π2ω,π2ω. 所以-π2≥-π2ω且2π3≤π2ω,所以ω∈⎝⎛⎦⎤0,34. 答案:⎝⎛⎦⎤0,34 2.将本例(3)改为:g (x )=-cos ⎝⎛⎭⎫-2x +π3⎝⎛⎭⎫x ∈⎣⎡⎦⎤-π2,π2, 则g (x )的单调递增区间为__________. 解析:g (x )=-cos ⎝⎛⎭⎫-2x +π3=-cos ⎝⎛⎭⎫2x -π3, 欲求函数g (x )的单调递增区间, 只需求y =cos ⎝⎛⎭⎫2x -π3的单调递减区间. 由2k π≤2x -π3≤2k π+π,k ∈Z ,得k π+π6≤x ≤k π+2π3,k ∈Z .故所给函数的单调递增区间为⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z ). 因为x ∈⎣⎡⎦⎤-π2,π2, 所以函数g (x )的单调递增区间是⎣⎡⎦⎤-π2,-π3,⎣⎡⎦⎤π6,π2. 答案:⎣⎡⎦⎤-π2,-π3,⎣⎡⎦⎤π6,π2命题点2 三角函数的奇偶性、对称性、周期性[例4] (1)若函数f (x )=sin x +φ3(φ∈[0,2π])是偶函数,则φ=( )A.π2B.2π3C.3π2D.5π3(2)函数f (x )=sin ⎝⎛⎭⎫x -π4的图象的一条对称轴是( ) A .x =π4B .x =π2C .x =-π4D .x =-π2(3)若函数y =cos ⎝⎛⎭⎫ωx +π6(ω∈N *)图象的一个对称中心是⎝⎛⎭⎫π6,0,则ω的最小值为( )A .1B .2C .4D .8(4)(2018·湘西自治州模拟)已知函数f (x )=sin(ωx -ωπ)(ω>0)的最小正周期为π,则f ⎝⎛⎭⎫π12等于( )A.12 B .-12C.32D .-32[解析] (1)由y =sin x +φ3是偶函数知φ3=π2+k π,k ∈Z ,即φ=3π2+3k π,k ∈Z ,又∵φ∈[0,2π],∴φ=3π2.(2)∵正弦函数图象的对称轴过图象的最高(低)点, 故令x -π4=k π+π2,k ∈Z ,∴x =k π+3π4,k ∈Z .即k =-1,则x =-π4.(3)由题知πω6+π6=k π+π2(k ∈Z )⇒ω=6k +2(k ∈Z )⇒ωmin =2,故选B.(4)由题意得2πω=π,所以ω=2,所以f (x )=sin(2x -2π)=sin 2x , 所以f ⎝⎛⎭⎫π12=sin π6=12. [答案] (1)C (2)C (3)B (4)A [方法提升][跟踪训练]3.(2018·泉州模拟)已知f (x )=cos(3x +φ)-3sin(3x +φ)为偶函数,则φ可以取的一个值为( )A.π6B.π3 C .-π6D .-π3解析:由已知得f (x )=2cos ⎣⎡⎦⎤3x +⎝⎛⎭⎫φ+π3为偶函数,由诱导公式可知φ+π3=k π.(k ∈Z ) 当k =0时,φ=-π3.答案:D4.已知函数f (x )=sin ⎝⎛⎭⎫ωx +π6-1最小正周期为2π3,则f (x )的图象的一条对称轴的方程是( )A .x =π9B .x =π6C .x =π3D .x =π2解析:已知函数f (x )的最小正周期为T =2πω=2π3,∴ω=3,则其对称轴方程为3x +π6=π2+k π,k ∈Z ,即x =π9+k π3,k ∈Z ,当k =0时,x =π9,故选A.答案:A5.同时具有性质:①最小正周期是π;②图象关于直线x =π3对称;③在⎣⎡⎦⎤-π6,π3上是增函数的一个函数是( )A .y =sin ⎝⎛⎭⎫x 2+π6 B .y =cos ⎝⎛⎭⎫2x +π3 C .y =sin ⎝⎛⎭⎫2x -π6 D .y =cos ⎝⎛⎭⎫x 2-π6解析:对于选项A ,y =sin ⎝⎛⎭⎫x 2+π6的最小正周期T =2π12=4π,故不满足①;对于选项B ,y =cos ⎝⎛⎭⎫2x +π3,由2k π≤2x +π3≤2k π+π,k ∈Z 可解得其单调递减区间为⎣⎡⎦⎤k π-π6,k π+π3,k ∈Z ,故不符合③;对于选项C ,令y =f (x )=sin ⎝⎛⎭⎫2x -π6,则f ⎝⎛⎭⎫π3=sin ⎝⎛⎭⎫2π3-π6=sin π2=1,为最大值,所以f (x )=sin ⎝⎛⎭⎫2x -π6的图象关于直线x =π3对称,且其周期T =2π2=π,具有性质①、②,由2k π-π2≤2x -π6≤2k π+π2,k ∈Z ,解得:x ∈⎣⎡⎦⎤k π-π6,k π+π3,k ∈Z ,从而当k =0时,有函数f (x )=sin ⎝⎛⎭⎫2x -π6在⎝⎛⎭⎫-π6,π3上是增函数,具有性质③,符合题意.对于选项D ,y =cos ⎝⎛⎭⎫x 2-π6的最小正周期T =2π12=4π,故不满足①. 答案:C[真题感悟]1.(2017·高考全国卷Ⅱ)函数f (x )=sin(2x +π3)的最小正周期为( )A .4πB .2πC .πD.π2解析:依题意得,函数f (x )=sin(2x +π3)的最小正周期T =2π2=π,选C.答案:C2.(2017·高考山东卷)函数y =3sin 2x +cos 2x 的最小正周期为( ) A.π2 B.2π3 C .πD .2π解析:y =3sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π6,T =2π2=π. 答案:C3.(2016·高考全国卷Ⅰ)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|≤π2,x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在⎝⎛⎭⎫π18,5π36上单调,则ω的最大值为( ) A .11 B .9 C .7D .5解析:由题意知:⎩⎨⎧-π4ω+φ=k 1π,π4ω+φ=k 2π+π2,则ω=2k +1,其中k ∈Z .因为f (x )在⎝⎛⎭⎫π18,5π36上单调, 所以5π36-π18=π12≤12×2πω,ω≤12.接下来用排除法.若ω=11,φ=-π4,此时f (x )=sin ⎝⎛⎭⎫11x -π4, f (x )在⎝⎛⎭⎫π18,3π44上单调递增,在⎝⎛⎭⎫3π44,5π36上单调递减,不满足f (x )在⎝⎛⎭⎫π18,5π36上单调,若ω=9,φ=π4,此时f (x )=sin ⎝⎛⎭⎫9x +π4,满足f (x )在⎝⎛⎭⎫π18,5π36上单调递减.答案:B。
三角函数的图像和性质知识点及例题讲解

三角函数的图像和性质一、用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是:(0,0) (2π,1) (,0) (23π,-1) (2,0)余弦函数y=cosx x [0,2]的图像中,五个关键点是:(0,1) (2π,0) (,-1) (23π,0) (2,1)二、正弦函数、余弦函数和正切函数的图象与性质:sin y x = cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值 当22x k ππ=+时,max 1y =;当22x k ππ=- 时,min 1y =-.当2x k π=时,max 1y =;当2x k ππ=+时,min1y =-.既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数 偶函数 奇函数单调性 在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦上是增函数; 在32,222k k ππππ⎡⎤++⎢⎥⎣⎦上是减函数. 在[]2,2k k πππ-上是增函数; 在[]2,2k k πππ+上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭上是增函数.对称性 对称中心(),0k π 对称轴2x k ππ=+对称中心,02k ππ⎛⎫+ ⎪⎝⎭对称轴x k π=对称中心,02k π⎛⎫⎪⎝⎭无对称轴函 数 性 质例作以下函数的简图(1)y=|sinx|,x ∈[0,2π], (2)y=-cosx ,x ∈[0,2π]例利用正弦函数和余弦函数的图象,求知足以下条件的x 的集合:21sin )1(≥x 21cos )2(≤x3、周期函数概念:关于函数()y f x =,若是存在一个非零常数T ,使适当x 取概念域内的每一个值时,都有:()()f x T f x +=,那么函数()y f x =就叫做周期函数,非零常数T 叫做那个函数的周期。
注意: 周期T 往往是多值的(如sin y x = 2π,4π,…,-2π,-4π,…都是周期)周期T 中最小的正数叫做()y f x =的最小正周期(有些周期函数没有最小正周期)sin y x =, cos y x =的最小正周期为2π (一样称为周期) 正弦函数、余弦函数:ωπ=2T 。
高三文科数学总复习课件:三角函数的图像与性质

递减区间.
第二十一页,编辑于星期日:二十二点 四十八 分。
备选例题.已知函数f (x) sin(x )( 0, 0 ) 是R上的偶函数,其图象关于点M (3 , 0)对称,且在
4
区间[0, ]上是单调函数,求和的值.
2
第二十二页,编辑于星期日:二十二点 四十八 分。
(方法一) 由于f (x)是R上的偶函数,所以f (x) f (x),
(其中 0) 6
6
2
(1)求函数 f (x) 的值域;
(2)若函数 y f (x)的图象与直线 y 1
的两个相邻交点间的距离为 ,求函数
y f (x)的单调增区间.
2
第十一页,编辑于星期日:二十二点 四十八分。
点评 研究三角函数 y Asin(x )( A 0, 0)
的单调性,基本思想是把 x 看作
f
6
1.
(1)求实数a的值;
(2)求f (x)的单调区间、周期和最值.
第十三页,编辑于星期日:二十二点 四十八分。
练习2.已知函数
f (x) cos(2x ) 2sin(x ) sin(x ).
3
4
4
(1)求函数f (x)的最小正周期和图象的对称轴方程;
(2)求函数f (x)在区间[ , ]上的值域.
的1 图象,
2
第八页,编辑于星期日:二十二点 四十八分。
第九页,编辑于星期日:二十二点 四十八分。
类型二 三角函数的图象与性质
定义域 周期性 奇偶性
值域、最值 单调性
对称性
第十页,编辑于星期日:二十二点 四十八分。
例1
设函数 f (x) sin(x ) sin(x ) 2 cos2 x,
三角函数的图像与性质
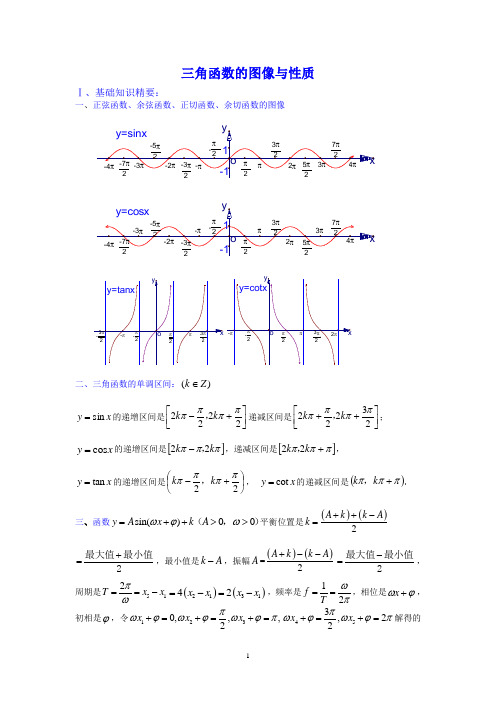
三角函数的图像与性质Ⅰ、基础知识精要:一、正弦函数、余弦函数、正切函数、余切函数的图像二、三角函数的单调区间:)(Z k ∈x y sin =的递增区间是⎥⎦⎤⎢⎣⎡+-2222ππππk k ,递减区间是⎥⎦⎤⎢⎣⎡++23222ππππk k ,;x y cos =的递增区间是[]πππk k 22,-,递减区间是[]πππ+k k 22,,tan y x =的递增区间是⎪⎭⎫ ⎝⎛+-22ππππk k ,, cot y x =的递减区间是()πππ+k k ,三、函数sin()y A x k ωϕ=++00A ω>>(,)平衡位置是()()2A k k A k ++-=+=最大值最小值2,最小值是k A -,振幅A =()()2A k k A +---=最大值最小值2,周期是512T x x πω==-()()213142x x x x =-=-,频率是12f T ωπ==,相位是ϕω+x ,初相是ϕ,令1230,,,2x x x πωϕωϕωϕπ+=+=+=453,22x x πωϕωϕπ+=+=解得的ϕ即为所求,关键是从“五点法”中的第一个零点(平衡点),0ϕω⎛⎫- ⎪⎝⎭作为突破口,从图象的升降情况找准该点的位置;其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω,凡是该图象与直线y k =的交点都是该图象的对称中心四、由y =sin x 的图象变换出y =sin(ωx +ϕ)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换移也常出现无论哪种变形,切记每一个变换总是对x 而言,即图象变换要看“变量”起多大变化而不是“角变化”多少.途径一:先平移变换再周期变换(伸缩变换)先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0)平移|ϕ|个单位,再将图象上各点的横坐标变为原来的ω1倍(ω>0),便得y =sin(ωx +ϕ)的图象途径二:先周期变换(伸缩变换)再平移变换先将y =sin x 的图象上各点的横坐标变为原来的ω1倍(ω>0),再沿x 轴向左(ϕ>0)或向右(ϕ<0=平移ωϕ||个单位,便得y =sin(ωx +ϕ)的图象五、由y =A sin(ωx +ϕ)的图象求其函数式:给出图象确定解析式y =A sin (ωx +ϕ)的题型,有时从寻找“五点”中的第一零点(-ωϕ,0)作为突破口,要从图象的升降情况找准..第一个零点的位置 六、对称轴与对称中心:sin y x =的对称轴为2x k ππ=+,对称中心为(,0) k k Z π∈; cos y x =的对称轴为x k π=,对称中心为2(,0)k ππ+; 对于sin()y A x ωφ=+和cos()y A x ωφ=+来说,对称中心与零点相联系,对称轴与最值点联系 tan y x =的对称中心为2(,0)k π.七、求三角函数的单调区间:一般先将函数式化为基本三角函数的标准式,要特别注意A 、ω的正负利用单调性三角函数大小一般要化为同名函数,并且在同一单调区间. 八、求三角函数的周期的常用方法:经过变形化成“sin()y A x k ωφ=++、cos()y A x k ωφ=++,tan()y A x k ωφ=++”的形式,再利用周期公式,另外还有图像法和定义法 九、判断三角函数的奇偶性()Z ∈k①y = sin (x +φ)是奇函数πϕk =⇔.②y = sin (x +φ)是偶函数2k πϕπ⇔=+.③y =cos (x +φ)是奇函数2k πϕπ⇔=+.④y = cos (x +φ)是偶函数k ϕπ⇔=.十、五点法作y =A sin (ωx +ϕ)的简图:五点取法是由ωx +ϕ取0、2π、π、2π3、2π来求. Ⅱ、典型例题精讲1. (2011课标5)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x=上,则cos 2θ= A .45-B .35-C .35D .45解析:本题考查三角公式和直线斜率定义,属于容易题.易知tan θ=2,cos θ=51±.由cos2θ=22cos 1θ-=35-.解法2:tan θ=2,cos2θ=cos 2θ-sin 2θcos 2θ+sin 2θ=1-tan 2θ1+tan 2θ=-35.选A . 2.(08全国Ⅰ 8)为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图象,只需将函数sin 2y x =的图象 A .向左平移5π12个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位 D .向右平移5π6个长度单位解:55cos 2sin 2sin 2,3612y x x x πππ⎛⎫⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭只需将函数sin 2y x =的图像向左平移5π12个单位得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像.选A .3.(01新课程)若b a =+=+<<<ββααπβαcos sin ,cos sin ,40,则A .a <bB .a >bC .ab <1D .ab >2解法1:利用sin cos ),m θθθϕ++其中tan nmϕ=,得),),0,,444444a b πππππππαβαβαβ=+=+∴+ <<<<<+<2sin()sin(),1))24444ππππαβαβ∴++∴++<<<1<<<1<<<a b ∴选A .解法2:0<<<sin >0,cos >0,sin >0,cos >0,>0,>04a b παβααββ∴∴ ,221sin 2>0,1sin 2000sin 2sin 22a b ><<<<<<παβαβαβ∴=+=+∴,22,1,21<2<a <b ∴,2 1<<<a b ∴选A .解法3:利用导数研究函数()sin cos f x x x =+在04π⎛⎫⎪⎝⎭,上的单调性.()cos sin f x x x '=- 在04π⎛⎫ ⎪⎝⎭,上恒大于0,故()f x 在04π⎛⎫⎪⎝⎭,上是增函数,所以()()()04f ff f παβ⎛⎫<<⎪⎝⎭,1<<<a b ∴选A .解法4:令0,30,αβ=0=15则0001sin cos15sin 30cos30,22a b =+==+=0151<<<a b ∴(特殊值估算法)选A .解法5:取04παβ→→,,则1,a b →,排除B 、C 、D (极限排除法)选A .4.(07全国Ⅰ12)函数22()cos 2cos2xf x x =-的一个单调增区间是 A .233ππ⎛⎫ ⎪⎝⎭,B .62ππ⎛⎫ ⎪⎝⎭,C .03π⎛⎫ ⎪⎝⎭,D .66ππ⎛⎫- ⎪⎝⎭,解:函数22()cos 2cos2x f x x =-=2cos cos 1x x --,从复合函数的角度看,原函数看作2()1g t t t =--,cos t x =,对于2()1g t t t =--,当1[1,]2t ∈-时,()g t 为减函数,当1[,1]2t ∈时,()g t 为增函数,当2(,)33x ππ∈时,cos t x =减函数,且11(,)22t ∈-, ∴ 原函数此时是单调增函数,选A .或者用排除法.求三角函数的单调区间:一般先将函数式化为基本三角函数的标准式,要特别注意A 、ω的正负.利用单调性比较函数大小一般要化为同名函数,并且在同一单调区间. 5.(08天津)已知函数()x f 是R 上的偶函数,且在区间[)+∞,0上是增函数. 令⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=75tan ,75cos ,72sinπππf c f b f a ,则 A . c a b << B . a b c << C .a c b << D . c b a <<解析:5(cos)(c 2os )77b f f ππ=-=,5(tan )(t 2an )77c f f ππ=-=. 因为2472πππ<<,所以220cos sin 1tan 7772πππ<<<<,所以b a c <<,选A .6.(2012新课标理9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
三角函数的图象、性质及应用(高中数学知识点讲解)

(5)不能认为y=tan
x在定义域上为增函数,应在区间
kπ-
π 2
,kπ
+
π 2
(k∈Z)内
为增函数.
知能拓展
考法一 关于三角函数图象的问题
例1 (1)(2018广东茂名化州二模,9)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<
φ<π)的部分图象如图所示,且f(α)=1,α∈
求φ及ω,从而
得到f(x)的解析式,由f(α)=1求α,进而得cos
2α
+
5π 6
.
A = 5,
(2)①根据已知表格中的数据可得方程组
π 3
ω
+
φ
=
π 2
,
解之可得函数f(x)的
5π 6
ω
+
φ
=
3π 2
,
解析式,进而可补全表格.
②由①并结合函数图象平移可得,g(x)=5sin
2
x
+
2θ -
π 3
-2x
实质上是y=tan
x与y=
π 3
-2x的复合,应
按复合函数单调性求解.
方法总结 三角函数的单调性问题的常见类型及解题策略
1.已知三角函数解析式求单调区间
(1)求函数的单调区间应遵循简单化原则,将解析式进行化简,并注意复合
函数单调性规律“同增异减”.
(2)求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)(其中ω>0)的单调区间时,要视“ωx
2π ω
=4×
7π 12
-
π 3
=π,得ω=2,故f(x)=3sin(2x+φ),将
三角函数的图像及性质
正弦函数的图象和性质正弦函数的图象和性质要点一:正弦函数性质类型一:正弦函数定义域与值域 例1.求函数lg(2sin 1)y x =-的定义域 【解析】依题意得2sin x -1>0,即1sin 2x >,∴52266k x k ππππ+<<+(k ∈Z ),∴函数的定义域为522,66x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭.例2.求下列函数的值域: (1)y=3―2sin x(2)2sin 23y x π⎛⎫=+ ⎪⎝⎭,,66x ππ⎡⎤∈-⎢⎥⎣⎦;【解析】 (1)∵-1≤sin x ≤1,∴-2≤2sin x ≤2,∴-2≤-2sin x ≤2,∴1≤3-2sin x ≤5,∴函数的值域为[1,5].(2)∵66x ππ-≤≤,∴20233x ππ≤+≤. ∴0sin 213x π⎛⎫≤+≤ ⎪⎝⎭.∴02sin 223x π⎛⎫≤+≤ ⎪⎝⎭,∴0≤y ≤2.∴函数的值域为[0,2]. 举一反三:【变式】 求y=cos 2x+4sin x ―2的值域. 【解析】y=cos 2x+4sin x ―2=―sin 2x+4sin x ―1 =―(sin x ―2)2+3. ∵-1≤sin x ≤1,∴当sin x=―1时,y min =―6;当sin x=1时,y max =2. ∴函数的值域为[-6,2]. 类型二:正弦函数单调性例3.求2sin 4y x π⎛⎫=- ⎪⎝⎭的单调区间.【解析】∵2sin 2sin 44y x x ππ⎛⎫⎛⎫=-=-- ⎪ ⎪⎝⎭⎝⎭,∴函数2sin 4y x π⎛⎫=- ⎪⎝⎭的递增区间就是函数2sin 4y x π⎛⎫=- ⎪⎝⎭的递减区间.∴322242k x k πππππ+≤-≤+(k ∈Z ),得372244k x k ππππ+≤≤+(k ∈Z ).∴函数2sin 4y x π⎛⎫=- ⎪⎝⎭的递增区间为372,244k k ππππ⎡⎤++⎢⎥⎣⎦(k ∈Z ).举一反三:【变式】求函数sin 23y x π⎛⎫=- ⎪⎝⎭的递减区间.【解析】已知函数sin 2sin 233y x x ππ⎛⎫⎛⎫=-=-- ⎪ ⎪⎝⎭⎝⎭.欲求该函数的单调递减区间,只需求sin 23y x π⎛⎫=- ⎪⎝⎭的单调递增区间.由222232k x k πππππ-≤-≤+(k ∈Z ),解得51212k x k ππππ-≤≤+(k ∈Z ). 所以原函数的单调递减区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z ).类型三:正弦函数的奇偶性 例4.判断下列函数的奇偶性:5())2f x x π=+;【解析】函数定义域为R ,且5()2s i n 2c o s 222f x x x x ππ⎛⎫⎛⎫=+=+=⎪⎪⎝⎭⎝⎭,显然有()()f x f x -=恒成立.∴函数5()22f x x π⎛⎫=+ ⎪⎝⎭为偶函数.举一反三:【变式1】()f x =; 【解析】由2sin x -1>0,即1s i n 2x >,得函数定义域为52,266k k ππππ⎛⎫++ ⎪⎝⎭(k ∈Z ),此定义域在x 轴上表示的区间不关于原点对称.∴该函数不具有奇偶性,为非奇非偶函数. 类型四:三角函数图象的综合应用例5.(1)方程lg sin x x =的解的个数为( ) A .0 B .1 C .2 D .3 (2)若02x π<<,则2x 与3sin x 的大小关系为( )A .23sin x x >B .23sin x x <C .23sin x x =D .与x 的取值有关【解析】(1) 作出lg y x =与sin y x =的图象,当52x π=时,5lg 12y π=<,5sin 12y π==,当92x π=时,9lg 12y π=>,lg y x =与sin y x =再无交点。
三角函数的图像与性质
1-
6
-
4
-
2
-
o
-1 -
-
2
4
6
因为终边相同的角的三角函数值相同,所以y=sinx的图象在……, 4 ,2 , 2 ,0, 0,2 , 2 ,4 ,……与y=sinx,x∈[0,2π ]的图象相同
y
-
-
-
x
1-
6
4
-
2
x
x 2
x sin 2
0 0 0
2
1
2
3
3 2
4
2
0
-1
0
y
x y= sin ,xR 2
1
-3 -2 - o
-1
2 3
4
y=sinx,xR
x
反思总结:五点法作图的基本步骤是什么?
五点法作图的基本步骤是:列表、描点、连线
反馈训练 : 画出下列函数的简图:
(1)y=1+sinx,x R
y 1
2
o -1
2
3 2
2
x
y=sinx,x[0, 2]
y
1
正弦曲 线
2
-4
-3
-2
-
o
-1
3
4
5
6
x
问题3: 如何作出余弦函数的图像?
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
正弦函数的图象 y=cosx=sin(x+ ), xR
(2)y=cos2x, x R
(3) y=cos(x+ ), xR
三角函数图像与性质
图3-4-2 A.2,- B.2,- C.4,- D.4,
自测后你觉得哪类题做起来困难呢?那我们一起来解决吧!
典例:
题型一三角函数的定义域和值域
(1)函数y= 的定义域为________.
A.向右平移 个单位B.向右平移 个单位C.向左平移 个单位D.向左平移 个单位
3.[2014·福建卷]将函数y=sinx的图像向左平移 个单位,得到函数y=f(x)的图像,则下列说法正确的是()
A.y=f(x)是奇函数B.y=f(x)的周期为π
C.y=f(x)的图像关于直线x= 对称D.y=f(x)的图像关于点 对称
导疑:由解析式求函数定义域应考虑________.
导学:由tanx-1 0得tanx 1所以x ________.
所以所求定义域为________.
(2)求下列函数的值域①y=2cos2x+2cosx②y=3cosx- sinx,x∈[0,π];
导疑:二次函数给定区间如何求值域?形如y=Asin(ωx+φ)函数的值域?
A. B.
C. D.
2.函数f(x)=2cos 是()
A.最小正周期为2π的奇函数B.最小正周期为2π的偶函数
C.最小正周期为2π的非奇非偶函数D.最小正周期为π的偶函数
3.函数f(x)=sin 的图象的一条对称轴是()
A.x= B.x= C.x=- D.x=-
4.比较大小:sin ________sin .
A.A=3,T= ,φ=- B.A=1,T= ,φ=
C.A=1,T= ,φ=- D.A=1,T= ,φ=-
图3-4-3图3-4-4
三角函数的图像和性质
一、复习引入:正弦线、余弦线:设任意角α的终边与单位圆相交于点P(x ,y),过P 作x 轴的垂线,垂足为M ,则有MP r y ==αsin ,OM r x==αcos向线段MP 叫做角α的正弦线,有向线段OM 叫做角α的余弦线.二、讲授新课:1、五点法作图描点法在要求不太高的情况下,可用五点法作出,y sin x,x [0,2]=∈π的图象上有五 点起决定作用,它们是 描出这五点后,其图象的形状基本上就确定了。
因此,在精确度要求不太高时,我们常常先描出这五个点,然后用平滑的曲线将它们连接起来,就得到在相应区间内正弦函数的简图,这种方法叫做五点法。
注意:(1)描点法所取的各点的纵坐标都是查三角函数表得到的数值,不易描出对应点的精确位置,因此作出的图象不够精确。
(2)几何法作图较为精确,但画图时较繁。
(3)五点法是我们画三角函数图象的基本方法,要切实掌握好。
(4)作图象时,函数自变量要用弧度制,这样自变量与函数值均为实数,因此在 x 轴、 y 轴上可以统一单位,作出的图象正规,便于应用。
2、正弦曲线下面是正弦函数y sin x,x R =∈的图象的一部分:-11y x-6π-5π6π5π-4π-3π-2π-π4π3π2ππf x () = sin x ()3、余弦曲线利用正弦曲线和诱导公式画出余弦曲线,3(0,0),(,1),(,0),(,1),(2,0)22πππ-π-11y x-6π-5π6π5π-4π-3π-2π-π4π3π2ππf x () = cos x ()4、正切曲线y=tanx3π2ππ2-3π2-π-π2oyx三、正弦余弦函数性质1奇偶性(1)余弦函数的图形当自变量取一对相反数时,函数y 取同一值。
由于cos(-x)=cosx ∴f(-x)= f(x).以上情况反映在图象上就是:如果点(x,y )是函数y=cosx 的图象上的任一点,那么,与它关于y 轴的对称点(-x,y)也在函数y=cosx 的图象上,这时,我们说函数y=cosx 是偶函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八讲 三角函数的图象与性质 真题试做►——————————————————— 1.(2013·高考天津卷)函数f(x)=sin2x-π4在区间0,π2上的最小值为( ) A.-1 B.-22 C.22 D.0 2.(2013·高考大纲全国卷)
若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=( ) A.5 B.4 C.3 D.2
3.(2013·高考安徽卷)已知函数f(x)=4cos ωx·sin(ωx+π4)(ω>0)的最小正周期为π. (1)求ω的值;
(2)讨论f(x)在区间[0,π2]上的单调性.
考情分析►——————————————————— 三角共有三部分内容,三角函数的图象及性质是其中的一个内容.对这个内容的考查,以图象的变换、函数的单调性、奇偶性、周期性、最值等作为热点内容.预计在2014年高考中,仍然会把三角函数的概念、周期性、单调性、有界性及图象的伸缩和平移等作为重点,并且往往与三角变换公式相互联系,有时也与平面向量,解三角形或不等式内容相互交汇,题型多以小而活的选择题、填空题来呈现,如果设置解答题一般与三角变换、解三角形、平面向量等知识进行综合考查,题目难度为中、低档.
考点一 三角函数的性质 三角函数的周期性、单调性、对称性、最值等是高考的热点,常与三角恒等变换交汇命题,在考查三角恒等变换的方法与技巧的同时,又考查了三角函数的性质,难度为中、低档.
(2013·高考湖南卷)已知函数f(x)=cos x·cos(x-π3).
(1)求f(2π3)的值; (2)求使f(x)<14成立的x的取值集合. 【思路点拨】 (1)利用三角恒等变形公式将f(x)变形为只含一个角的一种三角函数形式后求解.(2)根据余弦函数的性质变形为关于自变量x的不等式求解.
(1)求三角函数的周期、单调区间、最值及判断三角函数的奇偶性,往往是在定义域内,将三角函数式化为y=Asin(ωx+φ)+B的形式,然后再求解. (2)求函数f(x)=Asin(ωx+φ)(ω>0)的单调区间常用换元法:将ωx+φ作为一个整体,若
求单调增区间,令ωx+φ∈2kπ-π2,2kπ+π2(k∈Z);若求单调减区间,则令ωx+
φ∈
2kπ+π2,2kπ+
3π
2(k∈Z).值得注意的是,若ω<0,则需要利用诱导公式将其转换
为f(x)=Asin(ωx+φ)(ω>0)的形式,再用换元法求单调区间. 强化训练1 已知函数f(x)=3sin xcos x+cos2x+a. (1)求f(x)的最小正周期及单调递减区间;
(2)若f(x)在区间[-π6,π3]上的最大值与最小值的和为32,求a的值.
考点二 函数y=Asin(ωx+φ)的图象 关于函数y=Asin(ωx+φ)的图象,高考考查的内容不外乎以下三类: (1)由函数解析式作函数的图象; (2)利用已给三角函数的图象特点,求三角函数解析式; (3)函数y=Asin(ωx+φ)的图象变换. (1)(2013·高考四川卷) 函数f(x)=2sin(ωx+φ)ω>0,-π2( ) A.2,-π3 B.2,-π6
C.4,-π6 D.4,π3 (2)(2013·高考山东卷)将函数y=sin(2x +φ)的图象沿x轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( ) A.3π4 B.π4
C.0 D.-π4 【思路点拨】 (1)由图象确定周期,利用T=2πω求ω,再把(5π12,2)代入求φ;(2)利用平移规律求得解析式,再由偶函数求φ.
(1)已知函数y=Asin(ωx+φ)(A>0,ω>0)的图象求解析式时,常采用待定系数法,由图中的最高点、最低点或特殊点求A;由函数的周期确定ω;由图象上的关键点确定φ. (2)求函数的周期时,注意以下规律:相邻的最高点与最低点的横坐标之差的绝对值为
半个周期,最高点(或最低点)的横坐标与相邻零点差的绝对值为14个周期. (3)在用图象变换解题时,提倡先平移后伸缩,但先伸缩后平移也经常出现在题目中,所以必须熟练掌握,无论是哪种变换,切记每一个变换总是对字母x而言,即图象变换要看“变量”变化多少,而不是“角”变化多少. 强化训练2
(2013·济南市高三模拟考试)如图是函数y=Asin(ωx+φ)(x∈R,A>0,ω>0,0区间[-π6,5π6]上的图象,为了得到这个函数的图象,只需将y=sin x(x∈R)的图象上所有的点( ) A.向左平移π3个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变
B.向左平移π3个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 C.向左平移π6个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变 D.向左平移π6个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 考点三 三角函数图象与性质的综合应用 近几年关于三角函数综合应用的高考题不断求新求异,但考查的知识方法不变,首先是化简所给式子,然后结合三角函数的性质求解相关问题. 已知函数f(x)=sin2x+3sin xcos x+2cos2x(x∈R) (1)求函数f(x)的最小正周期和单调增区间; (2)函数f(x)的图象可以由函数y=sin 2x(x∈R)的图象经过怎样的变换得到?
【思路点拨】 (1)利用恒等变换把f(x)化为Asin(ωx+φ)+h的形式,然后再求周期与单调区间.(2)进行平移变换时,要注意x前的系数.
本题三处较为关键:(1)三角函数式的化简;(2)单调区间的求解;(3)图象变换;这三点正好也是三角中的重要的基础内容,在这里都得到了重点考查. 提醒:在求y=Asin(ωx+φ)的单调区间时,要特别注意A和ω的符号,必要时通过诱导公式先将ω的符号化为正的.
三角函数与三类知识的交汇 三角函数的图象与性质是高考考查的重点,近年来,三角函数与其他知识交汇命题成为高考的热点,由原来三角函数与平面向量的交汇渗透到三角函数与数列、圆、线性规划、复数、方程等知识的交汇. 一、三角函数与圆的交汇 (2013·高考江西卷)
如图,已知l1⊥l2,圆心在l1上、半径为1 m的圆O在t=0时与l2相切于点A,圆O沿l1以1 m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cos x,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( ) 【解析】 圆半径为1,设弧长x所对的圆心角为α,则α=x,如图所示,cos α2=1-t,即cos x2=1-t,则y=cos x=2cos2x2-1=2(1-t)2-1=2(t-1)2-1(0≤t≤1).其图象为开口向上,在[0,1]上的一段抛物线. 【答案】 B
本题巧妙地把三角函数与圆的知识相结合,弧长x因圆动而变,变中关系式不变(α=x,cosα2=1-t),见证了数学中的“以静制动”,求解此类问题的关键是,充分利用图形的几何性质,建立三角函数关系式,熟练运用二次函数关系式判断其图象,求解时应注意t的范围. 二、三角函数与数列的交汇
(2012·高考上海卷)设an=1nsin nπ25,Sn=a1+a2+„+an,在S1,S2,„,S100中,正数的个数是( ) A.25 B.50 C.75 D.100 【解析】 当1≤n≤24时,an>0,当26≤n≤49时,an<0,但其绝对值要小于1≤n≤24时相应的值;当51≤n≤74时,an>0;当76≤n≤99时,an<0,但其绝对值要小于51≤n≤74时相应的值,∴当1≤n≤100时,均有Sn>0,应选D. 【答案】 D
解决此类问题的关键:①能发现sin nπ25具有周期性;②结合1n,发现在一个“周期”内,正项的和大于其负项之和. 三、三角函数与线性规划的交汇 设函数f(θ)=3sin θ+cos θ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为12,32,求f(θ)的值;
(2)若点P(x,y)为平面区域Ω:x+y≥1,x≤1,y≤1,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值. 【解】 (1)由点P的坐标为12,32和三角函数定义得,sin θ=32,cos θ=12,
故f(θ)=3sin θ+cos θ=3×32+12=2.
(2)作出平面区域Ω(即三角形区域ABC),如图所示,其中A(1,0),B(1,1),C(0,1),于是0≤θ≤π2,又f(θ)=3sin θ+cos θ=2sinθ+π6,且π6≤θ+π6≤ 2π3,故当θ+π6=π2,即θ=π3时,f(θ)取到最大值2;当θ+π6=π6,即θ=0时,f(θ)
取到最小值1. 本题的亮点是借助线性规划包装三角命题,平淡中见新奇,通过线性规划应用引来“活水”,注入活力,全题皆活,符合新课程改革要求的命题趋势.求解此类问题的关键:熟练运用二元一次不等式组表示平面区域的方法——“选点法”,直线定边界,分清虚实;选点定区域,常选原点.准确作出可行域后,就可以借助图形直观地得出答案.
