九宫格详细解法
数独六宫格九宫格
6
42
73
6
2478
1
4
78
52
6
5
2136
7
94
13
2
721
95
6
5271
21
8
29
3
93
71
57
6
2
9
3
6
21
42
38
最多旳行、列或者宫格入手,用唯一解法和唯 余解法来解题。
2.不能猜测,填任何一种数之前必须要有充分旳根据才干填。
10/10/2024
2 1 3 54 6 9 7 8 8 7 5 12 9 4 63 6 4 9 3 87 1 2 5 1 5 7 4 3 26 89 42 8 6 9 1 5 3 7 39 6 7 5 8 2 1 4 564273891 9 32 8 1 4 7 5 6 7 8 1 9 65 3 4 2
第6行 6
2
5
第5行 2
45
6
第4行 1
3 65
第3行
第2行
5
第1行
6
2 1
45
第1列 第2列
第6行 2
3
六宫格
第3列 第4列
56
第5列 第6列
41
第5行 1
3
第4行
1632
第3行
4251
第2行 6
2
第1行 4
23
1
65
总结:1.从出现数字最多旳行、列或者宫格入手,用唯一解法和唯 余解法来解题。
2.不能猜测,填任何一种数之前必须要有充分旳根据才干填。
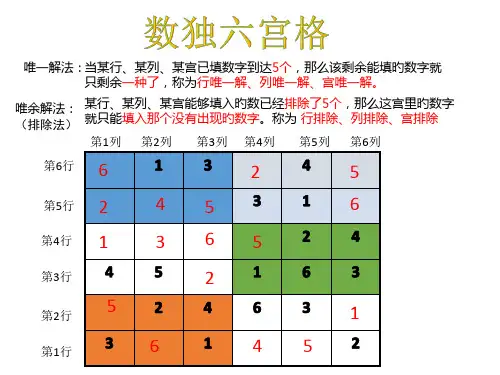
唯一解法:当某行、某列、某宫已填数字到达5个,那么该剩余能填旳数字就 只剩余一种了,称为行唯一解、列唯一解、宫唯一解。
九宫格难题解法

九宫格难题解法九宫格,也称数独,是一种独立于语言和文化的数学游戏。
它的规则很简单:在一个9×9的方格中填入数字1-9,使得每行、每列和每个3×3的小方格内都恰好包含1-9的数字,且不能重复。
虽然规则简单,但是九宫格的难度却是不小的,很多人在面对九宫格时都感到头疼。
本文将介绍一些九宫格难题的解法,希望能帮助读者提高九宫格的解题能力。
一、基本技巧首先,我们要讲一些基本的九宫格解题技巧。
这些技巧是解决九宫格问题的基础,掌握了这些技巧,对于初级和中级的九宫格难题都能迎刃而解。
1. 唯一候选数法唯一候选数法是指,在某个格子中只有一个数字是符合规则的,这个数字就是该格子的数字。
例如,在某个格子中只能填入数字6,那么这个格子的数字就是6。
这种方法在解决初级和中级的九宫格难题时非常有效。
2. 剪枝法剪枝法是指,在某个格子中填入一个数字后,根据规则来排除其他格子中的数字,从而减少待填数字的数量。
例如,在某个格子中填入数字6后,就可以排除该行、该列和该3×3小方格中所有的数字6,从而缩小了待填数字的范围。
3. 消除法消除法是指,在某行、某列或某个3×3小方格中,已经填入了8个数字,那么这一行、列或小方格中剩下的数字就只有一个,可以直接填入。
例如,在某行中已经填入了1、2、3、4、5、6、7和8,那么这一行中剩下的数字就只有9,可以直接填入。
二、高级技巧除了基本技巧之外,还有一些高级的九宫格解题技巧,这些技巧可以帮助我们解决那些难度较高的九宫格难题。
1. X-Wing法X-Wing法是指,在九宫格中,某两行或两列中只有两个格子可以填入某个数字,那么这两个格子就是该数字的唯一位置。
例如,在九宫格中,某两列中只有2个格子可以填入数字2,那么这两个格子就是数字2的唯一位置。
通过这种方法,我们可以排除其他行或列中的数字2,从而缩小待填数字的范围。
2. Swordfish法Swordfish法是指,在九宫格中,某三行或三列中只有三个格子可以填入某个数字,那么这三个格子就是该数字的唯一位置。
九宫格数独的技巧

九宫格数独的技巧数独是一种由九宫格组成的逻辑游戏,目标是在每个九宫格中填入数字1到9,使得每行、每列和每个九宫格内的数字都不重复。
虽然数独看似简单,但要解开一个完整的数独谜题可能需要一些技巧和策略。
下面是一些常用的九宫格数独解谜技巧:1.找出唯一解:用过的数字不能重复出现,所以可以通过排除法找出每个单元格的唯一可能解。
找到只有一个可能解的单元格,然后填入数字并继续解谜。
2.唯余法:在每个九宫格、每一行和每一列中,寻找缺失的数字。
如果一个数字在行、列或一些九宫格中只有一个空缺位置,那么该位置就是该数字的位置。
3.划定候选数:对于每个空白的单元格,可以列出其可能的数字。
这样一来,可以带入数字并查看是否会产生冲突。
如果格子只有一个可能的数字,那就填入该数字并继续解谜。
4.寻找唯一的区块:在一个九宫格中,对于每个数字,找到它们在该九宫格中唯一的可能位置。
填写这些数字,并以此继续解谜。
5. X-Wing法:如果一个数字在两行中的两个九宫格的同一列中只能出现在四个位置上,并且这四个位置形成一个矩形,那么可以断定该数字不能出现在任何其他相同列的位置上。
6. Swordfish法:如果一个数字在三行或三列的三个九宫格中只能出现在九个位置上,并且这九个位置形成一个鱼骨图,那么可以断定该数字不能出现在其他相同行或相同列的位置上。
7. XY-Wing法:如果三个候选数存在于三个单元格中,形成了一种特殊的关系,那么可以排除其中两个数字的所有可能。
这种关系通常形成一个三角形。
8. Chains法:通过连接候选数的链条,可以排除一些候选数。
其中,强链和弱链是最常见的链条。
强链包含两个候选数,通过连接同一数字的弱链,可以得出该数字不可能出现在一些单元格中。
这些技巧只是解九宫格数独的一些常用方法,数独的解法可以相当复杂,特定的解题技巧可能需要多次尝试才能掌握。
最重要的是,不要放弃,尝试不同的解题方法,并试图发现规律和数字之间的关系。
九宫格的解题过程

九宫格的解题过程第1步首先计算每行数字之和。
1-9九个数字之和:1+2+3+4+5+6+7+8+9=45九宫格共有三行,并且每行的数字之和相等,因此45/3=15,即每行数字之和为15。
第2步计算中间格的数字。
考虑第2行,第2列,和2条对角线的数字之和。
它们的总和为 15/4 = 60。
在它们的总和中,中间格子的数字出现了4次,其它位置格子的数字都出现了而且仅出现了1次。
所以,它们的总和=(4×中间格子的数字)+(其它8个数字)=(3×中间格子的数字)+(1-9九个数字之和)因此, 60=3×中间格子的数字+45,中间格子的数字等于5第3步,奇数不能出现在4个角上的格子里。
比如,如果数字9出现在角上的格子里,那么为了保证9所在行或所在列的数字和为15,必须需要4个数字,两两之和必须为6。
1,2,3,4,6,7,8中,只有2和4组成和为6的数字对,找到第2个和为6的数字对是不可能的。
因此,数字9不能出现在4个角上的格子里。
同样道理,1,3,7也不能出现在4个角上的格子里。
第4步,2,4,6,8必须填在4个角上的格子里,并且保证对角线数字和为15。
第5步,将1,3,7,9填入相应的格子里就完成了九宫格填数字任务,注意和为15的条件。
完成了填九宫格的任务后,我们进一步考虑,如果上面九宫格内所有数字都加数字1会发生什么呢即可不可以用数字2,3,4,5,6,7,8,9,10填九宫格,得到每一行,每一列,每一对角线的三个数字之和都相等的新九宫格呢。
显而易见,上面九宫格每行每列每对角线数字之和为18,奇数3,5,7,9处在4个角上的格子里,中间数6处在中间的格子里。
从1-9和2-10各九个数字所填充的九宫格可以得出下列规律:1)九个数字是由9个相连的整数构成的。
2)九个数字中正中间的数字填在九宫格的中间格子里。
1-9中的5,2-10中的6等。
3)每行每列的数字和等于中间数字的三倍。
九宫格的解题过程讲解

九宫格的解题过程第1步首先计算每行数字之和。
1-9九个数字之和:1+2+3+4+5+6+7+8+9=45九宫格共有三行,并且每行的数字之和相等,因此45/3=15,即每行数字之和为15。
第2步计算中间格的数字。
考虑第2行,第2列,和2条对角线的数字之和。
它们的总和为 15/4 = 60。
在它们的总和中,中间格子的数字出现了4次,其它位置格子的数字都出现了而且仅出现了1次。
所以,它们的总和=(4×中间格子的数字)+(其它8个数字)=(3×中间格子的数字)+(1-9九个数字之和)因此, 60=3×中间格子的数字+45,中间格子的数字等于5第3步,奇数不能出现在4个角上的格子里。
比如,如果数字9出现在角上的格子里,那么为了保证9所在行或所在列的数字和为15,必须需要4个数字,两两之和必须为6。
1,2,3,4,6,7,8中,只有2和4组成和为6的数字对,找到第2个和为6的数字对是不可能的。
因此,数字9不能出现在4个角上的格子里。
同样道理,1,3,7也不能出现在4个角上的格子里。
第4步,2,4,6,8必须填在4个角上的格子里,并且保证对角线数字和为15。
第5步,将1,3,7,9填入相应的格子里就完成了九宫格填数字任务,注意和为15的条件。
完成了填九宫格的任务后,我们进一步考虑,如果上面九宫格内所有数字都加数字1会发生什么呢?即可不可以用数字2,3,4,5,6,7,8,9,10填九宫格,得到每一行,每一列,每一对角线的三个数字之和都相等的新九宫格呢。
显而易见,上面九宫格每行每列每对角线数字之和为18,奇数3,5,7,9处在4个角上的格子里,中间数6处在中间的格子里。
从1-9和2-10各九个数字所填充的九宫格可以得出下列规律:1)九个数字是由9个相连的整数构成的。
2)九个数字中正中间的数字填在九宫格的中间格子里。
1-9中的5,2-10中的6等。
3)每行每列的数字和等于中间数字的三倍。
九宫数独解题技巧口诀

九宫数独解题技巧口诀九宫格数独是一种基于逻辑和推理的数字填空游戏。
每行、每列和每个宫格中都包含1到9的数字,且每个数字在每行、每列和每个宫格中只能出现一次。
九宫格数独的解题目标是填充所有的空格,使得每行、每列和每个宫格中的数字都是1到9的完整排列。
下面是九宫数独解题技巧口诀:1.九宫格数独,每行每列各数独:在九宫格数独中,每行、每列和每个宫格都是一个独立的数独。
这意味着在解决整个九宫格数独的过程中,我们需要分别解决三个不同的数独问题:行数独、列数独和宫格数独。
因此,要掌握每个数独的解题技巧,并能够熟练地应用于整个九宫格数独中。
2.缺一不可有一空:在解决九宫格数独时,我们经常会遇到一行、一列或一个宫格中有两个或多个空格需要填充的情况。
这时,我们可以使用“缺一不可有一空”的口诀来推理填空。
具体来说,如果一行中有两个空格需要填充,那么这两个空格必然是不同的数字;同理,如果一列或一个宫格中有两个空格需要填充,也是如此。
利用这个口诀,我们可以快速确定空格中的数字,进而解决整个九宫格数独。
3.逐行逐列遍历法:在解决九宫格数独时,我们可以使用逐行逐列遍历法来寻找可能填入的数字。
具体来说,我们可以先从某一行或某一列开始,逐个检查每个空格可能填入的数字,然后根据其他行或列中已经出现的数字来判断该空格中不能填入的数字。
通过逐行逐列遍历整个九宫格数独,我们可以逐步缩小可能填入的数字范围,最终找到正确的答案。
4.九个数字不重复:在九宫格数独中,每行、每列和每个宫格中的数字都不能重复。
因此,在填入数字时,我们需要时刻注意已经填入的数字,避免重复。
同时,我们也可以利用这个规则来判断某个数字是否填入错误,如发现有数字重复出现则说明解题思路有误需要重新思考。
5.相邻数字不矛盾:在九宫格数独中,相邻的两个数字不能矛盾。
具体来说如果一个空格所在的行或列中已经有一个确定的数字那么这个空格就不能再填入这个数字否则就会产生矛盾。
利用这个规则我们可以在解题过程中快速判断某个填入是否正确从而缩小解题范围提高解题效率。
九宫格数独解法
九宫格数独解法数独是一种非常受欢迎的逻辑数字游戏,它以一个 9x9 的方格为基础,被分为九个 3x3 的小方格。
游戏的目标是通过将数字 1-9 填入每个空格中,使得每一行、每一列和每一个小方格内数字均不重复。
九宫格数独的解法并不困难,但需要一定的逻辑思维和方法。
有许多不同的解决数独的方法,本文将介绍一种简单而有效的解法方法,帮助您在数独游戏中迅速找到答案。
第一步:观察与分析解决数独问题的第一步是观察并分析已有的数字。
观察数独方格,找出已经填入的数字。
这些已经确定的数字会帮助您确定其他数字的位置。
在观察数字的同时,应该注意到每个数字的分布情况。
这意味着我们要注意每一行、每一列和每一个小方格内是否已经有相同的数字。
如果某个数字在某一行、某一列或某一个小方格内已经出现,那么您就可以排除在这些位置中再次填入相同数字的可能性。
第二步:选择合适的数字当分析了已有数字之后,接下来就是根据已有数字选择合适的数字进行填充。
这需要一定的逻辑推理。
首先,我们可以通过观察某一行、某一列或某一个小方格内的缺失数字来判断哪个数字最适合填入。
例如,当某一行有八个数字已经确定时,我们可以确定剩下的数字只能是1-9 中的某一个数字,否则将无法满足数独的规则。
同样的,当某一个小方格内有八个数字已经确定时,也可以通过排除法来确定缺失的数字。
选择合适的数字还需要考虑到其他行、列和小方格的情况。
每一个数字需要在数独的每一行、每一列和每一个小方格中只出现一次。
因此,在选择数字时,必须综合考虑每一行、每一列和每一个小方格已经填入的数字。
第三步:尝试与回溯在选择了合适的数字之后,我们需要将这些数字填入数独方格中。
填充数字时,应该从数独方格中的第一个空格开始,并尝试填入一个数字。
填入数字后,我们需要进行一些检验。
首先,我们要检查数独的每一行、每一列和每一个小方格中是否已经存在相同的数字。
如果存在相同的数字,那么我们需要进行回溯,即将尝试填入的数字改为其他的候选数字。
九宫格的通解
九宫格的通解组成九宫格的九个数,不一定非得是等差数列或等差的三组数。
通过方程和等价变换,找到了使九宫格成立的通解,一共有两种形式。
等 差数列和等差的三组数,都只是第一种形式的特例。
一、首先确定中心位置的数。
九个数的和为S,中心数为X.则 34SX X S =+-. 解得X=S/9 为研究方便,每个数都减少X,九宫格依然成立,中心数变为0. a,b,为任意实数,当a,b,0三个数填入后,九宫格即确定下来。
图图2一、 令a>0,来分情况讨论,因为假如a<0,则-a>0,这两种情况在对称下是一致的。
1. 若0<a<b只看5个非负数,就可分析9个数的大小情况。
把九个数从小到大排列,方格中的编号即代表第几个数。
0<a<b<a+b<2a+b 依次用大一个编号的数减去小一个编号的数, 差值,依次为: a,b-a,a,a 为得出普遍规律令 b-a ≠a ,则a,b 的关系为0<a<b, 图3特例 b=3,a=1时得图4图42. 若0<b<a差值依次为b,a-b,b,a 令b ≠a −b 得a,b 的关系为 0<b<a ,图5特例图63. 若0<a<-b,此时2a+b 的正负无法确定。
可分为2a+b>0和2a+b<0来分析。
当2a+b>0时,得如图7,此时无法判断2a+b 与-a-b 的大小。
进一步分情况,3a+2b>0和3a+2b<0.图7当0<a<-b,2a+b>0,3a+2b>0时,得图图8 Array设-a-b=m,2a+b=n得a=m+n,-b=2m+n , 0<m<n则图8可表示为图9,这和图3在旋转和对称下是等价的。
图9 Array当0<a<-b,2a+b>0,3a+2b<0时,得图设2a+b=n,-a-b=n|得 a=m+n,-b=m+2n,0<n<m所以,图10和图5是等价的。
九宫格数学题的解法
1、九宫格是一种数学游戏,通常用于锻炼逻辑思维和空间想象
能力。
2、九宫格的解法有很多种,其中一种常见的方法是通过数列的
关系来求解。
3、例如,假设九宫格中的第一个格子填入数字1,第二个格子
填入数字2,依次类推,那么整个九宫格就可以表示为一个等差数列。
4、根据等差数列的性质,可以得到数列的前n项和公式为
Sn=n×(a1+an)/2,其中Sn表示前n项和,a1表示首项,an表示末项。
5、通过这个公式,可以依次求出九宫格中每个格子的数字,具
体方法是:将第一个格子的数字代入公式,计算出前两项之和,再依
次向后推算,直到计算出所有格子的数字为止。
6、当然,除了这种方法之外,还有许多其他的解法,例如通过
代数方程、几何形状等方式来求解。
不同的解法可能会涉及到不同
的数学知识和技巧,需要根据具体情况进行选择。
数字九宫格的解法
博学笃行自强不息
数字九宫格的解法
引言:
数字九宫格是一种数学智力游戏,它由一个3x3的网格组成,每个格子填入一个数字,使得每行、每列和对角线上的数字之和都相等。
本文将探讨数字九宫格的解法方法,以帮助读者更好地解决这类问题。
一、初步认识数字九宫格
数字九宫格的问题是一种经典的组合数学问题,它的解法方法可以
通过观察和推理来完成。
首先,我们需要明确每个格子可以填入的
数字范围是1-9,并且每个数字只能使用一次。
其次,由于行、列
和对角线上的数字之和都相等,我们可以得出每一行、每一列和两
条对角线上的数字之和都是相同的。
这个和我们称之为\
1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
。
。
1
口诀:戴九履一,左三右七,二四有肩,六八为足,五居中
央。 其实,只要记住“二四有肩,六八为足”就可以了。 要
使纵横斜各条线上之和都等于15,即九宫格之一:
2 9 4
7 5 3
6 1 8
上图按顺时针转动一周,可得到以下三个变化图: 九宫格
之二:
6 7 2
1 5 9
8 3 4
九宫格之三:
8 1 6
3 5 7
4 9 2
九宫格之四:
4 3 8
9 5 1
2 7 6
但是“二四有肩,六八为足“只是提示答案的快捷方法,并不
是具体的解法。下面介绍具体的解析过程: 1 +14( 5/9 或
6/8) 有效组合:1/5/9 和1/6/8 2 +13 (6/7 或 5/8 或
。
。
2
4/9) 有效组合:2/6/7和2/5/8、2/4/9 3 +12 (或 5/7 或
4/8) 有效组合:3/5/7和3/4/8 4 +11 (3/8 或 2/9或5/6)
有效组合:4/5/6 (*4/3/8、*4/2/9已重复,故删除) 以下
类推所得到的组合均已重复。 故满足条件的有效组合为上述
8组。 以上8组排列中2,4,6,8各出现三次(满足纵横斜三
条线),因此必然居于九宫格的角部(即肩、足);5出现4次(满
足纵横双斜四条线),故处于中间位置。九宫格的问题也就迎刃而
解了。 九宫格快速解法 将数字1~9填入九宫格中,使
横、纵、对角线上的三个数字之和相等。 以下为快速解法:
1) 将数字1~9依次填入九宫格中, 2) 1、8、9、2逆时针旋
转一位, 3) 3、6、7、4顺时针旋转一位即可。
九宫格快速解法
。
。
3
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求
