北理工《信号与系统》习题答案第6章答案(纯手写)
信号与系统课后答案(全)
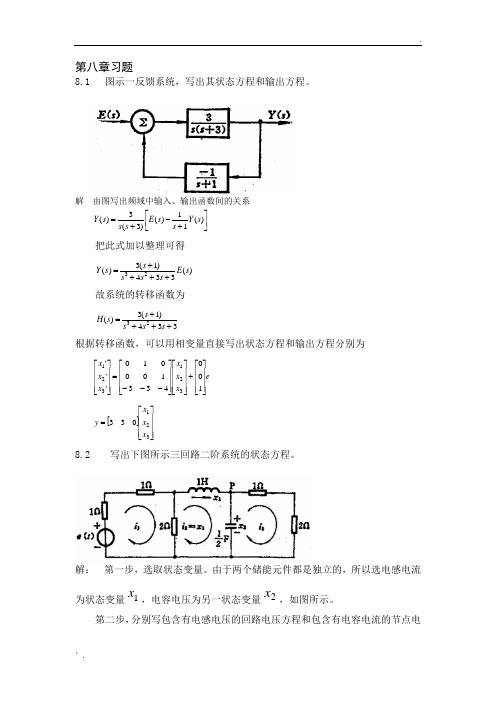
第八章习题8.1 图示一反馈系统,写出其状态方程和输出方程。
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数,可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。
解:第一步,选取状态变量。
由于两个储能元件都是独立的,所以选电感电流为状态变量1x,电容电压为另一状态变量2x,如图所示。
第二步,分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。
根据第二个回路的回路方程,并代入元件参数,则有112122'ixxx+--=312'21ixx-=第三步,上两式中1i和3i不是状态变量,要把它们表为状态变量。
由第一个回路有1124xie-=,即112141xei+=由第三个回路有323ix=,即2331xi=把1i和3i分别代入第二步中两式,并经整理,最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路,这里的激励函数)(t e是一压控电流源,输出电压)(t y由耦合电路的电阻L R上取得。
要求写出此电路的状态方程和输出方程。
解:第一步,选状态变量。
因为电感电流和电容电压等三个变量都是独立的,所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。
第二步,分别写回路方程或节点方程。
由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步,消去非状态变量。
信号与系统习题答案
解: (a )零输入响应
2 5 / 6 1 / 6 0, 1 1 / 3, 2 1 / 2
y0 [n] c1 (1 / 3) n c2 (1 / 2) n 由初始条件得 c1 13 / 3, c2 7 / 2 y0 [n] 13 / 3(1 / 3) n 7 / 2(1 / 2) n
第 10
(2-1b)P69
页
(b) (D2 3D 2) y(t ) 0; 2.1 求零输入响应
y(0) 1, y (0) 0
(1)
解:特征方程 2 3 2 0 1 1, 2 2
齐次解
yh (t ) c1e t c2e2t
( yh1) (t ) c1e t 2c2e2t
x1 ( t )
2 1 0 1 2 3 1
y2 (t ) y1 (t ) y1 (t 2)
y1 ( t )
t
t 1 2
0
Signals and Systems
机动 目录 上页 下页 返回 结束
第 7
(1-24)P37
页
练习: LTI系统输入输出如右图求输入为下图时的输出
并画出波形。
x(t )
(1-2)P35
第 1 页
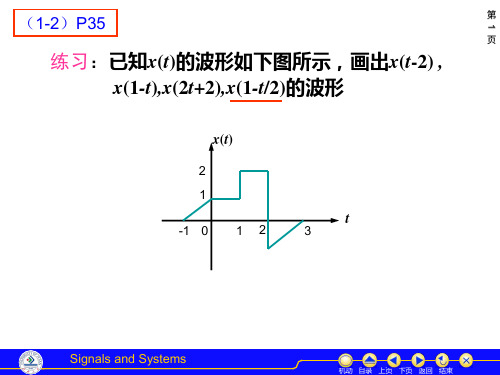
练习:已知x(t)的波形如下图所示,画出x(t-2) , x(1-t),x(2t+2),x(1-t/2)的波形
x(t)
2 1 -1 0 1 2
t
3
Signals and Systems
机动 目录 上页 下页 返回 结束
第
解:
-1
x(t)
2 1 0 1 2 3 t
2 页
信号与系统王明泉第六章习题解答

第6章线性时不变离散系统的时域分析6.1 学习要求(1)深刻理解离散时间信号的定义与时域特性;(2)会在时域中求解信号的各种变换和各种运算;(3)会建立简单离散系统的数学模型——差分方程;(4)会经典法和迭代法求解离散时间系统的响应和单位冲激响应,会画离散时间系统框图;(5)会计算卷积和,并用卷积法求解系统的零状态响应;(6)理解系统稳定和因果的充分必要性,会判断。
6.2 本章重点(1)基本的离散事件信号及其时域特性;(2)离散时间信号的时域变换和运算,特别是卷积和;(3)离散时间系统的数学模型——差分方程;(4)离散系统的输出响应、单位样值响应、零输入响应、零状态响应、6.3 本章的知识结构6.4 本章的内容摘要6.4.1 离散时间信号的定义离散时间信号是指仅在不连续的离散时刻有确定函数值,而在其它点上函数值未定义的信号,简称离散信号,也称序列,常用)(n x 表示。
6.4.2 常用的时间序列(1)单位冲激序列)(n δ⎩⎨⎧≠==0001)(n n n δ(2)单位阶跃序列)(n u⎩⎨⎧<≥=0001)(n n n u)(n u 可以看作是无数个单位采样序列信号之和:+-+-+-+=)3()2()1()()(n n n n n u δδδδ∑∞=-=0)(k k n δ)(n u 和)(n δ是差与和的关系,即)1()()(--=n u n u n δ(3)矩形序列)(n R N ⎩⎨⎧≥<-≤≤=)0(0)10(1)(N n n N n n R N 或矩形序列与阶跃序列、抽样序列的关系如下∑-=-=+-++-+-+=10)()1()2()1()()(N m N m n N n n n n n R δδδδδ)1()()(+--=N n u n u n R N(4)正弦序列)sin()(0φω+=n A n x式中,A 为幅度,φ为起始相位,0ω为正弦序列的数字域频率,Nπω20=。
信号与线性系统分析_(吴大正_第四版)习题答案第六章

. 学习参考. 第六章6.4 根据下列象函数及所标注的收敛域,求其所对应的原序列。
(1)1)(=z F ,全z 平面(2)∞<=z z z F ,)(3(3)0,)(1>=-z z z F(4)∞<<-+=-z z z z F 0,12)(2(5)a z az z F >-=-,11)(1(6)a z az z F <-=-,11)(1. 学习参考.6.5 已知1)(↔k δ,az z k a k -↔)(ε,2)1()(-↔z z k k ε,试利用z 变换的性质求下列序列的z 变换并注明收敛域。
. 学习参考 .(1))(])1(1[21k k ε-+ (3))()1(k k k ε-(5))1()1(--k k k ε (7))]4()([--k k k εε(9))()2cos()21(k k k επ. 学习参考.6.8 若因果序列的z 变换)(z F 如下,能否应用终值定理?如果能,求出)(lim k f k ∞→。
(1))31)(21(1)(2+-+=z z z z F (3))2)(1()(2--=z z z z F. 学习参考.6.10 求下列象函数的双边逆z 变换。
(1)31,)31)(21(1)(2<--+=z z z z z F (2)21,)31)(21()(2>--=z z z z z F (3)21,)1()21()(23<--=z z z z z F. 学习参考 .(4)2131,)1()21()(23<<--=z z z z z F. 学习参考.. 学习参考.. 学习参考.. 学习参考.6.11 求下列象函数的逆z 变换。
(1)1,11)(2>+=z z z F (2)1,)1)(1()(22>+--+=z z z z z z z F (5)1,)1)(1()(2>--=z z z z z F (6)a z a z az z z F >-+=,)()(32. 学习参考.. 学习参考.. 学习参考.6.13 如因果序列)()(z F k f ,试求下列序列的z 变换。
《信号与系统(第2版》【附录+习题答案】

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
信号与系统课后习题答案

第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中X (0-)为系统的初始状态。
(2)()()2f t y t e= (5)()()cos2y t f t t= (8)()()2y t f t =解:(2)()()2f t y t e=① 线性: 设()()()()1122,f t y t f t y t →→,则()()()()122212,f t f t y t ey t e==那么()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以是非线性的。
② 时不变性 设()()11,f t y t →则()()()()10122110,f t t f t y t ey t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t ey t t -==-,所以是时不变的。
③ 因果性因为对任意时刻 t1,()()121f t y t e=,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos2y t f t t=① 线性: 设()()()()1122,f t y t f t y t →→,则()()()()1122cos2,cos2y t f t t y t f t t==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t+→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性 设()()11,f t y t →则()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-,所以是时变的。
(完整版)信号与系统课后题答案
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
信号与系统习题及答案
信号与系统习题答案 习题一 1-7 绘出下列各信号的波形:
(1))4sin()()(tTTtutu; (2))4sin()2()(2)(tTTtuTtutu
1-9 粗略绘出下列各函数式的波形图:
(1) )()2()(tuetft ; (2) )()63()(2tueetftt ; (3))()55()(3tueetftt; (4))2()1()10cos()(tututetft。
T 0 图1 T 0 2T 图2
0 图1
1 2
图2 9 0
1-10 写出题图1-10(a)、(b)、(c)所示各波形的函数式。 图a:11()(2)(2)()(2)()(2)22fttututtutut (1)(2)(2)2tutut 图b:)2()1()()(tutututf 图c: )()()sin()(TtututTEtf 1-12 绘出下列各时间函数的波形图,注意它们的区别: (1) )]1()([tutut ; (2) )1(ttu; (3) )1()]1()([tututut ; 0 1ln32 图3 0 1 2
图4
1 1
0 1 2 3 t 2 1
(b) E T t (c)
f(t)
0 t (a) f(t) 1 2 -2
题图1-10
(4) )1()1(tut ; (5) )]1()()[1(tutut ;
(6))]3()2([tutut; (7))]3()2()[2(tutut;
1-4 对于下图所示信号,由f(t)求f(-3t-2),但改变运算顺序,先求f(3t)或先求f(-t),讨论 所得结果是否与原书中的结果一致。 方法一: 方法二: 1 0 1 图4 t 0 1 t 图5 2 0 1 图6 t 3 2 3 2 0 1 图7 t 3 1
信号与系统习题答案
R1
R2
is (t)
uo (t)
L
C
1H
1F
图 P3.23
图 P3.5 3.8 利用信号的奇偶性,判断图 P3.6 所示各信号的傅里叶级数所包含的分量。
f1 (t )
f2 (t)
" Tt
1
−T 2
−T
0
T
1
T
2
−T
2
Tt
−T
0
T
t
2
f3 (t ) 1
−T
−T
2
0
T
2
Tt
图 P3.6
3.9 f1 (t) 和 f 2 (t) 的波形如图 P3.7 所示,已知 f1 (t) 的傅里叶变换为 F1 ( jω) ,试根据已知的
(3)如果 f (t) 是周期为 2 的奇谐信号,且 f (t) = t ,0 < t < 1,请画出 f (t) 的波形,并求
出它的傅里叶系数。
3.6 已知周期信号 f (t) 前四分之一周期的波形如图 P3.4 所示,试分别绘出在下列条件下信
号在一个周期内的波形。
(1)是 t 的偶函数,其傅里叶级数只有偶次谐波。 (2)是 t 的偶函数,其傅里叶级数只有奇次谐波。 (3)是 t 的偶函数,其傅里叶级数有偶次谐波和奇次谐波。 (4)是 t 的奇函数,其傅里叶级数只有偶次谐波。 (5)是 t 的奇函数,其傅里叶级数只有奇次谐波。 (6)是 t 的奇函数,其傅里叶级数有偶次谐波和奇次谐波。
(1) f1 (t) = cos(wt) , f2 (t) = sin(wt) ;
(2) f1 (t) = cos(wt)
f2 (t) = sin(wt + 30° ) 。
信号与系统课后习题参考答案
题图2-10
2-11已知系统得微分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-12已知系统得差分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-13已知系统得微分方程,试求系统得单位冲激响应。
⑴
⑵
⑶
2-14已知系统得差分方程,试求系统得单位样值响应。
1-1试分别指出以下波形就是属于哪种信号?
题图1-1
1-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所示,试作出下列各信号得波形图,并加以标注。
题图1-3
⑴⑵⑶
⑷⑸⑹
⑺⑻⑼
1-4已知信号与波形如题图1-4中所示,试作出下列各信号得波形图,并加以标注。
题图1-4
⑴⑵⑶
⑷⑸⑹
⑵
⑶
⑷
⑸
⑹
2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)
⑵
⑶
⑷
⑸
⑹
2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-3
2-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-4
2-5已知,试求:
⑴⑵⑶
并作出她们得图形。
2-6系统如题图2-6所示,试求系统得单位冲激响应。已知其中各子系统得单位冲激响应分别为:
3-5设有一周期信号x(t),其复振幅为:
⑴x(t)就是实函数吗?⑵x(t)就是偶函数吗?⑶就是偶函数吗?
3-6设x(t)就是一基波频率为Ω得周期信号,其复振幅为,试用表示以下周期信号得复振幅。
⑴⑵
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H@i")=Ġ
‘½•@ƒg
ˆê•@
•@•@•@•e
ƒc•Yƒ…
ƒt
ƒŒ•k‚ÁC‚Ã
ƒWƒO‚V
•ã•F•\
ˆê•V
‚b
Or•\‚’ˆê•Œ
Ă
T— •Ê
ƒt
=ƒTŒ^•~–Ü
S•R
'a
‰Ÿ=Cb
H
{etr+uy
g)ktt'nZ
lr=r*t
)T-1
•qƒV
`‚݃–‰¥ƒD
(‚í ƒÁnt3=
•Œ:•L•g —[•u
n•••x‚ȃR
••
“‡•@•@ˆêˆêƒ‹é`
Xle‚è,Ž© ƒm‚¥‚Ì —[
`.•Œ•\
•L‚ñ
)
•‡Xki")-frxpi9rinW-;/n-in
ƒÇ‹¨ƒŠ•[~(ƒC)4‹w„JD
•xáí•LƒIJ•u4J]‘½ƒ_‚¢]••ƒÇ‚肯VetteŽš‘½X‚Æe‚•R•oƒÆ‚è=•`F|•\ƒfe~14•Œ,ƒR•v(gttƒÆ l:—[)`••••'•l•T•E/fGƒmƒŠ'/)]r‚Ì‚½‚߃‹7+ƒ`C••4‚¿‰ˆ••l•\•Œ•Œ%ƒC10‰_•••œ]•\‘½•Œ•¨ƒf|ƒ‚èƒÇ•^‚’”•C•Yƒ“•[•[•@•Cƒ†•Œ•\•R
ƒÅ‚Š
•çƒc•R•@‚Â
‚P•^
••
˜r
ˆøH••‚‚̂±ƒOƒŠ
(14r., flu= Bu)
-
{dln - *)")nm.
ƒÀL]•\ƒC•v
‚¶h•c|]•\
ƒIJ–h
•LƒŠ•[
ƒÔˆÕ
•l•õ•Œ•ê
•l‘½
rlƒˆ•g‰³•Œ•ã
•çT•AƒŒ
Z)
z@)n)
ƒK„_ ttn-4ƒŒ]•Œƒm•Vˆ±ƒS‚µ'ƒ`
t/-zo-irl )(bƒ_2~J‚¿
ƒO•t••ƒŠ•[
ƒiƒO
'1•]2ƒt
‚Ìä肽 •A
z(ƒÐ‚Â
‚»‚ñ”¢
ƒ‹
(ƒ‹•u)?‰¾•l=‚²
/.Į;3
‚ßP‹w–m
‚Ì
‘æ
•w•uƒM•[
zt.tu)tb/ H@)4=
(6•v‘½ƒÆ
•_
•ãƒ†
‚è•@•@•½‹ã
ˆê‚Q‹™ƒÇ‚ߕ܈Ú
•M
‘½
‡@ ?•ã•l
=
ƒÆ•@•@•@•@•@•R•ã
ƒX
’P‚Q•@‹¦Œ‚‚Q
‚S•@
•Nˆ¼
•lƒÆ•R‚¼‚¦‘½•‚•R
Z`ƒÇƒŒƒm
•Ýt~|•]2'ƒR•Œ
•‹ ƒÅ ,ƒ‹ ‚¤••
•\•Q ƒÆ‚È
“™ƒK
ƒÃ••=ƒJ
-2ƒ‹•]Z •\••ƒÆ(Yv\4) )'.
•ã‘½
2tvcYrtei! sy'
•¨ƒ‹
•Mt`L~hJ=
(/,
aa,X,.NJ
n2‚ª(
32L]r Š‹ŒËƒEŒË •k|~ƒÃƒÆ‚¤
–Ñ‘½
rt)
•R•M•MƒCƒŒ•l“ñƒÒ•ŒŠßl]~•v2Ž¥1]
=t•l|ƒe
11•Ê
tttƒÃ‚Ì‘½
n•\|)
(112)\ (el*)‚ñ•R•v‚Ë
]“ñ•Œw‚ê
]•\ —¢
7t4
HI((•lJƒm1)=
2/t/ ƒC•¡
•R‚±Y`ƒÇ
Jl),ƒm
•M•M
ƒT‚Ý1)ƒA
•LƒÎ
ƒv
•U‰ú‘½
n
4Zn
’¬•kƒŠ
_ƒ“ƒ‹
•Œ‘½
ƒŒ
•R‰~
•Œ•LƒŒ
•@
•@
•N•@
•E•]
•RŠª
•R•ã
‚½•@
•R•\
•C
ƒn‰³ƒA‚Ì•@•C•R•L•]‚¤•A•]Žµ•gäP•N~‚ñ •\•Œ•Œ‚µ‰³‚ñ•L‚y‚ë’†“©•R‰Â“ñ—•–ÁƒÄn
‘½~_
,‚Ó—[
/L
ƒÁ•koI‚‚ݑ½
l“ñƒÃJ‚‚݂½
,
W rCn)`ƒŠ
•¬_ƒ•lrc)•E)
ƒf™{2 ~2ƒÎ‚ê•›
ƒ†ƒ€
2ƒ‹
‚¦•ç
'•¡-2‚ñ
ˆê
ŠÇ••
‚ñ
“ñ
ƒÄwJeJ&))•X‚±‚ •Û)ƒ€‚ð“dF ttƒÄ
•©
==#‚̃An•\ƒU•¡•k
|•\
‚è,‚è
l- * aDtln +js;-'L
‡
ƒP•@•Ð
‚̃mƒÒ•@Ž‚
H`ƒÆJ‚¸ƒŠƒOƒ‰n•v
a‚è(h‚çntt
ƒÆ)ƒm
JQ•Œ ‚ñ '2L/4 H
@jft)'
‚ñ•L‚yˆê
ƒSƒÅ••‚Ì
‚¢ƒÅ
tt ƒÆ•\‚è•\ƒ‹,ƒC‹¦‚¦•\ƒÆ‚è 1“‡lf‚ñ‚¯•@ˆêˆê‚SŒŽƒÒ
‚k‚è‚e‚‰•A
O•g‚Ì‚ÝR••—[‚è•R•|Žqn•u~~•E2ƒÎ‚¦ƒun•\bttn]‚èƒÅƒR•]•••RˆêƒC‰³‚¾‚íƒA•@•@‚¢‚y‚S•R–Ù‚í•R•^
•@‚S•D
•\•@•A’m
•\ƒn‚µ•@•R•]•]•g‰Ï‚é
•@•@•@•C
ˆêƒ†•AƒO
•@ƒ…
‚Ε@••
•\•Œƒh
•R•^ƒt
I l-* et"(4,
/•\=|
/••aƒÇƒŒƒmH›¦
‚è
rc•\
•çd rl•F
•ÊhƒŠƒˆèI–µ•©-3-•ôƒAfh•\ƒ^ƒŠ
ƒnƒB
•ã
‚ê
•L
ƒM:ƒ\
`‚è‚ñ‚èr
L—Õ3=
ƒÎ•l
•Ä•kelƒ‹ƒŠ
‚S‚Q
•Rƒm•RƒÊƒÖ
•¬‘H
ƒ†‘½
