第5章 高Da数下多孔介质的传热与流动过程
《流体力学》第五章孔口管嘴管路流动
2 Av A
2g
P0
2 AvA
2g
H
p0
当淹没出流时:
H 0 (Z A Z B ) H' p0 p0 ' pa
A
A
H'
2 2 A v A B vB
H
B
C
2g
2 2 A v A B vB
2g
§5.2 孔口淹没出流
C
1 孔口 vc 2 gH 0 Q A 2 gH 0 A 2 gH 0 自由 c 1 2 出流 pA pC AvA H 0 ( Z A ZC ) 2g
§5.3 管嘴出流
从局部阻力系数图423中查得锐缘进口 ζ=0.5
管嘴真空现象及真空值通过C-C与B-B断面列 能量方程得到证明: 2 2 pC C vC pB B vB hl 2g 2g
2 l vB hl=突扩损失+沿程损失 ( m ) d 2g
A 1 vc vB vB Ac
第五章
孔口管嘴管路流动
孔口自由出流
pc
2 Av A
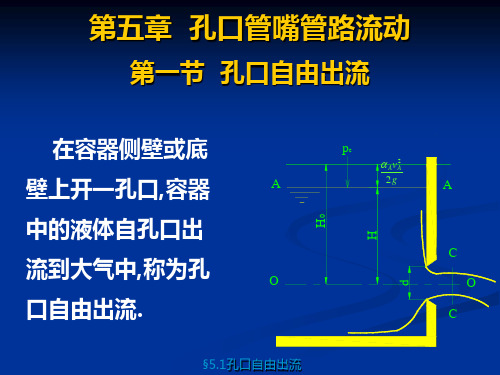
第一节
在容器侧壁或 底壁上开一孔口,容
A
2g
A
器中的液体自孔口
出流到大气中,称为
O
H0
H
C O C
孔口自由出流.
§5.1孔口自由出流
d
pc
2 Av A
A
2g
A
H0
H
C O O C
收缩断面:C-C断面 薄壁孔口:出流流股与孔口壁接触仅是一条周线, 这种条件的孔口称为薄壁孔口。 厚壁孔口(管嘴):若孔壁厚度和形状促使流股 收缩后又扩开,与孔壁接触形成面而不是线,这 种孔口称为厚壁孔口或管嘴。
2020年高中物理竞赛—传热学-第五章 对流换热:相似原理的应用等(共27张PPT) 课件

均匀热流边界 Nuf 4.82 0.0185Pef0.827
实验验证范围: Ref 3.6 103 ~ 9.05 105, Pef 102 ~ 104。
均匀壁温边界 Nuf 5.0 0.025Pef0.8
实验验证范围: Pef 100。
特征长度为内径,定性温度为流体平均温度。
第五章 对流换热
❖ 一般在关联式中引进乘数 (f / w )n 或(Prf / Prw )n
来考虑不均匀物性场对换热的影响。
第五章 对流换热
17
大温差情形,可采用下列任何一式计算。 (1)迪贝斯-贝尔特修正公式
Nuf 0.023 Ref0.8 Prfn ct
对气体被加热时,
ct
Tf Tw
0.5
当气体被冷却时, ct 1。
目的:完满表达实验数据的规律性、便于应用,特征数 关联式通常整理成已定准则的幂函数形式:
Nu c Ren Nu c Ren Prm Nu c(Gr Pr)n
式中,c、n、m 等需由实验数据确定,通常由图解法和
最小二乘法确定
第五章 对流换热
7
幂函数在对数坐标图上是直线
Nu c Ren lg Nu lg c nlg Re
n tg l2 ;
l1
c
Nu Re n
实验数据很多时,最好的方法是用最小二乘法由计算 机确定各常量
特征数关联式与实验数据的偏差用百分数表示
第五章 对流换热
8
① 回答了关于试验的三大问题:
(1) 实验中应测哪些量(是否所有的物理量都测) (2) 实验数据如何整理(整理成什么样函数关系) (3) 实物试验很困难或太昂贵的情况,如何进行试验? ② 所涉及到的一些概念、性质和判断方法:
流体力学第五章 孔口出流

(1)
H
H l
6 20
0.3m
(2)
v2 Lg
v2 Lg
(弗劳德数相等)
v
Lg
v2 Lg
v2L v L 8.9104m / s
L
L
qv vA qv vA
qv
vA vA
qv
vl 2qv
5
l 2 qv
F F
F
ma
l 2v2
l3
M M
FL F L
Fl
l4
qv vA qv vA
考虑在孔口射流断面上各点的水头、压强、速度沿孔口高度 的变化,这时的孔口称为大孔口。
小孔口(small orifice ):当孔口直径d(或高度e)与 孔口形心以上的水头高度H的比值小于0.1,即d/H<0.1时,
可认为孔口射流断面上的各点流速相等, 且各点水头亦相等, 这时的孔口称为小孔口。
2.根据出流条件的不同,可分为自由出流和淹没出流
防止泵前气穴的方法: 1. 降低吸水高度; 2. 降低吸水管、吸油管的局部沿程阻力; 3. 加大管径以降低流速;4.减少进水管输送长度。
5.5 相似原理
5.5.1 相似概念
力学相似是指实物流动与模型流动在对应点上物理量都 应该有一定的比例关系,具体包括几何相似、运动相似 及动力相似: 1)几何相似: 即模型流动与实物流动有相似的边界形 状,一切对应的线性尺寸成比例。
收缩系数
Cc
:
Cc
Cq Cv
0.64
阻力系数
:
1 Cv 2
1
0.06
流量系数 Cq :
Cq
qV qT
0.62
流速系数 Cv
0.97
多孔介质中的流动、传热与化学反应

多孔介质中的流动、传热与化学反应姜元勇; 徐曾和; 曹建立【期刊名称】《《金属矿山》》【年(卷),期】2019(000)004【总页数】5页(P1-5)【关键词】多孔介质; 流动; 传热; 化学反应; 跨尺度; 相互作用【作者】姜元勇; 徐曾和; 曹建立【作者单位】东北大学资源与土木工程学院辽宁沈阳110819【正文语种】中文【中图分类】TD80多孔介质是一种由固体骨架和孔隙(空隙)空间所组成的多相介质。
多孔介质的分布非常广泛,在人们的日常生活、工程实践和科学研究中比较常见,如煤层、岩体、球团矿和土壤等。
多孔介质中发生的流动过程、传热传质过程和化学反应过程具有重要的工程和科研价值,多年来一直受到众多研究者的关注[1-6]。
1 多孔介质中的流动多孔介质中的孔隙通道通常被流体所占据,在一定的能量梯度驱动下,流体便会沿着彼此联通的孔隙通道流动。
由于孔隙通道几何结构的复杂性,使得流体在多孔介质中流动时,孔隙流体与固体骨架之间的接触面构型也很复杂,很难进行精确描述[7]。
Bear[8]采用连续介质方法,将微观水平与宏观水平联系起来,通过引入表征体元(Representative Elementary Volume),给出了多孔介质物性参数的严格定义,如孔隙率、比面等,奠定了多孔介质流体动力学研究的基础。
流体在多孔介质中流动时,由于孔隙通道曲折、通道壁面不够光滑、流体具有一定的黏性等原因,造成多孔介质对于在其中流动的流体表现出一定的阻力作用[9]。
为了探究多孔介质中流动动力与阻力之间的关系,许多科研人员进行了不懈的努力。
早在1856年,Darcy就通过实验,研究了水在直立均质砂柱中的流动过程,获得了Darcy公式J=aq,也就是所谓的线性渗流定律(比流量与水力梯度成线性关系),此定律后来被进行了推广和理论证明。
实践中发现,Darcy定律主要反映黏性阻力的影响,具有一定的适用范围,即雷诺数满足Re=1~10。
多孔介质中的流体流动行为研究

多孔介质中的流体流动行为研究引言多孔介质是一种具有空隙或细小孔隙结构的物质,在实际生活和工程应用中广泛存在。
例如,我们身边的土壤、岩石、海绵等都属于多孔介质。
研究多孔介质中的流体流动行为不仅对于理解自然界的现象有重要意义,也对于工程应用中的地下水资源开发、油田开采、环境污染控制等具有重要的实际价值。
本文将介绍多孔介质中流体流动的一些基本概念和研究方法,以及与此相关的一些研究进展。
多孔介质中的流体流动多孔介质中的流体流动可以视为分为两个主要过程,即孔隙流动和边界流动。
孔隙流动指的是流体通过多孔介质中的孔隙进行传递、扩散和转移的过程。
而边界流动是指流体在多孔介质与外界界面上的流动过程。
这两个过程相互作用,共同决定了多孔介质中流体的传递性能以及整体的宏观流动行为。
研究方法研究多孔介质中的流体流动行为需要运用一系列的实验手段和数值模拟方法。
其中,流体力学的传统实验方法如渗流实验、测量渗透率和孔隙度等是最常用的手段之一。
通过这些实验可以获得多孔介质的渗透特性,进而分析流体在多孔介质中的传递规律。
此外,随着科学技术的进步,现代实验手段如X射线断层扫描、核磁共振等也被应用于多孔介质中的流体流动研究,能够提供更详细和精确的数据。
另一方面,数值模拟方法在多孔介质中流体流动的研究中也扮演着重要的角色。
如有限元方法、离散元方法等可以模拟多孔介质中复杂的孔隙结构,并通过数值模拟来分析流体在多孔介质中的流动规律。
数值模拟方法能够提供更加直观和清晰的流动图像和数据,帮助研究者更好地理解多孔介质中的流体行为。
研究进展在多孔介质中流体流动的研究中,流体渗流是一个重要而又复杂的问题。
研究者们发现,多孔介质中的流体渗流与多种因素有关,如孔隙结构、多孔介质的物理化学性质以及流体本身的性质等。
通过实验和数值模拟的方法,研究者们发现了一些有趣而又奇妙的现象。
例如,研究者们发现,多孔介质中流体的渗流速度与多孔介质的孔隙结构有关。
孔隙结构特征对于渗透率、渗透能力等渗流性质起着重要的调控作用。
第五章-传热学
h
' h,x
' h,y
cpuxtvytdxdy
8
单位时间内微元体热力学能的增加为
dU
d
cp
t
dxdy
于是根据微元体的能量守恒
h
dU
d
可得
2t x2
2t y2
dxdy
cpuxtvytdxdy
cp
t
dxdy
cptux tvy ttu xv y
2t x2
2t y2
2
20
cp
uxt
v t y
=
2t x2
2t y2
1
11 1
1
2
1 1
1
2
对流换热微分方程组简化为
h t tw tf y w
u v 0 x y
简化方程组只有4个方
程,但仍含有h、u、v、 p、t 等5个未知量,方
程组不封闭。如何求解?
uuxvuy1ddpxy2u2
u t x
v t y
26
第六节 相似理论基础
相似原理指导下的实验研究仍然是解决复杂对流换 热问题的可靠方法。
相似原理回答三个问题: (1)如何安排实验? (2)如何整理实验数据? (3)如何推广应用实验研究结果?
一、 相似原理的主要内容
1.物理现象相似的定义 2.物理现象相似的性质 3.相似特征数之间的关系 4.物理现象相似的条件
三、解的函数形式——特征数关联式
特征数是由一些物理量组成的无量纲数,例如毕 渥数Bi和付里叶数Fo。对流换热的解也可以表示成 特征数函数的形式,称为特征数关联式。
通过对流换热微分方程的无量纲化可以导出与对 流换热有关的特征数。
化工原理第五章传热过程计算与换热器

一.恒温差传热
T
t
tm T t
t
二.变温差传热
T
t1 0
T1
t1 浙江大学0本科生课程
过程工程原理
t
并流 t
0
T1 t2
t
A0 T1
T2 t2 t2
t
逆流 t
A0 第五章 传热过程计算与换热器
A T2
A T2 t1
A
13/25
§5.2.4 tm的计算
T1 t1
以冷、热流体均无相变、逆流流动为例:
t
T
11/2t5
1 1 b 1
T
KA 1 A1 Am 2 A2
Tw tw
考虑到实际传热时间壁两侧还有污垢热
阻,则上式变为:
t
1 1
KA 1 A1
Ra1
b
Am
Ra2
1
2 A2
浙江大学本科生课程 过程工程原理
第五章 传热过程计算与换热器
12/25
§5.2.4 tm的计算
Q KAtm
T1
T
浙江大学本科生课程 过程工程原理
第五章 传热过程计算与换热器
25/25
幻灯片2目录
习题课
浙江大学本科生课程 化工原理
第五章 传热过程计算与换热器
26/14
设 计 型
习题课 操作型 t1
LMTD法:
对数平均温差法
Q Ktm A
(1) T1
T2
Q mhc ph T1 T2 (2)
Q mc c pc t2 t1
浙江大学本科生课程
过程工程原理
第五章 传热过程计算与换热器
14/25
§5.2.4 tm的计算
第七章 多孔介质的渗流

Dt
pscT t
2 p 2 2 p p 2
K t Kp t
上式为不稳定渗流的基本方程
取 ( p) Kp 称为气体得导压系数,它是一个与
压力有关的变量。因而,无法采用原来的方法求解。
在通常情况下,我们可以采用线性化方法(求解非稳定 问题),稳定状态逐次替换法。在某些情况下可用自模解 的方法获得精确解,但后者往往限于典型问题,并最终要 求用数值方法求解常微分方程。
5.3 两相渗流问题
建立数学模型
设油水两种流体同时在多孔介质中流动,且流动服从达西定律。
对于油相的连续性方程为:
D(oS0 )
Dt
odivvo
0
对于水相的连续性方程为:
D( wSw )
Dt
wdivv w
0
饱和度方程:
S0 Sw 1
在考虑毛管力和重力影响时,油相和水相的a水渗是平流流面速动的度方夹分向角别与为:
(3)岩石的某些特征量,如长度、面积、
体积单位等等。
a 称为
窜流系数,
q为单位时间单位岩
无量纲量
石流经出过的因流次体分质析量得出窜流方程为:
q
a 0
(P2
P1 )
2 状态方程
P知为0压某力个已
无论是孔隙介质还是裂缝介质以及地层中流体均
是为可压缩的的,则裂缝和岩块的孔隙度的压缩特性
公式是:
气体在标准条件下的密度:
g ,sc
sc
Z sc RTsc
气体的体积系数 :
Bg
g,sc g
ZT Z scTsc
psc p
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.2.1物理模型及数学描述
矩形空腔的四壁不可渗漏,上下壁面 绝热。空腔中填充型砂,相变工质为 R113(沸点温度47.8℃)。 假设初始温度均为T0。腔底成为湿饱 和的液层;液层上方为干饱和的蒸汽 与残留不凝结性气体的混合物。 左壁面温度突升至T1,并维持不变, 腔内将形成一个稳定的自然对流,并 伴随工质的蒸发与冷凝传热。
多孔介质传热传质理论
刘伟
能源与动力工程学院 热科学与工程实验室
2013-7-25
1
主要内容
第1章 绪 论
第2章 多孔介质传热与流动的理论分析
第3章 土壤内的热质传输过程
第4章 有植物土壤内的传热传质分析
第5章 封闭多孔空腔及CPL系统传热传质分析
第6章 建筑物节能中的多孔介质流动与传热
2013-7-25
25
5.3
竖直封闭圆环内非饱和多孔 介质自然对流
5.3.1 物理模型与数学模型
2013-7-25
26
引入如下无量纲量
UgL Vg L Ul L Vl L Z R Z ,R ,U g , Vg ,U l , Vl , L L am am am am pk g g U v ,d L Vv , d L T T1 mL2 U v ,d , Vv , d ,P , ,m , am am cg g am T am g
(2) 运动方程
Vg / t Vg Vg mVg
气相: g g
g g g Pg g g g g Vg Vg Vl kg (5-4) 液相: l l Vl / t Vl Vl mVl l l Dl / kl l
以非饱和多孔介质的流动和传热理论建立 了矩形封闭腔体内的二维传热传质数理模 型,并对R113的蒸发相变进行了数值模拟。 根据计算结果着重讨论了流体瑞利数Ra, 介质达西数Da,腔体冷热端温差△T以及 形状比A的变化对其传热传质特性的影响, 得出一些有用的可指导工程实践的结论。
2013-7-25
4
2013-7-25
7
5.2.1.1 控制微分方程
(1) 连续性方程
不凝结性气体: 蒸汽:
gVg 0
(5-1)
v Vg Vv m
lVl m
(5-2) (5-3)
液体:
2013-7-25
8
5.2.1.1 控制微分方程
在日常生活中,多孔介质自然对流有着许 多的应用。 选取了两种具有代表性的封闭多孔材料: 竖直多孔圆环和倾斜矩形多孔腔中自然对 流现象进行研究。
2013-7-25
5
5.2 矩形封闭腔内非饱和多孔介质的传热传质
含湿多孔材料处于封闭围护结构体系中的热湿传递及相 变过程的理论研究,对建筑材料相变蓄能技术及相变工 质的恰当选择,具有重要的指导意义。 一般而言,工质在具有温度梯度的封闭腔内是以液态和 汽态的形式同时存在的;当封闭腔一侧受环境加热或冷 却时,在一定条件下内部的液体、蒸汽及残留气体会发 生运动,并发生蒸发与冷凝相变。 选用不同的相变工质,控制一定的工作温度(压力), 使在封闭腔的相应部位产生蒸发吸热或冷凝放热,就可 实现相变制冷或制热的目的,同时兼有相变蓄能的功能。 基于这一目的,本章模拟低温工质R113在矩形封闭腔 内的传热传质迁移过程。
2013-7-25
16
5.2.2.1 非饱和流动特性分析
图2(a)—(e)分别给出了当Da=10-4,A=5,T0=290K, Δ T=30℃时空腔内温度场、流函数场及内部蒸发量 场随Ra* =Λ Ra变化的场图。
(a)Λ Ra=104,Da=10-4
2013-7-25 17
(b)Λ Ra=105,Da=10-4
左右壁面为恒壁温边界:
X 0, 1, U g Vg U l Vl 0 X 1, 0, U g Vg U l Vl 0
初始条件: (X,Y, =0)=0
2013-7-25 15
5.2.2 计算结果及分析
为研究封闭腔内多孔介质中含湿非饱和的 自然对流行为,我们模拟了各种不同控制 参数Ra、Da、Δ T和A下温度场、流函数场、 蒸发量场等场量及换热系数的分布,下面 就各种因素对腔内流动与传热情况的影响 分别进行讨论。
T T0 Nu y / X ( x / L) Th T0 x 0
X 0
冷热端温差对传热的影响
2013-7-25
形状比A对传热的影响
24
5.2.2.4 结语
1)随着空腔内混合气体Ra数的增加,温度场逐渐扭曲,流场从 以Y=H/2对称到偏离对称,这说明对流的影响越来越强烈,当 Ra*=108时,在核心区差不多形成一个平行的强分层水平流动。 (2)随着对流的加强,蒸发、冷凝越来越旺盛。腔体底部靠近 热壁处是蒸发量最大的区域,冷凝量最大的区域则发生在腔体顶 部靠近冷壁处,如此,在封闭腔内形成稳定的自然循环流动。 (3)根据不同的流体瑞利数和介质达西数,我们可以将流体的 流动划分为四个区域,即导热区,强达西区,弱达西区,稳定对 流区。在弱达西区内,达西流动机制对增强传热的影响较小;在 稳定对流区,Nuh数不再受Da数影响。 (4)冷热端温差越大,腔体的传热能力越大。 (5)腔体的形状比越小,腔体的传热能力越强。
A
不 同 Da 数 下 Λ Ra 对 空 腔平 均 Nuh数的影响
无量纲传热系数Nuh
2013-7-25
1 m X X 0 dY A0 Nuh m h c
22
Da数对空腔传热系数的影响
2013-7-25
23
5.2.2.3 壁温Δ T及形状比A对传热的影响
第7章 多孔介质传热的实验研究
2013-7-25 2
第5章 高Da数下多孔介质的传 热与流动过程
矩形封闭腔内非饱和多孔介质的热质传输 特性研究
竖直封闭圆环内非饱和多孔介质热质传输 特性研究
倾斜矩形腔内非饱和多孔介质热质传输特 性研究 多孔介质中的场协同分析
2013-7-25 3
5.1 概述
201程
液相: Z方向: U l K l ( l ) Dl ( l ) l Z R方向: Vl Dl ( l ) l R Da U g U g 气相: Z方向: (U g Vg ) Pr Z R 2 Ug P U g Da ( ( R ) 2 ) gU g RaDa Z R R Z Da Vg Vg R方向: (U g Vg ) Pr Z R 2 Vg Vg P Vg Da ( ( R ) 2 ) gVg Da 2 R R R Z R
2013-7-25
12
引入如下无量纲量
UgL Vg L Ul L Vl L Z R Z ,R ,U g , Vg ,U l , Vl , L L am am am am pk g g U v ,d L Vv , d L T T1 mL2 U v ,d , Vv , d ,P , ,m , am am cg g am T am g
g kg ag g TL3 Ra , Pr , Da 2 , Le , Ja , g ag ag L Dva cg T a
a c c , v v , v v v , l l , l l l , g g g cg g g cg
g Kl L Dl Kl , Dl , am am m
2013-7-25
27
(1)连续性方程
( l lU l ) 1 ( l lVl R ) 液相: m Z R R ( v g (U g U v ,d )) 1 ( v g (Vg Vv ,d ) R) R113蒸汽: m Z R R ( a gU g ) 1 ( a gVg R ) 空气: 0 Z R R
Vv DTv g T Dlv l
(5-6)
2013-7-25
10
5.2.1.1 控制微分方程
(4) 能量方程
封闭腔中能量的平衡应同时考虑工质的流动传热和 相变换热。假设整个腔体中始终处于局部热力学平 衡态,即始终有Ts=Tl=Tg,则能量平衡的数学表达式 为: [ s ( c) s l ( c)l g ( v cv a ca )] T t
2013-7-25
18
(c)Λ Ra=106,Da=10-4
2013-7-25
19
(d)Λ Ra=107,Da=10-4
2013-7-25
20
(e)Λ Ra=108,Da=10-4
2013-7-25 21
5.2.2.2 传热特性分析
不 同 Λ Ra 下 Da 对 空 腔 平 均 Nuh数的影响
Da 1 Vg 1 Vg Vg Pr g g
Vl krl Vv
l P GDa c
Da 2 Vg Vg RaDak P g
