第二讲:树及其应用练习题目
数据结构树和二叉树习题

数据结构树和二叉树习题一、树的基本概念1.请简要描述树的基本概念及其特点。
答:树是由n(n≥0)个节点组成的有限集合。
其中:-若n=0,则为空树。
-若n>0,则树有且仅有一个称为根的节点,其他节点可以分为多个互不相交的有限集合,每个集合本身又是一棵树,称之为根的子树。
树的特点包括:-每个节点存放的数据可以是同种或不同种的数据类型。
-每个节点最多有一个父节点和多个子节点。
2.请列举树的应用场景。
答:树的应用场景包括但不限于以下几个方面:-文件系统:操作系统中的文件系统通常使用树来组织文件和目录。
-数据库:数据库中的索引通常使用树来存储和组织数据。
-编译原理:编译器使用语法树来解析源代码。
-社交网络:社交网络中的关注和粉丝关系可以表示为树。
二、二叉树3.请定义二叉树。
答:二叉树是一种特殊的树结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。
4.请画出以下二叉树的结构图:A/\BC/\/\DEFG答:以下是该二叉树的结构图:A/\BC/\/\DEFG5.请写出以下二叉树的前序遍历、中序遍历和后序遍历结果:/\23/\45答:-前序遍历结果:1,2,4,5,3-中序遍历结果:4,2,5,1,3-后序遍历结果:4,5,2,3,1三、二叉树的操作6.请实现二叉树的插入操作。
答:以下是二叉树的插入操作的示例代码:```class Node:def __init__(self, value):self.value = valueself.left = Noneself.right = Nonedef insert(root, value):if root is None:root = Node(value)else:if value < root.value:if root.left is None:root.left = Node(value)else:insert(root.left, value)else:if root.right is None:root.right = Node(value)else:insert(root.right, value)```7.请实现二叉树的查找操作。
二年级下册数学 知识点 应用题
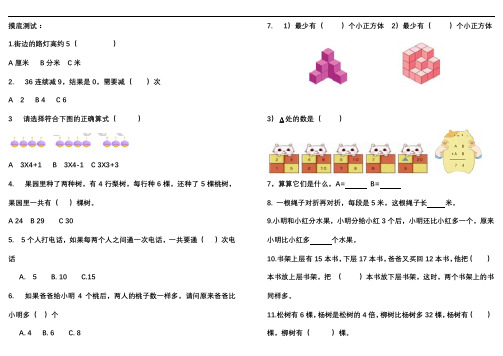
摸底测试:1.街边的路灯高约5()A厘米B分米C米2. 36连续减9,结果是0,需要减()次A 2B 4C 63 请选择符合下图的正确算式()A 3X4+1B 3X4-1C 3X3+34. 果园里种了两种树,有4行梨树,每行种6棵,还种了5棵桃树,果园里一共有()棵树。
A 24B 29C 305. 5个人打电话,如果每两个人之间通一次电话,一共要通()次电话A. 5B. 10C.156. 如果爸爸给小明4个桃后,两人的桃子数一样多,请问原来爸爸比小明多()个A. 4B. 6C. 8 7. 1)最少有()个小正方体2)最少有()个小正方体3)Δ处的数是()7,算算它们是什么,A= B=8. 一根绳子对折再对折,每段是5米,这根绳子长米。
9.小明和小红分水果,小明分给小红3个后,小明还比小红多一个,原来小明比小红多个水果。
10.书架上层有15本书,下层17本书,爸爸又买回12本书,他把()本书放上层书架,把()本书放下层书架,这时,两个书架上的书同样多。
11.松树有6棵,杨树是松树的4倍,柳树比杨树多32棵,杨树有()棵,柳树有()棵。
二年级春季物训班第一讲补充练习1.看图算式并计算2.计算3.计算1)3 X 3 X 20= 2) 3 X 3 X 20= 3) 2 X 3 X 50= 4) 4 X 20 X 9= 5) 2 X 9 X 5= 6) 5 X 7 X 8= 7) 9 X 4 X 5= 8) 7 X 5 X 6= 9)3 X 3X500 = 10)4 X 5 X 6= 11)900 X0= 12)900 X3=.二年级春季物训班第二讲补充练习3.如果1 个文具盒的价格等于3 支自动笔的价格,1支自动笔的价格等于5 支铅笔的价格。
3 个文具盒的价格等于支铅笔的价格。
5.如果1 只兔子的重量等于3 只小鸡的重量,2只狗的重量相当于4 只兔子的重量,那么:1 只狗的重量相当于只小鸡的重量。
11.如果 1 瓶可乐等于 1 杯茶和 1 杯奶的重量,2 杯奶的重量等于 1 杯茶的重量,1 瓶可乐相当于 杯牛奶的重量。
(完整版)种树问题练习题分类汇总

(完整版)种树问题练习题分类汇总种树问题是一个常见的考察生态环境保护与可持续发展的问题,在许多考试中都有相关题型出现。
下面是一份种树问题的练题分类汇总,供大家参考和练。
一、树木分类1. 请根据树木形态和叶子特征,将以下树木进行分类,并写出至少两个具体的例子。
- 针叶树类:- 例子1:松树- 例子2:云杉- 阔叶树类:- 例子1:梧桐树- 例子2:枫树2. 请说明以下树木的主要特征和用途。
- 柳树:- 主要特征:长而弯曲的枝条,细长的叶子- 用途:常用于修建生态堤岸和河岸防护。
- 桃树:- 主要特征:开白花、红花或者粉红花,果实肾形或球形- 用途:主要用于观赏和果实食用。
二、树木养护1. 针对以下描述,请写出正确的树木养护措施。
- 树木生长缓慢、叶子褪色:- 养护措施:适当施加合适的肥料,保持土壤湿润。
- 树干出现裂缝:- 养护措施:使用树胶封闭裂缝处,以防感染病菌。
2. 请说明以下树木养护的重要性和方法。
- 注水:- 重要性:保持树木的水分供应,促进生长。
- 方法:根据天气状况和树木需水情况,适时地进行浇水。
- 修剪:- 重要性:维持树木的形态和健康,促进枝条生长。
- 方法:根据树木枝条生长情况,定期修剪不合理的枝条。
三、树木病虫害防治1. 根据以下病虫害描述,请写出相应的防治措施。
- 树叶出现斑点、枯黄:- 防治措施:及时清除感染叶片,避免传染。
- 树干上出现无法自我修复的伤口:- 防治措施:擦拭受伤处并使用树胶封闭裂缝。
2. 请说明以下常见病虫害的特征和防治方法。
- 松树虱:- 特征:叶片上出现密集的小黑点,叶片逐渐枯萎。
- 防治方法:喷洒杀虫剂或清除感染的叶片。
- 褐树蟹:- 特征:树干上出现小洞,树皮逐渐剥落。
- 防治方法:清除受害的树皮,并使用防虫剂喷洒。
以上是一份种树问题的练习题分类汇总,希望对大家的学习和练习有所帮助。
继续加强对树木分类、养护和病虫害防治的了解,对于生态环境保护和可持续发展有着重要意义。
树与二叉树习题课

操作系统
操作系统的目录结构使用树形结构 来组织文件和目录,使得文件管理 变得有序和高效。
网络协议
网络协议中的路由协议使用树形结 构来计算最佳路径,使得数据包能 够快速、准确地传输到目标地址。
二叉树在计算机科学中的应用
01
排序算法
二叉搜索树是一种特殊的二叉树,用于实现高效的排序算法。插入节点
后序遍历
先遍历左子树,然后遍历 右子树,最后访问根节点。
02
二叉树的基本概念
二叉树的定义与性质
总结词
二叉树是一种特殊的树形结构,每个节点最多有两个子节点,通常称为左子节 点和右子节点。
详细描述
二叉树是一种树形数据结构,其中每个节点最多可以有两个子节点,通常称为 左子节点和右子节点。二叉树的性质包括平衡性、有序性等,这些性质对于二 叉树的遍历和查找等操作具有重要影响。
详细描述
构建二叉树的过程包括节点的插入、节点的删除等操作,这些操作需要遵循一定的规则以保证二叉树的性质。例 如,在插入节点时需要遵循左孩子右兄弟的规则,在删除节点时需要考虑如何维护二叉树的平衡性等。
03
树与二叉树的应用
树在计算机科学中的应用
数据结构
树是一种常见的数据结构,用于 表示层次关系和组织信息。在数 据库、文件系统、网页结构等方
总结词:考察复杂操作和 算法应用
2. 给定一棵二叉树,求其 二叉树的深度。
1. 设计一个算法,判断给 定的二叉树是否是平衡的。
3. 描述如何利用二叉树实 现一个优先级队列。
综合习题解析与解答
总结词:考察综合应用 和问题解决能力
01
2. 设计一个算法,实现 二叉树的镜像反转。
03
4. 给定一棵二叉搜索树, 删除其中的一个节点, 并保持其仍然是一棵二
树木练习题答案

树木练习题答案1. 解答第一题:树木是地球上最古老、最重要的生物之一。
它们扮演着保护土壤、吸收二氧化碳、提供氧气和提供栖息地的重要角色。
掌握树木的常见类别和特征对于我们认识自然界以及保护环境至关重要。
2. 解答第二题:树木的分类通常基于它们的特征、形态和生命周期。
在分类上,树木主要分为针叶树和阔叶树两大类。
2.1 针叶树:针叶树以其针状的叶片而得名,这些叶片通常较长且细长。
针叶树在适应干燥和寒冷环境方面具有独特的优势。
最常见的针叶树包括松树、云杉和冷杉等。
2.2 阔叶树:阔叶树的叶片宽而平坦,形状各异。
它们通常在温暖和湿润的环境中生长得更好。
一些典型的阔叶树包括橡树、枫树和桦树等。
3. 解答第三题:树木的主要特征是其树皮、树叶、花朵、果实以及生长习性等。
3.1 树皮:树木的树皮颜色、质地和形状各有不同。
例如,某些树木的树皮可能是光滑的,而其他树木的树皮则可能是粗糙的。
3.2 树叶:树叶的形态和大小也因树种而异。
一些树木的叶子呈尖形,而其他树木的叶子可能是圆形或心形。
3.3 花朵:花朵是树木进行繁殖的重要部分。
树木的花朵可以是鲜艳的,也可以是微小而不显眼的。
有些树木是花双性的,也就是说它们的花朵同时具有雄性和雌性的特征,而其他树木的花朵则是单性的。
3.4 果实:果实是树木成熟后产生的种子胚珠。
每种树木的果实都有独特的特征,有些树木的果实可以食用,而其他树木的果实可能会有毒。
3.5 生长习性:不同种类的树木在生长习性上也存在差异。
有些树木生长迅速,而其他树木生长缓慢而稳定。
4. 解答第四题:树木在人类生活中扮演着重要的角色。
它们为我们提供了木材、燃料和食物。
此外,树木对环境的影响也十分重要,它们能够调节气候、防止水土流失、为动物提供栖息地,并改善空气质量。
5. 结论:树木是地球上不可或缺的生物之一。
掌握树木的分类和特征可以帮助我们更好地了解自然界,加强对环境保护的认识。
我们应该珍惜树木,并意识到它们对我们生活和环境的重要性。
三年级奥数辅导题

还原问题(第一讲)“一个数加上3,乘以3,再减去3,最后除以3,结果还是3,这个数是几呢?”像这样已知一个数的变化过程和最后的结果,求原来的数,我们通常把它叫做“还原问题”。
解答“还原问题”一般采用倒推法,简单说,就是倒过来想。
原来加的,退回去用减;原来减的,退回去用加;原来乘的,退回去用除;原来除的,退回去用乘。
换句话说,从结果出发,按它变化的相反方向,一步一步倒着想,一步一步退还到原来的出发点,直到问题解决。
※一个数加上6,乘以3,再减去5得22,这个数是()。
※一个数加上5,乘5,减去5,再除以5,结果还是5,这个数是()。
※某数加上6,乘以6,减去6,除以6,其结果等于6,这个数是()。
※某数加上10,乘以10,减去10,除以10,结果等于10。
这个数是()。
※一个数的7倍加上3减去8乘以3得27,这个数()。
※一个数加上8,乘以8,减去8,再除以8,结果还是8.这个数是()。
※一个数减16加上24,再除以7得到9,这个数是()。
※某数加上3,乘5,再减去8,等于12,这个数是()。
※我爷爷说:“把我的年龄加上25,除以4,再减去23,最后乘以25,恰好是半百。
”请你猜猜我的爷爷今年()岁。
※有一位老人说:“把我的年龄加上4后除以3,再减去6,最后用5乘,恰巧是100岁。
”这位老人今年()岁。
※老爷爷说:“把我的年龄加上12,再用4除,然后减去15,再乘以10,恰好是100岁。
”老爷爷现在()岁。
植树问题(第一讲)植树造林,美化环境,造福人类,植树问题是数学中一种应用题,它有特殊的数量关系和解题规律,这类题主要研究总长度、树距、段数、树的棵数等数量之间的关系,此外像“上楼梯”、“锯木头”等许多相似的问题也可以转化为“植树问题”来解决或借助“植树问题”的思考方法来解决。
植树问题包括三个要素:1、总线路长;2、间距(株距);3、棵数。
只要知道三个要素中的两个,就可以求出第三个。
我们把植树问题分为不封闭路线和封闭路线两种情况。
树试题及答案
树试题及答案
1. 树的定义是什么?
答案:树是一种特殊的图,它是一个无环的连通图,其中任意两个节点之间有且仅有一条路径。
2. 什么是二叉树?
答案:二叉树是每个节点最多有两个子节点的树,这两个子节点被称为左子节点和右子节点。
3. 完全二叉树的定义是什么?
答案:完全二叉树是除了最后一层外,每一层都被完全填满,并且所有节点都尽可能地向左排列。
4. 请解释什么是平衡二叉树。
答案:平衡二叉树是一种特殊的二叉树,其中任何两个叶子节点的深度之差不超过1。
5. 树的深度和高度有何区别?
答案:树的深度是从根节点到最远叶子节点的最长路径上的节点数,而高度是从根节点到最远叶子节点的最长路径的长度。
6. 什么是二叉搜索树?
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
7. 描述树的遍历方法。
答案:树的遍历方法主要有前序遍历、中序遍历和后序遍历。
前序遍历先访问根节点,然后递归访问左子树和右子树;中序遍历先访问左
子树,然后访问根节点,最后访问右子树;后序遍历先访问左子树和右子树,最后访问根节点。
8. 如何判断一个二叉树是否是二叉搜索树?
答案:可以通过遍历二叉树并检查每个节点的左子节点值是否小于当前节点值,右子节点值是否大于当前节点值来判断。
9. 什么是树的子树?
答案:树的子树是由树的一个节点和它的所有后代节点组成的树。
10. 请解释什么是树的根节点。
答案:树的根节点是树中没有父节点的节点,它是树的起始点。
实验三 树及其应用2
实验三树及其应用实验目的:1.熟悉树的各种存储结构的特性。
2.应用树的结构解决具体问题。
实验内容:1.树的各种存储结构。
2.应用树的结构解决具体问题。
问题描述:很多涉及树的操作的算法都是以树的遍历操作为基础的。
试写一个程序,演示在二叉树上访问全部结点的操作。
实验要求:以二叉链表为存储结构,建立一棵二叉树,并对该二叉树进行先序、中序和后序遍历,分别输出每种遍历下的结点访问序列。
(1)把以下程序补充完整(2)编程输出二叉树的叶子结点测试数据:实验代码:#include<iostream.h>struct node{char data;node *left;node *right;};class tree{public:tree();void Create(node*);void Delete(node*);void Q(node*);void Z(node*);void H(node*);~tree();private:static node *root;};node* tree::root=0;tree::tree(){cout<<"输入树的根节点(如果为空输入#):\t";root=new node;cin>>root->data;Create(root);}void tree::Create(node *p){if(p){char x,y; node *q;cout<<"输入节点"<<p->data<<"的左孩子和右孩子:\t"; cin>>x>>y;if(x=='#')p->left=0;else{q=new node;q->data=x;p->left=q;}if(y=='#')p->right=0;else{q=new node;q->data=y;p->right=q;}Create(p->left);Create(p->right);}}//前序遍历void tree::Q(node *p=root){if(p){cout<<p->data<<' ';Q(p->left);Q(p->right);}}//中序遍历void tree::Z(node *p=root) {//写出算法的具体实现}//后序遍历void tree::H(node *p=root) {//写出算法的具体实现}//实现输出叶子结点的算法//tree::~tree(){Delete(root);}void tree::Delete(node *p) {if(p){Delete(p->left);Delete(p->right);delete p;}}void main(){tree h;cout<<"树的前序遍历:";h.Q();cout<<"\n树的中序遍历:";h.Z();cout<<"\n树的后序遍历:";h.H();}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[最优分解方案]
将一个正整数n分解成若干个互不相等的正整数的和,使得这些数的成绩最大。
输入:n(1<=n<=1000)
输出:乘积的最大值
样例:
输入:7
输出:12
第二讲:树及其应用
1、用链表方法建立二叉树,并输出先序,中序,后序的 遍历结果。用#表示空
输入:abd##eh##I##cf##g##
输出:
abdehicfg
dbheiafcg
dhiebfgca
2、根据两种遍历顺序确定树结构
输入:
二叉树的前序遍历顺序与中序遍历顺序
输出:
二叉树的后序遍历顺序
样例:
输入:
abcdefg
cbdafeg
输出:
cdbfgea
3、[石子合并问题]
有n堆石子,每堆有一个重量,每次把2堆石子合并成1堆,付出的代价为这两堆石子的重量
之和,如果把这n堆石子最后合并成1堆石子,怎样合并才能使付出的代价最小,求出最小的代
价.,例如n=5,重量 分别为7、5、2、4、6。付出的代价最小:54
输入:
第一行:石子数量n
第二行:n堆石子的重量
输出:
合并后付出的最小代价
样例:
输入:
5
7 5 2 4 6
输出:
54
