最小生成树数据结构课程设计报告
课程设计-最小生成树
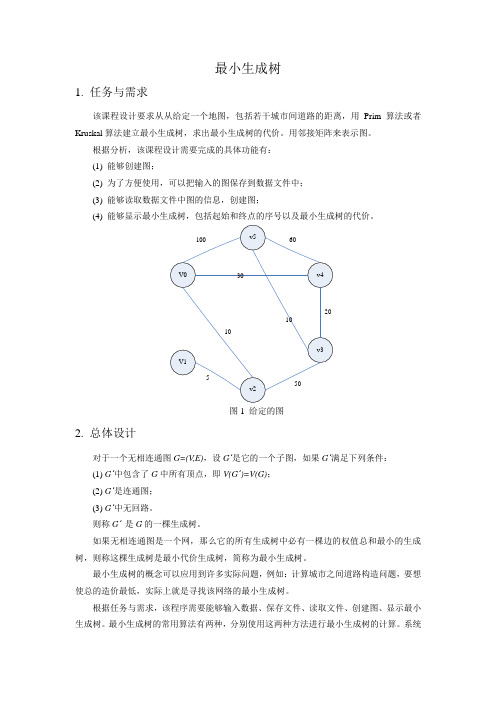
最小生成树1. 任务与需求该课程设计要求从从给定一个地图，包括若干城市间道路的距离，用Prim算法或者Kruskal算法建立最小生成树，求出最小生成树的代价。
用邻接矩阵来表示图。
根据分析，该课程设计需要完成的具体功能有：(1) 能够创建图；(2) 为了方便使用，可以把输入的图保存到数据文件中；(3) 能够读取数据文件中图的信息，创建图；(4) 能够显示最小生成树，包括起始和终点的序号以及最小生成树的代价。
图1 给定的图2. 总体设计对于一个无相连通图G=(V,E)，设G’是它的一个子图，如果G’满足下列条件：(1) G’中包含了G中所有顶点，即V(G’)=V(G)；(2) G’是连通图；(3) G’中无回路。
则称G’是G的一棵生成树。
如果无相连通图是一个网，那么它的所有生成树中必有一棵边的权值总和最小的生成树，则称这棵生成树是最小代价生成树，简称为最小生成树。
最小生成树的概念可以应用到许多实际问题，例如：计算城市之间道路构造问题，要想使总的造价最低，实际上就是寻找该网络的最小生成树。
根据任务与需求，该程序需要能够输入数据、保存文件、读取文件、创建图、显示最小生成树。
最小生成树的常用算法有两种，分别使用这两种方法进行最小生成树的计算。
系统功能模块如图：图2 系统功能模块图3. 详细设计3.1 最小生成树算法常见的两种构造最小生成树的算法是Prim算法和Kruskal算法。
1. Prim算法假设G=(V,E)为一网络，其中V为网络中的顶点集合，E为网络中的所有带权边集合。
设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，集合T存放G的最小生成树的边。
令集合U的初值为U={u0}（假设从u0出发），集合T的初值为T={}。
从所有u∈U，v∈V-U两个顶点构成的边中，选取具有最小权值的边(u,v)，将顶点v加入集合U中，将边(u,v)加入集合T中。
如此不断重复，直到U=V时，最小生成树构造完毕，这时候集合T中包含了最小生成树的所有边。
数据结构课程设计报告java最小生成树
上海电力学院数据结构（JAVA）课程设计题目:____最小生成树_______学生姓名：_****___________学号：_____*******_______院系：计算机科学与技术学院专业年级： ______*****___级20**年 *月**日目录1.设计题目 (1)2.需求分析 (1)1）运行环境 (1)2）输入的形式和输入值的范围 (1)3）输出的形式描述 (1)4）功能描述 (1)5）测试数据 (1)3.概要设计 (1)1）抽象数据类型定义描述 (1).2）功能模块设计 (1)3）模块层次调用关系图 (2)4.详细设计。
实现概要设计中定义的所有的类的定义及类中成员函数，并对主要的模块写出伪码算法。
(2)5.调试分析。
包括调试过程中遇到的问题及解决的方法、算法的时间空间复杂性分析、经验体会。
(6)6.用户使用说明。
详细列出每一步的操作说明。
(7)7. 测试结果 (7)8.附录：程序设计源代码 (9)一、设计题目1).问题描述若要在 n 个城市之间建设通信网络，只需要架设n-1 条线路即可。
如何以最低的经济代价建设这个通信网，是一个网的最小生成树问题。
2). 基本要求以邻接多重表存储无向带权图，利用克鲁斯卡尔算法或普瑞姆算法求网的最小生成树。
二、需求分析1）运行环境软件在JDK运行，硬件支持windows系统2）输入的形式和输入值的范围自动生成顶点数据在10~20之间；各个顶点之间权值在25~50之间；通过程序改动亦可生成已知顶点权值之间的最小生成树，需将随机生成代码改为edge edge[]={new edge(0,1,16),new（0,2,18）......}；将已知顶点、权值通过其函数输入再生成其所对应最小生成树。
3）输出的形式描述输出随机生成顶点个数以及各个顶点之间权值；然后输出本次生成顶点之间构成的最小生成树。
4）功能描述该程序会自动生成介于10~20个数顶点模拟各城市，再随机生成介于25~50之间数值作为权值模拟各个城市间的距离，并同时生成此次顶点、权值相对应的最小生成树，模拟各城市间的最小距离，最小生成树。
实验八 图的最小生成树
浙江大学城市学院实验报告课程名称数据结构与算法实验项目名称实验八图的最小生成树实验成绩指导老师（签名）日期1.一.实验目的和要求2.掌握图的最小生成树的概念。
3.掌握生成最小生成树的Prim算法（用邻接矩阵表示图）。
1、二.实验内容2、编写用邻接矩阵表示无向带权图时图的基本操作的实现函数, 主要包括：①初始化邻接矩阵表示的无向带权图 void InitMatrix(adjmatrix G); ②建立邻接矩阵表示的无向带权图 void CreateMatrix(adjmatrix G, int n) （即通过输入图的每条边建立图的邻接矩阵）; ③输出邻接矩阵表示的无向带权图void PrintMatrix(adjmatrix G, int n) （即输出图的每条边）。
把邻接矩阵的结构定义以及这些基本操作实现函数存放在头文件Graph1.h 中。
3、编写生成最小生成树的Prim算法函数void Prim(adjmatrix G, edgset CT,int n)以及输出边集数组的函数void PrintEdge(edgeset CT, int n)。
编写测试程序（即主函数）, 通过调用上述函数首先建立并输出无向带权图, 然后生成最小生成树并输出（即输出边集）。
要求: 把边集数组的结构定义、Prim算法函数、输出边集数组的函数PrintEdge 以及主函数存放在文件test8.cpp中。
测试数据如下:填写实验报告, 实验报告文件取名为report8.doc。
5.上传实验报告文件report8.doc与源程序文件test8.cpp及Graph1.h到Ftp服务器上自己的文件夹下。
三.函数的功能说明及算法思路函数: void InitMatrix(adjmatrix GA)功能: 初始化邻接矩阵表示的无向带权图函数: void CreateMatrix(adjmatrix GA,int n)功能: 建立邻接矩阵表示的无向带权图函数: void PrintMatrix(adjmatrix GA,int n)功能: 输出邻接矩阵表示的无向带权图函数: void Prim(adjmatrix GA,edgeset CT,int n)功能: 生成最小生成树思路：设从连通带权图G = { V, E }中的某一顶点u0 出发；选择与它关联的具有最小权值的边<u0, v>, 将其顶点加入到生成树的顶点集合U中；以后每一步从一个顶点在U中, 而另一个顶点在V-U中的各条边中选择权值最小的边<u, v>,把该顶点加入到集合U中；如此继续下去, 直到图中的所有顶点都加入到生成树顶点集合U中为止。
数据结构实验报告 最小生成树
实验报告六（数学学院08级4班080204015 余燕川）实验目的:通过对图的基本知识的学习, 掌握图的基本概念, 构造最小生成树, 在此基础上上机实践, 调试程序。
实验题目:对一个给定的图G（V, E）, 构造最小生成树。
三、实验分析:1.假设网G（V, E）是连通的, 从顶点u出发构造G的最小生成树T, 开始时, 记T=（U, B）, 其中U是T顶点集合, B是T的边集合；2、开始时U={u0 }( u0 ∈V)B=空,重复执行下述操作:在所有的u ∈U,V∈V-U组成的边(u,v)中找出一条权值最小的边（u0,v0）并入边集B中,同时将v0加入顶点集U,直到U=V为止, 此时T中必中必有n-1条边, 则T=（U, B）为G的最小生成树。
四、实验部骤:（1）构写程序的大体框架；（2）具体编写每个操作的程序；（3）程序的检查；（4）程序的调试；五、程序调试问题:输入顶点后, 边的信息输不进去；如下图：六、实验结果:输入顶点数为5, 边数为8, 顶点为v1,v2,v3,v4,v5;后面出现了问题。
七、实验程序:#define MAXSIZE 100#define max 10typedef char datatype;typedef struct{datatype vexs[MAXSIZE];int edges[MAXSIZE][MAXSIZE];int n,e;}graph;struct{char end;int len;}minedge[max];void Creatgraph(graph *ga){int i,j,k,w;printf("Please put the number of graph's vexs and edges:");scanf("%d,%d",&(ga->n),&(ga->e));printf("shu rui ding dian:\n");for(i=0;i<ga->n;i++)scanf("%2c\n",&(ga->vexs[i]));for(i=0;i<ga->n;i++)for(j=0;j<ga->n;j++)ga->edges[i][j]=100;for(k=0;k<ga->e;k++){printf("shu rui %d tiao bian de xu hao i,j and quan zhi w:",k+1);scanf("%d,%d,%d\n",&i,&j,&w);ga->edges[i][j]=w;ga->edges[j][i]=w;}}void prim(graph *g,char u){int v,k,j=0,min;for (v=1;v<=g->n;v++)if(v!=u){minedge[v].end=u;minedge[v].len=g->edges[v][u];}minedge[u].len=0;for(k=1;k<g->n;j++){min=minedge[k].len;v=j;}if(min==MAXSIZE){printf("error!");}printf("zui xiao sheng cheng shu:");printf("%d %d",v,minedge[v].end);minedge[v].len=-minedge[v].len; for(j=1;j<=g->n;j++)if(g->edges[j][v]<minedge[j].len) {minedge[j].len=g->edges[j][v]; minedge[j].end=v;}}void main(){int i,j;graph *g;g=(graph *)malloc(sizeof(graph)); Creatgraph(g);printf("Sheng cheng shu:\n"); prim(g,g->vexs[0]);}。
最小生成树-课程设计报告
课程设计报告问题描述:已知一个无向连通网表示n个城市以及城市间可能设置的通信线路，其中网的顶点表示城市，边表示两个城市之间的线路，赋于边上的权值表示相应的代价。
对于n个点的连通网能建立许多不同的生成树，每一棵生成树都可以是一个通信网。
我们要选择一棵生成树，使总的耗费最小（1）需求分析：在N地建设网络保证连通即可求最小的架设方式，任务完成可分为两个部分：A 存储N中任意两地之间的权（采用邻接表，邻接矩阵）B 用prim和克鲁斯卡尔两种算法分别求出N地中最优架设方式即最小生成树。
C 按顺序输出生成树中各条边以及它们的权值。
（2）概要设计：程序分为两大部分 1 存储部分，2 算法部分；存储部分分为邻接矩阵和邻接表，而且包含了两者直接的互相转换；算法部分分为普里母算法和克鲁斯卡尔算法。
Prim算法的思想：假设V是图中顶点的集合,E是图中边的集合,TE为最小生成树中的边的集合,则prim算法通过以下步骤可以得到最小生成树:1:初始化:U={u 0},TE={f}。
此步骤设立一个只有结点u 0的结点集U 和一个空的边集TE作为最小生成树的初始形态,在随后的算法执行中,这个形态会不断的发生变化,直到得到最小生成树为止。
2:在所有u∈U,v∈V－U的边(u,v)∈E中,找一条权最小的边(u 0,v 0)，将此边加进集合TE中，并将此边的非U中顶点加入U中。
此步骤的功能是在边集E中找一条边,要求这条边满足以下条件:首先边的两个顶点要分别在顶点集合U和V－U中,其次边的权要最小。
找到这条边以后,把这条边放到边集TE中,并把这条边上不在U中的那个顶点加入到U中。
这一步骤在算法中应执行多次,每执行一次,集合TE和U都将发生变化,分别增加一条边和一个顶点,因此,TE和U是两个动态的集合,这一点在理解算法时要密切注意。
3:如果U=V,则算法结束;否则重复步骤2。
可以把本步骤看成循环终止条件。
我们可以算出当U=V时,步骤2共执行了n－1次(设n为图中顶点的数目),TE中也增加了n－1条边,这n－1条边就是需要求出的最小生成树的边。
最小生成树问题课程设计
最小生成树问题课程设计一、课程目标知识目标：1. 理解最小生成树的概念，掌握其定义及性质；2. 学会运用普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法求解最小生成树问题；3. 了解最小生成树在实际问题中的应用，如网络设计、电路设计等。
技能目标：1. 能够运用普里姆和克鲁斯卡尔算法解决最小生成树问题，并进行算法分析；2. 能够运用所学知识解决实际问题，具备一定的算法设计能力；3. 能够通过合作与交流，提高问题分析和解决问题的能力。
情感态度价值观目标：1. 培养学生对数据结构与算法的兴趣，激发学习热情；2. 培养学生的团队合作意识，学会倾听、尊重他人意见；3. 培养学生面对问题勇于挑战、积极进取的精神。
课程性质：本课程为计算机科学与技术专业的高年级课程，旨在帮助学生掌握图论中的最小生成树问题及其求解方法。
学生特点：学生具备一定的编程基础和图论知识，对算法有一定的了解，但可能对最小生成树问题尚不熟悉。
教学要求：结合学生特点，采用案例教学、任务驱动等方法，注重理论与实践相结合，培养学生的实际操作能力和创新思维。
通过本课程的学习，使学生能够将所学知识应用于实际问题中，提高解决复杂问题的能力。
二、教学内容1. 最小生成树概念与性质- 定义、性质及定理- 最小生成树的构建方法2. 普里姆算法- 算法原理与步骤- 算法实现与复杂度分析- 举例应用3. 克鲁斯卡尔算法- 算法原理与步骤- 算法实现与复杂度分析- 举例应用4. 最小生成树在实际问题中的应用- 网络设计- 电路设计- 其他领域应用案例5. 算法比较与优化- 普里姆与克鲁斯卡尔算法的比较- 算法优化方法及其适用场景6. 实践环节- 编程实现普里姆和克鲁斯卡尔算法- 分析并解决实际问题- 小组讨论与成果展示教学内容依据课程目标进行选择和组织，注重科学性和系统性。
参考教材相关章节，制定以下教学安排：第1周：最小生成树概念与性质第2周：普里姆算法第3周：克鲁斯卡尔算法第4周：最小生成树在实际问题中的应用第5周：算法比较与优化第6周：实践环节与总结三、教学方法本课程将采用以下多样化的教学方法，以激发学生的学习兴趣和主动性：1. 讲授法：教师通过生动的语言和形象的比喻，对最小生成树的概念、性质、算法原理等基础知识进行讲解，使学生快速掌握课程内容。
数据结构课程设计报告(最小生成树)
《数据结构》课程设计报告课程名称：最小生成树课题负责人名（学号）:同组成员名单（角色）：指导教师：评阅成绩：评阅意见：提交报告时间：2011年12月19日最小生成树计算机科学与技术专业学生：指导老师：[摘要]选择一颗生成树，使之总的消费最少，也就是要构造连通网的最小代价生成树（简称为最小生成树）的问题，一颗生成树的代价就是树上各边的代价之和，构造最小生成树可以有多种算法，其中多数算法利用了MST的性质。
关键词：最小生成树连通图普里姆算法克鲁斯卡尔算法 MST一、设计目的1.了解并掌握数据结构与算法的设计方法，具备初步的独立分析和设计能力；2.初步掌握软件开发过程的问题分析、系统设计、程序编码、测试等基本方法和技能；3.提高综合运用所学的理论知识和方法独立分析和解决问题的能力；4.训练用系统的观点和软件开发一般规范进行软件开发，培养软件工作者所应具备的科学的工作方法和作风。
二、算法思想分析该设计的要求是在n个城市之间建设网络，不仅要保证连通，还要求是最经济的架设方法。
根据克鲁斯卡尔和普里姆算法的不同之处，该程序将城市个数大于十个时应用普里姆算法求最小生成树，而城市个数小于十个时则应用克鲁斯卡尔进行计算。
1.算法思想1)普里姆（Prim）算法思想a)选择从0节点开始，并选择0节点相关联的最小权值边，将与这条边相关联的另一顶点出列；b)在出列的节点中相关联的所有边中选择一条不与另一个已出列的节点相关联的权值最小的边，并将该边相关联的节点出列；c)重复b)直到所有的节点出列。
2)克鲁斯卡尔（Kruskal）算法思想为了使生成树上总的权值之和最小，应该使每一条边上的权值尽可能的小，所以应从权值最小的边选起，直至选出n-1条不能构成回路的权值最小的边位置。
具体做法如下：首先构造一个含n个顶点的森林，然后按权值从小到大从连通图中选择不使森林中产生回路的边加入到森林中去，直至该森林变成一棵树为止，这棵树便是连通图的最小生成树。
数据结构实验报告十二—最小生成树问题
问题描述：若要在n个城市之间建设通信网络，只需要架设n-1条线路即可。
如何以最低的经济代价建设这个通信网，是一个网的最小生成树问题。
一、需求分析：需定义结构体数组，根据权值逐一选择边。
二、概要设计：抽象数据类型：需定义结构体数组，存储每条边的起点，终点，权值。
算法的基本思想：1、图的信息的读取：定义结构体数组，存储每条边的起点，终点，权值。
2、对每条边在数组中的位置处理：选边需从最小的开始，故按边的权值从小到大进行排序。
3、边的选取：从最小的边的开始，若边的两端点不属于同一集合，则选取该边。
并将该边的两个顶点所在的两个集合合并成为一个。
因为有n个顶点，故只需选取n-1条边。
程序的流程程序由三个模块组成：输入模块：读入图的信息（顶点和边，用结构体数组进行存储）。
处理模块：Kruskal算法。
输出模块：将结果输出。
三、详细设计算法的具体步骤：struct G{int fromvex;int endvex;int weight;}GE[100],cur[100];void swap(G* GE,int i,int j){ //交换函数int temp=GE[i].fromvex;GE[i].fromvex=GE[j].fromvex;GE[j].fromvex=temp;temp=GE[i].endvex;GE[i].endvex=GE[j].endvex;GE[j].endvex=temp;temp=GE[i].weight;GE[i].weight=GE[j].weight;GE[j].weight=temp;}void Kruskal(int n){int i,j,k=0,pos=-1,m1,m2;bool** s=new bool *[n];//定义一个二维数组，用来判断是否为同一类for(i=0;i<n;i++)s[i]=new bool[n];for(i=0;i<n;i++){for(j=0;j<n;j++){if(i==j)s[i][j]=true; //初始化数组elses[i][j]=false;}}while(k<n-1){for(i=0;i<n;i++){if(s[i][GE[k].fromvex]==1)m1=i;if(s[i][GE[k].endvex]==1)m2=i;}if(m1!=m2){//判断是否为同一类,如果为同一类（该类中所有的点到起点和终//点的边在s数组中赋为1），cur[++pos].fromvex=GE[k].fromvex;cur[pos].endvex=GE[k].endvex;cur[pos].weight=GE[k].weight;for(i=0;i<n;i++){if(s[m1][i] || s[m2][i])//把该点添加到该类，并和并两个类s[m1][i]=1;elses[m1][i]=0;s[m2][i]=0;}}k++;}for(i=0;i<n;i++){delete []s[i];}}int main(){int i,j;int numVertex,numEdge;cout<<"请输入点的个数和边的条数："<<endl;cin>>numVertex>>numEdge;cout<<"请输入边的起始位置和边的权值："<<endl;for(i=0;i<numEdge;i++)cin>>GE[i].fromvex>>GE[i].endvex>>GE[i].weight;for(i=0;i<numEdge;i++)for(j=i;j<numEdge;j++){if(GE[j].weight<GE[i].weight)//将边的权值按从小到大排列swap(GE,i,j);}Kruskal(numEdge);for(i=0;i<numVertex-1;i++)cout<<cur[i].fromvex<<"->"<<cur[i].endvex<<":"<<cur[i].weight<<endl; system("pause");return 0;}四、调试分析：将选边的过程输出来检验算法的正确性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
河北科技大学课程设计报告学生姓名：白云学号：Z********* 专业班级：计算机113班课程名称：数据结构课程设计学年学期： 2 01 3—2 014学年第2学期指导教师：**2014年6月课程设计成绩评定表目录一、需求分析说明 (1)1.1最小生成树总体功能要求 (1)1.2基本功能 (1)1.3 模块分析 (1)二、概要设计说明 (1)2.1设计思路 (1)2.2模块调用图 (2)2.3数据结构设计 (2)2.3.1.抽象数据类型 (2)2.3.2方法描述 (2)三、详细设计说明 (3)3.1主函数模块 (3)3.2邻接表输出子模块 (3)3.3邻接矩阵输出子模块 (3)3.4创建邻接矩阵子模块 (3)3.5创建邻接表子模块 (3)3.6 Prim子模块 (3)3.7 Kruscal子模块 (4)四、调试分析 (4)4.1实际完成情况说明 (4)4.2 出现的问题及解决方案 (4)4.3程序中可以改进的地方 (4)六、课程设计总结 (7)七、测试数据 (7)八、参考书目 (7)一、需求分析说明1.1最小生成树总体功能要求在n个城市之间建设网络，只需保证连通即可，求最经济的架设方法。
存储结构采用多种。
求解算法多种。
1.2基本功能在n个城市之间建设网络，只需要架设n-1条线路，建立最小生成树即可实现最经济的架设方法。
程序可利用克鲁斯卡尔算法或prim算法生成最小生成树。
1.3 模块分析主模块：用于生成界面和调用各个子模块。
Kruscal模块：以kruscal算法实现最小生成树。
Prim模块：以prim算法实现最小生成树。
邻接表模块：用邻接表方式存储图。
邻接表输出模块：输出邻接表。
邻接矩阵模块：用邻接矩阵方式存储图。
邻接矩阵模块：输出邻接矩阵。
二、概要设计说明2.1设计思路问题的解决分别采用普利姆算法以及克鲁斯卡尔算法。
1) 普利姆算法就是先选择根，把它放入一个集合U中，剩余的顶点放在集合V中。
然后选择该顶点与V中顶点之间权值最小的一条边，以此类推，如果达到最后一个则返回上一个顶点。
2) 克鲁斯卡尔算法就是写出所有的顶点，选择权最小的边，然后写出第二小的，以此类推，最终要有一个判断是否生成环，不生成则得到克鲁斯卡尔的最小生成树。
2.2模块调用图2.3数据结构设计2.3.1.抽象数据类型ADT Graph{数据对象 V：v是具有相同特征的数据元素的集合，成为顶点集。
数据关系 R：R={VR}VR={<v,w>|v,w属于v且p(v,w)表示从v到w的弧，谓词p(v,w)定义了弧<v,w>的意义或信息}基本操作：1）GreatGraph(&G,V,VR)初始条件：V是图的顶点集，VR是图中弧的集合。
操作条件：按V和VR的定义构造图G。
2）LocateVex(G,u)初始条件：图G存在，u和G中顶点有相同的特征。
操作条件：若G中存在顶点u，则返回该顶点在图中的位置，否则返回其他信息。
2.3.2方法描述#define int_max 10000 /*节点不可达的距离*/#define max 20 /*数组最大长度*/int creatMGraph_L(MGraph_L &G) //用邻接矩阵存储void ljjzprint(MGraph_L G) //输出邻接矩阵int creatadj(algraph &gra,MGraph_L G) //用邻接表存储图void adjprint(algraph gra) //输出邻接表int prim(int g[][max],int n) //prim算法void kruscal_arc(MGraph_L G ,algraph gra) //最小生成树kruscal算法三、详细设计说明3.1主函数模块首先调用creatMGraph_L()函数进行邻接矩阵的初始化，然后调用creatadj()函数进行邻接表的初始化，然后根据用户输入判断switch()调用哪个模块。
3.2邻接表输出子模块首先判断是否超出了数据的个数，如果没有则输出邻接表的头节点，如果头节点的指针域不为空则输出下一个表结点，以此类推。
3.3邻接矩阵输出子模块判断是否超出了数据的个数，如果没有则输出G.arcs[i][j].adj中的值。
3.4创建邻接矩阵子模块输入顶点和弧的个数，再输入顶点与顶点之间的权值，生成邻接矩阵3.5创建邻接表子模块根据表结构定义一个表，设置表头结点为空，再循环生成其它结点并连接到上一个结点的后面。
3.6 Prim子模块标志顶点1加入U集合，形成n-1条边的生成树，寻找满足边的一个顶点在U，另一个顶点在V中的最小边，顶点K加入U，修改由顶点K到其他顶点边的权值，最后得到最小生成树。
3.7 Kruscal子模块确定弧的结点，以及弧的权，比较弧的权的大小并对权小的赋值，确定结点的位置，确保不能生成换，最后的到最小生成树。
四、调试分析4.1实际完成情况说明程序完成了prim和kruscal求一个图的最小生成树，并对图以邻接表和邻接矩阵的形式进行存储。
4.2 出现的问题及解决方案1)数据之间类型不同，引发数据间交换紊乱。
指针空间未分配导致系统随机给出一个错误的数据2)在寻找下一个结点时，寻找到最小权值边，将其两端的顶点信息及变的权值存储道辅助数组中。
在设计解决这些问题时用多个for循环嵌套查找，判断。
3)一些小细节尤其要注意，比如变量的定义，定义的位置。
4.3程序中可以改进的地方程序中对于一些没有最小生成树的图，没有判断功能。
还有就是进行完一个图的运算要关闭程序再重新输入新的图。
五、用户使用说明输入正确的数据程序执行菜单邻接矩阵存储邻接表存储Prim算法Kruscal算法六、课程设计总结通过这次课程设计，我收获了不少的东西。
我选择的题目是最小生成树，这个问题看这简单，但是做起来有非常大的困难。
平时我们很注重理论学习，但现在看来，实践也是非常重要的，两者缺一不可。
在这期间我遇到了不少的问题，问同学，查资料，虽然过程是辛苦琐碎的，但最后成果出来还是很鼓舞人心的。
七、测试数据1：城市的个数和线路个数：5,62：各个城市的名称：a,b,c,d,e3：每条路径的权值：a d 1 , a b 1 , b c 1 , b d 1 , d e 1 , c e 2八、参考书目[1]汤文兵.数据结构.北京：清华大学出版社，2011[2]李春葆.数据结构——习题与解析.北京：清华大学出版社，2010[3]Mark Allen Weiss. Data Structures and Algorithm Analysis in C: Second Edition. New York:MITPress, 2007[4]郭翠英.C语言课程设计案例精编.北京：中国水利出版社，2011源代码#include <iostream.h>#include <malloc.h>#include <stdio.h>//using namespace std;#define int_max 10000#define inf 9999#define max 20typedef struct ArcCell{int adj;char *info;}ArcCell,AdjMatrix[20][20];typedef struct {char vexs[20];//定义一个顶点数组AdjMatrix arcs;//定义一个邻接矩阵int vexnum;int arcnum;}MGraph_L;int localvex(MGraph_L G,char v){int i=0;while(G.vexs[i]!=v){++i;}return i;}int creatMGraph_L(MGraph_L &G){char v1,v2;int i,j,w;cout<<"请输入城市个数和总道路的个数:"<<endl;cin>>G.vexnum>>G.arcnum;for(i=0;i!=G.vexnum;++i){cout<<"输入城市名"<<i+1<<endl;cin>>G.vexs[i];}for(i=0;i!=G.vexnum;i++)for(j=0;j!=G.vexnum;++j){G.arcs[i][j].adj=int_max;G.arcs[i][j].info=NULL;}for(int k=0;k!=G.arcnum;++k){cout<<"请输入两城市之间的距离:"<<endl;cin>>v1>>v2>>w;//输入一条边依附的两点及权值i=localvex(G,v1);j=localvex(G,v2);G.arcs[i][j].adj=w;// G.arcs[j][i].adj=w;}cout<<"***********************************************"<<endl;cout<<"图创建成功"<<endl;cout<<"请根据如下进行操作"<<endl;return G.vexnum;}void ljjzprint(MGraph_L G){//输出邻接矩阵int i,j;for(i=0;i!=G.vexnum;++i){for(j=0;j!=G.vexnum;++j)if(G.arcs[i][j].adj==10000){ cout<<"0"<<" ";}else{cout<<G.arcs[i][j].adj<<" ";}cout<<endl;}}typedef struct arcnode{ //定义表结点int adjvex;//该弧指向的顶点在图中的位置struct arcnode *nextarc;//链域，指向下一条边或弧的结点char *info;//该弧的信息}arcnode;typedef struct vnode{//临街链表顶点头结点char data;//数据arcnode *firstarc;//链域}vnode,adjlist;typedef struct {//表的定义adjlist vertices[max];//定义头结点int vexnum,arcnum;//图的当前顶点数和弧数int kind;//图的种类标志}algraph;typedef struct acr{//弧的定义int pre;//弧的一结点int bak;//弧的另一结点int weight;//弧的权}edg;int creatadj(algraph &gra,MGraph_L G){//用邻接表存储图int i=0,j=0;arcnode *arc,*tem,*p;for( i=0;i!=G.vexnum;++i){//邻接表的初始化gra.vertices[i].data=G.vexs[i];//将abcde放入顶点信息域gra.vertices[i].firstarc=NULL;//指针域为空}for( i=0;i<G.vexnum;i++){for( j=0;j<G.vexnum;j++){if(gra.vertices[i].firstarc==NULL){if(G.arcs[i][j].adj!=int_max&&j<G.vexnum){arc=(arcnode *)malloc(sizeof(arcnode));arc->adjvex=j;gra.vertices[i].firstarc=arc;arc->nextarc=NULL;p=arc;}}else{if(G.arcs[i][j].adj!=int_max&&j!=G.vexnum){tem=(arcnode *)malloc(sizeof(arcnode));tem->adjvex=j;p->nextarc=tem;tem->nextarc=NULL;p=tem;}}}}gra.vexnum=G.vexnum;gra.arcnum=G.arcnum;return 1;}void adjprint(algraph gra){//输出邻接表int i;for(i=0;i!=gra.vexnum;++i){arcnode *p;cout<<gra.vertices[i].data<<i<<"->";p=gra.vertices[i].firstarc;while(p!=NULL){cout<<"->"<<p->adjvex;p=p->nextarc;}cout<<endl;}}typedef struct{int adjvex;int lowcost;}closedge;int prim(int g[][max],int n){//prim算法int lowcost[max],prevex[max];//lowcost[]存储当前集合U分别到剩余结点的最短路径prevex[]存储最短路径在U中的结点int i,j,k,min;for(i=2;i<=n;i++){lowcost[i]=g[1][i];//初始化prevex[i]=1;//顶点未加入到最小生成树中}lowcost[1]=0;//标志顶点1加入U集合for(i=2;i<=n;i++){//形成n-1条边的生成树min=inf;k=0;for(j=2;j<=n;j++)if((lowcost[j]<min)&&(lowcost[j]!=0)){min=lowcost[j];k=j;}printf("(%d,%d) %d\t",prevex[k]-1,k-1,min);lowcost[k]=0;//顶点K加入Ufor(j=2;j<=n;j++)if(g[k][j]<lowcost[j]){lowcost[j]=g[k][j];prevex[j]=k;}printf("\n");}return 0;}int arcvisited[100];//kruscal弧标记数组int find(int arcvisited[] ,int f){while(arcvisited[f]>0)f=arcvisited[f];return f;}void kruscal_arc(MGraph_L G ,algraph gra) {//最小生成树kruscal算法edg edgs[20];int i,j,k=0;for(i=0;i!=G.vexnum;++i)for(j=i;j!=G.vexnum;++j){if(G.arcs[i][j].adj!=10000){edgs[k].pre=i;edgs[k].bak=j;edgs[k].weight=G.arcs[i][j].adj;++k;}}int x,y,m,n;int buf,edf;for(i=0;i!=gra.arcnum;++i)arcvisited[i]=0;for(j=0;j!=G.arcnum;++j){m=10000;for(i=0;i!=G.arcnum;++i){if(edgs[i].weight<m){m=edgs[i].weight;x=edgs[i].pre;y=edgs[i].bak;n=i;}}buf=find(arcvisited,x);edf=find(arcvisited,y);edgs[n].weight=10000;if(buf!=edf){arcvisited[buf]=edf;cout<<"("<<x<<","<<y<<")"<<m;cout<<endl;}}}void main(){algraph gra;MGraph_L G;int i,j,d,g[20][20];char a='a';d=creatMGraph_L(G);creatadj(gra,G);cout<<"*****************************************"<<endl;cout<<"**1.用邻接矩阵存储:*********************"<<endl;cout<<"**2.用邻接表存储:*********************"<<endl;cout<<"**3.PRIM算法实现:*********************"<<endl;cout<<"**4.KRUSCAL算法实现:*********************"<<endl; int s;char y='y';while(y='y'){cout<<"请选择菜单:"<<endl;cin>>s;switch(s){case 1:cout<<"用邻接矩阵存储为:"<<endl;ljjzprint(G);break;case 2:cout<<"用邻接表存储为:"<<endl;adjprint(gra);break;case 3:for(i=0;i!=G.vexnum;++i)for(j=0;j!=G.vexnum;++j)g[i+1][j+1]=G.arcs[i][j].adj;cout<<"PRIM算法最经济的架设方法为:"<<endl;prim(g,d);break;case 4:cout<<"KRUSCAL算法最经济的架设方法为:"<<endl;kruscal_arc(G,gra);break;}cout<<endl<<"是否继续？y/n:";cin>>y;if(y=='n')break;}}。