我做的位似课件
合集下载
位似精品PPT课件
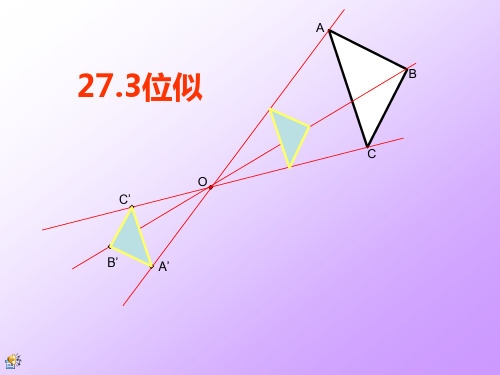
y A′(2,1), B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
你还有其他办法吗?试试看.
练一练:
1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比 y
A
C
o
D
B
x
练一练:
2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以 原点O为位似中心,将这个三角形放大为原来的2倍.
y
o
x
A
C
B
结束语
当你尽了自己的最大努力时,失败 也是伟大的,所以不要放弃,坚持
以0为中心把△ABC 缩小为原来的一半。
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0) y
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
y
A'
6
4 A
3
2
B'
C
1
B
o
2
4
6
还有其他办法吗?
C'
x
12
在平面直角坐标系中, △ABC三个顶点的坐标分别 为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2,将△ABC放大.
放大后对应点的坐标分别是多少?
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
你还有其他办法吗?试试看.
练一练:
1.如图表示△AOB和把它缩小后得到的△COD,求它们的相似比 y
A
C
o
D
B
x
练一练:
2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以 原点O为位似中心,将这个三角形放大为原来的2倍.
y
o
x
A
C
B
结束语
当你尽了自己的最大努力时,失败 也是伟大的,所以不要放弃,坚持
以0为中心把△ABC 缩小为原来的一半。
位似完整版课件

三个顶点的坐标所发生的变化. (1)沿y轴正向平移3个单位长度; (2)关于x轴对称; (3)以C为位似中心,将△ABC放大2倍; (4)以C为中心,将△ABC顺时针旋转180°.
当堂练习
1.将平面直角坐标系中某个图形的各点坐标做 如下变化,其中属于位似变换的是( C ) A.将各点的纵坐标乘以2,横坐标不变 B.将各点的横坐标除以2,纵坐标不变 C.将各点的横坐标、纵坐标都乘以2 D.将各点的纵坐标减去2,横坐标加上2
4.如图,正方形ABCD和正方形OEFG中, 点A和点F的坐 标分别为 (3,2),(-1,-1),则两个正方形的位似中 心的坐标是____(_1_,__0_)或__(_-__5_,__-__2.)
课堂小结
坐标变化规律
平面直角坐标系 中的位似变换
平面直角坐标 系中的位似
平面直角坐标系中 的位似图形的画法
x
-6
标的变化.
-8
把AB缩小后A,B的对应点为A ' ( 2 ,1 ),B' ( 2 , 0 );A"(- 2,- 1 ),B"( - 2 , 0 ).
y
2.如图,△ABC三个顶
8
点坐标分别为A(2,
6 A'
C'
3),B(2,1),C(
4A
2 B' C
6, 2),以点O为位似
-12 -10 -8 -6 -4 -2 O
B 2
4
6
8 910 12 x
中心,相似比为2,将 △ABC放大,观察对应 C"
B" -2 -4
A" -6
顶点坐标的变化.
-8
把△ABC放大后A,B,C的对应点为:
当堂练习
1.将平面直角坐标系中某个图形的各点坐标做 如下变化,其中属于位似变换的是( C ) A.将各点的纵坐标乘以2,横坐标不变 B.将各点的横坐标除以2,纵坐标不变 C.将各点的横坐标、纵坐标都乘以2 D.将各点的纵坐标减去2,横坐标加上2
4.如图,正方形ABCD和正方形OEFG中, 点A和点F的坐 标分别为 (3,2),(-1,-1),则两个正方形的位似中 心的坐标是____(_1_,__0_)或__(_-__5_,__-__2.)
课堂小结
坐标变化规律
平面直角坐标系 中的位似变换
平面直角坐标 系中的位似
平面直角坐标系中 的位似图形的画法
x
-6
标的变化.
-8
把AB缩小后A,B的对应点为A ' ( 2 ,1 ),B' ( 2 , 0 );A"(- 2,- 1 ),B"( - 2 , 0 ).
y
2.如图,△ABC三个顶
8
点坐标分别为A(2,
6 A'
C'
3),B(2,1),C(
4A
2 B' C
6, 2),以点O为位似
-12 -10 -8 -6 -4 -2 O
B 2
4
6
8 910 12 x
中心,相似比为2,将 △ABC放大,观察对应 C"
B" -2 -4
A" -6
顶点坐标的变化.
-8
把△ABC放大后A,B,C的对应点为:
位似教学课件

又因为 点A是∆ADE和 ∆ABC的公共点,点D和点B是对应点,点E和点C 是对应点,直线BD与CE交于点A,所以∆ADE和 ∆ABC是位似图形. 所以:∆ADE∽ ∆ABC 解:(2) DE∥BC.理由是: 因为:∆ADE和 ∆ABC是位似图形, 所以:∠ADE=∠B 则:DE∥BC.
如图,D,E分别AB,AC上的点.
A C C′ O B′ B
,画△
A′
2.分别在OA、OB、OC的反向延长线上取点A″、B″、
C″ ,使
A″ A C
,画△A″B″C″
C″
o
B B″
A
D′
A′ C′ B′ B C
C′ C
D
O A A′ B B′
O
(1)
( 2)
1.(1)、(2)两幅图中的图形相似吗? 2.还有其它特点吗?
A
D′
A′
C′ B′ B
C′ C D O A B B′
C
A′
O
两个多边形相似,对应顶点的连线相交于一点, 对应边互相平行,这样的两个图形叫做位似图形。 这个点叫做位似中心。 利用位似形可以将一个图形放大或缩小。
位似图形的任意一对对应点到位似中心的距离之 比等于位似比。
: 1.按如下方法将△ABC的三边缩小来原来的 如图所示,任取一点O,• 连AO,• BO,CO,并取它们 的中点D,E,F,得△DEF,则下列说法中正确的个数 是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形; B ③△ABC与△DEF是周长的比为2:1; ④△ABC与△DEF面积比为4:1
B
F
C
某小区原有一矩形花坛,现 小区进行规划。 (1)在原地将花坛扩建,使对应边变为原来的 4倍。 (2)在异地修建一块矩形草坪,使它与花坛的 对应边的比为5:1。 你能设计出图纸吗?
如图,D,E分别AB,AC上的点.
A C C′ O B′ B
,画△
A′
2.分别在OA、OB、OC的反向延长线上取点A″、B″、
C″ ,使
A″ A C
,画△A″B″C″
C″
o
B B″
A
D′
A′ C′ B′ B C
C′ C
D
O A A′ B B′
O
(1)
( 2)
1.(1)、(2)两幅图中的图形相似吗? 2.还有其它特点吗?
A
D′
A′
C′ B′ B
C′ C D O A B B′
C
A′
O
两个多边形相似,对应顶点的连线相交于一点, 对应边互相平行,这样的两个图形叫做位似图形。 这个点叫做位似中心。 利用位似形可以将一个图形放大或缩小。
位似图形的任意一对对应点到位似中心的距离之 比等于位似比。
: 1.按如下方法将△ABC的三边缩小来原来的 如图所示,任取一点O,• 连AO,• BO,CO,并取它们 的中点D,E,F,得△DEF,则下列说法中正确的个数 是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形; B ③△ABC与△DEF是周长的比为2:1; ④△ABC与△DEF面积比为4:1
B
F
C
某小区原有一矩形花坛,现 小区进行规划。 (1)在原地将花坛扩建,使对应边变为原来的 4倍。 (2)在异地修建一块矩形草坪,使它与花坛的 对应边的比为5:1。 你能设计出图纸吗?
人教版九年级下册位似—两个位似图形坐标之间的关系课件
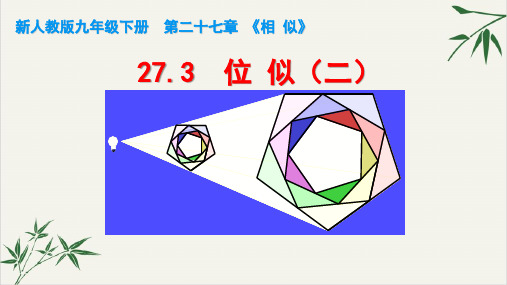
A
y
D
A′
B
D′
B′
C
C′ o
x
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
A′′ (3,-3 ), B′′ ( 4,-1 ), C′′ ( 2,0 ), D′′ ( 1,-2 )
A
y
D
B
C ′′
Co
x
B ′′
D ′′
A ′′
巩固训练
1. 在平面直角坐标系中,四边形 OABC 的顶点 坐标分别为 O (0,0),A (6,0),B (3,6),C (-3,3). 以原点 O 为位似中心,画出四边形 OABC 的位似图形,使它与四边形 OABC 的相 似是 2 : 3.
A′(-3,3),B′(-4,1),C′(-2,0),D′(-1,2).
或 A′′(3,-3),B′′(4,-1),C′′(2,0),D′′ (1,-2).
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的
坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出
它的一个以原点O为位似中心,位似比为1:2的位似图形.
投影—“动” 悉重难点
解:画法一:将四边 形 OABC 各顶点的坐
标都乘 2 ;在平面 3
直角坐标系中描点O
(0,0),A' (4,0),B'
(2,4),C′ (-2,2),
用线段顺次连接O,
A',B',C'.
y 6
4 C
C' 2
-4
O
-2
-4
B B'
A' A 6x
位似图形PPT课件

2.9位似图形
☞ 回顾与反思
• 什么叫相似多边形? • 什么叫相似多边形的相似比? • 判断两个三角形相似有哪些方法?
位似图形的概念,什么是位似中心,位似 比?
(1) 两个图形相似(2) 每组对应
点所在的直线都交于一点,那么这 样的两个图形叫做位似图形, 这个点 叫做位似中心, 这时的相似比又称为 位似比.
中心的距离,它们的比与位似比有什么关系?FELB O
G
K D
H C
位似图形有何性质?
• 位似图形的对应点和位似中心的关系 • 任意一对对应点到位似中心的距离之 比
• 例1.如图, • (1)如果DE∥BC,那么△ADE和△ABC是位似图 形吗?为什么?
(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗?为什么?
3 下列四边形ABCD和四边形EFGD是位似图形,它们的位似 中心是( ) A.点 B.点F C.点G D.点D
4 已知上图中,AE∶ED=3∶2,则四边形ABCD与 四边形EFGD的位似比为( ) A. 3∶2 B. 2∶3 C. 5∶2 D. 5∶3
(1)在各图中,位似图形的 位似中心与这两个 图形有什么位置关系?
(1)位似中心在两个图形的同侧; (2)位似中心在两个图形的之间; (3)位似中心在两个图形的内部; (4)位似中心在两个图形的一条对应边上; (5)位似中心在两个图形的一个对应顶点处;
A
在如图中任取一对对应点,度量这两个点到位似
从几方面回答?
A
D
E
B
C
练习
1、下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等; B.两个图形如果是位似图形,那么这两个图形不一定相似; C.两个图形如果是相似图形,那么这两个图形一定位似; D.两个图形如果是位似图形,那么这两个图形一定相似。
☞ 回顾与反思
• 什么叫相似多边形? • 什么叫相似多边形的相似比? • 判断两个三角形相似有哪些方法?
位似图形的概念,什么是位似中心,位似 比?
(1) 两个图形相似(2) 每组对应
点所在的直线都交于一点,那么这 样的两个图形叫做位似图形, 这个点 叫做位似中心, 这时的相似比又称为 位似比.
中心的距离,它们的比与位似比有什么关系?FELB O
G
K D
H C
位似图形有何性质?
• 位似图形的对应点和位似中心的关系 • 任意一对对应点到位似中心的距离之 比
• 例1.如图, • (1)如果DE∥BC,那么△ADE和△ABC是位似图 形吗?为什么?
(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗?为什么?
3 下列四边形ABCD和四边形EFGD是位似图形,它们的位似 中心是( ) A.点 B.点F C.点G D.点D
4 已知上图中,AE∶ED=3∶2,则四边形ABCD与 四边形EFGD的位似比为( ) A. 3∶2 B. 2∶3 C. 5∶2 D. 5∶3
(1)在各图中,位似图形的 位似中心与这两个 图形有什么位置关系?
(1)位似中心在两个图形的同侧; (2)位似中心在两个图形的之间; (3)位似中心在两个图形的内部; (4)位似中心在两个图形的一条对应边上; (5)位似中心在两个图形的一个对应顶点处;
A
在如图中任取一对对应点,度量这两个点到位似
从几方面回答?
A
D
E
B
C
练习
1、下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等; B.两个图形如果是位似图形,那么这两个图形不一定相似; C.两个图形如果是相似图形,那么这两个图形一定位似; D.两个图形如果是位似图形,那么这两个图形一定相似。
(位似图形)PPT课件

(2)位似与平移、轴对称、旋转一样,是图形的变换 方式,但位似可以改变图形的位置和大小,其他 变换只能改变图形的位置,即位似是图形的相似 变换,而其他变换是图 形的全等变换 .
1. 《XXXXX》P77T4 2. 《XXXXX》P77T6
知2-练
知识点 3 位似图形的画法
知3-导
利用位似可以把一个图形放大或缩小. 例3 【开放题】如图,已知四边形 ABCD, 将四边形ABCD
3∶6=1∶2,
1
所以△ABC∽△A′B′C′,且位似比为 2 .
所以
AC AC
1 2
,即
5 AC
1 2
,
所以A′C′=10 .
(2)根据题意,得 S△ABC
即
7
, 1 S△ABC
AC
2
AC
1 4
,
S△ABC 4
所以S △A′B′C′=7×4=28.
总结
知2-讲
(1)位似图形是相似图形, 所以它具有相似图形的一 切特征 .
知3-讲
画法二:位似中心在四边形的边上,如图,以AD边 上一点为位似中心,四边形A1B1C1D1就是所求作的 图形 .
知3-讲
总结
画位似图形的步骤: (1)确定位似中心(位似中心可以在图形外部,也可以在
图形内部, 还可以在图形的边上或在某一个顶点处); (2)分别连接位似中心和能代表原图的关键点,并延长; (3)根据位似比,确定所画位似图形的关键点的位置; (4)顺次连接所作各点,得到放大或缩小的图形. 注意:画位似图形时,要弄清位似比,即分清是已知图形 与新图形的位似比,还是新图形与已知图形的位似比 .
点的连线是否交于一点 .
知1-练
1. 《XXXXX》P77T1 2. 《XXXXX》P77T2
1. 《XXXXX》P77T4 2. 《XXXXX》P77T6
知2-练
知识点 3 位似图形的画法
知3-导
利用位似可以把一个图形放大或缩小. 例3 【开放题】如图,已知四边形 ABCD, 将四边形ABCD
3∶6=1∶2,
1
所以△ABC∽△A′B′C′,且位似比为 2 .
所以
AC AC
1 2
,即
5 AC
1 2
,
所以A′C′=10 .
(2)根据题意,得 S△ABC
即
7
, 1 S△ABC
AC
2
AC
1 4
,
S△ABC 4
所以S △A′B′C′=7×4=28.
总结
知2-讲
(1)位似图形是相似图形, 所以它具有相似图形的一 切特征 .
知3-讲
画法二:位似中心在四边形的边上,如图,以AD边 上一点为位似中心,四边形A1B1C1D1就是所求作的 图形 .
知3-讲
总结
画位似图形的步骤: (1)确定位似中心(位似中心可以在图形外部,也可以在
图形内部, 还可以在图形的边上或在某一个顶点处); (2)分别连接位似中心和能代表原图的关键点,并延长; (3)根据位似比,确定所画位似图形的关键点的位置; (4)顺次连接所作各点,得到放大或缩小的图形. 注意:画位似图形时,要弄清位似比,即分清是已知图形 与新图形的位似比,还是新图形与已知图形的位似比 .
点的连线是否交于一点 .
知1-练
1. 《XXXXX》P77T1 2. 《XXXXX》P77T2
位似 PPT课件 18 人教版
13、人生最大的错误是不断担心会犯错。
•
14、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。
•
15、不管怎样,仍要坚持,没有梦想,永远到不了远方。
•
16、心态决定命运,自信走向成功。
•
17、第一个青春是上帝给的;第二个的青春是靠自己努力的。
•
18、励志照亮人生,创业改变命运。
•
OE=2OB, OF=2OC,连接D,E,F, 还有其他方法吗?
E
B
O
B
C
F
A
D F
O
E D
C A
(3)如果在射线AO,BO,CO上分别取点D,E,F使
D结O果=会OA得,E到O一=O个B与,F△O=AOBCC,全那等么的,结△果D又E会F,.怎即样它呢们?的位
似比是1∶1.
还记得用凸透镜放大图形的方法吗?这种方法 放大前后的图形是什么关系?你能使它们的相似比 为3和4吗?
∆ADE和 ∆ABC是位似图形, ∆ADE∽ ∆ABC
∠ADE=∠B
DE∥BC.
如图:△ABC与 △FED是位似图形说明为什么AB∥DE?
A B
C
D
oE
F
练一练 如图,已知△ABC∽△DEF,
A
它们对应顶点的连线
AD,BE,CF相交于点O,这 D
两个三角形是不是位似三
角形?BBiblioteka E0FC• 位似图形:
A DE
A BC
E
D
A
B
CD
EB
C
例题欣赏
☞
• 如图所示,作出一个新图形,使
新图形与原图形对应线段的比
是2∶1.
