西街中学2015-2016高三第2次月考试题
北京市西城区2016届高三二模考试数学文试题(全WORD版含官方参考答案及评分标准)
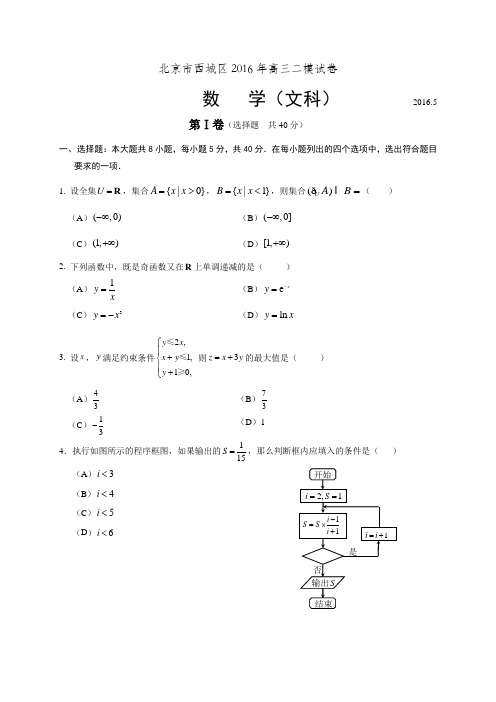
北京市西城区2016年高三二模试卷数 学(文科) 2016.5第Ⅰ卷(选择题 共40分)一、 选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 设全集U =R ,集合{|0}A x x =>,{|1}B x x =<,则集合()U A B = ð( ) (A )(,0)-∞ (B )(,0]-∞ (C )(1,)+∞(D )[1,)+∞2. 下列函数中,既是奇函数又在R 上单调递减的是( ) (A )1y x=(B )e xy -= (C )3y x =-(D )ln y x =3. 设x ,y 满足约束条件2,1,10,y x x y y ++⎧⎪⎨⎪⎩≤≤≥ 则3z x y =+的最大值是( )(A )43(B )73(C )13-(D )14.执行如图所示的程序框图,如果输出的115S =,那么判断框内应填入的条件是( ) (A )3i < (B )4i < (C )5i <(D )6i <5. 在∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若1sin()3A B +=,3a =,4c =,则sin A =( )(A )23(B )14(C )34(D )166. “0m n >>”是“曲线221mx ny +=为焦点在x 轴上的椭圆”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件7.某市家庭煤气的使用量x (m 3)和煤气费()f x (元) 满足关系, 0<,()(), .C x A f x C B x A x A ≤ìïï=íï+->ïî已知某家庭今年前三个月的煤气费如下表:若四月份该家庭使用了20 m 3的煤气,则其煤气费为( ) (A )11.5元 (B )11元 (C )10.5元 (D )10元8. 设直线l :340x y a ++=,圆22 (2)2C x y :-+=,若在直线l 上存在一点M ,使得过M 的圆C 的切线MP ,MQ (,P Q 为切点)满足90PMQ ?o ,则a 的取值范围是( )(A )[18,6]-(B )[6-+ (C )[16,4]-(D )[66---+第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 已知复数(2i)(1i)z =-+,则在复平面内,z 对应点的坐标为_____.10. 设平面向量,a b 满足||||2==a b ,()7⋅+=a a b ,则向量,a b 夹角的余弦值为_____. 11. 某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为_____.12.设双曲线C 的焦点在x 轴上,渐近线方程为y x =,则其离心率为____;若点(4,2)在C 上,则双曲线C 的方程为____.13. 设函数22, 1,()log , 1,x x f x x x -⎧<=⎨⎩≥ 那么1[()]2f f -=____;若函数()y f x k =-有且只有两个零点,则实数k 的取值范围是_____.14. 在某中学的“校园微电影节”活动中,学校将从微电影的“点播量”和“专家评分”两个角度来进行评优. 若A 电影的“点播量”和“专家评分”中至少有一项高于B 电影,则称A 电影不亚于B 电影. 已知共有5部微电影参展,如果某部电影不亚于其他4部,就称此部电影为优秀影片. 那么在这5部微电影中,最多可能有____部优秀影片.正(主)视图侧(左)视图俯视图 11 2三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2()(1)cos f x x x =. (Ⅰ)求函数()f x 的定义域和最小正周期;(Ⅱ)当π(0,)2x ∈时,求函数()f x 的值域.16.(本小题满分13分)已知数列{}n a 的前n 项和n S 满足432n n a S -=,其中n *∈N . (Ⅰ)求证:数列{}n a 为等比数列;(Ⅱ)设142n n b a n =-,求数列{}n b 的前n 项和n T .17.(本小题满分14分)如图,在周长为8的矩形ABCD 中,,E F 分别为,BC DA 的中点. 将矩形ABCD 沿着线段EF 折起,使得60DFA ∠= . 设G 为AF 上一点,且满足//CF 平面BDG .(Ⅰ)求证:EF DG ⊥;(Ⅱ)求证:G 为线段AF 的中点;(Ⅲ)求线段CG 长度的最小值.18.(本小题满分13分)FE GA BD C⇒E C某中学有初中学生1800人,高中学生1200人. 为了解学生本学期课外阅读时间,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.(Ⅰ)写出a 的值;(Ⅱ)试估计该校所有学生中,阅读时间不小于30个小时的学生人数;(Ⅲ)从阅读时间不足10个小时的样本学生中随机抽取2人,求至少抽到1名高中生的概率.19.(本小题满分13分)已知函数2()()x af x x a -=+.(Ⅰ)若()1f a '=,求a 的值;(Ⅱ)设0a ≤,若对于定义域内的任意1x ,总存在2x 使得21()()f x f x <,求a 的取值范围.20.(本小题满分14分)已知抛物线C :24x y =,过点)0)(,0(>m m P 的动直线l 与C 相交于B A ,两点,抛物线C 在点A 和点B 处的切线相交于点Q ,直线BQ AQ ,与x 轴分别相交于点F E ,.(Ⅰ)写出抛物线C 的焦点坐标和准线方程; (Ⅱ)求证:点Q 在直线y m =-上;(Ⅲ)判断是否存在点P ,使得四边形PEQF 为矩形?若存在,求出点P 的坐标;若不存在,说明理由.O 时间(小时)10 2030 40 50 高中生组O 时间(小时)10203040 50 初中生组北京市西城区2016年高三二模试卷参考答案及评分标准高三数学(文科) 2016.5一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.C 3.B 4.C 5.B 6.D 7.A 8.C 二、填空题:本大题共6小题,每小题5分,共30分. 9.(3,1) 10.3411.3 12 22184x y -=13.12 1(,)2+∞ 14.5注:第12,13题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:函数()f x 的定义域为{|x x ∈R ,且ππ,}2x k k ≠+∈Z . ……………… 2分又因为2()(1)cos f x x x =2(1x =……………… 3分2cos cos x x x =1cos 222x x+=……………… 7分 π1sin(2)62x =++, ……………… 9分 所以()f x 的最小正周期为2ππ2T ==.(验证知其定义域与之相符) …………… 10分 (Ⅱ)解:由π(0,)2x ∈,得ππ7π2666x <+<, ……………… 11分所以1πsin(2)126x -<+≤,所以当π(0,)2x ∈时,3()(0,]2f x ∈,即函数()f x 在区间π(0,)2的值域为3(0,]2. ……………… 13分16.(本小题满分13分)(Ⅰ)证明:因为432n n a S -=, ○1 所以当1n =时,11432a S -=,解得12a =; ………………… 2分 当2n ≥时,11432n n a S ---=, ○2 …………………3 分 由○1—○2,得11443()0n n n n a a S S -----=, 所以14n n a a -=, 由12a =,得0n a ≠,所以14nn a a -=,其中2n ≥. 故{}n a 是首项为2,公比为4的等比数列. …………………6 分(Ⅱ)解:由(Ⅰ),得124n n a -=⨯. ………………… 8分所以 114442n n n b a n n -=-=-. 则{}n b 的前n 项和011(44)(48)(44)n n T n -=-+-++- 011(444)(484)n n -=+++-+++ ……………… 10分 14(44)142n n n -+=-- 241223n n n -=--. ………………13分17.(本小题满分14分)(Ⅰ)证明:因为在折起前的矩形ABCD 中,,E F 分别为,BC DA 的中点, 所以EF FD ⊥,EF FA ⊥, 又因为FD FA F = ,所以EF ⊥平面DFA . ………………2分 又因为DG ⊂平面DFA ,所以EF DG ⊥. ………………4分 (Ⅱ)证明:因为在折起前的矩形ABCD 中,,E F 分别为,BC DA 的中点,所以在立体图中,////AB EF CD .即在立体图中,四边形ABCD 为平行四边形.连接AC ,设AC BD O = ,则AO CO =. ………………6分 又因为//CF 平面BDG ,CF ⊂平面ACF ,平面ACF 平面BDG OG =, 所以//CF OG ,所以在ACF ∆中,OG 为中位线,即G 为线段AF 的中点. ………………9分 (Ⅲ)解:因为G 为线段AF 的中点,60DFA ∠= 所以DFA ∆为等边三角形,且DG FA ⊥, 又因为EF DG ⊥,EF FA F = , 所以DG ⊥平面ABEF . 设BE 的中点为H ,连接,GH CH , 易得四边形DGHC 为平行四边形, 所以CH ⊥平面ABEF ,所以222CG GH CH =+. ………………11分 设DF x =,由题意得CH DG ==,42GH CD x ==-,所以222219(42))16164CG x x x x =-+=-+, ………………13分 所以当3219x =时,2min 4819CG =. 所以线段CG. ………………14分18.(本小题满分13分)(Ⅰ)解:0.03a =. ………………3分 (Ⅱ)解:由分层抽样,知抽取的初中生有60名,高中生有40名. ………………4分 因为初中生中,阅读时间不小于30个小时的学生频率为(0.020.005)100.25+⨯=, 所以所有的初中生中,阅读时间不小于30个小时的学生约有0.251800450⨯=人, ………………6分 同理,高中生中,阅读时间不小于30个小时的学生频率为(0.030.005)100.35+⨯=,学生人数约有0.351200420⨯=人.F EGA B D COH所以该校所有学生中,阅读时间不小于30个小时的学生人数约有450420870+=人. ………………8分 (Ⅲ)解:记“从阅读时间不足10个小时的样本学生中随机抽取2人,至少抽到1名高中生”为事件A , ………………9分初中生中,阅读时间不足10个小时的学生频率为0.005100.05⨯=,样本人数为0.05603⨯=人.高中生中,阅读时间不足10个小时的学生频率为0.005100.05⨯=,样本人数为0.05402⨯=人. ………………10分记这3名初中生为123,,A A A ,这2名高中生为12,B B ,则从阅读时间不足10个小时的样本学生中随机抽取2人,所有可能结果有10种,即:12(,)A A ,13(,)A A ,11(,)A B ,12(,)A B ,23(,)A A ,21(,)A B ,22(,)A B ,31(,)A B ,32(,)A B ,12(,)B B ,而事件A 的结果有7种,它们是11(,)A B ,12(,)A B ,21(,)A B ,22(,)A B ,31(,)A B ,32(,)A B ,12(,)B B , 所以7()10P A =. ………………13分19.(本小题满分13分)(Ⅰ)证明:函数()y f x =的定义域{|}D x x x a =∈≠-R 且,由题意,()f a '有意义,所以0a ≠.求导,得244()()2()()(3)()()()x a x a x a x a x a f x x a x a +--⋅++⋅-'==-++. ………………3分 所以24241()1164a f a a a '===, 解得12a =±. ………………5分(Ⅱ)解:“对于定义域内的任意1x ,总存在2x 使得21()()f x f x <”等价于“()f x 不存在最小值”. ………………6分① 当0a =时, 由1()f x x=,得()f x 无最小值,符合题意. ………………8分② 当0a <时,令4()(3)()0()x a x a f x x a +⋅-'=-=+,得x a =- 或 3x a =. ………………9分随着x 的变化时,()f x '与()f x 的变化情况如下表:………………11分 所以函数()f x 的单调递减区间为(,3)a -∞,(,)a -+∞,单调递增区间为(3,)a a -.因为当x a >时,2()0()x af x x a -=>+,当x a <时,()0f x <,所以min ()(3)f x f a =.所以当13x a =时,不存在2x 使得21()()f x f x <.综上所述,a 的取值范围为{0}a ∈. ………………13分20.(本小题满分14分)(Ⅰ)解:焦点坐标为(0,1),准线方程为1y =-. ………………2分 (Ⅱ)证明:由题意,知直线l 的斜率存在,故设l 的方程为m kx y +=. 由方程组2,4,y kx m x y =+=⎧⎨⎩ 得2440x kx m --=,由题意,得216160k m ∆=+>.设11(,)A x y ,22(,)B x y ,则124x x k +=,124x x m =-, ………………4分 由抛物线方程24x y =,得214y x =,所以12y x '=,所以抛物线在点A 处的切线方程为)(21411121x x x x y -=-, 化简,得2114121x x x y -=, ○1 同理,抛物线在点B 处的切线方程为2224121x x x y -=. ○2 ………………6分联立方程○1○2,得22221141214121x x x x x x -=-,即))((41)(21212121x x x x x x x +-=-,因为21x x ≠,所以)(2121x x x +=, 代入○1,得1214y x x m ==-, 所以点12(,)2x x Q m +-,即(2,)Q k m -. 所以点Q 在直线y m =-上. ………………8分 (Ⅲ)解:假设存在点P ,使得四边形PEQF 为矩形,由四边形PEQF 为矩形,得EQ FQ ⊥,即AQ BQ ⊥,所以1-=⋅BQ AQ k k ,即1212121-=⋅x x .由(Ⅱ),得1)4(414121-=-=m x x ,解得1m =.所以(0,1)P .………………10分 以下只要验证此时的四边形PEQF 为平行四边形即可.在○1中,令0=y ,得)0,21(1x E . 同理得)0,21(2x F .所以直线EP 的斜率为1122001x x k EP -=--=,直线FQ 的斜率12122221)1(0xx x x k FQ -=+---=,………………12分 所以FQ EP k k = ,即FQ EP //.同理EQ PF //.所以四边形PEQF 为平行四边形.综上所述,存在点)1,0(P ,使得四边形PEQF 为矩形.………………14分。
2015-2016学年青海省西宁市第四高级中学高一上学期第二次月考数学试题(word版)

2015-2016学年青海省西宁市第四高级中学高一上学期第二次月考数学试题(word 版)一、 选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U=R,集合A={x|x≥1},B={x|0≤x<5},则集合(∁U A)∩B=( ). A.{x|0<x<1}B.{x|0≤x<1}C.{x|0<x≤1}D.{x|0≤x≤1}2.如果集合A ={x |x =2k π+π,k ∈Z},B ={x |x =4k π+π,k ∈Z},则( ) A.A B B.B A C.A = B D.A ∩B =∅3.设A ={x ∈Z||x |≤2},B ={y |y =x 2+1,x ∈A },则B 的元素个数是( ) A.5 B.4 C.3 D.2 4、8.下列四组函数中,表示同一函数的是( ).A .f (x )=|x |,g (x )=2xB .f (x )=lg x 2,g (x )=2lg xC .f (x )=1-1-2x x ,g (x )=x +1 D .f (x )=1+x ·1-x ,g (x )=1-2x5. 下列函数中,既是偶函数又在()0,+∞上单调递增的是( ) A .2y x =- B .y x = C .2x y = D .12log y x =6. 若log 2 a <0,b⎪⎭⎫⎝⎛21>1, 则( ).A .a >1,b >0B .a >1,b <0C .0<a <1,b >0D .0<a <1,b <07.设A ={x |x 2+x -6=0},B ={x |ax +1=0},满足AB ,则a 取值的集合是 ( )A .{31,21-}B .{21-} C .{31} D .{31,21,0-}8.已知f (x )是一次函数,且2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )的解析式为( ) A.3x -2 B.3x +2 C.2x +3 D.2x -39. 已知函数f (x )=⎩⎨⎧0≤ 30log 2x x f x x ),+(>,,则f (-10)的值是( ).A .-2B .-1C .0D .110.设f(x)为定义在R 上的奇函数.当x>0时,f(x)=2x +2x+b(b 为常数),则f(-1)等于( ).A.-3B.-1C.1D.311.已知2lg(x -2y )=lg x +lg y ,则xy 的值为( ) A.1B.4C.1或4D. 14 或412.方程2x =2-x 的根所在区间是( ).A .(-1,0)B .(2,3)C .(1,2)D .(0,1)二.填空题:(本大题共4小题,每小题5分,共20分)13. 求满足1)21(+x >x -24的x 的取值集合是14. 设1.52.42.46.0,7.0,6.0===c b a ,则c b a ,,的大小关系是 15. .若定义在区间(-1,0)内的函数f (x )=log 2a (x +1)满足f (x )>0,则a 的取值范围是__ _16. 已知函数()()2,1在m x e x f x -+=内有零点,()()()6,4ln 在m x x g -=内有零点,若m 为整数,则m 的值为 三.解答题:(本大题共6小题,共70分) 17.(12分)计算下列各式的值:(1)()31213125.0141027.010833818730081.0⨯-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+∙⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯------(2)()4log 18log 2log 3log 166626∙+-18. (12分)集合{}{}121,52-≤≤+=≤≤-=m x m x B x x A 。
唐山市2015―2016学年度高三年级第二次模拟考试文科数学试题参考答案_图文

(19)解: A E D A E B C B M N C D (Ⅰ)分别取 BE,CE 中点 M,N,连接 AM,MN,DN,由已知可得△ABE,△DCE 均为腰长为 4 的等腰直角三角形,所以 AM⊥BE,且 AM=2 2.又∵平面 ABE⊥平面 BCE,且交线为 BE,∴AM⊥平面 BEC,同理可得:DN⊥平面 BEC,且 DN=2 2.∴AM∥DN,且AM=DN,∴四边形 AMND 为平行四边形.∴AD∥MN,又∵MN平面 BEC,AD / 平面 BEC,∴AD∥平面 BEC.(Ⅱ)点 E 到平面 ABC 的距离,也就是三棱锥 E -ABC 的高 h.连接 AC,MC,在 Rt△EMC 中有 MC= EM2+EC2=2 10,在 Rt△AMC 中有 AC= AM2+MC2=4 3.可得 AC2+AB2=BC2,所以△ABC 是直角三角形.B A E M C D …6 分 1 1 1 1 由 VE—ABC=VA—BEC 得 ·AB·AC·h= · BE·EC·AM, 3 2 3 2 4 6 可知 h=. 3 4 6 ∴点 E 到平面 ABC 的距离为. 3 (20)解:(Ⅰ)设 l:x=my+4,A(x1,y1,B(x2,y2.将 x=my+4 代入 y2=4x 得 y2-4my-16=0,y1+y2=4m,y1y2=-16.…3 分 y1 4y1 4y1 4 4 kAM=== 2 =,同理 kBM=, x1+4 y2 + 16 y - y y y - y y - y1 1 2 1 2 2 1 1 所以 kAM+kBM=0.高三文科数学答案第 6 页共4页…12 分…6 分(y1-y22 16m2+64 k 4 (Ⅱ)===-m+≥4, kAM·kBM -16m -16m -m 当且仅当 m=-2 时等号成立, k 故的最小值为 4. kAM·kBM (21)解: 2 k x +(1-kx-k (x+1(x-k (Ⅰ)f (x=x+1-k-==, x x x …12 分(ⅰ)k≤0 时,f (x>0,f (x在(0,+∞上单调递增;(ⅱ)k>0 时,x∈(0,k,f (x<0;x∈(k,+∞,f (x>0,所以 f (x在(0,k上单调递减,f (x在(k,+∞上单调递增.2 …5 分 3 3 k 3 (Ⅱ)因 k>0,由(Ⅰ)知 f (x+k2-的最小值为 f (k+k2-=+k-kln k-, 2 2 2 2 k2 3 k 3 由题意得+k-kln k-<0,即+1-ln k-<0. 2 2 2 2k 2 k 3 1 1 3 k -2k+3 令 g (k=+1-ln k-,则 g (k=-+ 2=>0,2 2k 2 k 2k 2k2 …8 分所以 g (k在(0,+∞上单调递增,又 g (1=0, k2 3 所以k∈(0,1时,g (k<0,于是+k-kln k-<0; 2 2 k2 3 k∈(1,+∞时,g (k>0,于是+k-kln k->0. 2 2 故 k 的取值范围为 0<k<1.(22)解:(Ⅰ)因为AE 与圆 O 相切于点 A,所以∠CAE=∠CBA;因为四边形 ABCD 内接于圆 O,所以∠CBA=∠ADE;又已知∠ADE=∠BDC,所以∠BDC=∠CAE,故 A,E,D,F 四点共圆.(Ⅱ)由(Ⅰ)得∠ADE=∠AFE=∠BDC,又∠BDC=∠BAC(同弧所对的圆周角相等),所以∠AFE=∠BAC,故 AB∥EF.(23)解:x=1+cos φ,(Ⅰ)由(φ 为参数,0<φ<π)得(x-12+y2=1(0<y≤1),y=sin φ.π 所以曲线 C1 的极坐标方程为ρ=2cos θ(0<θ<).…5 分 2 高三文科数学答案第 7 页共4页…12 分…5 分…10 分(Ⅱ)由题意可设A(ρ1,θ,C(2,θ(0<θ <π ), 2 则|AC|=2-ρ1=2-2cos θ,|BC|=2+ρ1=2+2cos θ,所以|AC|·|BC|=4sin2θ∈(0,4.…10 分(24)解:1-3x, x<-1,(Ⅰ)当 m=2 时,f (x=3-x,-1≤x≤1,3x-1, x>1. 5 =f (-1=4, 3 5 得 f (x<4 的解集为 x|-1<x<. 3 由 f (x的单调性及f ( y { } …5 分(Ⅱ)由f (x≥2m 得|x+1|≥m (2-|x-1|,因为 m<0, 1 所以- |x+1|≥|x-1|-2, m 在同一直角坐标系中画出 1 y=|x-1|-2 及 y=- |x+1|的图像, m 1 根据图像性质可得-≥1,即-1≤m<0, m 故 m 的最小值为-1.-1 -2 O 1 3 x …10 分高三文科数学答案第 8 页共4页。
2015高三数学理科西城二模解析

π π f x f x =4 2 2
③显然 f x 是增函数,所以
故选①②
注:第 10,11,12 题第一问 2 分,第二问 3 分;第 14 题多选、漏选或错选均不得分.
又因为 A1 E ⊥ DE , DC DE D , 所以 A1 E ⊥ 平面 BCDE 4分
⑵ 解 : 因 为 A1 E ⊥ 平 面 BCDE , DE ⊥ BE , 所 以 A1 E,DE ,BE 两 两 垂 直 , 以
EB ,ED ,EA1 分别为 x 轴、 y 轴和 z 轴,如图建立空间直角坐标系, 5 分
2 0 2 1 C5 C5 2 C0 2 C1 5 5C5 5 C5 P ( X 2) , , P ( X 1) , 2 2 2 C10 9 C10 9 C10 9
……8 分
所以 X 的颁布列为:
X P
0
2 9
1
5 9
2
2 9
5 2 所以 E ( X ) 0 1 2 1 . 9 9 9
x2 2x 4 1 4 1 x 2 4
2
1分
x 1 3 1 4 1 x 2 4
2 2
求导,得 f x
0,
4分
2 , 所以函数 f x 在区间 , 2 ,2 , 2 , 上单调递减.5 分
5.
64 4 x 2 64 64 , 即x4 当且仅当 4 x 4x 2 4 64 32 , x x x
6.
(a1 a21 ) 21 21 ,所以选 B. 2
2015届高三第二次月考试卷(正稿)

浏阳六中2015届高三第二次月考试卷(理科数学)(时量:120分钟 满分:150分)、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
R ,集合 A {x|x(x 3)0},则 C R A=(0 ”是“ ABC 为直角三角形”的()B •必要不充分条件D •既不充分又不必要条件点() A .向左平移一个单位长度,再把所得各点的横坐标缩短为原来的6 B. 向右平移一个单位长度,再把所得各点的横坐标缩短为原来的 6 C. 向左平移一个单位长度,再把所得各点的横坐标伸长为原来的 6 D. 向右平移一个单位长度,再把所得各点的横坐标伸长为原来的 65 .设a, b 是两个非零向量,则下列结论不正确的是()A.若存在一个实数 k 满足a kb ,则a 与b 共线C. a bA. ( ,0) U (3,)B. (,3]C.[0,3]D. (0,3)3.设m,n 是两条不同的直线,是两个不同的平面,给出下列条件,能得到m 的是A ., m B . m C . m n, n D . m// n,nx4.为了得到函数y 2sin (), xR 的图像,只需把函数2sin x, x R 的图像上所有的B.若ab ,则a1.已知全集U uuu uuur2.在 ABC 中,“ AB BC A .充分不必要条件C •充要条件1 一 、倍(纵坐标不变)31 一 、倍(纵坐标不变)3倍(纵坐标不变)D.若a 与b 为两个方向相同的向量r r rr a b ab,则 6.若变量 x, y 满足约束条件 x A.0 B. 1 C. 2 3 0 1 0,则 y 1 D. -2 2x 的最大值为( )记 APB ,则 sin2 的值是()16 63 16 16 A . B . C . D . —65 65 63 652 3 4sin( x x xx8.已知函数 f(x) 1 x2 3 4)( 0)的部分图象如右图所示, ,代B 是图象与x 轴的交点, 7 .函数y 设P 是图象的最高点 2011x2011则下列结论正确的是(A. f (x)在(—1,0)上恰有两个零点B. f (x)在(0,1) 上恰有一个零点C. f (x)在(—1,0)上恰有一个零点D.f (x)在(0,1)上恰有两个零点9.已知函数f (x) 2x 3 x 1,函数 1 0, 2g(x) a sinx2a 2 a 0,若存6在为风 0,1 ,使得f (xd X 2成立,则实数 a 的取值范围是(A. 1 2 10.式子 (a,b,c)满足(a,b, c) (b,c,a) (c, a, b), 则称 (a,b,c)为轮换对称式.给出如下三个式子:① (a,b, c) abc ;②(a,b,c) a 2b 2③(A, B,C) cosC cos(A B) 2cos C (代 B,C 是ABC 的内角).其中,为轮换对称式的个数是( A . 0B .1) C . 2恒成立,则k的最大值是_________ .15. 如图,在正方形ABCD中,已知N为正方形内(含边界)任意一点,则AB 2 , M为BC的中点,若uuuu UULTAM AN的取值范围是 __________三、解答题:本大题共6小题,共75分•解答应写出文字说明、证明过程或演算步骤.16 .(本小题满分12分)在厶ABC中,角A, B , C所对的边分别为a,b,c,已知函数1f(x) cosx cos(x A) cosA (x R).(i)求函数f(x)的最小正周期和最大值;(n)若函数f (x)在x 处取得最大值,求a(cos B cosC)的值.3 (b c)sin A17.(本题满分12分)在等差数列{a n}中,a= 3,其前n项和为S n,等比数列{b n}的各项均为正数,b1= 1,公比为q,且b2 + S2= 12, q =芝.(I)求{a n}与{b n}的通项公式;1 1 1 1 2(n)证明:3韦 + S2+ (3)18.(本小题满分12分)已知函数fx x22x a I nx , a R.(I )当a 4时,求f (x)的极值;;(n )若f x在区间(0,1)上无极值点,求a的取值范围;二、填空题:本大题共5小题,每小题5分,L 2 511.已知.3 cosx sin x ,贝U cos(——3 6(单位:cm )如下图12 .某几何体的三视图2cm .1 x213.已知函数y若g x 1 f x 1,则g共25分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西街中学2015—2016学年度高三第2次月考 英语试题 本试题分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试用时120分钟。 第I卷 第一部分 听力(共两节,满分30分)
第一节 (共5小题;每小题1.5分,满分7.5分) 听下面5段对话。每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。听完每段对话后,你都有10秒钟的时间来回来有关小题和阅读下一小题。每段对话仅读一遍。 1.What will Mary do on weekends? A.Work at the store. B.Read some books. C.Go to the seaside. 2.What does the man imply? A.He is busy with school. B.He plays tennis perfectly. C.He doesn't like the weather. 3.What can we learn from the conversation? A.The woman has been to Paris. B.The man lives in Paris now. C.The man used to live in London. 4.What is the woman? A.A teacher. B.A doctor. C.A student. 5.How many people will attend the party? A.15. B.135. C.150. 第二节 (共15小题;每小题1.5分,满分22.5分)
听下面5段对话或独白。每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。每段对话或独白读两遍。 听下面一段对话,回答第6和第7两个小题。 6.What happened to the man? A.His bike was hit by a car. B.He got injured in a car accident. C.The wheels of his bike were stolen. 7.When did the accident take place? A.This morning. B.Last weekend. C.Last Monday. 听下面一段对话,回答第8至第10三个小题。 8.In which season does the man probably feel lazy? A.Spring. B.Autumn. C.Winter. 9.What does the woman think of the summer evenings? A.Hot. B.Boring. C.Comfortable. 10.How does the woman get through the hot daytime? A.By staying indoors. B.By walking in the park. C.By taking a cold shower. 听下面一段对话,回答第11至第13三个小题。 11.Where is Hans now? A.In Germany. B.In America. C.In France. 12.How long had Hans studied music before getting married? A.3 years. B.6 years. C.8 years. 13.What do we know about Hans? A.He began to study English since high school. B.He hasn't played soccer for many years. C.He studied music since the 5th grade. 听下面一段对话,回答第14至第17四个小题。 14.How did the man know about the hotel? A.From a friend. B.From the Internet. C.From a guide book. 15.What was good about the hotel? A.The smell. B.The bed. C.The appearance. 16.Why did the man keep the windows shut? A.To keep quiet. B.To avoid the dust. C.To make the room warm. 17.What was the result of the man's complaint? A.He was given a free one-night stay. B.He was offered a discount. C.He got his money back. 听下面一段独白,回答第18至第20三个小题。 18.What is the prize of the competition? A.A visit to the radio station. B.A job offer in Europe. C.A trip to Europe. 19.What does the speaker say about the story? A.It cannot be fiction. B.It must be over 1,000 words long. C.It can be something that one hasn't experienced. 20.What is the closing date for entries? A.October 1st. B.October 15th. C.October 25th.
第二部分 阅读理解(共两节,满分40分) 第一节 (共15小题;每小题2分,满分30分) 阅读下列短文,从每题所给的四个选项(A、B、C、和D)中,选出最佳选项,并在答题卡上将该项涂黑。 A Figuring out how to lose weight is a challenge for many of us, particularly considering that the quickest path to weight loss is different for everyone. Of course, the common methods are always proper diet and exercise, which not only work in weight loss, but also keep a body healthy. Of course you've heard this before — the challenge is to follow through. Others have lost weight by following these simple guidelines, and so can you. Set small, practical goals. If you have a lot of weight to lose, try for 5 pounds, relax a bit and then go for 5 more. Start a regular exercise program and stick with it. Don't be afraid of those sweat suits and pants! Do extra exercise in addition to your regular program. Park at the far end of the parking lot and walk; take the stairs instead of the lift. Healthy foods are an important ingredient in losing weight. Eat low-fat, high-fiber foods such as salads and vegetables pastas. Choose foods that you like. Learn to prepare healthful, low-calorie foods that taste good by checking healthy cook books for new recipes. Eating well doesn't have to mean eating dull. Eat smaller, more frequent meals. This way, your body starts to increase its metabolism(新陈代谢) so that calories are burned faster. Also, mini-meals can prevent overeating. Plan ahead and keep a food diary. Keep the fridge stocked with healthy foods such as vegetables and fruit, and you'll be less likely to run out for high-calorie, high-fat junk food. This will help you know where you can improve your diet. 21. The underlined words “stick with it” in the third paragraph can best be replaced by “______ ”. A. put it in a place carelessly B. continue doing it C. finish doing it quickly D. give up doing it 22. Which of the following should be kept in your fridge if you want to lose weight according to the passage? A. Butter B. Chocolates C. Hamburgers. D. Apples 23. What is the best title for the passage? A. How to lose weight B. How to cook healthy foods C. How to exercise to lose weight D. How to eat to lose weight
