福州最牛,厦门一中榜上有名:2022年NOIOnline能力测试福建学生成绩公示
第二十二届全国中学生生物学竞赛福建赛区

张金言
厦门外国语学校
陈敏
叶从鑫
古田一中
陆晓燕
施悦雯
厦门一中
张琦
林丹彤
漳州立人学校
曾祥辉杜平英
江陈艳
厦门一中
兰福彬
蒋倩倩
龙岩一中
钟圣
汪杰
浦城一中
甘萍金建芳
王钰玺
安溪一中
余联金林进旺
李安莉
永定一中
李富丽曹水香
三
等
奖
(65名)
黄铎
厦门六中
洪彩凤陈丽环
蔡星星
晋江一中
卢晖陈晓佳
郭逸青
漳州立人学校
张朝胜曾祥辉
张硕刘冰妍
蔡熙阳
莆田一中
朱嘉冀
陈军
莆田二中
陈丽钦黄贞贞
许梅榕
莆田二中
陈丽钦黄贞贞
吴嘉彬
厦大附中
梁军胡福评
郭正元
福安一中
黄爱芳施淑娟
李铭坚
泉州一中
刘剑平张玲玲
郭晓婷
厦门一中
林静
洪佳铭
莆田二中
陈丽钦黄贞贞
石炜贤
漳州正兴学校
杨惠敏赵碧华
许唯佳
诏安一中
陈喜容沈宝明
朱海清
厦门外国语学校
陈敏
卫楷
陈泽众
连城一中
杨德胜吴金鸾
张一佳
泉州七中
卢晓剑黄小燕
陈琳燕
仙游一中
黄玉清
郭灵韵
漳州一中
陈颖芳黄静娜
沈艳琼
南安一中
马华章江海泉
陈志君
漳州立人学校
张朝胜杜平英
杨柏炜
诏安一中
沈宝明陈细容
二
等
2021-2022学年福建省厦门第一中学高一上学期入学考试数学试题(解析版)

2021-2022学年福建省厦门第一中学高一上学期入学考试数学试题一、单选题1 ) A .2± B .4±C .2D .4【答案】A【解析】,所以所求为4的平方根,按平方根的定义计算即可.【详解】,4的平方根为2±. 故选:A【点睛】本题考查平方根的计算,解题的关键是认真审题,本题属于基础题.2.据厦门中学生助手微信公众号统计,2020年厦门市全社会用于基础建设的资金约为100553000000元,这个数用科学记数法表示为( ) A .1.00553×1010元; B .1.00553×10 11 元; C .1.00553×1012元; D .1.00553×1013元【答案】B【分析】直接用科学计数法法表示即可.【详解】解:根据科学计数法可知:11100553000000 1.0055310=⨯, 所以,这个数用科学记数法表示为111.0055310⨯元. 故选:B3.已知,a b 满足方程组51234a b a b +=⎧⎨-=⎩,则a b +的值为( )A .4B .﹣4C .2D .﹣2【答案】A【分析】解方程得2b =,2a =,再计算a b +即可.【详解】解:因为51234a b a b +=⎧⎨-=⎩,所以3153634a b a b +=⎧⎨-=⎩,所以1632b =,即2b =,所以1252a b =-=, 所以4a b += 故选:A4.如图是一块长、宽、高分别为6cm 、4cm 、3cm 的长方体木块,一只蚂蚁要从长方体木块的一个顶点A 处,沿着长方体的表面到长方体上和A 相对的顶点B 处吃食物,那么它需要爬行的最短路径的长是()A.97cm B.85cm C.9cm D.(3213)+cm 【答案】B【分析】把这个长方体中蚂蚁所走的路线放到一个平面内,在平面内线段最短,结合勾股定理,即可求解.【详解】第一种情况:把所看的前面和上面组成一个平面,如图所示,则这个长方形的长和宽分别为9和4,所以所走的路程最短线段为229497;第二种情况:把看到的左面与上面组成一个长方形,如图所示,则这个长方形的长和宽分别为7和6,所以所走的路程最短线段为227685;第三种情况:把看到的前面与右面组成一个长方形,如图所示,则这个长方形的长和宽分别为10和3,所以所走的路程最短线段为22+=;103109故选:B.5.函数2和在同一直角坐标系内的图象可以是()y ax b y ax bx c=+=++A .B .C .D .【答案】C【分析】分类讨论,0a >和0a <时,由一次函数的单调性与二次函数图象的开口方向,排除一些选项,再由b 的正负,确定二次函数对称轴的位置,从而可得最后结果. 【详解】若a >0,则一次函数y =ax +b 为增函数,二次函数y =ax 2+bx +c 的开口向上,故可排除A ;若a <0,同理可排除D. 对于选项B ,由直线可知a >0,b >0,从而02ba-<,而二次函数的对称轴在y 轴的右侧,故应排除B. 故选:C.6.一同学在n 天假期中观察: (1)下了7次雨,在上午或下午; (2)当下午下雨时,上午是晴天; (3)一共有5个下午是晴天; (4)一共有6个上午是晴天. 则n 最小为( ) A .7 B .9C .10D .11【答案】B【分析】可假设上下午下雨的天数,然后计算出上下午晴天的天数,直到找到符合题意的情况,可得答案.【详解】假设上午或下午下了7次雨,则应有下午或上午下雨0次,即下午或上午有7个是晴天,与一共有5个下午是晴天以及一共有6个上午是晴天都不符合,故假设不成立;假设上午或下午下了6次雨,则应有下午或上午下雨1天,即下午或上午有6个是晴天,与一共有5个下午是晴天不符合,故假设不成立;假设上午或下午下了5次雨,则应有下午或上午下雨2天,即下午或上午有5个是晴天,与一共有6个上午是晴天不符合,故假设不成立;假设上午或下午下了4次雨,则应有下午或上午下雨3天,那么都加上3个上下午都晴天,即上午晴6天,下午晴7天,与题意不符合,故假设不成立;故假设下午下了4次雨,则应有上午下雨3天,那么都加上2个上下午都晴天,即有5个下午是晴天,有6个上午是晴天,与题意都符合,故n 最小为4329++= ; 故选:B7.已知(3)1y x x a =-+-+是关于x 的二次函数, 当x 的取值范围在15x ≤≤时,y 在1x =时取得最大值,则实数a 的取值范围是( )A .9a =B .5a =C .9a ≤D .5a ≤【答案】D【分析】由题知对应的二次函数开口向下,对称轴为32ax -=-且在15x ≤≤时,y 随着x 的增大而减小,进而解不等式312a--≤即可得答案. 【详解】解:()2(3)131y x x a x a x =-+-+=---+,开口向下,对称轴为32ax -=-, 因为当x 的取值范围在15x ≤≤时,y 在1x =时取得最大值, 所以,x 的取值范围在15x ≤≤时,y 随着x 的增大而减小, 所以312ax -=-≤,解得5a ≤. 所以,实数a 的取值范围是5a ≤. 故选:D8.正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,正方形BEFG 的边长为4,则DEK 的面积为( )A .10B .12C .14D .16【答案】D【分析】根据题意,连接,,BD GE FK ,则////BD GE FK ,进而得GDEGBES S=,GEKGEFSS=,再计算面积即可得答案.【详解】解:如图,连接,,BD GE FK ,则////BD GE FK , 所以,在梯形BEGD 中,GDEGBES S=(等底等高),在梯形GEKF 中,GEKGEFS S=(等底等高)所以,16GDEGEKGBEGEFBEFGDEKSSS SSS +=+===.故选: D9.如图,矩形ABCD 的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数241k k y x++=的图像上,若点A 的坐标为(2,3)--,则正数k 的值为( )A .1B .2C .4D .5【答案】A【分析】设()00,C x y ,进而根据题意得006x y =,即200416k x y k =+=+,再解方程即可得答案.【详解】解:设()00,C x y ,因为矩形ABCD 的对角线BD 经过坐标原点,点A 的坐标为(2,3)--所以,设直线BD 的方程为()0y mx m =≠,()()002,,,3B y D x --,所以0023y m mx =-⎧⎨-=⎩,所以006x y =,因为点C 在反比例函数241k k y x++=的图像上,所以200416k x y k =+=+,即2450k k +-=,解得1k =或5k =-(舍)所以,正数k 的值为1k =. 故选:A10.如图,AB 是⊙O 的直径, 点C 是⊙O 上一点,AD 与过点C 的切线垂直,垂足为D ,直线DC 与AB 的延长线交于点P ,弦CE 平分ACB ∠,交AB 于点F ,连接BE ,72BE =.下列四个结论:①AC 平分DAB ∠;②2·PF PB PA=;③若12BC OP =,则阴影部分的面积为749π344-;④若24PC =,则3tan 4PCB ∠=.其中正确的是( )A .①②B .③④C .①②④D .①②③【答案】C【分析】连接OC ,结合切线的性质得//OC AD ,进而根据平行线的性质判断①;根据几何关系证明PC PF =,再根据PCB PAC △△得2PC PB PA =⋅判断②;连接AE ,根据几何关系证明OBC 是等边三角形,进而计算阴影部分面积判断③;由PCB PAC △△得tan tan BC PBPCB PAC AC PC∠=∠==,再设PB x =,则14PA x =+,根据2PC PB PA =⋅解得18PB =,进而可判断④;【详解】解:对于①,连接OC ,OA OC =,OAC OCA ∴∠=∠, ∵PC 是圆O 的切线,AD CD ⊥,∴90OCP D ︒∠=∠=,∴//OC AD , ∴CAD OCA OAC ∠=∠=∠,即AC 平分DAB ∠,故①正确; 对于②,∵AB 是直径,∴90ACB ︒∠=,90PCB ACD ︒∴∠+∠=, 又90CAD ACD ︒∠+∠=,CAB CAD PCB ∴∠=∠=∠,又,ACE BCE PFC CAB ACE ∠=∠∠=∠+∠,PCF PCB BCE ∠=∠+∠,PFC PCF ∴∠=∠,PC PF ∴=,∵P ∠是公共角,PCB PAC ∴△△,::PA C PB PC P =∴,2P PC B PA =∴⋅,即2PF PB PA =⋅,故②正确;对于③,连接AE ,∵ACE BCE ∠=∠,∴AE BE =,∴AE BE =,又∵AB 是直径,∴90AEB ︒∠=,∴227214AB BE ==⨯=,∴7OB OC ==,∵PD 是切线,∴90OCP ︒∠=,∵12BC OP =,∴BC 是Rt OPC 的中线,∴BC OB OC ==,即OBC 是等边三角形,∴60BOC ︒∠=, ∴24960493,743606BOC BOC S S ππ==⨯⨯=△扇形, ∴ 阴影部分面积为4949364π-,故③错误; 对于④,PCB PAC △△,∴PB BCPC AC=,tan tan BC PB PCB PAC AC PC ∴∠=∠==, 设PB x =,则14PA x =+,2P PC B PA =∴⋅,224(14)x x ∴=+,解得1218,32x x ==-,18PB ∴=,183tan 244PB PCB PC ∠===,故④正确. 故选:C二、双空题11.如图,在平面直角坐标系xOy 中,把由两条射线AE ,BF 和以AB 为直径的半圆所组成的图形叫作图形C (注:不含AB 线段).已知(1,0),(1,0)A B -,AE ∥BF ,且半圆与y 轴的交点D 在射线AE 的反向延长线上.①当一次函数y=x+b 的图象与图形C 恰好只有一个公共点时,b 的取值范围为_________;②已知平行四边形AMPQ (四个顶点A ,M ,P ,Q 按顺时针方向排列)的各顶点都在图形C 上,且不都在两条射线上,则点M 的横坐标x 的取值范围为_________. 【答案】 2b =11b -<<; 21x -<<-或20x ≤<. 【分析】根据直线与半圆的交点个数,讨论y x b =+的位置并确定边界情况下b 的值,即可得参数范围;讨论M 在射线AE ,AD 上以及G 为BD 中点,M 在DG 、GB ,射线BF 上,结合已知条件判断是否有满足要求的平行四边形AMPQ 即可.【详解】由图知:若y x b =+在射线,BF AE 之间时,与图形C 恰好只有一个公共点, 当BF 与y x b =+重合,1b =-; 当AE 与y x b =+重合,1b =;若y x b =+与图形C 12=,即2b = 又y x b =+过一、二、三象限,故2b =综上,2b =11b -<<时,一次函数y=x+b 的图象与图形C 恰好只有一个公共点. 1、当M 在射线AE 上,A ,M ,P ,Q 按顺时针方向排列,则PQ 必在AM 上方,即,P Q 在AM 上不含,A M 两点,所以02PQ <<,而//AM PQ 且AM PQ =,故02AM <<21x -<<-; 2、当M 在AD 上,则PQ 必在AM 下方,结合题图,不存在满足条件的平行四边形AMPQ ; 3、如下图,若G 为BD 中点,连接OG ,当M 在DG 上,过M 作MQ OG ⊥交BD 于Q ,则OG 垂直平分MQ ,再连接A 和其垂足并延长交射线BF 于P ,此时,四边形AMPQ 为平行四边形,满足题设,则20x ≤4、当M 在上图GB 上,则PQ 必在AM 下方,结合上图,不存在满足条件的平行四边形AMPQ ;5、当M 在射线BF 上,则PQ 必在AM 下方,此时P 与B 重合,Q 在射线AE 上,显然不满足A ,M ,P ,Q 不都在两条射线上,不存在满足条件的平行四边形AMPQ ; 综上,21x -<<-或202x ≤<. 【点睛】关键点点睛:判断是否存在平行四边形AMPQ 时,注意讨论M 的位置情况,根据平行四边形的性质判断不同情况下是否可以找到满足条件的平行四边形. 三、填空题 120,21x >-且5x y +=,则x 的取值范围是______. 【答案】172x << 【分析】021x >-,根据分式、根式的性质列不等式组求x 的范围即可. 【详解】0,21x >- 所以70210x x ->⎧⎨->⎩,可得172x <<.故答案为:172x << 13.操场上站成一排的100名学生进行报数游戏,规则是:每位同学依次报自己的顺序数的倒数加1.如:第一位同学报111+,第二位同学报112+,第三位同学报113+,……这样得到的100个数的积为__________. 【答案】101【分析】用数学符号表示出每位同学的报数,再直接相乘即可. 【详解】设第n 位同学的报数为n a ,则111n n a n n+=+=, 则121002310110112100a a a ;故答案为:101.14.为了参加中考体育测试,厦门中学的甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传球三次.三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?____.(填:甲或乙或一样大) 【答案】乙【分析】根据古典概型概率公式计算可得.【详解】三次传球后,所有可能结果为:(乙、甲、乙)、(乙、甲、丙)、(乙、丙、甲)、(乙、丙、乙)、(丙、甲、乙)、(丙、甲、丙)、(丙、乙、甲)、(丙、乙、丙), 球回到甲脚下的概率:14P =; 球回到乙脚下的概率:38P =; 所以球回到乙脚下的概率大. 故答案为:乙.15.如图是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图中∠ACB =20°)时最为合适,已知货车车厢底部到地面的距离AB =1.5m ,木板超出车厢部分AD =0.5m ,则木板CD 的长度为________.(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m ).【答案】4.9m【分析】根据ACB ∠的正弦函数和AB 的长度求AC 的长,再加上AD 即可. 【详解】解:由题意可知:AB BC ⊥.∴在Rt ABC △中,sin AB ACB AC∠=, 1.5 1.54.39sin sin 200.3420AB AC ACB ∴===≈∠︒,4.390.5 4.89 4.9(m)CD AC AD ∴=+=+=≈.故答案为:4.9m.16.如图所示,正方形ABCD的面积为12,ABE△是等边三角形,点E在正方形ABCD 内,在对角线AC上有一点P,使PD PE+的和最小,则这个最小值为______.【答案】23【分析】连接PB,由正方形的对称性可知PB PD=,所以PD PE PB PE BE+=+≥,求出BE的长可知答案【详解】连接PB,因为正方形ABCD的面积为12,所以1223AB==,因为ABE△是等边三角形,所以23BE AB==,因为P为正方形ABCD对角线AC上一点,所以PB PD=,所以23PD PE PB PE BE+=+≥=,当,,B P E共线时取等号所以PD PE+的最小值为23,故答案为:23四、解答题17.计算(先化简,再求值):223122111a a aa a--+--+1-5a=【答案】1【分析】根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.【详解】解:∵a =1<,∴10a -<, 原式=22312211a a a a -----=()21111a a a a a -++-- =11-1a a - =1(1)a a -=1 ∴原式的值为1.18.已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根.(1)是否存在实数k ,使得()()12123222x x x x --=-成立?若存在,求出k 的值;若不存在,请说明理由; (2)求使12212x x x x +-的值为整数的实数k 的整数值. 【答案】(1)存在,95k = (2)235k =---,,【分析】(1)利用反证法先假设存在实数k ,使得()()12123222x x x x --=-成立,根据一元二次方程有两个实数根可得95k =,因此原假设不成立,故不存在; (2)根据题意()22212121221121244224411x x x x x x k x x x x x x k k +++-=-=-=-=-++,可得1k +能被4整除,即可求出k 的值.【详解】(1)假设存在实数k ,使得()()12123222x x x x --=-成立,一元二次方程24410kx kx k -++=的两个实数根,()2400Δ(4)441160k k k k k k ≠⎧∴⇒<⎨=--⋅+=-⎩,(不要忽略判别式的要求), 由韦达定理得1212114x x k x x k +=⎧⎪+⎨=⎪⎩,()()()()2221212121212129322252942k x x x x x x x x x x x x k +∴--=+-=+-=-=-, 95k ⇒=但0k <,∴不存在实数k ,使得()()12123222x x x x --=-成立.(2)()22212121221121244224411x x x x x x k x x x x x x k k +++-=-=-=-=-++, ∴要使其值是整数,只需要1k +能被4整除,故1124k +=±±±,,,即021335k =---,,,,,, 0k <,235k ∴=---,,.19.某校九年级共有80名同学参与数学科托底训练.其中(1)班30人,(2)班25人,(3)班25人,厦门中学生助手在托底训练后对这些同学进行测试,并对测试成绩进行整理,得到下面统计图表.班级平均数中位数 众数(1)班 75.2 m 82 (2)班 71.2 68 79 (3)班 72.87575(1)表格中的m 落在________组;(填序号)①40≤x <50, ②50≤x <60, ③60≤x <70,④70≤x <80, ⑤80≤x <90, ⑥90≤x ≤100. (2)求这80名同学的平均成绩;(3)在本次测试中,(2)班小颖同学的成绩是70分,(3)班小榕同学的成绩是74分,这两位同学成绩在自己所在班级托底同学中的排名,谁更靠前?请简要说明理由. 【答案】(1)④ (2)73.2分(3)小颖在自己班级的排名更靠前,理由见解析 【分析】(1)根据成绩分布直方图判断即可; (2)结合表中数据,计算平均数即可; (3)根据表中的中位数大小分析判断即可.【详解】(1)解:根据题意,(1)班成绩在4050x ≤<内的有1人,在5060x ≤<内的有3人,在6070x ≤<内的有6人,在7080x ≤<内的有7人,此时共17人, 所以,(1)班成绩的中位数m 在7080x ≤<内,故选序号④.(2)解:根据题意,(1)班的平均成绩为75.2分,共30人,(2)班的平均成绩为71.2分,共25人,(3)班的平均成绩为72.8分,共25人, 所以,这80名同学的平均成绩为75.23071.22572.82573.280x ⨯+⨯+⨯==分.(3)解:小颖同学在自己班级的托底同学中排名更靠前.理由:因为7068>,所以小颖同学成绩处于自己班级托底同学的中上水平; 因为7475<,所以小榕同学成绩处于自己班级托底同学的中下水平,且这两个班的参加托底训练的人数相同,所以小颖在自己班级的排名更靠前.20.木匠黄师傅用长AB =3,宽BC =2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:方案一:直接锯一个半径最大的圆;方案二:圆心O 1、O 2分别在CD 、AB 上,半径分别是O 1C 、O 2A ,锯两个外切的半圆拼成一个圆;方案三: 沿对角线AC 将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆; 方案四:锯一块小矩形BCEF 拼到矩形AFED 下面,利用拼成的木板锯一个尽可能大的圆.(1)写出方案一中圆的半径;(2)通过计算说明方案二和方案三中,哪个圆的半径较大? (3)在方案四中,设CE =x (0<x <1),圆的半径为y . ①求y 关于x 的函数解析式;②当x 取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大. 【答案】(1)1 (2)方案三半径较大(3)①答案见解析;②x =12时,最大为54,方案四时可取的圆桌面积最大【分析】(1)直接利用CB 的长即可求出圆的半径.(2)分别利用勾股定理以及相似三角形的判定与性质得出两半径长进而求出答案. (3)首先得出所截出圆的直径最大为3x -或2x +两者中较小的一个,再利用一次函数增减性得出即可.【详解】(1)因为长方形的长宽分别为3,2,那么直接取圆直径最大为2, 则方案一中的半径最大为1;(2)如图1,方案二中连接O 1,O 2,过O 1作O 1E ⊥AB 于E ,方案三中,过点O 分别作AB ,BF 的垂线,交于M ,N ,此时M ,N 恰为⊙O 与AB ,BF 的切点.方案二:设半径为r ,在Rt △O 1O 2E 中,∵O 1O 2=2r ,O 1E =BC =2,O 2E =AB -AO 2-CO 1=3-2r , ∴(2r )2=22+(3-2r )2,解得1312r =. 方案三:设半径为r ,在△AOM 和△OFN 中,∵∠A =∠FON ∠OMA =∠FNO ,∴△AOM ∽△OFN , ∴OM FN AM ON =,∴23r r r r -=-,解得65r =. 比较知,方案三半径较大;(3)①∵EC =x ,∴新拼图形水平方向跨度为3-x ,竖直方向跨度为2+x . 类似(1),所截出圆的直径最大为3-x 或2+x 较小的.a .当3-x <2+x 时,即当1>x >12时,y =12(3-x ); b .当3-x =2+x 时,即当x =12时,y =12(3-12)=54;c .当3-x >2+x 时,即当0<x <12时,y =12(2+x ). ②当x >12时,y =12(3-x )<12(3-12)=54;当x =12时,y =12(3-12)=54;当x <12时,y =12(2+x )<12(2+12)=54,∴方案四中,当x =12时,y 最大为54.∵1<1312<65<54,∴方案四时可取的圆桌面积最大.21.已知:直角梯形OABC 中,BC ∥OA ,∠AOC =90°,以AB 为直径的圆M 交OC 于D ,E ,连结AD ,BD ,BE .(1)在不添加其他字母和线的前提下..............,直接..写出图1中的两对相似三角形. (2)直角梯形OABC 中,以O 为坐标原点,A 在x 轴正半轴上建立直角坐标系(如图2), 若抛物线223(0)y ax ax a a =--<经过点A .B .D ,且B 为抛物线的顶点. ①求抛物线的解析式.②在x 轴下方的抛物线上是否存在这样的点P :过点P 作PN ⊥x 轴于N ,使得△P AN 与△OAD 相似?若存在,求出点P 的坐标;若不存在,说明理由. 【答案】(1)△OAD ∽△CDB . △ADB ∽△ECB (2)①2y x 2x 3=-++;②存在,(-2,-5)【分析】(1)由圆周角定理知:90,ADB ∠=︒首先可联想到的相似三角形是,BCD DOA ,易知BAD BED ∠=∠,可得的另一对相似三角形是Rt ,Rt BAD BED ∠.(2)①根据抛物线的解析式,易求得,,B D A 的坐标,也就得到了,,,OA OD CD BC 的长,根据(1)中的相似三角形,即可根据对应的成比例线段求出a 的值,即可求出抛物线的方程. ②由①易得△OAD 为等腰三角形,根据抛物线的解析式设出P 点坐标,然后根据PN =AN 的条件来求出P 点坐标.【详解】(1)如图1,因为AB 为直径,所以90,ADB ∠=︒ 所以90,CDB ADO ∠+∠=︒ 因为90,OAD ADO ∠+∠=︒所以OAD CDB ∠=∠,又因为90C O ∠=∠=︒, 所以△OAD ∽△CDB.因为BAD BED ∠=∠,C ADB ∠=∠,所以△ADB ∽△ECB. △OAD ∽△CDB . △ADB ∽△ECB (2)①顶点B (1,-4a ), ∵△OAD ∽△CDB ,∴=DC CB OA OD又∵ax 2-2ax -3a =0,可得A (3,0) 又OC =-4a ,OD =-3a ,CD =-a ,CB =1, ∴133-=-a a ∴21a = ∵0a < ∴1a =- 故抛物线的解析式为:2y x 2x 3=-++ ②假设存在,设P (x ,-x 2+2x +3)∵△P AN 与△OAD 相似,且△OAD 为等腰三角形, ∴PN =AN ,当x <0(x <-1)时,-x +3=-(-x 2+2x +3),x 1=-2,x 2=3(舍去), ∴P (-2,-5).当x >0(x >3)时,x -3= -(-x 2+2x +3), x 1=0,x 2=3(都不合题意舍去) 符合条件的点P 为(-2,-5).22.如图,在矩形ABCD 中,46AB AD E ==,,是AD 边上的一个动点,将四边形BCDE 沿直线BE 折叠,得到四边形BC D E '',连接AC AD '',.(1)若直线DA 交BC '于点F ,求证:EF BF =; (2)当433AE AC D ''△是等腰三角形; (3)在点E 的运动过程中,求AC D ''△面积的最小值. 【答案】(1)证明见解析 (2)证明见解析 (3)4【分析】(1)根据题意证明FEB FBE ∠=∠即可证明结论;(2)分别过点A 作AG BC ⊥'于点G AH C D ⊥'',于点H ,进而根据几何关系证明AH 是C D ''垂直平分线即可证明结论;(3)作点A 关于BE 的对称点A ',点A '落在以点B 为圆心,以AB 为半径的弧AM 上.设弧AM 交BC 于点M ,过点A '作A N CD '⊥于N ,进而得当点A '落在点M 处时,A CD '的面积最小,再根据142AC D A CDSC DC SM '''=⋅==即可得答案.【详解】(1)证明:∵四边形ABCD 是矩形,∴//AD BC . ∴FEB EBC ∠=∠.根据对称可得FBE EBC ∠=∠, ∴FEB FBE ∠=∠.∴BF EF =.(2)证明:如图2,分别过点A 作AG BC ⊥'于点G AH C D ⊥'',于点H , ∵四边形ABCD 是矩形, ∴90BAD ∠=︒.∴433343tan AE A B B A E ===∠∴30ABE ∠=︒.∴9060FEB ABE ∠=︒-∠=︒. ∴60FBE FEB ∠=∠=︒.∴30ABG FBE ABE ∠=∠-∠=︒. ∴122AG AB ==. 根据对称可得90BC D C ∠''=∠=,C D CD ''=. ∴90BC D C GA C HA ∠''=∠'=∠'=. ∴四边形AGC H '是矩形. ∴2AG C H ='=.∴AH 是C D ''的垂直平分线. ∴AC AD '='.(3)解:根据对称可得点C '与点D '的对称点分别为点C D ,. 作点A 关于BE 的对称点A ',如图3.由对称性得ACDAC D BA BA ''''=≌,. ∴A CDAC DSS''=,点A '落在以点B 为圆心,以AB 为半径的弧AM 上.设弧AM 交BC 于点M ,过点A '作A N CD '⊥于N . 由垂线段最短知BA A N BM MC '+'≥+. ∵BA BM '=,∴A N MC '≥.∴当点A '落在点M 处时,A CD '的面积最小. 即A CD '的面积最小.此时2MC BC BM =-=.142AC D A CDSC DC SM '''=⋅==. ∴AC D ''△面积的最小值为4。
2022同安一中滨海校区喜报内容

2022同安一中滨海校区喜报内容
1、同安一中:
永远的神,无可替代!物理类5人进入全省前100名,历史类5人进入全省前100名,600分以上501人,特控上线率90%。
2、同安二中:
进步飞快,超常发挥!600分以上78人,物理类最高分649,历史类最高分625,特控上线率65.08%。
3、斗门一中:
稳居第三,中规中矩最高分646,特控上线率30%。
4、同安市实验中学:
600分以上5人,物理类最高分620,历史类最高分584,
特控上线率23.72%。
5、北师大同安附中最高分617。
6、同安一中平沙校区最高分630。
7、华中师大同安附中600分以上4人,物理类最高分619,历史类最高分602,特控上线率22.9%。
8、省实金湾学校物理类最高分592,历史类最高分576。
9、同安一中附属实验学校600分以上18人,物理类最高分680,
历史类最高分631,特控上线率19.9%。
作为一所民办公助学校,这个高考成绩足够亮眼。
第二十二届“希望杯”全国数学邀请赛厦门市八年级获奖情况公布
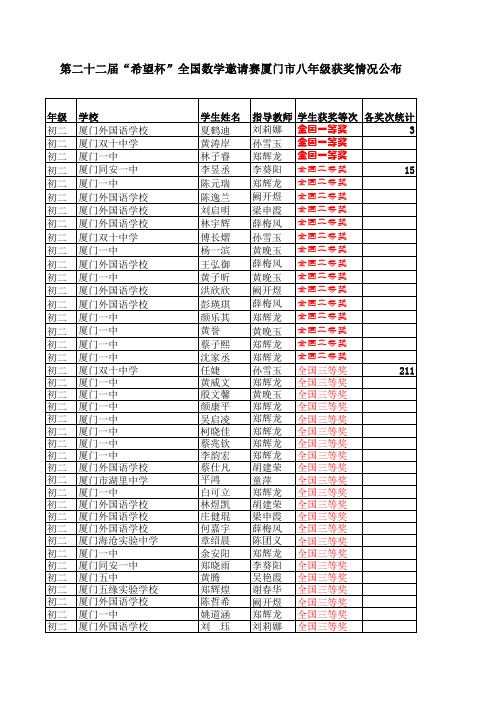
初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二 初二
厦门外国语学校 肖 宜 厦门外国语学校 郑润丰 厦门双十中学 张煜风 厦门双十中学 王晨霖 厦门十一中 张宇辰 厦门一中 吴凡 厦门一中 曾正 厦门一中 游路加 厦门一中 吴品萱 厦门同安一中 陈秀梅 厦门同安一中 高 恬 厦门同安一中 林 薇 厦门同安一中 黄雅兰 厦门同安一中 洪 妍 厦门同安一中 张剑岚 厦门同安一中 邵禹铭 厦门翔安一中 郭增佳 厦门英才学校 方艺鸿 厦门五缘实验学校 纪聪杰 厦门五缘实验学校 江薇 厦门五缘实验学校 曾昊 厦门外国语学校 陈 轲 厦门外国语学校 曲玥玥 厦门外国语学校 黄 宇 厦门双十中学 白若泰 厦门市莲花中学 王维 厦门市湖里区蔡塘学校 郑晓婷 厦门市槟榔中学 荆远方 厦门九中 卜昕月 厦门一中 陈见淳 厦门一中 陈嘉琪 厦门一中 许文熙 厦门一中 郑佳欣 厦门第六中学 涂锦程 厦门第六中学 李欧阳 厦门第六中学 刘雅文 厦门大同中学(兴华校区) 姚毓群 厦门同安一中 张睿 厦门市启悟中学 苏文宇 厦门五缘实验学校 刘航尔 厦门外国语学校 陈思曲 厦门外国语学校 阮聪逸 厦门市汀溪中学 叶栋梓 厦门一中 李途越 厦门一中 康梓屹 厦门五中 罗蔚榕 厦门五缘实验学校 刘豪
全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖 全国三等奖
福建省厦门第一中学2021-2022学年高二上学期暑假作业质量检查数学试题答案

x 24 .
5
(3)
设
a
与
3a
2b
的夹角为
,
则
a
(3a
2b )
3a
2
2a
b
12
6
6
,
则
cos
| aa|(|33aa22bb)|
6 26
1 2
,
第 1页,共 3页
又 0, ,
a
与
3a
2b
的夹角
.
3
18. 4 ,过程略 5
19. 解: (I )S 1 ab sin C 3 (a 2 b 2 c 2) ,所以
a
|
2
,
|
b
|
3.
a
b
|
a
|
|
b
|
cos120
2
3
(
1
)
3
,
2
|
3a
2b
|2
9
|
a
|2
4 |
b
|2
12a
b
36
,
|
3a
2b
|
6.
(2
)
若
b
垂直,
则
(
xa
b)
(a
3b )
xa2
(3x
1)a
b
3b 2
4x 27 (3x 1) (3) 24 5x 0 ,
AO 平面 A1BC ,则 AO A1B ;
(Ⅱ) 在平面 A1BC 内作 OH A1B 于 H,连接 AH,
AO 平面 A1BC , OH A1B ,
A1B AH ,
福建省一级达标高中名单

福建省一级达标高中名单
一、福州市(8所):
福州三中、福州八中、福州高级中学、福州格致中学、福州四中、福州二中、福清一中、长乐一中
二、厦门市(12所):
厦门一中、厦门双十中学、厦门六中、厦门外国语学校、厦门集美中学、厦门科技中学、同安一中、厦门翔安一中、厦门湖滨中学、厦门松柏中学、厦门十中、北师大厦门海沧附属实验中学
三、漳州市(7所):
漳州一中、龙海一中、龙海二中、漳州三中、长泰一中、云霄一中、诏安一中
四、泉州市(22所):
泉州一中、泉州五中、泉州七中、泉州培元中学、泉州城东中学、南安一中、南安国光中学、南安华侨中学、南安侨光中学、晋江养正中学、晋江季延中学、晋江侨声中学、晋江一中、晋江南侨中学、晋江毓英中学、永春一中、永春三中、安溪一中、惠安一中、德化一中、石狮石光中学、石狮一中
五、莆田市(8所):
莆田一中、莆田二中、仙游一中、莆田六中、莆田五中、莆田四中、莆田华侨中学、莆田十中
六、三明市(7所):
三明一中、三明二中、尤溪一中、大田一中、永安一中、三明九中、沙县一中
七、南平市(3所):
南平一中、建阳一中、邵武一中
八、龙岩市(7所):
龙岩一中、永定一中、漳平一中、武平一中、上杭一中、长汀一中、龙岩二中
九、宁德市(3所):
宁德一中、古田一中、福鼎一中
十、省属学校(2所):
福州一中、福建师大附中。
福建省厦门市2022-2023学年高一上学期学业水平测试数学试题(含解析)

2022-2023学年上学期高一年级学业水平测试数学试题满分:150分考试时间:120分钟考生注意:1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将答题卡交回.一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2,1,0,1,2A =--,{}|1B x x =≤≤,则A B = ()A.{}2,1,0,1-- B.{}1,0,1- C.{}0,1 D.{}2,1,0,1,2--【答案】B 【解析】【分析】根据集合,A B ,按照交集的定义直接运算即可.【详解】因为{}2,1,0,1,2A =--,{}|1B x x =≤≤,所以{}1,0,1A B =- .故选:B .2.已知命题2:0,0p x x ∀<>,则p 的否定是()A.20,0x x ∀<<B.20,0x x ∀<≤C.20,0x x ∃<<D.20,0x x ∃<≤【答案】D 【解析】【分析】根据含有量词的命题否定方法来求解.【详解】因为命题2:0,0p x x ∀<>,所以p 的否定是20,0x x ∃<≤.故选:D.3.已知lg 2,lg 3a b ==,则2log 12=()A.a +bB.2a -bC.2a b a+ D.2a b a+【答案】C 【解析】【分析】根据换底公式将2log 12写为lg12lg 2,再用对数运算法则展开,将lg 2,lg 3a b ==代入即可.【详解】解:因为lg 2,lg 3a b ==,而2lg12lg 4lg 32lg 2lg 32log 12lg 2lg 2lg 2a ba+++====.故选:C4.已知角α顶点在坐标原点,始边与x 轴非负半轴重合,终边与单位圆交于点34,55P ⎛⎫- ⎪⎝⎭,则πtan(π)cos 2αα⎛⎫--+ ⎪⎝⎭=()A.3215B.1115C.815-D.2915-【答案】A 【解析】【分析】通过三角函数定义得出角α的三角函数值,利用诱导公式化简表达式后求出数值.【详解】角α终边与单位圆交于点34,55P ⎛⎫- ⎪⎝⎭,则3cos 5α=-,4sin 5α=,4tan 3α=-.πtan(π)cos 2αα⎛⎫--+ ⎪⎝⎭4432tan sin 3515αα=-+=+=.故选:A.5.已知函数2()21xf x a =-+为奇函数,则不等式3()5f x <的解集为()A.(2,)-+∞B.(2,)+∞ C.(,2)-∞- D.(,2)-∞【答案】D 【解析】【分析】根据()f x 是奇函数求出参数a 的值,求解不等式.【详解】函数()f x 定义域为R ,又()f x 为奇函数,所以(0)10f a =-=,故1a =,经检验符合题意;不等式3()5f x <,即231215x-<+,22215x >+,215x +<,24x <,所以2x <.故选:D.6.已知函数()e x f x x =+,()ln g x x x =+,3()h x x x =+的零点分别为a ,b ,c ,则()A.a b c <<B.a c b<< C.c b a<< D.c a b<<【答案】B 【解析】【分析】结合函数单调性,根据零点的定义列方程,确定各函数零点的正负情况,即可比较,,a b c 的大小.【详解】显然:函数()e x f x x =+,()ln g x x x =+,3()h x x x =+在定义域内都是增函数,又()e 0e 00a a f a a a a =+=⇒=->⇒<,而()ln 0g b b b =+=中的0b >,令()32()100h c c c c c c =+=+=⇒=,a ∴,b ,c 的大小顺序为:a c b <<,故选:B .7.若不等式2221x mx m -+-<<的解集为(),2n 则m n -=()A.-2B.-1C.0D.1【答案】C 【解析】【分析】由题可得22y x mx m =+-对称轴在(),2n 之间,最小值大于-2,且221x mx m +-=的两个根为,2n ,列出相应不等式,找到关于,n m 的范围,再根据韦达定理解出,m n 的值,计算m n -即可.【详解】解:因为不等式2221x mx m -+-<<的解集为(),2n ,而22y x mx m =+-开口向上,所以有22mn ≤-≤,且最小值大于-2,即2254m ->-,解得:285m <,且221x mx m +-=的两个根为,2n ,所以2+221n m n m =-⎧⎨=--⎩,解得:35m n =⎧⎨=-⎩,11m n =-⎧⎨=-⎩,当35m n =⎧⎨=-⎩时,不符合285m <,故舍,所以11m n =-⎧⎨=-⎩,所以0-=m n .故选:C8.已知函数()2223,0log 2,0x x x f x x x ⎧+-≤=⎨->⎩,则方程()()f f x k =的实数解的个数至多是()A.5B.6C.7D.8【答案】B 【解析】【分析】根据复合方程问题,换元()t f x =,作函数图象分别看内外层分别讨论方程()()f f x k =根的个数情况,即可得答案.【详解】设()t f x =,则()()ff x k =化为()f t k =,又()2223,0log 2,0x x x f x x x ⎧+-≤=⎨->⎩,所以()()10322f f f ⎛⎫=-=-= ⎪⎝⎭,()1144f f ⎛⎫-=-= ⎪⎝⎭,如图为函数()f x的大致图象:由图可得,当3k >-时,()f t k =有两个根1212,2t t -,即()2t f x =<-或()12t f x =>,此时方程()()f f x k =最多有5个根;当43k -<≤-时,()f t k =有三个根1231121,10,42t t t -<<--<<<<,即()21f x -<<-或()10f x -<<或()1142f x <<,此时方程()()f f x k =最多有6个根;当4k =-时,()f t k =有两个根1211,4t t =-=,即()1f x =-或()14f x =,此时方程()()f f x k =有4个根;当4k <-时,()f t k =有一个根104t <<,即()104f x <<,此时方程()()f f x k =有2个根;综上,方程()()f f x k =的实数解的个数至多是6个.故选:B .二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.9.已知集合{}{}0,A x x B x x a =>=≥,若x A ∈是x B ∈的充分条件,则a 可以是()A.-1B.0C.1D.2【答案】AB 【解析】【分析】根据充分条件的概念,得出集合之间的包含关系,即可得出a 的范围,选出选项.【详解】解:因为x A ∈是x B ∈的充分条件,所以A B ⊆,所以有0a ≤.故选:AB10.若0a >且0a b +<,则()A.1ab <- B.22a b <C.2b aa b+<- D.33b a b+<【答案】BCD 【解析】【分析】由0a >且0a b +<,得出0b <,结合作差比较法和基本不等式可得答案.【详解】对于A ,因为0a >且0a b +<,所以0b <,所以10a a b b b ++=>,即1a b>-,A 不正确;对于B ,由选项A 可知0a b ->,所以()()220a b a b a b -=-+<,即22a b <,B 正确;对于C ,由于,a b 异号,所以0,0a b b a <<,所以2b a a b ⎛⎫⎛⎫-+-≥ ⎪ ⎪⎝⎭⎝⎭,由于等号只能在a b =时取到,所以2b a a b ⎛⎫⎛⎫-+-> ⎪ ⎪⎝⎭⎝⎭,即2b a a b +<-,C 正确;对于D ,因为b a b <+,所以33b a b +<,D 正确.故选:BCD.11.已知sin 5α=,7cos 225β=,π,0,2αβ⎛⎫∈ ⎪⎝⎭,则()A.αβ<B.2a b> C.π6β>D.π3αβ+<【答案】AC 【解析】【分析】根据平方公式、二倍角公式、和差角公式,结合正弦函数与余弦函数的单调性,逐项判断即可.【详解】因为27cos 212sin 25ββ=-=,所以29sin 25β=,又π0,2β⎛⎫∈ ⎪⎝⎭,所以3sin 5β=,所以1sin sin 2αβ<<,即πsin sin sin 6αβ<<,又函数sin y x =,在π0,2⎛⎫⎪⎝⎭上单调递增,π,0,2αβ⎛⎫∈ ⎪⎝⎭,则π6αβ<<,故A 正确,C 正确;因为π0,2α⎛⎫∈ ⎪⎝⎭,所以257cos cos 2525αβ==>=,又函数cos y x =,在()0,π上单调递减,所以2a b <,故B 不正确;因为π0,2β⎛⎫∈ ⎪⎝⎭,3sin 5β=,所以4cos 5β==,所以()254535π1cos cos cos sin sin cos 5555532αβαβαβ+=-=⨯-⨯=<=,又()0,παβ+∈,所以π3αβ+>,故D 不正确.故选:AC.12.已知定义在R 上的函数()f x 不恒等于零,()0f π=,且对任意的,x y ∈R ,有(2)(2)()()f x f y f x y f x y +=+-,则()A.(0)2f = B.()f x 是偶函数C.()f x 的图象关于点(π,0)中心对称 D.2π是()f x 的一个周期【答案】ABC 【解析】【分析】分别给,x y 取适当值代入条件,通过代数表达式判断函数性质.【详解】对于A ,令y x =得(2)(2)(2)(0)f x f x f x f +=,又函数()f x 不恒等于零,所以(0)2f =,选项A 正确;对于B ,令y x =-得(2)(2)(0)(2)2(2)f x f x f f x f x +-==,所以(2)(2)f x f x -=,故函数()f x 是偶函数,选项B 正确;对于C,D ,令π2t x +=,π2t y -=得(π)(π)()(π)0f t f t f t f ++-==,即(π)(π)f t f t +=--,()()()4π2πf t f t f t +=-+=,所以函数()f x 是周期函数,且周期为4π,选项D 错误;又()f x 是偶函数,即(π)(π)f t f t -=-,所以(π)(π)(π)(π)0f t f t f t f t ++-=++-=,即(π)(π)f t f t +=--,所以()f x 的图象关于点(π,0)对称,选项C 正确.故选:ABC.三、填空题:本题共4小题,每小题5分,共20分.13.已知()123f x x +=-,则()4f =______________.【答案】3【解析】【分析】根据函数解析式凑项法得()f x 的解析式,从而可求()4f 的值.【详解】因为()()123215f x x x +=-=+-,所以()25f x x =-,则()42453f =⨯-=.故答案为:3.14.已知扇形的圆心角为π4,弧长为2π3,则该扇形的面积为__________.【答案】8π9##8π9【解析】【分析】根据圆心角和弧长求得半径,根据弧长和半径利用扇形面积公式即可求得结果.【详解】解:记扇形的半径为r ,因为圆心角π4α=,弧长2π3l =,所以l r α=,即2ππ34r =,解得83r =,所以扇形的面积112π88π22339S lr ==⨯⨯=.故答案为:8π915.若关于x 的方程141k x xx x+=+有解,则k 的取值范围为_____________.【答案】[)9,+∞【解析】【分析】根据方程,讨论0x >,0x <时,可将方程141kx xx x+=+化为22145k x x=++有解,结合基本不等式及函数特点,即可求得k 的取值范围.【详解】方程141kx xx x +=+转化为114k x x x x ⎛⎫=++ ⎪ ⎪⎝⎭,当0x >时,方程为22111445k x x x x x x ⎛⎫⎛⎫=++=++ ⎪⎪⎝⎭⎝⎭,当0x <,22111445k x x x x x x ⎛⎫⎛⎫=----=++ ⎪⎪⎝⎭⎝⎭,即方程22145k x x =++有解,又20x >,2214559x x ++≥+=,当且仅当2214x x =,即212x =时,取到最小值9,所以函数[)221459,y x x∞=++∈+,所以k 的取值范围为[)9,+∞.故答案为:[)9,+∞.16.声音是由物体的振动产生的能引起听觉的波,每一个音都是由纯音合成的,纯音的数学模型是函数sin πy A t ω=.某技术人员获取了某种声波,其数学模型记为()y H t =,部分图象如图所示,对该声波进行逆向分析,发现它是由两种不同的纯音合成的,满足()()9sin 2πsin π0810H t t t ωω=+<<,其中50.8663H ⎛⎫≈- ⎪⎝⎭,则ω=_________.(1.732≈)【答案】3【解析】【分析】将53t =代入()H t ,结合题干数据可得05πsin 3ω⎛⎫⎪⎭=⎝,又()10H =,可得3ω=或6ω=,又1不是()H x 的周期,从而可求出满足题意的ω的值.【详解】由()()9sin 2πsin π0810H t t t ωω=+<<,且50.8663H ⎛⎫≈- ⎪⎝⎭,得5595sin 2πsin π33103H ω⎛⎫⎛⎫⎛⎫=⨯+⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0.86610π95π395πsinsin sin 31032103ω⎛⎫⎛⎫=+=-≈-+ ⎪ ⎪⎝⎭⎝⎭,3 1.732≈,所以3 1.7320.86622≈=,所以05πsin 3ω⎛⎫ ⎪⎭=⎝.由图可知()991sin 2πsin πsin π01010H ωω=+==,故ππ,k k ω=∈Z ,即,k k ω=∈Z .因为08ω<<,且05πsin 3ω⎛⎫⎪⎭=⎝,所以3ω=或6ω=.由图可知,1不是()H x 的周期,当6ω=时,()9sin 2πsin 6π10H t t t =+,此时()()()()991sin 2π1sin 6π1sin 2πsin 6π1010H t t t t t H t +=+++=+=,周期为1,不符合题意.当3ω=时,()9sin 2πsin 3π10H t t t =+,易知()()1H t H t +≠,满足题意.综上,3ω=.故答案为:3.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知函数()122xxf x =-.(1)若()32f x =,求x 的值;(2)判断函数()f x 的奇偶性并证明.【答案】(1)1x =;(2)()f x 为奇函数,证明见解析.【解析】【分析】(1)由()32f x =可得13222xx -=,解指数方程即可求解;(2)求出()f x -,结合奇函数的定义即可判断.【小问1详解】由()32f x =,可得13222xx -=,即()2223220x x -⋅-=,解得122=-x (舍)或22x =,解得1x =.【小问2详解】()f x 的定义域为R ,且()()112222x xx x f x f x ---=-=-=-,故函数()f x 为奇函数.18.已知函数()21xf x x =+(1)根据定义证明函数()f x 在()1,+∞单调递减;(2)若不等式()f x b <对一切实数x 都成立,求b 的取值范围.【答案】(1)证明见解析(2)1,2⎛⎫+∞⎪⎝⎭【解析】【分析】(1)根据函数单调性步骤取值、作差、变形、定号、下结论证明即可;(2)判断函数的奇偶性,结合单调性求解函数的最值,即可得b 的取值范围.【小问1详解】证明:任取121x x >>,则()()()()()()()()22122112121212122222221212121111111x x x x x x x x x x x x f x f x x x x x x x --+---=-==++++++,因为121x x >>,所以()()22121221110,10,0x x x x x x ++>->-<,所以()()120f x f x -<,即()()12f x f x <,故函数()f x 在()1,+∞单调递减;【小问2详解】因为函数()21x f x x =+的定义域为R ,所以()()21xf x f x x --==-+,故()f x 为奇函数,由(1)知函数()f x 在()1,+∞单调递减,任取120x x ≤<,则()()()()()()()()22122112121212122222221212121111111x x x x x x x x x x x x f x f x x x x x x x --+---=-==++++++,因为120x x ≤<,所以()()22121221110,10,0x x x x x x ++>--,所以()()120f x f x -<,即()()12f x f x <,故函数()f x 在[)0,1单调递增;所以此时()()max 112f x f ==,又()00f =且0x =是方程()0f x =唯一的根,所以[)0,x ∈+∞时,()10,2f x ⎡⎤∈⎢⎥⎣⎦,又()f x 为奇函数,所以()11,22f x ⎡⎤∈-⎢⎥⎣⎦不等式()f x b <对一切实数x 都成立,则()max 12b f x >=即b 的取值范围是1,2⎛⎫+∞⎪⎝⎭.19.某同学用“五点法”画函数()()πsin ,0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭在某一个周期内的图像时,列表并填入了部分数据,如下表:x ωϕ+0π2π3π22πxπ37π12()f x 022-0(1)请将上表数据补充完整,并根据表格数据做出函数()y f x =在一个周期内的图像;(2)将()y f x =的图形向右平移()0θθ>个单位长度,得到()y g x =的图像,若()y g x =的图像关于y 轴对称,求θ的最小值.【答案】(1)答案见解析(2)2π3【解析】【分析】)(1)根据表格,分别求得,,A ωϕ,即可得到函数()f x 的解析式,从而得到其函数图像;(2)根据题意,由函数图像变换,列出方程即可求得θ的最小值.【小问1详解】x ωϕ+0π2π3π22πxπ12π37π125π613π12()f x 022-0由表中数据可得,2A =,7ππ4123T =-,所以πT =,则2π2πω==,当π3x =时,π2x ωϕ+=,则π6ϕ=-,所以()π2sin 26f x x ⎛⎫=- ⎪⎝⎭【小问2详解】由题意可得,()()ππ2sin 22sin 2266g x x x θθ⎡⎤⎛⎫=--=-- ⎪⎢⎥⎣⎦⎝⎭,因为()y g x =的图像关于y 轴对称,则ππ2π62k θ--=+,k ∈Z ,解得ππ3k θ=--,k ∈Z且0θ>,所以当1k =-时,min 2π3θ=20.中国梦蕴含航天梦,航天梦助力中国梦.2022年11月29日23时08分,搭载神舟十五号载人飞船的长征二号F 遥十五运载火箭在酒泉卫星发射中心成功点火发射,实现了神舟十五号航天员乘组与神舟十四号航天员乘组太空在轨轮换.已知火箭起飞质量x (单位:kg )是箭体质量M (单位:kg )和燃料质量m (单位:kg )之和.在发射阶段,不考虑空气阻力的条件下,火箭的最大速度v (单位:km/s )和x 的函数关系是ln ln v a x b M =+,其中,a b 为常数,且当燃料质量为0kg 时,火箭的最大速度为0km/s .已知某火箭的箭体质量为kg M ,当燃料质量为()2e 1kg M -时,该火箭最大速度为4km/s .(1)求该火箭的最大速度v 与起飞质量x 之间的函数关系式;(2)当燃料质量至少是箭体质量的多少倍时,该火箭最大速度可达到8km/s ?【答案】(1)2ln 2ln v x M=-(2)燃料质量至少是箭体质量的()4e 1-倍时,该火箭最大速度可达到8km/s 【解析】【分析】(1)有题意可得()20ln ln 4ln e ln a M b M a M b M =+⎧⎪⎨=+⎪⎩,求得,a b 的值,即可得该火箭的最大速度v 与起飞质量x 之间的函数关系式;(2)设m kM =且0k >,根据(1)中关系式,代入即可解得k 的值,从而得答案.【小问1详解】因为火箭的最大速度v (单位:km/s )和x 的函数关系是ln ln v a x b M =+,又0m =时,x m M M =+=,0v =;()2e 1m M =-时,2e x m M M =+=,4v =,所以()20ln ln 4ln e ln a M b M a M b M=+⎧⎪⎨=+⎪⎩,解得2,2a b ==-,所以2ln 2ln v x M =-;【小问2详解】设m kM =且0k >,则()1x m M k M =+=+,又2ln 2ln v x M =-所以8v =时可得()82ln 12ln k M M =+-,即()()14lnln 1k Mk M+==+,解得4e 1k =-故燃料质量至少是箭体质量的()4e 1-倍时,该火箭最大速度可达到8km/s .21.已知函数()2cos sin f x x x x m =-+在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值为32.(1)求函数()f x 的解析式;(2)当,22ππx ⎡⎤∈-⎢⎥⎣⎦时,对于给定的实数a ,若方程()f x a =有解,则记该方程所有解的和为a S ,求a S 的所有可能取值.【答案】(1)()1sin 262πf x x ⎛⎫=++ ⎪⎝⎭(2)a S 的所有可能取值为ππππ,,0,,3663--.【解析】【分析】(1)根据三角恒等变换化简函数()f x ,利用正弦型函数的性质求得最大值,即可得m 的值,从而得函数()f x 的解析式;(2)根据,22ππx ⎡⎤∈-⎢⎥⎣⎦,确定函数()f x 的单调性及取值情况,作出函数()y f x =的图象,根据方程的根与函数对称性分类讨论得所有a S 取值即可.【小问1详解】()2311π1cos sin 2cos 2sin 222262f x x x x m x x m x m ⎛⎫=-+=++-=++- ⎪⎝⎭,因为π0,2x ⎡⎤∈⎢⎥⎣⎦,所以ππ7π2,666x ⎡⎤+∈⎢⎥⎣⎦,所以()max 13122f x m =+-=,则1m =,则()1sin 262πf x x ⎛⎫=++ ⎪⎝⎭;【小问2详解】当,22ππx ⎡⎤∈-⎢⎥⎣⎦,则π5π7π2,666x ⎡⎤+∈-⎢⎥⎣⎦,所以当ππ,23x ⎡⎤∈--⎢⎥⎣⎦时函数单调递减,ππ,36x ⎡⎤∈-⎢⎥⎣⎦时函数单调递增,当ππ,62x ⎡⎤∈⎢⎥⎣⎦时函数单调递减,又π5π1π7π1ππ1sin 0,sin 0,sin 0262262662f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-+==+=-=-+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,ππ11ππ13sin ,sin 32226222f f ⎛⎫⎛⎫⎛⎫-=-+=-=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则可得函数()y f x =的图象如下:对于给定的实数a ,若方程()f x a =有解,则当32a =时,方程的根为π6x =,此时π6a S =;当13,22a ⎛⎫∈ ⎪⎝⎭时,方程的两根关于直线π6x =对称,此时π3a S =;当12a =时,方程的根有三个1π3x =-,23,x x 关于直线π6x =对称,此时ππ033a S =-+=;当10,2a ⎛⎫∈ ⎪⎝⎭,方程有四个根,12,x x 关于直线π3x =-对称,34,x x 关于直线π6x =对称,此时2πππ333a S =-+=-;当0a =时,方程的根有三个123πππ,,262x x x =-=-=,此时ππππ2626a S =--+=-;综上,a S 的所有可能取值为ππππ,,0,,3663--.22.已知函数()ln(2)ln f x x x a =+++,()e ln(2)x g x a x =-+.(1)当1a =时,解不等式()1f x x <+;(2)证明:当1a ≥时,函数()f x 有唯一的零点x 0,且0()0g x >恒成立.【答案】(1)(2,e 2)--;(2)证明见解析.【解析】【分析】(1)由对数型函数的单调性直接求解即可;(2)由()f x 在(2,)-+∞上单调递增,利用零点存在性定理可知存在唯一的01(2,0)x a∈-,由00ln ln(2)x a x +=-+化简后可得0001()ln 2g x x a x =+++,利用均值不等式及等号成立条件即可得证.【小问1详解】当1a =时,()ln(2)f x x x =++,由()1f x x <+可得ln(2)1x +<,解得02e x <+<,即2e 2x -<<-,故不等式的解为(2,e 2)--.【小问2详解】因为y x =与ln(2)y x =+均为增函数,所以()f x 在(2,)-+∞上单调递增,当1a ≥时,(0)ln 2ln 0f a =+>,1111(2)2ln ln 21210f a a a a a-=-++=-≤-=-<,所以存在唯一的01(2,0)x a∈-,使得0()0f x =,即函数()f x 有唯一零点0x ,所以00ln(2)ln 0x x a +++=,即00ln ln(2)x a x +=-+,所以00ln ln(2)e e x a x +-+=,即001e2x a x =+,所以000000011()e ln(2)ln 22ln 22x g x x x a x a x x α=-+=++=++-+++,因为012x a >-,所以0120x a+>>,所以0()2ln ln 0g x a a ≥=-+≥,当且仅当01x =-与1a =时等号成立.当01x =-时,由00ln ln(2)x a x +=-+知ln 1a =,即e a =,所以等号不成立,所以0()0g x >.。
厦门市教育局处室业务公文 - 厦门一中

厦门市教育局处室业务公文2015年厦门市中小学生游泳锦标赛团体总分成绩公告高中组第一名:厦门一中第二名:科技中学第三名:厦门外国语学校第四名:厦门二中第五名:双十中学第六名:厦门六中初中组第一名:厦门一中第二名:厦门外国语学校第三名:双十中学第四名:莲花中学第五名:大同中学第六名:湖滨中学小学组第一名:公园小学第二名:大同小学第三名:湖里中心小学第四名:外国语附属小学第五名:群惠小学第六名:厦门实验小学各组别成绩公告小学组男子小学甲组自由泳全能成绩第一名:谢芳翔(公园小学) 第五名:洪榕骏(大同小学)第二名:林博文(公园小学) 第六名:林俊荣(湖里中心)第三名:伍喆恺(大同小学) 第七名:陈琛(外国语附)第四名:郭泽宏(公园小学) 第八名:周彥豆(金鸡亭)男子小学甲组仰泳全能成绩第一名:苏径舟(大同小学) 第五名:蔡炜程(大同小学)第二名:陈泓禹(公园小学) 第六名:陈秉键(湖里中心)第三名:李振宇(大同小学) 第七名:林录(大同小学)第四名:朱泽恺(大同小学)男子小学甲组蛙泳全能成绩第一名:周果(公园小学) 第五名:羊祉霖(实验小学) 第二名:谢志鑫(湖里中心) 第六名:吴柏熠(大同小学) 第三名:黄昱(公园小学) 第七名:林瀚之(实验小学) 第四名:徐畅(大同小学) 第八名:朱旭(公园小学)男子小学甲组蝶泳全能成绩第一名:陈思融(公园小学) 第五名:王芃霁(公园小学) 第二名:蒋昕哲(大同小学) 第六名:尤文祺(大同小学) 第三名:陈哲翀(大同小学) 第七名:蔡明昊(大同小学) 第四名:连锦鑫(公园小学)女子小学甲组自由泳全能成绩第一名:毛子萱(公园小学) 第五名:王忆欣(公园小学) 第二名:严杨彤欣(公园小学)第三名:万贝贝(大同小学)第四名:杨亭萱(大同小学)女子小学甲组仰泳全能成绩第一名:李诗淇(大同小学) 第三名:何玏(外国语附) 第二名:黄鑫瑜(公园小学) 第四名:杨渊滋(公园小学)女子小学甲组蛙泳全能成绩第一名:李畅(群惠小学) 第五名: 王涵宇(大同小学) 第二名: 杨若童(外国语附) 第六名: 朱玥含(公园小学) 第三名: 张雅贤(公园小学) 第七名: 陈艺萌(金鸡亭)第四名: 朱宇佳(公园小学)第一名:黄筱睿(公园小学) 第五名: 黎欣叶(外国语附) 第二名: 杜馨悦(公园小学) 第六名: 陈韵(公园小学) 第三名: 汪宇轩(大同小学)第四名: 林龙晓钰(大同小学)男子小学乙组自仰全能成绩第一名:白治鸣(公园小学) 第五名: 傅子函(外国语附) 第二名: 王子豪(公园小学) 第六名: 谢卓晟(公园小学) 第三名: 黄燦(大同小学) 第七名:汪承典(公园小学) 第四名: 柯肖阳(大同小学) 第八名: 黄鋆瀚(大同小学)女子小学乙组自仰全能成绩第一名:王佳华(公园小学) 第五名: 魏宇鸿(公园小学) 第二名: 刘邑暄(公园小学) 第六名: 陈昕瑶(公园小学) 第三名: 林晗璐(公园小学) 第七名:陈林怡(公园小学) 第四名: 陈裕欣(公园小学) 第八名: 谢静宜(公园小学)男子小学丙组自仰全能成绩第一名:林泓钰(公园小学) 第五名: 张逸诚(公园小学) 第二名: 钟宇轩(公园小学) 第六名: 许哲岩(大同小学) 第三名: 苏俊宇(大同小学) 第七名:严宸浩(思明二实) 第四名: 朱宇卿(大同小学) 第八名: 陈加乐(湖明小学)第一名: 陈佳慧(大同小学) 第五名: 林佳颖(公园小学) 第二名: 陈婉琪(公园小学) 第六名: 胡怡琳(公园小学) 第三名: 陈馨(湖里中心) 第七名:林岢臻(湖里中心) 第四名: 陈娜(公园小学) 第八名: 蔡佳烨(公园小学)男子高中组50米自由泳名次第一名: 陈珂(厦门一中) 第四名: 黄逸昆(厦门六中) 第二名: 何毅翔(海沧实验) 第五名: 吴斯桓(科技中学) 第三名: 石舒吉(厦门一中) 第六名:朱晨飞(双十中学)男子高中组100米自由泳名次第一名: 陈珂(厦门一中) 第四名:吴斯桓(科技中学) 第二名: 公思逸(厦门一中) 第五名:许铭浩 (双十中学) 第三名: 石舒吉(厦门一中)男子高中组200米自由泳名次第一名: 陈珂(厦门一中) 第五名: 欧阳桐澄(双十中心) 第二名:公思逸(厦门一中) 第六名:李米姿(外国语)第三名: 黄子回(厦门二中) 第七名:杨慧鑫(外国语)第四名:许博韬(外国语)男子高中组50米仰泳名次第一名: 刘星辰(厦门一中) 第五名:黄逸昆(厦门六中) 第二名:周政霆(厦门二中) 第六名:吴斯桓(科技中学) 第三名:何毅翔 (海沧实验) 第七名:沈国政(科技中学)第四名:林洪鹏(科技中学)男子高中组100米仰泳名次第一名: 刘星辰(厦门一中) 第四名:黄恺恩(外国语)第二名:黄逸昆(厦门二中) 第五名:杨慧鑫(外国语)第三名:沈国政 (科技中学) 第六名:黄仕豪(外国语)男子高中组200米仰泳名次第一名:黄子回 (厦门一中) 第二名: 黄恺恩(外国语)男子高中组50米蛙泳名次第一名: 王天翼(厦门一中) 第三名: 连智和(科技中学) 第二名:张廷嘉(双十中学) 第四名:蓝坤仲(双十中学)男子高中组100米蛙泳名次第一名: 王天翼(厦门一中) 第二名:许铭浩(双十中学)男子高中组200米蛙泳名次第一名:王天翼 (厦门一中) 第三名:黄仕豪(外国语)第二名:欧阳桐澄(双十中学)男子高中组50米蝶泳名次第一名: 周政霆(厦门二中) 第四名:石舒吉(厦门一中) 第二名:林洪鹏(科技中学) 第五名:张廷嘉(双十中学) 第三名: 沈国政(科技中学) 第六名:朱晨飞(双十中学)男子高中组100米蝶泳名次第一名: 周政霆(厦门二中) 第四名: 公思逸(厦门一中) 第二名:黄子回(厦门二中) 第五名:许博韬(外国语)第三名: 林洪鹏(科技中学) 第六名:李米姿(外国语)男子高中组200米个人混合泳名次第一名: 刘星辰(厦门一中) 第三名: 黄恺恩(外国语) 第二名: 许博韬(外国语)男子高中组4×50米混合泳接力名次第一名:刘星辰王天翼公思逸陈珂(厦门一中)第二名:沈国政连智和林洪鹏吴斯桓(科技中学)女子高中组50米自由泳名次第一名: 林佳欣(厦门六中) 第四名: 陈妍(厦门一中)第二名: 贾瑞云(康桥中学) 第五名:洪语汐(厦门一中)第三名: 吴稷(湖滨中学) 第六名:兰雨萱(双十中学)女子高中组100米自由泳名次第一名: 陈芷欣(外国语) 第四名: 肖金特(厦门一中) 第二名: 贾瑞云(康桥中学)第三名: 吴稷(湖滨中学)女子高中组200米自由泳名次第一名: 陈芷欣(外国语) 第四名: 陈逸如(外国语) 第二名: 贾瑞云(康桥中学) 第五名:肖金特(厦门一中)第三名: 孙蔓琳(厦门一中) 第六名:陈思静(双十中学)女子高中组50米仰泳名次第一名: 林佳欣(厦门六中) 第二名: 陈妍(厦门一中)女子高中组100米仰泳名次第一名: 林佳欣(厦门六中) 第三名: 肖金特(厦门一中) 第二名: 陈妍(厦门一中)女子高中组50米蛙泳名次第一名: 陈诗宇(科技中学) 第三名: 周心彤(厦门一中) 第二名: 孙蔓琳(厦门一中) 第四名: 于鹭日方(双十中学)女子高中组100米蛙泳名次第一名: 陈诗宇(科技中学) 第三名: 陈楚凌(外国语) 第二名: 周心彤(厦门一中)女子高中组200米蛙泳名次第一名: 陈诗宇(科技中学) 第四名: 陈楚凌(外国语) 第二名: 洪语汐(厦门一中) 第五名: 周心彤(厦门一中) 第三名: 孙蔓琳(厦门一中)女子高中组200米个人混合泳名次第一名: 陈芷欣(外国语) 第三名: 陈逸如(外国语) 第二名: 洪语汐(厦门一中)男子初中组50米自由泳名次第一名: 陈彦安(湖里实验) 第五名: 洪雨鑫(厦门一中) 第二名: 周翰泽(厦门一中) 第六名: 庄煜航(外国语) 第三名: 谢愽政(外国语) 第七名:林行健(双十中学) 第四名: 黄进琰(大同中学) 第八名: 陈诗远(双十中学)男子初中组100米自由泳名次第一名: 陈彦安(湖里实验) 第四名: 郑上锟(厦门一中) 第二名: 袁大一(大同中学) 第五名: 佘宁(大同中学) 第三名: 陈泽胧(厦门一中) 第六名:张鸿迈(双十中学)男子初中组200米自由泳名次第一名: 陈彦安(湖里实验) 第四名: 王瀚鸿(厦门一中) 第二名: 袁大一(大同中学) 第五名: 陈俊翔(外国语) 第三名: 谢愽政(外国语) 第六名:谢晨昀(莲花中学)男子初中组400米自由泳名次第一名: 郑上锟(厦门一中) 第三名: 谌业顺(莲花中学) 第二名: 袁大一(大同中学)男子初中组50米仰泳名次第一名: 陈润泽(厦门一中) 第五名: 许奕洋(莲花中学) 第二名: 周翰泽(厦门一中) 第六名: 佘宁(大同中学) 第三名: 陈诗远(双十中学) 第七名:张鸿迈(双十中学) 第四名: 曾鸿鸣(外国语)男子初中组100米仰泳名次第一名: 洪雨鑫(厦门一中) 第四名: 黄进琰(大同中学) 第二名: 陈诗远(双十中学) 第五名: 苏睿哲(厦门五中) 第三名: 谌业顺(莲花中学)男子初中组200米仰泳名次第一名: 郑上锟(厦门一中) 第三名: 曾鸿鸣(外国语) 第二名: 洪雨鑫(厦门一中) 第四名: 谢晨昀(莲花中学)男子初中组50米蛙泳名次第一名: 陈润泽(厦门一中) 第五名: 邱至枰(外国语) 第二名: 杨骐宇(湖滨中学) 第六名: 洪怀璟(双十中学) 第三名: 谢愽政(外国语) 第七名:孙伟峪(双十中学) 第四名: 陈阳(集美中学) 第八名:王相哲(集美中学)男子初中组100米蛙泳名次第一名: 陈泽胧(厦门一中) 第五名: 颜奇圻(双十中学) 第二名: 杨骐宇(湖滨中学) 第六名: 孙伟峪(双十中学) 第三名: 邱至枰(外国语) 第七名:刘子辰(槟郎中学) 第四名: 陈阳(集美中学) 第八名:王皓(槟郎中学)男子初中组200米蛙泳名次第一名: 陈泽胧(厦门一中) 第五名: 庄煜航(外国语) 第二名: 谌业顺(莲花中学) 第六名: 姚博文(莲花中学) 第三名: 陈韻鑫(厦门一中) 第七名:刘子辰(槟郎中学) 第四名: 邱至枰(外国语)男子初中组50米蝶泳名次第一名: 周翰泽(厦门一中) 第五名: 黄进琰(大同中学) 第二名: 杨骐宇(湖滨中学) 第六名: 颜奇圻(双十中学) 第三名: 陈韻鑫(厦门一中) 第七名:苏睿哲(厦门五中)男子初中组100米蝶泳名次第一名: 陈韻鑫(厦门一中) 第三名: 陈俊翔(外国语) 第二名: 王瀚鸿(厦门一中)男子初中组200米蝶泳名次第一名: 王瀚鸿(厦门一中) 第二名: 洪怀璟(双十中学)男子初中组4X50米自由泳接力名次第一名:周翰泽洪雨鑫陈润泽郑上锟(厦门一中)第二名:邱至枰陈俊翔庄煜航谢愽政(外国语)第三名:颜奇圻林行健张鸿迈洪怀璟(双十中学)第四名:谢晨昀许奕洋傅逸昇谌业顺(莲花中学)男子初中组4X50米混合泳接力名次第一名:陈润泽陈泽胧陈韻鑫王瀚鸿(厦门一中)第二名:曾鸿鸣邱至枰陈俊翔谢愽政(外国语)第三名:陈诗远颜奇圻洪怀璟张鸿迈(双十中学)第四名:谌业顺许奕洋谢晨昀傅逸昇(莲花中学)女子初中组50米自由泳名次第一名: 陈俊如(厦门一中) 第五名: 林慧婷(大同中学) 第二名: 林颖(科技中学) 第六名: 王艺锜(双十中学)第四名: 吴佳文(大同中学) 第八名:周思妹(厦门二中)女子初中组100米自由泳名次第一名: 黄蕾(厦门一中) 第四名: 刘子榆(外国语) 第二名: 朱卓琳(莲花中学) 第五名: 林颖(科技中学) 第三名: 陈俊如(厦门一中) 第六名:林慧婷(大同中学)女子初中组400米自由泳名次第一名: 黄蕾(厦门一中) 第二名: 朱卓琳(莲花中学)女子初中组50米仰泳名次第一名: 苏斐(厦门一中) 第五名: 吴佳文(大同中学) 第二名: 冯政骁(大同中学) 第六名: 王艺锜(双十中学) 第三名: 郑昕昀(双十中学) 第七名:李文君(松柏中学) 第四名: 林颖(科技中学)女子初中组100米仰泳名次第一名: 王滢(厦门一中) 第三名: 陈美霖(外国语) 第二名: 苏斐(厦门一中) 第四名: 杨雅霖(外国语)女子初中组200米仰泳名次第一名: 苏斐(厦门一中) 第三名: 陈美霖(外国语)女子初中组50米蛙泳名次第一名: 陈俊如(厦门一中) 第四名: 黄心怡(外国语) 第二名: 田祖扬(外国语) 第五名: 刘子榆(外国语) 第三名: 关小未(湖滨中学) 第六名:周思妹(厦门二中)女子初中组100米蛙泳名次第一名: 王滢(厦门一中) 第五名: 冯政骁(大同中学) 第二名: 黄心怡(外国语) 第六名: 刘佳佳(厦门一中) 第三名: 田祖扬(外国语) 第七名:关小未(湖滨中学) 第四名: 郑昕昀(双十中学) 第八名:李文君(松柏中学)女子初中组200米蛙泳名次第一名: 施予欣(厦门一中) 第四名: 刘子榆(外国语) 第二名: 王滢(厦门一中) 第五名: 杨雅霖(外国语) 第三名: 田祖扬(外国语)女子初中组50米蝶泳名次第一名: 方昕捷(双十中学) 第三名: 刘佳佳(厦门一中) 第二名: 郑昕昀(双十中学)女子初中组200米蝶泳名次第一名: 黄蕾(厦门一中) 第三名: 刘佳佳(厦门一中)女子初中组4X50米自由泳接力名次第一名:王滢苏斐黄蕾陈俊如(厦门一中)第二名:杨雅霖黄心怡田祖扬陈美霖(外国语)女子初中组4X50米混合泳接力名次第一名:王滢苏斐刘佳佳陈俊如(厦门一中)第二名:杨雅霖田祖扬陈美霖刘子榆(外国语)男子小学甲组4X50米自由泳接力名次第一名:林博文周果陈泓禹谢芳翔(公园小学)第二名:伍喆恺李振宇蒋昕哲苏径舟(大同小学)男子小学甲组4X50米混合泳接力名次第一名:林博文周果陈泓禹陈思融(公园小学)第二名:伍喆恺李振宇吴柏熠苏径舟(大同小学)女子小学甲组4X50米自由泳接力名次第一名:严杨彤欣毛子萱黄筱睿黄鑫瑜(公园小学)第二名:王涵宇汪宇轩万贝贝李诗淇(大同小学)女子小学甲组4X50米混合泳接力名次第一名:严杨彤欣张雅贤黄筱睿毛子萱(公园小学)男子小学乙组4X50米自由泳接力名次第一名:白治鸣柯肖阳陈博浒李霖(公园小学)第二名:王子豪卓辰宇林伟烨陈颖钊(湖里中心)第三名:谢卓晟李哲昊庄朋桥黄鋆瀚(大同小学)男子小学乙组4X50米混合泳接力名次第一名:王子豪卓辰宇林伟烨陈颖钊(湖里中心)第二名:白治鸣廖文博傅子函柯肖阳(公园小学)第三名:陈叙中李哲昊庄朋桥黄鋆瀚(大同小学)男子小学乙组4X50米打腿接力名次第一名:赖子杰汪承典李宇恒吕阳(公园小学)第二名:王子豪卓辰宇林语桐陈颖钊(湖里中心)第三名:陈叙中陈仁泽杨宝霖谢卓晟(大同小学)女子小学乙组4X50米自由泳接力名次第一名:陈裕欣魏宇鸿林晗璐王佳华(公园小学)第二名:苏雯茜朱文卿杨奕涵周露(大同小学)女子小学乙组4X50米混合泳接力决赛成绩第一名:谢静宜陈昕瑶陈林怡王佳华(公园小学)第二名:杨奕涵朱文卿苏雯茜周露(大同小学)女子小学乙组4X50米打腿接力名次第一名:陶易彤陈彤陈静怡刘邑暄(公园小学)第二名:刘萌萌周芷妍吴灵钰肖彦涵(湖里中心)男子小学丙组4X50米自由泳接力名次第一名:朱宇卿许哲岩王锴涵苏俊宇(大同小学)第二名:钟宇轩林泓钰杨镒祯张逸诚(公园小学)第三名:卓锴欣杜睿恩郑钰衡周宬佑(外国语附)第四名:谢永祺陈思恒陈仡童庆阳(湖里中心)男子小学丙组4X50米混合泳接力名次第一名:朱宇卿袁朗苏俊宇许哲岩(大同小学)第二名:钟宇轩杨镒祯张逸诚林泓钰(公园小学)第三名:刘学谦童庆阳陈思恒谢永祺(湖里中心)第四名:周宬佑卓锴欣郑钰衡杜睿恩(外国语附)男子小学丙组4X50米打腿接力名次第一名:苏俊宇吴一乐陈彦达朱宇卿(大同小学)第二名:林智贤王子昊徐浩宸陈宇浩(公园小学)第三名:谢永祺蔡旻晏陈思恒童庆阳(湖里中心)第四名:杜睿恩卓锴欣郑钰衡周宬佑(外国语附)女子小学丙组4X50米自由泳接力名次第一名:陈婉琪黄嘉欣胡怡琳林佳颖(公园小学)第二名:陈馨林岢臻曾含钰薛玮祺(湖里中心)女子小学丙组4X50米混合泳接力名次第一名:曾含钰郭璐宁陈馨林岢臻(湖里中心)第二名:胡怡琳陈娜陈婉琪黄嘉欣(湖里中心)女子小学丙组4X50米打腿接力名次第一名:张文程蔡佳烨陈静妍许玲珠(公园小学)第二名:陈馨郑钰琳林岢臻骆璇睿(湖里中心)厦门市教育局体卫艺教处2015年8月6日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福州最牛,厦门一中榜上有名:2022年NOIOnline能力测试福建学生成绩公示【主图】2022年3月31日星期四之前,我在厦门创客群里,全程发布了NOI Online能力测试的C++比赛信息,这是官方组织的在线的一次比赛。
现在成绩出来了,我们一起来看看。
01福建学生成绩:入门组前25%名单证书编号省份准考证号姓名性别总分学校年级CCF-NOI ONLINE-5-1132 福建FJ-00359李世奥男235泉州师范学院附属鹏峰中学初二CCF-NOI ONLINE-5-1133 福建FJ-00405林陈恩男235 福鼎市第六中学初一CCF-NOI ONLINE-5-1134 福建FJ-00586孙正晖男235福建省长乐第一中学初二CCF-NOI ONLINE-5-1135 福建FJ-00628王祉杰男235福建省福州延安中学初二CCF-NOI ONLINE-5-1195 福建FJ-00883郑融生男230 厦门市华侨中学初三CCF-NOI ONLINE-5-1196 福建FJ-00910周子臻男230 福州三牧中学初三CCF-NOI ONLINE-5-1217 福建FJ-00383李昕宸男225福建省长乐华侨中学初二CCF-NOI ONLINE-5-1237 福建FJ-00145陈睿鹏男220 长乐区航城中学初三CCF-NOI ONLINE-5-1238 福建FJ-00243黄彬鸿男220福建省南安第一中学初一CCF-NOI ONLINE-5-1301 福建FJ-00877郑锦翼男205 福州市温泉小学小学CCF-NOI ONLINE-5-1360 福建FJ-00058陈俊秀男200石狮市中英文实验学校初二CCF-NOI ONLINE-5-1361 福建FJ-00379李奕辰男200 福州立志中学初二CCF-NOI ONLINE-5-1362 福建FJ-00406林诚凯男200福建省南安第一中学初一CCF-NOI ONLINE-5-1363 福建FJ-00463林子檬男200 福州三牧中学初三CCF-NOI ONLINE-5-1364 福建FJ-00543潘伟文男200福建省长乐华侨中学初二CCF-NOI ONLINE-5-1365 福建FJ-00730许翔宇男200厦门大学附属实验中学初一CCF-NOI ONLINE-5-1366 福建FJ-00806余杰瑞男200 个人报名初二CCF-NOI ONLINE-5-1523 福建FJ-00257黄景烁男190厦门大学附属实验中学初一CCF-NOI ONLINE-5-1524 福建FJ-00280黄一涵男190福建省南安第一中学初一CCF-NOI ONLINE-5-1566 福建FJ-00262黄凌风男185福建省南安第一中学初一CCF-NOI ONLINE-5-1567 福建FJ-00542潘可慕女185福建省泉州第一中学初一CCF-NOI ONLINE-5-1568 福建FJ-00614王子乐男185福建省晋江市养正中学高一CCF-NOI ONLINE-5-1569 福建FJ-00831张承武男185 个人报名初一CCF-NOI ONLINE-5-1605 福建FJ-00039陈鸿睿男180 长乐区航城中学初三CCF-NOI ONLINE-5-1606 福建FJ-00108陈禹恩男180福建省泉州第一中学初二CCF-NOI ONLINE-5-1607 福建FJ-00230洪宜鲲男180福建省泉州市第七中学初一CCF-NOI ONLINE-5-1670 福建FJ-00283黄逸天男175 福州三牧中学初三CCF-NOI ONLINE-5-1671 福建FJ-00813俞昊岑男175福州市鼓楼实验小学小学CCF-NOI ONLINE-5-1672 福建FJ-00841张凯铭男175福建省南安第一中学高一CCF-NOI ONLINE-5-1827 福建FJ-00012蔡善桢男170闽江学院附属中学初一CCF-NOI ONLINE-5-1828 福建FJ-00110陈禹宸男170福建省泉州第一中学初二CCF-NOI ONLINE-5-1829 福建FJ-00185冯盛振男170 个人报名高一CCF-NOI ONLINE-5-1830 福建FJ-00192甘君阳男170 福州树德学校初二CCF-NOI ONLINE-5-1832 福建FJ-00485刘博仁男170福建省南安第一中学初一CCF-NOI ONLINE-5-1833 福建FJ-00491刘锦程男170福建省福州第十八中学初二CCF-NOI ONLINE-5-1834 福建FJ-00610王泽钦男170 泉州市城东中学初一CCF-NOI ONLINE-5-1835 福建FJ-00681吴奕多男170 福州三牧中学初二CCF-NOI ONLINE-5-1836 福建FJ-00757杨钧富男170厦门大学附属实验中学初三CCF-NOI ONLINE-5-1943 福建FJ-00086陈思衔男165 福州市温泉小学小学CCF-NOI ONLINE-5-1944 福建FJ-00375李湛橙男165 个人报名小学CCF-NOI ONLINE-5-1946 福建FJ-00680吴弈辰男165福建省福清第一中学初三CCF-NOI ONLINE-5-1947 福建FJ-00926祝钒男165 个人报名初二CCF-NOI ONLINE-5-2000 福建FJ-00299黄睿男160福州格致中学鼓山校区初二CCF-NOI ONLINE-5-2002 福建FJ-00857张恺瑄男160 福州现代中学初一CCF-NOI ONLINE-5-2041 福建FJ-00019蔡姗珊女155 福州市温泉小学小学CCF-NOI ONLINE-5-2043 福建FJ-00477林梓楠女155福建省长乐第一中学高一CCF-NOI ONLINE-5-2044 福建FJ-00684吴宸宇男155 现代中学初一CCF-NOI ONLINE-5-2045 福建FJ-00800阴若诚男155 福州三牧中学初二CCF-NOI ONLINE-5-2046 福建FJ-00891郑泓轩男155福建省长乐华侨中学初一CCF-NOI ONLINE-5-2161 福建FJ-00328柯致远男145福州市长乐区航城中学初一CCF-NOI ONLINE-5-2162 福建FJ-00510刘熠宁男145福建省福州第十九中学初二CCF-NOI ONLINE-5-2163 福建FJ-00539欧定兴男145福建省泉州第一中学初二CCF-NOI ONLINE-5-2164 福建FJ-00939邹子豪男145福建省泉州实验中学初三CCF-NOI ONLINE-5-2341 福建FJ-00010蔡坤阳男140南安市洪濑中心小学小学CCF-NOI ONLINE-5-2342 福建FJ-00036陈浩宇男140 莆田擢英中学初二CCF-NOI ONLINE-5-2343 福建FJ-00052陈举文男140福建省福州延安中学初一CCF-NOI ONLINE-5-2345 福建FJ-00074陈穆奚男140福建省泉州第一中学初一CCF-NOI ONLINE-5-2346 福建FJ-00080陈深然男140福建省泉州第一中学初二CCF-NOI ONLINE-5-2347 福建FJ-00105陈颖姗女140福建省福州市鼓山中学初一CCF-NOI ONLINE-5-2348 福建FJ-00148陈麒润男140 泉州第五中学小学CCF-NOI ONLINE-5-2349 福建FJ-00186冯萧逸男140 福州市钱塘小学小学CCF-NOI ONLINE-5-2350 福建FJ-00209郭正炫男140福建省福州屏东中学初一CCF-NOI ONLINE-5-2351 福建FJ-00212郭子锜男140 泉州第五中学初二CCF-NOI ONLINE-5-2352 福建FJ-00216韩聿宸男140福建省连江县黄如论中学初二CCF-NOI ONLINE-5-2353 福建FJ-00218何鸿楷男140 福州三牧中学初一CCF-NOI ONLINE-5-2354 福建FJ-00238胡炫辰男140 福州三牧中学初二CCF-NOI ONLINE-5-2355 福建FJ-00270黄诗焜男140福建省福州杨桥中学初二CCF-NOI ONLINE-5-2356 福建FJ-00271黄世成男140福建省福州第十九中学初二CCF-NOI ONLINE-5-2358 福建FJ-00323康锴男140 福州铜盘中学初二CCF-NOI ONLINE-5-2360 福建FJ-00327柯渝铭男140福州市长乐区实验小学小学CCF-NOI ONLINE-5-2361 福建FJ-00348李侯煦男140 福州三牧中学初二CCF-NOI ONLINE-5-2362 福建FJ-00355李敏增男140 福鼎市第六中学初二CCF-NOI ONLINE-5-2363 福建FJ-00378李奕博男140 厦门实验中学初二CCF-NOI ONLINE-5-2364 福建FJ-00384李昱涵男140厦门大学附属实验中学初二CCF-NOI ONLINE-5-2366 福建FJ-00403林博飞男140 长乐区朝阳中学初一CCF-NOI ONLINE-5-2367 福建FJ-00446林新程男140福建省福州杨桥中学初二CCF-NOI ONLINE-5-2369 福建FJ-00479林煜轩男140福建省福州第十九中学初一CCF-NOI ONLINE-5-2370 福建FJ-00505刘昊天男140福建省泉州第一中学初二CCF-NOI ONLINE-5-2371 福建FJ-00525罗诺睿瑄男140 个人报名小学CCF-NOI ONLINE-5-2372 福建FJ-00567石力恒男140福建省泉州第一中学初一CCF-NOI ONLINE-5-2373 福建FJ-00581孙浚皓男140 福州市钱塘小学小学CCF-NOI ONLINE-5-2374 福建FJ-00649吴承锦男140福州市城门中心小学小学CCF-NOI ONLINE-5-2375 福建FJ-00652吴翰琦男140 福州华侨中学初一NOI ONLINE-5-2377 福建00671 晨男140 柘荣三中初二CCF-NOI ONLINE-5-2378 福建FJ-00683吴峥男140福建省泉州第一中学初一CCF-NOI ONLINE-5-2379 福建FJ-00725许俊荣男140福建省惠安广海中学初二CCF-NOI ONLINE-5-2380 福建FJ-00727许铭辰男140 个人报名小学CCF-NOI ONLINE-5-2382 福建FJ-00751杨本初男140 福州三牧中学初二CCF-NOI ONLINE-5-2383 福建FJ-00809余煊男140福建省福州延安中学初一CCF-NOI ONLINE-5-2384 福建FJ-00814俞炫帆男140 钱塘文博小学小学CCF-NOI ONLINE-5-2385 福建FJ-00833张高畅男140福建省泉州第一中学初一CCF-NOI ONLINE-5-2386 福建FJ-00878郑凯仁男140福建省泉州第一中学初二CCF-NOI ONLINE-5-2387 福建FJ-00886郑义萱女140福建省长乐华侨中学初一CCF-NOI ONLINE-5-2388 福建FJ-00911周子骞男140 个人报名小学CCF-NOI ONLINE-5-2389 福建FJ-00933庄瑜男140 莆田第二中学高一NOI ONLINE-5-2390 福建00936 翰男140 福州市钱塘小学小学CCF-NOI ONLINE-5-2391 福建FJ-00937卓语萱女140 个人报名小学入门组福建省报名994名,上榜111名,1-3等奖截取25%,最低分为140分。
