第1章难点探究专题:特殊平行四边形中的动态问题-2020秋北师大版九年级数学上册习题(共12张PPT)
[初中数学++]第一章+特殊平行四边形+小结与复习+课件+北师大版九年级数学上册
![[初中数学++]第一章+特殊平行四边形+小结与复习+课件+北师大版九年级数学上册](https://img.taocdn.com/s3/m/19d3ca75657d27284b73f242336c1eb91a3733e7.png)
又∵∠BAD = 60°, ∴△ABD是等边三角形.
AO
B
C
∴ AB = BD = 6, AO 3 3,AC 6 3.
D
针对训练
1. 如图,在 □ABCD 中,对角线 AC 与 BD 相交于点 O,
AB = 5 ,OA = 2,OB = 1. 求证:□ABCD 是菱形.
证明:在 △AOB 中,
第一章 特殊的平行四边形
小结与复习
复习回顾
特殊四边形的关系
平行四边形
矩形 有一个角是直角且邻边相等
菱形
正方形
几种特殊四边形的性质:
边
角
四个角 矩形 平行且相等
都是直角
对角线
对称性
中心对称图形 互相平分且相等
轴对称图形
菱形
平行
对角相等
且四边相等 邻角互补
互相垂直平分
中心对称图形 轴对称图形
正方 平行
B
∵ AB = 5,OA = 2,OB = 1. ∴ AB2 = AO2 + OB2.
A
O
C
∴ △AOB 是直角三角形,∠AOB 是直角. D
∴ AC⊥BD.
∴ □ABCD 是菱形 (对角线垂直的平行四边形是菱形).
2. 如图,两张等宽的矩形纸条交叉重叠在一起,猜想
重叠部分的四边形 ABCD 是什么形状?说说你的理由.
两组对 边平行
一个角是直角且一组邻边相等
巩固练习,深化提高
1. 一个菱形的两条对角线的长分别为 4 cm 和 8 cm,求 它的边长. 【选自教材P26 复习题 第1题】
2 5 cm
2. 如图,若四边形 ABCD 的对角线 AC 与 BD 相交于点 О,
上册 小专题训练 特殊平行四边形的性质与判定-2020秋九年级北师大版数学全一册作业课件

17、只会幻想而不行动的人,永远也体会不到收获果实时的喜悦。 11、谁说“机会面前,人人平等”,新东方相信,个人奋斗制胜、攫取成功的精神财产将永远贫富不均。在浩瀚的生命之岸,你应该自豪地告诉
世界,你追求过,你奋斗过,你为辉煌的人生从来没有放弃过希望,从来没有停止过拼搏。而这个造就了万物的世界也将自豪而欣慰地回答你 :只要奋斗不息,人生终将辉煌。
9、强大的信心,能克服来自大自然和内心的恶魔,产生无往不胜的勇气。 71、从来就没有救世主也不靠神仙皇帝,要创造幸福生活必须全靠我们自已。 18. 世界会向那些有目标和远见的人让路。 13、自己打败自己是最可悲的失败,自己战胜自己是最可贵的胜利。 66、与其是无数遍地重温那个虚幻的玫瑰式的梦,还不如去一个静静的湖畔采一朵金黄色的野菊花。 17. 只有使自己自卑的心灵自信起来,弯曲的身躯才能挺直;只有使自己懦弱的体魄健壮起来,束缚的脚步才能迈开;只有使自己狭隘的心胸开 阔起来,短视的眼光才能放远;只有使自己愚昧的头脑聪明起来,愚昧的幻想才能抛弃! 10、彩虹绚烂多姿,是在与狂风暴雨争斗之后;枫叶似火燃烧,是在与秋叶的寒霜争斗之后;雄鹰的展翅高飞,是在与坠崖的危险争斗之后 。他们保持着奋斗的姿态,才铸就了他们的成功。
2020北师大版九年级数学上册 特殊平行四边形(重点知识点)

【文库独家】北师大版九上数学第一章特殊平行四边形(重点知识点)1、平行四边形(复习八下)(1)定义:两组对边分别平行的四边形是平行四边形.(2)性质平行四边形的邻角互补,对角相等;平行四边形的对边平行且相等;平行四边形的对角线互相平分;平行四边形是中心对称图形,对角线的交点为对称中心;附加:若一条直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交点为中点,且这条直线二等分平行四边形的面积;两平行线间的距离处处相等.(3)判定方法定义:两组对边分别平行的四边形是平行四边形;判定方法1:两组对边分别相等的四边形是平行四边形;判定方法2:对角线互相平分的四边形是平行四边形;判定方法3:一组对边平行且相等的四边形是平行四边形.2、矩形(1)定义:有一个内角是直角的平行四边形是矩形.(2)性质具有平行四边形的一切性质;矩形的四个角都是直角;矩形的对角线相等;矩形是轴对称图形;又是中心对称图形。
(3)、判定方法定义:有一个角是直角的平行四边形是矩形;判定方法1:有三个角是直角的四边形是矩形;判定方法2:对角线相等的平行四边形是矩形.3、菱形(1)定义:有一组邻边相等的平行四边形叫做菱形.(2)性质具有平行四边形的一切特征;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形.(3)判定方法定义:有一组邻边相等的平行四边形叫做菱形;判定方法1:四条边都相等的四边形是菱形;判定方法2:对角线互相垂直的平行四边形是菱形.4、正方形(1)定义:有一组邻边相等的矩形叫做正方形;(2)性质正方形具有四边形、平行四边形、矩形、菱形的一切特征.边——四边相等、邻边垂直、对边平行;角——四角都是直角;对角线——①相等,②互相垂直平分,③每条对角线平分一组对角;正方形是轴对称图形,有4条对称轴.(3)判定方法:判定一:一组邻边相等的矩形是正方形;判定二:一个角是直角的菱形是正方形.5、梯形(1)梯形的定义:一组对边平行且另一组对边不平行的四边形是梯形(2)梯形的性质及其判定;梯形是特殊的四边形所具有四边形所具有的一切性质,此外它的上下两底平行.一般用一组对边平行且不相等的四边形是梯形来判断.(3)等腰梯形的性质和判定:①性质:等腰梯形在同一底边上的两个内角相等,两腰相等,两底平行,两对角线相等,是轴对称图形,只有一条对称轴(底的中垂线就是它的对称轴).②判定方法:两腰相等的梯形是等腰梯形;同一底边上的两个角相等的梯形是等腰梯形;对角线相等的梯形是等腰梯形.(4)直角梯形:有一个角是直角的梯形叫做直角梯形.6、多边形的内外角和与外角和n边形内角和等于(n-2)·180°;任意多边形的外角和都等于360°.7、平面图形的密铺对于正多边形来说,只有正三角形、正方形和正六边形可以密铺.一般三角形、一般四边形有的也可以密铺.8、中心对称图形1·如果一个图形绕着它的中心点旋转180°后能与原图形重合,那么这个图形叫做中心对称图形,这个中心点叫做对称中心。
2020北师大版九年级数学上册 特殊平行四边形-正方形知识点2

【文库独家】北师大版九上数学第一章特殊平行四边形-正方形【基础知识概述】1.正方形定义:(1)有一组邻边相等并且有—个角是直角的平行四边形叫做正方形.(2)正方形既是有一组邻边相等的矩形,又是有—个角是直角的菱形.(3)既是矩形又是菱形的四边形是正方形.2.正方形的特征:正方形具有四边形、平行四边形、矩形、菱形的一切特征.(1)边——四边相等、邻边垂直、对边平行.(2)角——四角都是直角.(3)对角线——①相等;②互相垂直平分;③每条对角线平分一组对角.(4)是轴对称图形,有4条对称轴.3.正方形的识别方法:(1)一组邻边相等的矩形是正方形.(2)—个角是直角的菱形是正方形.4.正方形与矩形、菱形、平行四边形的关系:矩形、菱形、正方形都是特殊的平行四边形,它们的包含关系如图12-2-13.5.正方形的面积:正方形的面积等于边长的平方或者等于两条对角线乘积的一半.【例题精讲】例1如图12-2-14,已知过正方形ABCD对角线BD上一点P,作PE⊥BC于E,作PF ⊥CD于F.试说明AP=EF.分析:由PE⊥BC,PF⊥CD知,四边形PECF为矩形,故有EF=PC,这时只需证AP=CP,由正方形对角线互相垂直平分知AP=CP.解:连结AC、PC,∵四边形ABCD为正方形,∴BD垂直平分AC,∴AP=CP.∵PE⊥BC,PF⊥CD,∠BCD=90°,∴四边形PECF为矩形,∴PC=EF,∴AP=EF.注意:①在正方形中,常利用对角线互相垂直平分证明线段相等.②无论是正方形还是矩形经常通过连结对角线证题,这样可以使分散条件集中.思考:由上述条件是否可以得到AP⊥EF.提示:可以,延长AP交EF于N,由PE∥AB,有∠NPE=∠BAN.又∠BAN=∠BCP,而∠BCP=∠PFE,故∠NPE=∠PFE,而∠PFE+∠PEF=90°,所以∠NPE+∠PEF=90°,则AP⊥EF.例2如图12-2-15,△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB,试说明四边形BEDF是正方形.解:∵∠ABC=90°,DE⊥BC,∴DE∥AB,同理,DF∥BC,∴BEDF是平行四边形.∵BD平分∠ABC,DE⊥BC,DF⊥AB,∴DE=DF.又∵∠ABC=90°,BEDF是平行四边形,∴四边形BEDF是正方形.思考:还有没有其他方法?提示:(有一种方法可以证四边形DFBE为矩形,然后证BE=DE,可得.另一种方法,可证四边形DFBE为菱形,后证一个角为90°可得)注意:灵活选择正方形的识别方法.例3 如图12-2-16所示,四边形ABCD是正方形,△ADE是等边三角形,求∠BEC的大小.分析:等边三角形和正方形都能提供大量的线段相等和角相等,常能产生一些等腰三角形,十分便于计算.在本题中,必须注意等边三角形与正方形不同的位置关系.在(1)图中,△ABE和△DCE都是等腰三角形,顶角都是150°,可得底角∠AEB与∠DEC都是15°,则∠BEC为30°.而在(2)图中,等边三角形在正方形内部,△ABE和△DCE是等腰三角形,顶角是30°,可得底角∠AEB和∠DEC为75°,再利用周角可求得∠BEC=150°.解:(1)当等边△ADE在正方形ABCD外部时,AB=AE,∠BAE=90°+60°=150°,所以∠AEB=15°.同理可得∠DEC=15°,则∠BEC=60°-15°-15°=30°.(2)当等边△ADE在正方形ABCD内部时,AB=AE,∠BAE=90°-60°=30°,所以∠AEB=75°.同理可得∠DEC=75°,则∠BEC=360°-75°-75°-60°=150°.【中考考点】会用正方形的性质来解决有关问题,并能用正方形的定义来判断四边形是否为正方形.【命题方向】本节出题比较灵活,填空题、选择题、证明题均可出现.正方形是特殊的平行四边形,考查正方形的内容,实质上是对平行四边形知识的综合,涉及正方形知识的题型较多,多以证明题形式出现.【常见错误分析】已知如图12-2-18,△ABC中,∠C=90°,分别以AC和BC为边向外作正方形ACFH和正方形BCED,HM⊥BA的延长线于M,DK⊥AB的延长线于K.试说明AB=DK+HM.错解:延长DK到S,使KS=HM,连结SB.∵∠2=∠3,∠2+∠4=90°,∴∠3+∠4=90°.在△ABC和△SDB中,∵∠ACB=∠SBD=90°,BC=BD,∠2=90°-∠4=∠5∴△ABC与△SDB重合,∴AB=SD=SK+DK,即AB=HM+DK.分析指导:由于S、B、C三点共线未经证明,所以∠2=∠3的理由是不充足的,因此又犯了思维不严密的错误.正解:如图12-2-18,延长DK交CB延长线于S,下面证KS=MH.在△ACB和△SBD中,∵BD=BC,∠SBD=∠ACB=90°,又∠2=∠3=∠5,∴△ACB与△SBD重合,∴AB=DS,BS=AC=AH.在△BKS和△AMH中,∵∠1=∠2=∠3,∠AMH=∠SKB=90°,BS=AH,∴△BKS与△AMH重合,∴KS=HM,∴AB=DK+HM.【学习方法指导】正方形是最特殊的平行四边形,它既是一组邻边相等的矩形,又是有一个角为直角的菱形,所以它的性质最多,易混淆.故最好把平行四边形、矩形、菱形、正方形列表写出它们的定义、性质、判定,这样更容易记忆和区分.。
2020年北师大版九年级数学上册第一章特殊的平行四边形易错题专练(含详解)
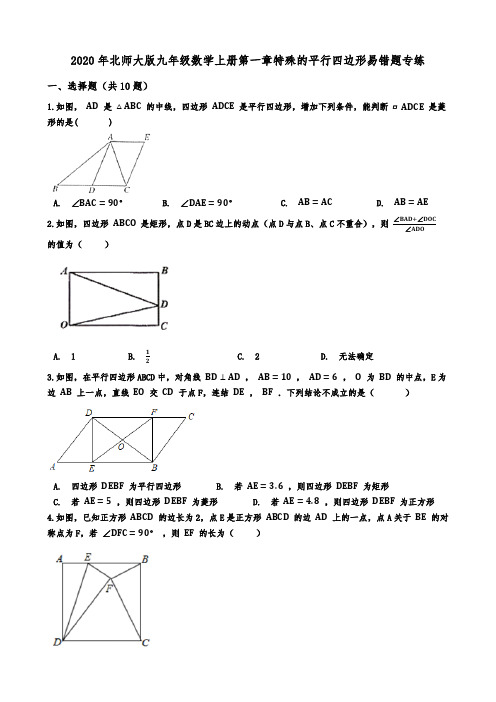
2020年北师大版九年级数学上册第一章特殊的平行四边形易错题专练一、选择题(共10题)1.如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断▱ADCE是菱形的是( )A. ∠BAC=90°B. ∠DAE=90°C. AB=ACD. AB=AE2.如图,四边形ABCO是矩形,点D是BC边上的动点(点D与点B、点C不重合),则∠BAD+∠DOC∠ADO的值为()C. 2D. 无法确定A. 1B. 123.如图,在平行四边形ABCD中,对角线BD⊥AD,AB=10,AD=6,O为BD的中点,E为边AB上一点,直线EO交CD于点F,连结DE,BF.下列结论不成立的是()A. 四边形DEBF为平行四边形B. 若AE=3.6,则四边形DEBF为矩形C. 若AE=5,则四边形DEBF为菱形D. 若AE=4.8,则四边形DEBF为正方形4.如图,已知正方形ABCD的边长为2,点E是正方形ABCD的边AD上的一点,点A关于BE的对称点为F,若∠DFC=90°,则EF的长为()A. 37B. 23C. 25D. 7105.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E. PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为()A. 4B. 245C. 6 D. 4856.如图,在平行四边形ABCD中,点O是对角线BD的中点,过点O作线段EF,使点E点F分别在边AD,BC上(不与四边形ABCD顶点重合),连结EB,EC设ED=kAE,下列结论:①若k=1,则BE=CE;②若k=2,则△EFC与△OBE面积相等:③若△ABE≌△FEC,则EF⊥BD.其中正确的是()A. ①B. ②C. ③D. ②③7.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF 上的点A′处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为()A. 12√3 B. 13√3 C. 14√3 D. 15√38.七巧板是大家熟悉的一种益智玩具,用七巧板能拼出许多有趣的图案.小李将块等腰直角三角形硬纸板(如图①)切割七块,正好制成一副七巧板(如图②),已知AB=40cm,则图中阴影部分的面积为()A. 25cm2B. 1003cm2 C. 50cm2 D. 75cm29.如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△ AA1A2;再以对角线OA2为边作第三个正方形OA2A3B3,连接A1A3,得到△ A1A2A3,再以对角线OA3为边作第四个正方形OA2A4B4,连接A2A4,得到△ A2A3A4,…,设△ AA1A2,△A1A2A3,△ A2A3A4,…,的面积分别为S1, S2, S3,…,如此下去,则S2020的值为()A. 122020B. 22018 C. 22018+ 12D. 101010.把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为()A. 7+3 √2B. 7+4 √2C. 8+3 √2D. 8+4 √2二、填空题(共8题)11.如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于12AB的长为半径作弧,两弧相交于M,N两点,直线MN交AD于点E,连接CE,则CE的长为________.12.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为________°.13.如图,矩形纸片ABCD,AB=6cm,BC=8cm,E为边CD上一点.将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN=________cm.14.如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=√2 HM;③在点M的运动过程中,四边形CEMD可能成为菱形;④无论点M运动到何处,∠CHM一定大于135°.以上结论正确的有________(把所有符合题意结论的序号都填上).15.如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为________.16.如图,菱形ABCD的边长是4,∠ABC=60°,点E,F分别是AB,BC边上的动点(不与点A,B,C重合),且BE=BF,若EG//BC,FG//AB,EG与FG相交于点G,当△ADG为等腰三角形时,BE的长为________.17.如图,正方形ABCD的边长为6,E是边AB的中点,F是边AD上的一个动点,EF=GF,且∠EFG=90°,则GB+GC的最小值为________.18.如图,在菱形纸片ABCD中,AB=3,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为________.三、解答题(共7题)19.如图,过平行四边形ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB、BC.CD、DA于点P、M、Q、N.(1)求证:△ PBE≌△ QDE;(2)顺次连接点P、M、Q、N,求证:四边形PMQN是菱形.20.如图1,在矩形ABCD中,AB=5,BC=8,点E,F分别为AB,CD的中点.(1)求证:四边形AEFD是矩形;(2)如图2,点P是边AD上一点,BP交EF于点O,点A关于BP的对称点为点M,当点M落在线段EF 上时,则有OB=OM.请说明理由;21.如图,正方形ABCD,G是BC边上任意一点(不与B、C重合),DE⊥AG于点E,BF//DE,且交AG于点F.(1)求证:AF−BF=EF;(2)四边形BFDE是否可能是平行四边形,如果可能请指出此时点G的位置,如不可能请说明理由.22.用周长相等的正方形ABCD和长方形AEFG,按如图所示的方式叠放在一起(其中点E在AB上,点G在AD延长线上,EF和DC交于点H),正方形ABCD的边长为m,长方形AEFG长为x,宽为y(y<m<x).(1)写出x、y 、m之间的等量关系;(2)求证:HC=HF;(3)若四边形DHFG为正方形,求x、y(用含有m的代数式表示);(4)比较四边形BEHC与四边形DHFG面积的大小,并说明理由.23.如图,在正方形ABCD中,E是CD边的中点,AC与BE相交于点F,连接DF.(1)在不增加点和线的前提下,直接写出图中所有的全等三角形;(2)连接AE,试判断AE与DF的位置关系,并证明你的结论;(3)延长DF交BC于点M,试判断BM与MC的数量关系.(直接写出结论)24.如图,正方形ABCD的边长为6.E,F分别是射线AB,AD上的点(不与点A重合),且EC⊥CF,M为EF的中点.P为线段AD上一点,AP=1,连结PM .(1)求证:CE=CF;(2)当△PMF为直角三角形时,求AE的长;(3)记BC边的中点为N,连结MN,若MN=√17,则△PMF的面积为________.(在横线上直接写出答案)25.如图1,矩形ABCD中,AB=3,BC=4 ,将矩形ABCD绕着点A顺时针旋转,得到矩形BEFG.(1)当点E落在BD上时,则线段DE的长度等于________ ;(2)如图2,当点E落在AC上时,求△ BCE的面积;(3)如图3,连接AE、CE、AG、CG,判断线段AE与CG的位置关系且说明理由,并求CE 2+AG 2的值;(4)在旋转过程中,请直接写出S△BCE+S△ABG的最大值.答案一、选择题1.解:A 、若 ∠BAC =90° ,则AD=BD=CD=AE ,∵四边形ADCE 是平行四边形,则此时四边形ADCE 为菱形,符合题意;B 、若 ∠DAE =90° ,则四边形ADCE 是矩形,不符合题意;C 、若 AB =AC ,则∠ADC=90°,则四边形ADCE 是矩形,不符合题意;D 、若 AB =AE ,而AB >AD ,则AE ≠AD ,无法判断四边形ADCE 为菱形,不符合题意. 故答案为:A.2.解:如图,过点D 作 DE//AB 交AO 于点E ,∵ 四边形 ABCO 是矩形 ∴AB//OC ∵DE//AB∴AB//DE,DE//OC ∴∠BAD =∠ADE,∠DOC =∠ODE∴∠BAD +∠DOC∠ADO=∠BAD +∠DOC ∠ADE +∠ODE=∠BAD +∠DOC ∠BAD +∠DOC=1故答案为:A.3.A.∵四边形ABCD 是平行四边形 ∴ DC//AB ∴ ∠FDO =∠EBO ∵ O 为 BD 的中点 ∴ DO =BO在 △FDO 与 △EBO 中 {∠FDO =∠EBODO =BO∠DOF =∠BOE ∴ △FDO ≅△EBO(ASA) ∴ DF =BE 又∵ DC//AB∴四边形 DEBF 为平行四边形, 故A 选项不符合题意; B.假设 DE ⊥AB∵ BD ⊥AD , AB =10 , AD =6∴BD=2−AD2=8∴S△ABD=12AD×BD=12×6×8=24∴DE=2S△ABDAB=4.8∵DE⊥AB∴AE=√AD2−DE2=3.6则当AE=3.6时,DE⊥AB∵四边形DEBF为平行四边形∴四边形DEBF为矩形,故B选项不符合题意;C.∵AE=5,AB=10∴E是AB中点∵BD⊥AD∴DE=AE=BE∵四边形DEBF为平行四边形∴四边形DEBF为菱形,故C选项不符合题意;D.当AE=4.8时与AE=3.6时矛盾,则DE不垂直于AB ,则四边形DEBF不为矩形,则也不可能为正方形,故D选项符合题意,故答案为:D.4.解:如图,延长EF交CD于M,连接BM,∵四边形ABCD是正方形,∴AB=BC,∠A=∠BCD=90°,∵将△ABE沿直线BE对折得到△BEF,∴∠A=∠BFE=∠BFM=90°,AB=BF=BC,在Rt △BFM与Rt △BCM中,{BF=BCBM=BM,∴Rt △BFM≌Rt △BCM(HL),∴MF=MC,∴∠MFC=∠MCF,∵∠MFC+∠DFM=90°,∠MCF+∠FDM=90°,∴∠MFD=∠MDF,∴MD=MF=MC ,∵正方形ABCD 的边长为2,∴MF=MC=DM=1,设AE=EF=x ,∵ DE 2+DM 2=EM 2 ,即 (2−x)2+12=(x +1)2,解得: x =23.∴EF =23.故答案为:B.5.解:连接BP ,∵菱形ABCD 的周长为20,∴AB=BC=20÷4=5,又∵菱形ABCD 的面积为24,∴S ABC =24÷2=12,又S ABC = S ABP +S CBP∴S ABP +S CBP =12,∴ 12AB •PF +12BC •PE =12 ,∵AB=BC ,∴ 12AB •(PE +PF)=12∵AB=5,∴PE+PF=12× 25 = 245 .故答案为:B.6.解:当k =1时,DE=AE ,不能证明△BAE ≌△CDE ,∴BE ≠CE ;故①错误;当k =2时,DE=2AE ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD=BC ,∵点O是BO的中点,∴OB=OD,∵∠EOD=∠FOB,∴△EOD≌△FOB,∴DE=BF,∴AD − DE=BC − BF,∴AE=CF,∴BF=2CF,∴SΔEFC=13SΔBEC=13•12S四边形ABCD=16S四边形ABCD,∵SΔBOE=SΔDOE=12SΔBDE,∴SΔBOE=16S四边形ABCD,∴SΔEFC=SΔBOE,故②正确;连接DF,如图:∵△ABE≌△FEC,∴AE=FC,∴DE=BF,∵DE∥BF,∴四边形DEBF是平行四边形,不能证明DEBF是菱形,∴EF与BD无法证明互相垂直,故③错误;∴正确的选项只有②;故答案为:B.7.解:∵EN=1,∴由中位线定理得AM=2,由折叠的性质可得A′M=2,∵AD∥EF,∴∠AMB=∠A′NM,∵∠AMB=∠A′MB,∴∠A′NM=∠A′MB,∴A′N=2,∴A′E=3,A′F=2∴NG=EN=1,∴A ′G=1,由勾股定理得MG= √22−12=√3 ,∴BE=DF=MG= √3 ,∴OF :BE=2:3,解得OF= 2√33 ,∴OD= √3 - 2√33 = √33 . 故答案为:B .8.解:如图,设OF =EF =FG =x ,∴OE =OH =2x ,在Rt △EOH 中,EH =2 √2 x ,由题意EH =20cm ,∴20=2 √2 x ,∴x =5 √2 ,∴阴影部分的面积=(5 √2 )2=50(cm 2), 故答案为:C .9.解:如图∴OA=AA1=A1B1=1,∴S1=12× 1×1=12,∵∠OAA1=90°,∴OA12=12+12=2,∴OA2=A2A3=2,∴S2=12× 2×1=1,同理可求:S3=12× 2×2=2,S4=4…,∴S n=2n﹣2,∴S2020=22018,故答案为:B.10.解:如图,过点M作MH⊥A′R于H,过点N作NJ⊥A′W于J.由题意△EMN是等腰直角三角形,EM=EN=2,MN=2√2,∵四边形EMHK是矩形,∴EK=A′K=MH=1,KH=EM=2,∵△RMH是等腰直角三角形,∴RH=MH=1,RM=√2,同法可证NW=√2,由题意AR=RA′=A′W=WD=4,∴AD=AR+RM+MN+NW+DW=4+ √2 + 2√2 + √2 +4=8+ 4√2,故答案为:D.二、填空题11.解:连接BE,如图:由题意可知,MN垂直平分AB,∴AE=BE,∴∠EBA=∠A=45°,则∠AEB=90°,在等腰直角三角形ABE中,AB=4,∴BE=AE= 2√2,∵四边形ABCD为菱形,∴∠EBC=∠AEB=90°,在Rt△BCE中,由勾股定理,则CE=√42+(2√2)2=2√6;故答案为:2√6 .12.解:∵四边形ABCD是正方形,∴∠ACB=∠BAC=45°,∴∠2+∠BCP=45°,∵∠1=∠2,∴∠1+∠BCP=45°,∵∠BPC=180°﹣∠1﹣∠BCP,∴∠BPC=135°,故答案为:135.13.解:连接AC,FC.由翻折的性质可知,BE垂直平分线段CF,∴FM⊥BE,∴F.M,C共线,FM=MC,∵AN=FN,∴MN=1AC,2∵四边形ABCD是矩形,∴∠ABC=90°,AC=5(cm),∴AC=√AB2+BC2=√62+82=10(cm),∴MN=12故答案为5.14.解:如图,连接DH,HM.由题可得,AM=BE,∴AB=EM=AD,∵四边形ABCD是正方形,EH⊥AC,∴EM=AD,∠AHE=90°,∠MEH=∠DAH=45°=∠EAH,∴△MEH≌△DAH(SAS),∴∠MHE=∠DHA,MH=DH,∴∠MHD=∠AHE=90°,△DHM是等腰直角三角形,∴DM=√2 HM,故②符合题意;当∠DHC=60°时,∠ADH=60°﹣45°=15°,∴∠ADM=45°﹣15°=30°,∴Rt△ADM中,DM=2AM,即DM=2BE,故①符合题意;∵CD∥EM,EC∥DM,∴四边形CEMD是平行四边形,∵DM>AD,AD=CD,∴DM>CD,∴四边形CEMD不可能是菱形,故③符合题意,∵点M是边BA延长线上的动点(不与点A重合),且AM<AB,∴∠AHM<∠BAC=45°,∴∠CHM>135°,故④符合题意;由上可得符合题意结论的序号为①②③.故答案为:①②③④.15.如图,过点A作AH⊥DF的延长线于点H,∵在正方形ABCD中,对角线AC与BD交于点O,∴O为AC中点∵F点是AE中点,∴OF是△ACE的中位线,∴CE=2OF=6∴G点是AD的中点,∴FG是△ADE的中位线,DE =1∴GF= 12∴CD=CE-DE=4,∴AD=CD=4∴AE= √42+22=2√5∴DF= 12 AE= √5∴S △AFD = 12 AD ·GF= 12 FD ·AH即 12 ×4×1= 12 × √5 ×AH∴AH= 4√55∴点A 到DF 的距离为 4√55 , 故答案为: 4√55 .16.解:如图,连接AC 交BD 于O ,∵菱形ABCD 的边长是4,∠ABC=60°,∴AB=BC=4,∠ABD=30°,AC ⊥BD ,BO=DO ,AO=CO ,∵EG ∥BC ,FG ∥AB ,∴四边形BEGF 是平行四边形,又∵BE=BF ,∴四边形BEGF 是菱形,∴∠ABG=30°,∴点B ,点G ,点D 三点共线,∵AC ⊥BD ,∠ABD=30°,∴AO= 12 AB=2,BO= √AB 2−AO 2=√42−22=2√3 ,∴BD= 4√3 ,AC=4,同理可求BG= √3 BE ,即BE= BG √3 , 若AD=DG'=4时, ∴BG'=BD-DG'= 4√3−4 ,∴BE' =√3−4√3=4−4√33 ;若AG''=G''D 时,过点G''作G''H ⊥AD 于H ,∴AH=HD=2,∵∠ADB=30°,G''H ⊥AD ,∵HD2+HG''2=DG''2,解得:HG'' =2√33,DG''=2HG'' =4√33,∴BG''=BD-DG''= 4√3−4√33=8√33,∴BE''= 83,综上所述:BE为83或4−4√33.17.解:如图,取AD的中点M,连接GM,延长MG交BC的延长线于J,在AB上截取AN,使得AN=AF,连接FN.作点C关于GJ的对称点K,连接GK,BK.∵四边形ABCD是正方形,∴AD=AB,∵AM=MD.AE=EB,∴AM=AE,∵AF=AN,∴FM=NE,∵∠A=∠GFE=90°,∴∠AFE+∠AEF=90°,∠AFE+∠GFM=90°,∠ANF=∠AFN=45°,∴∠GFM=∠FEN,∵FG=FE,∴△FGM≌△EFN(SAS),∴∠GMF=∠ENF,∵∠ANF=∠AFN=45°,∴∠GMF=∠FNE=135°,∴∠DMG=45°,设MJ交CD于R,∵∠D=∠JCR=90°,∴∠DMR=∠DRM=∠CRJ=∠CJR=45°,∴DM=DR=CR=CJ=3,∵C,K关于MJ对称,∴KJ=CJ=2,∠MJK=∠MJC=45°,GC=GK,∴BK= √KJ 2+BJ 2=√32+(3+6)2=3√10 , ∵GC+GB=GK+GB ≥BK ,∴GC+GB ≥3√10 ,∴GC+GB 的最小值为 3√10 ,故答案为: 3√10 .18.解:如图,连接BE ,BD ,∵四边形ABCD 为菱形,∠A =60°,∴AB =3=BC =CD ,∠A =60°=∠C ,∴△BCD 是等边三角形,∵E 是CD 中点,∴DE = 32 =CE ,BE ⊥CD ,∠EBC =30°, ∴BC=2CE=3∴BE = √BC 2−CE 2 = 32√3 ,∵CD ∥AB ,∴∠ABE =∠CEB =90°,由折叠可得AF =EF ,∵EF 2=BE 2+BF 2 ,∴EF 2= 274 +(3﹣EF )2,∴EF = 218 ,故答案为: 218 .三、解答题19. (1)证明:∵四边形ABCD 是平行四边形, ∴EB=ED ,AB ∥CD ,∴∠EBP=∠EDQ ,在△PBE 和△QDE 中,{∠EBP =∠EDQEB =ED ∠BEP =∠DEQ,∴△PBE ≌△QDE (ASA );(2)证明:如图所示:∵△PBE≌△QDE,∴EP=EQ,同理:△BME≌△DNE(ASA),∴EM=EN,∴四边形PMQN是平行四边形,∵PQ⊥MN,∴四边形PMQN是菱形.20. (1)证明:∵四边形ABCD是矩形,∴AB=CD,AB∥CD,∠A=90°,∵AE=EB,DF=FC,∴AE=DF,AE∥DF,∴四边形AEFD是平行四边形,∵∠A=90°,∴四边形AEFD是矩形.(2)解:如图2中,连接PM.BM.∵四边形AEFD是矩形,∴EF∥AD,∵BE=AE,∴BO=OP,由翻折可知,∠PMB=∠A=90°,∴OM=OB=OP.21. (1)证明:∵正方形ABCD,∴AB=AD,∠BAF+∠DAE=90°,∵DE⊥AG,∴∠ADE=∠BAF,又∵BF//DE,∴∠BFA=90°=∠AED,∴△ABF≌△DAE(AAS),∴AF=DE,AE=BF,∴AF−BF=AF−AE=EF;(2)不可能,理由是:如图,若要四边形BFDE是平行四边形,已知DE∥BF,则当DE=BF时,四边形BFDE为平行四边形,∵DE=AF,∴BF=AF,即此时∠BAF=45°,而点G不与B和C重合,∴∠BAF≠45°,矛盾,∴四边形BFDE不能是平行四边形.22. (1)解:∵正方形ABCD和长方形AEFG周长相等,∴4m=2x+2y,即x+y=2m;(2)解:∵HC=m−y,HF=x−m=2m−y−m=m−y,∴HC=HF;(3)解:∵四边形DHFG为正方形,∴DH=HF,即y=m−y,,解得y=m2m;∴x=2m−y=32(4)解:S BEHC=m(m−y),S DHFG=y(x−m)=y(2m−y−m)=y(m−y),∵m>y,∴m(m−y)>y(m−y),即S四边形BEHC>S四边形DHFG .23. (1)解:∵四边形ABCD是正方形,∴AB=AD=BC=DC,∠DAC=∠BAC=∠DCA=∠BCA=45°,又∵AF=AF,∴△ADF≌△ABF,∵AC=AC,∴△ADC≌△ABC,∵CF=CF,∴△CDF≌△CBF,∴全等的三角形有:△ADF≌△ABF,△ADC≌△ABC,△CDF≌△CBF. (2)解:AE⊥DF.证明:设AE与DF相交于点H.∵四边形ABCD是正方形,∴AD=AB,∠DAF=∠BAF.又∵AF=AF,∴△ADF≌△ABF.∴∠1=∠2.又∵AD=BC,∠ADE=∠BCE=90°,DE=CE,∴△ADE≌△BCE.∴∠3=∠4.∵∠2+∠4=90°,∴∠1+∠3=90°,∴∠AHD=90°.∴AE⊥DF.(3)解:如图,∵∠ADE=90°,AE⊥DF.∴∠1+∠5=90°,∠3+∠1=90°.∴∠3=∠5,∵∠3=∠4,∴∠4=∠5.∵DC=BC ,∠DCM=∠BCE=90°,∴△DCM ≌△BCE.∴CE=CM ,又∵E 为CD 中点,且CD=CB ,∴CE= 12 CD= 12 BC ,∴CM= 12 CB ,即M 为BC 中点,∴BM=MC.24. (1)证明:∵四边形ABCD 是正方形,∴BC=CD ,∠CBE=∠CDF=∠BCD=90°,又∵EC ⊥CF ,∴∠ECF=90°,∴∠ВСЕ+∠ECD=∠BCD=90°,∠DCF+∠ECD=∠ECF=90°,∴∠BCE=∠DCF ,在△BCE 和△DCF 中 { ∠BCE = ∠DCFBC =CD∠CBE = ∠CDF =90∘ , ∴△BCE ≌△DCF (ASA ),∴CE=CF ;(2)解:①当∠MPF=90°时,如图所示,,∵四边形ABCD是正方形,边长为6,∴AВ=AD=6,设BE=x,则由(1)得△BCE≌△DCF,∴DF=BE=x,∴AF=6-x,AE=6+x,又∵AP=1,∴PF=5-x,又∵M是EF中点,且MP⊥AD,AE⊥AD,∴MP//AE,MP= 12АE,∵PFAF =MPAE=12,∴5−x6−x =12,解得x=4,∴AЕ=6+4=10;②当∠PMF=90°时,如图所示,连接PE,设BE=DF=x,则АЕ=6-x,PF=5+x,∵M是EF中点,PM⊥EF,∴РЕ=PF=5+x,在Rt△AEP中,由勾股定理得AE2+AP2=PE2,∴(6-x)2+1=(5+x)2,解得x= 611 ,∴AE=6- 611 = 6011 ,故AE 的长为10或 6011 ;(3)7解:(3)如图,以A 为坐标原点,AD 为x 轴正半轴,AB 为y 轴正半轴建立直角坐标系,∵四边形ABCD 为正方形,边长为6,N 为BC 中点,AP=1,∴N (3,6),Р(1,0),设E (0,t ),则BE=|t-6|,∴F 的坐标为(12-t ,0),∵M 为EF 中点,∴M 的坐标为(6- 12 t , 12 t ),∴MN 2=( 12 t-3)2+( 12 t-6)2=( √17 )2 ,解得t 1=4,t 2=14,①当t=4时,点M 为(4,2),F 为(8,0),∴S △PMF = 12 (x F -x P )·y M = 12 ×7×2=7,②当t=14时,M 为(-1,7),F 为(-2,0),∵F 在射线AD 上,∴此时不符合题意,综上:△PMF 的面积为7,故答案为:7.25. (1)2(2)解:当点E 落在AC 上时,过点B 作BM ⊥AC 于点M ,在 RtΔABC 中,由勾股定理得:AC =√AB 2+BC 2=√32+42=5 ,∵ ΔABC 是直角三角形,BM ⊥AC ,∴ 12×3×4=12·BM ·AC ,∴ BM =125 ,在 RtΔBME 中,由勾股定理得:ME =√BE 2−BM 2=√32−(125)2=95 ,在 RtΔBMC 中,由勾股定理得:MC =√BC 2−BM 2=√42−(125)2=165 ,∴ CE =MC −ME =165−95=75 , ∴ S ΔBCE =12·CE ·BM =12×75×125=4225 ; (3)解:线段AE 与CG 的位置关系是垂直,理由如下:证明:连接AC 、EG ,设AE 与CG 相交于点N ,AE 与BC 相交于点P ,由旋转的性质知: ∠ABE =∠CBG , AB =BE ,BC =BG , ∴在等腰 ΔABE 和等腰 ΔCBG 中得到: ∠EAB =180°−∠ABE 2 , ∠BCG =180°−∠CBG 2 , ∴ ∠EAB =∠BCG ,∵ ∠1=∠2 ,∴ ∠CNP =∠ABP =90° ,即AE⊥CG;∵AE⊥CG,∴CE2+AG2=CN2+NE2+AN2+NG2=(CN2+AN2)+(NE2+NG2)=AC2+EG2,由矩形的性质可以得到:EG=AC=5,∴CE2+AG2=AC2+EG2=52+52=50;(4)解:过点C作CH⊥直线BE于点H,过点G作EQ⊥直线AB于点Q,∴SΔBCE=12·CH·BE,SΔABG=12·GQ·AB,∵AB=BE=3∴S△BCE+S△ABG=12·CH·BE+12·GQ·AB=12×3×(CH+GQ),∴当CH+GQ最大时,S△BCE+S△ABG最大,在旋转过程中,0≤CH≤4,0≤GQ≤4,∴0≤CH+GQ≤8,∴当点A、B、E三点共线时,CH+GQ=8,此时最大,∴S△BCE+S△ABG的最大值为:12×3×8=12 .解:(1)解:当E落在BD上时,如图所示:∵四边形ABCD是矩形,∴每个内角都等于90°,∵AB=3,BC=4,由勾股定理得:BD=√AB2+AD2=√AB2+BC2=√32+42=5,由旋转的性质可知:AB=BE=3,∴DE=BD−BE=5−3=2,故答案为:2;。
北师大版九年级数学上册第一章特殊平行四边形全部教案

第一章特殊平行四边形1菱形的性质与判定第1课时菱形的定义和性质1.经历从现实生活中抽象出图形的过程,了解菱形的概念及其与平行四边形的关系.2.体会菱形的轴对称性,经历利用折纸等活动探索菱形性质的过程,发展合情推理的能力.3.在证明菱形的性质和运用性质定理解决问题的过程中进一步发展学生的逻辑推理能力.重点理解并掌握菱形的概念与性质定理.难点菱形性质定理的证明及运用.一、情境导入课件出示教材第2页情境图,提出问题:你能从这几幅图中发现你熟悉的图形吗?你认为它们有什么样的共同特征呢?学生:图片中有八年级学过的平行四边形.教师:请同学们观察,这些平行四边形与下图的平行四边形ABCD相比较,还有什么不同点吗?学生:这些平行四边形不仅对边相等,而且任意两条邻边也相等.教师:同学们观察得很仔细.像这样,有一组邻边相等的平行四边形叫做菱形.二、探究新知1.菱形的性质教师:菱形是特殊的平行四边形,它具有一般平行四边形的所有性质.你能列举一些这样的性质吗?学生:菱形的对边平行且相等,对角相等,对角线互相平分.教师:同学们,你认为菱形还具有哪些特殊的性质?请你与同伴交流.学生讨论交流后,教师点评.教师:请同学们用菱形纸片折一折,回答下列问题:(1)菱形是轴对称图形吗?如果是,它有几条对称轴?对称轴之间有什么位置关系?(2)菱形中有哪些相等的线段?学生分小组进行折纸活动后讨论交流,回答问题,教师点评,并进一步讲解:①菱形是轴对称图形,有两条对称轴.对称轴是菱形对角线所在的直线,两条对角线互相垂直.②菱形的四条边相等.2.证明菱形的性质教师:通过折纸活动,同学们已经对菱形的性质有了初步的理解,下面我们要对菱形的性质进行严格的逻辑证明.课件出示:已知:如图,在菱形ABCD 中,AB =AD ,对角线AC 与BD 相交于点O. 求证:(1)AB =BC =CD =AD ;(2)AC ⊥BD.分析:①菱形不仅对边相等,而且邻边相等,这样就可以证明菱形的四条边都相等. ②因为菱形是平行四边形,所以点O 是对角线AC 与BD 的中点;又因为在菱形中可以得到等腰三角形,这样就可以利用“三线合一”来证明结论.学生写出证明过程,进行组内交流对比,教师点评. 证明:(1)∵四边形ABCD 是菱形,∴AB =CD ,AD =BC(菱形的对边相等). 又∵AB =AD ,∴AB =BC =CD =AD. (2)∵AB =AD ,∴△ABD 是等腰三角形. 又∵四边形ABCD 是菱形,∴OB =OD(菱形的对角线互相平分). 在等腰三角形ABD 中, ∵OB =OD , ∴AO ⊥BD ,即AC ⊥BD. 三、举例分析例 如图,在菱形ABCD 中,对角线AC 与BD 相交于点O, ∠BAD =60°,BD =6,求菱形的边长AB 和对角线AC 的长.分析:①因为菱形的邻边相等,一个内角是60°,所以可以得到等边△ABD ,BD =6,菱形的边长也是6.②由菱形的对角线互相垂直,可以得到直角△AOB ;由菱形的对角线互相平分,可以得到OB =3,根据勾股定理可以求出OA 的长度;再一次根据菱形的对角线互相平分,即AC =2OA ,求出AC 的长.解:∵四边形ABCD 是菱形, ∴AB =AD(菱形的四条边相等), AC ⊥BD(菱形的对角线互相垂直),OB =OD =12BD =12×6 =3(菱形的对角线互相平分).在等腰三角形ABD 中,∵∠BAD =60°,∴△ABD是等边三角形.∴AB=BD=6.在Rt△AOB中,由勾股定理,得OA2+OB2=AB2,∴OA=AB2-OB2=62-32=3 3.∴AC=2OA=63(菱形的对角线互相平分).四、练习巩固教材第4页“随堂练习”.五、小结1.什么叫做菱形?2.菱形有哪些性质?六、课外作业教材第4~5页习题1.1第1~4题.本节课的主要教学内容为菱形的定义和性质.学生已经学习了平行四边形的性质,这是本节课的知识基础.关于菱形的定义和性质,就是在平行四边形的基础上进一步强化条件得到的.课堂上通过折纸活动,让学生直观地感知图形的特点,激发学生学习的兴趣和积极性,教师要引导学生积极思考,抓住表面现象中的本质.在性质的证明和应用过程中,教师要鼓励学生大胆探索新颖独特的证明思路和方法,提倡证明方法的多样性,并引导学生在与其他同学的交流中进行证明方法的比较,优化证明方法,有利于提高学生的逻辑思维水平.第2课时菱形的判定1.探索证明菱形的判定方法,掌握证明的基本要求、方法及思路.2.经历运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,发展抽象思维.3.经历实际操作,探索菱形判定定理的证明过程,发展合情推理的能力.4.在具体问题的证明过程中,有意识地渗透试验论证、逆向思维的思想,提高学生解决问题的能力.重点菱形判定定理的证明及应用.难点菱形的判定方法的综合运用.一、复习导入1.菱形的定义是什么?2.菱形有哪些性质?教师:同学们对菱形的性质都掌握得很好,那么怎样判定一个四边形是菱形呢?这就是我们这节课所要研究的内容.二、探究新知1.菱形的判定方法一教师:根据菱形的定义,有一组邻边相等的平行四边形是菱形.这可以作为菱形的第一种判定方法.2.菱形的判定方法二课件出示:用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可动的十字,四周围上一根橡皮筋,做成一个四边形.教师转动木条,提出问题:(1)转动木条,这个四边形总有什么特征?(2)继续转动木条,什么时候橡皮筋围成的四边形变成菱形?引导学生猜想:当木条互相垂直时,平行四边形的一组邻边相等,此时四边形为菱形.教师:你能证明你的猜想吗?学生独立完成,指名板演,教师点评.已知:如图,在▱ABCD 中,对角线AC 与BD 相交于点O ,AC ⊥BD. 求证: ▱ABCD 是菱形.证明:∵四边形ABCD 是平行四边形, ∴OA =OC. 又∵AC ⊥BD ,∴BD 是线段AC 的垂直平分线. ∴BA =BC.∴四边形ABCD 是菱形(菱形的定义). 3.菱形的判定方法三教师:已知线段AC ,你能用尺规作图的方法作一个菱形ABCD ,使AC 为菱形的一条对角线吗?学生独立尝试作图,教师点评,并进一步讲解用尺规作菱形的方法:如图,分别以A ,C 为圆心,以大于12AC 的长为半径作弧,两条弧分别相交于点B ,D ,依次连接A ,B ,C ,D.教师:你能说明得到的四边形为什么是菱形吗?学生小组讨论交流,找到原因:该四边形四边相等. 教师:你能证明四边相等的四边形是菱形吗? 学生独立完成,指名板演,教师点评.已知:如图,在四边形ABCD 中,AB =BC =CD =DA. 求证: 四边形ABCD 是菱形.证明:∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.又∵AB=BC,∴四边形ABCD是菱形(菱形的定义).教师:你能用折纸等办法得到一个菱形吗?学生动手操作,教师巡视指导.三、举例分析例已知:如图,在▱ABCD中,对角线AC与BD相交于点O,AB=5,OA=2,OB=1.求证:▱ABCD是菱形.思考:(1)观察题目中的数据,AB,OA,OB有什么数量关系?(2)利用勾股定理的逆定理能否判定△ABO是直角三角形?(3)如果可以得到直角三角形,那么利用菱形的哪一个判定定理进行判断?四、练习巩固1.教材第7页“随堂练习”.2.教材第7页习题1.2第1题.五、小结1.怎样判定一个四边形是菱形?2.通过本节课的学习,你还学到了哪些知识?六、课外作业教材第7页习题1.2第2,3题.在本节课中,课前复习为本节课的探究作了有效的铺垫.学生资源的灵活运用提高了学生参与探究的兴趣,证明思路的分析过程让学生体会了逆向思维、一题多解等数学思想.另外,学生通过经历试验—猜想—证明—应用的探索过程提高了自身的科学素养.第3课时菱形的性质与判定的应用1.能灵活运用菱形的性质定理及判定定理解决一些相关问题,并掌握菱形面积的求法.2.经历菱形的性质定理及判定定理的应用过程,体会数形结合、转化等思想方法.重点菱形的性质定理与判定定理的综合应用及菱形面积的求法.难点等宽纸条交叉部分为菱形的证明及菱形面积的综合应用.一、复习导入1.如图①,在菱形ABCD中,AB=6.(1)求AD,DC,BC的长.(2)对角线AC与BD有什么位置关系?(3)若∠ADC =120°,求AC 的长.图①图②2.如图②,在▱ABCD 中添加一个条件使其成为菱形.添加方式1:________________________________________________________________________.添加方式2:________________________________________________________________________.二、探究新知 1.课件出示:如图,四边形ABCD 是边长为13 cm 的菱形,其中对角线BD 长10 cm .求:(1)对角线AC 的长度; (2)菱形ABCD 的面积.解:(1)∵四边形ABCD 是菱形,∴∠AED =90°(菱形的对角线互相垂直), DE =12BD =12×10=5(cm )(菱形的对角线互相平分).∴在Rt △ADE 中,由勾股定理可得:AE =AD 2-DE 2=132-52=12(cm ).∴AC =2AE =2×12=24(cm )(菱形的对角线互相平分). (2)S 菱形ABCD = S △ABD + S △CBD =2×S △ABD =2×12×BD ×AE=BD ×AE =10×12 =120( cm 2).注意:学生对于第一个问题的解决比较容易,但是学生的书写过程不规范;对于第二个问题,学生很容易求一边上的高,经过讨论、交流、点拨后学生能接受这种方法.在实际过程中教师应追问学生菱形的面积和对角线有什么关系,引起学生的思考,进而突破这一教学难点.2.课件出示教材第87页图1-7,提出问题:两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?为什么?分析:由图可知,重叠部分为平行四边形,且相邻的两边对应的高相等,由平行四边形的面积,可证平行四边形ABCD为菱形.三、举例分析例(变式训练)如上图,四边形ABCD是菱形,其中对角线BD长12 cm,AC长16 cm.求:(1)菱形的边长;(2)菱形一条边上的高.分析:灵活运用菱形的面积等于对角线乘积的一半求出面积进而求出一边上的高.教师:同学们,在我们刚才完成的例题及变式训练中你有什么感悟或经验?教师引导学生总结经验,帮助学生形成解题思路.四、练习巩固1.教材第9页“随堂练习”第1,2题.2.教材第10页习题1.3第5题.五、小结通过本节课的学习,你有哪些收获?还有什么疑问?六、课外作业1.教材第9页习题1.3第1~4题.2.如图,在四边形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求出此时菱形AECD的面积.本节课的教学内容是菱形的性质定理与判定定理的综合运用.通过课前复习,加深学生对菱形的性质定理及判定定理的记忆.在教学中,通过例题讲解,帮助学生总结经验并形成解题思路.学生对于几何题的规范答题是在课堂上需要重点强调的,这是培养学生严谨细致的数学素养的一个手段.同时,在教学中应注意学生解题的反思过程,例如由例题及变式训练完成反思过程后,学生的思维得到了升华,同时对于同类题目的突破方式有了初步的框架,能促进以后的学习,从本质上讲学习就是在学生不断反思中完成的.2矩形的性质与判定第1课时矩形的定义和性质1.了解矩形的概念,理解并掌握矩形的性质定理.2.经历探索矩形的概念和性质定理的过程,发展学生合情推理的意识.3.培养学生严谨的推理能力,掌握几何思维方法,体会逻辑推理的思维价值.重点矩形的性质定理的理解及应用. 难点矩形的性质定理的应用.一、情境导入课件出示教材第11页情境图,提出问题: 这三幅图片中都含有一些特殊的平行四边形.观察这些特殊的平行四边形,你能发现它们有什么样的共同特征?学生讨论交流后汇报,教师点评,并进一步讲解:有一个角是直角的平行四边形叫做矩形. 教师:你还能举出一些生活中矩形的例子吗? 二、探究新知1.探究矩形的性质定理教师出示一个平行四边形活动框架,完成以下探究.(1)改变平行四边形活动框架,将框架夹角∠α变为90°,平行四边形成为一个矩形,这说明平行四边形与矩形具有怎样的从属关系?学生:矩形是平行四边形的特例,属于平行四边形,因此它具有平行四边形所有的性质. (2)用橡皮筋做出两条对角线,这两条对角线有什么关系? 学生:橡皮筋的长度相等,因此矩形的两条对角线相等. (3)矩形是轴对称图形吗?如果是,它有几条对称轴? 学生:矩形是轴对称图形,它有2条对称轴.(4)你认为矩形还具有哪些特殊性质?学生:矩形的四个角都是直角,对角线相等. 教师:你能证明这些结论吗?学生独立完成,指名板演,教师点评,得到如下定理:矩形的四个角都是直角. 矩形的对角线相等.2.探究直角三角形的性质定理课件出示教材第12页图1-9,提出问题:如图,矩形ABCD 的对角线AC 与BD 交于点E ,那么BE 是Rt △ABC 中一条怎样的特殊线段?它与AC 有什么大小关系?由此你能得到怎样的结论?学生观察、思考后发现:AE =12AC ,BE =12BD ,BE 是Rt △ABC 的中线.由此归纳直角三角形的一个性质定理:直角三角形斜边上的中线等于斜边的一半. 三、举例分析例1 如图,在矩形ABCD 中,两条对角线相交于点O ,∠AOB =60°,AB =4 cm ,求这个矩形对角线的长.分析:利用矩形对角线相等且平分得到OA =OB ,由于∠AOB =60°,∴△AOB 为等边三角形,则OA =AB =4 cm ,∴AC =BD =2OA =8 cm .例2 如图,在△ABC 中,∠A =2∠B ,CD 是△ABC 的高,E 是AB 的中点,求证:DE =12AC.分析:本题可从E 是AB 的中点切入,考虑应用三角形中位线定理.应用三角形中位线必需找到另一个中点.可以取BC 的中点F ,也可以取AC 的中点G.学生分四人小组,合作探究不同的证法.证法一:取BC 的中点F ,连接EF ,DF ,如图①. ∵E 为AB 中点,∴EF ∥AC.∴∠FEB =∠A.∵∠A =2∠B ,∴∠FEB =2∠B.∵DF =12BC =BF ,∴∠1=∠B.∴∠FEB =2∠B =2∠1=∠1+∠2.∴∠1=∠2.∴DE =EF =12AC.证法二:取AC 的中点G ,连接DG ,EG ,如图②. ∵CD 是△ABC 的高,∴在Rt △ADC 中,DG =12AC =AG .∵E 是AB 的中点,∴GE ∥BC.∴∠1=∠B. ∴∠GDA =∠A =2∠B =2∠1.又∠GDA =∠1+∠2,∴∠1+∠2=2∠1. ∴∠2=∠1.∴DE =DG =12AC.四、练习巩固1.教材第13页“随堂练习”.2.如图,从矩形ABCD 的顶点C 作对角线BD 的垂线与∠BAD 的平分线相交于点E.求证:AC =CE.分析:要证AC =CE ,可以考虑证明∠E =∠CAE.∵AE 平分∠BAD ,∴∠DAE =∠BAE ,且∠CAE =∠DAE -∠DAC.另外一个条件是CE⊥BD,过点A作AF⊥BD于点F,则AF∥CE,可以将∠E转化为∠FAE,∠FAE=∠BAE-∠FAB.现在只要证明∠BAF=∠DAC即可,而实际上,∠BAF =∠BDA=∠DAC,问题迎刃而解.五、小结1.什么叫矩形?2.矩形有哪些性质?3.矩形有几条对称轴?六、课外作业教材第13~14页习题1.4第1~4题.本节课依据新课标的要求,设计的每个环节都是以学生为主体,在学生已有的知识经验的基础上,让学生自己动手探究完成,提高学生的探索创新思维和创造能力.首先,从矩形的定义和平行四边形的性质引入,提出问题,让学生猜想矩形应具有的性质,调动学生的思维积极性,激发探究欲望.教学过程中,先利用平行四边形活动框架,让学生通过观察、测量、思考、讨论等活动,得出矩形的性质.在解决问题的过程中发展了学生的合情推理意识.再引导学生进行推理证明及应用,通过探索证明,发展了学生的思维能力,帮助他们在自主探索与合作交流过程中真正理解和掌握矩形的性质定理,体验数学学习过程中的探索性、挑战性以及推理的严谨性.第2课时矩形的判定1.理解和掌握矩形的判定定理.2.经历探索、猜测、证明的过程,发展学生的推理论证能力.3.通过对比已学的知识,体会证明过程中所运用的归纳、概括以及转化等数学思想方法.重点理解和掌握矩形的判定定理.难点矩形的判定定理的应用.一、情境导入课前准备小木板和橡皮筋,制作一个如图所示的平行四边形活动框架.用两根橡皮筋分别套在两个相对的顶点上,拉动一对不相邻的顶点时,平行四边形的形状会发生什么变化?二、探究新知1.矩形的判定定理1根据上面的实践活动提出问题:(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?(2)当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?学生讨论交流后回答,教师点评,并归纳:矩形的判定定理1:对角线相等的平行四边形是矩形.矩形的判定定理1的证明过程:(1)学生独立画出图形,在教师引导下写出已知、求证;(2)对比平行四边形和菱形的判定定理的证明,对已知、求证进行分析;(3)请学生交流大体思路;(4)用规范的数学语言写出证明过程;(5)同学之间进行交流,找出自己还存在的问题.2.矩形的判定定理2教师:我们知道,矩形的四个角都是直角.反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?请证明你的结论,并与同伴交流.学生讨论交流后回答,教师点评,并引导学生归纳:矩形的判定定理2:有三个角是直角的四边形是矩形.矩形的判定定理2的证明过程:(1)学生独立画出图形,在教师引导下写出已知、求证;(2)对比平行四边形和菱形的判定定理的证明,对已知、求证进行分析;(3)请学生交流大体思路;(4)用规范的数学语言写出证明过程;(5)同学之间进行交流,找出自己还存在的问题.三、举例分析例1实际问题:(1)如果仅有一根足够长的绳子,如何判断一个四边形是平行四边形?(2)如果仅有一根足够长的绳子,如何判断一个四边形是菱形?(3)如果仅有一根足够长的绳子,如何判断一个四边形是矩形?学生分小组讨论后回答,教师点评,并总结:先利用“两组对边分别相等的四边形是平行四边形”证明是平行四边形,再由“对角线相等的平行四边形是矩形”得证.例2如图,在▱ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB =4,求▱ABCD的面积.学生独立完成,指名板演,教师点评.四、练习巩固1.教材第16页“随堂练习”.2. 已知:如图,在菱形ABCD中,对角线AC与BD相交于点O, CM∥BD,DM∥AC.求证:四边形OCMD是矩形.五、小结1.通过本节课的学习,你有什么收获?2.矩形的判定定理有哪些?六、课外作业教材第16页习题1.5第1~3题.对于本节课的知识,不能机械地照搬教材内容,而应该对教材内容进行再加工,灵活运用,使教材内容得到升华.课堂是学生展示自己的一个舞台,在课堂教学中,给予学生充分的时间和空间展示自己,不仅有利于提高学生学习的积极性,更有利于教师发现学生的独到见解和新思维、新想法,同时还能发现学生存在的问题,这对于课堂教学是非常有利的.几何教学对学生想象能力要求比较高,有些学生在这方面很有优势,而有些学生可能要差一点,课堂教学不能过急.此外,几何教学中要合理把握学生的课堂兴奋点,合理安排时间,力图让学生在注意力最集中时完成最重要的知识内容,掌握本节课重要的学习方法.还要注意的是,不要让思维活跃的学生的回答掩盖了其他学生的疑问,应该争取关注每一个学生.第3课时矩形的性质与判定的应用1.能够运用矩形的性质定理和判定定理解决问题.2.经历矩形的性质与判定的应用过程,发展学生的推理论证能力.3.通过学生独立完成证明的过程,让学生体会数学的严谨性.重点矩形的性质定理与判定定理的应用.难点灵活地运用矩形的性质定理与判定定理解决问题.一、复习导入1.如图①,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5 cm,则∠DAO=__________,AC=__________ cm,S矩形ABCD=__________ cm2.2. 如图②,四边形ABCD是平行四边形,添加一个条件________________,可使它成为矩形.二、探究新知课件出示:如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE.求AE的长.学生小组合作完成本题的求解,教师点评并板书:解:∵四边形ABCD是矩形,∴AO =BO =DO =12BD(矩形的对角线相等且互相平分),∠BAD =90°(矩形的四个角都是直角). ∵ED =3BE , ∴BE =OE.又∵ AE ⊥BD ,∴AB =AO.∴AB =AO =BO.即 △ABO 是等边三角形. ∴∠ABO =60°.∴∠ADB =90°-∠ABO =30°. 在Rt △AED 中, ∵∠ADE =30°, ∴AE =12AD =12×6=3.注意:本题的解法不唯一,采取小组合作时,应当鼓励学生提出自己不同的意见. 三、举例分析例 如图,在△ABC 中,AB =AC ,AD 为∠BAC 的平分线,AN 为△ABC 的外角∠CAM 的平分线,CE ⊥AN ,垂足为E.求证:四边形ADCE 是矩形.证明:∵AD 平分∠BAC ,AN 平分∠CAM , ∴∠CAD =12∠BAC ,∠CAN =12∠CAM.∴∠DAE =∠CAD +∠CAN =12(∠BAC +∠CAM)=12×180°=90°.在△ABC 中,∵AB =AC ,AD 为∠BAC 的平分线, ∴AD ⊥BC.∴∠ADC =90°. 又∵CE ⊥AN ,∴∠CEA =90°.∴四边形ADCE 为矩形(有三个角是直角的四边形是矩形). 四、练习巩固1.在上一题中,条件不变,连接DE ,交AC 于点F(如图①). (1)试判断四边形ABDE 的形状,并证明你的结论. (2)线段DF 与AB 有怎样的关系?请证明你的结论.图①2.如图②,四边形ABCD是由两个全等的等边△ABD和△CBD组成,点M,N分别是BC和AD的中点.求证:四边形BMDN是矩形.五、小结通过本节课的学习,你有什么收获?还有哪些疑问?六、课外作业教材第18~19页习题1.6第1~5题.的培养提到首位,达到本节课所要完成的真正目标.3正方形的性质与判定第1课时正方形的定义和性质1.理解正方形的概念和性质定理,通过由一般到特殊的研究方法,分析平行四边形、矩形、菱形、正方形的概念及性质之间的区别与联系.2.在探索正方形的性质定理的过程中,发展学生的合情推理能力.3.培养学生勇于探索、团结协作交流的精神,激发学生学习的积极性与主动性.重点理解正方形的定义和性质.难点选择适当的方法解决有关正方形的问题.一、情境导入教师:大家小时候都做过风车吗?在准备材料的时候,我们往往会先折一张正方形的纸片.那么大家能用一张长方形的纸片折出一个正方形吗?学生动手操作,引导学生在动手操作中对正方形产生感性认识,并感知正方形与矩形的关系.教师:结合菱形和矩形的定义,想一想,什么样的四边形是正方形?学生思考后回答,教师点评,并归纳:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.说明:其定义包括了两层意思:①有一组邻边相等的平行四边形(菱形);②有一个角是直角的平行四边形(矩形).所以说正方形既是菱形又是矩形.教师:这节课我们就来深入地了解正方形.(板书课题)二、探究新知教师:正方形都具有哪些性质呢?学生:由正方形的定义可知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.所以它应该具备菱形和矩形的所有性质.教师:你能详细说一说正方形的性质吗?学生:正方形的四个角都是直角,四条边都相等.正方形的两条对角线相等并且互相垂直平分.由学生的回答归纳出:正方形的性质定理1:正方形的四个角都是直角,四条边相等.正方形的性质定理2:正方形的对角线相等且互相垂直平分.教师:同学们能尝试完成这两个定理的证明吗?学生独立完成,并相互交流,教师点评.教师:正方形有几条对称轴?学生思考或者画图验证.三、举例分析例1如图,在正方形ABCD 中,E 为CD 边上一点,F 为BC 延长线上一点,且CE =CF.BE 与DF 之间有怎样的关系?请说明理由.解:BE =DF,且BE⊥DF.理由如下:(1)∵四边形ABCD 是正方形,∴BC =DC,∠BCE =90°(正方形的四条边相等,四个角都是直角).∴∠DCF =180°-∠ BCE =180°-90°=90°.∴∠BCE =∠ DCF.又∵ CE =CF,∴△BCE ≌△DCF.∴BE =DF.(2)延长BE 交DF 于点M(如图).∵△BCE ≌△DCF,∴∠CBE =∠ CDF.∵∠DCF =90°,∴∠CDF +∠ F =90°.∴∠CBE +∠ F =90°.∴∠BMF=90°.∴BE⊥DF.例2平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗?与同伴交流.学生尝试画图,教师点评,并进一步讲解,课件出示如下图:四、练习巩固1.如图,在正方形ABCD中,对角线AC与BD相交于点O,图中有多少个等腰三角形?。
上册 小专题训练 特殊平行四边形的性质与判定-2020秋九年级北师大版数学全一册作业课件
2. 走过了千山万水,我们才慢慢的懂得:没有人喜欢孤独,虽然。我们不得不承认,这就是爱情,这就是生活。
15. 乐观者在灾祸中看到机会;悲观者在机会中看到灾祸。 9. 叹气是最浪费时间的事情,哭泣是最浪费力气的行径。 5. 一个人的快乐,不是因为他拥有的多,而是因为他计较的少。 20. 茂盛的禾苗需要水分;成长的少年需要学习。 4. 干涉原则,就是不以人的好恶之心刻意去添减改变大自然。 10. 征服畏惧、建立自信的最快最确实的方法,就是去做你害怕的事,直到你获得成功的经验。 12. 销售世界上第一号的产品——不是汽车,而是自己。在你成功地把自己推销给别人之前,你必须百 19. 人生最精彩的不是实现梦想的瞬间,而是坚持梦想的过程。 13. 相信就是强大,怀疑只会抑制能力,而信仰就是力量。 6. 没有什么事情有象热忱这般具有传染性,它能感动顽石,它是真诚的精髓。 14. 人之所以平凡,在于无法超越自己。 4. 不怕路远,就怕志短 15. 大场面也许可以看出性格然而是小事件在培养性格 3. 人性最可怜的就是:我们总是梦想着天边的一座奇妙的玫瑰园,而不去欣赏今天就开在我们窗口的玫瑰。 5. 读一书,增一智。(?) 6. 仍然在途中,只好相信雨過後有彩虹。 11. 生命不是要超越别人,而是要超越自己。 14. 不吃饭则饥,不读书则愚。
