人教版八年级上册第11章三角形课件第十一章 数学活动
合集下载
最新人教部编版八年级数学上册《第十一章 三角形【全章】》精品PPT优质课件

2.完成练习册本课时内容。
学习体会 1、本节课你学到了哪些基本知识? 2、本节课你学到了哪些解题方法? 3、还有哪些知识和方法上的问题?
Thank you!
Good Bye!
11.1 与三角形有关的线段
即三角形两边的和大于第三边. B
C
由不等式②③移项可得 BC >AB -AC, BC >AC -AB.由此你能得出什么结论?
A
三角形两边的差小于第三边.
B
C
问题:下列长度的三条线段能否组成三角形?为 什么?(1)3,4,5;(2)5,6,11;(3)5,6,10. 解:(1)能.因为3 + 4>5,3 + 5>4,4 + 5>3,
解:①如果 4 cm 长的边为底边,设腰长为 x cm,则
4 + 2x = 18. 解得 x = 7. ②如果 4 cm 长的边为腰,设底边长为 x cm,则
4×2 + x = 18. 解得 x = 10.
因为4 + 4<10,不符合三角形两边的和大于第 三边,所以不能围成腰长为 4 的等腰三角形.
基础巩固
随堂演练
1.下列说法:①等边三角形是等腰三角形;②
三角形按边分类可分为等腰三角形、等边三角形、
不等边三角形;③三角形的两边之差大于第三边;
④三角形按角分类应分为锐角三角形、直角三角
形、钝角三角形. 其中正确的有( B )
A.1个
B.2个
C.3个
D.4个
2.已知三角形的一边长为 5 cm,另一 边长为 3 cm .则第三边的长 x 的取值范围是 __2_c_m__<__x_<__8_c_m___.
拓展延伸 3.等腰三角形的周长为 20 厘米. (1)若已知腰长是底长的 2 倍,求各边的长; (2)若已知一边长为 6 厘米,求其他两边的长.
学习体会 1、本节课你学到了哪些基本知识? 2、本节课你学到了哪些解题方法? 3、还有哪些知识和方法上的问题?
Thank you!
Good Bye!
11.1 与三角形有关的线段
即三角形两边的和大于第三边. B
C
由不等式②③移项可得 BC >AB -AC, BC >AC -AB.由此你能得出什么结论?
A
三角形两边的差小于第三边.
B
C
问题:下列长度的三条线段能否组成三角形?为 什么?(1)3,4,5;(2)5,6,11;(3)5,6,10. 解:(1)能.因为3 + 4>5,3 + 5>4,4 + 5>3,
解:①如果 4 cm 长的边为底边,设腰长为 x cm,则
4 + 2x = 18. 解得 x = 7. ②如果 4 cm 长的边为腰,设底边长为 x cm,则
4×2 + x = 18. 解得 x = 10.
因为4 + 4<10,不符合三角形两边的和大于第 三边,所以不能围成腰长为 4 的等腰三角形.
基础巩固
随堂演练
1.下列说法:①等边三角形是等腰三角形;②
三角形按边分类可分为等腰三角形、等边三角形、
不等边三角形;③三角形的两边之差大于第三边;
④三角形按角分类应分为锐角三角形、直角三角
形、钝角三角形. 其中正确的有( B )
A.1个
B.2个
C.3个
D.4个
2.已知三角形的一边长为 5 cm,另一 边长为 3 cm .则第三边的长 x 的取值范围是 __2_c_m__<__x_<__8_c_m___.
拓展延伸 3.等腰三角形的周长为 20 厘米. (1)若已知腰长是底长的 2 倍,求各边的长; (2)若已知一边长为 6 厘米,求其他两边的长.
秋人教版八年级数学上册课件:第十一章 三角形 11.3.1 多边形(共23张PPT)

18
多边形的分类
A
在图1中,画出任意一边所在的
D
直线,整个多边形都在直线的
同侧,这样的多边形叫做凸多 B 图1 C 边形.
图2中,多边形ABCD不在CD A 所在直线的同侧,就不是凸多
边形,叫凹多边形.
没有特别说明,我们研究的 多边形都是指凸多边形.
C
B
图 2
D
19
正多边形
正方形的各个角都相等,各条 边都相等。
•
16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021年9月14日星期二5时26分6秒17:26:0614 September 2021
•
17、儿童是中心,教育的措施便围绕他们而组织起来。下午5时26分6秒下午5时26分17:26:0621.9.14
正三角形 正方形
菱形
矩形
21
合作完成
如图,在正方形ABCD中,你能用五种不 同的方法把正方形面积四等分吗?
A
D
B
C
22
脑筋急转弯
一张桌子有四个角,如果锯掉一个角还有多少个角?
5个
答案:3个、 4个 或5个!
4个
3个
23
课堂小结
1、多边形的定义 在平面内,由一些线段首尾顺次相接组成的图形
2、多边形的内角
形。
n3
自学课本P19、20页,回答以下问题: 问题二:
(1)什么叫多边形的内角?什么叫多边 形的外角?n 边形有几个内角、几个外角?
(2)什么叫多边形的对角线?你能说出 一些常见多边形的对角线的条数吗? (3)你还有什么疑惑或提出其它问题吗?
12
可表示为:五边形ABCDE或五边形AEDCB
多边形的分类
A
在图1中,画出任意一边所在的
D
直线,整个多边形都在直线的
同侧,这样的多边形叫做凸多 B 图1 C 边形.
图2中,多边形ABCD不在CD A 所在直线的同侧,就不是凸多
边形,叫凹多边形.
没有特别说明,我们研究的 多边形都是指凸多边形.
C
B
图 2
D
19
正多边形
正方形的各个角都相等,各条 边都相等。
•
16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021年9月14日星期二5时26分6秒17:26:0614 September 2021
•
17、儿童是中心,教育的措施便围绕他们而组织起来。下午5时26分6秒下午5时26分17:26:0621.9.14
正三角形 正方形
菱形
矩形
21
合作完成
如图,在正方形ABCD中,你能用五种不 同的方法把正方形面积四等分吗?
A
D
B
C
22
脑筋急转弯
一张桌子有四个角,如果锯掉一个角还有多少个角?
5个
答案:3个、 4个 或5个!
4个
3个
23
课堂小结
1、多边形的定义 在平面内,由一些线段首尾顺次相接组成的图形
2、多边形的内角
形。
n3
自学课本P19、20页,回答以下问题: 问题二:
(1)什么叫多边形的内角?什么叫多边 形的外角?n 边形有几个内角、几个外角?
(2)什么叫多边形的对角线?你能说出 一些常见多边形的对角线的条数吗? (3)你还有什么疑惑或提出其它问题吗?
12
可表示为:五边形ABCDE或五边形AEDCB
人教版八年级数学上册课件:第十一章三角形 11.2 第一

A. 30° C. 120°
B. 60° D. 140°
课前预习
5. 如图11-2-1,BE,CF都是△ABC的角平分线,且 ∠BDC=110°,则∠A= 40° .
课堂讲练
新知1 三角形的内角
典型例题
【例1】 如图11-2-2,在△ABC中,∠A=60°,∠B=40°,
点D,E分别在BC,AC的延长线上,则∠1=
3. 如图11-2-7,∠1+∠2+∠3+∠4的度数为 360°.
课后作业
4. 如图11-2-8,在△ABC中,将∠C沿DE折叠,使顶点C
落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,
则∠2的度数为
. 40°
5. 在△ABC中,∠B,∠C的平分线交于点O,若 ∠BOC=132°,则∠A= 84° .
课后作业
解:(1)60° (2)没变化. 理由如下: ∵在△ABC中,∠A=30°, ∴∠ABC+∠ACB=180°-30°=150°. ∵∠BXC=90°, ∴∠XBC+∠XCB是一个定值,等于90°. ∴∠ABX+∠ACX=150°-(∠XBC+∠XCB)=60°. ∴∠ABX+∠ACX的大小无变化.
.
80°
课堂讲练
模拟演练 1. 如图11-2-3,AD是∠CAE的平分线,∠B=35°, ∠DAE=60°,则∠ACD=( D )
A. 25° C. 60°
B. 85° D. 95°
课堂讲练
新知2 直角三角形
典型例题
【例2】如图11-2-4,在△ABC中,∠BAC=50°,∠B=60°,
AE⊥BC于点E,CD平分∠ACB且分别与AB,AE交于点D,F,求 ∠AFC的度数.
A. 45° C. 45°或135°
八年级数学上册第十一章三角形本章小结课件新版新人教版

A组
布置作业
作业1 欣赏下面两组美丽的图案,看看中间空缺 处应补上什么图形才完成平面镶嵌?
B组
布置作业
作业2 根据所学知识,请你设计一个正多边形镶 嵌的图案.
作业3 回顾本节学习活动的过程,写一篇关于 “镶嵌”知识的小论文.
探究多边形能平面镶嵌的条件
问题3 在边长相等的正三角形、正方形、正五边 形、正六边形中取一种正多边形镶嵌,哪几种正多边形 可以进行平面镶嵌?
(1) 正三角形 、 正方形 、 正六边形 能单独 镶嵌, 正五边形 不能单独镶嵌.
(2)用同种正多边形能进行镶嵌的条件是 _a_x_=_3_6_0°__,_x_表__示__正_多__边_形__的_每__一_个__内__角_的__度__ _数_,__a_表__示_正__多_边__形_的__个__数 .
探究多边形能平面镶嵌的条件
问题4 在边长相等的正三角形、正方形、正五边 形、正六边形中取两种正多边形镶嵌,哪两种正多边形 可以进行平面镶嵌?
设 n 表示正多边形的边数. (1) n =3和4 、n = 3和6 能镶嵌,
_n =_3_和_5,_n_=_4和_5_,_n_=_4和_6_,_n_= 5_和_6不能镶 嵌.
探究多边形能平面镶嵌的条件
问题5 用形状、大小相同的三角形能否进行平面 镶嵌?四边形呢?
课堂小结
(1)解决本节课中的问题,用到了什么数学知识? (2)你能举出多边形镶嵌平面的例子,并指出为什么
可以进行镶嵌吗?
布置作业
作业1 欣赏下面两组美丽的图案,看看中间空缺 处应补上什么图形才完成平面镶嵌?
探究多边形能平面镶嵌的条件
问题4 在边长相等的正三角形、正方形、正五边 形、正六边形中取两种正多边形镶嵌,哪两种正多边形 可以进行平面镶嵌?
布置作业
作业1 欣赏下面两组美丽的图案,看看中间空缺 处应补上什么图形才完成平面镶嵌?
B组
布置作业
作业2 根据所学知识,请你设计一个正多边形镶 嵌的图案.
作业3 回顾本节学习活动的过程,写一篇关于 “镶嵌”知识的小论文.
探究多边形能平面镶嵌的条件
问题3 在边长相等的正三角形、正方形、正五边 形、正六边形中取一种正多边形镶嵌,哪几种正多边形 可以进行平面镶嵌?
(1) 正三角形 、 正方形 、 正六边形 能单独 镶嵌, 正五边形 不能单独镶嵌.
(2)用同种正多边形能进行镶嵌的条件是 _a_x_=_3_6_0°__,_x_表__示__正_多__边_形__的_每__一_个__内__角_的__度__ _数_,__a_表__示_正__多_边__形_的__个__数 .
探究多边形能平面镶嵌的条件
问题4 在边长相等的正三角形、正方形、正五边 形、正六边形中取两种正多边形镶嵌,哪两种正多边形 可以进行平面镶嵌?
设 n 表示正多边形的边数. (1) n =3和4 、n = 3和6 能镶嵌,
_n =_3_和_5,_n_=_4和_5_,_n_=_4和_6_,_n_= 5_和_6不能镶 嵌.
探究多边形能平面镶嵌的条件
问题5 用形状、大小相同的三角形能否进行平面 镶嵌?四边形呢?
课堂小结
(1)解决本节课中的问题,用到了什么数学知识? (2)你能举出多边形镶嵌平面的例子,并指出为什么
可以进行镶嵌吗?
布置作业
作业1 欣赏下面两组美丽的图案,看看中间空缺 处应补上什么图形才完成平面镶嵌?
探究多边形能平面镶嵌的条件
问题4 在边长相等的正三角形、正方形、正五边 形、正六边形中取两种正多边形镶嵌,哪两种正多边形 可以进行平面镶嵌?
人教版初中数学八年级上册第十一章 全等三角形 11.2三角形全等的判定课件
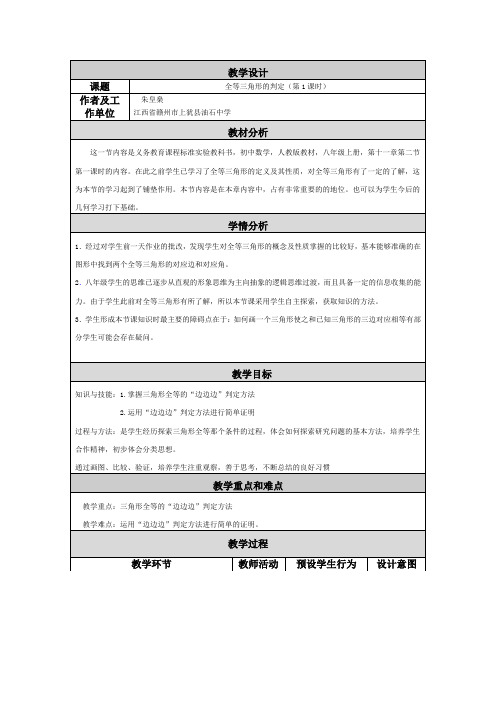
一、复习全等三角形概念及性质如图,如果△ABC≌△A′B′C′,那么请找出图中相等的线段和相等的角,并说明理由。
A′ABCB′C′二、新课导入又上节课内容可知如果△ABC≌△A′B′C′一定满足 AB= A′B′,BC= B′C′,AC= A′ C′∠A=∠ A′,∠B=∠ B′,∠C=∠ C那反过来,如果两个三角形满足这六个条件,那么这两个三角形全等吗?那满足上述条件中的一部分能否保证两个三角形全等呢?三、学生探究问题1:△ABC和△A′B′C′满足以上条件中的一个有几种情况?满足两个有几种情况?问题2,:既然△ABC和△A′B′C′满足以上条件中的一个或两个都不一定能证明这两个三角形全等,那满足三个条件可以吗?教师提问并根据实际情况找学生回答提出问题教师引导学生从角和边两个方面分析一个条件,两个条件各有几种可能。
教师引导学生找出三个条件共有哪些情况教师提问,先让学生试着自己画图,然后给出正确画法。
学生回答:AB= A′B′BC= B′C′AC= A′ C′∠A=∠ A′∠B=∠ B′∠C=∠ C′理由:全等三角形的对应角相等。
全等三角形的对应边相等。
学生思考后回答:全等学生产生疑问,从而进一步探索学生动手实践,尽量举出反例,得出由一个或两个条件不一定能得到全等的结论。
学生主动思考三个条件时可以出现哪些情况。
学生先根据自己的想法画两个三边对应相等的三角形,遇到问题后找老师解决。
然后观察思考并得出结论“SSS”。
复习并为本节内容奠定基础使学生明确探究方向并且激发学生兴趣学生自己实践得到一个或两个条件不能证明全等,加深学生对此知识的理解。
学生自己找出不同情况,有助于学生理解和后续三角形全等的其他判定方法的引出以学生探究为主,注重过程和学生的亲身体验,培养学生碳素,发现的能力。
人教版八年级数学上册第11章数学活动镶嵌优课件

正三角形和正方形能镶嵌 正三角形和正六边形能镶嵌
60°×3+90°×2=360°
60°×4 + 120°=360° 60°×2+120°×2=360°
正方形和正六边形不能镶嵌
正方形和正八想
正三角形和正十 二边形能否镶嵌?
正八边形和正方形 正十二边形和正三角形
90° 135° 135°
60°
150° 150°
3
1
2
4 3
1
2
探究3:
用几个形状、大小相同的任意三 角形能镶嵌成一个平面图案吗?四 边形呢?
2 31
3
1
2
3
1
2
3
1
2
23
1
1
32
23
1
3
1
2
3
1
2
∵ ∠1+∠2+∠3=180° ∴2(∠1+∠2+∠3)=360°
所以 任意三角形能镶嵌成平面图案
2 34
1 43
1
2
4
3
1
2
2 34 1
1 43 2
4
3
1
2
因为 ∠1+∠2+∠3+∠4=360°
所以任意四边形能 镶嵌成平面图案
归纳
1 .平面镶嵌的条件是:拼接在同一 个点的各个角的和等于360度 .
2 .任意三角形一定可以镶嵌. 任意四 边形一定可以镶嵌.在正多边形里只 有正三角形、正四边形、正六边形可 以镶嵌,而其他的正多边形不可镶 嵌. 3 .正三角形和正方形、正三角形和正 六边形、正八边形和正方形、正十二边 形和正三角形能镶嵌.
把平面的一部分完全覆盖,叫做用多边 形覆盖平面或平面镶嵌.
60°×3+90°×2=360°
60°×4 + 120°=360° 60°×2+120°×2=360°
正方形和正六边形不能镶嵌
正方形和正八想
正三角形和正十 二边形能否镶嵌?
正八边形和正方形 正十二边形和正三角形
90° 135° 135°
60°
150° 150°
3
1
2
4 3
1
2
探究3:
用几个形状、大小相同的任意三 角形能镶嵌成一个平面图案吗?四 边形呢?
2 31
3
1
2
3
1
2
3
1
2
23
1
1
32
23
1
3
1
2
3
1
2
∵ ∠1+∠2+∠3=180° ∴2(∠1+∠2+∠3)=360°
所以 任意三角形能镶嵌成平面图案
2 34
1 43
1
2
4
3
1
2
2 34 1
1 43 2
4
3
1
2
因为 ∠1+∠2+∠3+∠4=360°
所以任意四边形能 镶嵌成平面图案
归纳
1 .平面镶嵌的条件是:拼接在同一 个点的各个角的和等于360度 .
2 .任意三角形一定可以镶嵌. 任意四 边形一定可以镶嵌.在正多边形里只 有正三角形、正四边形、正六边形可 以镶嵌,而其他的正多边形不可镶 嵌. 3 .正三角形和正方形、正三角形和正 六边形、正八边形和正方形、正十二边 形和正三角形能镶嵌.
把平面的一部分完全覆盖,叫做用多边 形覆盖平面或平面镶嵌.
人教版八年级上册第十一章 三角形全章课件(共8份)6
1、不是井里没有水,而是你挖的不够深。不是成功来得慢,而是你努力的不够多。 2、孤单一人的时间使自己变得优秀,给来的人一个惊喜,也给自己一个好的交代。 3、命运给你一个比别人低的起点是想告诉你,让你用你的一生去奋斗出一个绝地反击的故事,所以有什么理由不努力! 4、心中没有过分的贪求,自然苦就少。口里不说多余的话,自然祸就少。腹内的食物能减少,自然病就少。思绪中没有过分欲,自然忧就少。大悲是无泪的,同样大悟无言。缘来尽量要惜,缘尽就放。人生本来就空,对人家笑笑,对自己笑笑,笑着看天下,看日出日落,花谢花开,岂不自在,哪里来的尘埃! 5、心情就像衣服,脏了就拿去洗洗,晒晒,阳光自然就会蔓延开来。阳光那么好,何必自寻烦恼,过好每一个当下,一万个美丽的未来抵不过一个温暖的现在。 6、无论你正遭遇着什么,你都要从落魄中站起来重振旗鼓,要继续保持热忱,要继续保持微笑,就像从未受伤过一样。 7、生命的美丽,永远展现在她的进取之中;就像大树的美丽,是展现在它负势向上高耸入云的蓬勃生机中;像雄鹰的美丽,是展现在它搏风击雨如苍天之魂的翱翔中;像江河的美丽,是展现在它波涛汹涌一泻千里的奔流中。 8、有些事,不可避免地发生,阴晴圆缺皆有规律,我们只能坦然地接受;有些事,只要你愿意努力,矢志不渝地付出,就能慢慢改变它的轨迹。 9、与其埋怨世界,不如改变自己。管好自己的心,做好自己的事,比什么都强。人生无完美,曲折亦风景。别把失去看得过重,放弃是另一种拥有;不要经常艳羡他人,人做到了,心悟到了,相信属于你的风景就在下一个拐弯处。 10、有些事想开了,你就会明白,在世上,你就是你,你痛痛你自己,你累累你自己,就算有人同情你,那又怎样,最后收拾残局的还是要靠你自己。 11、花开不是为了花落,而是为了开的更加灿烂。 12、随随便便浪费的时间,再也不能赢回来。 13、不管从什么时候开始,重要的是开始以后不要停止;不管在什么时候结束,重要的是结束以后不要后悔。 14、当你决定坚持一件事情,全世界都会为你让路。 15、只有在开水里,茶叶才能展开生命浓郁的香气。 16、别想一下造出大海,必须先由小河川开始。 17、不要让未来的你,讨厌现在的自己,困惑谁都有,但成功只配得上勇敢的行动派。 18、人生最大的喜悦是每个人都说你做不到,你却完成它了! 19、如果你真的愿意为自己的梦想去努力,最差的结果,不过是大器晚成。 20、不忘初心,方得始终。 11、失败不可怕,可怕的是从来没有努力过,还怡然自得地安慰自己,连一点点的懊悔都被麻木所掩盖下去。不能怕,没什么比自己背叛自己更可怕。 12、跌倒了,一定要爬起来。不爬起来,别人会看不起你,你自己也会失去机会。在人前微笑,在人后落泪,可这是每个人都要学会的成长。 13、要相信,这个世界上永远能够依靠的只有你自己。所以,管别人怎么看,坚持自己的坚持,直到坚持不下去为止。 14、也许你想要的未来在别人眼里不值一提,也许你已经很努力了可还是有人不满意,也许你的理想离你的距离从来没有拉近过......但请你继续向前走,因为别人看不到你的努力,你却始终看得见自己。 11、失败不可怕,可怕的是从来没有努力过,还怡然自得地安慰自己,连一点点的懊悔都被麻木所掩盖下去。不能怕,没什么比自己背叛自己更可怕。 12、跌倒了,一定要爬起来。不爬起来,别人会看不起你,你自己也会失去机会。在人前微笑,在人后落泪,可这是每个人都要学会的成长。 15、所有的辉煌和伟大,一定伴随着挫折和跌倒;所有的风光背后,一定都是一串串揉和着泪水和汗水的脚印。 13、看,坚持自己的坚持,直到坚持不下去为止。 16、成功的反义词不是失败,而是从未行动。有一天你总会明白,遗憾比失败更让你难以面对。 14、也许你想要的未来在别人眼里不值一提,也许你已经很努力了可还是有人不满意,也许你的理想离你的距离从来没有拉近过 ...... 但请你继续向前走,因为别人看不到你的努力,你却始终看得见自己。 15、所有的辉煌和伟大,一定伴随着挫折和跌倒;所有的风光背后,一定都是一串串揉和着泪水和汗水的脚印。 17、没有一件事情可以一下子把你打垮,也不会有一件事情可以让你一步登天,慢慢走,慢慢看,生命是一个慢慢累积的过程。 16、成功的反义词不是失败,而是从未行动。有一天你总会明白,遗憾比失败更让你难以面对。 18、努力也许不等于成功,可是那段追逐梦想的努力,会让你找到一个更好的自己,一个沉默努力充实安静的自己。 17、没有一件事情可以一下子把你打垮,也不会有一件事情可以让你一步登天,慢慢走,慢慢看,生命是一个慢慢累积的过程。 18、努力也许不等于成功,可是那段追逐梦想的努力,会让你找到一个更好的自己,一个沉默努力充实安静的自己。 19、你相信梦想,梦想才会相信你。有一种落差是,你配不上自己的野心,也辜负了所受的苦难。 19、你相信梦想,梦想才会相信你。有一种落差是,你配不上自己的野心,也辜负了所受的苦难。 20、生活不会按你想要的方式进行,它会给你一段时间,让你孤独、迷茫又沉默忧郁。但如果靠这段时间跟自己独处,多看一本书,去做可以做的事,放下过去的人,等你度过低潮,那些独处的时光必定能照亮你的路,也是这些不堪陪你成熟。所以,现在没那么糟,看似生活对你的亏欠,其实都是祝愿。 20、生活不会按你想要的方式进行,它会给你一段时间,让你孤独、迷茫又沉默忧郁。但如果靠这段时间跟自己独处,多看一本书,去做可以做的事,放下过去的人,等你度过低潮,那些独处的时光必定能照亮你的路,也是这些不堪陪你成熟。所以,现在没那么糟,看似生活对你的亏欠,其实都是祝愿。
新人教版八年级数学上册第11章全等三角形精品课件
M B′ C 图11.2-11
需要更完整的资源请到 新世纪教 育网 -
C′
活动三.知识应用,例题解析. 例4.如图11.2-12,AC⊥BC,BD⊥AD,AC=BD. 求证BC=AD. C 证明:∵AC⊥BC,BD⊥AD, D ∴∠C与∠D都是直角. 在Rt△ABC和Rt△BAD中,
AB BA AC=BD
A
B
图11.2-12
∴Rt△ABC≌Rt△BAD(HL). ∴BC=AD.
需要更完整的资源请到 新世纪教 育网 -
活动四.知识巩固,课堂练习 1.课本第14页小练习. 2.中考链接: (1)(江西)如下左图,已知AB=AD,那么添加下列一个条件后,仍无 法判定⊿ABC≌⊿ADC的是 ( ) A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90° E B
第11章全等三角形 第2节全等三角形的判定 -直角三角形全等的斜边直角边定理
需要更完整的资源请到 新世纪教 育网 -
教学目标
知识技能:理解直角三角形全等的判定定理,并能灵活地运用 直角三角形全等的判定定理,进行有条理的简单的推理,并能 利用它解决实际问题. 数学思考:懂得直角三角形全等的判定定理是确定两个直角三 角形全等的思考方法. 解决问题:经历探索三角形全等判定方法的过程,体会利用操 作、归纳获得数学结论的过程. 情感态度:体验数学模型与实际生活中的问题之间的联系.
需要更完整的资源请到 新世纪教 育网 -
活动二.交流合作,探索结论. 1.探究8.任意画出一个Rt△ABC,使∠C=90°.再画一个 Rt△A′B′C′,使B′C′=BC,A′B′=AB.把画好的Rt△A′B′C′剪 下,放到Rt△ABC上,它们全等吗? 画一个Rt△A′B′C′,使B′C′=BC,A′B′=AB: (1′=BC. (3).以B′为圆心,AB为半径画弧,交射线C′N于点A′. MB′CC′ABA′N图11.2-11 (4).连接A′B′.
