2013考研 高等数学 基础班(第24-25课)
2013成人高考专升本高等数学真题及答案

2013年成人高等学校专升本招生全国统一考试高等数学(二)答案必须答在答题卡上指定的位置,答在试卷上无效.......。
选择题一、选择题:1~10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填涂在答题卡相应题号的信点..........上.。
1、22limx cos xx π→= A.2πB. 2π-C.2πD. 2π-2、设函数ln 3x y e =-,则dy dx = A. x eB. 13x e +C.13D. 13x e -3、设函数()ln(3)f x x =,则'(2)f =A. 6B. ln 6C.12D.164、设函数3()1f x x =-在区间(,)-∞+∞A.单调增加B.单调减少C.先单调增加,后单调减少D.先单调减少,后单调增加5、21dx x ⎰=A.1C x+B. 2ln x C +C. 1C x-+ D.21C x+6、2(1)x d dt t dx +⎰= A. 2(1)x +B. 0C.31(1)3x +D. 2(1)x +7、曲线||y x =与直线2y =所围成的平面图形的面积为A. 2B. 4C. 6D. 88、设函数cos()z x y =+,则(1,1)|zx∂=∂ A. cos 2B. cos 2-C. sin 2D. -sin 29、设函数yz xe =,则2z x y∂∂∂=A. x eB. y eC. yxeD.x ye10、设A ,B 是两随机事件,则事件A B -表示A.事件A ,B 都发生B.事件B 发生而事件A 不发生C.事件A 发生而事件B 不发生D.事件A ,B 都不发生非选择题二、填空题:11~20小题,每小题4分,共40分,将答案填写在答题卡相应题...... 号后..。
11、3123x xlimx→-= _______________.12、设函数ln ,1,(),1x x f x a x x ≥⎧=⎨-<⎩在1x =处连续,则a = _______________.13、曲线23354y x x x =-+-的拐点坐标为_______________. 14、设函数1x y e +=,则''y = _______________.15、31(1)xx lim x→∞+= _______________.16、设曲线22y x ax =+在点(1,2)a +处的切线与直线4y x =平行,则a =_______. 17、3x dx e =⎰_______________. 18、131(3)x dx x -+=⎰_______________. 19、0x dx e -∞=⎰_______________.20、设函数2ln z y x =+,则dz =_______________.三、解答题:21~28题,共70分。
高等数学基础形成性作业及答案1-4

⾼等数学基础形成性作业及答案1-4⾼等数学基础形考作业1:第1章函数第2章极限与连续(⼀)单项选择题⒈下列各函数对中,(C )中的两个函数相等. A.2)()(x x f =,x x g =)( B. 2)(x x f =,x x g =)(C.3ln )(xx f =,x x g ln 3)(= D.1)(+=x x f ,11)(2--=x x x g ⒉设函数)(x f 的定义域为),(+∞-∞,则函数)()(x f x f -+的图形关于(C )对称.A. 坐标原点B. x 轴C. y 轴D.x y =⒊下列函数中为奇函数是(B ). A.)1ln(2x y += B. x x y cos =C.2x x a a y -+=D.)1ln(x y +=⒋下列函数中为基本初等函数是(C ). A.1+=x y B. x y -=C.2xy = D.,1x x y ⒌下列极限存计算不正确的是(D ). A.12lim 22=+∞→x x x B. 0)1ln(lim 0=+→x xC. 0sin lim=∞→x x x D. 01sin lim =∞→x x x⒍当0→x 时,变量(C )是⽆穷⼩量.A. x x sinB. x 1C. xx 1sin D. 2)ln(+x⒎若函数)(x f 在点0x 满⾜(A ),则)(x f 在点0x 连续。
A.)()(lim 00x f x f x x =→ B. )(x f 在点0x 的某个邻域内有定义C.)()(lim 00x f x f x x =+→ D. )(lim )(lim 0x f x f x x x x -+→→=(⼆)填空题⒈函数)1ln(39)(2x x x x f ++--=的定义域是()+∞,3.⒉已知函数x x x f +=+2)1(,则=)(x f x 2-x .⒊=+∞→xx x0,)1()(1x k x x x x f x ,在0=x 处连续,则=ke .⒌函数?≤>+=0,sin 0,1x x x x y 的间断点是0=x .⒍若A x f x x =→)(lim 0,则当0x x →时,A x f -)(称为时的⽆穷⼩量0x x →。
南昌大学2012-2013第一学期研究生课表

2012—2013学年第一学期研究生课程表二○一二年七月目录法学院硕士研究生课程表............................................................................................................................................................1-2 马克思主义学院研究生课程表......................................................................................................................................................3-4 公共管理学院硕士研究生课程表 (5)经济与管理学院硕士研究生课程表................................................................................................................................................6-8 人文学院哲学系硕士研究生课程表.............................................................................................................................................9-10 人文学院历史学系硕士研究生课程表 (11)人文学院新闻与传播学系、影视艺术研究中心硕士研究生课程表 (12)人文学院中国语言文学系硕士研究生课程表.................................................................................................................................13-14 外国语学院硕士研究生课程表 (15)艺术与设计学院硕士研究生课程表 (16)教育学院硕士研究生课程表......................................................................................................................................................17-18 生命科学与食品工程学院硕士研究生课程表.................................................................................................................................19-22 理学院化学系硕士研究生课程表................................................................................................................................................23-24 理学院数学系硕士研究生课程表 (25)理学院物理系硕士研究生课程表................................................................................................................................................26-27 材料科学与工程学院、理学院管理科学与工程系硕士研究生课程表 (28)机电工程学院硕士研究生课程表.................................................................................................................................29-31 信息工程学院计算机系硕士研究生课程表 (32)信息工程学院计算中心、电子信息工程系硕士研究生课程表 (33)信息工程学院信息管理系、电气与自动化工程系硕士研究生课程表 (34)目录建筑工程学院硕士研究生课程表....................................................................................................................................35-37 环境与化学工程学院硕士研究生课程表...........................................................................................................................38-40 马克思主义学院、建筑工程学院、环境与化学工程学院博士研究生课程表 (41)机电工程学院博士研究生课程表 (42)理学院博士研究生课程表 (43)材料科学与工程学院博士研究生课程表 (44)经济与管理学院2012—2013学年第一学期硕士研究生课程表经济与管理学院2012—2013学年第一学期硕士研究生课程表经济与管理学院2012—2013学年第一学期硕士研究生课程表人文学院历史学系2012—2013学年第一学期硕士研究生课程表人文学院新闻与传播学系、影视艺术研究中心2012—2013学年第一学期硕士研究生课程表人文学院中国语言文学系2012—2013学年第一学期硕士研究生课程表生命科学与食品工程学院2012—2013学年第一学期硕士研究生课程表生命科学与食品工程学院2012—2013学年第一学期硕士研究生课程表理学院物理系2012—2013学年第一学期硕士研究生课程表信息工程学院计算机系2012—2013学年第一学期硕士研究生课程表信息工程学院电子信息工程系2012—2013学年第一学期硕士研究生课程表信息工程学院信息管理系、电气与自动化工程系2012—2013学年第一学期硕士研究生课程表建筑工程学院2012—2013学年第一学期硕士研究生课程建筑工程学院2012—2013学年第一学期硕士研究生课程环境与化学工程学院2012—2013学年第一学期硕士研究生课程表环境与化学工程学院2012—2013学年第一学期硕士研究生课程表环境与化学工程学院2012—2013学年第一学期硕士研究生课程表马克思主义学院、建筑工程学院、环境与化学工程学院2012—2013学年第一学期博士研究生课程表机电工程学院、信息工程学院2012—2013学年第一学期博士研究生课程表。
浙江省2013年高等教育课堂教学改革项目
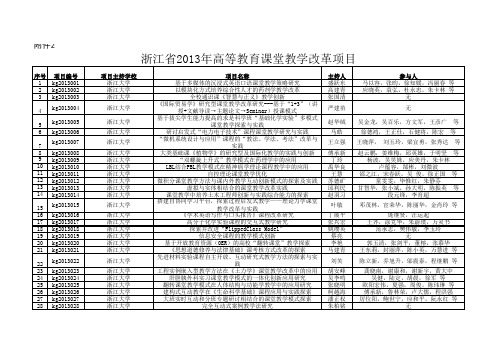
29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
kg2013029 kg2013030 kg2013031 kg2013032 kg2013033 kg2013034 kg2013035 kg2013036 kg2013037 kg2013038 kg2013039 kg2013040 kg2013041 kg2013042 kg2013043 kg2013044 kg2013045 kg2013046 kg2013047 kg2013048 kg2013049 kg2013050 kg2013051 kg2013052 kg2013053 kg2013054 kg2013055 kg2013056 kg2013057 kg2013058 kg2013059 kg2013060 kg2013061 kg2013062 kg2013063 kg2013064
65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82ቤተ መጻሕፍቲ ባይዱ83 84 85 86 87 88 89 90 91
kg2013065 kg2013066 kg2013067 kg2013068 kg2013069 kg2013070 kg2013071 kg2013072 kg2013073 kg2013074 kg2013075 kg2013076 kg2013077 kg2013078 kg2013079 kg2013080 kg2013081 kg2013082 kg2013083 kg2013084 kg2013085 kg2013086 kg2013087 kg2013088 kg2013089 kg2013090 kg2013091
高等数学第十章曲线积分与曲面积分(考研辅导班内部资料)

ds L ( L 表示曲线 L 的弧长 ) .
L
积函数可用积分曲线方程作变换.
( 6) 奇偶性与对称性 如果积分弧段 L (AB ) 关于 y 轴对称,
f (x, y)ds 存在,则
L( AB )
f ( x, y)ds
L ( AB )
0,
f ( x, y) 关于 x是奇函数 ,
2
f ( x, y)ds,f ( x, y) 关于 x是偶函数 .
切线的方向余弦是一个常量。 所以, 当积分曲线是直线时, 可能采用两类不同的曲线积分的
转换。
定理 4 (格林公式)
设 D 是由分段光滑的曲线 L 围成,函数 P( x, y), Q (x, y) 及其一阶偏导数在 D 上连续,
则有
P(x, y)dx Q (x, y)d y
Q P dxdy
L
Dx x
设 L (AB ) 的平面曲线: 其参数方程: x
分别是 和 ,则
(t), y
(t) ,起点和终点对应的参数取值
Pdx Qdy
L ( AB)
{ P( (t ), (t)] (t) Q[( (t), (t )] (t )}dt
设 L (AB ) 的空间曲线 :其参数方程: x (t), y (t ), z w(t ) ,起点和终点对应的
表示曲线的线密度。 定义 2 第二类曲线积分(对坐标的曲线积分)
( 1)平面曲线 L( AB) 的积分:
P(x, y)dx Q( x, y)dy
L ( AB )
( 2)空间曲线 L( AB) 的积分:
n
lim
(T ) 0
[ f ( k , k ) xk
k1
f ( k , k ) yk ]
考研数学一高等数学模拟试卷249_真题(含答案与解析)-交互

考研数学一(高等数学)模拟试卷249(总分60, 做题时间90分钟)1. 选择题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.把当x→0 +时的无穷小量α=tanx-x,β=∫x (1-cos )dt,γ=( ) x-1排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列次序是SSS_SINGLE_SELA α,β,γ.B γ,β,α.C β;α,γ.D γ,α,β.分值: 2答案:C解析:即当x→0 +时α是比β高阶的无穷小量,α与β应排列为β,α.故可排除(A)与(D).即当x→0 +时γ是较α高阶的无穷小量,α与γ应排列为α,γ.可排除(B),即应选(C).2.设f'(a)>0,则ヨδ>0,有SSS_SINGLE_SELA f(x)≥f(a)(x∈(a-δ,a+δ)).B f(x)≤f(a)(x∈(a-δ,a+δ)).C f(x)>f(a)(x∈(a,a+δ)),f(x)<f(a)(x∈(a-δ,a)).D f(x)<f(a)(x∈(a,a+δ)),f(x)>f(a)(x∈(a-δ,a)).分值: 2答案:C解析:直接由定义出发f'(a)=>0.由极限的保序性ヨδ>0,当x∈(a-δ,a+δ),x≠a时>0.f(x)>f(a) (x∈(a,a+δ)),f(x)<f(a) (x∈(a-δ,a)).因此选(C).3.设常数α>0,I1=∫π/2dx,I2=∫π/2dx,则SSS_SINGLE_SEL AI1>I2.BI1<I2.CI1 =I2.DI1与I2的大小与α的取值有关.分值: 2答案:A解析:I1-I2当0<x<π/4时cosx>sinx,又0<x<-x,所以I1-I2>0.故选(A).4.下列函数在点(0,0)处不连续的是SSS_SINGLE_SELABCD分值: 2答案:C解析:直接证(C)中f(x,y)在点(0,0)处不连续.当(x,y)沿直线y=x趋于点(0,0)时因此f(x,y)在点(0,0)处不连续.故选(C).5.SSS_SINGLE_SELA 绝对收敛.B 条件收敛.C 发散.D 敛散性与a有关.分值: 2答案:B解析:由莱布尼兹法则知原级数收敛.因此是条件收敛.选(B).2. 填空题1.设y=sinx 2.则dy/d(x 3 )=_______.SSS_FILL答案:正确答案:2cosx 2/3x解析:用微分之商来求.2.∫a arctan dx(a>0)=_______.SSS_FILL分值: 2答案:正确答案:a/2解析:利用分部积分法.3.已知方程y"+ y=0的两个特解y1 =e x,y2=x,则该方程满足初值y(0)=1,y'(0)=2的解y=_______.SSS_FILL分值: 2答案:正确答案:e x +x解析:因y1,y2线性无关,该方程的通解y=C1e x +C2x.由初始条件得C1 =1,C1+C2=2 C1=1,C2=1 y=e x +x.4.曲线在M(1,1,2)处的切线方程为_______,法平面方程为_______.SSS_FILL分值: 2答案:正确答案:;y-x=0解析:M0在曲线上,M处的切向量=-4i+4j=4{-1,1,0}. M处切线方程法平面方程-(x-1)+(y-1)=0,即y-x=0.5.设D为圆域x 2 +y 2≤x,则I= dσ=_______.SSS_FILL答案:正确答案:4╱9解析:D如图9.3.用极坐标变换,D的极坐标表示:-π/2≤0≤π/2,0≤r≤cosθ,于是I=∫-π/2π/2dθ∫cosθ r.rdr1/3cos 3θdθ3. 解答题解答题解答应写出文字说明、证明过程或演算步骤。
13年专升本高数真题答案
共 7 页,第 1 页2013年河南省普通高等学校选拔优秀专科毕业生进入本科阶段学习考试高等数学 答案及解析一、选择题(每小题2分,共60分)1.答案:C【解析】:易知,需满足,即,故应选C.⎩⎨⎧>-≤≤-0111x x 21≤<x 2.答案:D【解析】:因为,则,,故应选D.1()1f x x =-()[]x x x x f f 11111-=--={}[()]f f f x =()[]x xx x f f =--=1113.答案:B【解析】:因为为奇函数,则也为奇函数,应选B.()x x -+21ln )y x =-∞<<+∞4.答案:B 【解析】:因为,故是的可去间断点,应选B.22lim 2sin lim 00==→→xxx x x x 0x =()f x 5.答案:A【解析】:当时,,则与是等价无穷小0x →()1112lim 11lim00=-++=--+→→x x x xxx x x x x x --+11x 量,应选A.6.答案:C【解析】:因,应选C.0()()lim x f x g x x →--=()()()()()()()()b a x x g g x f x f x x g g f x f x x x +=--+-=--+-→→→0lim 0lim 00lim 0007.答案:B【解析】:因为曲线,则,故对应点处的法线cos (0,0)sin x a t a b y b t=⎧>>⎨=⎩t a b t a t b dt dx dt dy dx dy cot sin cos //-=-==4π=t 斜率为,应选B.ba8.答案:D【解析】: 因为,则,应选D.()()f x g x '=2d (sin )f x =()()xdx x g xdx x x f 2sin sin cos sin 2sin 22='9.答案:A【解析】:设函数具有任意阶导数,且,则;()f x 2()[()]f x f x '=()()()()[]322x f x f x f x f ='='';()()[]()()[]42!332x f x f x f x f ='⨯='''()()()[]()()[]534!4432x f x f x f x f ='⨯⨯=()()n f x =1![()]n n f x +10.答案:A【解析】:方程两边对求导,其中看作的函数,,所以x yxy e+=y x y ()1+'⋅=+'+x ex y x yx ,应选A.()()11--=--=--=='++x y y x y xy xy x y e e x dy dx x y x y x 11.答案:B【解析】:因为,则在上单调增加,应选B.()0(0)f x x a ''><<()f x '[0,]a 12.答案:A【解析】:点是曲线的拐点,则,故,应选A.(0,1)32y x bx c =++()()00,10=''=y y 0,1b c ==13.答案:A【解析】:因为,则2216x y x x +=+--()()3221-+++=x x x ;;()()543221lim 621lim 222=⎪⎪⎭⎫ ⎝⎛-+++=⎪⎭⎫ ⎝⎛--++-→-→x x x x x x x x ()()∞=⎪⎪⎭⎫ ⎝⎛-+++=⎪⎭⎫ ⎝⎛--++→→3221lim 621lim 323x x x x x x x x 故是曲线的垂直渐近线,应选A.3=x 14.答案:B【解析】: 因为,则,故应选B.()xxf x e e -=-()()C e e dx e ex F x x x x++=-=--⎰15.答案:D【解析】: 根据不定积分的相关性质,易知,正确,应选D.22d ()d ()d f x x f x x =⎰16.答案:D【解析】:因为为奇函数,故,应选D.x x sin 20sin 2=⎰-dx x x ππ17.答案:A 【解析】:方程两边对求导,得,则,故221()d x x f t t xe ++=⎰x ()x x xe e x f +++=+222()()x x e x e x f 2-+=,应选A.()f x '=x xe 18.答案:C【解析】:由P 无穷广义积分的结论可知,应选C.19.答案:B【解析】:微分方程的阶数是指微分方程中最高导数的阶数,应选B.20.答案:B【解析】:对方程分离变量,得,两边积分,得,代入,2d 2d 0y xy x -=xdx y dy 22=C x y+=-21(1)1y =-,故方程的特解是,应选B.0=C 21y x -=21.答案:C【解析】:向量的方向角需满足,应选C.1cos cos cos 222=++γβα22.答案:B【解析】:直线的方向向量与平面法向量平行,故与垂直相交,应选B.L π23.答案:D【解析】:缺少变量的二次曲面方程为柱面,应选D.共 7 页,第 3 页24.答案:C 【解析】:,应选C.0x y →→=()()41421lim 42lim 0000-=++-=++-→→→→xy xy xy xy y x y x 25.答案:B【解析】:因为,则22(,23)z fx y x y =-+zy∂=∂1223yf f ''-+26.答案:A 【解析】:因为为X 型积分,则交换积分次序后,Y 型积分的2 22 00 2d (, )d (, )d x I x f x y y x f x y y =+⎰⎰⎰积分区域为:,故可以化为,应选A.(){}282,20,y x y y y x -≤≤≤≤I 2d (, )d y f x y x ⎰⎰27.答案:C 【解析】: 积分,应选C. 122 01d d x x y y =⎰⎰21213121210321102=⋅=⋅⎰⎰x x ydy dx x 28. 答案:D【解析】:参数方程,则,应L ()10,2≤≤⎩⎨⎧==y yy y x 22d d Lxy x x y +=⎰[]1522105141042===+⋅⋅⎰⎰y dy y dy y ydy y y 选D.29.答案:C 【解析】:因为,则收敛半径,收敛区间为,应选C.121lim lim 1=++=∞→+∞→n n u u n n n n 1=R (1,1)-30.答案:A【解析】:A 为交错级数,且单调递减,,故收敛;B 、C 中,11+n 011lim=+∞→n n 111sinlim ,1111ln lim ==⎪⎭⎫ ⎝⎛+∞→∞→nn n n n n 且发散,故B 、C 均发散;D 中,故D 发散;应选A.∑∞=11n n∞=∞→!lim n n nn 二、填空题(每小题2分,共20分)31.答案:既不充分也不必要【解析】:函数在点有定义与极限存在没有关系,故为既不充分也不必要()f x 0x 0lim ()x x f x →条件.32.答案:32【解析】:因为,故.2331lim --∞→==⎪⎭⎫⎝⎛-e e x p pxx p =3233.答案:21【解析】:因为函数为连续函数,则,得,故.()()a x x a a a e x axx =+-=-+-→→2cos lim ,1lim 0a a =-121=a 34.答案:32x -【解析】:因为,则,故.421f x x ⎛⎫=⎪⎝⎭()21x x f =()32x x f -='35.答案:C x x ++sin 2ln 【解析】:2cos d 2sin x x x x +=+⎰()Cx x x x x x d ++=++⎰sin 2ln sin 2sin 236.答案:π32【解析】:,则.21221,cos -=⋅-=⋅⋅>=<→→→→→→ba ba b a 32,π>=<→→b a 37.答案:1-+=-xCex y 【解析】:由一阶线性微分方程的通解公式得,.()1-+=+=⎪⎭⎫ ⎝⎛+⎰⎰=---⎰⎰xxxdx dx Cex C dx xe e C dx xe e y 38.答案:-5【解析】:令,则,将代入方程,则,()xyz z y x y x F 22,-++=xy F yz F z x 21,21-='-='1,0==y x 2-=z 故.52121101010-=---=''-=∂∂======y x y x z x y x xyyz F F xz39.答案:542=-+z y x 【解析】:令,故点处的切平面法向量,故切()1,2,2,,,22-='='='-+=z y x F y F x F z y x z y x F ()5,2,1{}1,4,2-平面方程为,即.()()()052412=---+-z y x 542=-+z y x 40.答案:()()nn n n x 44101-⋅-∑∞=+【解析】:.()()()()∑∑∞=+∞=--=⎪⎭⎫ ⎝⎛--=-+⋅=-+==010441441414411414411n nn n nn n x x x x x x f 三、计算题(每小题5分,共50分)41..011lim ln(1)x x x →⎡⎤-⎢⎥+⎣⎦共 7 页,第 5 页【解析】:原式=.()()()()21211lim 2111lim 1ln lim 1ln 1ln lim 200200-=+-=-+=-+=+-+→→→→x x x x x x x x x x x x x x42.已知函数由方程所确定,求.()x x y =arctanyx=d d x y 【解析】:方程两边同时对求导,可知,,即y 2222222222111yx y x x yx x x y x xy ++'⋅+='-⋅+,故.2222y x y x x y x x y x ++'=+'-d d xy yx yx y x x y x x +-=+'-='=2243.求不定积分.x ⎰【解析】:.Cx x x x C t t t t dt tt t t dtt t t t tdt dx x tx tdt dx ++-=++-⋅=+-+-⋅=+-⋅==⎰⎰⎰⎰==arctan arctan arctan arctan 111arctan 1arctan arctan arctan 22222222244.设,求.21,0(),0x x x f x e x ⎧+≤⎪=⎨>⎪⎩31(2)d f x x -⎰【解析】:.()()()e e t t dt e dt t dt tf dx x f ttt x +=+⎪⎪⎭⎫ ⎝⎛+=++==----=-⎰⎰⎰⎰313121013100121131245.求微分方程的通解.23xy y y e '''+-=【解析】:原方程对应的齐次方程为,则特征方程为,特征根为,02=-'+''y y y 0122=-+r r 21,121=-=r r 故原方程对应的齐次方程的通解为.又知不是特征根,则原方程的()为任意常数2121211,,C C e C eC y x x+=-1=λ特解可设为,代入原方程可得,即,故原方程的通解为xAe y =*xxxxe Ae Ae Ae 32=-+23=A .x x xe eC e C y 232121++=-46.设,求全微分.2+sin2+xyu x y e =d u 【解析】:方法一:由题意可知,所以,2cos 2,2xy xy xe y yu ye x x u +=∂∂+=∂∂.()()dy xe y dx ye x dy yudx x u du xy xy +++=∂∂+∂∂=2cos 22方法二:对等式两边同时求微分,可知.()()()()dyxe y dx ye x ydx xdy e ydy xdx xy d e ydy xdx de y d dx du xy xy xy xy xy +++=+⋅++=++=++=2cos 222cos 222cos 222sin 247.一平面过点且平行于向量和,求此平面方程.(1,0,1)-{2,1,1}a =-{1,1,2}b =- 【解析】:由题意可知,所求平面平行于向量和,则所求平面的法向量,即{2,1,1}a =-{1,1,2}b =- →→→⨯=b a n ,又知平面过点,由平面的点法式方程可知,平面方{}3,5,135211112--=--=--=⨯=→→→→→→→→→k j i kj ib a n (1,0,1)-程为,即.()()01351=+---z y x 435=--z y x 48.计算,其中是由所围成的闭区域.d d xyDex y ⎰⎰D 1,,2,0y y x y x ====【解析】:由题意可知,如图所示,该区域为Y 型区域,则.d d x yDe x y ⎰⎰()()()1232112122121021-=-=-=⎪⎪⎭⎫ ⎝⎛==⎰⎰⎰⎰e y e dy e y dy ye dx e dy y y x yyx 49.计算积分,其中为曲线上从点到点2222(210)d (215)d Lx xy y x x xy y y +-++--+⎰L cos y x =π,02A ⎛⎫ ⎪⎝⎭一段弧.π,02B ⎛⎫- ⎪⎝⎭【解析】:由题意可知,,则()()152,,102,2222+--=+-+=y xy x y x Q y xy x y x P ,即,说明该曲线积分与积分路径无关,选取直线路径y x x Q y x y P 22,22-=∂∂-=∂∂xQy P ∂∂=∂∂,故⎪⎭⎫ ⎝⎛-→=22:,0ππx y .2222(210)d (215)d Lxxy y x x xy y y +-++--+⎰()ππππππ1012103103222232--=⎪⎪⎭⎫ ⎝⎛+=+=⎰--x x dx x 50.求幂级数的收敛域.0(1)2(1)nn n x n ∞=-+∑【解析】:该幂级数的为非标准不缺项的类型,令,则原幂级数可变形为,因为t x =-1()∑∞=+012n n nn t ,则幂级数的收敛半径为,故幂级数的收敛区间()()2221121lim lim11=++=+∞←+∞←n n u u n n n n nn ()∑∞=+012n nn n t 2=R ()∑∞=+012n n n n t 为;()2,2-当时,级数收敛;当时,级数收敛发散;2-=t ()()∑∞=+-011n n n 2=t ()∑∞=+011n n共 7 页,第 7 页则幂级数的收敛域为,故原幂级数的收敛域为.()∑∞=+012n n n n t [)2,2-0(1)2(1)nn n x n ∞=-+∑[)3,1-四、应用题(每小题6分,共12分)51.某房地产公司有50套公寓要出租,当月租金定为2000元时,公寓会全部租出去,当月租金每增加100元时,就会多一套公寓租不出去,而租出去的公寓每月需花费200元的维修费,试问租金定为多少可获得最大收入?最大收入是多少?【解析】:设租金定位元时,收入为,则,即x ()x S ()()200100200050-⎪⎭⎫⎝⎛--=x x x S ,令,得唯一的驻点,又知()()2000,14000721002≥-+-=x x x x S ()07250=+-='x x S 3600=x ,则为的极小值点,结合实际情况,也就是对应的最大值,所以当租金定位3600()0501<-=''x S 3600=x ()x S 元时,有最大收入,最大收入为115600元.52.曲线,直线以及轴围成一平面图形,试求平面图形绕轴旋转一周所得旋转体3(0)y x x =≥2x y +=y D D y 的体积.【解析】:由题意可知,如图所示,该区域为X 型区域,则体积=.()()ππππ151453222221053214213=⎪⎪⎭⎫ ⎝⎛--=--=--⎰⎰x x x dx x x x dx x x x 五、证明题(8分)53.设在区间上连续,且,证明:方程在区间(0,1)内有且仅有一个实根.()f x [0,1]()1f x <02()d 1xx f t t -=⎰【证明】:存在性:令,因为在区间上连续,则在区间上()()[]1,0,120∈--=⎰x dt t f x x F x()f x [0,1]()x F [0,1]也连续,而且,由零点定理可知,在区间(0,1)内至少存在一点()()()()()1,011,1010<>-=-=⎰x f dt t f F F ξ,使得;()0=ξF 唯一性:因为,则在区间(0,1)内单调递增,故方程在()()()()1,02<>-='x f x f x F ()x F 02()d 1xx f t t -=⎰区间(0,1)内至多有一实根;综上所述,方程在区间(0,1)内有且仅有一个实根.2()d 1xx f t t -=⎰。
武忠祥教授高等数学考研第二三章
x
lim
______.
x0 f ( x02x) f ( x0 x)
【1】
【例 2】(2011年2,3)已知 f ( x) 在 x 0 处可导,且 f (0) 0,
则
lim
x0
x2
f
(
x) 2 x3
f
(
x3
)
(A) 2 f (0).
(B) f (0).
(C) f (0).
(D) 0.
【例3】(2013年,1)设函数 y f ( x) 由方程 y x e x(1 y)
2) ( x ) x 1
3) (a x ) a x ln a
5) (loga
x)
1 x lna
7) (sin x) cos x
4) (e x ) e x 6) (ln x ) 1
x 8) (cos x) sin x
9) (tan x) sec2 x
10) (cot x) csc2 x
第二章 导 数 与 微 分
2023最新整理收集 do
something
考试内容概要
(一)导数与微分的概念
1. 导数的概念
定义1(导数)
f ( x0 )
lim y lim x0 x x0
f ( x0 x) x
f ( x0 )
f ( x0 )
lim
x x0
f (x) x
f ( x0 ) x0
f ( x0 ) 0 定理9(极值的第一充分条件)
设 f ( x) 在 U( x0 , ) 内可导,且 f ( x0 ) 0(或 f ( x) 在 x0 处连续)
(1)若 x x0 时, f ( x) 0; x x0 时, f ( x) 0, 则 f 在 x0 处取极大值.
3500份课程课后习题答案与大家分享~~
3500份课后答案,很值得收藏,这里只介绍了一部分。
还有很多,可以去课后答案网(/bbs)查找。
##################【公共基础课-答案】####################新视野大学英语读写教程答案(全)【khdaw】/bbs/viewthread.php?tid=108&fromuid=896767概率论与数理统计教程(茆诗松著) 高等教育出版社课后答案/bbs/viewthread.php?tid=234&fromuid=896767高等数学(第五版)含上下册高等教育出版社课后答案/bbs/viewthread.php?tid=29&fromuid=896767新视野英语听力原文及答案课后答案【khdaw】/bbs/viewthread.php?tid=586&fromuid=896767线性代数(同济大学应用数学系著) 高等教育出版社课后答案/bbs/viewthread.php?tid=31&fromuid=89676721世纪大学英语第3册(1-4)答案【khdaw】/bbs/viewthread.php?tid=285&fromuid=896767概率与数理统计第二,三版(浙江大学盛骤谢式千潘承毅著) 高等教育出版社课后答案/bbs/viewthread.php?tid=32&fromuid=896767复变函数全解及导学[西安交大第四版]【khdaw】/bbs/viewthread.php?tid=142&fromuid=896767大学英语精读第三版2册课后习题答案/bbs/viewthread.php?tid=411&fromuid=896767线性代数(第二版)习题答案/bbs/viewthread.php?tid=97&fromuid=89676721世纪(第三册)课后答案及课文翻译(5-8)【khdaw】/bbs/viewthread.php?tid=365&fromuid=896767大学英语精读第2册课文翻译(上外)【khdaw】/bbs/viewthread.php?tid=598&fromuid=896767新视野英语视听说教程1-4答案【khdaw】/bbs/viewthread.php?tid=2639&fromuid=896767物理学教程(马文蔚)答案/bbs/viewthread.php?tid=1188&fromuid=896767毛邓三课后思考题答案(高教版)高等教育出版社【khdaw】/bbs/viewthread.php?tid=1263 &fromuid=896767##################【通信/电子/电气/自动化类--答案】####################电路第四版(邱关源著) 高等教育出版社课后答案/bbs/viewthread.php?tid=259&fromuid=896767电路第五版(邱关源罗先觉著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=4097&fromuid=896767数字电子技术基础第四版(阎石著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=215&fromuid=896767模拟电子技术基础(第三版华成英主编)习题答案/bbs/viewthread.php?tid=242&fromuid=896767通信原理第5版(樊昌信著) 国防工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=34&fromuid=896767电磁场与电磁波西安电子科技大学(第二版)/bbs/viewthread.php?tid=588&fromuid=896767《信号与系统》第二版(郑君里)高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=994&fromuid=896767电机学(张松林著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=356&fromuid=896767《数字信号处理》(第二版)西安电子科技大学(丁玉美)课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=882&fromuid=896767高频电子线路(曾兴雯著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1110&fromuid=896767模拟电子技术基础简明教程第三版(杨素行著) 高等教育出版社课后答案/bbs/viewthread.php?tid=166&fromuid=896767##################【计算机/软件/网络/信息/数学类--答案】#################### C程序设计第三版(谭浩强著) 清华大学出版社课后答案/bbs/viewthread.php?tid=80&fromuid=896767C语言程序设计教程第三版(谭浩强张基温著) 高等教育出版社课后答案/bbs/viewthread.php?tid=79&fromuid=896767复变函数与积分变换第四版(张元林西安交大著) 高等教育出版社课后答案/bbs/viewthread.php?tid=612&fromuid=896767离散数学(第三版)(耿素云屈婉玲张立昂著) 清华大学出版社课后答案/bbs/viewthread.php?tid=293&fromuid=896767谭浩强C++程序设计习题答案/bbs/viewthread.php?tid=420&fromuid=896767《微机原理与接口技术》清华(冯博琴吴宁)版课后答案/bbs/viewthread.php?tid=707&fromuid=896767严蔚敏《数据结构(c语言版)习题集》答案/bbs/viewthread.php?tid=102&fromuid=896767数据库系统概论(王珊萨师煊著) 清华大学出版社课后答案/bbs/viewthread.php?tid=991&fromuid=896767《计算机网络第四版》答案【khdaw】/bbs/viewthread.php?tid=340&fromuid=896767《数学物理方法》(梁昆淼第二版)习题解答/bbs/viewthread.php?tid=334&fromuid=896767谢希仁版《计算机网络教程》课后答案/bbs/viewthread.php?tid=203&fromuid=896767清华大学《数据结构》习题+课后答案/bbs/viewthread.php?tid=249&fromuid=896767数据结构习题集(C版)答案/bbs/viewthread.php?tid=374&fromuid=896767刘绍学版《近世代数基础》课后习题答案/bbs/viewthread.php?tid=177&fromuid=896767计算机组成原理习题&答案唐朔飞高等教育出版社【khdaw】/bbs/viewthread.php?tid=984&fromuid=896767离散数学(左孝凌著) 上海科学技术文献出版社课后答案/bbs/viewthread.php?tid=466&fromuid=896767计算机网络(第4版)清华(Andrew S.Tanenbaum)版答案(中文版)/bbs/viewthread.php?tid=201&fromuid=896767耿国华数据结构课后答案/bbs/viewthread.php?tid=103&fromuid=896767计算机操作系统(汤子赢著) 西安电子科技大学课后答案/bbs/viewthread.php?tid=1083&fromuid=896767《编译原理》课后习题答案/bbs/viewthread.php?tid=175&fromuid=896767《常微分方程》王高雄高等教育出版社课后答案/bbs/viewthread.php?tid=567&fromuid=896767##################【物理/光学/声学/热学/力学类--答案】####################理论力学第六版(哈尔滨工业大学理论力学教研室著) 高等教育出版社课后答案/bbs/viewthread.php?tid=932&fromuid=896767理论力学第六版(哈尔滨工业大学理论力学教研室编著) 高等教育出版社【khdaw】/bbs/viewthread.php?tid=461&fromuid=896767《热力学统计物理》汪志诚(第三版)高教出版社(手抄版)习题答案【khdaw】/bbs/viewthread.php?tid=84&fromuid=896767原子物理学褚圣麟版课后答案【khdaw】/bbs/viewthread.php?tid=368&fromuid=896767《物理学教程》(马文蔚著) 高等教育出版社【khdaw】/bbs/viewthread.php?tid=2782&fromuid=896767《光学》姚启钧第三版高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=178&fromuid=896767大学物理实验报告与部分范例陈金太厦门大学【khdaw】/bbs/viewthread.php?tid=2350&fromuid=896767梁昆淼数学物理方法第三版的课后答案/bbs/viewthread.php?tid=2600&fromuid=896767《理论力学教程》周衍柏高等教育出版社完整版课后答案【khdawlxywyl】/bbs/viewthread.php?tid=676&fromuid=896767固体物理(黄昆版) 课后习题答案【khdaw】/bbs/viewthread.php?tid=339&fromuid=896767哈工大《理论力学》第6版(赵诒枢尹长城沈勇著) 华中科技大学出版社课后答案/bbs/viewthread.php?tid=1033&fromuid=896767热力学统计物理汪志诚第三版高等教育出版课后答案【khdaw】/bbs/viewthread.php?tid=289&fromuid=896767《量子力学教程》周习勋课后习题答案【khdaw】/bbs/viewthread.php?tid=388&fromuid=896767《原子物理学》杨福家版部分答案高等教育出版社【khdaw】/bbs/viewthread.php?tid=1065&fromuid=896767热力学·统计物理汪志诚高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=566&fromuid=896767《固体物理教程》王矜奉山东大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=1645&fromuid=896767##################【化学/环境/生物/医学/制药类--答案】#################### 物理化学(董元彦著) 科学出版社课后答案/bbs/viewthread.php?tid=412&fromuid=896767化工原理(陈敏恒著) 化学工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=704&fromuid=896767生物化学第三版(王镜岩朱圣庚著) 高等教育出版社课后答案/bbs/viewthread.php?tid=241&fromuid=896767遗传学第三版(朱军著) 农业大学出版社课后答案/bbs/viewthread.php?tid=39&fromuid=896767有机化学(汪小兰著) 高等教育出版社课后答案/bbs/viewthread.php?tid=841&fromuid=896767武汉大学版《无机化学》(第三版) 上册【khdaw】/bbs/viewthread.php?tid=196&fromuid=896767有机化学(徐寿昌著) 高教出版社课后答案/bbs/viewthread.php?tid=1752&fromuid=896767物理化学习题及答案【khdaw】/bbs/viewthread.php?tid=965&fromuid=896767有机化学第二版(胡宏纹著) 高等教育出版社课后答案/bbs/viewthread.php?tid=41&fromuid=896767分析化学第三版武汉大学课后答案/bbs/viewthread.php?tid=199&fromuid=896767武汉大学版<无机化学>(第三版) 下册【khdaw】/bbs/viewthread.php?tid=200&fromuid=896767物理化学第四版(傅献彩著) 高等教育出版社课后答案/bbs/viewthread.php?tid=3611&fromuid=896767##################【土建/机械/车辆/制造/材料类--答案】#################### 西工大机械原理配套作业题答案/bbs/viewthread.php?tid=570&fromuid=896767机械设计基础(第五版) 杨可桢程光蕴李仲生高教版课后答案/bbs/viewthread.php?tid=2316&fromuid=896767材料力学第4版(刘鸿文)答案(有附件)/bbs/viewthread.php?tid=1931&fromuid=896767材料力学课后答案/bbs/viewthread.php?tid=96&fromuid=896767材料力学(范钦珊主编著) 高等教育出版社课后答案/bbs/viewthread.php?tid=120&fromuid=896767机械设计基础(第五版) 答案7-18章杨可桢程光蕴李仲生/bbs/viewthread.php?tid=2570&fromuid=896767《结构力学习题集》课后答案【khdaw】/bbs/viewthread.php?tid=3016&fromuid=896767电工学第六版秦曾煌高等教育出版社课后答案/bbs/viewthread.php?tid=2986&fromuid=896767机械原理学习指南(第二版)(孙恒著) 课后答案/bbs/viewthread.php?tid=569&fromuid=896767机械原理高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=664&fromuid=896767电力电子技术试题习题考题及答案题解【khdaw】/bbs/viewthread.php?tid=1169&fromuid=896767机械原理习题+答案【khdaw_cola】/bbs/viewthread.php?tid=1210&fromuid=896767材料力学第四版(刘鸿文著) 高等教育出版社课后答案/bbs/viewthread.php?tid=2461&fromuid=896767机械设计及答案【khdaw_cola】/bbs/viewthread.php?tid=1172&fromuid=896767材料力学(I)第四版(孙训方)高等教育出版社课后答案/bbs/viewthread.php?tid=5342&fromuid=896767##################【经济/金融/营销/管理/电子商务类--答案】####################高鸿业版西方经济学习题答案(微观.宏观)【khdaw】/bbs/viewthread.php?tid=92&fromuid=896767西方经济学(微观部分) (高鸿业著) 中国人民大学出版社课后答案/bbs/viewthread.php?tid=2817&fromuid=896767袁卫统计学(第二版)习题答案【khdaw】/bbs/viewthread.php?tid=98&fromuid=896767曼昆《经济学原理》题目及课后答案/bbs/viewthread.php?tid=162&fromuid=896767统计学(贾俊平第二版)中国人民大学出版社课后答案/bbs/viewthread.php?tid=42&fromuid=896767运筹学教程第三版(甘应爱胡运权等著) 清华大学出版社课后答案/bbs/viewthread.php?tid=7016&fromuid=896767高鸿业版西方经济学习题答案(第三版)/bbs/viewthread.php?tid=1277&fromuid=896767西方经济学(宏观部分)第四版(高鸿业著) 中国人民大学出版社课后答案/bbs/viewthread.php?tid=7171&fromuid=896767财务管理学课后答案荆新王化成中国人民大学出版社/bbs/viewthread.php?tid=3433&fromuid=896767西方经济学课后答案(高鸿业著) 人民大学出版社/bbs/viewthread.php?tid=6189&fromuid=896767克鲁格曼_国际经济学(第六版)的教师手册(含习题答案)/bbs/viewthread.php?tid=237&fromuid=896767微观经济学第二版(高鸿业著) 西方经济学课后答案/bbs/viewthread.php?tid=577&fromuid=896767罗宾斯《管理学(第7版)》课后习题答案【khdaw】/bbs/viewthread.php?tid=513&fromuid=896767曼昆宏观经济学习题答案及讲义【khdaw】/bbs/viewthread.php?tid=115&fromuid=896767##################【法学/哲学/心理学/政治学类--答案】####################毛邓三课后答案(高教版) 课后答案【khdaw】/bbs/viewthread.php?tid=1184&fromuid=896767《马克思主义基本原理概论》最新版课后题答案(部分)及复习资料【khdaw】/bbs/viewthread.php?tid=1406&fromuid=896767马克思主义哲学原理课后习题答案【khdaw】/bbs/viewthread.php?tid=512&fromuid=896767马克思主义基本原理概论课后思考题答案【khdaw】/bbs/viewthread.php?tid=1145&fromuid=896767马基(马克思主义基本原理概论)课后思考题答案【khdaw】/bbs/viewthread.php?tid=1371&fromuid=896767《逻辑学》课后练习题及参考答案【khdaw】/bbs/viewthread.php?tid=2980&fromuid=896767##################【文学/史学/外语/教育类--答案】#################### 《中国近现代史纲要》课后答案(高教版)【khdaw】/bbs/viewthread.php?tid=1154&fromuid=896767《中国教育史》孙培青主编(华东师范大学出版社)习题答案【khdaw】/bbs/viewthread.php?tid=89&fromuid=896767《大学日语》汉译日标准答案【khdaw】/bbs/viewthread.php?tid=2954&fromuid=896767俄语模拟真题下载【khdaw】/bbs/viewthread.php?tid=859&fromuid=896767。
考研数学二(填空题)模拟试卷142(题后含答案及解析)
考研数学二(填空题)模拟试卷142(题后含答案及解析)题型有:1.1.极限=_______.正确答案:e2;涉及知识点:函数、极限、连续2.若=______.正确答案:5解析:令2x3=y,则故=3+2=5.知识模块:极限、连续与求极限的方法3.曲线上对应于t=1点处的法线方程为______。
正确答案:解析:当t=1时,,则由此可得法线的斜率为一1,因此可得法线方程为即知识模块:一元函数微分学4.设随机变量X与Y相互独立,且EX=μ1,EY=μ2,DX=σ12,DY=σ22,则COV(XY,X)=__________.正确答案:μσ2.解析:COV(XY,X)=E(XYX)-E(XY).EX=E(X2Y)一EX.E(XY),因为随机变量X与Y相互独立,所以cov(XY,X)=E(X2)EY-EX.EX.EY=[DX+(EX)2]EY-(EX)2.EY =(σ12+μ12)μ2-μ12μ2=μ2σ12.知识模块:概率论与数理统计5.由方程χyz+所确定的函数z=z(χ,y)在点(1,0,-1)处的全微分dz =_______.正确答案:dχ-dy 涉及知识点:多元函数微积分6.y=sin4x+cos4x,则y(n)=___________(n≥1).正确答案:4n一1cos(4x+π)解析:知识模块:一元函数微分学7.=______。
正确答案:解析:设计算可得于是知识模块:一元函数积分学8.设f(x)的一个原函数为xf’(x)dx=_________.正确答案:解析:知识模块:高等数学9.设f(x)是以T为周期的连续函数,且F(x)=∫0xf(t)dt+bx也是以T为周期的连续函数,则b=_______.正确答案:∫0Tf(t)dt.解析:F(x+T)=∫0x+Tf(t)dt+b(x+T)=∫0xf(t)dt+bx+∫xx+Tf(t)dt+bT=F(x)+∫xx+Tf(t)dt+bT=F(x)+∫0Tf(t)dt+bT,由F(x+T)=F(x),得b=∫0Tf(t)dt.知识模块:高等数学部分10.设a>0,则I=∫-aa=_________。
