安徽省黄山市歙县高考数学全真模拟试卷理(含解析)
安徽省黄山市高考数学三模试卷(理科)

安徽省黄山市高考数学三模试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)集合,则集合为()A . {1,2}B . {1}C . {2}D . {0,1}2. (2分) (2016高二下·芒市期中) 设复数z满足z(2﹣3i)=6+4i(i为虚数单位),则|z|=()A . 4B . 2C .D . 13. (2分)若sin2x、sinx分别是sinθ与cosθ的等差中项和等比中项,则cos2x的值为()A .B .C .D .4. (2分) (2015高二下·福州期中) (1+cosx)dx等于()A . πB . 2C . π﹣2D . π+25. (2分)执行如图所示的程序框图,则输出的s的值为()A . -7B . -5C . 2D . 96. (2分)(2017·张掖模拟) 若一个几何体的三视图如图所示,则该几何体的外接球的体积为()A . πB . πC . πD . π7. (2分)已知函数f(x)是定义在R上的偶函数,且对任意,都有f(x-1)=f(x+3)。
当时,f(x)=2x+1设函数f(x)在区间[-2,0]上的反函数为f-1(x),则f-1(19)的值为()A . -log23B . -2log23C . 1-2log23D . 3-2log238. (2分) (2017高二下·故城期中) 已知函数y=ax2+bx+c,其中a,b,c∈{0,1,2},则不同的二次函数的个数共有()A . 256个B . 18个C . 16个D . 10个9. (2分) (2019高三上·洛阳期中) 双曲线的对称轴与坐标轴重合,两个焦点分别为、,虚轴的一个端点为,若是顶角为的等腰三角形,则双曲线的离心率为()A .B .C .D .10. (2分) (2019高三上·双鸭山月考) 将函数的图象向右平移个单位长度后得到函数的图象,则函数的最大值为()A .B .C . 1D .11. (2分) (2016高三上·沙市模拟) 已知边长为的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD,则四面体的外接球的表面积为()A . 25πB . 26πC . 27πD . 28π12. (2分)关于函数有下列命题:①由f(x1)=f(x2)=0可得x1-x2必是的整数倍;②f(x)的表达式可改写为;③f(x)的图象关于点对称;④f(x)的图象关于直线对称;⑤f(x)在区间上是增函数;其中正确的是()A . ②③⑤B . ①② ③C . ②③ ④D . ①③⑤二、填空题 (共4题;共4分)13. (1分) (2016高二上·衡水开学考) 在平面直角坐标系中,O是坐标原点,两定点A,B满足| |=||= • =2,则点集{P| =x +y ,|x|+|y|≤1,x,y∈R}所表示的区域的面积是________.14. (1分)(2018·齐齐哈尔模拟) 已知实数满足条件若的最小值为 ,则实数 ________.15. (1分)在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“有99%以上的把握认为吸烟与患肺癌有关”.对以下说法:(1)在100个吸烟者中至少有99人患有肺癌;(2)某个人吸烟,那么这个人有99%的概率患有肺癌;(3)在100个吸烟者中一定有患肺癌的人;(4)在100个吸烟者中可能一个患肺癌的人也没有.其中正确的是________ .(填上所有正确的序号)16. (1分) (2016高二上·嘉峪关期中) 已知数列满足a1=1,an+1=2an+1(n∈N*).则通项公式为________.三、解答题 (共5题;共55分)17. (10分)(2019高二下·富阳月考) 在中,角所对的边分别为 .若.(1)求角的大小;(2)若的面积为,且,求的值.18. (10分)(2016·深圳模拟) 如图,四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2.(1)求证:平面PAB⊥平面ABCD;(2)若PA=PB,求二面角A﹣PC﹣D的余弦值.19. (10分)(2016·黄山模拟) 如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.(1)求x<2且y>1的概率;(2)求随机变量ξ的分布列与数学期望.20. (15分)已知点M(3,1),直线ax﹣y+4=0及圆(x﹣1)2+(y﹣2)2=4(1)求过M点的圆的切线方程(2)若直线ax﹣y+4=0与圆相交于A,B两点,且弦AB的长为2 ,求a的值(3)若电P(x,y)是圆上的任意一点,求k= 的取值范围.21. (10分) (2019高三上·双鸭山月考) 已知函数,其中为常数.(1)若直线是曲线的一条切线,求实数的值;(2)当时,若函数在上有两个零点.求实数的取值范围.四、选修4-4:坐标与参数方程 (共1题;共10分)22. (10分)(2016·中山模拟) 在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的参数方程为(ϑ为参数,且0≤ϑ<2π),曲线l的极坐标方程为ρ= (k是常数,且k∈R).(1)求曲线C的普通方程和曲线l直角坐标方程;(2)若曲线l被曲线C截的弦是以(,1)为中点,求k的值.五、选修4-5:不等式选讲 (共1题;共10分)23. (10分) (2019高三上·汉中月考) 已知函数,且的解集为.(1)解不等式:;(2)若均为正实数,且满足,求证: .参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共5题;共55分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、四、选修4-4:坐标与参数方程 (共1题;共10分) 22-1、22-2、五、选修4-5:不等式选讲 (共1题;共10分)23-1、23-2、。
2020年安徽省黄山市高考数学二模试卷(理科) (含答案解析)
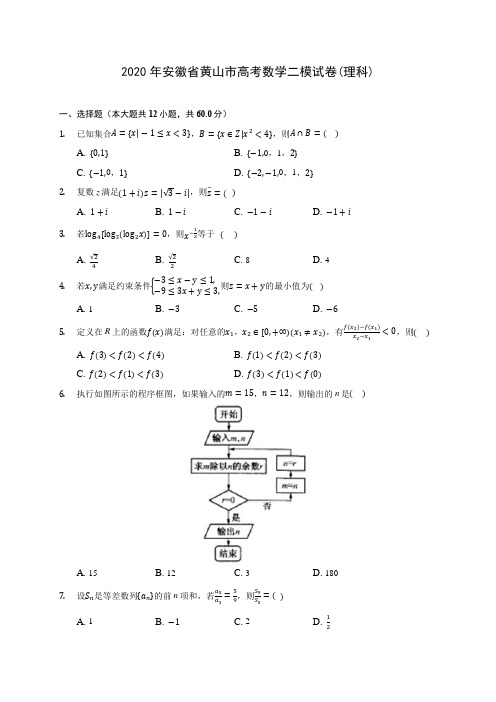
2020年安徽省黄山市高考数学二模试卷(理科)一、选择题(本大题共12小题,共60.0分)1. 已知集合A ={x|−1≤x <3},B ={x ∈Z|x 2<4},则A ∩B =( )A. {0,1}B. {−1,0,1,2}C. {−1,0,1}D. {−2,−1,0,1,2}2. 复数z 满足(1+i)z =|√3−i|,则z −=( )A. 1+iB. 1−iC. −1−iD. −1+i3. 若log 4[log 3(log 2x)]=0,则x −12等于 ( )A. √24B. √22C. 8D. 44. 若x,y 满足约束条件{−3≤x −y ≤1,−9≤3x +y ≤3,则z =x +y 的最小值为( )A. 1B. −3C. −5D. −65. 定义在R 上的函数f(x)满足:对任意的x 1,x 2∈[0,+∞)(x 1≠x 2),有f(x 2)−f(x 1)x 2−x 1<0,则( )A. f(3)<f(2)<f(4)B. f(1)<f(2)<f(3)C. f(2)<f(1)<f(3)D. f(3)<f(1)<f(0)6. 执行如图所示的程序框图,如果输入的m =15,n =12,则输出的n 是( )A. 15B. 12C. 3D. 1807. 设S n 是等差数列{a n }的前n 项和,若a5a 3=59,则S9S 5=( )A. 1B. −1C. 2D. 128. 若某同学连续3次考试的名次(3次考试均没有出现并列名次的情况)不超过3,则称该同学为班级的尖子生.根据甲、乙、丙、丁四位同学过去连续3次考试名次的数据,推断一定是尖子生的是( )A. 甲同学:平均数为2,众数为1B. 乙同学:平均数为2,方差小于1C. 丙同学:中位数为2,众数为2D. 丁同学:众数为2,方差大于19. 若角α的顶点在原点,始边与x 轴的非负半轴重合,终边落在直线y =−4x 上,且x ≤0,则( )A. sinα=−√1717B. cosα=4√1717C. tanα=−4D. 以上都错10. 已知四棱柱ABCD −A 1B 1C 1D 1中,AA 1⊥平面ABCD ,且底面ABCD 是正方形,AB =2,CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为( )A. 12B. √1010 C. √105D. 1511. 已知双曲线C:x 2−y 23=1,F 1为双曲线C 的左焦点,D 为双曲线C 右支上的动点,点G(1,2),则|DF 1|+|DG|的最小值为( )A. 2B. √5C. √5+2D. 412. 已知函数f(x)=e x −e −x ,若对任意的x ∈(0,+∞),f(x)>mx 恒成立,则m 的取值范围为( )A. (−∞,1)B. (−∞,1]C. (−∞,2)D. (−∞,2]二、填空题(本大题共4小题,共20.0分)13. 若(1−2x)2018=a 0+a 1x +a 2x 2+⋯+a 2018x 2018(x ∈R),则(a 0+a 1)+(a 0+a 2)+(a 0+a 3)+⋯+(a 0+a 2018)=________(用数字作答). 14. 函数f(x)=log 2(x −1)的零点是__________.15. 在平行四边形中,AB =4,AD =3,∠BAD =60°,点E 在BC 上,且BE ⃗⃗⃗⃗⃗ =2EC⃗⃗⃗⃗⃗ ,F 是DC 的中点,则AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ = ______ .16. 已知点P(t,4)在抛物线y 2=4x 上,抛物线的焦点为F ,那么|PF|= ______ . 三、解答题(本大题共7小题,共82.0分)17. 在△ABC 中角A ,B ,C 所对的边分别是a ,b ,c ,b =√2,c =1,cosB =34.(1)求sin C 的值; (2)求△ABC 的面积.18.如图,长方体ABCD−A1B1C1D1中,E是D1C1的中点,AB=2,BC=BB1=1.(Ⅰ)求证:平面DB1C1⊥平面DCC1D1;(Ⅱ)求二面角D−EB1−C1的余弦值.19.已知椭圆C:x2a2+y2b2=1(a>b>0)的左,右顶点分别是A1,A2,右焦点为F,直线l:bx−ay+√3ab=0与以线段A1A2为直径的圆相切.(1)求椭圆C的离心率;(2)设点P(√2,y0)(y0>0)在椭圆C上,且PF=1,求y0的值.20.某商场以分期付款方式销售某利商品,根据以往资料统计,顾客购买该商品选择分期付款的期数ξ的分布列为:其中0<a<1,0<b<1.(1)求购买该商品的3位顾客中,恰有2位选择分2期付款的概率:(2)商场销售,一件该商品,若顾客选择分2期付款,则商场获得的利润为200元;若顾客选择分3期付款,则商场获得的利润为250元:若顾客选择分4期付款,则商场获得的利润为300元.商场销售两件该商品所获得的利润记为X(单位:元).(ⅰ)求X的分布列;(ⅰ)若P(X≤500)≥0.8,求X的数学期望EX的最大值.21.已知函数f(x)=e x−ax,a∈R.(1)若f(x)在定义域内无极值点,求实数a的取值范围;(2)求证:当0<a<1,x>0时,f(x)>1恒成立.22.在平面直角坐标系xOy中,曲线C的参数方程为{x=−1+2cosφy=2sinφ(其中φ为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l1的极坐标方程为ρ=2sin(θ+π4),设l1与C相交于A,B两点,AB的中点为M,过点M作l1的垂线l2交C于P,Q两点.(1)写出曲线C的普通方程与直线l1的直角坐标方程;(2)求|PQ||MP|⋅|MQ|的值.23.已知函数f(x)=|x+1|−|4−2x|.(1)求不等式f(x)≥13(x−1)的解集;(2)若函数f(x)的最大值为m,且2a+b=m(a>0,b>0),求2a +1b的最小值.-------- 答案与解析 --------1.答案:C解析:解:A={x|−1≤x<3},B={x∈Z|x2<4}={−1,0,1},则A∩B={−1,0,1},故选:C.求出B中的元素,从而求出A、B的交集即可.本题考查了集合的运算,考查不等式问题,是一道基础题.2.答案:A解析:本题主要考查复数的应用,属于中档题.解:由题意得,z=|√3−i|1+i =21+i=2(1−i)(1+i)(1−i)=1−i,则z=1+i,故选A.3.答案:A解析:本题主要考查对数运算,由log4[log3(log2x)]=0可得log2x=3,即可得出x=23=8,进一步得出答案,属于基础题.解:因为log4[log3(log2x)]=0,所以log3(log2x)=1,即log2x=3,即x=23=8,所以x−12=8−12=2√2=√24.故选A.4.答案:C解析:【试题解析】解:作出x ,y 满足约束条件{−3≤x −y ≤1−9≤3x +y ≤3,表示的平面区域,如图所示的阴影部分:由z =x +y 可得y =−x +z ,则z 表示直线y =−x +z 在y 轴上的截距,截距越小,z 越小,由题意可得,{1=x −y−9=3x +y ,解得A(−2,−3),当y =−x +z 经过点A 时,z 最小, 由A(−2,−3),此时z =x +y =−5. 故选:C .作出不等式组表示的平面区域,由z =x +y 可得y =−x +z ,则z 表示直线y =−x +z 在y 轴上的截距,截距越小,z 越小,结合图象可求z 的最小值.本题主要考查了线性目标函数在线性约束条件下的最值的求解,解题的关键是明确z 的几何意义.5.答案:D解析:本题考查函数单调性的应用,属于基础题. 根据函数的单调性,即可得出结论. 解:若对任意的x 1,x 2∈[0,+∞)(x 1≠x 2),有f(x 2)−f(x 1)x 2−x 1<0,则函数f(x)满足在[0,+∞)上单调递减, 则f(3)<f(1)<f(0), 故选:D .6.答案:C解析:解:模拟程序的运行,可得 m =15,n =12 r =3不满足条件r =0,执行循环体,m =12,n =3,r =0 满足条件r =0,退出循环,输出n 的值为3.故选:C.由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基础题.7.答案:A解析:本题考查等差数列的性质与求和,属于基础题.利用等差数列的前n项和的计算公式及等差数列的性质即可求解.解:∵S9=9(a1+a9)2=9a5,S5=5(a1+a5)2=5a3,∴S9S5=9a55a3=95×59=1.故选A.8.答案:B解析:本题考查了平均数、中位数、众数、方差的定义及意义,根据题意利用排除法即可得到结果.解:根据题意可得甲可以是1,1,4,丙可以是2,2,4,丁可以是2,2,5,对于乙同学,平均数为2,若有名次超过3,则方差一定大于1,所以乙同学连续3次考试的名次都不超过3,因此一定是尖子生的是乙.故选B.9.答案:C解析:本题考查了任意角的三角函数的定义,属于基础题.利用任意角三角函数定义直接求解即可.解:根据题意,在角α的终边上取一点(−1,4),则r=√(−1)²+4²=√17,故sinα=yr =4√17=4√1717;cosα=xr =−1√17=−√1717;tanα=yx=−4.故选C.10.答案:D解析:解:如图,连接AD1,B1D1,则∠B1AD1为异面直线AB1与BC1所成角,由已知可得:AB1=AD1=√5,B1D1=2√2.∴cos∠B1AD1=2×5×5=15.∴异面直线AB1与BC1所成角的余弦值为15.故选:D.由已知画出图形,找出异面直线AB1与BC1所成角,再由余弦定理求解.本题考查异面直线所成角的求法,是基础的计算题.11.答案:C解析:本题考查双曲线的定义,属于中档题.由双曲线定义可知|DF1|−|DF2|=2,则|DF1|+|DG|=|DF2|+|DG|+2,当且仅当G,D,F2三点共线时|DF2|+|DG|最小为|GF2|,即可得解.解:设F2为双曲线C的右焦点,则F2(2,0).由已知,得|DF1|−|DF2|=2,即|DF1|=|DF2|+2,所以|DF1|+|DG|=|DF2|+|DG|+2≥|GF2|+2,当且仅当G,D,F2三点共线时取等号.因为|GF2|=√(1−2)2+22=√5,所以|DF2|+|DG|+2≥|GF2|+2=√5+2,故|DF1|+|DG|的最小值为√5+2.故选C.12.答案:D解析:解:令g(x)=e x−e−x−mx,x∈(0,+∞),则g′(x)=e x+e−x−m,x∈(0,+∞),易得函数y=e x+e−x>2在x∈(0,+∞)恒成立,故当m≤2时,g′(x)≥0在x∈(0,+∞)恒成立,故g(x)在(0,+∞)递增,又g(0)=0,故f(x)<mx恒成立,当m>2时,∵g′(x)在x∈(0,+∞)递增,故存在x0∈(0,+∞)恒成立,使得g′(x0)=0,故g(x)在(0,x0)递减,在(x0,+∞)递增,又g(0)=0,则g(x0)<0,这与g(x)>0恒成立矛盾,故m≤2,即m的范围是(−∞,2],故选:D.求出函数的导数,通过讨论m的范围,结合函数的单调性确定m的范围即可.本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.13.答案:2018解析:本题考查二项式定理的应用,二项式定理系数的性质,考查计算能力,属于中档题.令x =0,则a 0=1,令x =1,可计算得答案.解:在(1−2x)2018=a 0+a 1x +a 2x 2+⋯+a 2018x 2018中,令x =0,则a 0=1,令x =1,则a 0+a 1+a 2+a 3+⋯+a 2018=(−1)2018=1,故(a 0+a 1)+(a 0+a 2)+(a 0+a 3)+⋯+(a 0+a 2018)=2 017a 0+a 0+a 1+a 2+a 3…+a 2018=2 018.故答案为:2 018.14.答案:2解析:本题主要考查函数的零点与方程的根的关系,属于基础题型,直接求解即可.解:令log 2(x −1)=0,解得x =2,所以函数f(x)=log 2(x −1)的零点是2;故答案为2.15.答案:2解析:建立平面直角坐标系,求出AE ⃗⃗⃗⃗⃗ ,BF ⃗⃗⃗⃗⃗ 的坐标进行计算即可.本题考查了平面向量的数量积运算,属于中档题.解:以AB 为x 轴,以A 为原点建立平面直角坐标系,如图,则A(0,0),B(4,0),C(112,3√32),D(32,3√32),E(5,√3),F(72,3√32). ∴AE ⃗⃗⃗⃗⃗ =(5,√3),BF ⃗⃗⃗⃗⃗ =(−12,3√32), ∴AE ⃗⃗⃗⃗⃗ ⋅BF ⃗⃗⃗⃗⃗ =5×(−12)+√3×3√32=2.故答案为:2.建立平面直角坐标系,求出AE ⃗⃗⃗⃗⃗ ,BF ⃗⃗⃗⃗⃗ 的坐标进行计算即可.本题考查了平面向量的数量积运算,属于中档题.16.答案:5解析:本题考查了抛物线的标准方程及其性质,考查了推理能力与计算能力,属于基础题.点P(t,4)在抛物线y 2=4x 上,代入解得t ,利用|PF|=t +1即可得出.解:点P(t,4)在抛物线y 2=4x 上,其准线方程为x =−1,∴42=4t ,解得t =4.那么|PF|=t +1=5.故答案为:5.17.答案:(本题满分为12分)解:(1)∵b =√2,c =1,cosB =34.∴sinB =√1−cos 2B =√74, ∴由正弦定理可得:sinC =csinB b =1×√74√2=√148…4分 (2)∵c <b ,C 为锐角, ∴由(1)可得:cosC =√1−sin 2C =5√28, ∴sinA =sin(B +C)=sinBcosC +cosBsinC =√74×5√28+34×√148=√144, ∴S △ABC =12bcsinA =12×√2×1×√144=√74…12分解析:(1)利用同角三角函数基本关系式可求sin B ,由正弦定理可得sin C 的值.(2)由c <b ,可得C 为锐角,由(1)可得cos C ,利用两角和的正弦函数公式可求sin A 的值,利用三角形面积公式即可得解.本题主要考查了同角三角函数基本关系式,正弦定理,两角和的正弦函数公式,三角形面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.18.答案:解:(Ⅰ)证明:∵ABCD −A 1B 1C 1D 1是长方体,∴B 1C 1⊥平面DCC 1D 1,又B 1C 1⊂平面DB 1C 1,∴平面DB 1C 1⊥平面DCC 1D 1.(Ⅱ)以D 1为坐标原点,以D 1A 1、D 1C 1、D 1D 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系,如图所示:则D(0,0,1),B 1(1,2,0),E(0,1,0),DE ⃗⃗⃗⃗⃗⃗ =(0,1,−1),EB 1⃗⃗⃗⃗⃗⃗⃗ =(1,1,0).设n⃗ =(x 0,y 0,z 0)是平面DEB 1的一个法向量, ∵{DE ⃗⃗⃗⃗⃗⃗ ⋅n ⃗ =0EB ⃗⃗⃗⃗⃗ 1⋅n ⃗ =0,∴{y 0−z 0=0x 0+y 0=0, 令z 0=1,则x 0=−1,y 0=1,n⃗ =(−1,1,1), 易知平面EB 1C 1的一个法向量为D 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =(0,0,1),cos <n ⃗ ,D 1D ⃗⃗⃗⃗⃗⃗⃗⃗ >=n ⃗⃗ ⋅D 1D⃗⃗⃗⃗⃗⃗⃗⃗ |n ⃗⃗ ||D 1D ⃗⃗⃗⃗⃗⃗⃗⃗ |=√3×1=√33, 显然,二面角D −EB 1−C 1是钝角,∴二面角D −EB 1−C 1的余弦值为−√33.解析:本题考查了面面垂直的判定、二面角的求解,属于中档题.(Ⅰ)由B 1C 1⊥平面DCC 1D 1,即可得平面DB 1C 1⊥平面DCC 1D 1.(II)以D 1为坐标原点,以D 1A 1、D 1C 1、D 1D 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系,求得平面DEB 1的一个法向量和平面EB 1C 1的一个法向量即可得二面角D −EB 1−C 1的余弦值. 19.答案:(1)直线l :bx −ay +√3ab =0与以线段A 1A 2为直径的圆相切, 即√3ab22=a ,即a 2=2b 2.设F (c,0),c >0,由于a 2=b 2+c 2.a 2=2c 2, 故c a =√22,(2)由(1)可知,a=√2c,b=c.所以椭圆方程可为:x2+2y2=2c2.因为点P(√2,y0) ( y0>0)在椭圆C上,2+2y02=2c2,即1+y02=c2.由F(c,0),c>0,且PF=1,可得√(√2−c)2+y2=1,(y0>0)解得y0=1.解析:本题考查椭圆的离心率和椭圆的性质,属于中档题.(1)利用椭圆的几何性质求解即可;(2)根据直线与椭圆的位置关系求解即可.20.答案:解:(1)设购买该商品的3位顾客中,选择分2期付款的人数为η,依题意,得η~B(3,0.4),则P(η=2)=C32(0.4)2×(1−0.4)=0.288,故购买该商品的3位顾客中,恰有2位选择分2期付款的概率为0.288;(2)解:(ⅰ)依题意,X的取值分别为400,450,500,550,600.P(X=400)=0.4×0.4=0.16,P(X=450)=2×0.4a=0.8a,P(X=500)=2×0.4b+a2=0.8b+a2,P(X=550)=2ab,P(X=600)=b2.所以X的分布列为:(ⅰ)P(X≤500)=P(X=400)+P(X=450)+P(X=500)=0.16+0.8(a+b)+a2.根据题意知0.4+a+b=1,得a+b=0.6,得b=0.6−a,由P(X≤500)≥0.8,得0.16+0.48+a2≥0.8,解得a≥0.4或a≤−0.4.又a>0,则a≥0.4.又b>0,得0.6−a>0,解得a<0.6.所以a∈[0.4,0.6).EX =400×0.16+450×0.8a +500×(0.8b +a 2)+1100ab +600b 2=520−100a .当a =0.4时,EX 的最大值为480.所以X 的数学期望EX 的最大值为480.解析:本题考查离散型随机变量的分布列和期望,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.(1)由题意知购买该商品的3位顾客中恰有2位选择2期付款人数为η,得η~B(3,0.4),根据概率公式得到结果.(2)根据顾客采用的付款期数ξ的分布列对应于η的可能取值为400元,450元,500元,550元,600元.得到变量对应的事件的概率,写出变量的分布列并求出期望的最大值.21.答案:解:(1)由题意知f′(x)=e x (x−1)+ax 2,令g(x)=e x (x −1)+a ,(x ≠0),则g′(x)=e x ⋅x ,当x <0时,g′(x)<0,g(x)在(−∞,0)上单调递减,当x >0时,g′(x)>0,g(x)在(0,+∞)上单调递增,又g(0)=a −1,∵f(x)在定义域内无极值点,∴a >1,又当a =1时,f(x)在(−∞,0)和(0,+∞)上都单调递增也满足题意,所以a ≥1;(2)证明:f′(x)=e x (x−1)+ax 2,令g(x)=e x (x −1)+a ,由(1)可知g(x)在(0,+∞)上单调递増,又{g(0)=a −1<0g(1)=a >0,所以f′(x)存在唯一的零点x 0∈(0,1), 故f(x)在(0,x 0)上单调递减,在(x 0,+∞)上单调递増,∴f(x)≥f(x 0),由e x 0(x 0−1)+a =0知f(x 0)=e x 0>1,即当0<a <1,x >0时,f(x)>1恒成立.解析:本题考查函数的导数的应用,考查分类讨论思想的应用,考查转化思想以及计算能力.(1)求出导函数,构造函数g(x)=e x(x−1)+a(x≠0),求出g′(x)=e x⋅x,通过当x<0时,当x>0时,判断导函数的符号,判断函数的单调性,转化求解即可.(2)求出f′(x)=e x(x−1)+ax2,令g(x)=e x(x−1)+a,求出函数的最值,证明结论即可.22.答案:解:(1)由曲线C的参数方程{x=−1+2cosφy=2sinφ,消去参数φ,得曲线C的普通方程为(x+1)2+y2=4.由曲线l1的极坐标方程ρsin(θ−π4)=√22,得ρsinθ+ρcosθ=1,将x=ρcosθ,y=ρsinθ代入,得l1的直角坐标方程为x+y−1=0;(2)由l1⊥l2,得直线l2的斜率k l2=−1k l1=1,所以l2的倾斜角为π4,又l2过圆心(−1,0),所以l2的方程为y=x+1,与x+y−1=0联立,得AB的中点M(0,1),故l2的参数方程为{x=tcosπ4y=1+tsinπ4,(t为参数),即{x=√22ty=1+√22t,(t为参数),代入(x+1)2+y2=4中,化简、整理得t2+2√2t−2=0,设P,Q对应的参数分别为t1,t2,则由韦达定理得t1·t2=−2,又线段PQ为圆的直径,所以|PQ|=4,所以|PQ||MP|⋅|MQ|=4|−2|=2.解析:本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题型.(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.(2)利用一元二次方程根和系数关系式的应用求出结果.23.答案:解:(1)f(x)=|x+1|−|4−2x|={x−5,x<−13x−3,−1≤x≤2−x+5,x>2,因为f(x)≥13(x−1),所以{x<−1x−5≥13(x−1)或{−1≤x≤23x−3≥13(x−1)或{x>2−x+5≥13(x−1),解得1≤x≤2或2<x≤4.故不等式f(x)≥13(x−1)的解集为[1,4].(2)由(1)可知f(x)的最大值m=f(2)=3.因为2a+b=3(a>0,b>0),所以2a +1b=13(2a+b)(2a+1b)=13(2ab+2ba+5)≥13×(2×2+5)=3,当且仅当a=b=1时,等号成立,故2a +1b的最小值是3.解析:(1)将函数f(x)化为分段函数的形式,再分类讨论去掉绝对值,解不等式组后取并集即可得到解集;(2)由(1)知,2a+b=3,再利用基本不等式即可求得所求式子的最小值.本题考查绝对值不等式的解法以及利用基本不等式求最值,考查计算能力,属于基础题.。
安徽省黄山市高考数学一模试卷(理科)

安徽省黄山市高考数学一模试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2019高三上·临沂期中) 已知集合则()A .B .C .D .2. (2分)若复数(a∈R,i为虚数单位)是纯虚数,则实数a的值为()A . -6B . 13C .D .3. (2分) (2016高二上·桃江期中) 设等比数列{an}的前n项和为Sn ,若S5、S4、S6成等差数列.则数列{an}的公比为q的值等于()A . ﹣2或1B . ﹣1或2C . ﹣2D . 14. (2分)(2019·内蒙古模拟) 已知双曲线的左、右顶点分别为,点是双曲线上与不重合的动点,若,则双曲线的离心率为()A .B .C . 4D . 25. (2分)(2016·诸暨模拟) 已知△ABC中,AC=2,AB=4,AC⊥BC,点P满足 =x +y ,x+2y=1,则•( + )的最小值等于()A . ﹣2B . ﹣C . ﹣D . ﹣6. (2分) (2017高二上·张家口期末) 任取,直线y=k(x+2)与圆x2+y2=4相交于A,B 两点,则的概率为()A .B .C .D .7. (2分)为了得到函数的图象,只需把函数的图象()A . 向左平移个单位B . 向左平移个单位C . 向右平移个单位D . 向右平移个单位8. (2分)(2018·自贡模拟) 如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的分别为63,36,则输出的()A . 3B . 6C . 9D . 189. (2分) (2016高一下·舒城期中) 等差数列{an}中,a1=1,a3+a5=14,其前n项和Sn=100,则n=()A . 9B . 10C . 11D . 1210. (2分) (2016高三上·武邑期中) 如图是一个空间几何体的三视图,则该空间几何体的表面积是()A .B .C .D .11. (2分)抛物线x2=4y的焦点坐标为()A . (﹣1,0)B . (1,0)C . (0,﹣1)D . (0,1)12. (2分) (2019高一上·江苏月考) 已知函数,,则函数的值域为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2016高一上·台州期末) 已知函数f(x)是奇函数,当x>0时,f(x)=x3+1,则f(﹣2)=________.14. (1分)(2020·聊城模拟) 已知的展开式中的系数为,则实数 ________15. (1分) (2015高三上·保定期末) 设函数,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x﹣2y在D上的最大值为________ .16. (1分)设数列{an}中,a1=2,an+1=an+n+1,则通项an=________.三、解答题:解答应写出文字说明.证明过程或演算步骤. (共7题;共68分)17. (10分) (2019高一下·嘉兴期中) 设锐角的内角,,的对边分别为,,,且(1)求角的大小;(2)若,求的面积.18. (13分)网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.(1)表中的 ________,中位数落在________组,扇形统计图中组对应的圆心角为________°;(2)请补全频数分布直方图;(3)该校准备召开利用网络资源进行自主学习的交流会,计划在组学生中随机选出两人进行经验介绍,已知组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.组别学习时间频数(人数)A8B24CDE4小时以上419. (10分) (2019高一上·株洲月考) 如图,在三棱锥中,平面平面为等边三角形,且分别为的中点.(1)求证:平面;(2)求证:平面平面;20. (5分)(2017·运城模拟) 已知椭圆的右焦点为F(2,0),M为椭圆的上顶点,O 为坐标原点,且△MOF是等腰直角三角形.(Ⅰ)求椭圆的方程;(Ⅱ)过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1 , k2 ,且k1+k2=8,证明:直线AB过定点().21. (10分) (2016高三上·集宁期中) 已知函数f(x)=alnx﹣ax﹣3(a≠0).(1)讨论f(x)的单调性;(2)若f(x)+(a+1)x+4﹣e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数).22. (10分)以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为,若直线l过点P,且倾斜角为,圆C以M为圆心,3为半径.(1)求直线l的参数方程和圆C的极坐标方程;(2)设直线l与圆C相交于A,B两点,求|PA|•|PB|.23. (10分)设函数f(x)=|x﹣1|+ |x﹣3|.(1)求不等式f(x)>2的解集;(2)若不等式f(x)≤﹣3a(x+ )的解集非空,求实数a的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题:解答应写出文字说明.证明过程或演算步骤. (共7题;共68分) 17-1、17-2、18-1、18-2、18-3、19-1、19-2、20-1、21-1、21-2、22-1、22-2、23-1、23-2、。
2017年安徽省黄山市高考数学二模试卷(理科)(解析版)

2017年安徽省黄山市高考数学二模试卷〔理科〕一、选择题:本大题共12个小题,每题5分,共60分.在每题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={﹣2,﹣1,0,1,2},∁R B={x|≥0},则A∩B=〔〕A.{﹣1,0,1}B.{﹣1,0}C.{﹣2,﹣1,0}D.{0,1,2}2.复数z=〔a+i〕〔﹣3+ai〕〔a∈R〕,假设z<0,则a的值是〔〕A.a=B.a=﹣C.a=﹣1 D.a=13.已知数列{a n}的前n项和为S n,且a1=2,a n=S n+1〔n∈N*〕,则S5=〔〕+1A.31 B.42 C.37 D.474.在△ABC中,B〔﹣2,0〕,C〔2,0〕,A〔x,y〕,给出△ABC满足条件,就能得到动点A的轨迹方程下表给出了一些条件及方程:条件方程①△ABC周长为10C1:y2=25②△ABC面积为10C2:x2+y2=4〔y≠0〕③△ABC中,∠A=90°C3: +=1〔y≠0〕则满足条件①,②,③的轨迹方程依次为〔〕A.C3,C1,C2B.C1,C2,C3C.C3,C2,C1D.C1,C3,C25.在区间[0,8]上随机取一个x的值,执行如图的程序框图,则输出的y≥3的概率为〔〕A.B.C.D.6.过圆锥顶点的平面截去圆锥一部分,所得几何体的三视图如下图,则原圆推的体积为〔〕A.1 B. C. D.7.已知a=〔x2﹣1〕dx,b=1﹣log23,c=cos,则a,b,c的大小关系是〔〕A.a<b<c B.c<a<b C.a<c<b D.b<c<a8.已知m>1,x,y满足约束条件,假设目标函数z=ax+by〔a>0,b>0〕的最大值为3,则+〔〕A.有最小值B.有最大值C.有最小值D.有最大值9.《中国诗词大会》〔第二季〕亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.假设《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有〔〕A.144种B.288种C.360种D.720种10.已知圆C:x2+y2=1,点P为直线+=1上一动点,过点P向圆C引两条切线PA,PB,A,B为切点,则直线AB经过定点〔〕A.B.C.D.11.函数f〔x〕=与g〔x〕=〔|x+a|+1〕的图象上存在关于y轴对称的点,则实数a的取值范围是〔〕A.〔﹣∞,3﹣2ln2]B.[3﹣2ln2,+∞〕C.[,+∞〕 D.〔﹣∞,] 12.将函数y=sin〔x〕的图象向左平移3个单位,得函数y=sin〔x+φ〕〔|φ|<π〕的图象〔如图〕,点M,N分别是函数f〔x〕图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan〔φ﹣θ〕的值为〔〕A.1﹣B.2﹣C.1+D.﹣2+二、填空题〔每题5分,总分值20分,将答案填在答题纸上〕13.已知=〔,〕,||=1,|+2|=2,则在方向上的投影为.14.假设随机变量X~N〔2,32〕,且P〔X≤1〕=P〔X≥a〕,则〔x+a〕2〔ax﹣〕5展开式中x3项的系数是.15.祖暅〔公元前5﹣6世纪〕,祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,則积不容异.”这句话的意思是:两个等高的几何体假设在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环知总成立.据此,短轴长为4cm,长轴为6cm的椭球体的体积是cm3.16.设A〔n〕表示正整数n的个位数,a n=A〔n2〕﹣A〔n〕,A为数列{a n}的前202项和,函数f〔x〕=e x﹣e+1,假设函数g〔x〕满足f[g〔x〕﹣]=1,且b n=g〔n〕〔n∈N*〕,则数列{b n}的前n项和为.三、解答题〔本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.〕17.△ABC中,角A,B,C所对的边分别为a,b,c,向量=〔,1〕,=〔cosA+1,sinA〕,且•的值为2+.〔1〕求∠A的大小;〔2〕假设a=,cosB=,求△ABC的面积.18.如图,四棱锥P﹣ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=,M在PC上,且PA∥面MBD.〔1〕求证:M是PC的中点;〔2〕在PA上是否存在点F,使二面角F﹣BD﹣M为直角?假设存在,求出的值;假设不存在,说明理由.19.2016世界特色魅力城市200强新鲜出炉,包括黄山市在内的28个中国城市入选.美丽的黄山风景和人文景观迎来众多宾客.现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:合计赞成“自助游”不赞成“自助游”男性30女性10合计100〔1〕假设在100这人中,按性别分层抽取一个容量为20的样本,女性应抽11人,请将上面的列联表补充完整〔在答题卡上直接填写结果,不需要写求解过程〕,并据此资料能否在犯错误的概率不超过0.05前提下,认为赞成“自助游”是与性别有关系?〔2〕假设以抽取样本的频率为概率,从旅游节游客中随机抽取3人赠送精美纪念品,记这3人中赞成“自助游”人数为X,求X的分布列和数学期望.附:K2=P〔K2≥k〕k20.已知椭圆E : +=1〔a >〕的离心率e=,右焦点F〔c,0〕,过点A 〔,0〕的直线交椭圆E于P,Q两点.〔1〕求椭圆E的方程;〔2〕假设点P关于x轴的对称点为M,求证:M,F,Q三点共线;〔3〕当△FPQ面积最大时,求直线PQ的方程.21.已知函数f〔x〕=〔ax2+x﹣1〕e x+f'〔0〕.〔1〕讨论函数f〔x〕的单调性;〔2〕假设g〔x〕=e﹣x f〔x〕+lnx,h〔x〕=e x,过O〔0,0〕分别作曲线y=g〔x〕与y=h〔x〕的切线l1,l2,且l1与l2关于x轴对称,求证:﹣<a <﹣.[选修4-4:坐标系与参数方程]22.已知曲线C的极坐标方程为ρ=,过点P〔1,0〕的直线l交曲线C于A,B两点.〔1〕将曲线C的极坐标方程的化为普通方程;〔2〕求|PA|•|PB|的取值范围.[选修4-5:不等式选讲]23.已知函数f〔x〕=|x﹣2|,g〔x〕=|x+1|﹣x.〔1〕解不等式f〔x〕>g〔x〕;〔2〕假设存在实数x,使不等式m﹣g〔x〕≥f〔x〕+x〔m∈R〕能成立,求实数m的最小值.2017年安徽省黄山市高考数学二模试卷〔理科〕参考答案与试题解析一、选择题:本大题共12个小题,每题5分,共60分.在每题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={﹣2,﹣1,0,1,2},∁R B={x|≥0},则A∩B=〔〕A.{﹣1,0,1}B.{﹣1,0}C.{﹣2,﹣1,0}D.{0,1,2}【考点】交集及其运算.【分析】解不等式求出∁R B,根据补集与交集的定义计算即可.【解答】解:集合A={﹣2,﹣1,0,1,2},∁R B={x|≥0}={x|x<﹣2或x≥1},∴B={x|﹣2≤x<1}则A∩B={﹣2,﹣1,0}.故选:C.2.复数z=〔a+i〕〔﹣3+ai〕〔a∈R〕,假设z<0,则a的值是〔〕A.a=B.a=﹣C.a=﹣1 D.a=1【考点】复数的基本概念.【分析】z=〔a+i〕〔﹣3+ai〕=﹣4a+〔a2﹣3〕i<0,利用实部小于0,虚部等于0,即可求解.【解答】解:z=〔a+i〕〔﹣3+ai〕=﹣4a+〔a2﹣3〕i<0,∴a=,故选A.3.已知数列{a n}的前n项和为S n,且a1=2,a n=S n+1〔n∈N*〕,则S5=〔〕+1A.31 B.42 C.37 D.47【考点】数列递推式.【分析】a n+1=S n+1〔n∈N*〕,可得S n+1﹣S n=S n+1〔n∈N*〕,变形为:S n+1+1=2〔S n+1〕〔n∈N*〕,利用等比数列的通项公式即可得出.【解答】解:∵a n+1=S n+1〔n∈N*〕,∴S n+1﹣S n=S n+1〔n∈N*〕,变形为:S n+1+1=2〔S n+1〕〔n∈N*〕,∴数列{S n+1}为等比数列,首项为3,公比为2.则S5+1=3×24,解得S5=47.故选:D.4.在△ABC中,B〔﹣2,0〕,C〔2,0〕,A〔x,y〕,给出△ABC满足条件,就能得到动点A的轨迹方程下表给出了一些条件及方程:条件方程①△ABC周长为10C1:y2=25②△ABC面积为10C2:x2+y2=4〔y≠0〕③△ABC中,∠A=90°C3: +=1〔y≠0〕则满足条件①,②,③的轨迹方程依次为〔〕A.C3,C1,C2B.C1,C2,C3C.C3,C2,C1D.C1,C3,C2【考点】轨迹方程.【分析】①中可转化为A点到B、C两点距离之和为常数,符合椭圆的定义,利用定义法求轨迹方程;②中利用三角形面积公式可知A点到BC距离为常数,轨迹为两条直线;③中∠A=90°,可用斜率或向量处理.【解答】解:①△ABC的周长为10,即AB+AC+BC=10,∵BC=4,∴AB+AC=6>BC,故动点A的轨迹为椭圆,与C3对应;②△ABC的面积为10,∴BC•|y|=10,即|y|=5,与C1对应;③∵∠A=90°,∴=〔﹣2﹣x,﹣y〕〔2﹣x,﹣y〕=x2+y2﹣4=0,与C2对应.故选:A.5.在区间[0,8]上随机取一个x的值,执行如图的程序框图,则输出的y≥3的概率为〔〕A.B.C.D.【考点】程序框图.【分析】利用分段函数,求出输出的y≥3时,x的范围,以长度为测度求出相应的概率.【解答】解:由题意,0≤x≤6,2x﹣1≥3,∴2≤x≤6;6<x≤8,,无解,∴输出的y≥3的概率为=,故选B.6.过圆锥顶点的平面截去圆锥一部分,所得几何体的三视图如下图,则原圆推的体积为〔〕A.1 B. C. D.【考点】由三视图求面积、体积.【分析】由三视图可得底面圆的半径为=2,圆锥的高为=2,即可求出原圆推的体积.【解答】解:由三视图可得底面圆的半径为=2,圆锥的高为=2,∴原圆推的体积为=,故选D.7.已知a=〔x2﹣1〕dx,b=1﹣log23,c=cos,则a,b,c的大小关系是〔〕A.a<b<c B.c<a<b C.a<c<b D.b<c<a【考点】定积分;对数值大小的比较.【分析】估算a,b,c的值,即可比较大小.【解答】解:∵a=〔x2﹣1〕dx=〔x3﹣x〕|=﹣1=﹣≈﹣0.667,b=1﹣log23=1﹣≈﹣0.59,c=cos=﹣≈﹣0.866,∴c<a<b,故选B.8.已知m>1,x,y满足约束条件,假设目标函数z=ax+by〔a>0,b>0〕的最大值为3,则+〔〕A.有最小值B.有最大值C.有最小值D.有最大值【考点】简单线性规划.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数可得a+5b=3,然后利用基本不等式求得+有最小值.【解答】解:由约束条件作出可行域如图,联立,解得A〔1,5〕,化目标函数z=ax+by〔a>0,b>0〕为y=,由图可知,当直线y=过A时,直线在y轴上的截距最大,z有最大值为a+5b=3.∴+=〔+〕〔〕=.当且仅当a=5b,即a=,b=时,上式等号成立.故选:A.9.《中国诗词大会》〔第二季〕亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.假设《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有〔〕A.144种B.288种C.360种D.720种【考点】排列、组合的实际应用.【分析】根据题意,分2步进行分析:①、用倍分法分析《将进酒》、《望岳》和另两首诗词的排法数目,②、用插空法分析《山居秋暝》与《送杜少府之任蜀州》的排法数目,由分步计数原理计算可得答案.【解答】解:根据题意,分2步进行分析:①、将《将进酒》、《望岳》和另两首诗词的4首诗词全排列,有A44=24种顺序,由于《将进酒》排在《望岳》前面,则这4首诗词的排法有=12种,②、这4首诗词排好后,不含最后,有4个空位,在4个空位中任选2个,安排《山居秋暝》与《送杜少府之任蜀州》,有A43=12种安排方法,则后六场的排法有12×12=144种;故选:A.10.已知圆C:x2+y2=1,点P为直线+=1上一动点,过点P向圆C引两条切线PA,PB,A,B为切点,则直线AB经过定点〔〕A.B.C.D.【考点】直线与圆的位置关系.【分析】根据题意设P的坐标为P〔4﹣2m,m〕,由切线的性质得点A、B在以OP为直径的圆C上,求出圆C的方程,将两个圆的方程相减求出公共弦AB所在的直线方程,再求出直线AB过的定点坐标.【解答】解:因为P是直线+=1的任一点,所以设P〔4﹣2m,m〕,因为圆x2+y2=1的两条切线PA、PB,切点分别为A、B,所以OA⊥PA,OB⊥PB,则点A、B在以OP为直径的圆上,即AB是圆O和圆C的公共弦,则圆心C的坐标是〔2﹣m,〕,且半径的平方是r2=,所以圆C的方程是〔x﹣2+m〕2+〔y﹣〕2=,①又x2+y2=1,②,②﹣①得,〔2m﹣4〕x﹣my+1=0,即公共弦AB所在的直线方程是:〔2m﹣4〕x ﹣my+1=0,即m〔2x﹣y〕+〔﹣4x+1〕=0,由得x=,y=所以直线AB恒过定点〔,〕,故选B.11.函数f〔x〕=与g〔x〕=〔|x+a|+1〕的图象上存在关于y轴对称的点,则实数a的取值范围是〔〕A.〔﹣∞,3﹣2ln2]B.[3﹣2ln2,+∞〕C.[,+∞〕 D.〔﹣∞,]【考点】函数的图象;函数零点的判定定理.【分析】画出函数f〔x〕的图象,求出函数g〔x〕=〔|x+a|+1〕的最小值,利用已知条件转化列出不等式求解即可.【解答】解:函数f〔x〕=的图象如图:g〔x〕=〔|x+a|+1〕,当且仅当x=﹣a时取等号,函数y=ln〔﹣x〕与与=〔|x+|+1〕在x<0有解,而且g〔x〕=〔|x+a|+1〕看作g〔x〕=〔|x|+1〕向左平移而得,当a时,函数f〔x〕=与g〔x〕=〔|x+a|+1〕的图象上存在关于y轴对称的点,所以实数a的取值范围是:[,+∞〕.故选:C.12.将函数y=sin〔x〕的图象向左平移3个单位,得函数y=sin〔x+φ〕〔|φ|<π〕的图象〔如图〕,点M,N分别是函数f〔x〕图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan〔φ﹣θ〕的值为〔〕A.1﹣B.2﹣C.1+D.﹣2+【考点】由y=Asin〔ωx+φ〕的部分图象确定其解析式.【分析】根据函数图象的变换,求得φ的值,由正弦函数的性质,求得M和N 的坐标,利用余弦定理求得θ的值,即可求得tan〔φ﹣θ〕.【解答】解:函数y=sin〔x〕的图象向左平移3个单位,可得:y=sin[〔x+3〕]=sin〔x+〕,则φ=,∴M〔﹣1,〕,N〔3,﹣〕,则丨OM丨=2,丨ON丨=2,丨MN丨=2,cosθ==﹣,由0<θ<π,则θ=,则tan〔φ﹣θ〕=tan〔﹣〕=﹣tan=﹣tan〔﹣〕=﹣=﹣〔2﹣〕=﹣2+,tan〔φ﹣θ〕的值﹣2+,故选D.二、填空题〔每题5分,总分值20分,将答案填在答题纸上〕13.已知=〔,〕,||=1,|+2|=2,则在方向上的投影为﹣.【考点】平面向量数量积的运算.【分析】运用向量模的公式和向量的平方即为模的平方,可得•,再由在方向上的投影为,计算即可得到所求.【解答】解:=〔,〕,||=1,|+2|=2,可得||=1,|+2|2=4,即为2+4•+42=4,即有1+4•+4=4,•=﹣,可得在方向上的投影为=﹣.故答案为:﹣.14.假设随机变量X~N〔2,32〕,且P〔X≤1〕=P〔X≥a〕,则〔x+a〕2〔ax﹣〕5展开式中x3项的系数是1620.【考点】二项式系数的性质.【分析】根据正态分布的概率性质求出a的值,再化〔x+a〕2〔ax﹣〕5=〔x2+6x+9〕;利用展开式的通项公式求出含x2的系数,即可求出对应项的系数.【解答】解:随机变量X~N〔2,32〕,均值是2,且P〔X≤1〕=P〔X≥a〕,∴a=3;∴〔x+a〕2〔ax﹣〕5=〔x+3〕2〔3x﹣〕5=〔x2+6x+9〕;又展开式的通项公式为T r+1=•〔3x〕5﹣r•=〔﹣1〕r•35﹣r••,令5﹣=1,解得r=,不合题意,舍去;令5﹣=2,解得r=2,对应x2的系数为〔﹣1〕2•23•=270;令5﹣=3,解得r=,不合题意,舍去;∴展开式中x3项的系数是6×270=1620.故答案为:1620.15.祖暅〔公元前5﹣6世纪〕,祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,則积不容异.”这句话的意思是:两个等高的几何体假设在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为2b,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面β上.以平行于平面β的平面于距平面β任意高d处可横截得到S圆及S环两截面,可以证明S圆=S环知总成立.据此,短轴长为4cm,长轴为6cm的椭球体的体积是16πcm3.【考点】旋转体〔圆柱、圆锥、圆台〕.【分析】利用圆柱、圆锥的体积公式,即可得出结论.【解答】解:由题意,短轴长为4cm,长轴为6cm的椭球体的体积是=16πcm3.故答案为16π.16.设A〔n〕表示正整数n的个位数,a n=A〔n2〕﹣A〔n〕,A为数列{a n}的前202项和,函数f〔x〕=e x﹣e+1,假设函数g〔x〕满足f[g〔x〕﹣]=1,且b n=g〔n〕〔n∈N*〕,则数列{b n}的前n项和为n+3﹣〔2n+3〕•〔〕n.【考点】数列的求和.【分析】先根据n的个位数的不同取值推导数列的周期,由周期可求得A=2,再由函数f〔x〕为R上的增函数,求得g〔x〕的解析式,即有b n=g〔n〕=1+〔2n ﹣1〕•〔〕n,再由数列的求和方法:分组求和和错位相减法,化简整理即可得到所求和.【解答】解:n的个位数为1时有:a n=A〔n2〕﹣A〔n〕=0,n的个位数为2时有:a n=A〔n2〕﹣A〔n〕=4﹣2=2,n的个位数为3时有:a n=A〔n2〕﹣A〔n〕=9﹣3=6,n的个位数为4时有:a n=A〔n2〕﹣A〔n〕=6﹣4=2,n的个位数为5时有:a n=A〔n2〕﹣A〔n〕=5﹣5=0,n的个位数为6时有:a n=A〔n2〕﹣A〔n〕=6﹣6=0,n的个位数为7时有:a n=A〔n2〕﹣A〔n〕=9﹣7=2,n的个位数为8时有:a n=A〔n2〕﹣A〔n〕=4﹣8=﹣4,n的个位数为9时有:a n=A〔n2〕﹣A〔n〕=1﹣9=﹣8,n的个位数为0时有:a n=A〔n2〕﹣A〔n〕=0﹣0=0,每10个一循环,这10个数的和为:0,202÷10=20余2,余下两个数为:a201=0,a202=2,∴数列{a n}的前202项和等于:a201+a202=0+2=2,即有A=2.函数函数f〔x〕=e x﹣e+1为R上的增函数,且f〔1〕=1,f[g〔x〕﹣]=1=f〔1〕,可得g〔x〕=1+=1+,则g〔n〕=1+〔2n﹣1〕•〔〕n,即有b n=g〔n〕=1+〔2n﹣1〕•〔〕n,则数列{b n}的前n项和为n+[1•〔〕1+3•〔〕2+5•〔〕3+…+〔2n﹣1〕•〔〕n],可令S=1•〔〕1+3•〔〕2+5•〔〕3+…+〔2n﹣1〕•〔〕n,S=1•〔〕2+3•〔〕3+5•〔〕4+…+〔2n﹣1〕•〔〕n+1,两式相减可得S=+2[〔〕2+〔〕3+〔〕4+…+〔〕n]﹣〔2n﹣1〕•〔〕n+1=+2•﹣〔2n﹣1〕•〔〕n+1,化简可得S=3﹣〔2n+3〕•〔〕n,则数列{b n}的前n项和为n+3﹣〔2n+3〕•〔〕n.故答案为:n+3﹣〔2n+3〕•〔〕n.三、解答题〔本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.〕17.△ABC中,角A,B,C所对的边分别为a,b,c,向量=〔,1〕,=〔cosA+1,sinA〕,且•的值为2+.〔1〕求∠A的大小;〔2〕假设a=,cosB=,求△ABC的面积.【考点】余弦定理;正弦定理.【分析】〔1〕由已知及平面向量数量积的运算可求sin〔A+〕=1,结合A的范围即可得解A的值.〔2〕利用同角三角函数基本关系式可求sinB,进而利用正弦定理可求b的值,根据三角形面积公式即可计算得解.【解答】解:〔1〕∵=2+.∴.〔2〕∵,∴,∴由,得,∴.18.如图,四棱锥P﹣ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=,M在PC上,且PA∥面MBD.〔1〕求证:M是PC的中点;〔2〕在PA上是否存在点F,使二面角F﹣BD﹣M为直角?假设存在,求出的值;假设不存在,说明理由.【考点】二面角的平面角及求法;棱锥的结构特征.【分析】〔1〕连AC交BD于E,连ME,推导出E是AC中点,PA∥ME,由此能证明M是PC的中点.〔2〕取AD中点O,以O为原点,OA,OE,OP所在直线分别为x轴,y轴,z 轴建立空间直角坐标系,利用向量法求出存在F,使二面角F﹣BD﹣M为直角,此时.【解答】证明:〔1〕连AC交BD于E,连ME.∵ABCD是矩形,∴E是AC中点.又PA∥面MBD,且ME是面PAC与面MDB的交线,∴PA∥ME,∴M是PC的中点.解:〔2〕取AD中点O,由〔1〕知OA,OE,OP两两垂直.以O为原点,OA,OE,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系〔如图〕,则各点坐标为.设存在F满足要求,且,则由得:,面MBD的一个法向量为,面FBD的一个法向量为,由,得,解得,故存在F,使二面角F﹣BD﹣M 为直角,此时.19.2016世界特色魅力城市200强新鲜出炉,包括黄山市在内的28个中国城市入选.美丽的黄山风景和人文景观迎来众多宾客.现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:赞成“自助游”不赞成“自助合计游”男性30女性10合计100〔1〕假设在100这人中,按性别分层抽取一个容量为20的样本,女性应抽11人,请将上面的列联表补充完整〔在答题卡上直接填写结果,不需要写求解过程〕,并据此资料能否在犯错误的概率不超过0.05前提下,认为赞成“自助游”是与性别有关系?〔2〕假设以抽取样本的频率为概率,从旅游节游客中随机抽取3人赠送精美纪念品,记这3人中赞成“自助游”人数为X,求X的分布列和数学期望.附:K2=P〔K2≥k〕k【考点】独立性检验的应用.【分析】〔1〕根所给数据得到列联表,利用公式求得K2,与临界值比较,即可得到结论.〔2〕X的所有可能取值为:0,1,2,3,求出相应的概率,即可得到X的分布列、数学期望.【解答】解:〔1〕合计赞成“自助游”不赞成“自助游”男性301545女性451055合计7525100将2×2列联表中的数据代入计算,得K2的观测值:,∵<3.841,∴在犯错误的概率不超过0.05前提下,不能认为赞成“自助游”与性别有关系.〔2〕X的所有可能取值为:0,1,2,3,依题意,X的分布列为:X0123P〔X〕.20.已知椭圆E : +=1〔a >〕的离心率e=,右焦点F〔c,0〕,过点A 〔,0〕的直线交椭圆E于P,Q两点.〔1〕求椭圆E的方程;〔2〕假设点P关于x轴的对称点为M,求证:M,F,Q三点共线;〔3〕当△FPQ面积最大时,求直线PQ的方程.【考点】椭圆的简单性质.【分析】〔1〕由椭圆的离心率公式,计算可得a与c的值,由椭圆的几何性质可得b的值,将a、b的值代入椭圆的方程计算可得答案;〔2〕根据题意,设直线PQ的方程为y=k〔x﹣3〕,联立直线与椭圆的方程可得〔3k2+1〕x2﹣18k2x+27k2﹣6=0,设出P、Q的坐标,由根与系数的关系的分析求出、的坐标,由向量平行的坐标表示方法,分析可得证明;〔3〕设直线PQ的方程为x=my+3,联立直线与椭圆的方程,分析有〔m2+3〕y2+6my+3=0,设P〔x1,y1〕,Q〔x2,y2〕,结合根与系数的关系分析用y1.y2表示出△FPQ的面积,分析可得答案.【解答】解:〔1〕由,c=ea=×=2,则b2=a2﹣c2=2,∴椭圆E的方程是.〔2〕证明:由〔1〕可得A〔3,0〕,设直线PQ的方程为y=k〔x﹣3〕,由方程组,得〔3k2+1〕x2﹣18k2x+27k2﹣6=0,依题意△=12〔2﹣3k2〕>0,得.设P〔x1,y1〕,Q〔x2,y2〕,则,∵,由〔2﹣x1〕y2﹣〔x2﹣2〕y1=〔2﹣x1〕•k〔x2﹣3〕﹣〔x2﹣2〕•k〔x1﹣3〕=,得,∴M,F,Q三点共线.〔3〕设直线PQ的方程为x=my+3.由方程组,得〔m2+3〕y2+6my+3=0,依题意△=36m2﹣12〔m2+3〕>0,得.设P〔x1,y1〕,Q〔x2,y2〕,则.∴=,令t=m2+3,则,最大,∴,即时,S△FPQ∴S最大时直线PQ的方程为.△FPQ21.已知函数f〔x〕=〔ax2+x﹣1〕e x+f'〔0〕.〔1〕讨论函数f〔x〕的单调性;〔2〕假设g〔x〕=e﹣x f〔x〕+lnx,h〔x〕=e x,过O〔0,0〕分别作曲线y=g〔x〕与y=h〔x〕的切线l1,l2,且l1与l2关于x轴对称,求证:﹣<a<﹣.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【分析】〔1〕求出函数的导数,通过讨论a的范围求出函数的单调区间即可;〔2〕求出直线l1的方程,设l1与y=g〔x〕的切点为〔x1,y1〕,得到,根据函数的单调性求出a的范围即可.【解答】解:由已知得f'〔x〕=[ax2+〔2a+1〕x]e x,f'〔0〕=0,所以f〔x〕=〔ax2+x ﹣1〕e x.〔1〕f'〔x〕=[ax2+〔2a+1〕x]e x=[x〔ax+2a+1〕]e x.①假设a>0,当或x>0时,f'〔x〕>0;当时,f'〔x〕<0,所以f〔x〕的单调递增区间为;单调递减区间为.②假设a=0,f〔x〕=〔x﹣1〕e x,f'〔x〕=xe x,当x>0时,f'〔x〕>0;当x<0时,f'〔x〕<0,所以f〔x〕的单调递增区间为〔0,+∞〕;单调递减区间为〔﹣∞,0〕.③假设,当或x<0时,f'〔x〕<0;当时,f'〔x〕>0,所以f〔x〕的单调递增区间为;单调递减区间为.④假设,故f〔x〕的单调递减区间为〔﹣∞,+∞〕.⑤假设,当或x>0时,f'〔x〕<0;当时,f'〔x〕>0,所以f〔x〕的单调递增区间为;单调递减区间为.当a>0时,f〔x〕的单调递增区间为;单调递减区间为.当a=0时,f〔x〕的单调递增区间为〔0,+∞〕;单调递减区间为〔﹣∞,0〕.,当时,f〔x〕的单调递增区间为;单调递减区间为.当时,f〔x〕的单调递减区间为〔﹣∞,+∞〕;当时,f〔x〕单调递增区间为;单调递减区间为,〔0,+∞〕;〔2〕证明:g〔x〕=e﹣x f〔x〕+lnx=﹣e﹣x〔ax2+x﹣1〕e x+lnx=ax2+x﹣1+lnx,设l2的方程为y=k2x,切点为〔x2,y2〕,则,所以x2=1,y2=e,k2=e.由题意知k1=﹣k2=﹣e,所以l1的方程为y=﹣ex,设l1与y=g〔x〕的切点为〔x1,y1〕,则.又,即,令,在定义域上,u'〔x〕>0,所以〔0,+∞〕上,u〔x〕是单调递增函数,又,所以,即,令,则,所以,故.[选修4-4:坐标系与参数方程]22.已知曲线C的极坐标方程为ρ=,过点P〔1,0〕的直线l交曲线C于A,B两点.〔1〕将曲线C的极坐标方程的化为普通方程;〔2〕求|PA|•|PB|的取值范围.【考点】简单曲线的极坐标方程.【分析】〔1〕利用极坐标方程的转化方法,可得结论;〔2〕直线l的参数方程为为参数〕,将代入得〔cos2α+2sin2α〕t2+2tcosα﹣1=0,利用参数的几何意义,即可求|PA|•|PB|的取值范围.【解答】解:〔1〕由得ρ2〔1+sin2θ〕=2,得曲线C的普通方程为.〔2〕由题意知,直线l的参数方程为为参数〕,将代入得〔cos2α+2sin2α〕t2+2tcosα﹣1=0,设A,B对应的参数分别为t1,t2,则,∴|PA|•|PB|的取值范围为.[选修4-5:不等式选讲]23.已知函数f〔x〕=|x﹣2|,g〔x〕=|x+1|﹣x.〔1〕解不等式f〔x〕>g〔x〕;〔2〕假设存在实数x,使不等式m﹣g〔x〕≥f〔x〕+x〔m∈R〕能成立,求实数m的最小值.【考点】函数恒成立问题.【分析】〔1〕通过讨论x的范围,去掉绝对值,求出各个区间的x的范围,取并集即可;〔2〕问题转化为m≥〔|x﹣2|+|+1|〕min,根据绝对值的性质求出m的最小值即可.【解答】解:〔1〕由题意不等式f〔x〕>g〔x〕可化为|x﹣2|+x>|x+1|,当x<﹣1时,﹣〔x﹣2〕+x>﹣〔x+1〕,解得x>﹣3,即﹣3<x<﹣1;当﹣1≤x≤2时,﹣〔x﹣2〕+x>x+1,解得x<1,即﹣1≤x<1;当x>2时,x﹣2+x>x+1,解得x>3,即x>3,综上所述,不等式f〔x〕>g〔x〕的解集为{x|﹣3<x<1或x>3}.〔2〕由不等式m﹣g〔x〕≥f〔x〕+x〔m∈R〕可得m≥|x﹣2|+|x+1|,∴m≥〔|x﹣2|+|+1|〕min,∵|x﹣2|+|x+1|≥|x﹣2﹣〔x+1〕|=3,∴m≥3,故实数m的最小值是3.2017年4月21日。
2020年安徽省黄山市高考(理科)数学二模试卷 (解析版)

2020年高考数学二模试卷(理科)一、选择题(共12个小题)1.已知集合A ={x |x 2﹣6x +5≤0},B ={x |y =√x −3},A ∩B =( ) A .[1,+∞)B .[1,3]C .(3,5]D .[3,5]2.若复数z 满足(z ﹣1)(i ﹣1)=i ,则z 对应的点在第( )象限. A .一B .二C .三D .四3.已知log 5a =25,b 15=25,(25)c =5,则( )A .a <b <cB .b <a <cC .c <b <aD .a <c <b4.已知变量x ,y 满足约束条件{x +y ≥2x −2y +4≥02x −y −4≤0,若x 2+y 2+2x ≥k 恒成立,则实数k 的最大值为( ) A .40B .9C .8D .725.已知函数f (x )的定义域为D ,满足:①对任意x ∈D ,都有f (x )+f (﹣x )=0,②对任意x 1,x 2∈D 且x 1≠x 2,都有f(x 1)−f(x 2)x 1−x 2>0,则称函数f (x )为“成功函数“,下列函数是“成功函数”的是( ) A .f (x )=tan x B .f (x )=x +sin x C .f(x)=ln 2−x2+xD .f (x )=e ﹣x ﹣e x6.任取一个自然数,如果它是偶数,我们就把它除以2,如果它是奇数,我们就把它乘3再加上1,在这样的变换下,我们就得到一个新的自然数.如果反复使用这个变换,我们就会得到一串自然数,最终我们都会陷在4→2→1这个循环中,这就是世界数学名题“3x +1问题”.如图所示的程序框图的算法思路源于此,执行该程序框图,若N =6,则输出的i =( )A .6B .7C .8D .97.{a n }为等差数列,若a 2019a 2020<−1,且它的前n 项和S n 有最小值,那么当S n 取得最小正值时,n =( ) A .2019B .2020C .4039D .40408.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲.乙.丙.丁四地新增疑似病例数据,一定符合该标志的是( ) A .甲地:总体均值为3,中位数为4 B .乙地:总体均值为1,总体方差大于0 C .丙地:中位数为2,众数为3 D .丁地:总体均值为2,总体方差为39.如图,角α的顶点在坐标原点O ,始边在y 轴的非负半轴,终边经过点P (﹣3,﹣4),角β的顶点在原点O ,始边在x 轴的非负半轴,终边OQ 落在第二象限,且tan β=﹣2,则tan ∠QOP 的值为( )A .﹣2B .−211C .−112D .−1210.在长方体ABCD ﹣A 1B 1C 1D 1中,AB =√2,BC =CC 1=1,平面α过长方体顶点D ,且平面α∥平面AB 1C ,平面α∩平面ABB 1A 1=l ,则直线l 与BC 1所成角的余弦值为( ) A .√33B .√32C .√36D .√6611.点F 2是双曲线C :x 29−y 23=1的右焦点,动点A 在双曲线左支上,直线l 1:tx ﹣y +t ﹣2=0与直线l 2:x +ty +2t ﹣1=0的交点为B ,则|AB |+|AF 2|的最小值为( ) A .8B .5√3C .9D .6√312.设函数f (x )在定义域(0,+∞)上是单调函数,且∀x ∈(0,+∞),f (f (x )﹣e x +x )=e .若不等式2f (x )﹣f ′(x )﹣3≥ax 对x ∈(0,+∞)恒成立,则a 的取值范围是( ) A .(﹣∞,e ﹣2]B .(﹣∞,e ﹣1]C .(﹣∞,2e ﹣3]D .(﹣∞,2e ﹣1]二、填空题(本大题共4小题,每小题5分,共20分.请在答题卷的相应区域答题.) 13.(x +2)9=a 0+a 1(x +1)+a 2(x +1)2+…+a 9(x +1)9,则a 1+a 2+…+a 9= (用数字作答).14.已知函数f (x )={x ,x ≤1log 2(x −1),x >1,则函数y =f (f (x ))﹣1的所有零点构成的集合为 .15.在△ABC 中,D 为AB 边的中点,∠C =90°,AC =4,BC =3,E ,F 分别为边BC ,AC 上的动点,且EF =1,则DE →⋅DF →最小值为 .16.已知点A (0,4),抛物线C :x 2=2py (0<p <4)的准线为1,点P 在C 上,作PH ⊥l 于H ,且|PH |=|PA |,∠APH =120°,则抛物线方程为 .三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.请在答题卷的相应区域答题.)(一)必考题:共60分.17.已知a,b,c分别是△ABC三个内角A,B,C所对的边,且bcosC+√3bsinC−a−c=0.(1)求B;(2)若b=2,且sin A,sin B,sin C成等差数列,求△ABC的面积.18.如图,已知边长为2的菱形ABCD,其中∠BAD=120°,AE∥CF,CF⊥平面ABCD,AE=√33,CF=√3.(1)求证:平面BDE⊥平面BDF;(2)求二面角D﹣EF﹣B的大小.19.已知椭圆Γ:x2a2+y2b2=1(a>b>0)的离心率为√22,左右焦点分别为F1,F2,且A、B分别是其左右顶点,P是椭圆上任意一点,△PF1F2面积的最大值为4.(1)求椭圆Γ的方程.(2)如图,四边形ABCD为矩形,设M为椭圆Γ上任意一点,直线MC、MD分别交x 轴于E、F,且满足AE2+BF2=AB2,求证:AB=2AD.20.在党中央的英明领导下,在全国人民的坚定支持下,中国的抗击“新型冠状肺炎”战役取得了阶段性胜利,现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心,对某中型商品实行分期付款方式销售,根据以往资料统计,顾客购买该商品选择分期付款的期数ξ的分布列为ξ456P 0.4 a b其中0<a <1,0<b <1.(1)求购买该商品的3位顾客中,恰有1位选择分4期付款的概率;(2)商场销售一件该商品,若顾客选择分4期付款,则商场获得的利润为2000元;若顾客选择分5期付款,则商场获得的利润为2500元;若顾客选择分6期付款,则商场获得的利润为3000元,假设该商场销售两件该商品所获得的利润为X (单位:元), (i )设X =5500时的概率为m ,求当m 取最大值时,利润X 的分布列和数学期望; (ii )设某数列{x n }满足x 1=0.4,x n =a ,2x n +1=b ,若a <0.25,求n 的最小值. 21.已知函数f (x )=e x ﹣a (x +1)(a ∈R ). (1)讨论函数f (x )极值点的个数;(2)当a =1时,不等式f (x )≥kx 1n (x +1)在[0,+∞)上恒成立,求实数k 的取值范围.选考题:共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,曲线C 1的参数方程为{x =2cosαy =√3sinα(α为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρsin(θ+π4)=√22,且在极坐标下点P (1,π2).(1)求曲线C 1的普通方程和曲线C 2的直角坐标方程; (2)若曲线C 1与曲线C 2交于A ,B 两点,求1|PA|+1|PB|的值.[选修4--5:不等式选讲]23.已知实数x ,y 满足x +4y =2. (1)若|1+y |<|x |﹣2,求x 的取值范围; (2)若x >0,y >0,求4x+1y 的最小值.参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卷的相应区域答题.)1.已知集合A ={x |x 2﹣6x +5≤0},B ={x |y =√x −3},A ∩B =( ) A .[1,+∞)B .[1,3]C .(3,5]D .[3,5]【分析】分别求出集合A 、B ,从而求出A ∩B 即可. 解:∵集合A ={x |x 2﹣6x +5≤0}={x |1≤x ≤5}, B ={x |y =√x −3}={x |x ≥3}, ∴A ∩B =[3,5], 故选:D .【点评】本题考查了集合的运算,考查二次函数以及二次根式的性质,是一道基础题. 2.若复数z 满足(z ﹣1)(i ﹣1)=i ,则z 对应的点在第( )象限. A .一B .二C .三D .四【分析】把已知等式变形,利用复数代数形式的乘除运算化简求得z ,进一步求出z 的坐标得答案.解:由(z ﹣1)(i ﹣1)=i ,得z ﹣1=ii−1=i(−1−i)(−1+i)(−1−i)=12−12i , ∴z =32−12i ,则z =32+12i . ∴z 对应的点的坐标为(32,12),在第一象限. 故选:A .【点评】本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.3.已知log 5a =25,b 15=25,(25)c =5,则( )A .a <b <cB .b <a <cC .c <b <aD .a <c <b【分析】化对数式为指数式判断a >1,求解b ∈(0,1),化指数式为对数式判断c <0,则答案可求.解:由log 5a =25,得a =525>50=1,由b 15=25,得b =(25)5∈(0,1),由(25)c =5,得c =log 255<0, ∴c <b <a . 故选:C .【点评】本题考查对数值的大小比较,考查有理指数幂与对数的运算性质,考查数学转化思想方法,是基础题.4.已知变量x ,y 满足约束条件{x +y ≥2x −2y +4≥02x −y −4≤0,若x 2+y 2+2x ≥k 恒成立,则实数k 的最大值为( ) A .40B .9C .8D .72【分析】已知x 、y 满足以下约束条件画出可行域,目标函数z =x 2+y 2+2x 是可行域中的点(x ,y )到原点的距离的平方减1,求出最小值,然后求解z 的最大值. 解:变量x ,y 满足约束条件{x +y ≥2x −2y +4≥02x −y −4≤0的可行域如图,x 2+y 2+2x 是点(x ,y )到(﹣1,0)的距离的平方减1,故最小值为点P 到(﹣1,0)的距离的平方加1,z =x 2+y 2+2x 的最小值为:(2)2−1=72 若x 2+y 2+2x ≥k 恒成立,即72≥k .k 的最大值为:72.故选:D .【点评】此题主要考查简单的线性规划问题,是一道中档题,要学会画图.考查转化思想的应用.5.已知函数f (x )的定义域为D ,满足:①对任意x ∈D ,都有f (x )+f (﹣x )=0,②对任意x 1,x 2∈D 且x 1≠x 2,都有f(x 1)−f(x 2)x 1−x 2>0,则称函数f (x )为“成功函数“,下列函数是“成功函数”的是( ) A .f (x )=tan x B .f (x )=x +sin x C .f(x)=ln 2−x2+xD .f (x )=e ﹣x ﹣e x【分析】由①对任意x ∈D ,都有f (x )+f (﹣x )=0,得f (﹣x )=﹣f (x )即函数为奇函数;②对任意x 1,x 2∈D 且x 1≠x 2,都有f(x 1)−f(x 2)x 1−x 2>0,即函数单调递增,然后结合选项进行判断即可.解:由①对任意x ∈D ,都有f (x )+f (﹣x )=0,得f (﹣x )=﹣f (x )即函数为奇函数;②对任意x 1,x 2∈D 且x 1≠x 2,都有f(x 1)−f(x 2)x 1−x 2>0,即函数单调递增,A :y =tan x 在定义域内不单调,不符合题意;B :由f (x )=x +sin x 可得f (﹣x )=﹣x ﹣sin x =﹣f (x )且由于f ′(x )=1+cos x ≥0恒成立,即f (x )在R 上单调递增,符合题意;C :结合复合函数单调性可知,y =ln2−x 2+x在(﹣2,2)内单调递减,不符合题意;D :y =e ﹣x ﹣e x 在定义域R 上单调递减,不符合题意. 故选:B .【点评】本题主要考查了函数单调性与奇偶性的判断,属于函数性质的综合应用. 6.任取一个自然数,如果它是偶数,我们就把它除以2,如果它是奇数,我们就把它乘3再加上1,在这样的变换下,我们就得到一个新的自然数.如果反复使用这个变换,我们就会得到一串自然数,最终我们都会陷在4→2→1这个循环中,这就是世界数学名题“3x +1问题”.如图所示的程序框图的算法思路源于此,执行该程序框图,若N =6,则输出的i =( )A.6B.7C.8D.9【分析】根据该程序的功能是利用循环结构计算n的值并输出相应的i的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.解:由题意,模拟程序的运行,可得n=6,i=1n不是奇数,n=3,i=2,不满足条件n=1;n是奇数,n=10,i=3,不满足条件n=1,执行循环体,n不是奇数,n=5,i=4;不满足条件n=1,执行循环体,n是奇数,n=16,i=5;不满足条件n=1,执行循环体,n不是奇数,n=8,i=6;不满足条件n=1,执行循环体,n不是奇数,n=4,i=7;不满足条件n=1,执行循环体,n不是奇数,n=2,i=8;不满足条件n=1,执行循环体,n不是奇数,n=1,i=9;满足条件n=1,退出循环,输出i的值为9.故选:D.【点评】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.7.{a n }为等差数列,若a 2019a 2020<−1,且它的前n 项和S n 有最小值,那么当S n 取得最小正值时,n =( ) A .2019 B .2020 C .4039 D .4040【分析】若a 2019a 2020<−1,且它的前n 项和S n 有最小值,可得a 2019<0,a 2020>0.a 2019+a 2020<0.再利用求和公式即可判断出结论. 解:若a 2019a 2020<−1,且它的前n 项和S n 有最小值,∴a 2019<0,a 2020>0. ∴a 2019+a 2020<0.S 4038=2019(a 1+a 4038)=2019(a 2019+a 2020)<0. S 4039=4039(a 1+a 4039)2=4039a 2020>0. 那么当S n 取得最小正值时,n =4039. 故选:C .【点评】本题考查了等差数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.8.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲.乙.丙.丁四地新增疑似病例数据,一定符合该标志的是( ) A .甲地:总体均值为3,中位数为4 B .乙地:总体均值为1,总体方差大于0 C .丙地:中位数为2,众数为3 D .丁地:总体均值为2,总体方差为3【分析】平均数和中位数不能限制某一天的病例超过7人,当总体方差大于0,不知道总体方差的具体数值,因此不能确定数据的波动大小,中位数和众数也不能确定,当总体平均数是2,若有一个数据超过7,则方差就接近3,符合要求. 解:∵平均数和中位数不能限制某一天的病例超过7人, 故A 不正确,当总体方差大于0,不知道总体方差的具体数值,因此不能确定数据的波动大小, 故B 不正确,中位数和众数也不能确定,故C不正确,当总体平均数是2,若有一个数据超过7,则方差就接近3,∴总体均值为2,总体方差为3时,没有数据超过7.故D正确.故选:D.【点评】本题考查数据的几个特征量,这几个量各自表示数据的一个方面,有时候一个或两个量不能说明这组数据的特点,若要掌握这组数据则要全面掌握.9.如图,角α的顶点在坐标原点O,始边在y轴的非负半轴,终边经过点P(﹣3,﹣4),角β的顶点在原点O,始边在x轴的非负半轴,终边OQ落在第二象限,且tanβ=﹣2,则tan∠QOP的值为()A.﹣2B.−211C.−112D.−12【分析】由已知可得:tanα=43.可得tan∠QOP=tan(α﹣β)=tanα−tanβ1+tanα⋅tanβ,代入即可得出.解:由已知可得:tanα=−4−3=43.∴tan∠QOP=tan(α﹣β)=tanα−tanβ1+tanα⋅tanβ=43−(−2)1+43×(−2)=−2.故选:A.【点评】本题考查了三角函数的定义、和差公式,考查了推理能力与计算能力,属于基础题.10.在长方体ABCD﹣A1B1C1D1中,AB=√2,BC=CC1=1,平面α过长方体顶点D,且平面α∥平面AB1C,平面α∩平面ABB1A1=l,则直线l与BC1所成角的余弦值为()A.√33B.√32C.√36D.√66【分析】由题意画出图形,得到平面α与平面ABB 1A 1的交线l ,找出异面直线所成角,由已知结合余弦定理求解. 解:如图,∵平面α过长方体顶点D ,且平面α∥平面AB 1C , ∴平面α与平面A 1DC 1 重合,在平面ABB 1A 1中,过A 1作A 1E ∥AB 1,则A 1E ∥DC 1,即A 1E 为平面α与平面ABB 1A 1的交线l , 连接AD 1,可得AD 1∥BC 1,又l ∥AB 1,则∠D 1AB 1 即为直线l 与BC 1所成角. 连接D 1B 1,由AB =√2,BC =CC 1=1,得AB 1=B 1D 1=√3,AD 1=√2,由余弦定理可得:cos ∠D 1AB 1=(√3)2+(√2)2−(√3)22×√3×√2=√66.即直线l 与BC 1所成角的余弦值为√66. 故选:D .【点评】本题考查异面直线所成角的求法,考查空间想象能力与思维能力,是中档题. 11.点F 2是双曲线C :x 29−y 23=1的右焦点,动点A 在双曲线左支上,直线l 1:tx ﹣y +t ﹣2=0与直线l 2:x +ty +2t ﹣1=0的交点为B ,则|AB |+|AF 2|的最小值为( ) A .8B .5√3C .9D .6√3【分析】由题意求出直线l 1,l 2的交点B 为圆心在(0,﹣2),半径为1的圆,由双曲线的定义可得|AF 2|=|AF 1|+2a ,所以|AB |+|AF 2|=|AB |+|AF 1|+6,当A ,F 1,B 三点共线时,|AB |+|AF 2|最小,过F 1与圆心的直线与圆的交点B 且在F 1和圆心之间时最小.解:由双曲线的方程可得a =3,b =√3,焦点F (﹣2√3,0), 可得|AF 2|=|AF 1|+2a =|AF 1|+6, 所以|AB |+|AF 2|=|AB |+|AF 1|+6,当A ,F 1,B 三点共线时,|AB |+|AF 2|最小,联立直线l 1,l 2的方程{tx −y +t −2=0x +ty +2t −1=0,可得{x =−t 2−1t 2+1y +2=2tt 2+1,消参数t 可得x 2+(y +2)2=1,所以可得交点B 的轨迹为圆心在(0,﹣2),半径为1的圆, 所以|AB |+|AF 2|=|AB |+|AF 1|+6≥|BF 1|﹣1+6=√(−2√3)2+22+5=9, 当过F 1与圆心的直线与圆的交点B 且在F 1和圆心之间时最小. 所以|AB |+|AF 2|的最小值为9, 故选:C .【点评】本题考查求轨迹方程及双曲线的性质,三点共线时线段之和最小,属于中档题. 12.设函数f (x )在定义域(0,+∞)上是单调函数,且∀x ∈(0,+∞),f (f (x )﹣e x +x )=e .若不等式2f (x )﹣f ′(x )﹣3≥ax 对x ∈(0,+∞)恒成立,则a 的取值范围是( ) A .(﹣∞,e ﹣2]B .(﹣∞,e ﹣1]C .(﹣∞,2e ﹣3]D .(﹣∞,2e ﹣1]【分析】先利用换元法求出f (x )的解析式,然后再用分离变量法,借助函数的单调性来解决问题.解:设f (x )﹣e x +x =t ,则f (t )=e ,∴f (x )=e x ﹣x +t ,令x =t 得f (t )=e t ﹣t +t =e ,解得t =1, ∴f (x )=e x ﹣x +1, f ′(x )=e x ﹣1,不等式2f (x )﹣f ′(x )﹣3≥ax ,x ∈(0,+∞).即:a ≤e xx−2.令g (x )=e xx−2,x ∈(0,+∞).g ′(x )=e x (x−1)2,可得x =1时,函数g (x )取得极小值即最小值.∵不等式2f (x )﹣f ′(x )﹣3≥ax 对x ∈(0,+∞)恒成立, ∴a ≤e ﹣2.∴a 的取值范围是(﹣∞,e ﹣2]. 故选:A .【点评】本题考查了利用导数研究函数的单调性极值与最值、方程与不等式解法、换元法、等价转化方法,考查了推理能力与计算能力,属于中档题.二、填空题(本大题共4小题,每小题5分,共20分.请在答题卷的相应区域答题.) 13.(x +2)9=a 0+a 1(x +1)+a 2(x +1)2+…+a 9(x +1)9,则a 1+a 2+…+a 9= 511 (用数字作答).【分析】在所给的等式中,分别令x =﹣1,x =0,可得要求式子的值. 解:∵(x +2)9=a 0+a 1(x +1)+a 2(x +1)2+…+a 9(x +1)9, ∴令x =﹣1,可得a 0=1.再令x =0,可得 1+a 1+a 2+…+a 9=29,∴a 1+a 2+…+a 9=511, 故答案为:511.【点评】本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.14.已知函数f (x )={x ,x ≤1log 2(x −1),x >1,则函数y =f (f (x ))﹣1的所有零点构成的集合为 {1,3,9} .【分析】函数y =f [f (x )]﹣1的零点,即求方程f [f (x )]﹣1=0的解,利用换元法进行求解即可.解:由y =f (f (x ))﹣1=0得f (f (x ))=1, 设t =f (x ),则等价为f (t )=1, 当x ≤1时,由f (x )=x =1得x =1,当x >1时,由f (x )=log 2(x ﹣1)=1得x =3, 即t =1或t =3,当x ≤1时,由f (x )=x =1,得x =1,由f (x )=x +1=3,得x =2(舍),故此时x =1,当x >1时,由f (x )=log 2(x ﹣1)=1得x =3,由f (x )=log 2(x ﹣1)=3,得x =9, 综上x =1,或x =3或x =9,所以函数y =f [f (x )]﹣1的所有零点所构成的集合为:{1,3,9} 故答案为:{1,3,9}.【点评】本小题主要考查函数的零点、方程的解法等基础知识,利用换元法结合数形结合是解决本题的关键.15.在△ABC 中,D 为AB 边的中点,∠C =90°,AC =4,BC =3,E ,F 分别为边BC ,AC 上的动点,且EF =1,则DE →⋅DF →最小值为154.【分析】建立平面直角坐标系,设E (x ,0),求出DE →⋅DF →的坐标,则DE →⋅DF →可表示为x 的函数,利用函数的性质得出最小值.【解答】解以三角形的直角边为坐标轴建立平面直角坐标系,如图:则A (0,4),B (3,0),C (0,0),D (32,2).设E (x ,0),则F (0,√1−x 2).0≤x ≤1.∴DE →=(x −32,﹣2),DF →=(−32,√1−x 2−2).∴DE →⋅DF →=94−32x +4﹣2√1−x 2=254−32x ﹣2√1−x 2. 令f (x )=254−32x ﹣2√1−x 2,则f ′(x )=−322x √1−x . 令f ′(x )=0得x =35.当0≤x <35时,f ′(x )<0,当35<x <1时,f ′(x )>0.∴当x =35时,f (x )取得最小值f (35)=154. 故答案为:154.【点评】本题考查了平面向量的数量积运算,建立坐标系是解题关键,属于中档题. 16.已知点A (0,4),抛物线C :x 2=2py (0<p <4)的准线为1,点P 在C 上,作PH⊥l于H,且|PH|=|PA|,∠APH=120°,则抛物线方程为x2=165y.【分析】设抛物线的焦点为F(0,p2),则|AF|=4−p2,由抛物线的定义可知,|PH|=|PF|=|PA|,不妨设点P在第一象限,过点P作PQ⊥y轴于点Q,则Q为AF的中点,结合∠APH=120°,可以用p表示出点P的坐标,然后将其代入抛物线方程,列出关于p 的方程,解之可得p的值,从而求得抛物线的方程.解:设抛物线的焦点为F(0,p2),|AF|=4−p2,由抛物线的定义可知,|PH|=|PF|,∵|PH|=|PA|,∴|PA|=|PF|,不妨设点P在第一象限,过点P作PQ⊥y轴于点Q,则Q为AF的中点,|AQ|=|FQ|=12|AF|=12(4−p2),∵∠APH=120°,∴∠APQ=120°﹣90°=30°,∴|PQ|=√3|AQ|=√32(4−p2),|OQ|=|FQ|+|OF|=12(4−p2)+p2=2+p4,∴点P的坐标为(√32(4−p2),2+p4),∵点P在抛物线C上,∴[√32(4−p2)]2=2p×(2+p4),化简得5p2+112p﹣192=0,解之得p=85或−24(舍负),∴抛物线方程为x2=165y.故答案为:x2=165y.【点评】本题考查抛物线的定义,求抛物线的标准方程,考查学生的分析能力和运算能力,属于中档题.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.请在答题卷的相应区域答题.)(一)必考题:共60分.17.已知a,b,c分别是△ABC三个内角A,B,C所对的边,且bcosC+√3bsinC−a−c=0.(1)求B;(2)若b=2,且sin A,sin B,sin C成等差数列,求△ABC的面积.【分析】(1)由正弦定理,三角函数恒等变换的应用化简已知等式,结合sin C>0,可得sin(B−π6)=12,又根据范围B−π6∈(−π6,5π6),可求B的值.(2)由等差数列的性质,正弦定理可得a+c=2b=4,又根据余弦定理可求ac的值,进而根据三角形的面积公式即可计算求解.解:(1)由bcosC+√3bsinC−a−c=0,则sinBcosC+√3sinBsinC=sinA+sinC,sinBcosC+√3sinBsinC=sin(B+C)+sinC,√3sinBsinC=sinCcosB+sinC,而sin C>0,√3sinB−cosB=1,所以2sin(B−π6)=1,可得sin(B−π6)=12,而B∈(0,π),又B−π6∈(−π6,5π6),所以B−π6=π6,故B=π3.(2)由sin A,sin B,sin C成等差数列,且b=2,所以2sin B=sin A+sin C,可得a+c=2b=4,又a2+c2﹣2ac cos B=b2,则(a+c)2−2ac−2accos π3=4,可得:16﹣3ac=4,所以ac=4,则S=12acsinB=12×4×√32=√3.【点评】本题主要考查了正弦定理,三角函数恒等变换的应用,等差数列的性质,余弦定理,三角形的面积公式在解三角形中的应用,考查了转化思想,属于基础题.18.如图,已知边长为2的菱形ABCD,其中∠BAD=120°,AE∥CF,CF⊥平面ABCD,AE=√33,CF=√3.(1)求证:平面BDE⊥平面BDF;(2)求二面角D﹣EF﹣B的大小.【分析】(1)证明BD⊥CF,BD⊥AC,推出BD⊥平面ACFE,得到OF⊥BD,推出AE⊥平面ABCD,证明AE⊥AO且FC⊥CO,OF⊥OE,证明OF⊥平面BDE,然后证明平面BDE⊥平面BDF.(2)以OA,OB所在的直线分别为x轴,y轴,过O做垂直于平面ABCD的为z轴建立空间直角坐标系.求出平面DEF的一个法向量,平面BEF的一个法向量,通过空间向量的数量积求解二面角D﹣EF﹣B的大小.【解答】(1)证明:因为AE∥CF,所以A、C、F、E四点共面.又CF⊥平面ABCD,而BD⊂平面ABCD,所以BD⊥CF,由菱形ABCD,所以,BD⊥AC,令BD∩AC=O,且CF∩AC=C,所以,BD⊥平面ACFE,而OF⊂平面ACFE,所以,OF⊥BD,因为AE∥CF且CF⊥平面ABCD,所以AE⊥平面ABCD,则AE⊥AO且FC⊥CO AE=√33,CF=√3,由菱形ABCD且∠BAD=120,所以AO=OC=1,故tan∠EOA=√33,tan∠FOC=√3,则∠EOA=π6,∠FOC=π3,所以∠EOF=π2,即OF⊥OE,又OE∩BD=O,所以OF⊥平面BDE,OF⊂平面BDF,平面BDE⊥平面BDF.(2)由菱形ABCD ,所以BD ⊥AC ,以OA ,OB 所在的直线分别为x 轴,y 轴,过O 作垂直于平面ABCD 的直线为z 轴建立空间直角坐标系. 则∠BAD =2π3,所以A (1,0,0),B(0,√3,0),D(0,−√3,0),F(−1,0,√3),E(1,0,√33),所以EF →=(−2,0,2√33),DF →=(−1,√3,√3),BF →=(−1,−√3,√3),令平面DEF 的一个法向量为n →=(1,y 1,z 1),且EF →=(−2,0,2√33),DF →=(−1,√3,√3),由n →⋅EF →=0,−2+2√33z 1=0,所以z 1=√3,由n →⋅DF →=0,−1+√3y 1+√3z 1=0,所以y 1=−2√33,即n →=(1,−2√33,√3),令平面BEF 的一个法向量为:m →=(1,y 2,z 2),且EF →=(−2,0,2√33),BF →=(−1,−√3,√3),由m →⋅EF →=0,−2+2√33z 2=0,所以z 2=√3,由n →⋅BF →=0,−1−√3y 2+√3z 2=0,所以y 2=2√33,即m →=(1,2√33,√3),所以cosθ=−cos <n →,m →>=−n →⋅m →|n →|⋅|m →|=−1−43+31+43+3=−12,则θ=23π, 即二面角D ﹣EF ﹣B 的大小为23π.【点评】本题考查直线与平面垂直的判定定理以及平面与平面垂直的判定定理得到应用,二面角的平面角的求法,考查空间想象能力,逻辑推理能力,以及计算能力,是中档题. 19.已知椭圆Γ:x 2a +y 2b =1(a >b >0)的离心率为√22,左右焦点分别为F 1,F 2,且A 、B 分别是其左右顶点,P 是椭圆上任意一点,△PF 1F 2面积的最大值为4. (1)求椭圆Γ的方程.(2)如图,四边形ABCD 为矩形,设M 为椭圆Γ上任意一点,直线MC 、MD 分别交x 轴于E 、F ,且满足AE 2+BF 2=AB 2,求证:AB =2AD .【分析】(1)由椭圆的离心率公式和三角形的面积公式,结合a ,b ,c 的关系,解方程可得所求椭圆方程;(2)设C (2√2,﹣t ),D (﹣2√2,﹣t ),t >0,可令M (x 0,y 0),运用直线方程和两直线的交点,化简整理,即可得证.解:(1)由题意可得e =c a =√22,又c 2=a 2﹣b 2,可得b =c ,而S ≤12×2c ×b =4,所以b =c =2,解得a 2=8,b 2=4, 所以椭圆的方程为x 28+y 24=1;(2)证明:设C (2√2,﹣t ),D (﹣2√2,﹣t ),t >0,可令M (x 0,y 0), 由k MC =0x 0−22,故MC 的方程为y ﹣y 0=0x 0−22(x ﹣x 0), 直线MC 交x 轴于E ,可令y =0,则x =y 0(2√2−x 0)y 0+t +x 0=2√2y 0+tx 0y 0+t ,即E (2√2y 0+tx 0y 0+t,0), 由k MD =0x 0+2√2,故MD 的方程为y ﹣y 0=0x 0+2√2(x ﹣x 0),直线MD 交x 轴于F ,可令y =0,则x =−y 0(2√2+x 0)y 0+t +x 0=−2√2y 0+tx 0y 0+t,即F (−2√2y 0+tx 0y 0+t,0),因为AE 2+BF 2=AB 2,所以(2√2y 0+tx 0y 0+t +2√2)2+(−2√2y 0+tx 0y 0+t−2√2)2=(4√2)2,可得16y 02+2t 2x 02(y 0+t)+32y 0y 0+t=16,即8y 02+t 2x 02+16y 02+16y 0t =8(y 0+t )2, 即t2x 02+16y 02=8t 2,而x28+y 024=1,所以x 02=8﹣2y 02,可得t 2(8﹣2y 02)+16y 02=8t 2,可得(16﹣2t 2)y 02=0,而M 为椭圆上一点,所以16﹣2t2=0,解得t=2√2,所以ABAD=2,即AB=2AD.【点评】本题考查椭圆的方程和性质,考查直线和椭圆的位置关系,考查直线方程的求法和应用,以及两点的距离公式,考查方程思想和化简运算能力,属于中档题.20.在党中央的英明领导下,在全国人民的坚定支持下,中国的抗击“新型冠状肺炎”战役取得了阶段性胜利,现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心,对某中型商品实行分期付款方式销售,根据以往资料统计,顾客购买该商品选择分期付款的期数ξ的分布列为ξ456P0.4a b其中0<a<1,0<b<1.(1)求购买该商品的3位顾客中,恰有1位选择分4期付款的概率;(2)商场销售一件该商品,若顾客选择分4期付款,则商场获得的利润为2000元;若顾客选择分5期付款,则商场获得的利润为2500元;若顾客选择分6期付款,则商场获得的利润为3000元,假设该商场销售两件该商品所获得的利润为X(单位:元),(i)设X=5500时的概率为m,求当m取最大值时,利润X的分布列和数学期望;(ii)设某数列{x n}满足x1=0.4,x n=a,2x n+1=b,若a<0.25,求n的最小值.【分析】(1)方法1:设恰有一位顾客选择分4期付款的概率的概率为P.由题可知:a+b=0.6,然后求解即可.方法2:由于3位顾客中恰有1位选择“分4期付款”,则另外两位均不选“分4期付款”,利用相互独立事件乘法乘积求解概率即可.(2)(ⅰ)由题可得X的值分别为4000,4500,5000,5500,6000.求出概率,得到分布列,然后求解期望即可.(ⅱ)由题可得x n+2x n+1=a+b=0.6,得到x n+1=−12x n+0.3,判断数列{x n﹣0.2}是等比数列,然后分类求解n的最小值.解:(1)方法1:设恰有一位顾客选择分4期付款的概率的概率为P.由题可知:a+b=0.6,则P=3×0.4×(a2+2ab+b2)=0.4×(a+b)2=0.4×0.62=0.432.方法2:由于3位顾客中恰有1位选择“分4期付款”,则另外两位均不选“分4期付款”,所以P=3×0.4×(1﹣0.4)×(1﹣0.4)=0.432.(2)(ⅰ)由题可得X的值分别为4000,4500,5000,5500,6000.P(X=4000)=0.4×0.4=0.16,P(X=4500)=2×0.4×a=0.8a,P(X=5000)=a2+2×0.4×b=a2+0.8b,P(X=5500)=2ab,P(X=6000)=b2,所以P(X=5500)=2ab≤2×(a+b2)2=0.362=0.18,取最大值的条件为a=b=0.3所以分布列为:X40004500500055006000P0.160.240.330.180.09∴E(X)=4000×0.16+4500×0.24+5000×0.33+5500×0.18+6000×0.09=4900.(ⅱ)解:由题可得x n+2x n+1=a+b=0.6,所以x n+1=−12x n+0.3,化简得x n+1−0.2=−12(x n−0.2),即{x n﹣0.2}是等比数列,首项为x1﹣0.2=0.2,公比为−1 2,所以x n−0.2=(0.4−0.2)×(−12)n−1,化简得x n=0.2[1+(−12)n−1]由题可知:(1)由题可知:a=x n=0.2[1+(−12)n−1]<0.6⇒(−12)n−1<2,显然对所有n∈一、选择题*都成立;(2)b=2x n+1=0.4[1+(−12)n]<0.6⇒(−12)n<12,也是对所有n∈N*都成立;(3)a=x n=0.2[1+(−12)n−1]<0.25⇒(−12)n−1<14当n为偶数时,上述不等式恒成立;当n为奇数时,(12)n−1<14,解得n>5即n≥5综上所述,n的最小值为5.【点评】本题考查离散型随机变量的分布列以及期望的求法,数列与函数的应用,考查转化思想以及计算能力,题目比较新颖,是难题.21.已知函数f(x)=e x﹣a(x+1)(a∈R).(1)讨论函数f(x)极值点的个数;(2)当a=1时,不等式f(x)≥kx1n(x+1)在[0,+∞)上恒成立,求实数k的取值范围.【分析】(1)求出导函数f'(x)=e x﹣a,通过①当a≤0时,②当a>0时,判断导函数的符号,判断函数的单调性,求解函数的极值即可.(2)当a=1时,由题即e x﹣x﹣1≥kxln(x+1)在[0,+∞)上恒成立,令h(x)=e x ﹣x﹣1﹣kxln(x+1)且h(0)=0,通过函数的导数,结合(ⅰ)当1﹣2k≥0时,(ⅱ)当1﹣2k<0时,判断函数的单调性求解函数的最值,推出结果.求解k的取值范围.解:(1)f'(x)=e x﹣a,①当a≤0时,f'(x)=e x﹣a>0,所以f(x)在R上单调递增,无极值.②当a>0时,令f'(x)=0,得x=lna,当x∈(﹣∞,lna)时,f'(x)<0;当x∈(lna,+∞)时,f'(x)>0即函数f(x)在(﹣∞,lna)上单调递减,在(lna,+∞)上单调递增,此时只有一个极值点.综上所述,当a≤0时,f(x)在R上无极值点;当a>0时,函数f(x)在R上只有一个极值点.(2)当a=1时,由题即e x﹣x﹣1≥kxln(x+1)在[0,+∞)上恒成立令h(x)=e x﹣x﹣1﹣kxln(x+1)且h(0)=0,则h′(x)=e x−1−k[ln(x+1)+xx+1](x≥0),令g(x)=h′(x)=e x−1−k[ln(x+1)+x x+1](x≥0),则g,(x)=e x−k[1x+1+1(x+1)2](x≥0)且g'(0)=1﹣2k,(ⅰ)当1﹣2k≥0时,即k≤12时,由于x≥0,e x≥1,而k[1x+1+1(x+1)2]≤12[1x+1+1(x+1)2]≤1,所以g'(x)≥0,故g(x)在[0,+∞)上单调递增,所以g(x)≥g(0)=0,即h'(x)≥0,故h(x)在[0,+∞)上单调递增,所以h(x)≥h(0)=0,即e x﹣x﹣1≥kxln(x+1)在[0,+∞)上恒成立,故k≤12符合题意.(ⅱ)当1﹣2k<0时,即k>12时g'(0)<0,由于g′(x)=e x−k[1x+1+1(x+1)2]在[0,+∞)上单调递增,令x =ln (2k )>0因为g′(ln2k)=eln2k−k[1ln2k+1+1(ln2k+1)2]>2k −2k=0,故在(0,ln 2k )上存在唯一的零点x 0,使g '(x 0)=0,因此,当x ∈(0,x 0)时,g '(x )<0,g (x )单调递减,所以g (x )<g (0)=0, 即h '(x )<0,h (x )在(0,x 0)上单调递减,故h (x )<h (0)=0,与题不符. 综上所述,k 的取值范围是(−∞,12].【点评】本题考查函数的导数的应用,考查转化思想以及计算能力,分类讨论思想的应用,是难题.选考题:共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,曲线C 1的参数方程为{x =2cosαy =√3sinα(α为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρsin(θ+π4)=√22,且在极坐标下点P (1,π2).(1)求曲线C 1的普通方程和曲线C 2的直角坐标方程; (2)若曲线C 1与曲线C 2交于A ,B 两点,求1|PA|+1|PB|的值.【分析】(1)直接利用转换关系,把参数方程、极坐标方程和直角坐标方程之间进行转换.(2)利用直线和曲线的位置关系式的应用和一元二次方程根和系数关系式的应用求出结果.解:(1)C 1的参数方程:{x =2cosαy =√3sinα(α为参数)得(x2)2+(3)2=1,曲线C 1的直角坐标方程:x 24+y 23=1.由ρsin(θ+π4)=√22,得√22ρsinθ+√22ρcosθ=√22, 所以曲线C 2的直角坐标方程为x +y ﹣1=0.(2)点P的极坐标为(1,π2),故其直角坐标为(0,1),由C2:x+y﹣1=0,则其参数方程为{x=−√22ty=1+√22t,将C2的参数方程代入曲线C1的方程x24+y23=1,得7t2+8√2t−16=0①由于△>0恒成立,不妨令方程①有两个不等实根t1、t2,由于t1t2=−167<0,所以t1、t2异号,且|PA|⋅|PB|=16 7,则|PA|+|PB|=|t1|+|t2|=|t1−t2|=√(t1+t2)2−4t1t2=(−827)2+647=247,1 |PA|+1|PB|=|PA|+|PB||PA|⋅|PB|=247167=32.【点评】本题考查的知识要点:参数方程、极坐标方程和直角坐标方程之间的转换,一元二次方程的根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.[选修4--5:不等式选讲]23.已知实数x,y满足x+4y=2.(1)若|1+y|<|x|﹣2,求x的取值范围;(2)若x>0,y>0,求4x+1y的最小值.【分析】(1)由x+4y=2,得y=12−x4,代入|1+y|<|x|﹣2,可得|32−x4|<|x|−2,即|6﹣x|<4|x|﹣8,然后对x分类求解,取并集得答案;(2)由x>0,y>0,且x+4y=2,得4x +1y=12(4x+1y)(x+4y),展开后利用基本不等式求最值.解:(1)由x+4y=2,得y=12−x4由|1+y|<|x|﹣2⇒|32−x4|<|x|−2,即|6﹣x|<4|x|﹣8,当x<0,则6﹣x<﹣4x﹣8⇒x<−143,∴x<−143;当0≤x ≤6时,则6﹣x <4x ﹣8⇒x >145,∴145<x ≤6; 当x >6时,则x ﹣6<4x ﹣8⇒x >23,∴x >6. 故x 的取值范围为{x |x <−143或x >145}; (2)∵x >0,y >0,且x +4y =2 ∴4x +1y=12(4x+1y )(x +4y)=12(4+4+16y x +x y)≥12(4+4+2√16)=8.当且仅当16y x=xy,即x =1,y =14时,4x+1y的最小值为8.【点评】本题考查绝对值不等式的解法,训练了利用基本不等式求最值,是中档题.。
安徽省黄山市高考数学三模试卷 理(含解析)

安徽省黄山市2015届高考数学三模试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1.(5分)若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4 B.C.4 D.2.(5分)已知集合M={x|y=lg(1﹣x)},集合N={y|y=2x,x∈R},则M∩N=()A.{x|x<1} B.{x|x>1} C.{x|0<x<1} D.∅3.(5分)已知(1+ax)(1+x)5的展开式中x2的系数为5,则a=()A.﹣4 B.﹣3 C.﹣2 D.﹣14.(5分)若以直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,已知直线l参数方程为(t为参数),曲线C的极坐标方程为ρ=4sinθ,则直线l被曲线C截得的弦长为()A.B.C.D.5.(5分)数列{a n}满足a1=1,a n+1=r•a n+r(n∈N*,r∈R且r≠0),则“r=1”是“数列{a n}成等差数列”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.(5分)执行如图所示的程序框图,则输出的S的值是()A.B.C.4 D.﹣17.(5分)过双曲线﹣=1(a>0,b>0)的右顶点A作斜率为﹣1的直线,该直线与双曲线的两条渐近线的交点分别为B、C.若=,则双曲线的离心率是()A.B.C.D.8.(5分)已知函数有且仅有3个实数根x1、x2、x3,则x12+x22+x32=()A.5 B.C.3 D.9.(5分)已知平面直角坐标系xOy上的区域D由不等式组确定,若M(x,y)为D上的动点,点A的坐标为(1,﹣1),且z=的最小值为﹣1,则实数a=()A.7 B.5 C.4 D.310.(5分)对于定义在区间M上的函数f(x),若满足对∀x1,x2∈M且x1<x2时,都有f(x1)≤f(x2),则称函数f(x)为区间M上的“非减函数”,若f(x)为区间上的“非减函数”,且f(0)=0,f(x)+f(1﹣x)=1;又当x∈时,f(x)≤2x﹣1恒成立.有下列命题:①∀x∈,f(x)≥0;②当x1,x2∈且x1≠x2时,f(x1)≠f(x2);③f()+f()+f()+f()=2;④当x∈时,f(f(x))≤f(x).其中正确命题有()A.②③B.①②③C.①②④D.①③④二、填空题(共5小题,每小题5分,满分25分)11.(5分)在区间上随机取一个数x,使得|x|﹣|x﹣1|≥1成立的概率为.12.(5分)一个总体中有100个个体,随机编号为0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k小组中抽取的号码个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码是.13.(5分)已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为.14.(5分)已知定义在R上的函数f(x),g(x)满足=a x,f′(x)g(x)<f(x)g′(x),+=,若有穷数列{}(n∈N•)的前n项和等于,则n=.(5分)已知△ABC中,AB边上的中线|CM|=2,若动点P满足=sin2θ+cos2θ(θ∈R),15.给出下列命题:①对∀θ∈R,∃λ∈R,使得=λ;②当θ∈(﹣,)时,存在唯一的θ,使=(+);③动点P在运动的过程中,(+)•的取值范围为;④若||=2,动点P在运动的过程中,||2+||2+||2的最小值为.以上命题中,其中正确命题的序号为.三、解答题(共6小题,满分75分)16.(12分)已知函数f(x)=2sinx(sinx+cosx),x∈R.(Ⅰ)求函数f(x)的最小正周期及单调增区间;(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足f(+π)=,cosC+(cosA﹣sinA)cosB=0,a=2,求△ABC的面积.17.(12分)某高校自主招生考试依次为自荐材料审查、笔试、面试共三轮考核.规定只有前一轮考核通过才能进入下一轮的考核,否则将被淘汰;三轮考核都通过才算通过该校的自主招生考试.学生甲参加该校自主招生考试三轮考试通过的概率分别为,,,各轮考核通过与否相互独立.学生乙参加该校自主招生考试三轮考试通过的概率分别为,,,且各轮考核通过与否相互独立,甲乙两人通过该校的自主招生考试与否互不影响.(Ⅰ)求甲乙恰有一人通过该高校自主招生考试的概率;(Ⅱ)甲所在中学为鼓励学生参加自主招生考试,每通过一轮分别奖励学生100元,200元,300元,记学生甲获得奖励的金额为X,求X的分布列及数学期望.18.(12分)已知正项数列{a n}的前n项和为S n,满足a n2=S n+S n﹣1(n≥2),a1=1.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,数列{b n}的前n项和为T n,证明:对任意n∈N•,都有T n<恒成立.19.(13分)如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置.(Ⅰ)如图2,当A1C⊥CD时,求证:A1C⊥平面BCDE;(Ⅱ)如图3,设平面A1CD与平面A1BE所成锐二面角为θ,当tanθ=时,求点C到平面A1BE的距离.20.(13分)如图,已知椭圆+=1(a>b>0)的离心率为,且过点(,).(Ⅰ)求该椭圆的方程;(Ⅱ)若A,B,C为椭圆上的三点(A,B不在坐标轴上),满足=+,直线OA,OB分别交直线l:x=3于M,N两点,设直线OA,OB的斜率为k1,k2.证明:k1•k2为定值,并求线段MN长度的最小值.21.(13分)已知函数f(x)=(x>﹣1).(Ⅰ)求函数f(x)的最小值;(Ⅱ)求证:()n+()n+…+()n+()n<(n∈N•)安徽省黄山市2015届高考数学三模试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4 B.C.4 D.考点:复数代数形式的乘除运算;复数求模.专题:数系的扩充和复数.分析:由题意可得 z==,再利用两个复数代数形式的乘除法法则化简为+i,由此可得z的虚部.解答:解:∵复数z满足(3﹣4i)z=|4+3i|,∴z====+i,故z的虚部等于,故选:D.点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,属于基础题.2.(5分)已知集合M={x|y=lg(1﹣x)},集合N={y|y=2x,x∈R},则M∩N=()A.{x|x<1} B.{x|x>1} C.{x|0<x<1} D.∅考点:交集及其运算.专题:集合.分析:求出M中x的范围确定出M,求出N中y的范围确定出N,找出M与N的交集即可.解答:解:由M中y=lg(1﹣x),得到1﹣x>0,即x<1,∴M={x|x<1},由N中y=2x>0,得到N={y|y>0},则M∩N={x|0<x<1},故选:C.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.3.(5分)已知(1+ax)(1+x)5的展开式中x2的系数为5,则a=()A.﹣4 B.﹣3 C.﹣2 D.﹣1考点:二项式系数的性质.专题:概率与统计.分析: 由题意利用二项展开式的通项公式求得展开式中x 2的系数为+a•=5,由此解得a 的值.解答: 解:已知(1+ax )(1+x )5=(1+ax )(1+x+x 2+x 3+x 4+x 5)展开式中x 2的系数为+a•=5,解得a=﹣1,故选:D .点评: 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题. 4.(5分)若以直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,已知直线l 参数方程为(t 为参数),曲线C 的极坐标方程为ρ=4sin θ,则直线l 被曲线C 截得的弦长为()A .B .C .D .考点: 参数方程化成普通方程.专题: 直线与圆;坐标系和参数方程.分析: 把直线l 的参数方程、曲线C 的极坐标方程都化为普通方程,利用圆心到直线l 的距离d 与半径r 求出弦长|AB|的值. 解答: 解:把直线l 的参数方程(t 为参数)化为普通方程是x+y ﹣3=0,把曲线C 的极坐标方程ρ=4sin θ变形为 ρ2=4ρsin θ,化为普通方程是x 2+y 2=4y ,即x 2+(y ﹣2)2=4, 它表示圆心为(0,2),半径r=2的圆; 则圆心到直线l 的距离为 d==,所以,直线l 被曲线C 截得的弦长为 |AB|=2=2=.故选:B .点评: 本题考查了直线的参数方程与圆的极坐标方程的应用问题,解题时可以化为普通方程进行解答,是基础题目.5.(5分)数列{a n}满足a1=1,a n+1=r•a n+r(n∈N*,r∈R且r≠0),则“r=1”是“数列{a n}成等差数列”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:阅读型.分析:把r=1代入给出的递推式,直接判断出数列{a n}是等差数列,再由给出的递推式,当r≠1时,配方后得到,说明数列{}是等比数列,求出其通项公式后可得a n,由a n看出,当r=时数列{a n}为等差数列,从而说明“r=1”是“数列{a n}成等差数列”的不必要条件.解答:解:当r=1时,等式a n+1=r•a n+r化为a n+1=a n+1,即a n+1﹣a n=1(n∈N*).所以,数列{a n}是首项a1=1,公差为1的等差数列;“r=1”是“数列{a n}成等差数列”的充分条件;当r不等于1时,由,得:,所以,数列{}是首项为,公比为r的等比数列所以,,.当r=时,a n=1.{a n}是首项为1,公差为0的等差数列.因此,“r=1”不是“数列{a n}成等差数列”的必要条件.综上可知,“r=1”是“数列{a n}成等差数列”的充分但不必要条件.故选A.点评:本题考查了必要条件、充分条件及充要条件,解答的关键是判断必要性,也是该题的难点,考查了由递推式求数列的通项公式,对于a n+1=pa n+q型的递推式,一般都可转化成一个新的等比数列.此题是中档题.6.(5分)执行如图所示的程序框图,则输出的S的值是()A.B.C.4 D.﹣1考点:程序框图.专题:图表型.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量S的值并输出.解答:解:程序运行过程中,各变量的值如下表示:是否继续循环 S i循环前/4 1第一圈是﹣1 2第二圈是 3第三圈是 4第四圈是4 5第五圈否故最后输出的S值为4.故选C.点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型.7.(5分)过双曲线﹣=1(a>0,b>0)的右顶点A作斜率为﹣1的直线,该直线与双曲线的两条渐近线的交点分别为B、C.若=,则双曲线的离心率是()A.B.C.D.考点:直线与圆锥曲线的综合问题;双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:分别表示出直线l和两个渐近线的交点,进而表示出和,进而根据=求得a和b的关系,进而根据c2﹣a2=b2,求得a和c的关系,则离心率可得.解答:解:直线l:y=﹣x+a与渐近线l1:bx﹣ay=0交于B(,),l与渐近线l2:bx+ay=0交于C(,),A(a,0),∴=(﹣,),=(,﹣),∵=,∴=,b=2a,∴c2﹣a2=4a2,∴e2==5,∴e=,故选C.点评:本题主要考查了直线与圆锥曲线的综合问题.要求学生有较高地转化数学思想的运用能力,能将已知条件转化到基本知识的运用.8.(5分)已知函数有且仅有3个实数根x1、x2、x3,则x12+x22+x32=()A.5 B.C.3 D.考点:函数与方程的综合运用.专题:计算题;压轴题.分析:根据函数f(x)的对称性可知=k有解时总会有2个根,进而根据方程有且仅有3个实数根可知必含有1这个根,进而根据f(x)=1解得x,代入x12+x22+x32答案可得.解答:解:∵方程有3个实数根,=k有解时总会有2个根,所以必含有1这个根令=1,解得x=2或x=0所以x12+x22+x32═02+12+22=5.故选A点评:本题主要考查了函数与方程的综合运用.利用了函数图象的对称性和方程根的分布,考查了学生分析问题的能力.9.(5分)已知平面直角坐标系xOy上的区域D由不等式组确定,若M(x,y)为D上的动点,点A的坐标为(1,﹣1),且z=的最小值为﹣1,则实数a=()A.7 B.5 C.4 D.3考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组对应的平面区域,利用向量数量积的定义将目标函数进行化简,结合z 的几何意义进行求解即可.解答:解:∵且的最小值为﹣1,∴x﹣y的最小值为﹣1,设z=x﹣y,作出不等式组对应的平面区域如图:由z=x﹣y,得y=x﹣z表示,斜率为1纵截距为﹣z的一组平行直线,∵x﹣y的最小值为﹣1,∴作出直线x﹣y=﹣1,则直线x﹣y=﹣1与y=2x﹣1相交于A,此时A为一个边界点,由,解得,即A(2,3),此时A也在直线x+y=a上,则a=2+3=5,即直线为x+y=5,平移直线y=x﹣z,当直线y=x﹣z经过点A时,直线y=x﹣z的截距最大,此时z最小,此时z min=2﹣3=﹣1,满足条件.故a=5,故选:B.点评:本题主要考查线性规划的基本应用,利用z的几何意义以及向量数量积将目标函数进行化简是解决本题的关键.,注意利用数形结合来解决.10.(5分)对于定义在区间M上的函数f(x),若满足对∀x1,x2∈M且x1<x2时,都有f(x1)≤f(x2),则称函数f(x)为区间M上的“非减函数”,若f(x)为区间上的“非减函数”,且f(0)=0,f(x)+f(1﹣x)=1;又当x∈时,f(x)≤2x﹣1恒成立.有下列命题:①∀x∈,f(x)≥0;②当x1,x2∈且x1≠x2时,f(x1)≠f(x2);③f()+f()+f()+f()=2;④当x∈时,f(f(x))≤f(x).其中正确命题有()A.②③B.①②③C.①②④D.①③④考点:命题的真假判断与应用.专题:函数的性质及应用.分析:对于①,由f(0)=0,然后直接利用“非减函数”的定义进行判断;对于②,由x∈时,f(x)≤2x﹣1恒成立得到f()≤,在等式f(x)+f(l﹣x)=l中,取x=得到f()=,而>,从而说明f()≥.利用两边夹的思想得到f()=.同理得到f()=.结合新定义即可得到结论;对于③,结合②的结论及等式f(x)+f(l﹣x)=l变形即可得到;对于④,当x∈时,判断f(x)与x的大小关系即可.正确.解答:解:对于①,因为f(0)=0,所以对∀x∈,根据“非减函数”的定义知f(x)≥0.所以①正确;对于②,因为当x∈时,f(x)≤2x﹣1恒成立,∴f()≤,又f(x)+f(l﹣x)=l,所以f()=,由而>,由“非减函数”的定义可知,所以f()≥.所以f()=.同理有f()=.当x∈时,由“非减函数”的定义可知,f()≤f(x)≤f(),所以f(x)=.所以②不正确;由②中,当x∈时,f(x)=.可得:所以③正确;f()=f()=,由f(x)+f(1﹣x)=1得:f()+f()=1,故f()+f()+f()+f()=2,故③正确;对于④,当x∈时,x≥2x﹣1,因为函数f(x)为区间D上的“非减函数”,所以f(x)≥f(2x﹣1),所以f(f(x))≤f(2x﹣1)≤f(x).所以④正确.故正确命题有:①③④.故选:D点评:本题考查了命题的真假判断与运用,考查了抽象函数的性质,解答的关键是正确理解新定义,考查了学生的抽象思维能力,是中档题.二、填空题(共5小题,每小题5分,满分25分)11.(5分)在区间上随机取一个数x,使得|x|﹣|x﹣1|≥1成立的概率为.考点:几何概型.专题:概率与统计.分析:由题意,本题符合几何概型,分别求出已知区间的长度,以及满足不等式的区间长度,利用长度比得到所求.解答:解:区间的长度为4,不等式|x|﹣|x﹣1|≥1等价于①,②,③,解①得x≥1;解②得∅;解③得∅,所以不等式的解集为:{x|x≥1},所以在区间上随机取一个数x,使得|x|﹣|x﹣1|≥1成立的概率为:;故答案为:.点评:本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型12.(5分)一个总体中有100个个体,随机编号为0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k小组中抽取的号码个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码是63.考点:系统抽样方法.专题:压轴题.分析:此问题总体中个体的个数较多,因此采用系统抽样.按题目中要求的规则抽取即可,在第k小组中抽取的号码个位数字与m+k的个位数字相同,由m=6,k=7得到要抽数字的个位数.解答:解:∵m=6,k=7,m+k=13,∴在第7小组中抽取的号码是63.故答案为:63.点评:当总体中个体个数较多而差异又不大时可采用系统抽样.要从容量为N的总体中抽取容量为n的样本,可将总体分成均衡的若干部分,然后按照预先制定的规则,从每一部分抽取一个个体,得到所需要的样本.13.(5分)已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为.考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:由已知中的三视图,可知该几何体是一个三棱柱切去一个三棱锥所得的组合体,分别求出体积后,相减可得答案.解答:解:由已知中的三视图,可知该几何体是一个三棱柱切去一个三棱锥所得的组合体,棱柱和棱锥的底面均为侧视图,故底面面积S=×4×4=8,棱柱的高为8,故体积为64,棱锥的高为4,故体积为:,故组合体的体积V=64﹣=,故答案为:点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.14.(5分)已知定义在R上的函数f(x),g(x)满足=a x,f′(x)g(x)<f(x)g′(x),+=,若有穷数列{}(n∈N•)的前n项和等于,则n=6.考点:数列的求和.专题:导数的综合应用;等差数列与等比数列.分析:由列出方程求出a的值,根据求导法则求出,结合条件判断出导数的符号,即可确定函数的单调性,由指数函数的单调性确定a的值,代入由条件和等比数列的前n项和公式求出n的值.解答:解:因为=a x,且,所以a+,化简得2a2﹣5a+2=0,解得a=或2,因为f′(x)g(x)<f(x)g′(x),所以=<0,则在定义域上单调递减,故a=,所以=,则有穷数列{}(n∈N•)是以为首项、公比的等比数列,因为有穷数列{}(n∈N•)的前n项和等于,所以,解得n=6,故答案为:6.点评:本题考查了等比数列的定义、前n项和公式,以及函数的导数与函数单调性关系,属于中档题.(5分)已知△ABC中,AB边上的中线|CM|=2,若动点P满足=sin2θ+cos2θ(θ∈R),15.给出下列命题:①对∀θ∈R,∃λ∈R,使得=λ;②当θ∈(﹣,)时,存在唯一的θ,使=(+);③动点P在运动的过程中,(+)•的取值范围为;④若||=2,动点P在运动的过程中,||2+||2+||2的最小值为.以上命题中,其中正确命题的序号为①③.考点:命题的真假判断与应用;平面向量数量积的运算.专题:平面向量及应用;简易逻辑.分析:由给出的等式结合共线向量基本定理可得C、P、M共线,由此判断①正确;由给出的向量等式可知P为△ABC的重心,求出,结合θ范围可得满足条件的θ有两个,判断②错误;由,得(+)•==2||||cosπ=﹣2||||,然后利用基本不等式求得(+)•的取值范围判断③正确;由已知求出||2+||2+||2的最小值说明④错误.解答:解:∵动点P满足=sin2θ+cos2θ(θ∈R),且sin2θ+cos2θ=1,又∵cos2θ∈,∴P在线段CM上,则对∀θ∈R,∃λ∈R,使得=λ正确,命题①正确;∵CM为AB边上的中线,若=(+),则P为△ABC的重心,此时=,∴,∵θ∈(﹣,),∴,则命题②错误;由判断①的过程知,P、M、C三点共线,即点P在CM上,而,故(+)•==2||||cosπ=﹣2||||,∵||+||=CM=2,由基本不等式可得:||||≤.∴﹣2,当P与M或C重合时(+)•最大为0,命题③正确;设(0≤λ≤1),则||2+||2+||2 ===4λ2+1+4λ2+1+4(λ﹣1)2=12λ2﹣8λ+6.当时,||2+||2+||2 有最小值为,故命题④错误.∴正确的命题是①③.故答案为:①③.点评:本题考查命题的真假判断与应用,着重考查了向量的数量积公式及其运算性质、三角函数的图象与性质、三角恒等变换公式和二次函数的性质等知识,属于中档题.三、解答题(共6小题,满分75分)16.(12分)已知函数f(x)=2sinx(sinx+cosx),x∈R.(Ⅰ)求函数f(x)的最小正周期及单调增区间;(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足f(+π)=,cosC+(cosA﹣sinA)cosB=0,a=2,求△ABC的面积.考点:三角函数中的恒等变换应用;正弦函数的图象.专题:三角函数的图像与性质;解三角形.分析:(Ⅰ)由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x﹣)+1,利用正弦函数的周期性和单调性即可得解;(Ⅱ)已知等式根据三角函数中的恒等变换应用化简可得tanB=,结合B∈(0,π)可求B,又化简f()=,可得△ABC为正三角形,结合a及三角形面积公式即可得解.解答:本小题满分为12分解:(Ⅰ)∵f(x)=2sinx(sinx+cosx)=2sin2x+2sinxcosx=1﹣cos2x+sin2x=sin(2x﹣)+1,∴函数f(x)的最小正周期为π…3分由2kπ﹣≤2x﹣≤2k(k∈Z)可得:kπkπ+(k∈Z),∴函数f(x)的单调增区间为:(k∈Z)…6分(Ⅱ)在△ABC中,cosC=﹣cos(A+B),及cosC+(cosA﹣sinA)cosB=0,可得:sinAsinB ﹣sinAcosB=0,而sinA≠0,∴tanB=,∵B∈(0,π),∴B=.又∵f()=sin(A+)+1=cosA+1=,∴cosA=,∴A=.∴△ABC为正三角形,又a=2,∴△ABC的面积S==2…12分点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,三角形面积公式的应用,属于基本知识的考查.17.(12分)某高校自主招生考试依次为自荐材料审查、笔试、面试共三轮考核.规定只有前一轮考核通过才能进入下一轮的考核,否则将被淘汰;三轮考核都通过才算通过该校的自主招生考试.学生甲参加该校自主招生考试三轮考试通过的概率分别为,,,各轮考核通过与否相互独立.学生乙参加该校自主招生考试三轮考试通过的概率分别为,,,且各轮考核通过与否相互独立,甲乙两人通过该校的自主招生考试与否互不影响.(Ⅰ)求甲乙恰有一人通过该高校自主招生考试的概率;(Ⅱ)甲所在中学为鼓励学生参加自主招生考试,每通过一轮分别奖励学生100元,200元,300元,记学生甲获得奖励的金额为X,求X的分布列及数学期望.考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.专题:概率与统计.分析:(Ⅰ)根据所给的概率,利用相互独立事件的概率乘法公式即可做出结果.(Ⅱ)根据学生甲得到教育基金的金额为X,X的次数的取值是0元,100元,300元,600元,根据互斥事件和相互独立事件同时发生的概率列出分布列,最后做出分布列和期望即可解答:解:(Ⅰ)设甲通过该校自荐材料审核、笔试、面试三轮分别为事件A1,A2,A3;通过高校自主招生考试为事件A,乙通过该校自荐材料审核、笔试、面试三轮分别为事件B1,B2,B3;通过高校自主招生考试为事件B,则事件A1,A2,A3相互独立,事件B1,B2,B3;相互独立,事件A,B相互独立.P(A)=P(A1,A2,A3)=P(A1)P(A2)P(A3)=P(B)=P(B1B2B3)=P(B1)P(B2)P(B3)=设甲乙恰有一人通过该校自主招生考生为事件C,则C=A,事件与A互斥,P(C)=P(A)=P(A)P()+P()=(Ⅱ)随机变量X的取值为0,100,300,600P(X=0)=,P(X=100)=,P(X=300)=,P(X=600)=X 0 100 300 600PEX=点评:考查运用概率知识解决实际问题的能力,相互独立事件是指,两事件发生的概率互不影响,而对立事件是指同一次试验中,不会同时发生的事件,遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.18.(12分)已知正项数列{a n}的前n项和为S n,满足a n2=S n+S n﹣1(n≥2),a1=1.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,数列{b n}的前n项和为T n,证明:对任意n∈N•,都有T n<恒成立.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(I)a n2=S n+S n﹣1(n≥2),当n≥3时,=S n﹣1+S n﹣2,两式相减可得:a n﹣a n﹣1=1(n≥3).当n=2时,也成立,即a n﹣a n﹣1=1(n≥2),利用等差数列的通项公式即可得出.(II)b n==,利用“裂项求和”、“放缩法”即可得出.解答:(I)解:∵a n2=S n+S n﹣1(n≥2),当n≥3时,=S n﹣1+S n﹣2,∴=S n﹣S n﹣2=a n+a n﹣1,∵a n>0,∴a n﹣a n﹣1=1(n≥3).又=S2+S1=a2+2a1,a1=1,a2>0,解得a2=2,∴a2﹣a1=1,∴a n﹣a n﹣1=1(n≥2).∴数列{a n}为等差数列,公差为1,∴a n=1+(n﹣1)=n.(II)证明:b n===,∴T n=+…++=<=.∴对任意n∈N•,都有T n<恒成立.点评:题考查了“裂项求和”、等差数列的通项公式、递推式的应用、“放缩法”,考查了推理能力与计算能力,属于中档题.19.(13分)如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置.(Ⅰ)如图2,当A1C⊥CD时,求证:A1C⊥平面BCDE;(Ⅱ)如图3,设平面A1CD与平面A1BE所成锐二面角为θ,当tanθ=时,求点C到平面A1BE的距离.考点:点、线、面间的距离计算;直线与平面垂直的判定.专题:综合题;空间位置关系与距离;空间角.分析:(Ⅰ)先证明BC⊥A1C,DE⊥A1C,A1C⊥CD,即可证明A1C⊥平面BCDE.(Ⅱ)延长CD,BE交于点F,则平面A1CD∩平面A1BE=A1F,过D作DQ⊥A1F,垂足为Q,连接EQ,证明∠DQE为二面角C﹣A1F﹣B的平面角,A1D⊥CD,建立如图所示的坐标系,求出平面A1BE的法向量,即可求出点C到平面A1BE的距离.解答:(Ⅰ)证明:∵∠C=90°,DE∥BC,∴BC⊥CD,BC⊥A1D,CD∩A1D=D,∴BC⊥平面A1CD,∴BC⊥A1C,DE⊥A1C,∵A1C⊥CD,CD∩BC=C,CD∩DE=D,DE∥BC,∴A1C⊥平面BCDE.(Ⅱ)解:延长CD,BE交于点F,则平面A1CD∩平面A1BE=A1F,过D作DQ⊥A1F,垂足为Q,连接EQ,∵BC⊥平面A1CD,DE∥BC,∴DE⊥平面A1CD,∴EQ⊥A1F,∴∠DQE为二面角C﹣A1F﹣B的平面角,即tanθ=tan∠DQE=,由图1,在直角三角形ABC中,∠C=90°,BC=3,AC=6,且DE∥BC,DE=2,∴AD=4,CD=2,图3中,DF=A1D=4,∴DQ==2,∴A1Q=QF=2,∴∠A1DF=90°,∴A1D⊥CD,∵A1D⊥DE,DC⊥DE,建立如图所示的坐标系,则D(0,0,0),C(2,0,0),B(2,3,0),E(0,2,0),A1(0,0,4)∴=(2,3,﹣4),=(﹣2,﹣1,0),设平面A1BE的法向量为=(x,y,z),则,取=(﹣1,2,1),∵=(0,3,0),∴点C到平面A1BE的距离为=.点评:本题主要考查直线与平面垂直的判定,考查二面角的平面角,考查点C到平面A1BE 的距离,知识综合强.20.(13分)如图,已知椭圆+=1(a>b>0)的离心率为,且过点(,).(Ⅰ)求该椭圆的方程;(Ⅱ)若A,B,C为椭圆上的三点(A,B不在坐标轴上),满足=+,直线OA,OB分别交直线l:x=3于M,N两点,设直线OA,OB的斜率为k1,k2.证明:k1•k2为定值,并求线段MN长度的最小值.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(I)由题意可得:,解得即可得出椭圆的标准方程.(II)设A(x1,y1),B(x2,y2),则,=1.由于满足=+,可得=.代入椭圆的方程化简可得:x1x2+4y1y2=0,即可证明k1k2为定值.设OA:y=k1x,OB:y=﹣x,令x=3,解得M,N.|MN|==,利用基本不等式的性质即可得出.解答:(I)解:由题意可得:,解得a=2,b=1,c=,∴椭圆的标准方程为:.(II)证明:设A(x1,y1),B(x2,y2),则,=1,①.∵满足=+,∴=.代入椭圆的方程可得:,化为++=1,由①可得:x1x2+4y1y2=0,∴k1k2=﹣为定值.设OA:y=k1x,OB:y=﹣x,令x=3,解得M(3,3k1),N.∴|MN|==≥3×=3,当且仅当时取等号,∴|MN|的最小值为3.点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、向量坐标运算、基本不等式的性质,考查了推理能力与计算能力,属于难题.21.(13分)已知函数f(x)=(x>﹣1).(Ⅰ)求函数f(x)的最小值;(Ⅱ)求证:()n+()n+…+()n+()n<(n∈N•)考点:利用导数求闭区间上函数的最值;利用导数研究函数的极值.专题:导数的综合应用;不等式的解法及应用.分析:(Ⅰ)求出f(x)的导数,求得增区间和减区间,即可得到最小值f(0)=1;(Ⅱ)由(Ⅰ)可得≥1,即e x≥x+1,即有x≥ln(x+1),当且仅当x=0取得等号,令1+x=,则﹣1≥ln,即k﹣n≥nln=ln()n.(当且仅当n=k取得等号),运用累加法,结合等比数列的求和公式和不等式的性质,即可得证.解答:解:(Ⅰ)函数f(x)=(x>﹣1)的导数为f′(x)=,由f′(x)>0可得x>0,由由f′(x)<0可得﹣1<x<0,即有f(x)在(﹣1,0)递减,在(0,+∞)递增,则x=0处f(x)取得极小值,也为最小值,且为f(0)=1;(Ⅱ)由(Ⅰ)可得≥1,即e x≥x+1,即有x≥ln(x+1),当且仅当x=0取得等号,令1+x=,则﹣1≥ln,即k﹣n≥nln=ln()n.(当且仅当n=k取得等号),将k从1到n取值,可得1﹣n≥ln()n.2﹣n≥ln()n…,(n﹣1)﹣n≥ln()n,n﹣n≥ln()n.则有()n≤e1﹣n,()n≤e2﹣n,…,()n≤e(n﹣1)﹣n,()n≤e n﹣n.即有()n+()n+…+()n+()n≤e1﹣n+e2﹣n+…+e(n﹣1)﹣n+e n﹣n==<(n∈N•).点评:本题考查导数的运用:求单调区间和极值、最值,同时考查不等式的证明,注意运用函数的最值和不等式的性质及等比数列的求和公式,属于中档题.。
安徽省黄山市2021届高三上学期第一次模拟数学(理)试卷 Word版含解析
2021年安徽省黄山市高考数学一模试卷(理科)一、选择题(本大题共10小题,每小题5分,共50分在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数z满足方程Z2+2=0,则z=()A.±i B.± C.﹣i D.﹣2.函数f(x)=lgx ﹣的零点所在的区间是()A.(0,1) B.(1,2) C.(2,3) D.(3,10)3.“tanx=”是“x=2kπ+(k∈Z)”成立的()A.充分不必要条件 B.必要不充分条件C.充分条件 D.既不充分也不必要条件4.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点之间的距离不小于该正方形边长的概率为()A. B. C. D.5.已知三个正态分布密度函数(x∈R,i=1,2,3)的图象如图所示,则()A.μ1<μ2=μ3,σ1=σ2>σ3 B.μ1>μ2=μ3,σ1=σ2<σ3C.μ1=μ2<μ3,σ1<σ2=σ3 D.μ1<μ2=μ3,σ1=σ2<σ36.已知双曲线﹣=1(a>0,b>0)的离心率e∈[,2],则一条渐近线与实轴所成角的取值范围是()A. B. C. D.7.如图1,已知点E、F、G分别是棱长为a的正方体ABCD﹣A1B1C l D1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上运动,当以M、N、Q、P为顶点的三棱锥P﹣MNQ的俯视图是如图2所示的等腰三角形时,点P到平面MNQ的距离为()A. a B. a C. a D. a8.数列{a n}满足a n+1=,若a1=,则a2021=()A. B. C. D.9.己知函数f(x)=tx,g(x)=(2﹣t)x2﹣4x+l.若对于任一实数x0,函数值f(x0)与g(x0)中至少有一个为正数,则实数t的取值范围是()A.(﹣∞,﹣2)∪(0,2] B.(﹣2,0)∪(﹣2,2] C.(﹣2,2] D.(0,+∞)10.由无理数引发的数学危机始终连续到19世纪.直到1872年,德国数学家戴德金从连续性的要求动身,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N=∅,M中的每一个元素都小于N中的每一个元素,则称(M,N)为戴德金分割试推断,对于任一戴德金分割(M,N),下列选项中,不行能成立的是()A. M没有最大元素,N有一个最小元素B. M没有最大元素,N也没有最小元素C. M有一个最大元素,N有一个最小元素D. M有一个最大元素,N没有最小元素三、填空题(本大题共5小题,每小题5分,共25分把答案填在答题卡的相应位置上)11.在极坐标系中,点P(2,)到极轴的距离为.12.已知两点A(1,0),B(l,1),O为坐标原点,点C在其次象限,且∠AOC=135°,设=+λ(λ∈R),则λ的值为.13.已知x>0,y>0,且2y+x﹣xy=0,若x+2y﹣m>0恒成立,则实数m 的取值范围是.14.执行如图所示的程序框图,则输出结果S的值为.15.在直角坐标系中,定义两点P(x1,y l),Q(x2,y2)之间的“直角距离为d(P,Q)=|x1﹣x2|+|y1﹣y2|.现有以下命题:①若P,Q是x轴上两点,则d(P,Q)=|x1﹣x2|;②已知两点P(2,3),Q(sin2α,cos2α),则d(P,Q)为定值;③原点O到直线x﹣y+l=0上任意一点P的直角距离d(O,P)的最小值为;④若|PQ|表示P、Q两点间的距离,那么|PQ|≥d(P,Q);其中为真命题的是(写出全部真命题的序号).三、解答题(本大题共6小题,共75分解答应写出文字说明、证明过程或演算步骤解答写在答题卡上的指定区域内)16.己知=(sin(θ﹣),﹣1),=(﹣1,3)其中θ∈(0,),且∥.(1)求sinθ的值;(2)已知△ABC 中,∠A=θ,BC=2+1,求边AC的最大值.17.四棱锥P﹣ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点(1)求证:QP⊥AC;(2)当二面角Q﹣AC﹣P的大小为120°时,求QB的长.18.甲、乙两人参与某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是,乙只能答对其中的5道题,规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分低于o分时记为0分(即最低为0分),至少得15分才能入选.(1)求乙得分的分布列和数学期望;(2)求甲、乙两人中至少有一人入选的概率.19.已知函数f(x)=lnx+cosx﹣(﹣)x的导数为f′(x),且数列{a n}满足a n+1+a n=nf′()+3(n∈N*).(1)若数列{a n}是等差数列,求a1的值:(2)若对任意n∈N*,都有a n+2n2≥0成立,求a1的取值范围.20.如图,已知椭圆Γ:=1(a>b>0)的离心率e=,短轴右端点为A,M(1,0)为线段OA的中点.(Ⅰ)求椭圆Γ的方程;(Ⅱ)过点M任作一条直线与椭圆Γ相交于两点P,Q,试问在x轴上是否存在定点N,使得∠PNM=∠QNM,若存在,求出点N的坐标;若不存在,说明理由.21.已知函数f(x)=ax﹣1﹣1n x.(1)若f(x)≥0对任意的x∈(0,+∞)恒成立,求实数a的取值范围;(2)求证:对任意的x∈N*,<e(其中e为自然对数的底,e≈2.71828).2021年安徽省黄山市高考数学一模试卷(理科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数z满足方程Z2+2=0,则z=()A.±i B.± C.﹣i D.﹣考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:设z=a+bi(a,b∈R),由于复数z满足方程Z2+2=0,可得a2﹣b2+2+2abi=0,利用复数相等即可得出.解答:解:设z=a+bi(a,b∈R),∵复数z满足方程Z2+2=0,∴(a+bi)2+2=0,∴a2﹣b2+2+2abi=0,∴,解得,∴z=.故选:A.点评:本题考查了复数的运算法则、复数相等,属于基础题.2.函数f(x)=lgx ﹣的零点所在的区间是()A.(0,1) B.(1,2) C.(2,3) D.(3,10)考点:函数零点的判定定理.专题:计算题;函数的性质及应用.分析:由函数的连续性及f(2)=lg2﹣=lg2﹣lg<0,f(3)=lg3﹣lg>0;从而推断.解答:解:函数f(x)=lgx ﹣在定义域上连续,f(2)=lg2﹣=lg2﹣lg<0,f(3)=lg3﹣lg>0;故f(2)f(3)<0;从而可知,函数f(x)=lgx ﹣的零点所在的区间是(2,3);故选C.点评:本题考查了函数的零点的判定定理的应用,属于基础题.3.“tanx=”是“x=2kπ+(k∈Z)”成立的()A.充分不必要条件 B.必要不充分条件C.充分条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的推断.专题:三角函数的求值;简易规律.分析:依据三角函数的性质结合充分条件和必要条件的定义进行推断即可.解答:解:若tanx=,则x=kπ+,k∈Z,则“tanx=”是“x=2kπ+(k∈Z)”成立的必要不充分条件,故选:B点评:本题主要考查充分条件和必要条件的推断,比较基础.4.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点之间的距离不小于该正方形边长的概率为()A. B. C. D.考点:几何概型.专题:概率与统计.分析:设正方形边长为1,则从正方形四个顶点及其中心这5个点中任取2个点,共有10条线段,4条长度为1,4条长度为,两条长度为,即可得出结论.解答:解:设正方形边长为1,则从正方形四个顶点及其中心这5个点中任取2个点,共有10条线段,其中4条长度为1,4条长度为,两条长度为,满足这2个点之间的距离不小于该正方形边长的有4+2=6条,∴所求概率为P==.故选:A点评:本题考查概率的计算,列举出满足条件的基本大事是关键.5.已知三个正态分布密度函数(x∈R,i=1,2,3)的图象如图所示,则()A.μ1<μ2=μ3,σ1=σ2>σ3 B.μ1>μ2=μ3,σ1=σ2<σ3C.μ1=μ2<μ3,σ1<σ2=σ3 D.μ1<μ2=μ3,σ1=σ2<σ3考点:正态分布曲线的特点及曲线所表示的意义.专题:数形结合.分析:正态曲线关于x=μ对称,且μ越大图象越靠近右边,第一个曲线的均值比其次和第三和图象的均值小,且二,三两个的均值相等,又有σ越小图象越瘦长,得到正确的结果.解答:解:∵正态曲线关于x=μ对称,且μ越大图象越靠近右边,∴第一个曲线的均值比其次和第三和图象的均值小,且二,三两个的均值相等,只能从A,D两个答案中选一个,∵σ越小图象越瘦长,得到其次个图象的σ比第三个的σ要小,故选D.点评:本题考查正态分布曲线的特点及曲线所表示的意义,考查密度函数中两个特征数均值和标准差对曲线的位置和外形的影响,是一个基础题.6.已知双曲线﹣=1(a>0,b>0)的离心率e∈[,2],则一条渐近线与实轴所成角的取值范围是()A. B. C. D.考点:双曲线的简洁性质.专题:圆锥曲线的定义、性质与方程;圆锥曲线中的最值与范围问题.分析:由及c2=a2+b2,得的取值范围,设一条渐近线与实轴所成的角为θ,可由tanθ=及0<θ<探求θ的取值范围.解答:解:∵e,∴2≤≤4,又∵c2=a2+b2,∴2≤≤4,即1≤≤3,得1≤≤.由题意知,为双曲线的一条渐近线的方程,设此渐近线与实轴所成的角为θ,则,即1≤tan θ≤.∵0<θ<,∴≤θ≤,即θ的取值范围是.故答案为:C.点评:本题考查了双曲线的离心率及正切函数的图象与性质等,关键是通过c2=a2+b2将离心率的范围转化为渐近线的斜率的范围.7.如图1,已知点E、F、G分别是棱长为a的正方体ABCD﹣A1B1C l D1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上运动,当以M、N、Q、P为顶点的三棱锥P﹣MNQ的俯视图是如图2所示的等腰三角形时,点P到平面MNQ的距离为()A. a B. a C. a D. a考点:点、线、面间的距离计算.专题:空间位置关系与距离.分析:可先由俯视图的特征推断出M,Q的位置,再求点到平面MNQ的距离即可.解答:解:∵点E、F、G分别是棱长为a的正方体ABCD﹣A1 B1C l D1的棱AA1、CC1、DD1的中点,点M、N、Q、P分别在线段DF、AG、BE、C1B1上运动,∴当以M、N、Q、P为顶点的三棱锥P﹣MNQ的俯视图是如图2所示的等腰三角形时,M与D重合,Q与E重合,N在线段AG上,此时点P到平面MNQ的距离等于点P到侧面AA1D1D的距离,∴点P到平面MNQ的距离等于正方体的棱长a.故选:D.点评:本题考查点到平面的距离的求法,是基础题,解题时要认真审题,留意空间思维力量的培育.8.数列{a n}满足a n+1=,若a1=,则a2021=()A. B. C. D.考点:数列递推式.专题:点列、递归数列与数学归纳法.分析:依据数列的递推关系得到数列为周期数列即可得到结论.解答:解:由递推数列可得,a1=,a2=2a1﹣1=2×﹣1=,a3=2a2=2×=,a4=2a3=2×=,a5=2a4﹣1=2×﹣1=,…∴a5=a1,即a n+4=a n,则数列{a n}是周期为4的周期数列,则a2021=a503×4+3=a3=,故选:B点评:本题主要考查递推数列的应用,依据递推关系得到数列{a n}是周期为4的周期数列是解决本题的关键.9.己知函数f(x)=tx,g(x)=(2﹣t)x2﹣4x+l.若对于任一实数x0,函数值f(x0)与g(x0)中至少有一个为正数,则实数t的取值范围是()A.(﹣∞,﹣2)∪(0,2] B.(﹣2,0)∪(﹣2,2] C.(﹣2,2] D.(0,+∞)考点:二次函数的性质.专题:函数的性质及应用.分析:不论t为何值,对于任一实数x,f(x)与g(x)的值至少有一个为正数,所以对t分类争辩,即t=0、t=2、t>2,t<﹣2 争辩f(x)与g(x)的值的正负,排解即可得出答案.解答:解:函数f(x)=tx,g(x)=(2﹣t)x2﹣4x+l.△=16﹣4×(2﹣t)×1=8+4t,①当t=0时,f(x)=0,△>0,g(x)有正有负,不符合题意,故排解C.②当t=2时,f(x)=2x,g(x)=﹣4x+1,符合题意,③当t>2时,g(x)=(2﹣t)x2﹣4x+l.f(x)=tx,当x取﹣∞时,f(x0)与g(x0)都为负值,不符合题意,故排解D④当t<﹣2时,△<0,∴g(x)=(2﹣t)x2﹣4x+l>0恒成立,符合题意,故B不正确,故选:A点评:本题考查一元二次方程的根的分布与系数的关系,考查分类争辩思想,排解转化思想,是中档题.10.由无理数引发的数学危机始终连续到19世纪.直到1872年,德国数学家戴德金从连续性的要求动身,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N=∅,M中的每一个元素都小于N中的每一个元素,则称(M,N)为戴德金分割试推断,对于任一戴德金分割(M,N),下列选项中,不行能成立的是()A. M没有最大元素,N有一个最小元素B. M没有最大元素,N也没有最小元素C. M有一个最大元素,N有一个最小元素D. M有一个最大元素,N没有最小元素考点:集合的表示法.专题:计算题;集合.分析:由题意依次举例对四个命题推断,从而确定答案.解答:解:若M={x∈Q|x<0},N={x∈Q|x≥0};则M没有最大元素,N有一个最小元素0;故A正确;若M={x∈Q|x <},N={x∈Q|x ≥};则M没有最大元素,N也没有最小元素;故B正确;M有一个最大元素,N有一个最小元素不行能,故C不正确;若M={x∈Q|x≤0},N={x∈Q|x>0};M有一个最大元素,N没有最小元素,故D正确;故选C.点评:本题考查了同学对新定义的接受与应用力量,属于基础题.三、填空题(本大题共5小题,每小题5分,共25分把答案填在答题卡的相应位置上)11.在极坐标系中,点P(2,)到极轴的距离为.考点:简洁曲线的极坐标方程.专题:坐标系和参数方程.分析:本题可以利用公式求出点的平面直角坐标,从而得到它在平面直角坐标系中与x轴的距离,即得到点P(2,)到极轴的距离.解答:解:∵在极坐标系中,点P(2,),∴ρ=2,.将极点与平面直角坐标系的原点重合,极轴与x 轴重合,正方向全都,建立平面直角坐标系,设P (x,y),则,.∴它在平面直角坐标系中与x轴的距离为:.∴到点P(2,)到极轴的距离为:.故答案为:.点评:本题考查了极坐标化成平面直角坐标,本题难度不大,属于基础题.12.已知两点A (1,0),B(l,1),O为坐标原点,点C在其次象限,且∠AOC=135°,设=+λ(λ∈R),则λ的值为.考点:平面对量的基本定理及其意义.专题:平面对量及应用.分析:由已知条件设出C点坐标(x0,﹣x0),所以求出向量的坐标带入即可求出λ.解答:解:依据已知条件设C(x0,﹣x0);∴由得:(x0,﹣x0)=(1,0)+λ(1,1);∴;∴解得.故答案为:.点评:考查依据∠AOC=135°能设出C(x0,﹣x0),由点的坐标求出向量的坐标,以及向量坐标的加法及数乘的坐标运算.13.已知x>0,y>0,且2y+x﹣xy=0,若x+2y﹣m>0恒成立,则实数m 的取值范围是m<8 .考点:基本不等式.专题:不等式的解法及应用.分析:变形利用基本不等式的性质可得x+2y==2(y﹣1)++4≥8,而x+2y﹣m>0恒成立,可得m<(x+2y)min.即可得出.解答:解:∵x>0,y>0,且2y+x﹣xy=0,∴x=>0,解得y >1.∴x+2y==2(y ﹣1)++4≥+4=8,当且仅当y=2,x=4时取等号.∴(x+2y )min=8.∵x+2y﹣m>0恒成立,∴m<(x+2y)min=8.故答案为:m<8.点评:本题考查了变形利用基本不等式的性质、恒成立问题的等价转化方法,属于基础题.14.执行如图所示的程序框图,则输出结果S的值为﹣.考点:程序框图.专题:计算题;算法和程序框图.分析:算法的功能是求S=cos+cos+…+cos的值,依据条件确定最终一次循环的n值,再利用余弦函数的周期性计算输出S的值.解答:解:由程序框图知:算法的功能是求S=cos+cos+…+cos的值,∵跳出循环的n值为2021,∴输出S=cos+cos+…+cos,∵cos+cos+cos+cos+cos+cos =cos+cos +cos﹣cos﹣cos﹣cos=0,∴S=cos+cosπ=﹣.故答案为:﹣.点评:本题考查了循环结构的程序框图,关键框图的流程推断算法的功能是关键.15.在直角坐标系中,定义两点P(x1,y l),Q(x2,y2)之间的“直角距离为d(P,Q)=|x1﹣x2|+|y1﹣y2|.现有以下命题:①若P,Q是x轴上两点,则d(P,Q)=|x1﹣x2|;②已知两点P(2,3),Q(sin2α,cos2α),则d(P,Q)为定值;③原点O到直线x﹣y+l=0上任意一点P的直角距离d(O,P)的最小值为;④若|PQ|表示P、Q两点间的距离,那么|PQ|≥d(P,Q);其中为真命题的是①②④(写出全部真命题的序号).考点:命题的真假推断与应用.专题:简易规律.分析:先依据直角距离的定义分别表示出所求的问题的表达式,然后依据确定值的性质进行判定即可.解答:解:①若P,Q是x轴上两点,则y1=y2=0,所以d(P,Q)=|x1﹣x2|,正确;②已知P(2,3),Q(sin2α,cos2α)(a∈R),则d(P,Q)=|2﹣sin2α|+|3﹣cos2α|=1+cos2α+2+sin2α=4为定值,正确;③设P(x,y),O(0,0),则d(0,P)=|x1﹣x2|+|y1﹣y2|=|x|+|y|=|x|+|x+1|,表示数轴上的x到1和0的距离之和,其最小值为1,故不正确;④若|PQ|表示P、Q两点间的距离,那么|PQ|=,d(P,Q)=|x1﹣x2|+|y1﹣y2|,由于2(a2+b2)≥(a+b)2,所以|PQ|≥2d(P,Q),正确;.故答案为:①②④.点评:本题考查两点之间的“直角距离”的定义,确定值的意义,关键是明确P(x1,y1)、Q(x2,y2)两点之间的“直角距离”的含义.三、解答题(本大题共6小题,共75分解答应写出文字说明、证明过程或演算步骤解答写在答题卡上的指定区域内)16.己知=(sin (θ﹣),﹣1),=(﹣1,3)其中θ∈(0,),且∥.(1)求sinθ的值;(2)已知△ABC中,∠A=θ,BC=2+1,求边AC的最大值.考点:平面对量共线(平行)的坐标表示;正弦定理.专题:平面对量及应用.分析:(1)利用向量共线定理由∥,可得=.由于θ∈(0,),∈,即可得出.变形sinθ=.(2)在△ABC 中,由正弦定理可得:,代入可得AC=3sinB,利用sinB≤1,即可得出.解答:解:(1)∵∥,∴=1,即=.∵θ∈(0,),∴∈.∴=.∴sinθ==+==.(2)在△ABC 中,由正弦定理可得:,∴=,∴AC=3sinB,当且仅当sinB=1,即时取等号,∴边AC的最大值是3.点评:本题考查了向量共线定理、正弦定理、三角函数的单调性,考查了计算力量,属于基础题.17.四棱锥P﹣ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点(1)求证:QP⊥AC;(2)当二面角Q﹣AC﹣P的大小为120°时,求QB的长.考点:二面角的平面角及求法;棱锥的结构特征.专题:空间位置关系与距离;空间角.分析:(1)由已知得PD⊥AC,AC⊥BD,从而AC⊥平面PDBQ,由此能证明AC⊥PQ.(2)设AC和BD的交点为O,连结OP,OQ,则∠POD是二面角P﹣AC﹣D的平面角,∠POQ是二面角P﹣AC﹣Q的平面角,∠POQ=120°,由此利用余弦定理能求出QB.解答:(1)证明:∵PD⊥面ABCD,AC⊂面ABCD,∴PD⊥AC,又菱形ABCD中,两对角线垂直,即AC⊥BD,又BD∩PD=D,∴AC⊥平面PDBQ,∴AC⊥PQ.(2)解:△PAC和△QAC都是以AC为底的等腰三角形,设AC和BD的交点为O,连结OP,OQ,则∠POD是二面角P﹣AC﹣D的平面角,由tan,得二面角P﹣AC﹣B大小120°,∴点Q与点P在平面ABCD的同侧,如图所示,∴∠POQ是二面角P﹣AC﹣Q的平面角,∴∠POQ=120°,在Rt△POD中,OP=,设QB=x,则Rt△OBQ中,OQ=,在直角梯形PDBQ中,PQ==,在△POQ中,由余弦定理得PQ==6﹣4x,故6﹣4x>0,且3x2﹣16x+5=0,解得x=,即QB=.点评:本题考查异面直线垂直的证明,考查线段长的求法,是中档题,解题时要认真审题,留意空间思维力量的培育.18.甲、乙两人参与某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是,乙只能答对其中的5道题,规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分低于o分时记为0分(即最低为0分),至少得15分才能入选.(1)求乙得分的分布列和数学期望;(2)求甲、乙两人中至少有一人入选的概率.考点:互斥大事的概率加法公式;相互独立大事的概率乘法公式;离散型随机变量及其分布列;离散型随机变量的期望与方差.专题:概率与统计.分析:(1)确定乙答题所得分数的可能取值,求出相应的概率,即可得到乙得分的分布列和数学期望;(2)由已知甲、乙至少答对2题才能入选,求出甲、乙入选的概率,利用对立大事,即可求得结论.解答:解:(1)乙答题所得分数为X,则X的可能取值为0,15,30.P(X=0)=+=P(X=15)==P(X=30)==乙得分的分布列如下X 0 15 30PEX=0×+15×+30×=(2)由已知甲、乙至少答对2题才能入选,记甲入选为大事A,乙入选为大事B,则P(A)=+=+=,P ()=1﹣=由(1)知:P(B)=P(X=15)+P(X=30)=,P ()=1﹣=,所求概率为P=1﹣P ()=点评:本题考查概率的计算,考查互斥大事的概率,考查离散型随机变量的分布列与期望,确定变量的取值,计算其概率是关键.19.已知函数f(x)=lnx+cosx ﹣(﹣)x的导数为f′(x),且数列{a n}满足a n+1+a n=nf ′()+3(n∈N*).(1)若数列{a n}是等差数列,求a1的值:(2)若对任意n∈N*,都有a n+2n2≥0成立,求a1的取值范围.考点:数列与函数的综合;利用导数争辩函数的单调性;利用导数求闭区间上函数的最值.专题:点列、递归数列与数学归纳法.分析:(1)求函数的导数,得到数列的递推关系式,依据数列{a n}是等差数列的通项公式进行求解即可求a1的值:(2)求出数列{a n}的通项公式,利用不等式a n+2n2≥0恒成立.利用参数分别法进行求解即可.解答:解:f′(x)=﹣sinx ﹣+,则f ′()=4;故a n+1+a n=πf ′()+3=4n+3,(1)若数列{a n}是等差数列,则a n=a1+(n﹣1)d,a n+1=a1+nd,则a n+1+a n=a1+(n﹣1)d+a1+nd=2a1+(2n﹣1)d=4n+3,解得d=2,a1=.(2)由a n+1+a n=4n+3,a n+2+a n+1=4n+7,两式相减得a n+2﹣a n=4,故数列{a2n﹣1}是首项为a1,公差为4的等差数列,数列{a2n}是首项为a2,公差为4的等差数列,又a1+a2=7,∴a2=7﹣a1,∴a n =.①当n为奇数时,a n=2n﹣2+a1,由a n+2n2≥0成立,即2n﹣2+a1+2n2≥0,转化为a1≥﹣2n2﹣2n+2,恒成立,设f(n)=﹣2n2﹣2n+2=﹣(n+)2+,∴f(n)max=f(1)=﹣2,∴a1≥﹣2.②当n为偶数时,a n=2n+3﹣a1,由a n+2n2≥0成立,即2n+3﹣a1+2n2≥0,转化为﹣a1≥﹣2n2﹣2n﹣3,恒成立,设g(n)=﹣2n2﹣2n﹣3=﹣(n+)2﹣,∴g(n)max=g(2)=﹣15,∴﹣a1≥﹣15.即a1≤15,综上﹣2≤a1≤15,即a1的取值范围是[﹣2,15].点评:本题主要考查等差数列的通项公式的应用已经递推数列的应用,考查同学的运算和推理力量,求出数列的递推关系是解决本题的关键.20.如图,已知椭圆Γ:=1(a>b>0)的离心率e=,短轴右端点为A,M(1,0)为线段OA的中点.(Ⅰ)求椭圆Γ的方程;(Ⅱ)过点M任作一条直线与椭圆Γ相交于两点P,Q,试问在x轴上是否存在定点N,使得∠PNM=∠QNM,若存在,求出点N的坐标;若不存在,说明理由.考点:直线与圆锥曲线的综合问题.专题:综合题;圆锥曲线的定义、性质与方程.分析:(Ⅰ)依据离心率,短轴右端点为A,M(1,0)为线段OA的中点,求出几何量,即可求椭圆Γ的方程;(Ⅱ)分类争辩,设PQ的方程为:y=k(x﹣1),代入椭圆方程化简,若∠PNM=∠QNM,则k PN+k QN=0,即可得出结论.解答:解:(Ⅰ)由已知,b=2,又,即,解得,所以椭圆方程为.…(4分)(Ⅱ)假设存在点N(x0,0)满足题设条件.当PQ⊥x轴时,由椭圆的对称性可知恒有∠PNM=∠QNM,即x0∈R;…(6分)当PQ与x轴不垂直时,设PQ的方程为:y=k(x﹣1),代入椭圆方程化简得:(k2+2)x2﹣2k2x+k2﹣8=0 设P(x1,y1),Q(x2,y2),则则==…(10分)若∠PNM=∠QNM,则k PN+k QN=0即=0,整理得4k(x0﹣4)=0由于k∈R,所以x0=4综上在x轴上存在定点N(4,0),使得∠PNM=∠QNM…(12分)点评:本题考查椭圆的几何性质与标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查同学的计算力量,属于中档题.21.已知函数f(x)=ax﹣1﹣1n x.(1)若f(x)≥0对任意的x∈(0,+∞)恒成立,求实数a的取值范围;(2)求证:对任意的x∈N*,<e(其中e为自然对数的底,e≈2.71828).考点:利用导数求闭区间上函数的最值.专题:计算题;证明题;函数的性质及应用;导数的综合应用.分析:(1)f(x)≥0可化为a ≥对任意的x∈(0,+∞)恒成立,令g(x)=,x∈(0,+∞);求g′(x)=﹣,从而求最值;(2)由(1)知,lnx≤x﹣1对任意的x∈(0,+∞)恒成立,从而可得ln(1+)<对任意k∈N*成立,从而可得到kln(1+k)﹣klnk<1,从而化简求得.解答:解:(1)由f(x)≥0得,a ≥对任意的x∈(0,+∞)恒成立,令g(x)=,x∈(0,+∞);∵g′(x)=﹣,∴当x∈(0,1)时,g′(x)>0,g(x)为增函数;当x∈(1,+∞)时,g′(x)<0,g(x)为减函数;故g max(x)=g(1)=1;∴a≥1;∴实数a的取值范围是[1,+∞);(2)证明:由(1)知,lnx≤x﹣1对任意的x∈(0,+∞)恒成立,当且仅当x=1时取等号,∴ln(1+)<对任意k∈N*成立,即ln(1+k)﹣lnk<;即kln(1+k)﹣klnk<1,∴(1+k)ln(1+k)﹣klnk<1+ln(1+k);故2ln2﹣1ln1<1+ln2,3ln3﹣2ln2<1+ln3,…,(1+n)ln(1+n)﹣nlnn<1+ln(1+n);累加得,(1+n)ln(1+n)<n+ln2+ln3+…+ln(n+1),即nln(n+1)<n+ln(n!),∴ln(n+1)<1+ln(n!),即ln(n+1)﹣ln<1;∴ln<1,即<e.点评:本题考查了导数的综合应用及恒成立问题的应用,属于中档题.。
2020年安徽省黄山市高考数学二模试卷(理科)(含答案解析)
2020年安徽省黄山市高考数学二模试卷(理科)一、选择题(本大题共12小题,共60.0分)1.已知集合,,A. B. C. D.2.若复数z满足,则对应的点在第象限.A. 一B. 二C. 三D. 四3.已知,则A. B. C. D.4.已知变量x,y满足约束条件,若恒成立,则实数k的最大值为A. 40B. 9C. 8D.5.已知函数的定义域为D,满足:对任意,都有,对任意,且,都有,则称函数为“成功函数“,下列函数是“成功函数”的是A. B.C. D.6.任取一个自然数,如果它是偶数,我们就把它除以2,如果它是奇数,我们就把它乘3再加上1,在这样的变换下,我们就得到一个新的自然数.如果反复使用这个变换,我们就会得到一串自然数,最终我们都会陷在这个循环中,这就是世界数学名题“问题”如图所示的程序框图的算法思路源于此,执行该程序框图,若,则输出的A. 6B. 7C. 8D. 97.为等差数列,若,且它的前n项和有最小值,那么当取得最小正值时,A. 2019B. 2020C. 4039D. 40408.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是A. 甲地:总体均值为3,中位数为4B. 乙地:总体均值为1,总体方差大于0C. 丙地:中位数为2,众数为3D. 丁地:总体均值为2,总体方差为39.如图,角的顶点在坐标原点O,始边在y轴的非负半轴,终边经过点,角的顶点在原点O,始边在x轴的非负半轴,终边OQ落在第二象限,且,则的值为A.B.C.D.10.在长方体中,,平面过长方体顶点D,且平面平面,平面平面,则直线l与所成角的余弦值为A. B. C. D.11.点是双曲线的右焦点,动点A在双曲线左支上,直线:与直线:的交点为B,则的最小值为A. 8B.C. 9D.12.设函数在定义域上是单调函数,且,若不等式对恒成立,则a的取值范围是A. B. C. D.二、填空题(本大题共4小题,共20.0分)13.,则______用数字作答.14.已知函数,则函数的所有零点构成的集合为______.15.在中,D为AB边的中点,,,,E,F分别为边BC,AC上的动点,且,则最小值为______.16.已知点,抛物线C:的准线为1,点P在C上,作于H,且,,则抛物线方程为______.三、解答题(本大题共7小题,共82.0分)17.已知a,b,c分别是三个内角A,B,C所对的边,且.求B;若,且sin A,sin B,sin C成等差数列,求的面积.18.如图,已知边长为2的菱形ABCD,其中,,平面ABCD,,.求证:平面平面BDF;求二面角的大小.19.已知椭圆:的离心率为,左右焦点分别为,,且A、B分别是其左右顶点,P是椭圆上任意一点,面积的最大值为4.求椭圆的方程.如图,四边形ABCD为矩形,设M为椭圆上任意一点,直线MC、MD分别交x轴于E、F,且满足,求证:.20.在党中央的英明领导下,在全国人民的坚定支持下,中国的抗击“新型冠状肺炎”战役取得了阶段性胜利,现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心,对某中型商品实行分期付款方式销售,根据以往资料统计,顾客购买该商品选择分期付款的期数的分布列为456P a b其中,.求购买该商品的3位顾客中,恰有1位选择分4期付款的概率;商场销售一件该商品,若顾客选择分4期付款,则商场获得的利润为2000元;若顾客选择分5期付款,则商场获得的利润为2500元;若顾客选择分6期付款,则商场获得的利润为3000元,假设该商场销售两件该商品所获得的利润为单位:元,设时的概率为m,求当m取最大值时,利润X的分布列和数学期望;设某数列满足,,,若,求n的最小值.21.已知函数.讨论函数极值点的个数;当时,不等式在上恒成立,求实数k的取值范围.22.在直角坐标系xOy中,曲线的参数方程为为参数,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,且在极坐标下点.求曲线的普通方程和曲线的直角坐标方程;若曲线与曲线交于A,B两点,求的值.23.已知实数x,y满足.若,求x的取值范围;若,,求的最小值.-------- 答案与解析 --------1.答案:D解析:解:集合,,,故选:D.分别求出集合A、B,从而求出即可.本题考查了集合的运算,考查二次函数以及二次根式的性质,是一道基础题.2.答案:A解析:解:由,得,,则.对应的点的坐标为,在第一象限.故选:A.把已知等式变形,利用复数代数形式的乘除运算化简求得z,进一步求出的坐标得答案.本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.3.答案:C解析:解:由,得,由,得,由,得,.故选:C.化对数式为指数式判断,求解,化指数式为对数式判断,则答案可求.本题考查对数值的大小比较,考查有理指数幂与对数的运算性质,考查数学转化思想方法,是基础题.4.答案:D解析:解:变量x,y满足约束条件的可行域如图,是点到的距离的平方减1,故最小值为点P到的距离的平方加1,的最小值为:若恒成立,即的最大值为:.故选:D.已知x、y满足以下约束条件画出可行域,目标函数是可行域中的点到原点的距离的平方减1,求出最小值,然后求解z的最大值.此题主要考查简单的线性规划问题,是一道中档题,要学会画图.考查转化思想的应用.5.答案:B解析:解:由对任意,都有,得即函数为奇函数;对任意,且,都有,即函数单调递增,A :在定义域内不单调,不符合题意;B:由可得且由于恒成立,即在R上单调递增,符合题意;C:结合复合函数单调性可知,在内单调递减,不符合题意;D:在定义域R上单调递减,不符合题意.故选:B.由对任意,都有,得即函数为奇函数;对任意,且,都有,即函数单调递增,然后结合选项进行判断即可.本题主要考查了函数单调性与奇偶性的判断,属于函数性质的综合应用.6.答案:D解析:解:由题意,模拟程序的运行,可得,n不是奇数,,,不满足条件;n是奇数,,,不满足条件,执行循环体,n不是奇数,,;不满足条件,执行循环体,n是奇数,,;不满足条件,执行循环体,n不是奇数,,;不满足条件,执行循环体,n不是奇数,,;不满足条件,执行循环体,n不是奇数,,;不满足条件,执行循环体,n不是奇数,,;满足条件,退出循环,输出i的值为9.故选:D.根据该程序的功能是利用循环结构计算n的值并输出相应的i的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.解析:解:若,且它的前n项和有最小值,,....那么当取得最小正值时,.故选:C.若,且它的前n项和有最小值,可得,再利用求和公式即可判断出结论.本题考查了等差数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.8.答案:D解析:【分析】本题考查数据分析,中位数,众数,方差等概念,属于基础题.逐一分析即可求得答案.【解答】解:由于甲地总体均值为3,中位数为4,即中间两个数第5、6天新增人数的平均数为4,因此之后的几天中感染人数可能大于7,故甲地不符合;乙地总体均值为1,因此这10天感染的人数总和为10,故这10天中可以有一天感染人数大于7,故乙地不符合;丙地中位数为2,众数为3,可以有一天感染人数为8,故丙地不符合;丁地由于总体均值为2,方差为3,故若有一天超过7,比如8,则故丁地符合,故选D.9.答案:A解析:解:由已知可得:..故选:A.由已知可得:可得,代入即可得出.本题考查了三角函数的定义、和差公式,考查了推理能力与计算能力,属于基础题.解析:解:如图,平面过长方体顶点D,且平面平面,平面与平面重合,在平面中,过作,则,即为平面与平面的交线l,连接,可得,又,则即为直线l与所成角.连接,由,得,,由余弦定理可得:.即直线l与所成角的余弦值为.故选:D.由题意画出图形,得到平面与平面的交线l,找出异面直线所成角,由已知结合余弦定理求解.本题考查异面直线所成角的求法,考查空间想象能力与思维能力,是中档题.11.答案:C解析:解:由双曲线的方程可得,,焦点,可得,所以,当A,,B三点共线时,最小,联立直线,的方程,可得,消参数t可得,所以可得交点B的轨迹为圆心在,半径为1的圆,所以,当过与圆心的直线与圆的交点B且在和圆心之间时最小.所以的最小值为9,故选:C.由题意求出直线,的交点B为圆心在,半径为1的圆,由双曲线的定义可得,所以,当A,,B三点共线时,最小,过与圆心的直线与圆的交点B且在和圆心之间时最小.本题考查求轨迹方程及双曲线的性质,三点共线时线段之和最小,属于中档题.12.答案:A解析:解:设,则,,令得,解得,,,不等式,即:.令,.,可得时,函数取得极小值即最小值.不等式对恒成立,.的取值范围是.故选:A.先利用换元法求出的解析式,然后再用分离变量法,借助函数的单调性来解决问题.本题考查了利用导数研究函数的单调性极值与最值、方程与不等式解法、换元法、等价转化方法,考查了推理能力与计算能力,属于中档题.13.答案:511解析:解:,令,可得.再令,可得,,故答案为:511.在所给的等式中,分别令,,可得要求式子的值.本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.14.答案:3,解析:解:由得,设,则等价为,当时,由得,当时,由得,即或,当时,由,得,由,得舍,故此时,当时,由得,由,得,综上,或或,所以函数的所有零点所构成的集合为:3,故答案为:3,.函数的零点,即求方程的解,利用换元法进行求解即可.本小题主要考查函数的零点、方程的解法等基础知识,利用换元法结合数形结合是解决本题的关键.15.答案:解析:解以三角形的直角边为坐标轴建立平面直角坐标系,如图:则,,,设,则.,..令,则.令得.当时,,当时,.当时,取得最小值.故答案为:.建立平面直角坐标系,设,求出的坐标,则可表示为x的函数,利用函数的性质得出最小值.本题考查了平面向量的数量积运算,建立坐标系是解题关键,属于中档题.16.答案:解析:解:设抛物线的焦点为,,由抛物线的定义可知,,,,不妨设点P在第一象限,过点P作轴于点Q,则Q为AF的中点,,,,,,点P的坐标为,点P在抛物线C上,,化简得,解之得舍负,抛物线方程为.故答案为:.设抛物线的焦点为,则,由抛物线的定义可知,,不妨设点P在第一象限,过点P作轴于点Q,则Q为AF的中点,结合,可以用p表示出点P的坐标,然后将其代入抛物线方程,列出关于p的方程,解之可得p的值,从而求得抛物线的方程.本题考查抛物线的定义,求抛物线的标准方程,考查学生的分析能力和运算能力,属于中档题.17.答案:解:由,则,,,而,,所以,可得,而,又,所以,故.由sin A,sin B,sin C成等差数列,且,所以,可得,又,则,可得:,所以,则.解析:由正弦定理,三角函数恒等变换的应用化简已知等式,结合,可得,又根据范围,可求B的值.由等差数列的性质,正弦定理可得,又根据余弦定理可求ac的值,进而根据三角形的面积公式即可计算求解.本题主要考查了正弦定理,三角函数恒等变换的应用,等差数列的性质,余弦定理,三角形的面积公式在解三角形中的应用,考查了转化思想,属于基础题.18.答案:证明:因为,所以A、C、F、E四点共面.又平面ABCD,而平面ABCD,所以,由菱形ABCD,所以,,令,且,所以,平面ACFE,而平面ACFE,所以,,因为且平面ABCD,所以平面ABCD,则且,,由菱形ABCD且,所以,故,,则,,所以,即,又,所以平面BDE,平面BDF,平面平面BDF.由菱形ABCD,所以,以OA,OB所在的直线分别为x轴,y轴,过O作垂直于平面ABCD的直线为z轴建立空间直角坐标系.则,所以0,,,,,,所以,,,令平面DEF的一个法向量为,且,,由,,所以,由,,所以,即,令平面BEF的一个法向量为:,且,,由,,所以,由,,所以,即,所以,则,即二面角的大小为.解析:证明,,推出平面ACFE,得到,推出平面ABCD,证明且,,证明平面BDE,然后证明平面平面BDF.以OA,OB所在的直线分别为x轴,y轴,过O做垂直于平面ABCD的为z轴建立空间直角坐标系.求出平面DEF的一个法向量,平面BEF的一个法向量,通过空间向量的数量积求解二面角的大小.本题考查直线与平面垂直的判定定理以及平面与平面垂直的判定定理得到应用,二面角的平面角的求法,考查空间想象能力,逻辑推理能力,以及计算能力,是中档题.19.答案:解:由题意可得,又,可得,而,所以,解得,,所以椭圆的方程为;证明:设,,,可令,由,故MC的方程为,直线MC交x轴于E,可令,则,即,由,故MD的方程为,直线MD交x轴于F,可令,则,即,因为,所以,可得,即,即,而,所以,可得,可得,而M为椭圆上一点,所以,解得,所以,即.解析:由椭圆的离心率公式和三角形的面积公式,结合a,b,c的关系,解方程可得所求椭圆方程;设,,,可令,运用直线方程和两直线的交点,化简整理,即可得证.本题考查椭圆的方程和性质,考查直线和椭圆的位置关系,考查直线方程的求法和应用,以及两点的距离公式,考查方程思想和化简运算能力,属于中档题.20.答案:解:方法1:设恰有一位顾客选择分4期付款的概率的概率为P.由题可知:,则.方法2:由于3位顾客中恰有1位选择“分4期付款”,则另外两位均不选“分4期付款”,所以.由题可得X的值分别为4000,4500,5000,5500,6000.,,,,,所以,取最大值的条件为所以分布列为:X40004500500055006000P.解:由题可得,所以,化简得,即是等比数列,首项为,公比为,所以,化简得由题可知:由题可知:,显然对所有都成立;,也是对所有都成立;当n为偶数时,上述不等式恒成立;当n为奇数时,,解得即综上所述,n的最小值为5.解析:方法1:设恰有一位顾客选择分4期付款的概率的概率为由题可知:,然后求解即可.方法2:由于3位顾客中恰有1位选择“分4期付款”,则另外两位均不选“分4期付款”,利用相互独立事件乘法乘积求解概率即可.由题可得X的值分别为4000,4500,5000,5500,求出概率,得到分布列,然后求解期望即可.由题可得,得到,判断数列是等比数列,然后分类求解n的最小值.本题考查离散型随机变量的分布列以及期望的求法,数列与函数的应用,考查转化思想以及计算能力,题目比较新颖,是难题.21.答案:解:,当时,,所以在R上单调递增,无极值.当时,令,得,当时,;当时,即函数在上单调递减,在上单调递增,此时只有一个极值点.综上所述,当时,在R上无极值点;当时,函数在R上只有一个极值点.当时,由题即在上恒成立令且,则,,则且,当时,即时,由于,,而,所以,故在上单调递增,所以,即,故在上单调递增,所以,即在上恒成立,故符合题意.当时,即时,由于在上单调递增,令因为,故在上存在唯一的零点,使,因此,当时,,单调递减,所以,即,在上单调递减,故,与题不符.综上所述,k的取值范围是.解析:求出导函数,通过当时,当时,判断导函数的符号,判断函数的单调性,求解函数的极值即可.当时,由题即在上恒成立,令且,通过函数的导数,结合当时,当时,判断函数的单调性求解函数的最值,推出结果.求解k的取值范围.本题考查函数的导数的应用,考查转化思想以及计算能力,分类讨论思想的应用,是难题.22.答案:解:的参数方程:为参数得,曲线的直角坐标方程:.由,得,所以曲线的直角坐标方程为.点P的极坐标为,故其直角坐标为,由:,则其参数方程为,将的参数方程代入曲线的方程,得由于恒成立,不妨令方程有两个不等实根、,由于,所以、异号,且,则,.解析:直接利用转换关系,把参数方程、极坐标方程和直角坐标方程之间进行转换.利用直线和曲线的位置关系式的应用和一元二次方程根和系数关系式的应用求出结果.本题考查的知识要点:参数方程、极坐标方程和直角坐标方程之间的转换,一元二次方程的根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.答案:解:由,得由,即,当,则,;当时,则,;当时,则,.故x的取值范围为或;,,且.当且仅当,即,时,的最小值为8.解析:由,得,代入,可得,即,然后对x分类求解,取并集得答案;由,,且,得,展开后利用基本不等式求最值.本题考查绝对值不等式的解法,训练了利用基本不等式求最值,是中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省黄山市歙县高考数学全真模拟试卷理(含解析)2016年安徽省黄山市歙县中学高考数学全真模拟试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A={x|x2<1},B={y|y=|x|},则A∩B=()A.?B.(0,1)C.2.设随机变量ξ~N(3,σ2),若P(ξ>4)=0.2,则P(3<ξ≤4)=()A.0.8 B.0.4 C.0.3 D.0.23.已知复数z=(i为虚数单位),则3=()A.1 B.﹣1 C.D.4.过双曲线﹣=1(a>0,b>0)的一个焦点F作两渐近线的垂线,垂足分别为P、Q,若∠PFQ=π,则双曲线的渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x5.将半径为1的圆分割成面积之比为1:2:3的三个扇形作为三个圆锥的侧面,设这三个圆锥底面半径依次为r1,r2,r3,那么r1+r2+r3的值为()A.B.2 C. D.16.如图是某算法的程序框图,则程序运行后输出的结果是()A.2 B.3 C.4 D.57.等差数列{a n}中,a3=7,a5=11,若b n=,则数列{b n}的前8项和为()A. B.C.D.8.已知(x﹣3)10=a0+a1(x+1)+a2(x+1)2+…+a10(x+1)10,则a8=()A.45 B.180 C.﹣180 D.7209.如图为三棱锥S﹣ABC的三视图,其表面积为()A.16 B.8+6C.16D.16+610.已知椭圆E: +=1(a>b>0)的左焦点F(﹣3,0),P为椭圆上一动点,椭圆内部点M(﹣1,3)满足PF+PM的最大值为17,则椭圆的离心率为()A.B.C.D.11.已知f(x)=,若函数y=f(x)﹣kx恒有一个零点,则k的取值范围为()A.k≤0 B.k≤0或k≥1 C.k≤0或k≥e D.k≤0或k≥12.已知数列{a n}的通项公式为a n=﹣2n+p,数列{b n}的通项公式为b n=2n﹣4,设c n=,若在数列{c n}中c6<c n(n∈N*,n≠6),则p的取值范围()A.(11,25)B.(12,22)C.(12,17)D.(14,20)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.)13.若平面向量、满足||=2||=2,|﹣|=,则在上的投影为.14.若数列{a n}满足a1=a2=1,a n+2=,则数列{a n}前2n项和S2n= .15.若直线ax+(a﹣2)y+4﹣a=0把区域分成面积相等的两部分,则的最大值为.16.已知函数f(x)=(a+1)lnx+x2(a<﹣1)对任意的x1、x2>0,恒有|f (x1)﹣f(x2)|≥4|x1﹣x2|,则a的取值范围为.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在△ABC中,角A,B,C所对的边分别为a,b,c,满足c=1,且cosBsinC+(a﹣sinB)cos(A+B)=0 (1)求C的大小;(2)求a2+b2的最大值,并求取得最大值时角A,B的值.18.如图,在四棱锥P﹣ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.(Ⅰ)求证:平面PBC⊥平面PCD;(Ⅱ)设点N是线段CD上一动点,且=λ,当直线MN与平面PAB所成的角最大时,求λ的值.19.如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.(Ⅰ)求x<2且y>1的概率;(Ⅱ)求随机变量ξ的分布列与数学期望.20.已知椭圆E: +=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(﹣1,).过椭圆E内一点P(1,)的两条直线分别与椭圆交于点A、C和B、D,且满足=λ,=λ,其中λ为实数.当直线AP平行于x轴时,对应的λ=.(Ⅰ)求椭圆E的方程;(Ⅱ)当λ变化时,k AB是否为定值?若是,请求出此定值;若不是,请说明理由.21.已知函数f(x)=,曲线y=f(x)在点x=e2处的切线与直线x﹣2y+e=0平行.(Ⅰ)若函数g(x)=f(x)﹣ax在(1,+∞)上是减函数,求实数a的最小值;(Ⅱ)若函数F(x)=f(x)﹣无零点,求k的取值范围.22.如图所示,AC为⊙O的直径,D为的中点,E为BC的中点.(Ⅰ)求证:DE∥AB;(Ⅱ)求证:AC?BC=2AD?CD.23.在平面直角坐标系中,直线l的参数方程为(t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=(1)求曲线C的直角坐标方程和直线l的普通方程;(2)若直线l与曲线C相交于A,B两点,求△AOB的面积.24.已知函数f(x)=|x﹣l|+|x﹣3|.(I)解不等式f(x)≤6;(Ⅱ)若不等式f(x)≥ax﹣1对任意x∈R恒成立,求实数a的取值范围.2016年安徽省黄山市歙县中学高考数学全真模拟试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A={x|x2<1},B={y|y=|x|},则A∩B=()A.?B.(0,1)C.【考点】交集及其运算.【分析】求出集合的等价条件,根据集合的基本运算进行求解即可.【解答】解:A={x|x2<1}={x|﹣1<x<1},B={y|y=|x|≥0},则A∩B=10,利用二项式定理的通项公式即可得出.【解答】解:(x﹣3)10=10,∴,故选:D.9.如图为三棱锥S﹣ABC的三视图,其表面积为()A.16 B.8+6C.16D.16+6【考点】由三视图求面积、体积.【分析】该三棱锥为长方体切去四个小三棱锥得到的,三棱锥的三条边长分别为,即可球心三棱锥的表面积【解答】解:由三视图可知该三棱锥为边长为2,4,4的长方体切去四个小棱锥得到的几何体.三棱锥的三条边长分别为,∴表面积为4×=16.故选:C.10.已知椭圆E: +=1(a>b>0)的左焦点F(﹣3,0),P为椭圆上一动点,椭圆内部点M(﹣1,3)满足PF+PM的最大值为17,则椭圆的离心率为()A.B.C.D.【考点】椭圆的简单性质.【分析】设右焦点为Q,求得Q(3,0),运用椭圆的定义可得即|PF|=2a﹣|PQ|,则|PM|+|PF|=2a+(|PM|﹣|PQ|)≤2a+|MQ|,当P,M,Q三点共线时,取得最大值,解得a=6,运用离心率公式,计算即可得到所求值.【解答】解:设右焦点为Q,由F(﹣3,0),可得Q(3,0),由椭圆的定义可得|PF|+|PQ|=2a,即|PF|=2a﹣|PQ|,则|PM|+|PF|=2a+(|PM|﹣|PQ|)≤2a+|MQ|,当P,M,Q共线时,取得等号,即最大值2a+|MQ|,由|MQ|==5,可得2a+5=17,所以a=6,则e===,故选:A.11.已知f(x)=,若函数y=f(x)﹣kx恒有一个零点,则k的取值范围为()A.k≤0 B.k≤0或k≥1 C.k≤0或k≥e D.k≤0或k≥【考点】分段函数的应用.【分析】根据函数与方程的关系,将条件转化为两个函数的交点个数问题,利用导数和数形结合进行求解即可.【解答】解:由y=f(x)﹣kx=0得f(x)=kx,作出函数f(x)和y=kx的图象如图,由图象知当k≤0时,函数f(x)和y=kx恒有一个交点,当x≥0时,函数f(x)=ln(x+1)的导数f′(x)=,则f′(0)=1,当x<0时,函数f(x)=e x﹣1的导数f′(x)=e x,则f′(0)=e0=1,即当k=1时,y=x是函数f(x)的切线,则当0<k<1时,函数f(x)和y=kx有3个交点,不满足条件.当k≥1时,函数f(x)和y=kx有1个交点,满足条件.综上k的取值范围为k≤0或k≥1,故选:B.12.已知数列{a n}的通项公式为a n=﹣2n+p,数列{b n}的通项公式为b n=2n﹣4,设c n=,若在数列{c n}中c6<c n(n∈N*,n≠6),则p的取值范围()A.(11,25)B.(12,22)C.(12,17)D.(14,20)【考点】数列递推式.【分析】化简a n﹣b n=﹣2n+p﹣2n﹣4,从而判断a n﹣b n,a n,b n的增减性,从而分类讨论以确定最小值,从而解得.【解答】解:∵a n﹣b n=﹣2n+p﹣2n﹣4,∴a n﹣b n随着n变大而变小,又∵a n=﹣2n+p随着n变大而变小,b n=2n﹣4随着n变大而变大,∴,(1)当(2)当,综上p∈(14,20),故选D.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.)13.若平面向量、满足||=2||=2,|﹣|=,则在上的投影为﹣1 .【考点】平面向量数量积的运算.【分析】对的两边平方便可求出,而可以得出在上的投影为,从而便可得出该投影的值.【解答】解:根据条件,==7;∴;∴在上的投影为.故答案为:﹣1.14.若数列{a n}满足a1=a2=1,a n+2=,则数列{a n}前2n项和S2n= 2n+n2﹣1 .【考点】数列递推式.【分析】由已知可得:n=2k﹣1时,a2k+1﹣a2k﹣1=2,为等差数列;n=2k时,a2k+2=2a2k,为等比数列.分组求和即可得出.【解答】解:∵数列{a n}满足a1=a2=1,a n+2=,∴n=2k﹣1时,a2k+1﹣a2k﹣1=2,为等差数列;n=2k时,a2k+2=2a2k,为等比数列.∴.故答案为:2n+n2﹣1.15.若直线ax+(a﹣2)y+4﹣a=0把区域分成面积相等的两部分,则的最大值为 2 .【考点】简单线性规划.。
