有限个广义φ-伪压缩映象迭代收敛性
ch2-1(二分、简单迭代)ami

∵ f ( x0 ) < 0,∴令a1 = x0 = 1.25, b1 = b = 1.5,
[a 得新的有根区间 1 , b1 ]
如此二分下去即可。 如此二分下去即可。现估计二分次数
x − xn < 0.005 ⇒ n ≥ 5.64
*
所以二分6次可达到要求。 所以二分6次可达到要求。
精确解为: 精确解为: x =1.324718
y = ϕ( x) 又 x = ϕ( x) 的解⇔ 的解 y = x
(两条线的交点) 两条线的交点)
迭代法的几何意义
y
y=x
y
y = ϕ ( x)
x
x
迭代法的几何意义
y
y=x
y
y=x
y=ϕ(x)
y=ϕ(x)
0
x1
x3 x5ξ x4 x2 x0
x
0
x3 x1 ξ x0 x2
x4
x
简单迭代法例题
只要二分足够多次(即充分大), 只要二分足够多次( k充分大),
则有 x* −xk < ε
. ε 这里 为预定的精度
区间二分法
对分区间次数的估计
bn − an b − a 由 x * −xn ≤ = n+1 < ε 2 2
不难得出: 不难得出:
ln( b − a) − lnε n> −1 ln 2
= (L
p−1
+L
p−2
+⋯+ 1) xn+1 − xn
简单迭代法收敛定理
1− L 1− L n xn+1 − xn ≤ L x1 − x0 = 1− L 1− L
p p
即
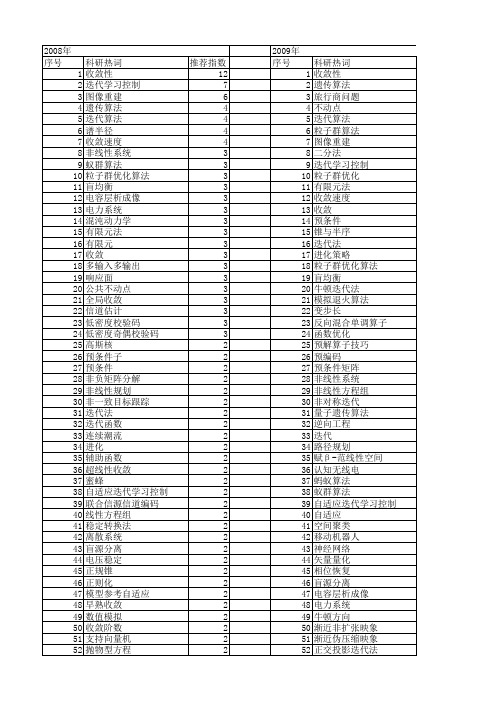
【国家自然科学基金】_迭代收敛_基金支持热词逐年推荐_【万方软件创新助手】_20140803
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词 收敛性 迭代学习控制 图像重建 遗传算法 迭代算法 谱半径 收敛速度 非线性系统 蚁群算法 粒子群优化算法 盲均衡 电容层析成像 电力系统 混沌动力学 有限元法 有限元 收敛 多输入多输出 响应面 公共不动点 全局收敛 信道估计 低密度校验码 低密度奇偶校验码 高斯核 预条件子 预条件 非负矩阵分解 非线性规划 非一致目标跟踪 迭代法 迭代函数 连续潮流 进化 辅助函数 超线性收敛 蜜蜂 自适应迭代学习控制 联合信源信道编码 线性方程组 稳定转换法 离散系统 盲源分离 电压稳定 正规锥 正则化 模型参考自适应 早熟收敛 数值模拟 收敛阶数 支持向量机 抛物型方程
模拟退火 栅格法 极大似然估计 权值修正 机器视觉 有限差分法 最佳逼近解 无线通信 无功优化 收敛性定理 支持向量机 扩散模型 惯性权重 悬索桥 序贯最小优化 对角占优 对称正定矩阵 对流扩散方程 实banach空间 变异策略 压缩传感 单调线性互补 共轭梯度 全局收敛性 全局收敛 位姿估计 优化 交会对接 中心路径方向 严格双α -对角占优矩阵 与文本无关 三维地电场 lyapunov-like函数 gauss-seidel迭代法 backstepping aor迭代法 魔方变换 高维 高斯滤波 高斯混合 马尔可夫随机场(mrf) 马尔可夫随机场 食物链生态进化算法 风量损失 频率分辨光学快门 预载恒流静压导轨 预测模型 预测控制 预测 预条件共轭梯度法 预条件lanczos算法 预应力钢结构 预信噪比 顺逆交替迭代技术
牛顿-拉夫森(Newton-Raphson)迭代法

§3.4 牛顿迭代法牛顿迭代法也称为牛顿-拉夫森(Newton-Raphson)迭代法,它是数值分析中最重要的方法之一,它不仅适用于方程或方程组的求解,还常用于微分方程和积分方程求解。
3.4.1 牛顿迭代法用迭代法解非线性方程时,如何构造迭代函数是非常重要的,那么怎样构造的迭代函数才能保证迭代法收敛呢?牛顿迭代法就是常用的方法之一,其迭代格式的来源大概有以下几种方式:1设],[)(2b a C x f ∈,对)(x f 在点],[0b a x ∈作泰勒展开: !2))((''))((')()(20000x x f x x x f x f x f -+-+=ξ略去二次项,得到)(x f 的线性近似式:))((')()(000x x x f x f x f -+≈。
由此得到方程=)(x f 0的近似根(假定≠)('0x f 0),)(')(000x f x f x x -=即可构造出迭代格式(假定≠)('k x f 0):)(')(1k k k k x f x f x x -=+ 公式(3.4.1)这就是牛顿迭代公式,若得到的序列{k x }收敛于α,则α就是非线性方程的根。
2 牛顿迭代法也称为牛顿切线法,这是由于)(x f 的线性化近似函数)(x l =))((')(000x x x f x f -+是曲线y =)(x f 过点))(,(00x f x 的切线而得名的,求)(x f 的零点代之以求)(x l 的零点,即切线)(x l 与x 轴交点的横坐标,如右图所示,这就是牛顿切线法的几何解释。
实际上,牛顿迭代法也可以从几何意义上推出。
利用牛顿迭代公式,由k x 得到1+k x ,从几何图形上看,就是过点))(,(k k x f x 作函数)(x f 的切线k l ,切线k l 与x 轴的交点就是1+k x ,所以有1)()('+-=k k k k x x x f x f ,整理后也能得出牛顿迭代公式: )(')(1k k k k x f x f x x -=+。
Banach空间中的逼近问题

Banach空间中的逼近问题常青【期刊名称】《重庆三峡学院学报》【年(卷),期】2012(028)003【摘要】Let E be a real Banach space, C is a nonempty closed convex subset of E and be a retract of E.A mapping P from E to C is a retraction.This paper, based on the [2] reference in the literature, removes the error of iterative sequences change and proves that the sequence {xn } converges stronglywith a common fixed point of T1, T2,……, Tu , if and only if lim inf d (x, F) = 0. Finally it presents two inferences on the basis of the corollary.%设E为实Banach空间,C为E上的非空闭凸子集且为E上的收缩核,P:E→C的保核收缩映象,文章在文献[2]的基础上,对带误差的迭代序列进行了修改,并证明了序列{xn}收敛于T1,T2,…,TN的公共不动点的充分必要条件为:limn→∞inf d(xn,F)=0,最后给出了在此基础上的两个推论.【总页数】5页(P24-28)【作者】常青【作者单位】重庆师范大学数学学院,重庆400047【正文语种】中文【中图分类】O177.91【相关文献】1.Banach空间中一类非线性变分包含问题解的存在性和逼近问题 [J], 谷峰2.Banach空间中增生算子的粘滞逼近问题 [J], 马乐荣;高兴慧;周海云3.Banach空间中一类新的κ-次增生型变分包含问题解的迭代逼近 [J], 谷峰4.Banach空间中一类伪压缩型变分包含问题解的迭代逼近 [J], 虞懿;曾六川5.自反Banach空间内一类新的广义混合平衡问题组的辅助原理和逼近可解性 [J], 丁协平因版权原因,仅展示原文概要,查看原文内容请购买。
带模糊映象的新一类广义混合拟变分包含的迭代算法

1 引言及预 备知识
广义模糊集值混合拟变分包含在数学 、 物理 、 工程、 经济等领域有广泛 的应用. 近年来 , 1 ] 文[ - 7
研 究 了多种 广义 模糊集 值 变分 包 含 问题 , 别 是 文 特
是 ( ) 单 调 的 集 值 映 象 , rn eg —m)n H, 一 且 a g(
维普资讯
20 0 8年 3月
四川师 范大学学报 ( 自然科学版 )
Junl f i unN r l n esy N trl c n e ora o c a oma U i ri ( a a Si c ) Sh v t u e
Ma ., 0 8 r 2 0
是模糊映象 , 且满足条件 ( ) : 存在函数 a: 一 [ ,] 0 1 使得对每一个 ∈X ,
D Lpc i 连续性和强单调性, —i ht s z 单值映象 Ⅳ的 ( , 口 一isht连续性 和 S关 于 Ⅳ的第 一 , )Lpci z 二变 量 的强 单调性 , 单值映象 日的 r强 一 一 单调性 , 和集值映象
H let 间 ,B X)与 2 i r空 b C( 分别 表示 的一切 非 空 有 界闭集 族 和 的非空 集族 , ・ ・ 是 C ) D( , ) B( 上 的 Hasof距离 . udr 设 是 上模糊 集族 , 映象 S : 一 取 )称为模 糊 映象. A = { ,, ,, 6 , 设 12 345,}
Vo . 1 31. No. 2
第3卷 l
第 2期
带模 糊映 象的新一 类广义混合 拟变分包含 的迭代算法
李红 刚 , 田有 先
( 重庆邮 电大学 应用数学研究所 , 重庆 4 0 6 ) 00 5
【国家自然科学基金】_任意banach空间_基金支持热词逐年推荐_【万方软件创新助手】_20140801
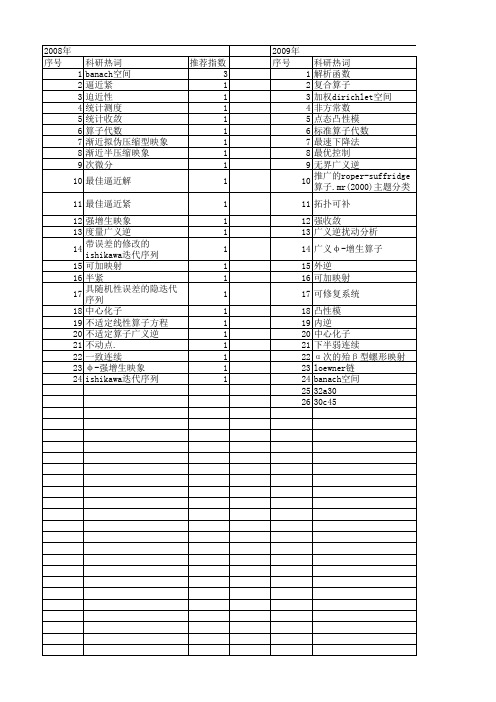
科研热词 推荐指数 banach空间 3 逼近紧 1 迫近性 1 统计测度 1 统计收敛 1 算子代数 1 渐近拟伪压缩型映象 1 渐近半压缩映象 1 次微分 1 最佳逼近解 1 最佳逼近紧 1 强增生映象 1 度量广义逆 1 带误差的修改的ishikawa迭代序列1 可加映射 1 半紧 1 具随机性误差的隐迭代序列 1 中心化子 1 不适定线性算子方程 1 不适定算子广义逆 1 不动点. 1 一致连续 1 φ -强增生映象 1 ishikawa迭代序列 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词 解析函数 复合算子 加权dirichlet空间 非方常数 点态凸性模 标准算子代数 最速下降法 最优控制 无界广义逆 推广的roper-suffridge算子.mr(2000)主题分 拓扑可补 强收敛 广义逆扰动分析 广义φ -增生算子 外逆 可加映射 可修复系统 凸性模 内逆 中心化子 下半弱连续 α 次的殆β 型螺形映射 loewner链 banach空间 32a30 30c45
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1
Hale Waihona Puke 2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
2011年 科研热词 推荐指数 非线性遍历定理 1 非常值多项式 1 逼近紧性 1 近可凹性 1 近严格凸性 1 谱 1 解析核 1 渐近非扩张型映射 1 渐近非扩张型半群 1 渐近φ -伪压缩映像 1 殆轨道 1 有界线性算子 1 度量投影算子 1 广义(ω 1)性质 1 广义(ω )性质 1 带误差修改的mann迭代 1 带误差修改的ishikawa迭代 1 巴拿赫空间 1 单值延拓性质 1 半群 1 任意banach空间 1 上半连续 1 一致lipschitz映像 1 opial条件 1 kk性质 1 banach空间 1
【浙江省自然科学基金】_变分_期刊发文热词逐年推荐_20140812
2009年 序号 1 2 3 4 5 6 7 8 9 10 14
科研热词 非扩张映射 非光滑 诸多方面 计算方法 算法效率 玻色-爱因斯坦凝聚 方法 数值 操控 技术 强收敛 山路引理 大气效应 地球 啁啾孤子 变分同化 变分不等式 公共不动点 严格伪压缩映射 α -逆强单调 p-laplacian gross-pitaevskii方程 gps掩星 clarke次微分
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
2011年 科研热词 近似解 变分迭代 非线性半变分不等式 非扩张映像 非光滑c-条件 闭凸集 等离子体 洛伦兹方程 洛仑兹方程 扰动 平衡问题 局部lipschitz函数 复合迭代算法 变分原理 发展方程 不动点 α -逆-强单调映像 推荐指数 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
科研热词 推荐指数 操控 2 孤子 2 非线性 1 钢带并联机器人 1 量点 1 邻域 1 视频修复 1 纹理合成 1 玻色.爱因斯坦凝聚 1 玻色-爱因斯坦凝聚 1 柔性手臂 1 有限元分析 1 整体变分 1 应变分 1 平衡态 1 孤波 1 失稳特性 1 圆弧弯曲截面 1 向异性 1 动力学 1 刚柔耦合 1 划痕 1 假设模态法 1 仿真 1 solitons 1 gross—pitaevskii方程 1 gross-pitaevskii方程 1 gross-pitaevskii equation 1 controlled manipulation 1 burgers系统 1 bose-einstein condensates 1
非线性方程组的迭代解法
4.2 非线性方程组的迭代解法 一、 一般概念1.非线性方程组的一般形式⎪⎪⎪⎩⎪⎪⎪⎨⎧===0),,,(0),,,(0),,,(21212211x x x fx x x f x x x f n nn n⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n x x x x 21令⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=)()()()(21x f x f x f x F n则向量形式如下:0)(=x F2.解非线性方程组的方法 (1)简单迭代法(2)线性化方法(即Newton 法)(3)求函数极小值的方法(即最速下降法) 二、简单迭代法RR nn x F →:)(把方程组:F (x )=0 改写成等价形式,即)19.4)((0)(x G x x F =⇔=适当选取初始向量D x ∈0,利用上述的等价形式,构成迭代公式:)20.4(,2,1,0),()()1( ==+k x G xk k其中G (x )为迭代函数 2.收敛性(1)非局部收敛定理(压缩映象原理)定理4.13 设G:R R nn D −→−⊂在闭区域D D⊂0上满足条件:(1)G 把D0映入自身, (2)G 在D0上是压缩映射,则有下列结论:(1)对任取的D x 0)0(∈,由迭代公式4.20产生的序列{}D x k 0)(∈,且收敛于方程组4.19在D0内的唯一解(2)成立误差估计式xxL x x L kk )0()1()(*1--≤- xx L xxk k kk L)1()()(*1---≤-下面给出简单迭代法(4.20)局部收敛定理定理4.14 设G:R R nn D −→−⊂,)int(*D x ∈是方程组4.19的解,G 在x *处可微。
若()xG *'的谱半径()()1*<'x G ρ,则存在开球{}D x x x D⊂<<-=0,*δδ,使对任意的D x0)0(∈,由迭代法4.20产生的序列{}D x k 0)(∈且收敛于x*。
注:(1)但是对于线性方程组来说,上述定理成为全局收敛性定理,而不是局部收敛性定理。
【国家自然科学基金】_弱收敛性_基金支持热词逐年推荐_【万方软件创新助手】_20140802
53 54 55 56 57 58 59 60 61 62 63 64 65
充分下降 修正的ncp函数 依概率收敛 伪单调 一致凸banach空间 wolfe-powell条件 opial's条件 n(o)rlund平均 kkt点 g-局部松弛强单 1 1 1 1 1 1 1 1 1 1 1
推荐指数 6 3 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 4 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
带误差的二阶隐迭代格式的收敛性
K为一个以£ 为系数的李普希兹算子 , 对任意给定 的U EK 以及实数 , 。 ,
旦兰[!3室 1
收稿 日期 :0 1— 5—2 21 0 0
二= ! 基生
) 男, , 辽宁省 交通 高等专科 学校教授 , 究方 向: 研 高等数 学及工程数学的应用研 究.
作者简 介 : 刘汝 臣(9 8 15
摘要 : 首先在 B nc aah空间 x 的 非 空 闭子 空 间上建 立 了一 类 由有 限具 公 共 李 普 希 兹
系数 的算 子集决 定 的带误 差的 二 阶隐迭 代格 式, 利用 压 缩 映像 原 理证 明 了该 二 阶 隐迭 代
格 式定义 的合理 性.其次 , 出 了该 二 阶隐迭代格 式 中各 个 点列 收敛 的 一个充 分 条件 , 给 其 结果 扩展及 推广 了一些 已有 的结 果.
希兹系数 的一个有限李普希兹算子集 , 满足 L>1 .定义集合 F ={ ∈K r , s i N , :, x= 1 }且假设
F≠ .假设数列 { } , } 。 { 是闭区间E ,]中的实序列 ,u } { } o1 { , 是 中的点列 , 并且 满足条件
1 准备知识
设 是 一个 以 l I l・l为范 数 的 B nc 间 , a ah空 是 的一个 非空 闭子空 间 , } 。 定义 在 上具 有 { 是 公 共 的李 普 希兹 系数 的一个 有 限李普 希兹算 子集 , 足 L >1 义集 合 F : { ∈K: 满 .定 = ,s 1
( . )及 12
∑ ( 一 +。 ∑LI < ∞, I< ∞ 1 a)< a, l + ∑L I l + l l u l
la .=1 i ̄ r
(.) 21
