2020年深圳中考5套红卷-第4套-数学答案及评分标准
2020深圳中考数学模拟试卷(含答案)最新

B2020深圳中考数学模拟试卷1.下列实数中,32-的倒数是 ( )A .32B .23C .32-3± D .23-2.刚刚过去的2017年,深圳经济成绩亮眼,全市GDP 超过2.2万亿元人民币,同比增长约8.8%,赶超香港已成事实。
数据“2.2万亿”用科学记数法表示为 ( ) A .130.2210⨯ B .122.210⨯C .112.210⨯D .132210⨯ 3.下列美丽的图案中,不是轴对称图形的是( )A B C D 4.下列运算正确的是 ( ) A .426a a a += B .2363()x y x y =C .222()m n m n -=-D .623b b b ÷=5.小明是一位运动达人,他通过佩戴智能手环来记录自己一个月(30天)每天所走的步数,并绘制成如下统计表:在每天所走的步数这组数据中,众数和中位数分别是 ( ) A .1.6,1.5 B .1.7,1.55, C .1.7,1.7 D .1.7,1.6 6.如图所示,在□ABCD 中,已知AC =4cm ,若△ACD 的周长为13cm ,则平行四边形的周长为 ( )A .18cmB .20cmC .24cmD .26c7.如图,是由若干个大小相同的小正方体组合而成的几何体,那么其三种视图中面积最大的是( A .主视图 B .俯视图 C .左视图 D .一样大 8.下列命题中正确的是( )A .两条直线被第三条直线所截,内错角相等B .平行四边形对角线相等C .三角形的外心到三角形三个顶点的距离相等D .对角线互相垂直的四边形是菱形 9.如图,△ABC 中,∠BAC =90°,AB =5,AC =10。
分别以点B 和点C 为圆心,大于12BC 径作弧,两弧相交于D 、E 两点,连接DE 交BC 于点H ,连接AH ,则AH的长为( ) A .5B.C.2D .10.某畅销书的售价为每本30元,每星期可卖出200本,书城准备开展“读书节活动”调查,如果调整书籍的售价,每降价2元,每星期可多卖出40本。
2020年深圳中考5套红卷-第三套-2020年深圳英语红卷

83 元,扫码付完款后发现余钱剩 3 元,设 A 型号的钢笔每支售价为 x 元,根据题意可列
出的方程为
A. 50 30 x x5
B. 50 33 x x5
C. 30 50 x x5
D. 50 30 x x5
11.如图,抛物线 y=ax2+bx+c 与 x 轴交于点 A(﹣1,0),顶点坐标(1,n),则下列结论:
D.6064
9.如图,CE 是∠ACD 的平分线,CD∥AB,,DE⊥CE,若∠DEB=32°,
则∠A 的度数为 A.62°
B.64°
C.68°
D.70°
10.某商店出售 A,B 两种型号的钢笔,已知 A 型号的钢笔比 B 型号的钢笔贵 5 元,小红用 50
元买了 A 型号的钢笔,用若干元买了相同数量 B 型号的钢笔,小红手机微信里的余钱共有
A. 6
B. 1 6
C. 1 6
2.下列美丽的图案,是中心对称图形但不是轴对称图形的是(
D.6 )
A.
B.
C.
3.将 0.2×450×105 的计算结果用科学记数法表示,其正确的是
A.9×106
B.90×105
C.0.9×107
D. D.900×104
4.如图,是一个正方体的表面展开图,则原正方体中与“功”字所在的面相对的面上标的
①ab<0;②8a+c<0;③4a+b<0;
④一元二次方程 ax2+(b+2)x+c=n+2x 有两个相等的实数根,
其中正确的有
A.1 个
B.2 个
C.3 个
D.4 个
12.如图,正方形 ABCD 边长为 2,BM、DN 分别是正方形的两个外角的平分线,点 P,Q
2020最新深圳中考数学模拟试卷5
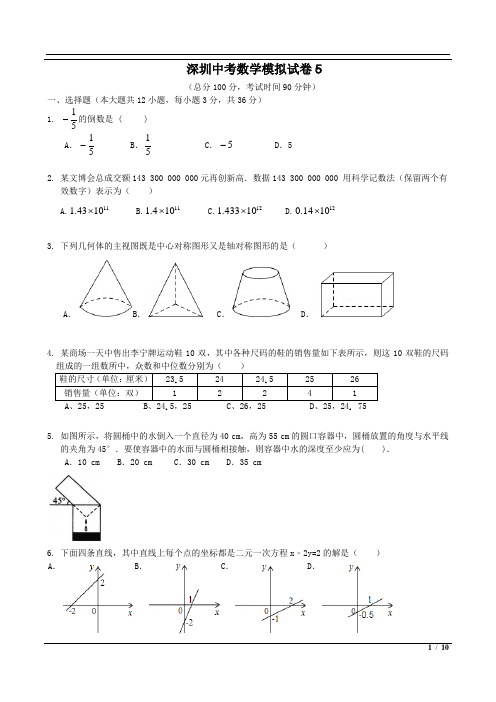
深圳中考数学模拟试卷5(总分100分,考试时间90分钟)一、选择题(本大题共12小题,每小题3分,共36分) 1. 的倒数是 ( ) A . B .C .D .52. 某文博会总成交额143 300 000 000元再创新高.数据143 300 000 000 用科学记数法(保留两个有 效数字)表示为( )A.111043.1⨯ B.11104.1⨯ C.1210433.1⨯ D.121014.0⨯3. 下列几何体的主视图既是中心对称图形又是轴对称图形的是( )A .B .C .D .4. 某商场一天中售出李宁牌运动鞋10双,其中各种尺码的鞋的销售量如下表所示,则这10双鞋的尺码A 、25,25B 、24.5,25C 、26,25 D 、25,24. 755. 如图所示,将圆桶中的水倒入一个直径为40 cm ,高为55 cm 的圆口容器中,圆桶放置的角度与水平线的夹角为45°.要使容器中的水面与圆桶相接触,则容器中水的深度至少应为( ). A .10 cm B .20 cm C .30 cm D .35 cm6. 下面四条直线,其中直线上每个点的坐标都是二元一次方程x ﹣2y=2的解是( ) A . B .C .D .51-51-515-7. 如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于()A.50°B.60°C.65°D.90°8. 希望中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是()A.被调查的学生有200人B.被调查的学生中喜欢教师职业的有40人C.被调查的学生中喜欢其他职业的占40%D.扇形图中,公务员部分所对应的圆心角为72°9. 下列命题,假命题是()A.平行四边形的两组对边分别相等B.两组对边分别相等的四边形是平行四边形C.矩形的对角线相等D.对角线相等的四边形是矩形10. 如图,⊙O1,⊙O,⊙O2的半径均为2cm,⊙O3,⊙O4的半径均为1cm,⊙O与其他4个圆均相外切,图形既关于O1O2所在直线对称,又关于O3O4所在直线对称,则四边形O1O4O2O3的面积为A.12cm2B.24cm2C.36cm2D.48cm2(第10题图)2/ 1011. 如图,将矩形ABCD 沿AE 折叠,点D 的对应点落在BC 上点F 处,过点F 作FG ∥CD ,连接EF ,DG ,下列结论中正确的有( )①∠ADG=∠AFG ;②四边形DEFG 是菱形;③DG 2=AE•EG;④若AB=4,AD=5,则CE=1.A .①②③④B .①②③C .①③④D .①②12. 已知二次函数2y ax bx c =++(a ≠0)的图象如图所示,有下列5个结论:①abc >0;②b <a+c ;③4a+2b+c >0;④2c <3b ;⑤a+b >m(am+b),(m ≠l 的实数).其中正确的结论有( )个.A .2个B .3个C .4个D .5个二、填空题(本大题共4小题,每小题3分,共12分) 13.分解因式:x xy xy +-22=14.某池塘里养了鱼苗10万条,根据这几年的经验知道,鱼苗成活率为95%,一段时间准备打捞出售,第一网捞出40条,称得平均每条鱼重2.5千克,第二网捞出25条,称的平均每条鱼重2.2千克,第三网捞出35条,称的平均每条鱼重2.8千克,试估计这池塘中鱼的重量为 千克。
2020年深圳中考5套红卷-第二套

B. ①②
C. ②④
D. ①③
图5
第二部分 非选择题
二.填空题(本大题共 4 小题,每小题 3 分,共 12 分)
13. 因式分解: a3 16a = ▲
.
14.
化简
a
a
b
b
b
a
2(a a2
b)2 b2
的结果是
▲
.
15. 如图 6,⊙O 的半径为 6,点 P 是⊙O 直径 AB 延长线上的一点, PT 切⊙O 于点 T,M 是 OP 的中点,射线 TM 与⊙O 交于点 C.
(2)(3 分)随着 P 点的运动,BD 的长是否会发生变化?若变化,请说明理由,若不变,请你求出 BD 的长;
(3)(3 分)如图 11-2,取 PB 中点 M,连接 DM,则 DM 的最大值为多少?请你直接写出来.
P
l
M AD N
O C
B
图 11-2
23.(9 分)如图 12,抛物线 y ax2 bx c 经过 A(2,0),B(6,0),C(0,-4)三点,一条长为 4 的
同学了解相关情况,请用列表或画树状图的方法求出选中小明的概率.
2020 深圳市中考 5 套红卷 数学试卷(第 2 套) 第 4 页(共 6 页)
20.(8 分)如图 9,等腰ΔABC 中,AB=AC,射线 CD 垂直于 BC,以点 A 为圆心,BC 为半径画弧,交射 线 CD 于点 D,连结 AD 交 BC 于点 E.
若 P 50 ,则图中阴影部分的面积为 ▲ .
图6
2020 深圳市中考 5 套红卷 数学试卷(第 2 套) 第 3 页(共 6 页)
16. 如图 7,在△ABC 中,AB=AC,延长 AB 到 D,使 BD=2AB,延长 BC 到 E,使 EC=BC,连接 ED.若
2020年深圳市中考数学模拟试卷(4)

2020年深圳市中考数学模拟试卷(4)一.选择题(共12小题,满分36分,每小题3分) 1.(3分)247的倒数是( )A .274B .187C .718D .782.(3分)下列图形中既是中心对称图形又是轴对称图形的是( )A .B .C .D .3.(3分)已知空气的单位体积质量为1.24×10﹣3克/厘米3,1.24×10﹣3用小数表示为( ) A .0.000124B .0.0124C .﹣0.00124D .0.001244.(3分)如图是一个正方体展开图,把展开图折叠成正方体后“抗”字一面相对面上的字是( )A .新B .冠C .病D .毒5.(3分)下列计算正确的是( ) A .a 3•a 2=a 6B .a 2+a 4=2a 2C .(3a 3)2=9a 6D .(3a 2)3=9a 66.(3分)如图,AC ∥BD ,AD 与BC 相交于O ,∠A =45°,∠B =30°,那么∠AOB 等于( )A .75°B .60°C .45°D .30°7.(3分)某鞋厂为了了解初中生穿鞋的尺码情况,对某中学八年级(2)班的20名男生进行了调查,统计结果如下表:则这20个数据的中位数和众数分别为( ) 尺码 37 38 39 40 41 42 人数344711A .4和7B .40和7C .39和40D .39.1和398.(3分)如图,在Rt △ABC 中,∠C =90°,AD 是角平分线,若BC =10cm ,BD :CD =3:2,则点D 到AB 的距离是( )A .6cmB .5cmC .4cmD .3cm9.(3分)二次函数y =﹣ax 2+a 与反比例函数y =ax的图象大致是( )A .B .C .D .10.(3分)下列说法中错误的是( )A .两组对边分别相等的四边形一定是平行四边形B .有三个角是直角的四边形一定是矩形C .有一组邻边相等的平行四边形一定是菱形D .对角线相等的四边形一定是正方形 11.(3分)给定一列按规律排列的数:1,34,59,716,…,则第n (n ≥1)个数为( )A .n 2−1n 2B .2n n 2C .2n−1n 2D .2n+1n 212.(3分)二次函数y =(x ﹣1)2﹣5的最小值是( ) A .1B .﹣1C .5D .﹣5二.填空题(共4小题,满分12分,每小题3分)13.(3分)把多项式x 2y ﹣6xy +9y 分解因式的结果是 .14.(3分)一个不透明盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是 . 15.(3分)如图,将边长为6的正方形ABCD 折叠,使点D 落在AB 边的中点E 处,折痕为FH ,点C 落在点Q 处,EQ 与BC 交于点G ,则△EBG 的周长是 cm .16.(3分)如图,已知直线y =﹣x +2分别与x 轴,y 轴交于A ,B 两点,与双曲线y =kx 交于E ,F 两点,若AB =2EF ,则k 的值是 .三.解答题(共7小题,满分52分)17.(5分)计算:(13)﹣1﹣|−√3|+3tan60°﹣(π﹣2020)0.18.(6分)先化简,再求值:x−1x+2•x 2−4x −2x+1,其中|x |=2.19.(7分)某品牌牛奶供应商提供A ,B ,C ,D 四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图. 根据统计图的信息解决下列问题:(1)本次调查的学生有多少人?(2)补全上面的条形统计图;(3)扇形统计图中C对应的中心角度数是;(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?20.(8分)如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E.(1)求证:BE2=EG•EA;(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.21.(8分)桃花中学计划购买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比买一块B型小黑板多20元,且购买5块A型小黑板和4块B型小黑板共需820元.(1)求购买一块A型小黑板和一块B型小黑板各需要多少元?(2)根据学校的实际情况,需购买A、B两种型号的小黑板共60块,并且购买A型小黑板的数量不少于购买B型小黑板的数量,请问学校购买这批小黑板最少要多少元?22.(9分)如图,直线y=−12x−3与x轴,y轴分别交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴的另一个交点为点B(2,0),点D是抛物线上一点,过点D作DE ⊥x轴于点E,连接AD,DC.设点D的横坐标为m.(1)求抛物线的解析式;(2)当点D在第三象限,设△DAC的面积为S,求S与m的函数关系式,并求出S的最大值及此时点D的坐标;(3)连接BC,若∠EAD=∠OBC,请直接写出此时点D的坐标.23.(9分)定义:在平面直角坐标系xOy中,对于点P和图形M,如果线段OP与图形M 有公共点时,就称点P为关于图形M的“亲近点”.已知平面直角坐标系xOy中,点A(1,√3),B(5,√3),连接AB.(1)在P1(1,2),P2(3,2),P3(5,2)这三个点中,关于线段AB的“亲近点”是;(2)若线段CD上的所有点都是关于线段AB的“亲近点”,点C(t,2√3t−3√3)、D (t+6,2√3t−3√3),求实数t的取值范围;(3)若⊙A与y轴相切,直线l:y=−√3x+b过点B,点E是直线l上的动点,⊙E半径为2,当⊙E上所有点都是关于⊙A的“亲近点”时,直接写出点E横坐标n的取值范围.2020年深圳市中考数学模拟试卷(4)参考答案与试题解析一.选择题(共12小题,满分36分,每小题3分) 1.(3分)247的倒数是( )A .274B .187C .718D .78【解答】解:247=187,187的倒数是718,故选:C .2.(3分)下列图形中既是中心对称图形又是轴对称图形的是( )A .B .C .D .【解答】解:A 、是轴对称图形,不是中心对称图形,故此选项错误; B 、是轴对称图形,是中心对称图形,故此选项正确; C 、是轴对称图形,不是中心对称图形,故此选项错误; D 、是轴对称图形,不是中心对称图形,故此选项错误; 故选:B .3.(3分)已知空气的单位体积质量为1.24×10﹣3克/厘米3,1.24×10﹣3用小数表示为( ) A .0.000124B .0.0124C .﹣0.00124D .0.00124【解答】解:把数据“1.24×10﹣3中1.24的小数点向左移动3位就可以得到为0.001 24.故选D .4.(3分)如图是一个正方体展开图,把展开图折叠成正方体后“抗”字一面相对面上的字是( )A.新B.冠C.病D.毒【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“抗”字一面相对面上的字是“病”,故选:C.5.(3分)下列计算正确的是()A.a3•a2=a6B.a2+a4=2a2C.(3a3)2=9a6D.(3a2)3=9a6【解答】解:A.a3•a2=a5,故本选项不合题意;B.a2与a4不是同类项,所以不能合并,故本选项不合题意;C.(3a3)2=9a6,正确,故本选项符合题意;D.(3a2)3=27a6,故本选项不合题意.故选:C.6.(3分)如图,AC∥BD,AD与BC相交于O,∠A=45°,∠B=30°,那么∠AOB等于()A.75°B.60°C.45°D.30°【解答】解:∵AC∥BD,∠B=30°,∴∠B=∠C=30°,又∵∠A=45°,∴∠AOB=∠A+∠C=45°+30°=75°;故选:A.7.(3分)某鞋厂为了了解初中生穿鞋的尺码情况,对某中学八年级(2)班的20名男生进行了调查,统计结果如下表:则这20个数据的中位数和众数分别为()尺码373839404142人数344711A.4和7B.40和7C.39和40D.39.1和39【解答】解:观察图表可知:有7人的鞋号为40,人数最多,即众数是40;中位数是第10、11人的平均数,即39;故选:C.8.(3分)如图,在Rt△ABC中,∠C=90°,AD是角平分线,若BC=10cm,BD:CD=3:2,则点D到AB的距离是()A.6cm B.5cm C.4cm D.3cm【解答】解:∵BC=10cm,BD:CD=3:2,∴CD=25×10=4,∵AD是角平分线,∴点D到AB的距离等于CD,即点D到AB的距离为4cm.故选:C.9.(3分)二次函数y=﹣ax2+a与反比例函数y=ax的图象大致是()A.B.C.D.【解答】解:当a >0时,抛物线开口向下,与y 轴交于正半轴,双曲线位于一、三象限,故C 、D 图象错误;当a <0时,抛物线开口向上,与y 轴交于负半轴,双曲线位于二、四象限,故B 图象错误,A 图象正确. 故选:A .10.(3分)下列说法中错误的是( )A .两组对边分别相等的四边形一定是平行四边形B .有三个角是直角的四边形一定是矩形C .有一组邻边相等的平行四边形一定是菱形D .对角线相等的四边形一定是正方形【解答】解:A 、两组对边分别相等的四边形一定是平行四边形,正确; B 、有三个角是直角的四边形一定是矩形,正确; C 、有一组邻边相等的平行四边形一定是菱形,正确; D 、对角线相等、平分、垂直的四边形一定是正方形,错误; 故选:D .11.(3分)给定一列按规律排列的数:1,34,59,716,…,则第n (n ≥1)个数为( )A .n 2−1n 2B .2n n2C .2n−1n 2D .2n+1n 2【解答】解:由已知观察可得,分母是自然数1,2,3,…,n 的平方,分子是正奇数, 则第n 个数是2n−1n ,故选:C .12.(3分)二次函数y =(x ﹣1)2﹣5的最小值是( ) A .1B .﹣1C .5D .﹣5【解答】解:二次函数y =(x ﹣1)2﹣5的最小值是﹣5. 故选:D .二.填空题(共4小题,满分12分,每小题3分)13.(3分)把多项式x 2y ﹣6xy +9y 分解因式的结果是 y (x ﹣3)2 . 【解答】解:原式=y (x 2﹣6x +9)=y (x ﹣3)2, 故答案为:y (x ﹣3)214.(3分)一个不透明盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是 16.【解答】解:画树状图得:∵共有12种等可能的结果,两次都摸到白球的有2种情况, ∴两次都摸到白球的概率是:212=16故答案为:16.15.(3分)如图,将边长为6的正方形ABCD 折叠,使点D 落在AB 边的中点E 处,折痕为FH ,点C 落在点Q 处,EQ 与BC 交于点G ,则△EBG 的周长是 12 cm .【解答】解:由翻折的性质得,DF =EF , 设EF =x ,则AF =6﹣x , ∵点E 是AB 的中点, ∴AE =BE =12×6=3,在Rt △AEF 中,AE 2+AF 2=EF 2, 即32+(6﹣x )2=x 2, 解得x =154, ∴AF =6−154=94, ∵∠FEG =∠D =90°, ∴∠AEF +∠BEG =90°, ∵∠AEF +∠AFE =90°, ∴∠AFE =∠BEG ,又∵∠A =∠B =90°,∴△AEF ∽△BGE ,∴BE AF=BG AE =EG EF , 即394=BG 3=EG 154,解得BG =4,EG =5,∴△EBG 的周长=3+4+5=12.故答案为:12.16.(3分)如图,已知直线y =﹣x +2分别与x 轴,y 轴交于A ,B 两点,与双曲线y =k x 交于E ,F 两点,若AB =2EF ,则k 的值是 34 .【解答】解:作FH ⊥x 轴,EC ⊥y 轴,FH 与EC 交于D ,如图,由直线y =﹣x +2可知A 点坐标为(2,0),B 点坐标为(0,2),OA =OB =2,∴△AOB 为等腰直角三角形,∴AB =2√2,∴EF =12AB =√2,∴△DEF 为等腰直角三角形,∴FD =DE =√22EF =1,设F 点横坐标为t ,代入y =﹣x +2,则纵坐标是﹣t +2,则F 的坐标是:(t ,﹣t +2),E 点坐标为(t +1,﹣t +1),∴t (﹣t +2)=(t +1)•(﹣t +1),解得t =12,∴E 点坐标为(32,12), ∴k =32×12=34.故答案为34.三.解答题(共7小题,满分52分)17.(5分)计算:(13)﹣1﹣|−√3|+3tan60°﹣(π﹣2020)0. 【解答】解:原式=3−√3+3√3−1=2+2√318.(6分)先化简,再求值:x−1x+2•x 2−4x 2−2x+1,其中|x |=2.【解答】解:原式=x−1x+2•(x+2)(x−2)(x−1)2 =x−2x−1. 当x =2时,原式=2−22−1=0. 19.(7分)某品牌牛奶供应商提供A ,B ,C ,D 四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:(1)本次调查的学生有多少人?(2)补全上面的条形统计图;(3)扇形统计图中C 对应的中心角度数是 144° ;(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A ,B 口味的牛奶共约多少盒?【解答】解:(1)本次调查的学生有30÷20%=150人;(2)C 类别人数为150﹣(30+45+15)=60人,补全条形图如下:(3)扇形统计图中C 对应的中心角度数是360°×60150=144°故答案为:144°(4)600×(45+30150)=300(人),答:该牛奶供应商送往该校的牛奶中,A ,B 口味的牛奶共约300盒.20.(8分)如图,已知矩形ABCD 的两条对角线相交于点O ,过点A 作AG ⊥BD 分别交BD 、BC 于点G 、E .(1)求证:BE 2=EG •EA ;(2)连接CG ,若BE =CE ,求证:∠ECG =∠EAC .【解答】证明:(1)∵四边形ABCD 是矩形,∴∠ABC =90°,∵AE ⊥BD ,∴∠ABC =∠BGE =90°,∵∠BEG =∠AEB ,∴△ABE ∽△BGE ,∴AE BE =BE EG ,∴BE 2=EG •EA ;(2)由(1)证得BE 2=EG •EA ,∵BE =CE ,∴CE 2=EG •EA ,∴CE EG =AE CE ,∵∠CEG =∠AEC ,∴△CEG ∽△AEC ,∴∠ECG =∠EAC .21.(8分)桃花中学计划购买A 、B 两种型号的小黑板,经洽谈,购买一块A 型小黑板比买一块B 型小黑板多20元,且购买5块A 型小黑板和4块B 型小黑板共需820元.(1)求购买一块A 型小黑板和一块B 型小黑板各需要多少元?(2)根据学校的实际情况,需购买A 、B 两种型号的小黑板共60块,并且购买A 型小黑板的数量不少于购买B 型小黑板的数量,请问学校购买这批小黑板最少要多少元?【解答】解:(1)设A 型小黑板x 元/块,B 型小黑板y 元/块,{x −y =205x +4y =820, 解得,{x =100y =80, 答:A 型小黑板100元/块,B 型小黑板80元/块;(2)设购买A 型小黑板a 块,学校购买这批小黑板共需m 元,a ≥60﹣a ,解得,a ≥30,m =100a +80(60﹣a )=20a +4800,∵m 随着a 的增大而增大,∴a =30时,m 有最小值为5400,答:学校购买这批小黑板最少要5400元.22.(9分)如图,直线y =−12x −3与x 轴,y 轴分别交于点A ,C ,经过点A ,C 的抛物线y =ax 2+bx ﹣3与x 轴的另一个交点为点B (2,0),点D 是抛物线上一点,过点D 作DE ⊥x 轴于点E ,连接AD ,DC .设点D 的横坐标为m .(1)求抛物线的解析式;(2)当点D 在第三象限,设△DAC 的面积为S ,求S 与m 的函数关系式,并求出S 的最大值及此时点D 的坐标;(3)连接BC ,若∠EAD =∠OBC ,请直接写出此时点D 的坐标.【解答】解:(1)在y =−12x ﹣3中,当y =0时,x =﹣6,即点A 的坐标为:(﹣6,0),将A (﹣6,0),B (2,0)代入y =ax 2+bx ﹣3得:{36a −6b −3=04a +2b −3=0, 解得:{a =14b =1, ∴抛物线的解析式为:y =14x 2+x ﹣3;(2)设点D 的坐标为:(m ,14m 2+m ﹣3),设DE 交AC 于F ,则点F 的坐标为:(m ,−12m ﹣3),∴DF =−12m ﹣3﹣(14m 2+m ﹣3)=−14m 2−32m , ∴S △ADC =S △ADF +S △DFC=12DF •AE +12•DF •OE=12DF •OA=12×(−14m 2−32m )×6=−34m 2−92m=−34(m +3)2+274, ∵a =−34<0, ∴抛物线开口向下,∴当m =﹣3时,S △ADC 存在最大值274, 又∵当m =﹣3时,14m 2+m ﹣3=−154, ∴存在点D (﹣3,−154),使得△ADC 的面积最大,最大值为274;(3)①当点D 与点C 关于对称轴对称时,D (﹣4,﹣3),根据对称性此时∠EAD =∠ABC .②作点D (﹣4,﹣3)关于x 轴的对称点D ′(﹣4,3),直线AD ′的解析式为y =32x +9,由{y =32x +9y =14x 2+x −3,解得{x =−6y =0或{x =8y =21, 此时直线AD ′与抛物线交于D (8,21),满足条件,综上所述,满足条件的点D 坐标为(﹣4,﹣3)或(8,21)23.(9分)定义:在平面直角坐标系xOy 中,对于点P 和图形M ,如果线段OP 与图形M有公共点时,就称点P 为关于图形M 的“亲近点”.已知平面直角坐标系xOy 中,点A (1,√3),B (5,√3),连接AB .(1)在P 1(1,2),P 2(3,2),P 3(5,2)这三个点中,关于线段AB 的“亲近点”是 P 2和P 3 ;(2)若线段CD 上的所有点都是关于线段AB 的“亲近点”,点C (t ,2√3t −3√3)、D(t +6,2√3t −3√3),求实数t 的取值范围;(3)若⊙A 与y 轴相切,直线l :y =−√3x +b 过点B ,点E 是直线l 上的动点,⊙E 半径为2,当⊙E 上所有点都是关于⊙A 的“亲近点”时,直接写出点E 横坐标n 的取值范围.【解答】解:(1)如图1:由“亲近点”的定义可以判断OP 2与OP 3与AB 线段有公共点,∴线段AB 的“亲近点”是P 2与P 3,故答案为P 2和P 3;(2)线段CD 上的所有点都是关于线段AB 的“亲近点”,∵t +6>t ,∴O 、A 、C 在一条直线上,O 、B 、D 在一条直线上,此时线段CD 上的所有点都是关于线段AB 的“亲近点”,∴√3=2√3t−3√3t, ∴t =3,∴√35=2√3t−3√36+t, ∴t =73,∴73≤t ≤3; (3)y =−√3x +b 过点B ,∴b =6√3,∴y =−√3x +6√3,如图2:过原点的直线与⊙A 相切于点F ,连接OA ,过点A 作AG ⊥x 轴,∵OA=2,AF=1,∴∠AOF=30°,∵AG=√3,OG=1,∴∠AOG=60°,∴∠FOG=30°,当⊙E与⊙A的切线相切时,⊙E上所有点都是关于⊙A的“亲近点”,∴OP⊥PE,∵Q(6,0),∴PQ=3,∵⊙E的半径PE=2,∴EQ=5,∴E点横坐标n=6−52=72;如图3:当⊙E与y轴相切时,⊙E上所有点都是关于⊙A的“亲近点”,∴E点横坐标n=2,∴2≤n≤7 2;。
2020年广东省深圳中考数学试卷含答案
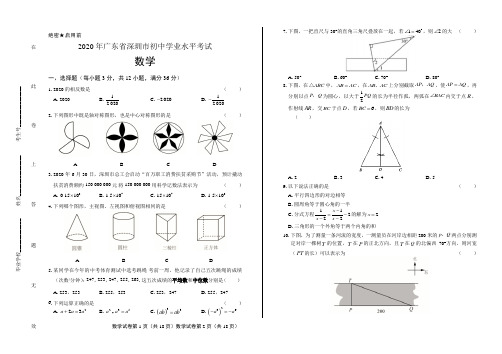
数学试卷第1页(共18页)数学试卷第2页(共18页)绝密★启用前2020年广东省深圳市初中学业水平考试数学一、选择题(每小题3分,共12小题,满分36分)1.2020的相反数是( )A .2020B .12020C .2020-D .12020- 2.下列图形中既是轴对称图形,也是中心对称图形的是( )ABCD3.2020年6月30日,深圳市总工会启动“百万职工消费扶贫采购节”活动,预计撬动扶贫消费额约150 000 000元.将150 000 000用科学记数法表示为( )A .80.1510⨯B .71.510⨯C .71510⨯D .81.510⨯ 4.下列哪个图形,主视图、左视图和俯视图相同的是( )ABCD5.某同学在今年的中考体育测试中选考跳绳.考前一周,他记录了自己五次跳绳的成绩(次数/分钟):247,253,247,255,263.这五次成绩的平均数...和中位数...分别是( ) A .253,253B .255,253C .253,247D .255,247 6.下列运算正确的是( )A .223a a a +=B .235a a a =C .()33ab ab =D .()236a a -=-7.下图,一把直尺与30°的直角三角尺叠放在一起,若°140∠=,则2∠的大 ( )A .50°B .60°C .70°D .80°8.下图,在ABC △中,AB AC =,在AB AC 、上分别截取AP AQ ,,使AP AQ =,再分别以点P Q ,为圆心,以大于12PQ 的长为半径作弧,两弧在BAC ∠内交于点R ,作射线AR ,交BC 于点D ,若6BC =,则BD 的长为( )A .2B .3C .4D .5 9.以下说法正确的是( )A .平行四边形的对边相等B .圆周角等于圆心角的一半C .分式方程11222x x x -=---的解为2x =D .三角形的一个外角等于两个内角的和10.下图,为了测量一条河流的宽度,一测量员在河岸边相距200米的p Q 、两点分别测定对岸一棵树T 的位置,T 在P 的正北方向,且T 在Q 的北偏西70°方向,则河宽(PT 的长)可以表示为 ( )毕业学校_____________ 姓名________________ 考生号________________________________ _____________-------------在------------------此------------------卷------------------上-------------------答-------------------题-------------------无-------------------效----------------数学试卷第3页(共18页)数学试卷第4页(共18页)A .°200tan70米B .°200tan 70米 C .°200sin70米 D .°200sin70米 11.二次函数()20y ax bx c a =++≠的顶点坐标为()1n -,,其部分图象如下图所示,以下结论错误..的是( )A .0abc >B .240ac b -<C .30a c +>D .关于x 的方程21ax bx c n ++=+无实数根12.下图,矩形纸片ABCD 中,612AB BC ==,,将纸片折叠,使点B 落在边AD 的延长线上的点G 处,折痕为EF ,点E F 、分别在边AD 和边BC 上.连接BG ,交CD 于点K ,FG 交CD 于点H .给出以下结论:①EF BG ⊥;②GE GF =;③GDK △和GKH △的面积相等;④当点F 与点C 重合时,°75DEF ∠=,其中正确..的结论共有 ( ) A .1个B .2个C .3个D .4个第二部分非选择题二、填空题(本题共4小题,每小题3分,共12分)13.分解因式:3m m -=________.14.一口袋内装有编号分别为1,2,3,4,5,6,7的七个球(除编号外都相同),从中随机摸出一个球,则摸出编号为偶数的球的概率是________.15.下图,在平面直角坐标系中,()()()003112O A B ,,,,,,反比例函数()0ky k x=≠的图象经过OABC 的顶点C ,则K =_______.16.下图,在四边形ABCD ,AC 与BD 相交于点O ,°90ABC DAC ∠=∠=,14tan 23BO ACB OD ∠==,,则ABD CBD S S △△=________.三、解答题(本题共7小题,共52分)17.(5分)计算:()10°12cos304π3-⎛⎫-+-- ⎪⎝⎭.18.(6分)先化简,再求值:2132211a a a a a +-⎛⎫++ ⎪-+-⎝⎭,其中2a =.19.(7分)以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调査了m 名新聘毕业生的专业情况,并将调查结果绘制成如下两幅不完整的统计图.请根据统计图提供的信息,解答下列问题.测试n %软件硬件40%总线30%数学试卷第5页(共18页)数学试卷第6页(共18页)(1)m =________,n =________; (2)请补全条形统计图;(3)在扇形统计图中,“软件”所对应的扇形的圆心角是________度;(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有________名. 20.(8分)如图,AB 为O 的直径,点C 在O 上,AD 与过点C 的切线互相垂直,垂足为D .连接BC 并延长,交AD 的延长线于点E .(1)求证:AE AB =;(2)若106AB BC ==,,求CD 的长.21.(8分)端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.(1)肉粽和蜜枣粽的进货单价分别是多少元?(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?22.(9分)背景:一次小组合作探究课上,小明将两个正方形按右图所示的位置摆放(点E A D 、、在同一条直线上),发现BE DG =且BE DG ⊥.小组讨论后,提出了三个问题,请你帮助解答:(1)将正方形AEFG 绕点A 按逆时针方向旋转,(如图1)还能得到BE DG =吗?若能,请给出证明;若不能,请说明理由;(2)把背景中的正方形分别改为菱形AEFG 和菱形ABCD ,将菱形AEFG 绕点A 按顺时针方向旋转,(如图2)试问当EAG ∠与BAD ∠的大小满足怎样的关系时,背景中的结论BE DG =仍成立?请说明理由;(3)把背景中的正方形分别改成矩形AEFG 和矩形ABCD 且,23AE AB AG AD ==,48AE AB ==,,将矩形AEFG 绕点A 按顺时针方向旋转(如图3),连接DE ,BG .小组发现:在旋转过程中,22DE BG +的值是定值,请求出这个定值.23.(9分)如图1,抛物线()230y ax bx a =+≠与x 轴交于()30A -,和()10B ,,与y 轴交于点C ,顶点为D . (1)求解抛物线解析式(2)连接AD DC CB ,,,将OBC △沿x 轴以每秒1个单位长度的速度向左平移,得到O B C '''△,点O B C 、、的对应点分别为点O B C '''、、,设平移时间为t 秒,当点O '与点A 重合时停止移动。
2020年深圳市中考总复习数学试卷五(含答案和解析)
2020年深圳市中考总复习数学试卷五一、选择题(本部分共12小题,每小题3分,共36分,每小题给出4个选项,其中只有一个是正确的) 1. 绝对值为5的实数是( )A .5±B .5C .5- D. 512.环境监测中PM 2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.数据0.0000025用科学记数法可以表示为( ) A .6105.2⨯ B .5105.2-⨯ C .6105.2-⨯ D .7105.2-⨯3.如图,下面是由四个完全相同的正方体组成的几何体,这个几何体的主视图是( )A .B .C .D .4.下列计算正确的是( )A .325a a a +=B .222(3)9a b a b -=-C .3226()ab a b -= D .623a b a a b ÷=5. 某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误..的是( ) A. 众数是80 B. 中位数是75 C .平均数是80 D. 极差是156.函数中,自变量x 的取值范围是( )A . x >1B . x <1C .51-≥xD .51≥x 7.如图,AB ∥CD ,∠ABE =60°,∠D =50°,则∠E 的度数为( )A .︒30B .︒20C .︒10D . ︒408.某工厂生产一种零件,计划在20天内完成,若每天多生产4个,则15天完成且还多生产10个.设原计划每天生产x 个,根据题意可列分式方程为( ) A . B . C . D .9.某市今年中考体育测试,其中男生测试项目有200米跑、1000米跑、立定跳远、投掷实心球、一分钟跳绳、引体向上、篮球半场来回运球上篮七个项目.考生须从这七个项目中选取两个项目,其中200米跑必选,剩下六个项目选一个,则两名男生在体育测试中所选项目完全相同的概率为( ) A .71 B .61 C .51 D .4110.如右图1,在矩形MNPQ 中,动点R 从点N 出发,沿N →P →Q →M 方向运动至点M 处停止.设点R 运动的路程为x ,图中阴影部分MNR △的面积为y ,如果y 关于x 的函数图象如图2所示,则矩形PQMN 的面积为( ) A .16 B .20 C .36 D .4511.以下说法正确的有( )①正八边形的每个内角都是135°; ②反比例函数y =﹣,当x <0时,y 随x 的增大而增大; ③长度等于半径的弦所对的圆周角为30°; ④分式方程13x 1=x x -的解为2x=3; A . 1个 B . 2个 C . 3个 D . 4个12.如右图,在平面直角坐标系中,直线y =﹣3x +3与x 轴、y 轴分别交于A 、B 两点, 以AB 为边在第一象限作正方形ABCD ,点D 在双曲线(k ≠0)上.将正方形沿x 轴负方向平移a 个单位长度后,点C 恰好落在该双曲线上,则a 的值是( )A .1B .2C .3D .4第二部分 非选择题二、填空题(本题共4小题,每小题3分,共12分) 13.分解因式:269mx mx m -+=_____________.14.如图,将⊙O 沿弦AB 折叠,使经过圆心O ,则∠OAB = .15.观察下列图形中点的个数,若按其规律再画下去,可以得到第n 个图形中所有点的个数为 (用含n 的代数式表示).16.如图,在四边形ABCD 中,AD ∥BC ,∠BCD=90°,∠ABC=45°,AD=CD ,CE 平分∠ACB 交AB 于点E ,在BC 上截取BF=AE ,连接AF 交CE 于点G ,连接DG 交AC 于点H ,过点A 作AN ⊥BC ,垂足为N ,AN 交CE 于点M .则下列结论;①CM=AF ;②CE ⊥AF ;③△ABF ∽△DAH ;④GD 平分∠AGC ,其中正确的序号是 .三、解答题(本题共7小题,其中第17题5分,第18题6分,第19题7分,第20题8分,第21题8分,第22题9分,第23题9分,共52分)17.计算: 02)14.3(32145sin 8-+-+⎪⎭⎫⎝⎛-︒⨯-π(第16题图)18.先化简,然后a在﹣1、1、2三个数中选一个合适的数代入求值.19.某校学生准备调查初一年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.(1)确定调查方式时,甲同学说:“我到初一(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到初一年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.类别频数(人数)频率武术类0.25书画类20 0.20棋牌类15 b器乐类合计a 1.00(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题:①a=_________,b=_________;②在扇形统计图中,器乐类所对应扇形的圆心角的度数是_________;③若该校初一年级有学生560人,请你估计大约有多少学生参加武术类校本课程.20.钓鱼岛是我国固有领土,为测量钓鱼岛东西两端A,B的距离,如下图,我勘测飞机在距海平面垂直高度为1千米的点C处,测得端点A的俯角为45°,然后沿着平行于AB的方向飞行3.2千米到点D,并测得端点B的俯角为37°,求钓鱼岛两端AB的距离.(结果精确到0.1千米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41)21.如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.(1)求证:∠ABE=∠EAD;(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.B OC D E B O C D P x yE F Q l 图1 图2 22.定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.如矩形OBCD 中,点C 为O ,B 两点的勾股点,已知OD =4,在DC 上取点E,DE=8.(1)如果点E 是O ,B 两点的勾股点(点E 不在点C ), 试求OB 的长;(2)如果OB =12,分别以OB,OD 为坐标轴建立如图2的直角坐标系,在x 轴上取点F (5,0).在线段DC 上取点P , 过点P 的直线l ∥y 轴,交x 轴于点Q .设DP=t.①当点P 在DE 之间,以EF 为直径的圆与直线l 相切,试求t 的值;②当直线l 上恰好有2点是E ,F 两点的勾股点时,试求相应t 的取值范围.23.如图,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(0,4),点B 的坐标为(4,0),点C 的坐标为(﹣4,0),点P 在AB 上,连结CP 与y 轴交于点D ,连结BD .过P ,D ,B 三点作⊙Q 与y 轴的另一个交点为E ,延长DQ 交⊙Q 于点F ,连结EF ,BF . (1)求直线AB 的函数解析式; (2)求证:∠BDE =∠ADP ;(3)设DE =x ,DF =y .请求出y 关于x 的函数解析式;(备用图)2020年深圳市中考总复习数学试卷五参考答案13. 2)3(-x m14. ︒3015. 2)1(+n16. ①②③④17.原式=1342222++-⨯……………………………………………………(3分) =2……………………………………………………(5分)131112)1()1)(1(111)1(2.182-+=-++-=-+-++⨯-+=a a a a a a a a a a a 原式当2=a 时,原式=513=-+a a …………………………(6分)19. 解:(1)∵调查的人数较多,范围较大, ∴应当采用随机抽样调查,∵到初一年级每个班随机调查一定数量的同学相对比较全面,∴丙同学的说法最合理.……………………………………………(1分) (2)①∵喜欢书画类的有20人,频率为0.20,∴a =20÷0.20=100,……………………………………………(2分) b =15÷100=0.15;……………………………………………(3分) ②∵喜欢器乐类的频率为:1﹣0.25﹣0.20﹣0.15=0.4,∴喜欢器乐类所对应的扇形的圆心角的度数为:360×0.4=144°;………………………(5分) ③喜欢武术类的人数为:560×0.25=140人.……………………………(7分)20. 解:过点A 作AE ⊥CD 于点E ,过点B 作BF ⊥CD 于点F . ∵AB ∥CD ,∴∠AEF =∠EFB =∠ABF =90°, ∴四边形ABFE 为矩形,题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ACDCBDCABBCB在Rt△AEC中,∠C=45°,AE=1千米.∴CE=AE=1(千米).在Rt△BFD中,∠BDF=37°,BF=1千米,∴DF==≈1.33千米,……………………………………………(6分)∴AB=EF=CD+DF﹣CE≈3.2+1.33﹣1=3.53≈3.5(千米).……………………(7分)答:钓鱼岛两端AB的距离约为3.5千米.…………………………(8分)21.解::(1)在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD,∵AE=AB,∴∠ABE=∠AEB,∴∠ABE=∠EAD;……………(3分)(2)∵AD∥BC,∴∠ADB=∠DBE,∵∠ABE=∠AEB,∠AEB=2∠ADB,∴∠ABE=2∠ADB,∴∠ABD=∠ABE﹣∠DBE=2∠ADB﹣∠ADB=∠ADB,∴AB=AD,又∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.…………………………(8分)22.(1)10(2)①4 ②4<t<923.解:(1)设直线AB的函数解析式为y=kx+4,代入(4,0)得:4k+4=0,解得:k=﹣1,则直线AB的函数解析式为y=﹣x+4;……(3分)(2)①由已知得:OB=OC,∠BOD=∠COD=90°,又∵OD=OD,∴△BOD≌△COD,∴∠BDO=∠CDO,∵∠CDO=∠ADP,∴∠BDE=∠ADP,…………………………………(6分)②连结PE,∵∠ADP是△DPE的一个外角,∴∠BDE=∠ABD+∠OAB,∵∠ADP=∠BDE,∠DEP=∠ABD,∴∠DPE=∠OAB,∵OA=OB=4,∠AOB=90°,∴∠OAB=45°,∴∠DPE=45°,∴∠DFE=∠DPE=45°,∵DF是⊙Q的直径,∴∠DEF=90°,∴△DEF是等腰直角三角形,∴DF=DE,即y=x;…………………………(9分)。
2020届深圳市中考数学模拟试卷有答案(word版)
广东省深圳市中考试卷数学试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.6的相反数是( )A .6-B .16-C .16D .6 2.260000000用科学计数法表示为( )A .90.2610⨯B .82.610⨯C .92.610⨯D .72610⨯3.图中立体图形的主视图是( )A .B .C .D .4.观察下列图形,是中心对称图形的是( )A .B . C.D .5.下列数据:75,80,85,85,85,则这组数据的众数和极差是( )A .85,10B .85,5 C.80,85 D .80,106.下列运算正确的是( )A .236a a a =gB .32a a a -= C. 842a a a ÷= D =7.把函数y x -向上平移3个单位,下列在该平移后的直线上的点是( )A .()2,2B .()2,3 C.()2,4 D .(2,5)8.如图,直线,a b 被,c d 所截,且//a b ,则下列结论中正确的是( )A .12∠=∠=B .34∠==∠ C.24180∠+∠=o D .14180∠+∠=o9.某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满,设大房间有x 个,小房间有y 个.下列方程正确的是( )A .7086480x y x y +=⎧⎨+=⎩B .7068480x y x y +=⎧⎨+=⎩ C. 4806870x y x y +=⎧⎨+=⎩ D .4808670x y x y +=⎧⎨+=⎩10.如图,一把直尺,60︒的直角三角板和光盘如图摆放,A 为60︒角与直尺交点,3AB =,则光盘的直径是( )A .3B .6 D .11.二次函数2(0)y ax bx c a =++≠的图像如图所示,下列结论正确是( )A .0abc >B .20a b +< C.30a c +< D .230ax bx c ++-=有两个不相等的实数根12.如图,A B 、是函数12y x=上两点,P 为一动点,作//PB y 轴,//PA x 轴,下列说法正确的是( )①AOP BOP ∆≅∆;②AOP BOP S S ∆∆=;③若OA OB =,则OP 平分AOB ∠;④若4BOP S ∆=,则16ABP S ∆=A .①③B .②③ C.②④ D .③④第Ⅱ卷(共90分)二、填空题(每题3分,满分12分,将答案填在答题纸上)13.分解因式:29a -=.14.一个正六面体的骰子投掷一次得到正面向上的数字为奇数的概率:.15.如图,四边形ABCD 是正方体,CEA ∠和ABF ∠都是直角且点,,E A B 三点共线,4AB =,则阴影部分的面积是.16.在Rt ABC ∆中,90?C ∠=,AD 平分CAB ∠,AD BE 、相交于点F ,且4,AF EF ==则AC =.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.计算:-1012sin )2π⎛⎫- ⎪⎝⎭. 18.先化简,再求值:2221111x x x x x ++⎛⎫-+ ⎪--⎝⎭,其中2x =. 19.某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:请根据上图完成下面题目:(1)总人数为__________人,a =__________,b =__________.(2)请你补全条形统计图.(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?20.已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在CFE ∆中,6,12CF CE ==,45?FCE ∠=,以点C 为圆心,以任意长为半径作AD ,再分别以点A 和点D 为圆心,大于12AD 长为半径做弧,交EF 于点,//B AB CD . (1)求证:四边形ACDB 为FEC ∆的亲密菱形;(2)求四边形ACDB 的面积.21.某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贯2元.(1)第一批饮料进货单价多少元?(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?22.如图在O e 中,2,BC AB AC ==,点D 为AC 上的动点,且cos B =. (1)求AB 的长度;(2)求AD AE ⋅的值;(3)过A 点作AH BD ⊥,求证:BH CD DH =+.23.已知顶点为A 抛物线2122y a x ⎛⎫=-- ⎪⎝⎭经过点3,22B ⎛⎫- ⎪⎝⎭,点5,22C ⎛⎫ ⎪⎝⎭. (1)求抛物线的解析式;(2)如图1,直线AB 与x 轴相交于点,M y 轴相交于点E ,抛物线与y 轴相交于点F ,在直线AB 上有一点P ,若OPM MAF ∠=∠,求POE ∆的面积;图1(3)如图2,点Q 是折线A B C --上一点,过点Q 作//QN y 轴,过点E 作//EN x 轴,直线QN 与直线EN 相交于点N ,连接QE ,将QEN ∆沿QE 翻折得到1QEN ∆,若点1N 落在x 轴上,请直接写出Q 点的坐标. 图2广东省深圳市中考试卷数学参考答案一、选择题1-5: ABBDA 6-10:BDBAD 11、12:CB二、填空题13.()()33a a +- 14.1215.8 三、解答题17.318.解:原式21(1)(1)11(1)1x x x x x x x -++-=⋅=-++ 把2x =代入得:原式13=19.解:(1)0.440100÷=(人)251000.25a =÷=,1000.1515b =⨯=(人), (2)如图:(3)6000.1590⨯=(人)20.解:(1)证明:由已知得:AC CD =,AB DB =由已知尺规作图痕迹得:BC 是FCE ∠的角平分线则:ACB DCB ∠=∠又//AB CD QABC DCB ∴∠=∠ACB ABC ∴∠=∠AC AB ∴=又,AC CD AB DB ==QAC CD DB BA ∴===∴四边形ACDB 是菱形ACD ∠Q 与FCE ∆中的FCE ∠重合,它的对角ABD ∠顶点在EF 上 ∴四边形ACDB 为FEC ∆的亲密菱形(2)解:设菱形ACDB 的边长为x可证:EAB FCE ∆∆∽ 则:FA AB FC CE =,即6126x x -= 解得:4x =过A 点作AH CD ⊥于H 点在Rt ACH ∆中,45?ACH ∠=AH ∴==∴四边形ACDB 的面积为:4⨯21.解:(1)设第一批饮料进货单价为x 元,则:1600600032x x ⋅=+ 解得:8x =经检验:8x =是分式方程的解答:第一批饮料进货单价为8元.(2)设销售单价为m 元,则: (8)200(10)6001200m m -⋅+-⋅≥化简得:2(8)6(10)12m m -+-≥解得:11m ≥答:销售单价至少为11元.22.解:(1)作AM BC ⊥,,2AB AC AM BC BC =⊥=Q112BM CM BC ===cos BM B AB ==Q Rt AMB ∆中,1BM =cos 1AB BM B ∴=÷==(2)连接DCAB AC =QACB ABC ∴∠=∠∵四边形ABCD 内接于圆O ,180ADC ABC ∴∠+∠=o ,180ACE ACB ∠+∠=o Q ,ADC ACE ∴∠=∠CAE ∠Q 公共EAC CAD ∴∆∆∽AC AE AD AC∴=2210AD AE AC ∴⋅===.(3)在BD 上取一点N ,使得BN CD =在ABN ∆和ACD ∆中31AB AC BN CD =⎧⎪∠=∠⎨⎪=⎩()ABN ACD SAS ∴∆≅∆AN AD ∴=,AN AD AH BD =⊥QNH HD ∴=,BN CD NH HD ==QBN NH CD HD BH ∴+=+=.23.解:(1)把点3,22B ⎛⎫- ⎪⎝⎭代入2122y a x ⎛⎫=-- ⎪⎝⎭,解得:1a =, ∴抛物线的解析式为:2122y x ⎛⎫=-- ⎪⎝⎭或274y x x =--; (2)设直线AB 解析式为:y kx b =+,代入点,A B 的坐标得: 122322k b k b ⎧-=+⎪⎪⎨⎪=-+⎪⎩,解得:21k b =-⎧⎨=-⎩,∴直线AB 的解析式为:21y x =--, 易求()0,1E ,70,4F ⎛⎫- ⎪⎝⎭,1,02M ⎛⎫- ⎪⎝⎭, 若OPM MAF ∠=∠,则当//OP AF 时,OPE EAE ∆∆∽,14334OP OE FA FE ===, 433OP FA ∴===, 设点(),21P t t --3= 解得1215t =-,223t =-, 由对称性知;当1215t =-时,也满足OPM MAF ∠=∠, 1215t ∴=-,223t =-都满足条件 POE ∆Q 的面积12OE l =⋅,POE ∴∆的面积为115或13.。
2020年广东省深圳市中考数学模拟试卷(4)
2020年广东省深圳市中考数学模拟试卷(4)一、选择题(本大题共12小题,每小题3分,共36分)1.(3分)下列各数中,最小的数是( )A .5B .3-C .0D .22.(3分)如图,直线a ,b 被直线c 所截,若//a b ,1110∠=︒,则2∠等于( )A .70︒B .75︒C .80︒D .85︒3.(3分)下列运算正确的是( )A .224a a a +=B .532a a a -=C .2222a a a =gD .5210()a a =4.(3分)如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )A .B .C .D .5.(3分)不等式组11841x x x ->⎧⎨+<-⎩的解集是( ) A .3x > B .3x < C .2x < D .2x >6.(3分)将含有30︒角的直角三角板OAB 如图放置在平面直角坐标中,OB 在x 轴上,若2OA =,将三角板绕原点O 顺时针旋转75︒,则点A 的对应点A '的坐标为( )A .(3,1)B .(1,3)-C .(2,2)-D .(2-,2)7.(3分)在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( )成绩(分)27 28 30 人数 2 3 1A .28,28,1B .28,27.5,1C .3,2.5,5D .3,2,5 8.(3分)“科学用眼,保护视力”是青少年珍爱生命的具体表现.科学证实:近视眼镜的度数y (度)与镜片焦距()x m 成反比例.如果500度近视眼镜片的焦距为0.2m ,则表示y 与x 函数关系的图象大致是( )A .B .C .D .9.(3分)在ABCD Y 中,8AD =,AE 平分BAD ∠交BC 于点E ,DF 平分ADC ∠交BC 于点F ,且2EF =,则AB 的长为( )A .3B .5C .2或3D .3或510.(3分)如图是抛物线2(0)y ax bx c a =++≠的部分图象,其顶点坐标为(1,)n ,且与x 轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①0a b c -+>;②30a b +=;③24()b a c n =-;④一元二次方程21ax bx c n ++=-有两个不相等的实数根.其中正确结论的个数是( )A .1B .2C .3D .4 11.(3分)从3-,1-,12,1,3这五个数中,随机抽取一个数,记为a ,若数a 使关于x 的不等式组1(27)330x x a ⎧+⎪⎨⎪-<⎩…无解,且使关于x 的分式方程2133x a x x --=---有整数解,那么这5个数中所有满足条件的a 的值之和是( )A .3-B .2-C .32-D .1212.(3分)平面直角坐标系中,已知(2,2)A 、(4,0)B .若在坐标轴上取点C ,使ABC ∆为等腰三角形,则满足条件的点C 的个数是( )A .5B .6C .7D .8二、填空(本大题共4小题,每小题3分,共12分.)13.(3分)分解因式:2228x y -= .14.(3分)若一个圆锥的底面圆半径为3cm ,其侧面展开图的圆心角为120︒,则圆锥的母线长是 cm .15.(3分)如图,已知双曲线k y x=与直线6y x =-+相交于A ,B 两点,过点A 作x 轴的垂线与过点B 作y 轴的垂线相交于点C ,若ABC ∆的面积为8,则k 的值为 .16.(3分)如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan ADE∠的值为.三、解答题(共7小题,满分18分)17.计算:29|4|2sin303+-+︒-.18.先化简,再求值:2221(1)21x xx x x x--÷+++,其中x的值从不等式组1214xx-⎧⎨-<⎩…的整数解中选取.19.为弘扬中华优秀传统文化,我市教育局在全市中小学积极推广“太极拳”运动.弘孝中学为争创“太极拳”示范学校,今年3月份举行了“太极拳”比赛,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:(1)该校七(1)班共有名学生;扇形统计图中C等级所对应扇形的圆心角等于度;并补全条形统计图;(2)A 等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生作为全班训练的示范者,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.20.在ABC ∆中,P 为边AB 上一点.(1)如图1,若ACP B ∠=∠,求证:2AC AP AB =g ;(2)若M 为CP 的中点,2AC =.①如图2,若PBM ACP ∠=∠,3AB =,求BP 的长;②如图3,若45ABC ∠=︒,60A BMP ∠=∠=︒,直接写出BP 的长.21.孝感市在创建国家级园林城市中, 绿化档次不断提升 . 某校计划购进A ,B 两种树木共 100 棵进行校园绿化升级,经市场调查: 购买A 种树木 2 棵,B 种树木 5 棵, 共需 600 元;购买A 种树木 3 棵,B 种树木 1 棵, 共需 380 元 .(1) 求A 种,B 种树木每棵各多少元?(2) 因布局需要, 购买A 种树木的数量不少于B 种树木数量的 3 倍 . 学校与中标公司签订的合同中规定: 在市场价格不变的情况下 (不 考虑其他因素) ,实际付款总金额按市场价九折优惠, 请设计一种购买树木的方案, 使实际所花费用最省, 并求出最省的费用 .22.(9分)如图,在Rt ABC ∆中,90C ∠=︒,点O 在AB 上,经过点A 的O e 与BC 相切于点D ,与AC ,AB 分别相交于点E ,F ,连接AD 与EF 相交于点G .(1)求证:AD 平分CAB ∠;(2)若OH AD ⊥于点H ,FH 平分AFE ∠,1DG =.①试判断DF 与DH 的数量关系,并说明理由;②求O e 的半径.23.(9分)在平面直角坐标系中, 已知抛物线2y x bx c =++的顶点M 的坐标为(1,4)--,且与x 轴交于点A ,点B (点A 在点B 的左边) ,与y 轴交于点C . (1) 填空:b = ,c = ,直线AC 的解析式为 ;(2) 直线x t =与x 轴相交于点H .①当3t =-时得到直线AN (如 图1),点D 为直线AC 下方抛物线上一点, 若COD MAN ∠=∠,求出此时点D 的坐标;②当31t -<<-时 (如 图2),直线x t =与线段AC ,AM 和抛物线分别相交于点E ,F ,P . 试证明线段HE ,EF ,FP 总能组成等腰三角形;如果此等腰三角形底角的余弦值为35,求此时t 的值 .2020年广东省深圳市中考数学模拟试卷(4)参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分)1.(3分)下列各数中,最小的数是( )A .5B .3-C .0D .2【解答】解:3025-<<<,则最小的数是3-,故选:B .2.(3分)如图,直线a ,b 被直线c 所截,若//a b ,1110∠=︒,则2∠等于( )A .70︒B .75︒C .80︒D .85︒【解答】解://a b Q ,13180∴∠+∠=︒,3180170∴∠=︒-∠=︒,2370∴∠=∠=︒, 故选:A .3.(3分)下列运算正确的是( )A .224a a a +=B .532a a a -=C .2222a a a =gD .5210()a a =【解答】解:A 、2222a a a +=,故此选项错误;B 、53a a -,无法计算,故此选项错误;C 、224a a a =g,故此选项错误; D 、5210()a a =,正确.故选:D .4.(3分)如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是( )A .B .C .D .【解答】解:观察该几何体发现:从正面看到的应该是三个正方形,上面1个,下面2个, 故选:C .5.(3分)不等式组11841x x x ->⎧⎨+<-⎩的解集是( )A .3x >B .3x <C .2x <D .2x >【解答】解:11841x x x ->⎧⎨+<-⎩①②, 解①得:2x >,解②得:3x >,则不等式的解集是:3x >.故选:A .6.(3分)将含有30︒角的直角三角板OAB 如图放置在平面直角坐标中,OB 在x 轴上,若2OA =,将三角板绕原点O 顺时针旋转75︒,则点A 的对应点A '的坐标为( )A .(31)B .(1,3)-C .(22)-D .(2-2)【解答】解:如图,Q 三角板绕原点O 顺时针旋转75︒,∴旋转后OA 与y 轴夹角为45︒,2OA =Q ,2OA ∴'=,∴点A '的横坐标为2222⨯= 纵坐标为222-=- 所以,点A '的坐标为(22)-.故选:C .7.(3分)在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( ) 成绩(分)27 28 30 人数 2 3 1A .28,28,1B .28,27.5,1C .3,2.5,5D .3,2,5 【解答】解:这组数据28出现的次数最多,出现了3次,则这组数据的众数是28; 把这组数据从小到大排列,最中间两个数的平均数是(2828)228+÷=,则中位数是28; 这组数据的平均数是:(27228330)628⨯+⨯+÷=,则方差是:2221[2(2728)3(2828)(3028)]16⨯⨯-+⨯-+-=; 故选:A .8.(3分)“科学用眼,保护视力”是青少年珍爱生命的具体表现.科学证实:近视眼镜的度数y (度)与镜片焦距()x m 成反比例.如果500度近视眼镜片的焦距为0.2m ,则表示y与x 函数关系的图象大致是( )A .B .C .D .【解答】解:根据题意近视眼镜的度数y (度)与镜片焦距x (米)成反比例,设k y x =, 由于点(0.2,500)在此函数解析式上,0.2500100k ∴=⨯=,100y x∴=. 故选:B .9.(3分)在ABCD Y 中,8AD =,AE 平分BAD ∠交BC 于点E ,DF 平分ADC ∠交BC 于点F ,且2EF =,则AB 的长为( )A .3B .5C .2或3D .3或5【解答】解:①如图1,在ABCD Y 中,8BC AD ==Q ,//BC AD ,CD AB =,//CD AB , DAE AEB ∴∠=∠,ADF DFC ∠=∠,AE Q 平分BAD ∠交BC 于点E ,DF 平分ADC ∠交BC 于点F ,BAE DAE ∴∠=∠,ADF CDF ∠=∠,BAE AEB ∴∠=∠,CFD CDF ∠=∠,AB BE ∴=,CF CD =,2EF =Q ,28BC BE CF EF AB EF ∴=+-=-=,5AB ∴=;②在ABCD Y 中,8BC AD ==Q ,//BC AD ,CD AB =,//CD AB , DAE AEB ∴∠=∠,ADF DFC ∠=∠,AE Q 平分BAD ∠交BC 于点E ,DF 平分ADC ∠交BC 于点F ,BAE DAE ∴∠=∠,ADF CDF ∠=∠, BAE AEB ∴∠=∠,CFD CDF ∠=∠, AB BE ∴=,CF CD =, 2EF =Q ,28BC BE CF AB EF ∴=+=+=, 3AB ∴=;综上所述:AB 的长为3或5. 故选:D .10.(3分)如图是抛物线2(0)y ax bx c a =++≠的部分图象,其顶点坐标为(1,)n ,且与x 轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①0a b c -+>; ②30a b +=; ③24()b a c n =-;④一元二次方程21ax bx c n ++=-有两个不相等的实数根. 其中正确结论的个数是( )A .1B .2C .3D .4【解答】解:Q 抛物线与x 轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线1x =,∴抛物线与x 轴的另一个交点在点(2,0)-和(1,0)-之间. ∴当1x =-时,0y >,即0a b c -+>,所以①正确; Q 抛物线的对称轴为直线12bx a=-=,即2b a =-, 332a b a a a ∴+=-=,所以②错误; Q 抛物线的顶点坐标为(1,)n ,∴244ac b n a-=,2444()b ac an a c n ∴=-=-,所以③正确; Q 抛物线与直线y n =有一个公共点,∴抛物线与直线1y n =-有2个公共点,∴一元二次方程21ax bx c n ++=-有两个不相等的实数根,所以④正确.故选:C .11.(3分)从3-,1-,12,1,3这五个数中,随机抽取一个数,记为a ,若数a 使关于x 的不等式组1(27)330x x a ⎧+⎪⎨⎪-<⎩…无解,且使关于x 的分式方程2133x a x x --=---有整数解,那么这5个数中所有满足条件的a 的值之和是( ) A .3-B .2-C .32-D .12【解答】解:解1(27)330x x a ⎧+⎪⎨⎪-<⎩…得1x x a ⎧⎨<⎩…,Q 不等式组1(27)330x x a ⎧+⎪⎨⎪-<⎩…无解,1a ∴„,解方程2133x a x x--=---得52a x -=, 52ax -=Q 为整数,1a „,3a ∴=-或1或1-,1a =-Q 时,原分式方程无解,故将1a =-舍去,∴所有满足条件的a 的值之和是2-,故选:B .12.(3分)平面直角坐标系中,已知(2,2)A 、(4,0)B .若在坐标轴上取点C ,使ABC ∆为等腰三角形,则满足条件的点C 的个数是( ) A .5B .6C .7D .8【解答】解:Q 点A 、B 的坐标分别为(2,2)、(4,0)B .AB ∴=①若AC AB =,以A 为圆心,AB 为半径画弧与坐标轴有3个交点(含B 点),即(0,0)、(4,0)、(0,4),Q 点(0,4)与直线AB 共线,∴满足ABC ∆是等腰三角形的C 点有1个;②若BC AB =,以B 为圆心,BA 为半径画弧与坐标轴有2个交点(A 点除外),即满足ABC ∆是等腰三角形的C 点有2个;③若CA CB =,作AB 的垂直平分线与坐标轴有两个交点,即满足ABC ∆是等腰三角形的C 点有2个;综上所述:点C 在坐标轴上,ABC ∆是等腰三角形,符合条件的点C 共有5个. 故选:A .二、填空(本大题共4小题,每小题3分,共12分.)13.(3分)分解因式:2228x y -= 2(2)(2)x y x y +- . 【解答】解:2222282(4)2(2)(2)x y x y x y x y -=-=+-. 故答案为:2(2)(2)x y x y +-.14.(3分)若一个圆锥的底面圆半径为3cm ,其侧面展开图的圆心角为120︒,则圆锥的母线长是 9 cm .【解答】解:设母线长为l ,则12023180lππ⨯=⨯ 解得:9l =. 故答案为:9.15.(3分)如图,已知双曲线k yx=与直线6y x=-+相交于A,B两点,过点A 作x轴的垂线与过点B作y轴的垂线相交于点C,若ABC∆的面积为8,则k的值为5.【解答】解法一:解:6kyxy x⎧=⎪⎨⎪=-+⎩,解得:113939x ky k⎧=--⎪⎨=+-⎪⎩,223939x ky k⎧=+-⎪⎨=-⎪⎩,即点A的坐标为(39k-39)k+-,点B的坐标为(39k-39k--,则29AC k=-,29BC k=-8ABCS∆=Q,∴182AC BC=g,即2(9)8k-=,解得:5k=.解法二:解:设点1(A x,16)x-,2(B x,26)x-Q双曲线kyx=与直线6y x=-+相交于A,B两点,∴方程(6)0kxx--+=有解,即:260x x k -+=有2个不相同的实根,126x x ∴+=,12x x k =,AC BC ⊥QC ∴点坐标为1(x ,26)x -2121AC x x BC x x ∴=-=- 8ABC S ∆=Q ,∴182AC BC =g ∴2211()82x x -= 整理得:21212()416x x x x +-=,36416k ∴-= 解得5k =, 故答案为:5.解法三:根据对称性设(,)A a b ,(,)B b a ,由题意:21()82ABC S a b ∆=-=,4a b ∴-=-. 又6a b +=Q ,1a ∴=,5b =, 5k ∴=.16.(3分)如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD 的面积是小正方形EFGH 面积的13倍,那么tan ADE ∠的值为23.【解答】解:设小正方形EFGH 面积是2a ,则大正方形ABCD 的面积是213a ,∴小正方形EFGH 边长是a ,则大正方形ABCD ,Q 图中的四个直角三角形是全等的,AE DH ∴=,设AE DH x ==,在Rt AED ∆中,222AD AE DE =+, 即22213()a x x a =++解得:12x a =,23x a =-(舍去), 2AE a ∴=,3DE a =,22tan 33AE a ADE DE a ∴∠===, 故答案为:23. 三、解答题(共7小题,满分18分)172|4|2sin 303-+︒-.【解答】2|4|2sin 303-+︒- 3419=++-1=-.18.先化简,再求值:2221(1)21x x x x x x --÷+++,其中x 的值从不等式组1214x x -⎧⎨-<⎩„的整数解中选取.【解答】解:2221(1)21x x x x x x --÷+++ 2(1)[1](1)(1)(1)x x x x x x +=-⨯++- 111()111x x x x x ++=-⨯++- 111x x x x -+=⨯+- 1xx =--, 解不等式组1214x x -⎧⎨-<⎩„得:512x -<…, 当2x =时,原式21xx =-=--. 19.为弘扬中华优秀传统文化,我市教育局在全市中小学积极推广“太极拳”运动.弘孝中学为争创“太极拳”示范学校,今年3月份举行了“太极拳”比赛,比赛成绩评定为A ,B ,C ,D ,E 五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:(1)该校七(1)班共有 50 名学生;扇形统计图中C 等级所对应扇形的圆心角等于 度;并补全条形统计图;(2)A 等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生作为全班训练的示范者,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率. 【解答】解:(1)由题意可知总人数48%50=÷=人;扇形统计图中C 等级所对应扇形的圆心角2050100%360144=÷⨯⨯︒=︒;补全条形统计图如图所示:故答案为:50,144; (2)列表如下:男 男 女 女 男 ---(男,男)(女,男) (女,男) 男 (男,男) ---(女,男) (女,男) 女 (男,女) (男,女) ---(女,女)女(男,女)(男,女)(女,女)---得到所有等可能的情况有12种,其中恰好抽中一男一女的情况有8种, 所以恰好选到1名男生和1名女生的概率82123==. 20.在ABC ∆中,P 为边AB 上一点.(1)如图1,若ACP B ∠=∠,求证:2AC AP AB =g ; (2)若M 为CP 的中点,2AC =.①如图2,若PBM ACP ∠=∠,3AB =,求BP 的长;②如图3,若45ABC ∠=︒,60A BMP ∠=∠=︒,直接写出BP 的长.【解答】解:(1)ACP B ∠=∠Q ,A A ∠=∠, ACP ABC ∴∆∆∽,∴AC ABAP AC=, 2AC AP AB ∴=g ;(2)①取AP 在中点G ,连接MG ,设AG x =,则PG x =,3BG x =-,M Q 是PC 的中点,//MG AC ∴, BGM A ∴∠=∠, ACP PBM ∠=∠Q , APC GMB ∴∆∆∽,∴AP AC GM BG=,即2213xx=-,x∴=,3AB=Q,3AP∴=,PB∴=②过C作CH AB⊥于H,延长AB到E,使BE BP=,设BP x=.45ABC∠=︒Q,60A∠=︒,CH∴=HE x=,222)CE x=+Q,PB BE=Q,PM CM=,//BM CE∴,60PMB PCE A∴∠=∠=︒=∠,E E∠=∠Q,ECP EAC∴∆∆∽,∴CE AEEP CE=,2CE EP EA∴=g,2332(1)x x x∴+++=,1x∴=,1PB∴.21.孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100 棵进行校园绿化升级,经市场调查:购买A种树木2 棵,B种树木5 棵,共需600 元;购买A种树木3 棵,B种树木1 棵,共需380 元.(1)求A种,B种树木每棵各多少元?(2)因布局需要,购买A种树木的数量不少于B种树木数量的3 倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.【解答】解:(1)设A种树每棵x元,B种树每棵y元,依题意得:25600 3380x yx y+=⎧⎨+=⎩,解得10080xy=⎧⎨=⎩.答:A种树每棵100 元,B种树每棵80 元;(2)设购买A种树木为a棵,则购买B种树木为(100)a-棵,则3(100)a a-…,解得75a ….设实际付款总金额是y 元, 则0.9[10080(100)]y a a =+-,即187200y a =+.180>Q ,y 随a 的增大而增大,∴当75a =时,y 最小 .即当75a =时,187572008550y =⨯+=最小值(元).答: 当购买A 种树木 75 棵,B 种树木 25 棵时, 所需费用最少, 最少为 8550元 .22.(9分)如图,在Rt ABC ∆中,90C ∠=︒,点O 在AB 上,经过点A 的O e 与BC 相切于点D ,与AC ,AB 分别相交于点E ,F ,连接AD 与EF 相交于点G .(1)求证:AD 平分CAB ∠;(2)若OH AD ⊥于点H ,FH 平分AFE ∠,1DG =.①试判断DF 与DH 的数量关系,并说明理由;②求O e 的半径.【解答】解:(1)如图,连接OD ,O Q e 与BC 相切于点D ,OD BC ∴⊥,90C ∠=︒Q ,//OD AC ∴,CAD ODA ∴∠=∠,OA OD =Q ,OAD ODA ∴∠=∠,CAD BAD ∴∠=∠,AD ∴平分CAB ∠.(2)①DF DH =,理由如下:FH Q 平分AFE ∠,AFH EFH ∴∠=∠,又DFG EAD HAF ∠=∠=∠,DFG EAD HAF ∴∠=∠=∠,DFG GFH HAF HFA ∴∠+∠=∠+∠,即DFH DHF ∠=∠,DF DH ∴=.②设HG x =,则1DH DF x ==+,OH AD ⊥Q ,22(1)AD DH x ∴==+,DFG DAF ∠=∠Q ,FDG FDG ∠=∠,DFG DAF ∴∆∆∽, ∴DF DG AD DF =, ∴112(1)1x x x+=++, 1x ∴=,2DF =Q ,4AD =,AF Q 为直径,90ADF ∴∠=︒,AF ∴==O ∴e 的半径为5. 23.(9分)在平面直角坐标系中, 已知抛物线2y x bx c =++的顶点M 的坐标为(1,4)--,且与x 轴交于点A ,点B (点A 在点B 的左边) ,与y 轴交于点C . (1) 填空:b = 2 ,c = ,直线AC 的解析式为 ;(2) 直线x t =与x 轴相交于点H .①当3t =-时得到直线AN (如 图1),点D 为直线AC 下方抛物线上一点, 若COD MAN ∠=∠,求出此时点D 的坐标;②当31t -<<-时 (如 图2),直线x t =与线段AC ,AM 和抛物线分别相交于点E ,F ,P . 试证明线段HE ,EF ,FP 总能组成等腰三角形;如果此等腰三角形底角的余弦值为35,求此时t 的值 .【解答】解: (1)Q 抛物线2y x bx c =++的顶点M 的坐标为(1,4)--, ∴212444b c b ⎧-=-⎪⎪⎨-⎪=-⎪⎩,解得:23b c =⎧⎨=-⎩, ∴抛物线解析式为:223y x x =+-,令0y =,得:2230x x +-=,解得:11x =,23x =-,(3,0)A ∴-,(1,0)B ,令0x =,得3y =-,(0,3)C ∴-,设直线AC 的解析式为:y kx b =+,将(3,0)A -,(0,3)C -代入,得:303k b b -+=⎧⎨=-⎩,解得:13k b =-⎧⎨=-⎩, ∴直线AC 的解析式为:3y x =--;故答案为: 2 ,3-,3y x =--.(2)①设点D 的坐标为2(,23)m m m +-, COD MAN ∠=∠Q ,tan tan COD MAN ∴∠=∠, ∴22(23)4m m m -=-+-,解得:m =30m -<<Q ,m ∴=故点D 的坐标为(-;②设直线AM 的解析式为y mx n =+,将点(3,0)A -、(1,4)M --代入,得:304m n m n -+=⎧⎨-+=-⎩,解得:26m n =-⎧⎨=-⎩,∴直线AM 的解析式为:26y x =--,Q 当x t =时,(3)3HE t t =---=+,(26)26HF t t =---=+,2(23)HP t t =-+-, 3HE EF HF HE t ∴==-=+,243FP t t =---, 222(3)43(3)0HE EF FP t t t t +-=++++=+>Q ,HE EF FP ∴+>,又HE FP EF +>,EF FP HE +>, ∴当31t -<<-时, 线段HE ,EF ,FP 总能组成等腰三角形; 由题意得:1325FP EF =,即21(43)3235t t t ---=+, 整理得:2526330t t ++=, 解得:13t =-,2115t =-, 31t -<<-Q , 115t ∴=-.。
广东省深圳市2020年中考数学试题与答案
广东省深圳市2020年中考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.2020的相反数是()A.2020B.12020C.2020-D.12020-2.下列图形中既是轴对称图形,也是中心对称图形的是()A.B.C.D.3.2020年6月30日,深圳市总工会启动“百万职工消费扶贫采购节”活动,预计撬动扶贫消费额约150000000元.将150000000用科学记数法表示为()A.0.15×108B.1.5×107C.15×107D.1.5×108 4.下列哪个图形,主视图、左视图和俯视图相同的是()A.圆锥B.圆柱C.三棱柱D.正方体5.某同学在今年的中考体育测试中选考跳绳.考前一周,他记录了自己五次跳绳的成绩(次数/分钟):247,253,247,255,263.这五次成绩的平均数和中位数分别是()A.253,253B.255,253C.253,247D.255,247 6.下列运算正确的是()A.a+2a=3a2B.235a a a⋅=C.33()ab ab=D.326()a a-=-7.一把直尺与30°的直角三角板如图所示,∠1=40°,则∠2=()A.50°B.60°C.70°D.80°8.如图,已知AB=AC,BC=6,尺规作图痕迹可求出BD=()A.2B.3C.4D.5 9.以下说法正确的是()A.平行四边形的对边相等B.圆周角等于圆心角的一半C.分式方程11222xx x-=---的解为x=2D.三角形的一个外角等于两个内角的和10.如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为()A.200tan70°米B.200tan70︒米C.200sin70°米D.200sin70︒米11.二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列说法错误的是( )A .B .4ac -b 2>0C .3a +c =0D .ax 2+bx +c =n +1无实数根12.如图,矩形纸片ABCD 中,AB =6,BC =12.将纸片折叠,使点B 落在边AD 的延长线上的点G 处,折痕为EF ,点E 、F 分别在边AD 和边BC 上.连接BG ,交CD 于点K ,FG 交CD 于点H .给出以下结论:∠EF ∠BG ;∠GE=GF ;∠∠GDK 和△GKH 的面积相等;∠当点F 与点C 重合时,∠DEF =75°.其中正确的结论共有( )A .1个B .2个C .3个D .4个二、填空题 13.分解因式:3x -x=__________.14.口袋内装有编号分别为1,2,3,4,5,6,7的七个球(除编号外都相同),从中随机摸出一个球,则摸出编号为偶数的球的概率是___.15.如图,在平面直角坐标系中,ABCO 为平行四边形,O (0,0),A (3,1),B (1,2),反比例函数(0)k y k x =≠的图象经过OABC 的顶点C ,则k =___.16.如图,已知四边形ABCD ,AC 与BD 相交于点O ,∠ABC =∠DAC =90°,14tan ,23BO ACB OD ∠==,则ABD CBD S S =___.三、解答题17.计算:101()2cos30|(4)3π--︒+--. 18.先化简,再求值:213(2)211a a a a a +-÷+-+-,其中a =2. 19.以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,现随机调查了m 名新聘毕业生的专业情况,并将调查结果绘制成如下两幅不完整的统计图:根据以上信息,解答下列问题:(1)m = ,n= ;(2)请补全条形统计图;(3)在扇形统计图中,“软件”所对应圆心角的度数是;(4)若该公司新聘600名毕业生,请你估计“总线”专业的毕业生有名.20.如图,AB为∠O的直径,点C在∠O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.(1)求证:AE=AB;(2)若AB=10,BC=6,求CD的长.21.端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元.(1)肉粽和蜜枣粽的进货单价分别是多少元?(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?22.背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE∠DG.小组讨论后,提出了三个问题,请你帮助解答:(1)将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:(2)把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE =DG 仍成立?请说明理由;(3)把背景中的正方形改成矩形AEFG 和矩形ABCD ,且23AE AB AG AD ==,AE =4,AB =8,将矩形AEFG 绕点A 按顺时针方向旋转(如图3),连接DE ,BG .小组发现:在旋转过程中, BG 2+DE 2是定值,请求出这个定值.23.如图1,抛物线y =ax 2+bx +3(a ≠0)与x 轴交于A (-3,0)和B (1,0),与y 轴交于点C ,顶点为D .(1)求解抛物线解析式;(2)连接AD ,CD ,BC ,将△OBC 沿着x 轴以每秒1个单位长度的速度向左平移,得到O B C '''∆,点O 、B 、C 的对应点分别为点O ',B ',C ',设平移时间为t 秒,当点O'与点A 重合时停止移动.记O B C '''∆与四边形AOCD 的重叠部分的面积为S ,请直接写出S 与时间t 的函数解析式;(3)如图2,过抛物线上任意一点M (m ,n )向直线l :92y =作垂线,垂足为E ,试问在该抛物线的对称轴上是否存在一点F ,使得ME -MF =14?若存在,请求F 点的坐标;若不存在,请说明理由.参考答案:1.C根据相反数的定义,即可求解.2020的相反数是:2020,故选C.本题主要考查求一个数的相反数,掌握相反数的定义是解题的关键.2.B根据轴对称图形与中心对称图形的概念求解.解:A、既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;B、既是轴对称图形,也是中心对称图形,故此选项符合题意;C、是轴对称图形,不是中心对称图形,故此选项不符合题意;D、不是轴对称图形,是中心对称图形,故此选项不符合题意.故选:B.此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.3.D科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.解:将150000000用科学记数法表示为1.5×108.故选:D.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.D分别得出圆锥体、圆柱体、三棱柱、正方体的三视图的形状,再判断即可.解:圆锥的主视图、左视图都是等腰三角形,而俯视图是圆,因此选项A不符合题意;圆柱体的主视图、左视图都是矩形,而俯视图是圆形,因此选项B不符合题意;三棱柱主视图、左视图都是矩形,而俯视图是三角形,因此选项C不符合题意;正方体的三视图都是形状、大小相同的正方形,因此选项D符合题意;故选:D.本题考查简单几何体的三视图,明确圆锥、圆柱、三棱柱、正方体的三视图的形状和大小是正确判断的前提.5.A根据题干找出基准数,排列出新数列,则找到平均数,再由从小到大排列找出中位数.求平均数可用基准数法,设基准数为250,则新数列为-4,3,-3,5,13,新数列的平均数为3,则原数列的平均数为253;对数据从小到大进行排列,可知中位数为253,故选A.此题考查中位数和平均数相关知识,难度一般.6.B根据合并同类项、同底数幂的乘法、幂的乘方、积的乘方逐项分析即可.A.a+2a=3a,该选项错误;B.235⋅=,该选项正确;a a aC.333=,该选项错误;()ab a bD.326-=,该选项错误;a a()故选B.本题考查了整式的运算,熟练掌握幂的运算法则是解答本题的关键.7.D如图:根据直角三角形的性质可得360︒∠=,然后再根据两直线平行,同旁内角互补解答即可.解:如图:∠含30°直角三角形∠360︒∠=∠直尺两边平行∠∠1+∠2+∠3=180°∠21803180︒︒∠=-∠-∠=.故答案为D.本题考查了直角三角形的性质和平行线的性质,其中灵活运用两直线平行、同旁内角互补的性质是解答本题的关键.8.B根据尺规作图的方法步骤判断即可.由作图痕迹可知AD为∠BAC的角平分线,而AB=AC,由等腰三角形的三线合一知D为BC重点,BD=3,故选B本题考查尺规作图-角平分线及三线合一的性质,关键在于牢记尺规作图的方法和三线合一的性质.9.A根据平行四边形的性质、圆周角定理、解分式方程以及三角形外角的性质逐项分析即可.解:A选项正确;B选项:同弧所对的圆周角等于圆心角的一半,故B选项错误;C选项:x=2为增根,原分式方程无解,故C选项错误;D选项:没有指明两个内角为不想邻的内角,故D选项错误.故答案为A.本题考查了平行四边形的性质、圆周角定理、解分式方程以及三角形外角的性质等知识,掌握相关性质、定理所关注的细节是解答本题的关键.10.B在直角三角形PQT中,利用PQ的长,以及∠PQT的度数,进而得到∠PTQ的度数,根据三角函数即可求得PT的长.解:在Rt∠PQT中,∠∠QPT=90°,∠PQT=90°-70°=20°,∠∠PTQ=70°,∠tan70PQPT︒=,∠200tan70tan70PQPT==︒︒,即河宽200tan70︒米,故选:B.此题考查了解直角三角形的应用-方向角问题,掌握方向角与正切函数的定义是解题的关键.11.B根据函数图象确定a、b、c的符号判断A;根据抛物线与x轴的交点判断B;利用抛物线的对称轴得到b=2a,再根据抛物线的对称性求得c=-3a即可判断C;利用抛物线的顶点坐标判断抛物线与直线y=n+1即可判断D.由函数图象知a<0,c>0,由对称轴在y轴左侧,a与b同号,得b<0,故abc>0,选项A 正确;二次函数与x轴有两个交点,故∆=240b ac->,则选项B错误,由图可知二次函数对称轴为x=-1,得b=2a,根据对称性可得函数与x轴的另一交点坐标为(1,0),代入解析式y=ax2+bx+c可得c=-3a,∠3a+c=0,选项C正确;∠二次函数y=ax2+bx+c的顶点坐标为(-1,n),∠抛物线与直线y=n+1没有交点,故D正确;故选:B.此题考查抛物线的性质,抛物线的图象与点坐标,抛物线的对称性,正确理解和掌握y=ax2+bx+c型抛物线的性质及特征是解题的关键.12.C由折叠的性质可得四边形EBFG是菱形从而判断∠∠正确;由角平分线定理即可判断DG≠GH,由此推出∠错误;根据F、C重合时的性质,可得∠AEB=30°,进而算出∠正确.连接BE,由折叠可知BO=GO,∠EG//BF,∠∠EGO=∠FBO,又∠∠EOG=∠FOB,∠∠EOG∠∠FOB(ASA) ,∠EG=BF,∠四边形EBFG是平行四边形,由折叠可知BE=EG,则四边形EBFG为菱形,故EF∠BG,GE=GF,∠∠∠正确;∠四边形EBFG为菱形,∠KG平分∠DGH,∠,DG≠GH,∠ S△GDK≠S△GKH,故∠错误;当点F与点C重合时,BE=BF=BC=12=2AB,∠∠AEB=30°,1752DEF DEB∠=∠=︒,故∠正确.综合,正确的为∠∠∠.故选C.本题考查矩形的性质,菱形的判断,折叠的性质,关键在于结合图形对线段和角度进行转换.13.x(x+1)(x-1)【解析】解:原式14.3 7用袋子中编号为偶数的小球的数量除以球的总个数即可得.解:∠从袋子中随机摸出一个球共有7种等可能结果,其中摸出编号为偶数的球的结果数为3,∠摸出编号为偶数的球的概率为37,故答案为:37.本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.15.-2连接OB ,AC ,交点为P ,根据O ,B 的坐标求解P 的坐标,再根据平行四边形的性质:对角线互相平分即可求出则C 点坐标,根据待定系数法即可求得k 的值.解:连接OB ,AC ,交点为P ,∠四边形OABC 是平行四边形,∠AP=CP ,OP=BP ,∠O (0,0),B (1,2),∠P 的坐标1,12⎛⎫ ⎪⎝⎭, ∠A (3,1),∠C 的坐标为(-2,1),∠反比例函数k y x=(k≠0)的图象经过点C , ∠k=-2×1=-2,故答案为-2.本题考查的是反比例函数图象上点的坐标特点,平行四边形的性质,求得C 点的坐标是解答此题的关键.16.332过B 点作BE//AD 交AC 于点E ,证明ADO EBO ∽,得到3,AO OE =再证明,ABE ACB ∠=∠利用1tan tan ,2BE AE ACB ABE CE BE ∠==∠==设,OE a =利用三角形的面积公式可得答案. 解:过B 点作BE//AD 交AC 于点E ,90,DAC ∠=︒∴ BE∠AD ,ADO EBO ∴∽, ∠,AO DO EO BO= 43BO OD = ∠3,4AO DO EO BO == 3,4AO OE ∴= 由1tan 2ACB ∠=, 1,2BE CE ∴= 2,CE BE ∴=90,,ABC BE AC ∠=︒⊥90,ABE CBE CBE ACB ∴∠+∠=︒=∠+∠,ABE ACB ∴∠=∠1tan tan ,2AE ACB ABE BE ∴∠=∠== 2,BE AE ∴=24,CE BE AE ∴==∠OAB OAD ABD CBD OCB OCD S S S S S S ∆∆+=+()()11221122AO AD AO BE AO AD BE AO OC AD BE OC OC AD OC BE •+•+===+•+• 设,OE a = 则3,4AO a = 7,4AE AO OE a ∴=+= 7,CE a = 8.OC OE CE a =+= 334.832ABDCBD a S AO S OC a ∆∆===故答案为:33217.2 分别计算负整数指数幂,锐角三角函数,绝对值,零次幂,再合并即可.解:101()2cos30|(4)3π--︒+--321=-31=2.=本题考查实数的运算,考查了负整数指数幂,锐角三角函数,绝对值,零次幂的运算,掌握以上知识是解题的关键.18.11a -,1. 先将分式进行化简,再把a 的值代入化简的结果中求值即可.213(2)211a a a a a +-÷+-+- 212(1)3(1)1a a a a a +-+-=÷-- 211(1)1a a a a ++=÷-- 211(1)1a a a a +-=⨯-+ 11a =- 当a=2时,原式1121==-. 本题考查了分式的化简求值,解决本题的关键是进行分式的化简.19.(1)50,10;(2)补全条形统计图见解析;(3)70°;(4)估计“总线”专业的毕业生有180名.(1)根据条形统计图和扇形统计图的数据计算即可.(2)先算出硬件专业的毕业生人数,再补充统计图即可.(3)先算出软件专业的占比,再利用周角相乘即可算出圆心角.(4)用600与总线所占比相乘即可求出.(1)由统计图可知155030%m ==,510%50n ==,n=10. (2)硬件专业的毕业生为5040%=20⨯人,则统计图为(3)软件专业的毕业生对应的占比为10100%=20%50⨯,所对的圆心角的度数为20%360=72⨯︒︒.(4)该公司新聘600名毕业生,“总线”专业的毕业生为60030%=180⨯名.本题考查条形统计图和扇形统计图的画图和信息获取,关键在于通过图象获取有用信息.20.(1)见解析;(2)245 CD=.(1)连接OC,由同旁内角互补得出AD//OC,可得∠OCB=∠E,即可推出∠ABE=∠E,AE=AB.(2)连接AC,由勾股定理求出AC,由∠EDC∠∠ECA得出相似比,求出CD即可.(1)证明:连接OC∠CD与∠O相切于C点∠OC∠CD又∠CD∠AE∠OC//AE∠∠OCB=∠E∠OC=OB∠∠ABE=∠OCB∠∠ABE =∠E∠AE =AB(2)连接AC∠AB 为∠O 的直径∠∠ACB =90°∠8AC ==∠AB =AE ,AC ∠BE∠EC =BC =6∠∠DEC =∠CEA, ∠EDC =∠ECA∠∠EDC ∠∠ECA ∠DC EC AC EA= ∠6248105EC CD AC EA =⋅=⨯=. 本题考查圆与三角形的综合性质及相似的证明和性质,关键在于合理作出辅助线将已知条件转换求解.21.(1)肉粽得进货单价为10元,蜜枣粽得进货单价为4元;(2)第二批购进肉粽200个时,全部售完后,第二批粽子获得利润最大,最大利润为1000元.(1)设肉粽和蜜枣粽的进货单价分别为x 、y 元,根据题意列方程组解答;(2)设第二批购进肉粽t 个,第二批粽子得利润为W ,列出函数关系式再根据函数的性质解答即可.(1)设肉粽和蜜枣粽的进货单价分别为x 、y 元,则根据题意可得:50306206x y x y +=⎧⎨-=⎩. 解此方程组得:104x y =⎧⎨=⎩. 答:肉粽得进货单价为10元,蜜枣粽得进货单价为4元;(2)设第二批购进肉粽t 个,第二批粽子得利润为W ,则(1410)(64)(300)2600W t t t =-+--=+,∠k =2>0,∠W 随t 的增大而增大,由题意2(300)t t ≤-,解得200t ≤,∠当t =200时,第二批粽子由最大利润,最大利润22006001000W =⨯+=,答:第二批购进肉粽200个时,全部售完后,第二批粽子获得利润最大,最大利润为1000元.此题考查二元一次方程组的实际应用,不等式的实际应用,一次函数解决实际问题,一次函数的性质,正确理解题意列出方程组或函数、不等式解决问题是关键.22.(1)见解析;(2)当∠EAG =∠BAD 时,BE =DG 成立;理由见解析;(3)22260BG DE +=.(1)根据四边形ABCD 和AEFG 是正方形的性质证明∠EAB ∠∠GAD 即可;(2)根据菱形AEFG 和菱形ABCD 的性质以及角的和差证明∠EAB ∠∠GAD 即可说明当∠EAG =∠BAD 时,BE =DG 成立;(3)如图:连接EB ,BD ,设BE 和GD 相交于点H ,先根据四边形AEFG 和ABCD 为矩形的性质说明∠EAB ∠∠GAD ,再根据相似的性质得到90GHE EAC ︒∠=∠=,最后运用勾股定理解答即可.(1)证明:∠四边形ABCD 为正方形∠AB =AD ,90DAB ︒∠=∠四边形AEFG 为正方形∠AE =AG ,90EAG ︒∠=∠EAB GAD ∠=∠在∠EAB 和∠GAD 中有:AE AG EAB GAD AB AD =⎧⎪∠=∠⎨⎪=⎩∠∠EAB ∠∠GAD∠BE =DG ;(2)当∠EAG =∠BAD 时,BE =DG 成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方法二:
2020 九年级数学教学质量检测 数学参考答案与评分标准 第 7 页 共 7 页
① 当 ABC ∽ MCN 时, MN = 6 10 ,∠MNB=45°,∠CNB=90° 5
∵
xN
18 5
2020 九年级数学教学质量检测 数学参考答案与评分标准 第 1 页 共 7 页
=
1
.
(x 1)(x 2)
--------------------------------1 分(累计 4 分)
∵ 2 x 2 ,且 x 为整数
由题 x 2,1
∴x0
--------------------------------1 分(累计 5 分)
∵ C(0, 3a) , D(0,3a)
∴直线 BC 与直线 BD 关于 x 轴对称
∴ x 轴上一点 P 到直线 BC,BD 的距离相等--------------------------------1 分(累计 3 分)
令 x 1 ,则 y 4a , F(1, 4a)
y ax2 2ax 3a 联立
∴ x , y 的值分别为 8,12.
---------------2 分(累计 4 分)
(2)设甲种水果售出 m kg,则乙种水果售出 (1000 m) kg,该平台利润为 w 元,则
m 1 (1000 m) 3
∴ m 250
---------------1 分(累计 5 分)
w (12 8)m (14 12)(1000 m) 1000a ,
∴ △ABD≌△MCD,
--------------------------------1 分(累计 4 分)
∴ DA = DM ,∠CDM=∠BDA
∴ ∠ADM=∠BDC=180°-∠BAC=120°
在△ADM 中,作 AM 边上的高 h
则 AD=2h , AM =2 3h
--------------------------------1 分(累计 5 分)
D
F
23. 解:(1)∵抛物线 y ax2 bx c 交 x 轴于点 A(- 1, 0) , B(3, 0)
设 y a(x 1)(x 3)
∵ C 点坐标为 (0,3)
∴ 3 a 1(3) , ∴ a 1 ∴ y (x 1)(x 3) .
--------------------------------1 分(累计 1 分) --------------------------------1 分(累计 2 分)
(其他方法酌情给分) (3)∵∠CNM=45°=∠CBA,∠CHN=∠MHB ∴△CHN∽△MHB
∴ CH NH MH BH
∵∠CHM=∠NHB ∴△CHM∽△NHB ∴∠HBN=∠CMH ∴∠1=∠MCN
∵ ABC 与 CMN 相似,∠CNM=∠CBA
∴∠MCN=∠ACB 或∠CAB -------------------------1 分(累计 5 分)
(4)750.
--------------------------------2 分(累计 7 分)
20. (1)证明:在正方形 ABCD 中,AD∥BC,
∴ ADE ECG , HAE 1.
∵ E 是 DC 的中点,
∵ HAE EAF, HAE 1
∴ EAF 1.
∴ FA=FG ∴ □AFGH 是菱形
--------------------------------1 分(累计 3 分) --------------------------------1 分(累计 4 分)
A
DH
2
4
E
3
B
FC
(2) ∵ □AFGH 是菱形 ∴ AG⊥FH, ∴ ∠2+∠4=90° ∵ ∠ADE=90° ∴∠2+∠DAE=90° ∴ ∠4=∠DAE ∵E 为 CD 中点
∴ DE=CE.
∴ △ADE≌△GCE.
∴ AE=EG,
--------------------------------1 分(累计 1 分)
同理△HDE≌△FCE.
∴ HE=FE.
--------------------------------1 分(累计 2 分)
∴四边形 AFGH 是平行四边形
2020 深圳市中考 5 套红卷 数学(第 4 套)答案及评分标准
第一部分 选择题
一、(本大题共 12 题,每小题 3 分,共 36 分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A B D C C D B D C B B
第二部分 非选择题 二、填空题:(本大题共 4 题,每小题 3 分,共 12 分)
22. 解:(1)连接 DO,BO,CO,
∵ D 是 BC 的中点,
∴ BD CD ,
2020 九年级数学教学质量检测 数学参考答案与评分标准 第 3 页 共 7 页
∴ ∠BOD=∠COD, ∵ OB=OC, ∴ OD⊥BC,
∵ 直线 DF 是⊙O 的切线,
∴ OD⊥DF, ∴ DF∥BC
A
--------------------------------1 分(累计 1 分)
∴ S菱形AFGH AH AB 5 4 20 --------------------------------1 分(累计 8 分)
(其他方法酌情给分)
21.
解:(1)
5x 10 12x 5
y y
160, 156;
---------------2 分(累计 2 分)
解得:
x 8, y 12;
1
G
∴ DE 1 DC 1 AD
2
2
2020 九年级数学教学质量检测 数学参考答案与评分标准
第2页 共7页
∵∠ADE=90°
∴tan∠DAE= DE 1 AD 2
∴tan∠4=
DH DE
1 2
∴DE=2 ∴AB=CD=2DE=4 ∴AH=5
--------------------------------2 分(累计 6 分) --------------------------------1 分(累计 7 分)
即 y x2 2x+3
2020 九年级数学教学质量检测 数学参考答案与评分标准 第 5 页 共 7 页
(2)对抛物线 y a(x 1)(x 3) ,令 x 0 ,则 y 3a , C(0, 3a)
对直线 l : y kx 3a ,令 x 0 ,则 y 3a , D(0,3a)
令 x 3 ,则 y 3k 3a 0 , ∴ k a ∴ y ax 3a
y l
C N
AO M
1
B
x
方法一:
① 当 ABC ∽ MCN 时,∠1=∠ACB=∠MCN tan 1 tan ACB 2 ,∠MNB=45°
求得直线 l : y 2x 6
∴ N(18 , 6) 55
6 18 构造如图所示的“一线三等角”,可得 G1(5 , 5 )
----------------------------1 分(累计 8 分)
∴ CA CB AB CH CA AH
设 BC 3BH =3k
∴ CA2 CB CH 12k 2
--------------------------------1 分(累计 7 分)
∴ CA 2 3k
∴ CA AB CB = 3k 3 CH AH CA 2 3k 2
∴ CH 2 3CA, AH 2 3AB
SCMN =( CM )2 ( 3 )2 9
SABC AC
10 10
2020 九年级数学教学质量检测 数学参考答案与评分标准 第 6 页 共 7 页
∴ SCMN
9 10
SABC
27 5
为最小,此时
xN
18 ,点 M 与点 O 重合 5
--------------------------------1 分(累计 7 分)
2020 九年级数学教学质量检测 数学参考答案与评分标准 第 4 页 共 7 页
∴△AEB≌△AEN ∴EN=BE,∠ABE=∠ANE ∴GA=GE+EB=GE+EN=GN ∴∠ANE=∠GAN=∠HAB+∠BAC 又∠ABE=∠HAB+∠AHB ∴∠AHB=∠BAC=60° ∵∠ACB=∠HCA ∴△CAB∽△CHA
∴ AB AC AM 2 3h 3 为定值 . --------------------------------1 分(累计 6 分) AD AD 2h
A
O
B
E
C
F D
M
(3)延长 GE 交 AC 于点 N,则∠AEN=∠GED ∵GE=GD ∴∠GED=∠GDE 由(1)BC∥DF ∴∠AEB=∠GDE ∴∠AEB=∠AEN ∵∠BAD=∠CAD,AE=AE
17. 解: 2 cos 30 3 2 12 (2020)0
= 2 3 ( 3 2) 2 3 1 2
= 3 3 22 3 1
= 1.
18.
解:
1 x2 1
1 x 1
x2 x
4 1
=
1 x2 1
x x2
1 1
(x
x 1 2)(x
2)
= 2 x x 1 (x 1)(x 1) (x 2)(x 2)
3
3
∴ CH +AH 2 3CA+ 2 3AB= 2
3
3
3
--------------------------------1 分(累计 8 分)
3(CA AB) 2 3 3AD 4 3 3
--------------------------------1 分(累计 9 分)
