数字逻辑课件第7章状态化简
数字逻辑设计及应用教学课件:7-5 同步状态机设计2

6、draw the logic circuit(略)
说明: 最小冒险法 所有未用状态 “安全”状态. 最小成本法 所有未用状态的下一状态作为无关项 电路的激励方程简单,不够安全.
15
合理的状态赋值
选择复位时容易进入的状态作为初始状态.
使每次转移时要发生改变的状态变量数最小化
Example 1(P558);Example 2(P566);Example 3(P570)
State diagram design(T-bird tail-light )
The Guessing Game
4
State table design(example 1)(P554)
1、transition table
2、minimize
S
AB 从23中选5种一共有
8!
5种编码5个状态,又有5!种
00
01
种 5!×3! Z 11 10
8! A0 初始状态 INIT A0 A1 共有 3、 State assignment. 5! · 5!×3! A上捕获一个0 A0 OK0 OK0 A1 A上捕获一个1 A1 OK,A值为0 OK0
Design
a clocked synchronous state machine with two inputs, X and Y, and one output, Z. The output should be 1 if the number of 1 inputs on X and Y since reset is a multiple of 4, and 0 otherwise. 对两个输入X和Y同时计数,当1的个数为4的 整数倍时输出为1.
数字电子技术优质课件精选——《逻辑代数的运算法则及其化简》

解:设A、B、C分别表示三个车间的开工状态
开工为1,不开工为0; G1和G2运行为1,停机为0。
010 011 100
AB BC CA
101
G2 A BC ABC ABC ABC
110 111
G1 G2
00 01
01 10 01 10 10 11
ABC ABC ABC ABC
⑶由逻辑式画出逻辑图 G1
&
20.6 组合逻辑电路的分析与综合
G2
&
&
&
&
&
&
&
&
AB C
AB
C
本章作业
G1 G2
00 01
01 10 01 10 10 11
20.6 组合逻辑电路的分析与综合
⑵ 由逻辑状态表写出逻辑式并化简
G1 ABC ABC ABC ABC A B C
G2 A BC ABC ABC ABC 0 0 0
用与非门构成逻辑电路
001
G1 AB BC CA
AB BC CA
B.
20.6 组合逻辑电路的分析与综合
1
&
A
& Y
A•B
1
B
. ⑴ 写出逻辑式 Y = AB AB = AB +AB
20.6 组合逻辑电路的分析与综合
⑵ 列逻辑状态表
AB
Y
数字逻辑基础卡诺图化简
101
0
110
0
1 2020/8/14 1 1
1
14
练习:三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
111
1
2020/8/14
15
(2)从最小项表达式画卡诺图 把表达式中所有的最小项在对应的小方块中填
入1,其余的小方块中填入0。
例4: 画出函数Y(A、B、C、D)= ∑m(0,3,5,7,9,12,15) 的卡诺图。
① 无关项的概念
对应于输入变量的某些取值下,输出函数的值可 以是任意的(随意项、任意项),或者这些输入变量的 取值根本不会(也不允许)出现(约束项),通常把这 些输入变量取值所对应的最小项称为无关项或任意项, 在卡诺图中用符号“×”表示,在标准与或表达式中用 ∑d( )表示。
例:当8421BCD码作为输入变量时,禁止码1010~ 1111这六种状态所对应的最小项就是无关项。
相邻 相邻
② 几何相邻的必须
逻辑相邻:变量的 取值按00、01、11、 10的顺序(循环码 ) 排列 。
图1-11 三变量卡诺图的画法
2020/8/14
12
不 相邻
相邻
相邻
图1-12 四变量卡诺图的画法
正确认识卡诺 图的“逻辑相邻”: 上下相邻,左右相 邻,并呈现“循环 相邻”的特性,它 类似于一个封闭的 球面,如同展开了 的世界地图一样。
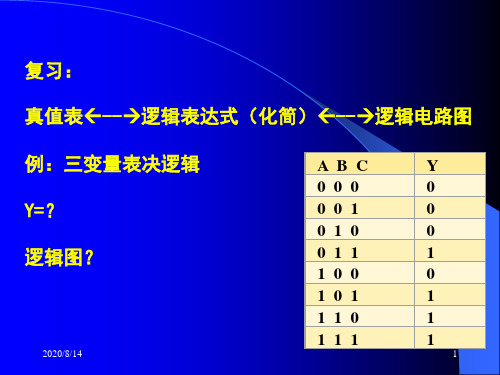
复习:
真值表--逻辑表达式(化简)--逻辑电路图
例:三变量表决逻辑 Y=? 逻辑图?
2020/8/14
数字逻辑电路(第五到七章)

图4-47 某移位寄存器的逻辑符号解:引脚图(b)中,CR为异步复位端,SH/LD端为右移/预置控制端,CP1和CP0为时钟输入端,二者相或,D S为串行输入端,D0~D7为预置信号输入端,Q7为串行输出端。
4.3.46 电路如图4-48所示,试画出其状态表。
图4-48 题4.46电路解:设Q A Q B Q C Q D初态为0000或0011,可构成模7移位型计数器。
4.3.47 现欲用2114构成2K×8的静态存储器,试画出其逻辑图。
解:2114RAM是1K×4位存储器,要求字、位分别扩展2倍。
先作位扩展产生8位I/O信号,再进行字扩展。
用与非门输入和输出信号(输入高位地址)分别作片选信号。
电路也可将字。
位分别扩展4倍。
155第5章同步时序电路和数字系统设计要求掌握用触发器和用MSI时序模块设计同步时序电路,了解并逐渐掌握VHDL语言及其电路设计方法。
5.1 学习要点5.1.1 由触发器和组合电路实现同步时序电路用触发器和组合电路实现同步时序电路的指导思想是尽可能少的触发器及门电路来实现电路的设计。
设计的过程如图5-1所示。
原始状态表图5-1 用触发器设计同步时序电路的过程1.原始状态表(图)的建立由逻辑功能文字描述到建立原始状态表(图)是时序电路设计的关键的一步,常因为状态图比状态表更直观,所以可先导出状态图,然后再列状态表。
该过程可分两步:(1) 列出电路所必须记住的不同的输入序列或输出序列的特征,以确定该电路应包含的状态,并列出这些状态(用符号S0,S1……表示)。
(2) 分别以这些状态为现态,考察在每一种可能输入组合作用下电路应转入哪个状态及其相应的输出。
如发现有尚未定义的新状态,则把这新状态补充到原来的状态图(表)中去,并构成完整的状态图(表)。
2.状态化简原始状态表(图)能正确地反映电路的逻辑要求,但不一定是最简的,其中某些状态有可能是等价的,它们可以合并。
状态的多少将直接影响到电路的规模。
数字逻辑基础教学课件PPT

(1)逻辑函数式→真值表 举例:例1-6(P9) (2)逻辑函数式→逻辑图 举例:例1-7(P10) (3)逻辑图→逻辑函数式 方法:从输入到输出逐级求取。
举例:例1-8(P10)
(4)真值表→函数式
方法:将真值表中Y为 1 的输入变量相与,取 值为 1 用原变量表示,0 用反变量表示, 将这 些与项相加,就得到逻辑表达式。这样得到的 逻辑函数表达式是标准与-或逻辑式。
断开为0;灯为Y,灯亮为1,灭为0。
真值表
AB Y 00 0 01 1 10 1 11 1
由“或”运算的真值表可知
“或”运算法则为:
有1出
0+0 = 0 1+0 = 1
1
0+1 = 1 1+1 = 1
全0为
0
⒊ 表达式
逻辑代数中“或”逻辑关系用“或”运算 描述。“或”运算又称逻辑加,其运算符为 “+”或“ ”。两变量的“或”运算可表示
0
卡诺图是一 种用图形描 述逻辑函数
的方法。
00 0 01 0 11 0
10 1
例:函数 F=AB + AC
ABC F
000 0
1 001 1 010 0
1 011 1
1 100 1
0
101 1 110 0
1 111 0
1.逻辑函数式
特点:
例:函数 F=AB + AC
(1)便于运算; (2)便于用逻辑图实现; (3)缺乏直观。
真值表
K
Y
0
1
1
0
由“非”运算的真值表可知 “非”运算法则为:
0 =1 1 =0
⒊ 表达式
“非”逻辑用“非”运算描述。“非”运 算又称求反运算,运算符为“-”或“¬”, “非”运算可表示为:
数电课件第七章

QN Q’
Q QN
……Alternate Holding
when S=0, R=0, If current state Q=QN’, hold the last state.
9
PRINCIPLES AND PRACTICES
R=0 and S=0
R=0 Q*=QN’
Function table
? ?
14
PRINCIPLES AND PRACTICES
2.
S-R
Latch
Logic symbol
State transition truth table
S R
Q Q
S_L R_L Q 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1
Q*
Using NAND Gates
Timing diagram
(1) (2)
(3)
(5) (4)
(6) (7) (8) (9)
(11)
(10)
(12)
13
PRINCIPLES AND PRACTICES
Minimum Pulse Width (最小脉冲宽度)
Minimum Pulse Width S
R
Q
tpLH(SQ) tpHL(RQ)
Simulation
R
Low level High level
S
11
PRINCIPLES AND PRACTICES
Characteristic equation
state transition truth table
S R 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1
数字逻辑设计第七章(2)D锁存器
RD DOUT[3:0]
Xi Yi Ci
X Y
S
CI CO
锁存器的应用
Si Ci+1
串行输入、串行输出 注意:时钟同步
QD Q C CLK
Xi Yi
时钟控制
再谈串行输入 加法器的实现
Ci
暂存
XY CI CO
S
Si
Ci+1
9
触发器
只在时钟信号的边沿改变其输出状态
正边沿 上升沿
负边沿 下降沿
CLK
Q
15
D锁存器 ——电平有效 D触发器 —— 边沿有效
触发器的应用
利用触发器作为移位寄存器(图1)
思考:能否将触发 器改为锁存器(图2) D
F/F
F/F
D Q Q1 D Q Q
CLK Q
CLK Q
D CLK
Q1 Q
16
CLK D
CLK
(图1)
latch
latch
Q1
DQ
DQ Q
CQ
CQ
(图1)
D触发器的定时参数
QQn+*1==SS++RR’’··QQ
Q —— 当前状态(原态、现态)
Q* —— 下一状态(新态、次态)
S·R = 0(约束条件)
31
J K C
C J K Qm Q
32
SQ
SQ
C 主 Qm C 从
RQ
RQ
逻辑符号 Q
JQ QL C
KQ
1 箝位
功能表
C=1期间,
JK Q
0 1
J的变化只引起 Qm改变一次
CLK=1时, 主锁存器不工作,Qm 保持不变 从锁存器工作,将 Qm 传送到输出端
数字逻辑基础卡诺图化简
1 0 0
1 0 1 1 1 0 1 1 1
2019/3/18
0
1 1 1
15
(2)从最小项表达式画卡诺图 把表达式中所有的最小项在对应的小方块中填 入1,其余的小方块中填入0。 例4: 画出函数Y(A、B、C、D)= ∑m(0,3,5,7,9,12,15) 的卡诺图。
2019/3/18
图1-14
A
相邻
2019/3/18 28
A
BC
相邻
2019/3/18
29
A
BC BD
Y A BC B D
2019/3/18 30
例8: 化简图示逻辑函数。 解:
1
2 多余 的圈
4
3
Y ACD ABC AC D ABC
2019/3/18
1
2
3
4
31
圈组技巧(防止多圈组的方法):
2019/3/18 22
m3
BCD
m11
图1-15
2019/3/18
两个最小项合并
23
图1-16
2019/3/18
四个最小项合并
24
2019/3/18
图1-17
八个最小项合并
25
(2)利用卡诺图化简逻辑函数 A.基本步骤: ① 画出逻辑函数的卡诺图; ② 合并相邻最小项(圈组); ③ 从圈组写出最简与或表达式。 关键是能否正确圈组 。 B.正确圈组的原则 ① 必须按2、4、8、2N的规律来圈取值为1的相 邻最小项; ② 每个取值为1的相邻最小项至少必须圈一次, 但可以圈多次; ③ 圈的个数要最少(与项就少),并要尽可能 大(消去的变量就越多)。
2019/3/18 37
数字逻辑课件——逻辑函数的表格化简法
再重复同样的方法,依次类推。我们可以逐步从(n-2), (n-3),…个变量项中得到含有(n-3),(n-4),…个 变量的各项,一直进行到最后一组以致其中各项已无法相邻合 并为止。
这时,在所有各项旁没有记号“√”的项就是我们需要的项, 称为质蕴涵项(Prime implicant),亦即不含多余变量的项, 也就是它再不能同其它项合并而得到变量更少的项了。
表1-3-9(c) (n-2)个变量的与项
组号
最小项 编号
变量
ABC D
2
10,11
-1 - 1
P7
14,15
7
P1 A B D,
P2 A B C ,
P3 A C D,
P4 A CD,
P5 ABC , P6 A CD, P7 B D
图1-3-19 函数以质蕴涵项表示
函数F就是这些质蕴涵项之和,但它不是最简的结 果。画出函数F的卡诺图,如图1-3-19所示。
13(b),
表1-3-13(a) 质蕴涵表
mi P
m0 m1 m3 m6 m7 m9 m11 m12 m15
P1
×
P2 × ×
P3
××
P4
××
××
P5
×
×
×
×
22
表1-3-13(b) 简化质蕴涵表
表1-3-13(c)
mi P
m0 m15
P1
m3
m6
m9 m12
×
P2 ×
P3
×
P4
×
×
P5
×
×
mi P
0
变量
ABCD 0000
状态化简_计算机逻辑设计_[共6页]
第 6 章 时序逻辑分析与设计
表 6.28
当前状态
A B C D E F G
例 6.17 状态表
下一个状态
x=0
x=1
B
C
D
F
F
E
B
G
F
C
E
D
F
G
输出 Z
1 1 0 1 0 0 0
解:
根据状态表,可以得出图 6.72 所示的隐含表。第一次划分时,将所有的状态放在同一个块中,即
P1 = (ABCDEFG) 第二次划分,将具有不同输出的状态分开,如图 6.72(a)所示,输出不同的状态肯定不等价。
所谓状态化简,就是要获得一个最小化的状态表。这个表不仅能正确地反映设计的全部需求, 而且状态的数目最少。若状态数能够减少,则原始设计中必定有一些状态与其他一些状态对状态 机整体表现所做的贡献是等价的。可以用下面的定义对此做出更正规的描述。
对于状态 Si 和 Sj,当且仅当每种可能的输入序列都产生相同的输出序列时,这两个状态 Si 和 Sj 才被称为等价。根据该定义可知,如果 Si 和 Sj 等价,那么 Si 和 Sj 对相同输入的对应次态 Su 和 Sv 也等价。
这意味着必须将状态 A、B、D 与状态 C、E、F、G 区分开。因此新的划分有两个块。
A
B BD/CF
C
×
×
D
CG
GF
×
E
×
×
√
×
F
×
× FE/ED × CD
G
×
×
EG
× CG EF/DG
A
B
C
DE
F
G
(a)
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X Y
A B C D E
0 C/1 C/1 B/ 1 D/ 1 D/ 1
1 B/ 0 E/0 E/0 B/ 1 B/ 1
S(t +1) / Z
Y(t +1) / Z
例2:化简图示原始状态表 :
1/0 S1 S2
1/0
0/0 S3
0/0
0/0 S3
次态维持
0/0 S1 1/1 S3 1/0 0/1 S5 后继状态等效 0/0 S2 1/1 S4 1/0 0/1 S1,S2 1/1 S3,S4 0/1 S5 1/0 0/0 S1 1/1
0/0 0/0 S2 1/1 S3,S4 0/1 S5 1/0
0/0 S1 1/1 1/0 0/0 S3 0/1 1/1 1/1 S6 1/0 0/1 次态循环 S3,S4 1/1 S5,S6 1/0 0/0 S4 0/1 0/0 0/0 S2 1/1
S1,S2 1/1 0/0
S5
在原始状态表中判断状态的等效
X Y
A B C D E
0 B/ 0 A/ 0 A/ 0 E/1 E/1
CF等效且 等效且AE,BE次态 等效且 次态 循环,所以AE等效 等效, 循环,所以 等效, 也等效。 也等效 X BE也等效。 X AE CF X X B X X X X CD DE D X X E X F
√
X C
请同学自己求出最大等效类、 请同学自己求出最大等效类、作出最小状态表
作业: 作业:P263~265 5.4 5.7(用Verilog HDL建模) ( 建模) 建模 补充题: 补充题: 1)画出满足下列要求的序列检测器原始状态 ) 图和最简状态表。 图和最简状态表。 输入X: 输入 …0 0 1 0 1 0 1 1 0 1… 输出Z: 输出 …0 0 0 0 1 0 1 0 0 1… 2)画出3位二进制码的串行奇偶检测器的原始状 )画出 位二进制码的串行奇偶检测器的原始状 态图和最简状态表 输入为X,每三位一组, 和最简状态表。 态图和最简状态表。输入为 ,每三位一组, 其中“ 的个数为偶数时 输出Z=1,否则 的个数为偶数时, 其中“1”的个数为偶数时,输出 , Z=0。 。
B C D E
BE
BC BE X X √ X X X X √
Y(t +1) / Z
1)作隐含表 )
A
B
C
D
2)求等效对 ) ● 顺序比较 所有“状态对”逐一检查、比较。 所有“状态对”逐一检查、比较。 等效: 等效:方格内画 √ ; 不等效: 不等效:方格内画 x ; 与其它状态对有关:方格内填写相关状态对。 与其它状态对有关:方格内填写相关状态对。
7.3.1 完全给定同步时序电路状态表的化简
完全给定同步时序电路是指其状态表中的所有 次态及输出都是确定的。 次态及输出都是确定的。
完全给定同步时序电路状态表的化简, 完全给定同步时序电路状态表的化简,是利 用状态之间的等效关系进行的。 用状态之间的等效关系进行的。 等效关系进行的
有 关 概 念 状态等效 假设状态S 假设状态SA和SB是完全给定同步时序电路状态 表中的两个状态,如果对于所有可能的输入序列, 表中的两个状态,如果对于所有可能的输入序列, 分别从S 分别从SA和SB出发,所得到的输出响应序列完全相 出发, 同,则两个状态是等效(等价)的,称SA和SB为等 则两个状态是等效(等价) 效对,记作:(SA,SB)。 效对,记作:( :(S 所有可能的输入序列,指输入序列的长度和结 所有可能的输入序列, 构是任意的。 构是任意的。
因为CF等效,所以 等效 因为 等效,所以AB等效 等效
现态 A B C D E F G
次态/输出 次态 输出 输入X=0 输入 C/0 F/0 F/0 D/1 C/0 C/0 C/1 输入X=1 输入 B/1 A/1 G/0 E/0 E/1 G/0 D/0
B C D E F G
CF X X BE X X A
完全给定同步时序电路原始状态表的化简过程, 完全给定同步时序电路原始状态表的化简过程,就 原始状态表的化简过程 是寻找最大等效类, 是寻找最大等效类, 将每个最大等价类中的所有状态合 并为一个新状态,从而得到最小状态表的过程。 最小状态表的过程 并为一个新状态,从而得到最小状态表的过程。 化简后的状态数等于最大等效类的个数。 化简后的状态数等于最大等效类的个数。源自Y(t +1) / Z
化简后的状态图: 化简后的状态图:
0/ 0
S1
1/ 1
S2
0/ 1
X 0 S S1 S1 / 0 S2 S2 / 1
1 S2 / 1 S1 / 0
S(t +1) / Z
1/ 0
利用隐含表进行完全给定同步时序电路状态表的化简 利用隐含表进行完全给定同步时序电路状态表的化简 完全 一般步骤: 一般步骤: 1)作隐含表 ) 2)寻找等效对 ) 3)求出最大等效类 ) 注意: 各最大等效类之间不应出现相同状态 注意:a)各最大等效类之间不应出现相同状态 b)原始状态表中的每一个状态必须属于某一个最 原始状态表中的每一个状态必须属于某一个最 大等效类 4)作出最小化状态表 )
●关联比较 若相关状态对都等效,则方格对应的状态对等效。 若相关状态对都等效,则方格对应的状态对等效。不增 加标志。 加标志。 若相关状态对有一个不等效, 若相关状态对有一个不等效,则方格对应的状态对不等 效。画 / 。
B C D E
BE
BC BE X X √ X X X X √
A
B
C
D
等效对为: 等效对为: (B,C),(D,E) , ) , )
在等效关系中,等效对是狭义的概念, 在等效关系中,等效对是狭义的概念,针对两个状态 而言。等效类是广义的概念,针对若干个状态而言, 而言。等效类是广义的概念,针对若干个状态而言,甚至 一个状态可称为等效类。 一个状态可称为等效类。
最大等效类
不是任何其它等效类子集的等效类称为最大等效类。 不是任何其它等效类子集的等效类称为最大等效类。
X Y
A B C D E
0 B/ 0 A/ 0 A/ 0 E/1 E/1
1 E/1 E/1 D/ 1 B/ 0 B/ 0
B C D E
A
B
C
D
Y(t +1) / Z
例1: 化简图示状态表。 : 化简图示状态表。
X Y
A B C D E
0 C/1 C/1 B/ 1 D/ 1 D/ 1
1 B/ 0 E/0 E/0 B/ 1 B/ 1
7.3.2 不完全给定同步时序电路状态表的化简
在原始状态图上判别状态的等效
输入/输出 输入 输出 S1 0/0 1/0 S2 0/0 1/0 0/0 1/0 S1,S2
S3
S4
S3
S4
次态相同
输入/输出 输入 输出 1/0 S1 1/0 0/0 S3 0/0 0/0 S3 S2 S1,S2 1/0
次态交错
输入/输出 输入 输出 1/0 S1,S2
7.3 状态化简 通过原始状态图就可以得到一张原始状态表。 通过原始状态图就可以得到一张原始状态表。 本节提出的问题是: 本节提出的问题是:这张状态表中的状态数是不是 最少?这直接关系到电路的繁简和优化。 最少?这直接关系到电路的繁简和优化。 当采用硬件描述语言建模时,关系到PLD器件 当采用硬件描述语言建模时,关系到PLD器件 中逻辑资源的有效占用。 中逻辑资源的有效占用。 为求得最简状态表, 为求得最简状态表,需要我们将等价的状态从 原始状态表中解析出来,进行化简后形成一张最简 原始状态表中解析出来, 状态表(最小状态表)。 状态表(最小状态表)。
3)求出最大等效类 ) 利用等效状态的对称性、自反性、传递性,求出等效类。 利用等效状态的对称性、自反性、传递性,求出等效类。 {B,C},{D,E},{A}。 , , 。 等效类 {B,C},{D,E},{A} 均不包含在任何其他等效类 , , , , 是最大等价类。 中, 所以 {A},{B,C},{D,E} 是最大等价类。 , , , , 4)作最小化状态表 ) 令S1={A},S2={B,C},S3={D,E} , , , ,
1 E/1 E/1 D/ 1 B/ 0 B/ 0
输出不相等,则不等效。例如: 和 输出不相等,则不等效。例如:C和D… 输出相等时: )次态相等,等效。如状态 输出相等时: 1)次态相等,等效。如状态D 和E等效; 等效; 等效 2)次态交错,等效。如状态 )次态交错,等效。如状态A 等效; 和B等效; 等效 3)后继状态等效,等效。此例 )后继状态等效,等效。 是否等效, 中B和C是否等效,要看 和 和 是否等效 要看E和 D是不是等效,因为 和D等 是不是等效, 是不是等效 因为E和 等 所以B和 等效 等效。 效,所以 和C等效。
从整体上讲, 从整体上讲,原始状态表已经反映了各状态在 任意输入序列下的输出。 任意输入序列下的输出。 等效状态可以合并为一个状态, 等效状态可以合并为一个状态,这种合并不会 改变电路的外部特性。 改变电路的外部特性。 等效状态的三个特点: 等效状态的三个特点: ),则 ●对称性:若(SA,SB),则(SB,SA)。 对称性: 。 ●自反性:对任何状态,( A,SA)。 自反性:对任何状态,(S ,( ),则 ●传递性:若(SA,SB)且(SB,SC),则(SA,SC)。 传递性:
等效(等价) 判断原始状态表中两个状态是否 等效(等价) 的标准: 的标准: 如果两个状态, 如果两个状态,对每一位可能的输入都满足下 列两个条件,则这两个状态等效。 列两个条件,则这两个状态等效。 第一,它们的输出完全相同。 第一,它们的输出完全相同。 第二,它们的次态属于下列情况之一: 第二,它们的次态属于下列情况之一: 1)次态相同 ) 2)次态交错或者次态维持 ) 3)后继状态等效 ) 4)次态循环 )
