山东省泰安市英雄山中学2019届高三文综10月月考试题
(解析版)山东省泰安市第一中学2018-2019学年高一10月学情检测语文试题

泰安一中2018-2019学年高一10月学情检测语文试题阅读下面的文字,完成小题。
汉字危机中国的书写交流进入键盘化时代只有十几年,任何一个初次接触电脑的人通过简单的学习都能迅速掌握文字输入。
随着电脑的普及,现在很多人写字总是提笔忘字,尤其是经常使用的汉字往往一下想不起来了,这跟他受过高等教育,掌握无数信息和知识的身份有点不符。
很多人纷纷惊呼汉字危机来了,拯救汉字刻不容缓。
书写是记忆汉字的最好方式,只有经常书写,才能记住一个字该怎么写。
过去用笔书写汉字基本上是音、形、义同时进行,键盘输入就出现问题了,它不是直接写汉字,而是让你在候选的字码中去选择正确的那个字。
这就是汉字在键盘输入时代面临的一个问题,换句话说,这就是音素文字和语素文字的最大区别。
所有音素文字(英语、德语、法语、西班牙语等)它们只有音和形,而且音形基本统一,打字本身就是书写过程。
我们是拼音解决汉字输入问题,而不是在键盘上打笔画。
五笔字型不会让你忘记一个汉字怎么写,但是可能会让你忽略它该怎么读;拼音输入可以让你知道一个字怎么读,却让你慢慢忘记它怎么写。
在信息时代,中国人开始遇到能说能读能输入但可能不会写的问题了。
这也暴露了汉字的自身局限问题。
网络时代屡屡出现新词,人们对“雷”、“囧”这类汉字就赋予了新的含义。
从每年出现的网络流行语中不难看出,新的词语越来越多,看上去也越来越没文化含量,继而还可能导致汉语的使用环境和美感越来越差。
网络语言通过互联网的病毒式传播迅速扩散全球,但死得也非常快。
它只是迎合某一类信息某一种情绪在传播的当口被创造出来,并随着这种氛围的消失而慢慢消亡,能留下来的凤毛麟角。
为了提高书写效率,方便学习和交流,开始出现俗字、新字,汉字的数量在不断增加,但却有不断简化的趋势。
是否要恢复繁体字的讨论没有太大意义,因为很多汉字究竟怎么写,它的结构组合究竟是什么意思你可能都觉得不重要了。
今天80%以上的中国人都会使用汉字,这其中多数人就像街头对话一样也仅仅是用来交流,而不是用来写作或研究。
高中政治 2024年山东省泰安市高考政治三模试卷

2024年山东省泰安市高考政治三模试卷一、选择题:本题共15小题,每小题3分,共45分。
每小题只有一个选项符合题目要求。
1.(3分)从1840年到1905年的几十年间,西方列强通过一个比一个苛刻的不平等条约,强迫中国割地、赔款,贪婪地攫取国的种种特权。
人民除遭受帝国主义压迫外,还要在本国封建主义、官僚资本主义残酷压迫下苦苦挣扎。
党领导人民经过28血奋战,取得新民主主义革命的伟大胜利,实现了民族独立、人民解放。
这说明,新民主主义革命的胜利()①彻底改变了中国人民和中华民族的前途命运②为当代中国的一切发展进步奠定了制度基础③是中华民族有史以来最为广泛而深刻的社会变革④使中华民族以崭新姿态屹立于世界民族之林A.①②B.①④C.②③D.③④2.(3分)近年来,绥宁县通过开展股份合作,搞活经营机制,在村集体、合作社、企业和农户之间建立紧密的利益联结机制导土地整体流转,带动社会资本投入,促进了农业生产发展和一二三产业融合,全县村集体经济收入2292.19万元,村均10.3元,同比增长3.4%。
该地的这一做法()①提高了土地资源配置效率,促进了农业增产农民增收②提高了农业规模化水平,促进农村集体经济发展壮大③通过农村基本经营制度的变革解放发展了农村生产力④说明完善分配激励机制有利于调动农民生产积极性A.①②B.①④C.②③D.③④3.(3分)深圳市龙岗区近年来加强产业链和人才、资金支持,培育战略性新兴产业集群;深化全过程创新生态链建设,推业企业数字化转型;主动帮助企业解决发展难点、堵点,越来越多的优秀企业和人才来到这里扎根发展。
2023年前三季度,生产总值达3487.79亿元,固定资产投资总额增长14.4%,规模上工业增加值达1540亿元,彰显了当地经济的活力与韧性。
这()①劳动力是自主创新的关键和衡量综合实力的重要指标②政府积极履行经济职能可以助力经济高质量发展③提升经济发展质量要主动淘汰落后产能,培育新动能④提高自主创新能力可以激发经济发展的内生动力A.①②B.①③C.②④D.③④4.(3分)下列对下面图片反映的经济现象推导过程符合经济学原理的是()①刺激消费政策持续发力②加强体育场馆和场地夜间设施建设③释放群众夜间体育消费的潜力A .①→②→③→⑤B .②→④→③→⑤C .③→⑤→②→①D .④→②→③→①④以精神文化需求替代物质生活需求⑤拉动当地经济增长A .①③B .①④C .②③D .②④5.(3分)十四届全国人大二次会议于2024年3月5日上午开幕。
2019年山东省泰安市高考数学二模试卷(文科)含答案解析

2019年山东省泰安市高考数学二模试卷(文科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数的共轭复数在复平面上对应的点位于()A.第一象限 B.第二象限 C.第三象限 D.第四象限2.已知集合A={x|y=},B={x|x2﹣2x<0},则()A.A∩B=∅B.A∪B=R C.B⊆A D.A⊆B3.设a,b,c∈R且a<b,则()A.>B.a2<b2C.a3<b3D.ac<bc4.设,,是非零向量,已知:命题p:∥,∥,则∥;命题q:若•=0,•=0则•=0,则下列命题中真命题是()A.p∨q B.p∧q C.(¬p)∧(¬q)D.¬p∨q5.=()A.B.﹣1 C.D.16.执行如图所示的程序框图,则输出i的值为()A.4 B.5 C.6 D.557.如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是()A.AC⊥SBB.AB∥平面SCDC.SA与平面SBD所成的角等于SC与平面SBD所成的角D.AB与SC所成的角等于DC与SA所成的角8.已知x,y满足条件,若z=2x+y的最大值为()A.9 B.8 C.7 D.69.已知双曲线﹣=1(a>0,b>0)的一条渐近线平行于直线l:y=2x+10,双曲线的一个焦点在直线l上,则双曲线的方程为()A.﹣=1 B.﹣=1C.﹣=1 D.﹣=110.将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.二、填空题:本大题共5小题,每小题5分.11.长方形ABCD中,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为______.12.已知直线ax+by﹣6=0(a>0,b>0)被圆x2+y2﹣2x﹣4y=0截得的弦长为2,则ab 的最大值为______.13.如图是一个几何体的三视图,则该几何体的体积是______.14.已知函数f(x)=,若存在x1,x2∈R,当0≤x1<4≤x2≤12时,f(x1)=f(x2),则x1f(x2)的最大值是______.15.给出下列命题:①某地2019年各月的平均气温(℃)数据的茎叶图如图,则这组数据的中位数为20;②函数f (x ﹣1)是偶函数,且在(0,+∞)上单调递增,则f (2)>f (log 2)>f [()2]③已知直线l 1:ax +3y ﹣1=0,l 2:x +by +1=0,则l 1⊥l 2的充要条件是=﹣3, 其中正确命题的序号是______(把你认为正确的序号都填上).三、解答题:本大题共6小题,满分75分.解答应写出文字说明、证明过程或演算步骤. 16.已知a ,b ,c 分别为△ABC 三个内角的对边,且cosC +sinC=.(Ⅰ)求∠B 的大小;(Ⅱ)若a +c=5,b=7,求的值. 17.某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”. (1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概0.01“”2人参加2405018.已知正项等差数列{a n}的首项为a1=2,前n项和为S n,若a1+3,2a2+2,a6+8成等比数列.(1)求数列{a n}的通项公式;(2)记P n=+++…+,Q n=+++…+,证明:P n≥Q n.19.如图,三棱柱ABC﹣A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B 是边长为2的正三角形,A1D=2,BC=1.(1)证明:MD∥平面ABC;(2)证明:BC⊥平面ABB1A1.20.已知椭圆C: +=1(a>b>0)的离心率为,F1,F2分别为椭圆的上、下焦点,过点F2作直线l与椭圆C交于不同的两点A,B,若△ABF1的周长为4.(1)求椭圆C的标准方程;(2)P是y轴上一点,以PA,PB为邻边作平行四边形PAQB,若点P的坐标为(0,﹣2),求平行四边形PAQB对角线PQ的长度的取值范围.21.已知函数f(x)=x2+mlnx+x(1)求f(x)的单调区间;(2)令g(x)=f(x)﹣x2,试问过点P(1,3)存在多少条直线与曲线y=g(x)相切?并说明理由.2019年山东省泰安市高考数学二模试卷(文科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数的共轭复数在复平面上对应的点位于()A.第一象限 B.第二象限 C.第三象限 D.第四象限【考点】复数代数形式的乘除运算.【分析】化简复数,得出其共轭复数.【解答】解:==,∴复数的共轭复数是+.故选:A.2.已知集合A={x|y=},B={x|x2﹣2x<0},则()A.A∩B=∅B.A∪B=R C.B⊆A D.A⊆B【考点】集合的包含关系判断及应用.【分析】求出集合A,B,根据集合包含关系的定义,可得答案.【解答】解:∵集合A={x|y=}=(﹣∞,2],B={x|x2﹣2x<0}=(0,2),故B⊆A,故选:C.3.设a,b,c∈R且a<b,则()A.>B.a2<b2C.a3<b3D.ac<bc【考点】不等关系与不等式.【分析】利用不等式的性质,结合反例一一判断即可.【解答】解:A.>,可知当a,b异号时不成立;B.a2<b2,可知当a=﹣1,b=1时不成立;C,a,b,c∈R且a<b,a3﹣b3=(a2﹣b2)(a+ab+b)<0成立;D.ac<bc,可知当c=0时不成立.故选:C.4.设,,是非零向量,已知:命题p:∥,∥,则∥;命题q:若•=0,•=0则•=0,则下列命题中真命题是()A.p∨q B.p∧q C.(¬p)∧(¬q)D.¬p∨q【考点】命题的真假判断与应用;平面向量数量积的运算.【分析】根据向量共线的性质以及向量数量积的应用,判断pq的真假即可.【解答】解:∵,,是非零向量,∴若∥,∥,则∥;则命题p是真命题,若•=0,•=0,则•=0,不一定成立,比如设=(1,0),=(0,1),=(2,0),满足•=0,•=0,但•=2≠0,则•=0不成立,即命题q是假命题,则p∨q为真命题.,p∧q为假命题.,(¬p)∧(¬q),¬p∨q都为假命题,故选:A.5.=()A.B.﹣1 C.D.1【考点】三角函数的化简求值.【分析】由条件利用两角和差的三角公式化简所给的式子,求得结果.【解答】解:==2•=2sin30°=1,故选:D.6.执行如图所示的程序框图,则输出i的值为()A.4 B.5 C.6 D.55【考点】程序框图.【分析】模拟执行程序,可得程序作用是对平方数列求和,当i的值为5时满足条件,退出循环,即可得解.【解答】解:模拟执行程序,可得程序作用是对平方数列求和,容易得到S4=30,S5=55>50,故输出i的值为5.故选:B.7.如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是()A.AC⊥SBB.AB∥平面SCDC.SA与平面SBD所成的角等于SC与平面SBD所成的角D.AB与SC所成的角等于DC与SA所成的角【考点】直线与平面垂直的性质.【分析】根据SD⊥底面ABCD,底面ABCD为正方形,以及三垂线定理,易证AC⊥SB,根据线面平行的判定定理易证AB∥平面SCD,根据直线与平面所成角的定义,可以找出∠ASO是SA与平面SBD所成的角,∠CSO是SC与平面SBD所成的角,根据三角形全等,证得这两个角相等;异面直线所成的角,利用线线平行即可求得结果.【解答】解:∵SD⊥底面ABCD,底面ABCD为正方形,∴连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;∵AB∥CD,AB⊄平面SCD,CD⊂平面SCD,∴AB∥平面SCD,故B正确;∵SD⊥底面ABCD,∠ASO是SA与平面SBD所成的角,∠CSO是SC与平面SBD所成的,而△SAO≌△CSO,∴∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,而这两个角显然不相等,故D不正确;故选D.8.已知x,y满足条件,若z=2x+y的最大值为()A.9 B.8 C.7 D.6【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,即可求出最大值.,【解答】解:作出不等式组对应的平面区域如图:(阴影部分).由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点A时,直线y=﹣2x+z的截距最大,此时z最大.由,解得,即A(2,3),代入目标函数z=2x+y得z=2×2+3=7.即目标函数z=2x+y的最大值为:7.故选:C.9.已知双曲线﹣=1(a>0,b>0)的一条渐近线平行于直线l:y=2x+10,双曲线的一个焦点在直线l上,则双曲线的方程为()A.﹣=1 B.﹣=1C.﹣=1 D.﹣=1【考点】双曲线的标准方程.【分析】先求出焦点坐标,利用双曲线﹣=1(a>0,b>0)的一条渐近线平行于直线l:y=2x+10,可得=2,结合c2=a2+b2,求出a,b,即可求出双曲线的方程.【解答】解:∵双曲线的一个焦点在直线l上,令y=0,可得x=﹣5,即焦点坐标为(﹣5,0),∴c=5,∵双曲线﹣=1(a>0,b>0)的一条渐近线平行于直线l:y=2x+10,∴=2,∵c2=a2+b2,∴a2=5,b2=20,∴双曲线的方程为﹣=1.故选:A.10.将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2,有|x1﹣x2|min=,则φ=()A. B.C.D.【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.【解答】解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ<)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min=,不妨x1=,x2=,即g(x)在x2=,取得最小值,sin(2×﹣2φ)=﹣1,此时φ=,不合题意,x1=,x2=,即g(x)在x2=,取得最大值,sin(2×﹣2φ)=1,此时φ=,满足题意.故选:D.二、填空题:本大题共5小题,每小题5分.11.长方形ABCD中,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为.【考点】几何概型.【分析】本题利用几何概型解决,这里的区域平面图形的面积.欲求取到的点到O的距离大于1的概率,只须求出圆外的面积与矩形的面积之比即可.【解答】解:根据几何概型得:取到的点到O的距离大于1的概率:==.故答案为:12.已知直线ax +by ﹣6=0(a >0,b >0)被圆x 2+y 2﹣2x ﹣4y=0截得的弦长为2,则ab的最大值为.【考点】直线与圆相交的性质.【分析】由圆的方程得到圆的半径为,再由弦长为2得到直线过圆心,即得到a 与b满足的关系式,再利用基本不等式即可得到结论.【解答】解:圆x 2+y 2﹣2x ﹣4y=0可化为(x ﹣1)2+(y ﹣2)2=5,则圆心为(1,2),半径为,又由直线ax +by ﹣6=0(a >0,b >0)被圆x 2+y 2﹣2x ﹣4y=0截得的弦长为2,则直线ax +by ﹣6=0(a >0,b >0)过圆心,即a +2b ﹣6=0,亦即a +2b=6,a >0,b >0,所以6=a +2b ≥2,当且仅当a=2b 时取等号,所以ab ≤,所以ab 的最大值为,故答案为:.13.如图是一个几何体的三视图,则该几何体的体积是 15 .【考点】由三视图求面积、体积.【分析】由三视图知该几何体是一个组合体:左边是三棱柱、右边是三棱锥,由三视图求出几何元素的长度,由柱体、锥体的体积公式求出几何体的体积.【解答】解:根据三视图可知几何体是一个组合体:左边是三棱柱、右边是三棱锥, 三棱柱底面是侧视图:等腰直角三角形,两条直角边是3,三棱柱的高是3; 三棱锥的底面也是侧视图,高是1,所以几何体的体积是V==15,故答案为:15.14.已知函数f(x)=,若存在x1,x2∈R,当0≤x1<4≤x2≤12时,f(x1)=f(x2),则x1f(x2)的最大值是.【考点】分段函数的应用.【分析】由题意作函数f(x)=的图象,从而可得1≤x1≤3,x1f(x2)=﹣x13+4,记g(x1)=﹣x13+4,则g′(x1)=﹣3+8x1=﹣3x1(3x1﹣8),从而判断函数的单调性及最值,从而求得.【解答】解:由题意作函数f(x)=的图象如下,,结合图象可知,3≤﹣+4x1≤4,解得,1≤x1≤3,故x1f(x2)=x1f(x1)=x1(﹣+4x1)=﹣x13+4,记g(x1)=﹣x13+4,g′(x1)=﹣3+8x1=﹣3x1(3x1﹣8),故g(x1)在[1,]上是增函数,在(,3]上是减函数,故x1f(x2)的最大值是g()=,故答案为:.15.给出下列命题:①某地2019年各月的平均气温(℃)数据的茎叶图如图,则这组数据的中位数为20;②函数f(x﹣1)是偶函数,且在(0,+∞)上单调递增,则f(2)>f(log2)>f[()2]③已知直线l1:ax+3y﹣1=0,l2:x+by+1=0,则l1⊥l2的充要条件是=﹣3,其中正确命题的序号是①②(把你认为正确的序号都填上).【考点】命题的真假判断与应用.【分析】①根据中位数的定义进行求解判断,②根据函数奇偶性和单调性的关系进行转化判断.③根据直线垂直的等价条件进行判断.【解答】解:①这组数据的中间两个数为20,20,则中位数为20;故①正确,②函数f(x﹣1)是偶函数,则函数f(x﹣1)关于x=0对称,则函数f(x)关于x=﹣1对称,则f(log2)=f(﹣3)=f(1),0<()2<1,2>1,∵f(x)在(0,+∞)上单调递增,∴f(2)>f(log2)>f[()2],故②正确,③当b≠0时,两直线的斜率分别为,,若=﹣3,则•()==﹣1,此时l1⊥l2,充分性成立.当a=0,b=0时,满足l1⊥l2成立,但=﹣3不成立,即必要性不成立,故=﹣3是l1⊥l2的充分不必要条件,故③错误,故答案为:①②.三、解答题:本大题共6小题,满分75分.解答应写出文字说明、证明过程或演算步骤.16.已知a,b,c分别为△ABC三个内角的对边,且cosC+sinC=.(Ⅰ)求∠B的大小;(Ⅱ)若a+c=5,b=7,求的值.【考点】余弦定理;正弦定理.【分析】(Ⅰ)根据两角和差的正弦公式以及正弦定理进行化简即可求∠B的大小;(Ⅱ)由余弦定理可求|AB||BC|=42,利用平面向量数量积的运算即可得解.【解答】解:(I)在△ABC中,∵cosC+sinC=,∴cosC +sinC=,∴sinBcosC +sinBsinC=sin (B +C ),∴sinBcosC +sinBsinC=sinBcosC +cosBsinC , ∴由于sinC ≠0,可得:sinB=cosB , ∴tanB=, ∵B ∈(0,π), ∴B=;(Ⅱ)∵B=,a +c=5,b=7,∴由余弦定理b 2=a 2+c 2﹣2accosB ,可得:49=a 2+c 2﹣ac=(a +c )2﹣3ac=175﹣3ac , 解得:ac=42,即|AB ||BC |=42, ∴=﹣|AB ||BC |cosB=﹣42×=﹣21.17.某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”. (1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概0.01“”2人参加24050【考点】独立性检验;频率分布直方图.【分析】(1)根据频率分布直方图,计算对应的数据,填写2×2列联表,计算观测值K2,对照数表得出结论;(2)根据分层抽样以及列举法求出对应的基本事件数,计算对应的概率值.【解答】解:(1)根据频率分布直方图,得;“课外体育达标”的学生数为200×(0.020+0.005)×10=50,其中男生人数为30,女生人数为20,22计算观测值:K2==≈6.6061<6.635,所以不能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关;(2)从课外体育达标学生中按分层抽样抽取5人,其中课外锻炼时间在[40,50)内有5×=4人,分别记为a、b、c、d,在[50,60)内有1人,记为E;从这5人中抽取2人,基本事件是ab、ac、ad、aE、bc、bd、bE、cd、cE、dE共10种,其中2人都在[40,50)内的基本事件是ab、ac、ad、bc、bd、cd共6种,故所求的概率为P==0.6.18.已知正项等差数列{a n}的首项为a1=2,前n项和为S n,若a1+3,2a2+2,a6+8成等比数列.(1)求数列{a n}的通项公式;(2)记P n=+++…+,Q n=+++…+,证明:P n≥Q n.【考点】数列的求和;等差数列与等比数列的综合.【分析】(1)通过设正项等差数列{a n}的公差为d,并利用首项和公差d表示出a2、a6,通过a1+3,2a2+2,a6+8成等比数列构造方程,进而计算可得结论;(2)通过(1)可知=,利用等比数列的求和公式计算可知P n=1﹣,通过裂项可知=﹣,进而并项相加即得结论.【解答】(1)解:设正项等差数列{a n}的公差为d,则d≥0,依题意,a2=2+d,a6=2+5d,∵a1+3,2a2+2,a6+8成等比数列,∴(6+2d)2=(2+3)(10+5d),整理得:36+24d+4d2=50+25d,即4d2﹣d﹣14=0,解得:d=2或d=﹣(舍),∴数列{a n}的通项公式a n=2n;(2)证明:由(1)可知==,由等比数列的求和公式可知P n=+++…+==1﹣,∵==﹣,∴Q n=+++…+=1﹣+﹣+…+﹣=1﹣,显然,当n≥1时≥,故P n≥Q n.19.如图,三棱柱ABC﹣A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B 是边长为2的正三角形,A1D=2,BC=1.(1)证明:MD∥平面ABC;(2)证明:BC⊥平面ABB1A1.【考点】直线与平面垂直的判定;直线与平面平行的判定.【分析】(1)取AB的中点H,连接HM,CH,根据线面平行的判定定理即可证明MD∥平面ABC;(2)根据三角形的边长关系证明三角形是直角三角形,然后结合线面垂直的判定定理即可证明BC⊥平面ABB1A1.【解答】证明:(1)取AB的中点H,连接HM,CH,∵D、M分别为CC1和A1B的中点,∴HM∥BB1,HM=BB1=CD,∴HM∥CD,HM=CD,则四边形CDMH是平行四边形,则CH=DM.∵CH⊂平面ABC,DM⊄平面ABC,∴MD∥平面ABC;(2)取BB1的中点E,∵△AA1B是边长为2的正三角形,A1D=2,BC=1.∴C1D=1,∵A1D⊥CC1,∴A1C1==,则A1B12+A1B12=4+1=5=A1C12,则△A1B1C1是直角三角形,则B1C1⊥A1B1,∵在正三角形BA1B1中,A1E=,∴A1E2+DE2=3+1=4=A1D12,则△A1DE是直角三角形,则DE⊥A1E,即BC⊥A1E,BC⊥A1B1,∵A1E∩A1B1=A1,∴BC⊥平面ABB1A1.20.已知椭圆C: +=1(a>b>0)的离心率为,F1,F2分别为椭圆的上、下焦点,过点F2作直线l与椭圆C交于不同的两点A,B,若△ABF1的周长为4.(1)求椭圆C的标准方程;(2)P是y轴上一点,以PA,PB为邻边作平行四边形PAQB,若点P的坐标为(0,﹣2),求平行四边形PAQB对角线PQ的长度的取值范围.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程;椭圆的简单性质.【分析】(1)由△ABF1的周长为4,离心率为,求出a,b,由此能求出椭圆C的标准方程.(2)设直线l的方程为y=kx﹣1,代入椭圆方程,得(2+k2)x2﹣2kx﹣1=0,由此利用韦达定理、弦长公式、换元法,结合已知条件能求出平行四边形PAQB对角线PQ的长度的取值范围.【解答】解:(1)∵△ABF1的周长为4,∴4a=4,解得a=,又e==,∴c=1,∴b==1,∴椭圆C的标准方程为=1.(2)设A(x1,y1),B(x2,y2),AB中点E(x0,y0),当直线斜率不存在时不成立,∴设直线l的方程为y=kx﹣1,①将①代入椭圆方程=1,整理得:(2+k2)x2﹣2kx﹣1=0,∴,,,,|PE|===,令t=2+k2,则t∈[2,+∞),∴∈(0,],∴|PE|====∈[1,2).∴平行四边形PAQB对角线PQ的长度的取值范围是[1,2).21.已知函数f(x)=x2+mlnx+x(1)求f(x)的单调区间;(2)令g(x)=f(x)﹣x2,试问过点P(1,3)存在多少条直线与曲线y=g(x)相切?并说明理由.【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,通过讨论m的范围,解关于导函数的不等式,从而得到函数的单调区间;(2)设切点为(x0,x0+mlnx0),求出切线斜率K,求出切线方程,切线过点P(1,3),推出关系式,构造函数g(x)(x>0),求出导函数,通过讨论①当m<0时,判断g(x)单调性,说明方程g(x)=0无解,切线的条数为0,②当m>0时,类比求解,推出当m>0时,过点P(1,3)存在两条切线,③当m=0时,f(x)=x,说明不存在过点P(1,3)的切线.【解答】解:(1)f(x)=x2+mlnx+x,(x>0),f′(x)=x++1==,①m≥0时,f′(x)>0,函数在(0,+∞)递增,②m<0时,令f′(x)>0,解得:x>,令f′(x)<0,解得:x<,∴f(x)在(0,)递减,在(,+∞)递增;(2)设切点为(x0,x0+mlnx0),则切线斜率k=1+,切线方程为y﹣(x0+alnx0)=(1+)(x﹣x0).因为切线过点P(1,3),则3﹣(x0+alnx0)=(1+)(1﹣x0).即m(lnx0+﹣1)﹣2=0.…①令g(x)=m(lnx+﹣1)﹣2(x>0),则g′(x)=m(﹣)=,①当m<0时,在区间(0,1)上,g′(x)>0,g(x)单调递增;在区间(1,+∞)上,g′(x)<0,g(x)单调递减,所以函数g(x)的最大值为g(1)=﹣2<0.故方程g(x)=0无解,即不存在x0满足①式.因此当m<0时,切线的条数为0.②当m>0时,在区间(0,1)上,g′(x)<0,g(x)单调递减,在区间(1,+∞)上,g′(x)>0,g(x)单调递增,所以函数g(x)的最小值为g(1)=﹣2<0.取x1=e1+>e,则g(x1)=a(1++e﹣1﹣﹣1)﹣2=ae﹣1﹣>0.故g(x)在(1,+∞)上存在唯一零点.取x2=e﹣1﹣<,则g(x2)=m(﹣1﹣+e1+﹣1)﹣2=me1+﹣2m﹣4=m[e1+﹣2(1+)].设t=1+(t>1),u(t)=e t﹣2t,则u′(t)=e t﹣2.当t>1时,u′(t)=e t﹣2>e﹣2>0恒成立.所以u(t)在(1,+∞)单调递增,u(t)>u(1)=e﹣2>0恒成立,所以g(x2)>0.故g(x)在(0,1)上存在唯一零点.因此当m>0时,过点P(1,3)存在两条切线.③当m=0时,f(x)=x,显然不存在过点P(1,3)的切线.综上所述,当m>0时,过点P(1,3)存在两条切线;当m≤0时,不存在过点P(1,3)的切线.2019年9月19日。
山东省泰安英雄山中学2018-2019学年高三上学期第三次月考试卷数学含答案

山东省泰安英雄山中学2018-2019学年高三上学期第三次月考试卷数学含答案班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知,,那么夹角的余弦值( )A.B.C .﹣2 D.﹣2. 设n S 是等差数列{}n a 的前项和,若5359a a =,则95SS =( ) A .1 B .2 C .3 D .43. 方程1x -= )A .一个圆B . 两个半圆C .两个圆D .半圆 4. 已知一三棱锥的三视图如图所示,那么它的体积为( )A .13 B .23C .1D .2 5. 若函数)1(+=x f y 是偶函数,则函数)(x f y =的图象的对称轴方程是( )]A .1=xB .1-=xC .2=xD .2-=x 6. 以下四个命题中,真命题的是( ) A .(0,)x π∃∈,sin tan x x =B .“对任意的x R ∈,210x x ++>”的否定是“存在0x R ∈,20010x x ++<C .R θ∀∈,函数()sin(2)f x x θ=+都不是偶函数D .ABC ∆中,“sin sin cos cos A B A B +=+”是“2C π=”的充要条件【命题意图】本题考查量词、充要条件等基础知识,意在考查逻辑推理能力.7. 已知全集I={1,2,3,4,5,6},A={1,2,3,4},B={3,4,5,6},那么∁I (A ∩B )等于( ) A .{3,4} B .{1,2,5,6} C .{1,2,3,4,5,6} D .∅8. 由直线与曲线所围成的封闭图形的面积为( )A B1C D9. 设复数1i z =-(i 是虚数单位),则复数22z z+=( ) A.1i - B.1i + C. 2i + D. 2i -【命题意图】本题考查复数的有关概念,复数的四则运算等基础知识,意在考查学生的基本运算能力. 10.已知函数,,若,则( )A1 B2 C3 D-111.设集合3|01x A x x -⎧⎫=<⎨⎬+⎩⎭,集合(){}2|220B x x a x a =+++>,若 A B ⊆,则的取值范围 ( )A .1a ≥B .12a ≤≤ C.a 2≥ D .12a ≤< 12.拋物线E :y 2=2px (p >0)的焦点与双曲线C :x 2-y 2=2的焦点重合,C 的渐近线与拋物线E 交于非原点的P 点,则点P 到E 的准线的距离为( ) A .4 B .6 C .8D .10二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.若复数12,z z 在复平面内对应的点关于y 轴对称,且12i z =-,则复数1212||z z z +在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限【命题意图】本题考查复数的几何意义、模与代数运算等基础知识,意在考查转化思想与计算能力.14.已知函数322()7f x x ax bx a a =++--在1x =处取得极小值10,则ba 的值为 ▲ .15.设平面向量()1,2,3,i a i =,满足1ia =且120a a ⋅=,则12a a += ,123a a a ++的最大值为 .【命题意图】本题考查平面向量数量积等基础知识,意在考查运算求解能力. 16.定义在R 上的可导函数()f x ,已知()f x y e=′的图象如图所示,则()y f x =的增区间是 ▲ .三、解答题(本大共6小题,共70分。
2019-2020学年泰安市英雄山中学高三语文期末考试试题及答案解析

2019-2020学年泰安市英雄山中学高三语文期末考试试题及答案解析一、现代文阅读(36分)(一)现代文阅读I(9分)阅读下面的文字,完成下面小题。
依赖一条邮路陈忠实①上世纪80年代初,我在自以为获得专业创作的最佳境地时,决定回归乡下祖居的老家,以求得一个耳目清静的环境,而不是陶渊明式的避世隐居。
我在这里可以坐下来潜心阅读世界名著,可以平心静气回嚼20年乡村生活,形成新的作品。
我几乎本能地关注着生活,尤其是乡村世界的变化,自然少不得一份报纸。
能否每天看到当日的地方报纸,成为一个小小的却也揪心的问题。
②我祖居的村子虽然距西安不过50华里,却是一个被地理环境限制着的“死角”,回到这样环境的老屋里,我首先想到如何能读到当天的报纸。
得知这里的邮递员仍旧是我熟悉的那位姓史的乡党,便找到他商量,把我所订的报纸投送到他每天必经的村子的我的一位亲戚家,由我走读上中学的儿子放晚学时顺便捎回来。
这样,每天傍晚,我停歇工作的时候,坐在祖居的小院里,借着尚未暗淡的天光,打开《参考消息》,看世界的这个和那个角落又发生了什么值得关注的大事和趣闻;还有贴近我生活的《西安晚报》,既有国家大事,更有城市和乡村的新鲜事。
我曾在该报上读到一位农村女人首创家庭养鸡场的新闻报道,竟然兴奋不已,随之便搭乘汽车追到西安西边的户县进行采访,先写了一篇报告文学发表在《西安晚报》,后又演绎成8万字的中篇小说《四妹子》,这是我写农村体制改革最用心也最得意的一部小说。
③每有或长或短的小说或散文写成,或者要投寄一封信,我便骑自行车赶到4公里远的邮政代办点。
代办点设在军校大门内右侧的一间小平房里,只有一位代办员。
我把自行车停在路边,便拿出要寄的稿件或信件走到办理窗口前,看着那张熟悉面孔的眼神里显示出“你来了”的意象,等着我先开口。
如果是寄信,我便会说要几张邮票;如果是寄稿件,便把封好的信递给他,让他在桌旁的磅秤上称一下重量,然后用算盘算出邮资。
我用他摆在窗台上的糨糊贴好邮票,再把装着文稿的信封给他。
山东肥城市泰西中学2019届高三10月月考文科综合试题
2018-2019学年肥城市泰西中学高三阶段性检测注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字迹工整,笔迹清楚。
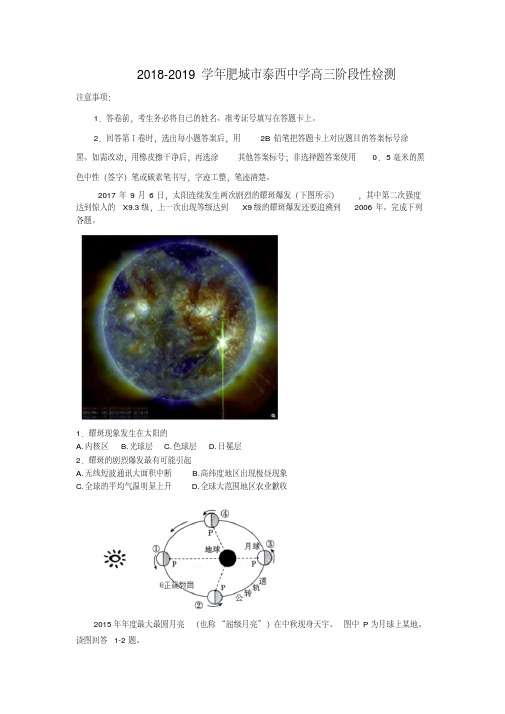
2017年9月6日,太阳连续发生两次剧烈的耀斑爆发(下图所示),其中第二次强度达到惊人的X9.3级,上一次出现等级达到X9级的耀斑爆发还要追溯到2006年。
完成下列各题。
1.耀斑现象发生在太阳的A. 内核区B. 光球层C. 色球层D. 日冕层2.耀斑的剧烈爆发最有可能引起A. 无线短波通讯大面积中断B. 高纬度地区出现极昼现象C. 全球的平均气温明显上升D. 全球大范围地区农业歉收2015年年度最大最圆月亮(也称“超级月亮”)在中秋现身天宇。
图中P为月球上某地。
读图回答1-2题。
3.中秋夜观赏“超级月亮”时,月球可能处于图中()A.①处B.②处C.③处D.④处4.月球上P地永远正对着地球,是因为月球公转与自转()A.方向相同,周期不同B.方向相同,周期相同C.自转周期小于公转周期D.自转速度大于公转速度下图曲线表示我国40o N某地某日太阳高度全天随时间变化状况。
读图回答5-7题。
5.该地所在经度是东经()A.100o B.105oC.120o D.130o6.此日太阳直射点的纬度为()A.0o B.13oNC.23.5oN D.23.5oS7.该日以后()A.当地昼长开始增长B.当地正午太阳偏西C.北京天气开始变冷D.南极圈地区结束极夜读中国冬夏季风的进展、进退与副热带高压脊的位移关系图,回答下面小题。
山东省泰安市宁阳一中2019届高三数学上学期10月月考试题理2019010802238
山东省泰安市宁阳一中2019届高三数学上学期10月月考试题理一、选择题(每小题5分,共12小题60分)1、设集合,,则( )A. B. C. D.2、在中,,则等于()A. B. C. D.3、已知函数,实数满足,则的所有可能值为()A.或B.C.D.或或4、已知命题,命题,则()A.为假B.为真C.为真D.为假5、已知是偶函数,它在上是减函数,若,则的取值范围是()A. B. C.D.6、已知,,则()A. B. C. D.7、已知函数,若存在实数,,,,当时满足,则的取值范围是( )A. B.C.D.8、函数的图象大致是()A.B.C. D.9、使得函数有零点的一个区间是()A. B. C. D.10、定义在上的函数的导函数为,已知是偶函数,且.若,且,则与的大小关系是( )A. B. C. D.不确定11、已知是定义在上的减函数,那么实数的取值范围是()A.B. C. D.12、已知函数的部分图像如图所示,则的图象可由的图象( )A.向右平移个长度单位B.向左平移个长度单位C.向右平移个长度单位D.向左平移个长度单位二、填空题(每小题5分,共4小题20分)13、已知向量,满足,,则__________.14、已知函数的图象向左平移个单位后与函数的图象重合,则正数的最小值为__________.15、已知为锐角,,则__________.16、若函数在上有最小值,则实数的取值范围为__________.三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)17、已知命题,且,命题,且.(Ⅰ)若,求实数的值;(Ⅱ)若是的充分条件,求实数的取值范围.18、已知向量,,函数,且图象上一个最高点的坐标为,与之相邻的一个最低点的坐标为.(1)求的解析式;(2)在中,是角所对的边,且满足,求角的大小以及的取值范围.19、设函数是自然对数的底数)(1)求函数的单调区间;(2)若关于的方程在区间上恰有两相异实根,求的取值范围;(3)当时,证明:20、设函数,其中.(Ⅰ)当时,求曲线在原点处的切线方程;(Ⅱ)试讨论函数极值点的个数;21、已知函数(其中且),函数在点处的切线过点.(Ⅰ)求函数的单调区间;(Ⅱ)若函数与函数的图像在有且只有一个交点,求实数的取值范围.22、已知函数.(1)判断函数的奇偶性,并证明;(2)若对于任意,不等式恒成立,求正实数的取值范围.宁阳一中2016级高三上学期阶段性考试(二)数学理科答案解析第1题答案D解析由已知得,故.第2题答案D因为,所以,所以,所以.第3题答案A ∵,∴,∴,当时,,,.当时,,∴或.第4题答案C 当时,,即命题为真命题,当时,,即命题为假命题,则为真,为假,为假,为真,则为真;故选C.第5题答案C因为是偶函数,它在上是减函数,则,所以的取值范围是,故选C.第6题答案D 由①, 所以②由①②可得③由①③得,.第7题答案D 如下图所示,设从左往右的零点依次为,则,又∵,∴,,故选D第8题答案B 因为,易知,当时,,当时,,排除A、C;又,易知当时,,此时单调递增,当时,,此时单调递减.第9题答案∴,由零点存在定理,可知选C第10题答案C由可知,当时,函数递减.当时,函数递增.因为函数是偶函数,所以,,即函数的对称轴为.所以若,则.若,则必有,则,此时由,即,综上,选C.第11题答案C 依题意,有且,解得,又当时,,当时,,所以,解得.故.第12题答案A 根据题中所给的图像,可知,故选A.第13题答案由,即,即,所以.第14题答案将的图象向左平移个单位后,得到函数的图象,又的图象与的图像重合,故,,所以(),又,故当时,取得最小值,为.第15题答案因为为锐角,所以,,所以.因为,所以,所以.第16题答案,令得或,令得,所以函数的单调递增区间为和,减区间为.所以要使函数在上有最小值,只需,即.第17题答案(1)∵,————2分(1)若,则有,解得:.————5分(2)是的充分条件,即分两种情况,或,解得:或、——------------10分.a4第18题答案(1);(2),(1)--------------------1分. --------------------2分∵图象上一个最高点的坐标为,与之相邻的一个最低点的坐标为.∴,∴,于是---------------------5分.所以. ---------------6分(2)∵,∴. ------------7分又,∴,----------------------------------8分∴. ---------------------------------9分∵,∴,于是,----------------10∴,所以.-------------------------12分第19题答案(1)的递增区间为递减区间为(2)第19题解析(1)------------------1分当时当时--------------2分的递增区间为递减区间为 ----------3分(2)由方程得------------4分令则-----------5分当时,递减当时,递增-------------------------7分又-------------------------9分(3)要证原不等式成立,只需证明成立---------------10分由(1)可知当时,又时,--------11分故即 ---------------------------12分第20题答案(Ⅰ)(Ⅱ)当时,无极值点;当时,有2个极值点;当时,有1个极值点第20题解析(Ⅰ)当时,-----------1分,则,-----2分∴,---------------3分∴曲线在原点处的切线方程为;---------4分(Ⅱ),--------------5分令当时,,所以,则,所以在上为增函数,所以无极值点;-------------6分当时,,所以,则,所以在上为增函数,所以无极值点;----------------------7分当时,,令,则,-------------9分当时,,,此时有2个极值点;-----10分当时,,此时有1个极值点;-------------11分综上:当时,无极值点;当时,有1个极值点;当时,有1个极值点.--------------12分第21题答案见解析第21题解析(Ⅰ),∴∴----------------------------------------1分∴函数在处的切线方程为,∵切线过点,∴,即,------------------2分∴,令,解得----------3分①当时,单调递增,单调递减,-----------------4分②当时,单调递减,单调递增-----------------5分.(Ⅱ)原题等价方程在只有一个根,即在只有一个根,令,等价函数在与轴只有唯一的交点,------------6分∴①当时,在递减,递增,当趋近于趋近于正无穷要是函数在与轴只有唯一的交点需或,所以或-------------------------------------8分②当时,在递增,递减,递增因为,当趋近于,趋近于负无穷,因为所以在与轴只有唯一的交点----------------------10分③当时,在的递增,∵,,∴函数在与轴只有唯一的交点,-------------------------------11分综上所述,的取值范围是或或.-------------12分第22题答案(1)在定义域上是奇函数;(2)的取值范围是.第22题解析(1)由,得且,∴函数的定义域为,------------------1分当时,,,-----------------5分所以,∴在定义域上是奇函数--------------------6分(2)由于, 当或时,恒成立,所以在上是减函数,-----------7分因为且,所以-----------------------8分 210,01(1)(7)x mx x x +>>---由及在上是减函数,所以,-----------------9分因为,所以在恒成立.---------10分设,,则,所以,所以当时,.所以在上是增函数,.--------------11分综上知符合条件的的取值范围是.-------------------------------12分。
2019届高考文数百强名校试题解析精编版:山东省乳山市第一中学2019届高三10月月考文数试题解析(解析版)
第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.(2019·昆明第一中学一摸)设集合{|12}A x x =-<<,集合B =N ,则A B =( )A.{0,1}B.{1}C.1D.{-1,0,1,2}【答案】A 【解析】试题分析:根据集合的运算法则,可知{}0,1A B =,故选A.考点:集合的运算.2.[2019·湖北卷]命题“0x ∃∈R Q ð,30x ∈Q ”的否定是( ) A.0x ∃∉R Q ð,30x ∈QB.0x ∃∈R Q ð,30x ∉QC.x ∀∉R Q ð,3x ∈QD.x ∀∈R Q ð,3x ∉Q【答案】D 【解析】试题分析:根据对特称命题的否定可知,是先改变量词,然后把结论否定.故所求否定为“x ∀∈R Q ð,3x ∉Q ”.所以选D. 考点:特称命题的否定.3.(2019·太原模拟)设()f x 为定义在R 上的奇函数,当0x ≥时,()()32x f x x a a =-+∈R ,则()2f -=( ) A.-1 B.-4 C.1D.4 【答案】B 【解析】试题分析:因为在R 上的奇函数0(0)0(0)32001f f a a =⇒=-⨯+=⇒=-;故当0x ≥时,()321x f x x =--,所以2(2)(2)[3221]4f f -=-=--⨯-=-. 考点:奇函数的定义和性质的应用.4.若命题“∃x 0∈R ,使x 20+(a -1)x 0+1<0”是假命题,则实数a 的取值范围为( )A .1≤a ≤3B .-1≤a ≤1C .-3≤a ≤1D .-1≤a ≤3 【答案】D 【解析】试题分析:x 2+(a -1)x +1≥0恒成立,所以(a -1)2-4≤0,得-1≤a ≤3,故选D. 考点:一元二次不等式的解集的形式与对应的方程的根的情况关系.5.已知偶函数f (x )在区间[0,+∞)上单调递增,则满足f (2x -2)<f (2)的x 的取值范围是( ) A .(-∞,0) B .(0,2) C .(0,22) D .(2,+∞) 【答案】B考点:应用偶函数的性质转化不等式. 6.“22ab >”是 “22log log a b >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B 【解析】 试题分析:22ab >的等价结果是a b >,22log log a b >的等价结果是0a b >>,故“22ab >”是 “22log log a b >”的必要不充分条件,故选B.考点:充要条件的判断.7.已知f (x )是定义在R 上的偶函数,g (x )是定义在R 上的奇函数,且g (x )=f (x -1),则f (2009)+f (2019)的值为( )A .-1B .1C .0D .无法计算 【答案】C 【解析】试题分析:由题意得g (-x )=f (-x -1),又因为f (x )是定义在R 上的偶函数,g (x )是定义在R上的奇函数,所以g (-x )=-g (x ),f (-x )=f (x ),∴f (x -1)=-f (x +1),∴f (x )=-f (x +2),∴f (x )=f (x +4),∴f (x )的周期为4,∴f (2009)=f (1),f (2019)=f (3)=f (-1),又∵f (1)=f (-1)=g (0)=0,∴f (2009)+f (2019)=0,故选C. 考点:奇偶函数的性质.8.[2019·长沙一中月考] 已知命题p :关于x 的函数y =x 2-3ax +4在[1,+∞)上是增函数,命题q :关于x 的函数y =(2a -1)x 在R 上为减函数,若p 且q 为真命题,则a 的取值范围是( ) A .a ≤23 B .0<a <12 C.12<a ≤23 D.12<a <1 【答案】C 【解析】试题分析:已知命题p 为真,则3a 2≤1,∴a ≤23;已知命题q 为真,则0<2a -1<1,∴12<a <1;综合以上得12<a ≤23,故选C.考点:函数单调性对应的条件,复合命题真值表.9.(2019·银川一中第三次月考)已知函数()()()f x x a x b =--(其中a b >)的图象如图1所示,则函数()x g x a b =+的图象是图2中的( )【答案】A 【解析】试题分析:由图象可得01,1a b <<<-.由01a <<得函数()x g x a b =+单调递减,故排除C,D 项;又当0x =时,()10g x b =+<,故排除B 项;A 项符合题意,故选A. 考点:函数图像的选择.10.关于函数f (x )=lg x 2+1|x |(x ∈R ,x ≠0),有下列命题:①函数y =f (x )的图象关于y 轴对称;②在区间(-∞,0)上,f (x )是减函数;③函数y =f (x )的最小值是lg2;④在区间(-∞,0)上,f (x )是增函数.其中准确的是( ) A .①② B .②④ C .①③ D .③【答案】C 【解析】试题分析:由函数f (x )的定义域为()-∞,0∪()0,+∞,且f (-x )=f (x ),所以f (x )为偶函数.当x >0时,f (x )=lg x 2+1x =lg ⎝⎛⎭⎫x +1x ≥lg2,函数f (x )在()-∞,-1,()0,1上为减函数,在()-1,0,()1,+∞上为增函数.故①③准确,所以选C.考点:函数的性质.第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.[2019·天津卷]已知集合{}+2<3A x x =∈R ,集合{}(-)(-2)<0B x x m x =∈R 且),,1(n B A -= 则m =__________,n = __________.【答案】1,1-考点:不等式的解集,集合的交集.12.已知幂函数f (x )=k ·x α的图象过点⎝ ⎛⎭⎪⎫12,22,则k +α=________【答案】32【解析】试题分析:∵f (x )=k ·x α是幂函数,∴k =1.又f (x )的图象过点⎝⎛⎭⎫12,22,∴⎝⎛⎭⎫12α=22,∴α=12.∴k +α=1+12=32.考点:幂函数的定义,幂函数的解析式的求解.13.设函数⎩⎨⎧+∞∈-∞∈=-),1(log ]1,(2)(81x x x x f x ,则满足41)(=x f 的x 值是_______.【答案】3 【解析】试题分析:令124x -=,解得2x =,不合题意,舍去,令811log 4x =,解得3x =,符合题意,所以x 值是3.考点:分段函数已知函数值求自变量.14.设f (x )=x 3+x ,x ∈R ,当0≤t ≤1时,f (m t)+f (1-m )>0恒成立,则实数m 的取值范围是________ 【答案】 【解析】试题分析:根据函数()f x 的性质,不等式()(1)0f mt f m +->,即()(1)f mt f m >-,即1mt m >-在[0,1]上恒成立.即()10g t mt m =-+>在[0,1]上恒成立,可知(0)10(1)10g m g m m =-+>⎧⎨=-+>⎩,解得1m <.考点:构造新函数.15.已知函数f (x )=⎩⎪⎨⎪⎧e -x -2(x ≤0),2ax -1(x >0)(a 是常数且a >0).对于下列命题:①函数f (x )的最小值是-1;②函数f (x )在R 上是单调函数;③若f (x )>0在⎣⎡⎭⎫12,+∞上恒成立,则a 的取值范围是a >1;④对任意x 1<0,x 2<0且x 1≠x 2,恒有f⎝⎛⎭⎫x 1+x 22<f (x 1)+f (x 2)2.其中准确命题的序号是________.【答案】①③④ 【解析】试题分析:如图,①准确;函数f (x )在R 上不是单调函数,②错误;若f (x )>0在⎣⎢⎡⎭⎪⎫12,+∞上恒成立,则2a ×12-1>0,a >1,③准确;由图象可知在(-∞,0)上对任意x 1<0,x 2<0且x 1≠x 2,恒有f ⎝⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2成立,④准确,所以准确命题的序号为①③④.考点:函数的性质.三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.(满分12分)已知1:2123x p --≤-≤,22:210(0)q x x m m -+-≤>,且p ⌝是q ⌝的必要不充分条件,求实数m 的取值范围. 【答案】9m ≥ 【解析】试题分析:首先确定出各个命题是真命题时对应的变量的范围,即先求出两个不等式的解集,再根据题中的条件,确定出p 是q 的充分不必要条件,再根据集合的真包含关系,求得参数的取值范围试题解析:由22210x x m -+-≤,得11m x m -≤≤+,......2分:{|1q A x x m ∴⌝=>+或1,0}x m m <->.......4分由12123x --≤-≤,得210x -≤≤. ......6分 :{|10p B x x ∴⌝=>或2}x <-......8分p ⌝是q ⌝的必要不充分条件,012,110m A B m m >⎧⎪∴⊆⇔-≤-⎨⎪+≥⎩9m ∴≥.......12分考点:充要条件的判断,参数的取值范围的求解.17.(满分12分)已知函数x a k x f -⋅=)((a k ,为常数,0>a 且1≠a )的图象过点)8,3(),1,0(B A . (1)求实数a k ,的值;(2)若函数1)(1)()(+-=x f x f x g ,试判断函数)(x g 的奇偶性,并说明理由【答案】(1)21,1==a k ; (2)奇函数. 【解析】试题分析:第一问应用点在曲线上的条件,点的坐标满足函数解析式,代入得到方程组,从而求得参数的值,第二问将函数()g x 的解析式求出来,利用定义确定出函数是奇函数.试题解析:(1)把)8,3(),1,0(B A 的坐标代入x a k x f -⋅=)(,得⎩⎨⎧=⋅=⋅-,8,13a k a k 解得21,1==a k ——6分(2)由(1)知xx f 2)(=,所以12121)(1)()(+-=+-=x x x f x f x g .此函数的定义域为R ,又 )(12122222221212)(x g x g x x x x x x x x x x -=+--=+⋅-⋅=+-=-----,所以函数)(x g 为奇函数.————12分考点:点在函数图像上的条件,函数奇偶性的判断. 18.(满分12分)已知函数f (x )=ax +1x 2(x ≠0,常数a ∈R). (1)讨论函数f (x )的奇偶性,并说明理由;(2)若函数f (x )在x ∈[3,+∞)上为增函数,求a 的取值范围.【答案】(1)0a =时,()f x 为偶函数,当0a ≠时,()f x 为非奇非偶函数; (2)227a ≥. 【解析】试题分析:第一问首先判断函数的定义域是否关于原点对称,对a 的取值实行讨论,判断()f x 和()f x -的关系,从而得到结果,第二问利用函数的导数在给定区间上大于等于零恒成立,从而转化为最值来处理,求得结果. 试题解析:(1)定义域为(,0)(0,)-∞+∞,关于原点对称.......1分当0a =时,21()f x x=,满足对定义域上任意x ,()()f x f x -=,∴0a =时,()f x 是偶函数;......3分当0a ≠时,(1)1f a =+,(1)1f a -=-,显然(1)(1)f f -≠且 (1)-(1)f f -≠, ∴当0a ≠时,()f x 是非奇非偶函数.......6分(2)由题意知'()0f x ≥在[3,)+∞上恒成立, …………… 7分所以32a x≥在[3,)+∞上恒成立, …………………8分 因为[3,)x ∈+∞,所以322(0,]27x ∈, ……………………..11分 所以227a ≥. ………………………..12分 考点:函数奇偶性的判断,函数在给定区间上单调增对应的参数的取值范围的确定. 19.(满分12分)已知函数f (x )=1-2a x -a 2x (a >1).(1)求函数f (x )的值域;(2)若当x ∈[-2,1]时,函数f (x )的最小值为-7,求此时f (x )的最大值 【答案】(1)(-∞,1); (2)716. 【解析】试题分析:第一问设a x =t >0,将函数换元,转化为关于t 的二次式,此时将问题转化为二次函数在某个区间上的值域问题,从而求得结果,第二问需要对底数a 实行讨论,判断函数在哪个点取得最值,从而求得结果.试题解析:设a x =t >0,则y =-t 2-2t +1=-(t +1)2+2.(1)∵t =-1∉(0,+∞),∴y =-t 2-2t +1在(0,+∞)上是减函数.∴y <1, 所以f (x )的值域为(-∞,1).————6分(2)∵x ∈[-2,1],a >1,∴t ∈⎣⎡⎦⎤1a 2,a ,由t =-1∉⎣⎡⎦⎤1a 2,a ,所以y =-t 2-2t +1在⎣⎡⎦⎤1a 2,a 上是减函数,∴-a 2-2a +1=-7,∴a =2或a =-4(不合题意,舍去).当t =1a 2=14时,y 有最大值.即y max =-⎝⎛⎭⎫142-2×14+1=716.————12分 考点:函数的值域和最值. 20.(满分13分)已知函数f(x)=21ax b x ++是定义在(-1,1)上的奇函数,且12()25f =. (Ⅰ)求函数f(x)的解析式;(Ⅱ)证明f(x)在(-1,1)上是增函数; (Ⅲ)解不等式f(t-1)+ f(t)<0. 【答案】(Ⅰ) 2()1xf x x =+;(Ⅱ)证明见解析; (Ⅲ)1{|}2t O t << 【解析】试题分析:第一问根据奇函数的性质(0)0f =,从而求得0b =,再根据12()25f =,代入求得1a =,从而求得函数解析式,第二问利用函数单调性的定义证明函数在定义域上是增函数,也能够应用导数来证明,第三问将式子移项,化简,将不等式转化为两个函数值的大小,利用函数的单调性,转化为两个自变量的大小,从而求得不等式的解集. 试题解析:(Ⅰ) ()f x 是(-1,1)上的奇函数 , (0)0f ∴= 0b ∴= (1分)又12()25f =2122151()2a ∴=+ 1a ∴= (2分)2()1x f x x ∴=+ (4分) (Ⅱ)证明:任设x 1、x 2∈(-1,1),且12x x <,则1121212222212122()(1)()()11(1)(1)x x x x x x f x f x x x x x ---=-=++++ 1211x x -<<< 1211x x ∴-<< (6分) 120x x ∴-<,且1210x x ->又221210,10x x +>+> 12()()0f x f x ∴-< 即12()()f x f x < (7分)()f x ∴在(-1,1)上是增函数 (8分)(Ⅲ)()f x 是奇函数 ∴不等式可化为(1)()()f t f t f t -<-=-即 (1)()f t f t -<- (9分) 又()f x 在(-1,1)上是增函数∴有111111t t t t-<-<⎧⎪-<<⎨⎪-<-⎩解之得12O t << (12分 ∴不等式的解集为1{|}2t O t << (13分)考点:奇函数的性质,函数解析式的求解,单调性的证明,不等式的求解. 21.(满分14分)已知函数f (x )=x 2+bx +c 满足条件:f (x -3)=f (5-x ),且方程f (x )=x 有相等实根.(1)求f (x )的解析式;(2)当x ∈[-1,+∞)时,f (x )≥2(a -1)x +a +14恒成立,求a 的取值范围. 【答案】(1)29()24f x x x =-+; (2)[3,11]-. 【解析】试题分析:第一问根据(3)(5)f x f x -=-,得出函数图像的对称轴1x =,从而求得2b =-,再根据方程230x x c -+=有相等实根,求得94c =,从而得到函数解析式,第二问将不等式转化为2022x ax a ≤--+在[1,)-+∞上恒成立,从而转化为最值来处理,从而求得结果. 试题解析:(1) 2()f x x bx c =++满足条件(3)(5)f x f x -=-,则函数()f x 的图象关于直线1x =对称,故2b =-,又方程有相等实根,即230x x c -+=有相等实根,故94c =,故29()24f x x x =-+;—6分 (2)由题意,得1()2(1)4f x a x a ≥-++,即2022x ax a ≤--+在[1,)-+∞上恒成立, 设2()22g x x ax a =--+,则min ()0g x ≥, 在[1,)-+∞上的最小值是2min2,[1,)()32,(,1)a a a g x a a ⎧--∈-+∞=⎨+∈-∞-⎩,10分又等价于103a a <-⎧⎨≤+⎩或2102a a a≥-⎧⎨≤--⎩ ……………………………………………….13分 解之,得[3,11]a ∈-. ……………………………………………14分. 考点:二次函数解析式的求解,恒成立问题的转化.。
2019-2020学年山东省泰安一中高三(上)月考地理试卷(10月份)
【解答】
该城市中利用智能化“风光路灯”需要风能和太阳能,故需要风能和太阳能比较丰富的地方,呼和浩特市温带大陆性气候,晴天多,太阳能和风能丰富,故C正确。
A.地形迎风坡,降水多,水汽足B.气温较低,降雪丰富,水分足
C.地形比较封闭,水汽不易扩散D.气温较高,蒸发量大,水汽足
【答案】
B
B
C
【考点】
常见地形地貌的特征及分布
影响气候的主要因素
大气的垂直分层及各层对人类活动的影响
【解析】
在等高线地形图上,等高线闭合且等高线数值中间高四周低则为山顶;两山顶之间相对低洼的部位为鞍部;高线闭合且等高线数值中间低四周高则为盆地;等高线向海拔低处凸为山脊;等高线向海拔高处凸为山谷,在等高线地形图上,等高线越密集,表示坡度越陡,等高线越稀疏,表示的坡度越缓。
【答案】
C
D
A
【考点】
能源矿产资源的开发与区域可持续发展
太阳能量的来源及其对地球的影响
正午太阳高度的变化
【解析】
根据上图可知,该城市中利用智能化“风光路灯”需要风能和太阳能。
一年中太阳能板摆动幅度的变化与一年中正午太阳高度的变化幅度是相同的,也就是正午太阳高度变化大,太阳能板摆动幅度变大,反之就小。
【解答】
A、木星不在地球公转轨道以内,不存在凌日现象,不符合题意。
B、水星和金星在地球公转轨道以内,会产生凌日现象,故正确。
C、火星和木星的公转轨道均在地球公转轨道以外,不存在凌日现象,不符合题意。
泰山区高中2018-2019学年上学期高三数学10月月考试题
泰山区高中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 抛物线x=﹣4y 2的准线方程为( ) A .y=1 B .y=C .x=1D .x=2.为了得到函数的图象,只需把函数y=sin3x 的图象( )A.向右平移个单位长度 B.向左平移个单位长度 C.向右平移个单位长度D.向左平移个单位长度3. 设a ,b ∈R ,i 为虚数单位,若2+a i1+i =3+b i ,则a -b 为( )A .3B .2C .1D .04. 已知实数y x ,满足不等式组⎪⎩⎪⎨⎧≤-≥+≤-5342y x y x x y ,若目标函数mx y z -=取得最大值时有唯一的最优解)3,1(,则实数m 的取值范围是( )A .1-<mB .10<<mC .1>mD .1≥m【命题意图】本题考查了线性规划知识,突出了对线性目标函数在给定可行域上最值的探讨,该题属于逆向问题,重点把握好作图的准确性及几何意义的转化,难度中等.5. 函数sin()y A x ωϕ=+在一个周期内的图象如图所示,此函数的解析式为( ) A .2sin(2)3y x π=+B .22sin(2)3y x π=+C .2sin()23x y π=-D .2sin(2)3y x π=-6. 沿一个正方体三个面的对角线截得几何体如图所示,则该几何体的侧视图为( )A .B .C .D .7. 为了解决低收入家庭的住房问题,某城市修建了首批108套住房,已知C B A ,,三个社区分别有低收入家 庭360户,270户,180户,现采用分层抽样的方法决定各社区所分配首批经济住房的户数,则应从C 社 区抽取低收入家庭的户数为( )A .48B .36C .24D .18【命题意图】本题考查分层抽样的概念及其应用,在抽样考查中突出在实际中的应用,属于容易题. 8. 函数f (x )=kx +bx +1,关于点(-1,2)对称,且f (-2)=3,则b 的值为( )A .-1B .1C .2D .49. 底面为矩形的四棱锥P -ABCD 的顶点都在球O 的表面上,且O 在底面ABCD 内,PO ⊥平面ABCD ,当四棱锥P -ABCD 的体积的最大值为18时,球O 的表面积为( ) A .36π B .48π C .60π D .72π10.定义运算,例如.若已知,则=( )A .B .C .D .11.已知函数22()32f x x ax a =+-,其中(0,3]a ∈,()0f x ≤对任意的[]1,1x ∈-都成立,在1 和两数间插入2015个数,使之与1,构成等比数列,设插入的这2015个数的成绩为T ,则T =( ) A .20152B .20153C .201523D .20152212.已知f (x )在R 上是奇函数,且f (x+4)=f (x ),当x ∈(0,2)时,f (x )=2x 2,则f (7)=( ) A .﹣2 B .2 C .﹣98 D .98二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.已知tan()3αβ+=,tan()24πα+=,那么tan β= .14.已知定义在R 上的奇函数()f x 满足(4)()f x f x +=,且(0,2)x ∈时2()1f x x =+,则(7)f 的值为 ▲ .15.已知函数5()sin (0)2f x x a x π=-≤≤的三个零点成等比数列,则2log a = . 16.如图是一个正方体的展开图,在原正方体中直线AB 与CD 的位置关系是 .三、解答题(本大共6小题,共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省泰安市英雄山中学2019届高三文综10月月考试题全卷满分300分。
考试用时150分钟。
一选择题(共35小题,每题4分,共140分)1. 下列说法正确的是A. 甲气压中心的名称是亚洲高压B. 丙地盛行风风向为西南风C. 乙处风力强于丙处D. 此季节太平洋上阿留申低压势力强大2. 据图可判断A. 甲气压中心是由于海陆热力性质的差异形成B. 此季节影响丙地盛行风形成的因素是海陆热力性质差异C. 此季节,乙地的气候特点是低温少雨D. 此季节,丙地的气候特点是高温少雨下图为世界某大洲局部地区某月等温线(单位:℃)分布示意图,据此完成下面小题。
3. M地气温最有可能是A. 18℃B. 22℃C. 28℃D. 32℃4. 导致甲、乙两地气温差异的主导因素是A. 纬度位置B. 海陆差异C. 地形起伏D. 洋流性质5. 图示季节,影响圣地亚哥的大气环流是A. 东南信风B. 副热带高压C. 盛行西风D. 东南季风6. 图中西南沿海地区海岸线曲折,多幽深的峡湾,其形成原因主要是A. 断裂下陷B. 火山作用C. 流水作用D. 冰川作用下图为江汉平原某河段示意图。
据此回答下列问题。
7. 有关该河段的叙述,正确的是A. 图中地貌主要发育于山前地带B. 该河段主要出现在河流发育初期C. 该河段北岸堆积,南岸侵蚀D. 该河段下蚀作用减弱,侧蚀作用加强8. 有关该河流地貌与人类活动关系的叙述,不正确的是A. 河漫滩平原土壤肥沃,利于耕作B. 该区域聚落一般沿河成线状分布C. 河流可方便聚落的对外联系和运输D. 南岸适合于建设港口下图,回答下列各题。
9.下列名山或山脉的地质构造与图中①处地质构造相类似的是A. 华山B. 喜马拉雅山C. 阿尔卑斯山D. 安第斯山10. 下列地区的地质构造与图中④处不同的是A. 渭河平原B. 汾河谷地C. 东非大裂谷D. 长江三峡11. 图中⑥处山地的成因为A. 背斜成山B. 向斜成山C. 褶皱隆起成山D. 断层上升成山12.2018年1月15日,德国和法国相继宣布将人民币纳入外汇储备,欧元区两大经济体对人民币投下信任票。
到目前,已有60多个国家和地区的中央银行或货币当局把人民币纳入外汇储备篮子。
这意味着①中国外汇储备安全性提高②中国在世界经济中的地位显著上升③人民币汇率稳定性增强④人民币国际化程度不断提高A.①②B.①③ C.②④ D.③④13.快递与外卖业的崛起,大量的塑料包装让执行了十年的“限塑令”再遇尴尬。
有网友建议:通过降低已有成熟替代品(如布袋、纸基包装、可降解材料等)的价格,实现“白色污染”与时俱进的治理。
下列供求曲线图示(图4)能正确反映该网友观点的是图4(注:P为价格,Q为数量,d1为可降解材料类包装的曲线,d2为塑料类包装的曲线)A.①→③B.①→④C.②→③D.②→④14.按中国石化销售有限公司与25家境内外投资者签署的相关协议,中国石化销售有限公司的注册资本将由人民币200亿元增至人民币28567亿元,持有7001%的股权;包括腾讯等25家投资者以现金共计107094亿元认购销售公司2999%的股权。
重组后,最终形成一个国有、民营、社会资本混合的产权结构。
这种结构①是公有制经济的重要实现形式和社会主义的根本经济特征②表明公有制经济是国民经济的主体,控制着国民经济的命脉③有利于公有制经济与非公有制经济平等参与市场竞争、共同发展④表明公有制经济和非公有制经济都是我国经济社会发展的重要基础A.①② B.①③ C.②③ D.③④15.2018年,农村集体产权制度改革试点县将增加到300个,力争到2021年底基本完成改革。
试点地区要在有序推进经营性资产股份合作制改革、赋予农民对集体资产股份权能等五个方面进行积极探索。
这表明①股份合作制创新了法定的公司形式②农民获得股份权益,增加了财产性收入③农民作为股东对公司债务承担无限责任④集体资产通过股份合作制改革能实现保值增值A.①② B.③④ C.①③ D.②④16.国资委在关于中央企业重组整合会上指出,央企通过重组整合,国有资本整体布局,行业结构、业务结构、资产质量都不断优化,企业规模实力、资源配置效率、创新水平、经营业绩都有效提升。
央企改革成功有利于①保证国有资产在社会总资产中占优势②增强央企活力,不断提高国有经济的控制力和影响力③促进国企强强联合,提高国有经济在国民经济中的比重④推动资源整合,实现国有资本的优化配置A.①④ B.②④ C.③④ D.②③17.如果不能打败对手,那就加入他们。
近年来,国内互联网企业界上演了多起“敌人变情人”的戏码:美团与大众点评、58同城与赶集、携程与去哪儿、滴滴出行和优步中国、世纪佳缘和百合网……这些企业通过直接并购或股权转换等方式实现了合并。
互联网企业合并旨在①实现优势互补,增强企业营利能力②提高企业的市场竞争力和经济效益③淘汰落后企业,促进社会资源合理配置④带动劣势企业走出困境,实现共赢发展A.①②B.③④C.①③D.②④18.十九大报告指出:“就业是最大的民生。
要坚持就业优先战略和积极就业政策,实现更高质量和更充分就业。
”为贯彻落实这一精神,政府应该①提供全方位的就业服务,做好高校毕业生的分配工作②大规模开展职业技能培训,注重解决结构性就业矛盾③树立正确的就业观念,实现多渠道多方式就业和创业④破除妨碍劳动力流动的体制弊端,使其都有发展机会A.①② B.①③ C.②④ D.③④19.零工经济是共享经济的一种重要的组成形式,是人力资源的一种新型分配形式,是互联网时代流行的新的用工方式。
它利用互联网和移动技术快速匹配供需方,在全职工作之外,增加一项临时工作。
零工经济①降低就业成本,大幅度提高劳动者的收入水平②增强劳动者就业的灵活性,也会带来劳动者维权的风险③有利于推动创新经济的发展,也给法律和政策的完善提出挑战④激发了人们的创造力,改变了当下劳动的性质和特点A.①② B.①④ C.②③ D.③④20.甲、乙、丙、丁四人准备用人民币10万元同时进行投资理财(如表1)表1假如一年后M股票的价格上涨了3%,欧元对人民币汇率上涨2%。
在不考虑其他因素的情况下,对四人收益由高到低的正确排序是A.丁>乙>甲>丙 B.丁>甲>乙>丙 C.乙>丁>丙>甲 D.乙>丙>丁>甲21.国务院批复的《基本养老保险基金投资管理办法》规定,养老基金在投资国债、银行债券等债权性资产的同时,可以投资股票、股票基金,但投资股票等权益类资产的比重不超过30%。
上述规定的主要目的是A.增强资本流动性,平抑资本市场的波动B.优化投资组合,追求收益与风险的平衡C.扩大投资渠道,实现投资收益的最大化 D.提高投资安全性,促进资本市场的增长22.十九大报告提出要深化金融体制改革,增强金融服务实体经济能力。
为实现这一目标,下列选项中正确的传导路径有①完善金融管理制度→防范化解系统性金融风险→为微商提供更好的金融服务②促进多层次资本市场健康发展→为实体经济拓宽融资渠道→增加实体经济资金供应③金融领域利用大数据→“物联网+”新的金融业态的发展→金融服务普惠到实体经济④保持金融市场的强监管态势→抑制金融市场投机性活动→提高金融资源的配置效率A.①② B.①④ C.②③ D.③④23.2018年3月,中共中央办公厅、国务院办公厅印发《关于提高技术工人待遇的意见》,指导企业深化工资分配制度改革,建立基于岗位价值、能力素质、业绩贡献的工资分配机制,强化工资收入分配的技能价值激励导向。
落实这一政策有利于①贯彻我国的按劳分配原则,健全再分配制度②提高技术工人生产积极性,助推企业转型升级③实现技高者多得、多劳者多得,增强技术工人获得感④快速解决技术工人短缺问题,优化劳动力供给结构A.①②B.①④ C.②③D.③④24. 这是罗马帝国鼎盛时期的一个案例:一个贵族垂涎另一个贵族的财产,而后者碰巧在帝国家庭中失宠,此时前者就可作为控方揭发后者的叛逆罪,如果被告被判处死刑,前者就可得到被告的一部分财产。
这说明A. 罗马法无法有效地解决财产纠纷问题B. 罗马法的缺陷使其成为贵族斗争的工具C. 罗马法不利于调和统治阶级内部的矛盾D. 贵族之间的矛盾已经影响到帝国的稳定25. “对建立在理性基础上的工业社会表示怀疑,不屑于表面的客观真实,致力于探索离奇别致的形式技巧。
”具有这一创作精神的作者是A. 雪莱B. 毕加索C. 雨果D. 巴尔扎克26. 清朝康熙年间,烧制出大量造型丰富和具有装饰图案的瓷器,而且在瓷器的纹饰中绘有欧洲的家族、公司、团体、城市等图案标志。
下列相关表述中正确的是A. 中国瓷器开始大量销往海外市场B. 清朝贵族生活方式的西方化C. 许多瓷器为满足市场需要而生产D. 这些产品都出自官营手工业27. 1958年8月1日,中国第一台计算机由张梓昌领衔研制的103型通用数字电子计算机研制成功,运行速度每秒1,500次;1959年,由张效样教授领衔研制的中国第一台大型数字电子计算机,运算速度达到每秒1万次。
这反映出A. 人当时中闻科技人才大量涌现B. 当时中国科研出现"左"倾冒进现象C. 新中国在部分科技领域取得突破D. 新中国计算机技术落后于欧美等国家28. 1955年,毛泽东指出:“农民的出路主要还在农村,他们可组织起来,向一切可发挥自己力量的地方和部门进军,向生产的深度与广度进军。
”毛泽东此番话意在鼓励农民A. 开展土地改革运动B. 走农业集体化的道路C. 成立农村人民公社D. 实行联产承包责任制29. 道家认为“人法地,地法天,天法道,道法自然”;儒家肯定人是自然界的一部分,认为人负有“仁民爱物”、善待自然的伦理义务。
这些观念A. 专注于保护生态环境B. 属于农耕经济的产物C. 受到天人感应说影响D. 强化了神权政治体制30. 历史叙述、历史解释和历史评价是历史学习能力的重要组成部分。
下面有关赵匡胤杯酒释兵权的记载中属于历史解释的是A. 赵匡胤劝守信等部将“自择善地,各守外藩,勿议除替”B. 宴会次日,赵匡胤等部将“皆称疾,请解军权。
上许之”C. 几个朝中大将唯命交权主要迫于赵匡胤已牢控中央禁军D. 赵匡胤使用和平手段成功地防止了军队的政变31. “1849年(英国)国会废除了臭名昭著的航海条例,这一决议从1850年开始生效……1840-1860年间,英国继续削减关税,许多商品的关税甚至被取消。
……1863-1866年间,通过与法国签订条约,大多数欧洲国家加入了自由贸易网络,即所谓的‘科布登———谢瓦利埃条约’网络。
”材料反映了A. 欧洲“一体化”进程加快B. 自由主义思想被世界多数国家接受C. 英国殖民霸主地位动摇D. 资本主义世界市场的基本形成32. 下表是中国部分时期县的数目变化统计表,据此可知A. 县制有利于社会变革B. 县制是小农经济的基础C. 县制有职责明确的优点D. 县是基本的行政区域33. 美国学者丹尼尔·贝尔指出:大众消费时代开始于20世纪20年代,技术革命加上市场的发展和分期付款购物法的传播,彻底打破了新教徒害怕负债的传统顾虑,最终导致消费社会的降临。
