天大2006年运筹学考研真题
2006考研数学(二)真题及参考答案

2006年全国硕士研究生入学考试数学(二)一、填空题 (1)曲线4sin 52cos x xy x x+=-的水平渐近线方程为 .(2)设函数231sin ,0,(),x t dt x f x x a x ⎧≠⎪=⎨⎪=⎩⎰在0x =处连续,则a = .(3)广义积分22(1)xdxx +∞=+⎰.(4)微分方程(1)y x y x-'=的通解是 . (5)设函数()y y x =由方程1yy xe =-确定,则A dy dx== .(6)设矩阵2112A ⎛⎫= ⎪-⎝⎭,E 为2阶单位矩阵,矩阵B 满足2B A BE =+,则B = . 二、选择题(7)设函数()y f x =具有二阶导数,且()0,()0f x f x '''>>,x ∆为自变量x 在0x 处的增量,y ∆与dy 分别为()f x 在点0x 处对应的增量与微分,若0x ∆>,则 (A )0.dy y <<∆ (B )0.y dy <∆<(C )0.y dy ∆<<(D )0.dy y <∆<【 】(8)设()f x 是奇函数,除0x =外处处连续,0x =是其第一类间断点,则()x f t dt ⎰是(A )连续的奇函数. (B )连续的偶函数(C )在0x =间断的奇函数 (D )在0x =间断的偶函数. 【 】(9)设函数()g x 可微,1()(),(1)1,(1)2g x h x e h g +''===,则(1)g 等于(A )ln 31-. (B )ln 3 1.--(C )ln 2 1.--(D )ln 2 1.-【 】(10)函数212xxx y C e C e xe -=++满足一个微分方程是(A )23.xy y y xe '''--= (B )23.xy y y e '''--=(C )23.xy y y xe '''+-=(D )23.xy y y e '''+-=(11)设(,)f x y 为连续函数,则140(cos ,sin )d f r r rdr πθθθ⎰⎰等于(A )22120(,).x xdx f x y dy -⎰⎰(B )22120(,).x dx f x y dy -⎰⎰(C )22120(,).y ydy f x y dx -⎰⎰(D )22120(,).y dy f x y dx -⎰⎰【 】(12)设(,)f x y 与(,)x y ϕ均为可微函数,且1(,)0y x y ϕ≠. 已知00(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点,下列选项正确的是(A )若00(,)0x f x y '=,则00(,)0y f x y '=. (B )若00(,)0x f x y '=,则00(,)0y f x y '≠. (C )若00(,)0x f x y '≠,则00(,)0y f x y '=. (D )若00(,)0x f x y '≠,则00(,)0y f x y '≠.【 】(13)设12,,,,a a a 均为n 维列向量,A 是m n ⨯矩阵,下列选项正确的是 (A )若12,,,,a a a 线性相关,则12,,,,Aa Aa Aa 线性相关. (B )若12,,,,a a a 线性相关,则12,,,,Aa Aa Aa 线性无关.(C )若12,,,,a a a 线性无关,则12,,,,Aa Aa Aa 线性相关.(D )若12,,,,a a a 线性无关,则12,,,,Aa Aa Aa 线性无关. 【 】(14)设A 为3阶矩阵,将A 的第2行加到第1行得B ,再将B 的第1列的-1倍加到第2列得C ,记110010001P ⎛⎫⎪= ⎪ ⎪⎝⎭,则(A )1.C P AP -= (B )1.C PAP -=(C ).T C P AP =(D ).TC PAP =三 解答题15.试确定A ,B ,C 的常数值,使得23(1)1()xe Bx Cx Ax o x ++=++,其中3()o x 是当30x x →时比的高阶无穷小.16.arcsin xxe dx e ⎰求. 17.{}22(,)1,0D x y x y x =+≤≥设区域,221.1DxyI dxdy x y +=++⎰⎰计算二重积分 18.{}110,sin (0,1,2,)n n n x x x x n π+<<== 设数列满足1lim n x x +→∞证明: (1) 存在,并求极限;211(2)lim()n x n x nx x +→∞计算. 19.sin 2cos sin cos .<a <b b b b b a a a a a πππ<++>++证明: 当0时, 20 设函数()()0,,f u +∞在内具有二阶导数且()22z fx y=+满足等式22220z zx y∂∂+=∂∂.(Ⅰ)验证()()0f u f u u'''+=;(Ⅱ)若()()()10,11,f f f u '==求函数的表达式. 21 已知曲线L 的方程为221,(0),4x l t y l t⎧=+≥⎨=-⎩(Ⅰ)讨论L 的凹凸性;(Ⅱ)过点(-1,0)引L 的切线,求切点00(,)x y ,并写出切线的方程; (Ⅲ)求此切线与L (对应于0x x ≤的部分)及x 轴所围成的平面图形的面积.22 已知非齐次线性方程组12341234123414351331x x x x x x x x ax x x bx +++=-⎧⎪++-=-⎨⎪++-=⎩有个线性无关的解Ⅰ证明方程组系数矩阵A 的秩()2r A =; Ⅱ求,a b 的值及方程组的通解.23 设3阶实对称矩阵A 的各行元素之和均为3,向量()()121,2,1,0,1,1TTαα=--=-是线性方程组A x =0的两个解, (Ⅰ)求A 的特征值与特征向量 (Ⅱ)求正交矩阵Q 和对角矩阵A,使得TQ AQ A =.真题解析一、填空题 (1)曲线4sin 52cos x xy x x+=-的水平渐近线方程为15y =4sin 11lim lim2cos 55x x xx y x x→∞→∞+==-(2)设函数2301sin ,0(),0xt dt x f x x a x ⎧≠⎪=⎨⎪=⎩⎰ 在x =0处连续,则a =132200()1lim ()lim 33x x sm x f x x →→==(3)广义积分22(1)xdxx +∞=+⎰1222222201(1)11110(1)2(1)2(1)22xdx d x x x x +∞+∞+∞+==-⋅=+=+++⎰⎰(4)微分方程(1)y x y x-'=的通解是xy cxe -=)0(≠x(5)设函数()y y x =由方程1yy xe =-确定,则0x dy dx==e-当x =0时,y =1,又把方程每一项对x 求导,y yy e xe y ''=--01(1)1x x y yyyye y xe ey e xe ===''+=-=-=-+(6) 设A = 2 1 ,2阶矩阵B 满足BA =B +2E ,则|B |= .-1 2解:由BA =B +2E 化得B (A -E )=2E ,两边取行列式,得|B ||A -E |=|2E |=4, 计算出|A -E |=2,因此|B |=2. 二、选择题(7)设函数()y f x =具有二阶导数,且()0,()0,f x f x x '''>>∆为自变量x 在点x 0处的增量,0()y dy f x x ∆与分别为在点处对应增量与微分,若0x ∆>,则[A](A )0dy y <<∆(B )0y dy <∆<(C )0y dy ∆<<(D )0dy y <∆<由()0()f x f x '>可知严格单调增加()0()f x f x ''>可知是凹的即知(8)设()f x 是奇函数,除0x =外处处连续,0x =是其第一类间断点,则()xf t dt ⎰是[B](A )连续的奇函数 (B )连续的偶函数(C )在x =0间断的奇函数 (D )在x =0间断的偶函数(9)设函数()g x 可微,1()(),(1)1,(1)2,g x h x e h g +''===则g (1)等于[C] (A )ln 31- (B )ln 31--(C )ln 21--(D )ln 21- ∵ 1()()()g x h x g x e +''=,1(1)12g e+= g (1)= ln 21--(10)函数212x x x y c e c xe -=++满足的一个微分方程是[D] (A )23x y y y xe '''--= (B )23x y y y e '''--=(C )23xy y y xe '''+-=(D )23xy y y e '''+-=将函数212x x x y c e c xe -=++代入答案中验证即可.(11)设(,)f x y 为连续函数,则14(cos ,sin )d f r r rd πθθθγ⎰⎰等于[C](A )2212(,)x xdx f x y dy -⎰⎰(B )2212(,)x dx f x y dy -⎰⎰(C )2212(,)y ydy f x y dx -⎰⎰(D )2212(,)y dy f x y dx -⎰⎰(12)设(,)(,)f xyxy ϕ与均为可微函数,且(,)0,y x y ϕ'≠已知00(,)(,)x y f x y 是在约束条件(,)0x y ϕ=下的一个极值点,下列选项正确的是[D](A )若0000(,)0,(,)0x y f x y f x y ''==则(B )若0000(,)0,(,)0x y f x y f x y ''=≠则 (C )若0000(,)0,(,)0x y f x y f x y ''≠=则 (D )若0000(,)0,(,)0x y f x y f x y ''≠≠则(,)(,)(,)(,)0(1)(,)(,)0(2)(,)0x x xy y y F f x y x y F f x y x y F f x y x y F x y λλϕλϕλϕϕ=+'''=+=⎧⎪'''=+=⎨⎪'==⎩令今000000(,)(,)0,(,)y y y f x y x y x y ϕλϕ''≠∴=-'代入(1) 得 00000000(,)(,)(,)(,)y xx y f x y x y f x y x y ϕϕ'''='今 00000000(,)0,(,)(,)0(,)0x y xy f x y f x y x y f x y ϕ''''≠∴≠≠则 故选[D] (13)设α1,α2,…,αs 都是n 维向量,A 是m ⨯n 矩阵,则( )成立.(A) 若α1,α2,…,αs 线性相关,则A α1,A α2,…,A αs 线性相关. (B) 若α1,α2,…,αs 线性相关,则A α1,A α2,…,A αs 线性无关. (C) 若α1,α2,…,αs 线性无关,则A α1,A α2,…,A αs 线性相关. (D) 若α1,α2,…,αs 线性无关,则A α1,A α2,…,A αs 线性无关. 解: (A)本题考的是线性相关性的判断问题,可以用定义解.若α1,α2,…,αs 线性相关,则存在不全为0的数c 1,c 2,…,c s 使得c 1α1+c 2α2+…+c s αs =0,用A 左乘等式两边,得c 1A α1+c 2A α2+…+c s A αs =0,于是A α1,A α2,…,A αs 线性相关.如果用秩来解,则更加简单明了.只要熟悉两个基本性质,它们是: 1. α1,α2,…,αs 线性无关⇔ r(α1,α2,…,αs )=s. 2. r(AB )≤ r(B ).矩阵(A α1,A α2,…,A αs )=A ( α1, α2,…,αs ),因此r(A α1,A α2,…,A αs )≤ r(α1, α2,…,αs ).由此马上可判断答案应该为(A).(14)设A 是3阶矩阵,将A 的第2列加到第1列上得B ,将B 的第1列的-1倍加到第2列上得C .记 1 1 0P = 0 1 0 ,则 0 0 1(A) C =P -1AP . (B) C =PAP -1. (C) C =P TAP . (D) C =PAP T. 解: (B)用初等矩阵在乘法中的作用得出B =PA , 1 -1 0C =B 0 1 0 =BP -1= PAP -1. 0 0 1三、解答题(15)试确定A ,B ,C 的常数值,使23(1)1()x e Bx Cx Ax o x ++=++其中3()o x 是当30x x →时比的高阶无穷小.解:泰勒公式2331()26xx x e x o x =++++代入已知等式得 23323[1()][1]1()26x x x o x Bx Cx Ax o x ++++++=++整理得233111(1)()()1()226BB xC B x C o x Ax o x ⎛⎫+++++++++=++ ⎪⎝⎭比较两边同次幂函数得B +1=A ①C +B +12=0 ② 1026B C ++= ③ 式②-③得120233B B +==-则 代入①得13A = 代入②得16C = (16)求arcsin xxe dx e ⎰.解:原式=22arcsin arcsin ()x x xx e t de e t dt e t =⎰⎰令21arcsin arcsin ()1t dttd t t t t =-=-+-⎰⎰2222arcsin arcsin 1(2)12(1)1t tdt t udu t u t t u u t t -=-+-==-+--⎰⎰令2arcsin 1t dut u =-+-⎰arcsin 11ln 21t u C t u -=-+++22arcsin arcsin 111ln 211x x x x x x e e e dx C e e e --∴=-++-+⎰. (17)设区域22{(,)||,0}D x y x y x =+≤≥,计算二重积分2211DxyI dxdy x y +=++⎰⎰.解:用极坐标系2201D xydxdy x y ⎛⎫= ⎪++⎝⎭⎰⎰11222002ln(1)ln 2122r I d dr r r ππππθ-==+=+⎰⎰. (18)设数列{}n x 满足10x π<<,1sin (1,2,3,)n n x x n +==证明:(1)1lim n n x +→∞存在,并求极限;(2)计算211lim n x n n n x x +→∞⎛⎫ ⎪⎝⎭. 证:(1)212sin ,01,2x x x n =∴<≤≥ 因此 1sin ,{}n n n n x x x x +=≤单调减少有下界()0n x ≥根据准则1,lim n n x A →∞=存在在1sin n n x x +=两边取极限得sin 0A A A =∴=因此1lim 0n n x +→∞=(2)原式21sin lim "1"n x n n n x x ∞→∞⎛⎫= ⎪⎝⎭为型 离散型不能直接用洛必达法则先考虑 22011s i n l i m l n 0s i n l i m t t t t t t t e t →⎡⎤⎢⎥⎣⎦→⎛⎫= ⎪⎝⎭用洛必达法则2011(cos sin )limsin 2t t t t t tt te→-=23233310()0()26cos sin limlim22t t t t t t t t t t tt t ee →→⎡⎤⎡⎤-+--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦==3330110()261lim26t t t t ee →⎛⎫-++ ⎪⎝⎭-==.(19)证明:当0a b π<<<时,1sin 2cos sin 2cos b b b b a a a aππ++>++. 证:令()sin 2cos f x x x x x π=++ 只需证明0a x π<<<时,()f x 严格单调增加()sin cos 2sin f x x x x x π'=+-+cos sin x x x π=-+()cos sin cos sin 0f x x x x x x x ''=--=-< ()f x '∴严格单调减少又()cos 0f ππππ'=+=故0()0()a x f x f x π'<<<>时则单调增加(严格)()()b a f b f a >>由则得证(20)设函数()(0,)f u +∞在内具有二阶导数,且()22Z fx y=+满足等式22220z zx y∂∂+=∂∂.(I )验证()()0f u f u u'''+=; (II )若(1)0,(1)1f f '== 求函数()f u 的表达式.证:(I )()()22222222;zx zy f x y f x y xyx yx y∂∂''=+=+∂∂++()()()()22222223222222zx y f x yf x yx x y x y ∂'''=+++∂++()()()()22222223222222zy x f x yf x yy x y x y ∂'''=+++∂++()2222222222()0()()0f x y z zf x yx y x yf u f u u'+∂∂''+=++=∂∂+'''∴+=代入方程得成立(II )令(),;,dp p dp du c f u p c p du u p u u'==-=-+=⎰⎰则22(1)1,1,()ln ||,(1)0,0()ln ||f c f u u c f c f u u '===+==∴= 由(21)已知曲线L 的方程221(0)4x t t y t t⎧=+≥⎨=-⎩(I )讨论L 的凹凸性;(II )过点(1,0)-引L 的切线,求切点00(,)x y ,并写出切线的方程; (III )求此切线与L (对应0x x ≤部分)及x 轴所围的平面图形的面积.解:(I )4222,42,12dx dy dy t t t dt dt dx t t-==-==-222312110(0)2dy d d y dx t dx dx dt t t t dt ⎛⎫⎪⎛⎫⎝⎭=⋅=-⋅=-<> ⎪⎝⎭处(0L t ∴>曲线在处)是凸(II )切线方程为201(1)y x t ⎛⎫-=-+⎪⎝⎭,设2001x t =+,20004y t t =-,则2223200000000241(2),4(2)(2)t t t t t t t t ⎛⎫-=-+-=-+⎪⎝⎭得200000020,(1)(2)001t t t t t t +-=-+=>∴=点为(2,3),切线方程为1y x =+(III )设L 的方程()x g y =则()3()(1)S g y y dy =--⎡⎤⎣⎦⎰ ()224024241t t y y x y -+==±-=±-+解出t 得由于(2,3)在L 上,由()232241()y x x y g y ===--+=得可知()30944(1)S y y y dy ⎡⎤=-----⎣⎦⎰ 3300(102)44y dy ydy =---⎰⎰3333220002(10)44(4)214(4)3y y yd y y =-+--=+⨯⨯-⎰8642213333=+-=- (22)已知非齐次线性方程组 x 1+x 2+x 3+x 4=-1,4x 1+3x 2+5x 3-x 4=-1,a x 1+x 2+3x 3+bx 4=1有3个线性无关的解.① 证明此方程组的系数矩阵A 的秩为2.② 求a,b 的值和方程组的通解.解:① 设α1,α2,α3是方程组的3个线性无关的解,则α2-α1,α3-α1是AX =0的两个线性无关的解.于是AX =0的基础解系中解的个数不少于2,即4-r(A )≥2,从而r(A )≤2.又因为A 的行向量是两两线性无关的,所以r(A )≥2.两个不等式说明r(A )=2.② 对方程组的增广矩阵作初等行变换:1 1 1 1 -1 1 1 1 1 -1(A |β)= 4 3 5 -1 -1 → 0 –1 1 –5 3 ,a 1 3b 1 0 0 4-2a 4a+b-5 4-2a由r(A )=2,得出a=2,b=-3.代入后继续作初等行变换:1 02 -4 2→ 0 1 -1 5 -3 .0 0 0 0 0得同解方程组x 1=2-2x 3+4x 4,x 2=-3+x 3-5x 4,求出一个特解(2,-3,0,0)T 和AX =0的基础解系(-2,1,1,0)T ,(4,-5,0,1) T.得到方程组的通解: (2,-3,0,0)T +c 1(-2,1,1,0)T +c 2(4,-5,0,1)T , c 1,c 2任意.(23) 设3阶实对称矩阵A 的各行元素之和都为3,向量α1=(-1,2,-1)T , α2=(0,-1,1)T 都是齐次线性方程组AX =0的解.① 求A 的特征值和特征向量.② 求作正交矩阵Q 和对角矩阵Λ,使得 Q T AQ =Λ.解:① 条件说明A (1,1,1)T =(3,3,3)T ,即 α0=(1,1,1)T 是A 的特征向量,特征值为3.又α1,α2都是AX =0的解说明它们也都是A 的特征向量,特征值为0.由于α1,α2线性无关, 特征值0的重数大于1.于是A 的特征值为3,0,0.属于3的特征向量:c α0, c ≠0.属于0的特征向量:c 1α1+c 2α2, c 1,c 2不都为0.② 将α0单位化,得η0=(33,33,33)T . 对α1,α2作施密特正交化,的η1=(0,-22,22)T , η2=(-36,66,66)T . 作Q =(η0,η1,η2),则Q 是正交矩阵,并且 3 0 0Q T AQ =Q -1AQ = 0 0 0 .0 0 0。
运筹学考研真题及答案

运筹学考研真题及答案运筹学考研真题及答案【篇一:1999-2016年南京航空航天大学824运筹学考研真题及答案解析汇编】p> 我们是布丁考研网南航考研团队,是在读学长。
我们亲身经历过南航考研,录取后把自己当年考研时用过的资料重新整理,从本校的研招办拿到了最新的真题,同时新添加很多高参考价值的内部复习资料,保证资料的真实性,希望能帮助大家成功考入南航。
此外,我们还提供学长一对一个性化辅导服务,适合二战、在职、基础或本科不好的同学,可在短时间内快速把握重点和考点。
有任何考南航相关的疑问,也可以咨询我们,学长会提供免费的解答。
更多信息,请关注布丁考研网。
以下为本科目的资料清单(有实物图及预览,货真价实):南京航空航天大学《运筹学》全套考研资料包含:一、南京航空航天大学《运筹学》历年考研真题及答案解析2016年南京航空航天大学《运筹学》考研真题(含答案解析)(11月份统一更新)2015年南京航空航天大学《运筹学》考研真题(含答案解析)2014年南京航空航天大学《运筹学》考研真题(含答案解析)2013年南京航空航天大学《运筹学》考研真题(含答案解析)2012年南京航空航天大学《运筹学》考研真题(含答案解析)2011年南京航空航天大学《运筹学》考研真题(含答案解析)2010年南京航空航天大学《运筹学》考研真题(含答案解析)2009年南京航空航天大学《运筹学》考研真题(含答案解析)2008年南京航空航天大学《运筹学》考研真题(含答案解析)2006年南京航空航天大学《运筹学》考研真题(含答案解析)2005年南京航空航天大学《运筹学》考研真题(含答案解析)2004年南京航空航天大学《运筹学》考研真题(含答案解析)2003年南京航空航天大学《运筹学》考研真题(含答案解析)2002年南京航空航天大学《运筹学》考研真题(含答案解析)2001年南京航空航天大学《运筹学》考研真题(含答案解析)2000年南京航空航天大学《运筹学》考研真题(含答案解析)1999年南京航空航天大学《运筹学》考研真题(含答案解析)二、南京航空航天大学《运筹学》期中期末试卷汇编三、南京航空航天大学《运筹学》考研复习笔记1、运筹学辅导讲义该部分为824运筹学辅导讲义2017版,由2016级高分学姐根据2017年考研动态编写,讲义按章节编写包含三个部分、第一个部分考研点睛(历年考试情况分析)、第二个部分考研知识点总结(知识点详细划分,重要内容均作了详细标记,可以直接切入考研重难点,避免一些不必要的时间浪费),第三部分直击考研(典型题型针对性联系)。
运筹学考研真题及答案

运筹学考研真题及答案运筹学考研真题及答案一、选择题1. 在线性规划中,若最优化问题的对偶问题有最优解,则原始问题也有最优解。
(正确)解析:线性规划理论中对偶定理:“若原始问题的对偶问题有可行解,且存在最优解,则原始问题也有最优解。
”2. 若在线性规划的单纯形法中,某一回路上的所有非基变量(非基变量为0)均为0,则这一问题无有限最优解。
(错误)解析:所有非基变量为0时,相应的基变量可以任意非负,问题有无穷多最优解。
3. 在线性规划中,若某元组在原始问题和对偶问题下都是可行解,则该元组是原始问题和对偶问题的最优解。
(错误)解析:若某元组在原始问题和对偶问题下都是可行解,则该元组满足原始问题的可行性和对偶问题的可行性,但并不一定是最优解。
4. 线性规划的最优性条件是原始问题的可行解和对偶问题的可行解所对应的目标函数值相等。
(正确)解析:线性规划理论中最优性条件:“若原始问题的可行解与对偶问题的可行解所对应的目标函数值相等,则解是原始问题和对偶问题的最优解。
”5. 线性规划的可行性要求约束条件为不等式约束。
(错误)解析:线性规划的可行性要求是所有约束条件都满足,包括等式约束和不等式约束。
二、填空题1. 与线性规划的相对论证法相对应的是(单纯形法)。
解析:线性规划的相对论证法和单纯形法是互为相对的两种求解方法。
2. 在线性规划中,若最优差异为0,则最优解是(非唯一)。
解析:最优差异为0意味着最优解是非唯一的,有多个最优解。
3. 线性规划的最优性条件是(对偶定理)与最优条件相对应。
解析:线性规划的最优性条件是对偶定理,而最优条件是原始问题的可行解和对偶问题可行解所对应的目标函数值相等。
4. 在线性规划中,若一个可行解在原始问题和对偶问题下都是最优解,则称为(互补性)条件。
解析:若一个可行解在原始问题和对偶问题下都是最优解,则满足互补性条件。
三、应用题1.某公司生产两种产品A和B,每个产品的制造工序及所需时间如下表,在一天内,公司有8小时的工时可用,每个工序只能由一名员工负责完成。
2006经管院运筹学试卷B
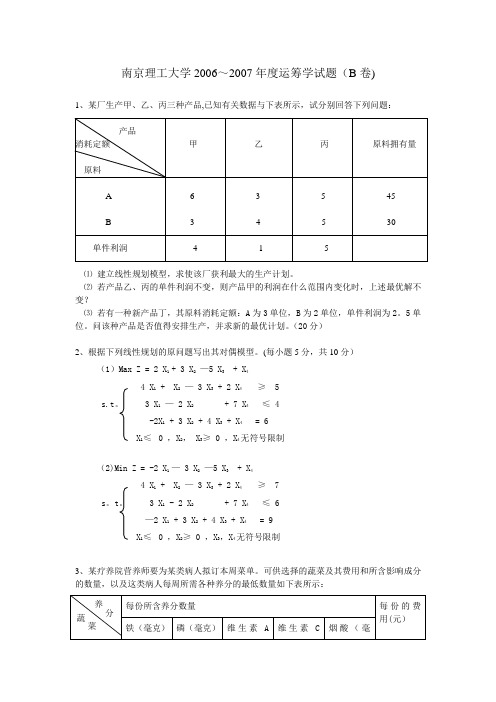
南京理工大学2006~2007年度运筹学试题(B卷)1、某厂生产甲、乙、丙三种产品,已知有关数据与下表所示,试分别回答下列问题:产品消耗定额甲乙丙原料拥有量原料A 6 3 5 45B 3 4 5 30单件利润 4 1 5⑴建立线性规划模型,求使该厂获利最大的生产计划。
⑵若产品乙、丙的单件利润不变,则产品甲的利润在什么范围内变化时,上述最优解不变?⑶若有一种新产品丁,其原料消耗定额:A为3单位,B为2单位,单件利润为2。
5单位。
问该种产品是否值得安排生产,并求新的最优计划。
(20分)2、根据下列线性规划的原问题写出其对偶模型。
(每小题5分,共10分)(1)Max Z = 2 X1 + 3 X2—5 X3 + X44 X1 + X2 — 3 X3 + 2 X4 ≥ 5s.t。
3 X1 — 2 X2 + 7 X4≤ 4-2X1 + 3 X2 + 4 X3 + X4 = 6X1≤ 0 ,X2, X3≥ 0 ,X4无符号限制(2)Min Z = -2 X1 — 3 X2—5 X3 + X44 X1 + X2 — 3 X3 + 2 X4 ≥ 7s。
t。
3 X1 - 2 X2 + 7 X4≤ 6—2 X1 + 3 X2 + 4 X3 + X4 = 9X1≤ 0 ,X2≥ 0 ,X3,X4无符号限制3、某疗养院营养师要为某类病人拟订本周菜单。
可供选择的蔬菜及其费用和所含影响成分的数量,以及这类病人每周所需各种养分的最低数量如下表所示:另外为了口味的需求,规定一周内所用卷心菜不多于2份,其它蔬菜不多于4份。
若病人每周需14份蔬菜。
问选用每种蔬菜各多少份?试着建立该问题的线性规划模型。
(不用求解,10分)4、有A1,A2,A3三座铁矿,每天要把生产的铁矿石运往B1,B2,B3,B4四个炼铁厂。
各矿的产量,各厂的销量(百吨/天)以及各厂矿间的运价(百元/百吨)如下表所示(1)试给出该运输问题的初始调运方案,并求出该初始调运方案对应的总运费。
天大2004年运筹学考研真题

所有答案必须写在答题册上,写在试题上无效。
一(12%)、填空1.设线性规划问题}{0max ≥=bx Ax cx 有最优解*x 和影子价格*y ,则线性规划}{该解是点:如果它在纯策略意义下无解,则它在意义下必有解。
二(23%)、某公司生产家用的清洁产品,为了在高度的市场竞争中增加市场份额,公司决定进行一次大规模的广告行动。
表1给出了公司准备做广告的三种产品名称、估计每做一单位广告(一个广告标准批量)使每种产品的市场份额增加量、公司拟定的广告后每种产品市场份额增加量的最低目标和两种可选的广告方式的单价。
C B X B B -1b 100200000M M M x 1x 2x 3x 4x 5x 6x 7x 80x 541/3114/3-1/3-1100x 14-1/30-2/31/30200x 23100σj400/3100/3M-400/3M-100/3M(1)请填完表中空白;(2)由表指出最优广告计划并求出相应的最低广告费用,此最优计划使每种产品的市场份额最低增量目标达成情况如何?求出对偶最优解Y*的实际意义。
中的互理:P )[max]z=CX,X ∈{X|AX ≤b,X ≥0},(D)[min]u=Yb,Y ∈{YA ≥b,Y ≥0},若,X Y 分别是(P)(D)的可行解,,s s X Y 分别是其相应的松弛变量,则,X Y 是(P),(D)的最优解的充要条件是:0s s YX Y X ==;并解释互补松弛定理的经济意义。
四(15%)、某工厂购进100台机器,准备用于生产A,B 两种产品。
若生产产品A,每台机器每年可收入45万,损坏率为65%,若生产产品B 每台机器年收入35万,损坏率为35%,估计三年后将有新的机器出现,旧的机器将全部淘汰。
请在下列两问中任选一问:1、试问每年就如何生产,使三年内的收入最多?运用动态规划方法具体计算求解。
2、写出用动态规划方法求解时的阶段变量、状态变量、决策变量、状态转移、阶段指标、指标函数、基本方程(递推公式),不必具体计算。
天津大学考研运筹学832真题及解析(09-13)

天津⼤学考研运筹学832真题及解析(09-13).2009~2013 年天津⼤学招收硕⼠学位研究⽣⼊学考试试题—832运筹学基础.⽬录天津⼤学招收2009年硕⼠学位研究⽣⼊学考试试题 (2)天津⼤学招收2010年硕⼠学位研究⽣⼊学考试试题 (8)天津⼤学招收2011年硕⼠学位研究⽣⼊学考试试题 (14)天津⼤学招收2012年硕⼠学位研究⽣⼊学考试试题 (19)天津⼤学招收2013年硕⼠学位研究⽣⼊学考试试题 (23)天津⼤学招收2009年硕⼠学位研究⽣⼊学考试试题共七题。
所有答案必须写在答题纸上,并写清楚题号,答案写在试题上⽆效。
⼀、单项选择题(共24分,每题3分)1、根据线性规划的互补松弛定理,影⼦价格⼤于零的资源⼀定剩余;安排⽣产的产品机会成本⼀定利润。
A、没有,⼩于B、没有,⼤于C、没有,等于D、有,等于2、⽬标线性规划模型的⼀个主要特点是引⼊了变量,模型的⽬标就是这些变量的极化。
A、正偏差,⼤B、负偏差,⼩C、正或负偏差,⼤D、正或负偏差,⼩3、线性规划模型中,若某⼀变量的⽬标函数系数发⽣变化,以下结果中不可能出现的是A、可⾏域改变B、可⾏域不变C、最优基不变,⽬标函数值改变D、最优基不变,⽬标函数值也不变4、将⾮平衡运输问题化为平衡运输问题,在表上相当于增加⼀个虚设的,在模型中相当于增加若⼲个变量A、产地,松弛B、销地,剩余C、产地或销地,松弛D、产地或销地,松弛或剩余5、⽹络最⼤流问题标号法的理论基础是: A、贝尔曼最优性原理B、K-T定理C、单纯性原理D、最⼤流最⼩截定理6、矩阵对策⼜称对策,它在纯策略意义下有解的充要条件是:该解为.A、⼆⼈有限,鞍点B、⼆⼈有限零和,鞍点C、⼆⼈有限零和,驻点D、⼆⼈有限零和,K-T点7、某⼈收益为x的效⽤为u(x),若u(x)对x边际递减,则他对风险的态度是。
A、风险中⽴B、厌恶风险C、追求风险D、⽆法确定8、基于蒙特卡洛法的系统模拟技术主要适⽤于对系统进⾏模拟。
2006年全国硕士研究生入学考试数学(四)答案解析与点评
= f ′(4x2 − y 2 ) ⋅ (8xdx − 2 ydy)
= 2 f ′(4x2 − y 2 ) ⋅ (4xdx − ydy)
于是 dz = 2 f ′(0)(4dx − 2dy) = 4dx − 2dy . (1, 2 )
可参见水木艾迪 2006 考研数学 36 计例 15-5 等题 (4)已知 a1, a2 为 2 维列向量,矩阵 A = (2a1 + a2 , a1 − a2 ) , B = (a1, a2 ) .若行列式
(2) 设函数 f (x) 在 x = 2 的某邻域内可导,且 f ′(x) = e f (x) , f (2) = 1则 f ′′′(2) = 2e3.
【解析与点评】由题设 f (x) 在 x = 2 的某邻域内可导以及 f ′(x) = e f (x) ,可知 f ′(x) 也在
x = 2 的同一邻域内可导,于是在该邻域内函数 f (x) 二阶可导,且
(3) 设 函 数 f (u) 可 微 , 且 f ′(0) = 1 , 则 z = f (4x 2 − y 2 ) 在 点 (1,2) 处 的 全 微 分 2
dz = 4dx − 2dy 。 (1, 2 )
【解析与点评】 该题为多元函数微分学基本题。利用一阶全微分形式不变性直接计算可得
dz = f ′(u)du = f ′(4x2 − y 2 ) ⋅ d (4x2 − y 2 )
2006 年全国硕士研究生入学统一考试 数学试题解析点评
水木艾迪考研辅导班命题研究中心
2006 年全国硕士研究生入学考试数学(四)
答案解析与点评
水木艾迪考研辅导班命题研究中心 清华大学数学科学系 刘坤林 谭泽光 俞正光 葛余博 1. 06 年考题仍然以基本的概念,理论和技巧为主, 注意考察基础知识的理解与简单综合运 用。除概率统计比 05 年考题难度略有增加以外,试卷难度普遍降低,估计平均难度系 数为 55-62%,平均分数为 80-83 分;而前几年为 38-45%,平均分数只有 60-63 分。 2. 各套试题共用题目比例有较大幅度提高,在大纲要求的共同范围内难度趋于统一。特别 是数三数四连续几年并无任何经济特色,正如我们在讲座和教学中强调的那样,考的是 数学,确切说是理工类数学的能力。这是对 07 年考生的重要参考。 3. 06 年考题进一步说明了我们在水木艾迪考研辅导中教学策略的正确性,教学内容的准 确性和有效性,包括基础班、强化班及考研三十六计冲刺班,对广大学员的教学引导与 训练,使更大面积的考生最大限度受益。 就四套试题的全局而言,水木艾迪考研辅导教学题型、方法与技巧在 06 年的考试 中得到完美的体现,许多试题为水木艾迪考研辅导教学或模拟试题的原题,还有大量 题目仅仅有文字和符号的差别,问题类型及所含知识点与所用方法完全相同,特别是 水木艾迪考研数学三十六计为广大学员提供了全盛的锐利武器。 在面向 07 年考研的水木艾迪考研辅导教学中,水木艾迪的全体清华大学教师将进 一步总结经验,不辜负广大考生的支持和赞誉,以独树一帜的杰出教学质量回报考生 朋友,为打造他们人生的 U-形转弯倾心工作,送他们顺利走上成功之路。
河海大学2006年运筹学试卷
2006-2007学年第一学期《运筹学》期末试卷(经济学专业03级)Class ID Number Name ScoreI.Tree/False(1) That the LP is unbounded means:(A) The feasible region is unbounded;(B) The incoming variable is available but the outgoing variable cannot be found;(C) All testing figures are zero for non-basic variables in the optimal table;(D) The corresponding minimum ratio is more than one when selecting the outgoing variable.(A, B, C, D)(2) That the LP is of alternate optima means:(A) One basic variable is equal to zero in optimal table;(B) The testing figure(s) of one (or more) non-basic variable is zero in optimal table;(C) The feasible region is unbounded;(D) The minimum ratio is zero as per to determine the outgoing variable.(A, B, C, D)(3) The shadow price of a resource is its market price.(4) If the feasible region of an LP problem is not empty, then at least one vertex is the optimal solution.(5) The non-basic variable in basic feasible solution must be zero.(6) If primal problem is of alternate optima, then its dual problem is also of alternate optima.(7) X1 and X2 are two different optimal solutions in an LP problem, and CX1=CX2. X is a point located on the segment linking X1 and X2. Then, CX1=CX2=CX.(8) X* and Y* are optimal solutions for primal and its dual problem respectively, then X* = Y*.(9) That a constant is added to objective function will not affect the optimal solution of an LP problem.II. To solve the LP problems below:(1) Max. Z = X 1 + X 2 +X 3 +X 4 s.t. X 1 + X 2 ≤ 3 X 3 +X 4 ≤ 2 X 1, X 2 , X 3, X 4≥ 0 Please find out the optimal solution of its dual.(2) The objective function of an LP is Max. Z = 2X1 - X2 +4X 3. This LP is of three constraints(resources #1,#2 and #3 respectively) with “≤”form. Below is a processing step by using simplex method. a) To complete this table;b) Is this table optimal? If “yes ”, then do c); if “no ”, then find out the optimal table. c) To write out the optimal solution and objective value.d) To write out the shadow prices of resources #1, #2 and #3, and describe the significances.III. To find the shortest path and its length from A to D:C1 59 8 B1 7 6D 6 C2 A 8 7 7 B2 5 C3 6VI To solve the transportation problem below (M is the last two places of your ID Number):IV.There is an LP problem below:Max. Z = -5X1 + 5X2 +13X3s.t. - X1 + X2+ X3≤2012X1 +4X2 +10X3 ≤90X1, X2 , X3≥0a)Solve it;b)Formulate its dual;c)If resource #1 is changed to 18, what will Z be? What will the optimal solutionbe?d)If resources #1 and #2 are increased by one unit respectively, what influences willbe happened to Z?e)What is the allowed range for C3?f)What is the allowed range for b2? If b2is decreased to 88, what is the optimalsolution?2006-2007学年第一学期《运筹学》期末试卷(经济学专业03级)Class ID Number Name Score I.判断(1) 线性规划无界的含义是:(A) 可行域无界;(B) 有入基变量但没有出基变量;(C) 最优表中,有非基本变量的检验数是零;(D) 选取出基变量时,对应的最小比值多于一个。
(NEW)运筹学教材编写组《运筹学》(第4版)笔记和课后习题(含考研真题)详解
线性规划问题的共同特征:
(1)每一个问题都用一组决策变量
表示某一方案,这组
决策变量的某一确定值就代表一个具体方案。一般这些变量的取值是非
负且连续的。
(2)存在有关的数据,如资源拥有量、消耗资源定额、创造新价值 量等,同决策变量构成互不矛盾的约束条件,这些约束条件可以用一组 线性等式或线性不等式来表示。
1.2 课后习题详解
本章无课后习题。
1.3 考研真题详解
本章只是对本课程的一个简单介绍,不是考试重点,所以基本上没 有学校的考研试题涉及到本章内容,因此,读者可以简单了解,不必作 为复习重点,本部分也就没有可选用的考研真题。Leabharlann 第2章 线性规划与目标规划
2.1 复习笔记
1.线性规划模型的概念及其一般形式
目 录
第1章 运筹学概论 1.1 复习笔记 1.2 课后习题详解 1.3 考研真题详解
第2章 线性规划与目标规划 2.1 复习笔记 2.2 课后习题详解 2.3 考研真题详解
第3章 对偶理论与灵敏度分析 3.1 复习笔记 3.2 课后习题详解 3.3 考研真题详解
第4章 运输问题 4.1 复习笔记 4.2 课后习题详解
2.线性规划问题的标准型及标准化 (1)线性规划的标准型
或
(2-4) (2-5) 线性规划的标准型要求:目标函数是Max型;约束条件是等式约 束;决策变量非负。 (2)线性规划的标准化方法
① 若要求目标函数实现最小化,即
,则只需将目标函数最
小化变换为求目标函数最大化,即令 ,于是得到
第13章 排队论
13.1 复习笔记 13.2 课后习题详解 13.3 考研真题详解 第14章 存储论 14.1 复习笔记 14.2 课后习题详解 14.3 考研真题详解 第15章 对策论基础 15.1 复习笔记 15.2 课后习题详解 15.3 考研真题详解 第16章 单目标决策 16.1 复习笔记 16.2 课后习题详解 16.3 考研真题详解 第17章 多目标决策 17.1 复习笔记
2006级运筹学试题A
天津师范大学考试试卷Array 2007—2008学年第二学期期末考试试卷(A 卷)科目:运筹学学院:管理学院专业:信管、物流一、基本计算题:(每小题15分,本大题共60分)1. 用表上作业法,求解下列产销平衡问题的最优调用方案和最2. 某企业生产两种产品A、B,市场销售前景很好。
这两种产品的单件销售利润为:A每台1000元,B每台800元。
两产品需要同一种材料,分别为6kg和4kg。
该材料的每周计划供应量为240kg,若不够时可议价购入此种材料不超过80kg。
由于议价原材料价格高于计划内价格,导致A、B产品的利润同样地降低100元。
该企业的决策者考虑:首先,企业要满足客户每周的基本要求:A24台、B18台。
第二,计划内的材料要充分使用完。
第三,努力使获得的利润更高。
试建立生产计划的数学模型。
3. 求下图所示网络中v s到v t的最大流和网络的最小割集。
弧旁的数字为容量。
4. 某市一工业局接省经委一对外加工任务,现有4kt材料拟分配给可以接受该项任务的甲、乙、丙三家工厂。
为计算简便起见,仅以千吨为单位进行分配。
据事先了解,各厂在分得该种材料之后,可为国家净创外汇如下所示(单位为万美元)。
问:(1)拟分配给各厂各多少千吨材料,可使国家获得的外二、综合计算题:(每小题20分,本大题共40分)1. 已知某工厂计划生产A1,A2,A3三种产品,各产品需要在甲、乙、丙设备上加工。
有关数据如下表。
试问:(1)如何充分发挥设备能力,使工厂获利最大?(2)若为了增加产量,可借用别的工厂的设备甲,每月可借用60台时,租金1.8万元,问是否合算?(3)若另有2种新产品A4、A5,其中每件A4需用设备12台时、设备乙5台时、设备丙10台时,每件获利2.1千元,每件A5需用设备甲4台时、设备乙4台时、设备丙12台时,每件获利1.87千元。
如A1、A2、A3设备台时不增加,分别回答这2种新产品是否合算?(42. 根据下面工程明细表绘制PERT网络图,并计算各事项的时。
