人教版一次函数单元测试题
人教版八年级数学下册 第十九章 一次函数 单元测试卷(含答案)

2019年八年级数学下册一次函数单元测试卷一、选择题1、对于函数y=-3x+1,下列结论正确的是()A.它的图象必经过点(-1,3)B.它的图象经过第一、二、三象限C.当x>1时,y<0 D.y的值随x值的增大而增大2、巴西奥运会期间,童童从宾馆出发前往奥体中心观看中国女排决战塞尔维亚,先匀速步行至轻轨车站,等了一会儿,童童搭乘轻轨至奥体中心观看演出,演出结束后,她搭乘朋友的车顺利到家。
其中x表示童童从宾馆出发后所用时间,y表示童童离宾馆的距离.下图能反映y与x的函数关系式的大致图象是3、向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止注水1分钟,然后继续注水,直至注满.则能反映注水量与注水时间函数关系的图象是( )A.B.C.D.4、若直线y=kx+b经过第二、三、四象限,则()A.k>0,b>0 B.k>0,b<0C.k<0,b>0D.k<0,b<05、在同一平面直角坐标系中,直线y=4x+1与直线y=﹣x+b的交点不可能在()A.第一象限B.第二象限C.第三象限D.第四象限6、用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )A. B. C. D.7、若点A(m,n)在的图像上,且2m-3n>6,则b的取值范围为A. b>2B. b>-2C. b<2D. b<-28、如图,已知:函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x +b>ax﹣3的解集是( )A.x>﹣5 B.x>﹣2 C.x>﹣3 D.x<﹣29、对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,ma x{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是( )A.0 B.2 C.3 D.410、已知直线y=34 x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的函数解析式是( )A.y=﹣x+8 B.y=﹣x+8 C.y=﹣x+3 D.y=﹣x+311、在A、B两地之间有汽车站C(C在直线AB上),甲车由A地驶往C,乙车由B地驶往A地,两车同时出发,匀速行驶.甲、乙两车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论中:①A、B两地相距440千米;②甲车的平均速度是60千米/小时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇,正确的结论有()A.1个B.2C.3个D.4个12、如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )A.B.C.D.二、填空题13、函数x32x1y-+-=的自变量x的取值范围是。
人教版八年级下册数学一次函数-单元测试题

人教版八年级下册数学一次函数单元测试题一、选择题:1.星期天,小明和小兵租用一艘皮划艇去嘉陵江游玩,他们先从上游顺流划行1小时,再停留0.5小时采集植物标本,然后加速划行0.5小时到下游,最后乘坐公交车1小时回到出发地,那么小明和小兵距离出发点的距离y随时间x变化的大致图象是()2.某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )3.向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止注水1分钟,然后继续注水,直至注满.则能反映注水量与注水时间函数关系的图象是( )4.一次函数y=2x﹣1的图象大致是()5.同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图,则满足y1≥y2的x 取值范围是()A.x≤﹣2 B.x≥﹣2 C.x<﹣2 D.x>﹣26.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 图描述了他上学的情景,下列说法中错误的是( )A.修车时间为15分钟B.学校离家的距离为2000米C.到达学校时共用时间20分钟D.自行车发生故障时离家距离为1000米7.若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式中总是成立的是( ) A.ab>0 B.a-b>0 C.a2+b>0 D.a+b>08.在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k不经过...的象限是( )A.第一象限B.第二象限C.第三象限D.第四象限9.已知一次函数y=-0.5x+2,当1≤x≤4时,y的最大值是().A.2 B.1.5 C.2.5 D.-610.在市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程s(米)与时间t (分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是()A.这次比赛的全程是500米B.乙队先到达终点C.比赛中两队从出发到1.1分钟时间段,乙队的速度比甲队的速度快D.乙与甲相遇时乙的速度是375米/分钟11.如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(1,1),B(3,1),C(2,2)当直线y=0.5x+b与△ABC有交点时,b的取值范围是( )A.-1≤b≤1 B.-1≤b≤0.5C.-0.5≤b≤0.5 D.-0.5≤b≤112.如图,在平面直角坐标系,直线y=﹣3x+3与坐标轴分别交于A,B两点,以线段AB为边,在第一象限内作正方形ABCD,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在直线y=3x﹣2上,则a的值为()A.1 B.2C.﹣1 D.﹣1.5二、填空题:13.3x﹣y=7中,变量是,常量是.把它写成用x的式子表示y的形式是.14.已知y-2与x成正比,且当x=1时, y=-6,则y与x的关系式是____________。
人教版八年级下册数学《一次函数》单元测试卷合集(含答案)
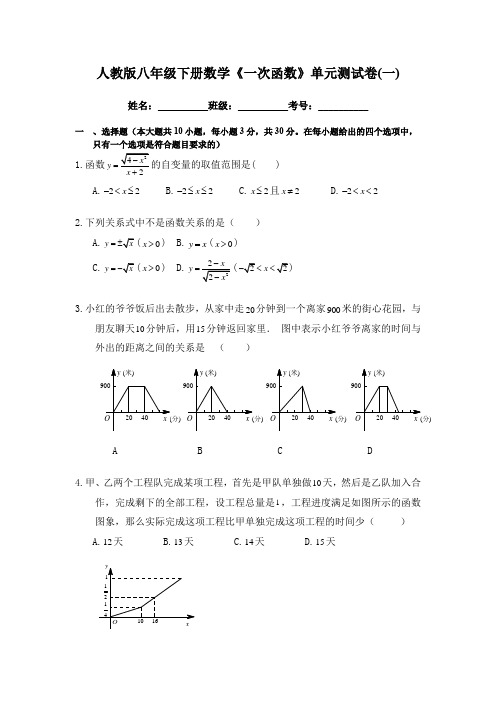
人教版八年级下册数学《一次函数》单元测试卷(一)姓名:__________班级:__________考号:__________一 、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的) 1.函数y =的自变量的取值范围是( )A.22x -<≤B.22x -≤≤C.2x ≤且2x ≠D.22x -<<2.下列关系式中不是函数关系的是( )A.y =0x >)B.y x =(0x >)C.y =(0x >) D.y(x <3.小红的爷爷饭后出去散步,从家中走20分钟到一个离家900米的街心花园,与朋友聊天10分钟后,用15分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )A B C D4.甲、乙两个工程队完成某项工程,首先是甲队单独做10天,然后是乙队加入合作,完成剩下的全部工程,设工程总量是1,工程进度满足如图所示的函数图象,那么实际完成这项工程比甲单独完成这项工程的时间少( ) A.12天 B.13天 C.14天 D.15天分)分)分)分)5.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。
在课堂上,李老师请学生画出自行车行进路程s (km )与行进时间t (小时)的函数图象的示意图,同学们画出的示意图如图所示,你认为正确的是( )6.如果(0)y kx k =≠的自变量增加4,函数值相应地减少16,则k 的值为( )A.4B.4-C.14D.14-7.你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为x ,瓶中水面的高度为y ,下面能大致表示上面故事情节的图象是( )A B C D8.如图,一只蚂蚁从O 点出发,沿着扇形OAB 的边缘匀速爬行一周,设蚂蚁的运动时间为t ,蚂蚁到O 点的距离..为S ,则S 关于t 的函数图象大致为( )9.如果一次函数的图象经过第一象限,且与轴负半轴相交,那么( )A .,B .,C .,D .,10.如图,在矩形ABCD 中,AB=2,1BC =,动点P 从点B 出发,沿路线B C D→→作匀速运动,那么ABP ∆的面积S 与点P 运动的路程x 之间的函数图象大致是( )二 、填空题(本大题共5小题,每小题3分,共15分)11.函数2113y x =+的自变量x 的取值范围是 .12.已知一次函数的图象过点与,则这个一次函数随的增大而 .13.函数1x y x-=的自变量x 的取值范围是 .14.已知一次函数y x a =-+与y x b =+的图象相交于点()8m ,,则a b +=______. y kx b =+y 0k >0b >0k >0b <0k <0b >0k <0b <()0,3()2,1y x D C P BAO31 1 3 Sx A .O1 1 3 Sx O3 Sx 3O1 1 3 SxB .C .D .2BAOA .B .C .D .S t S tS tStOOOO15.已知直线123141535y x y x y x ==+=+,,的图象如图所示,若无论x 取何值,y 总取12y y ,,3y ,中的最小值,则y 的最大值为 .三 、解答题(本大题共7小题,共55分)16.等腰ABC ∆周长为10cm ,底边BC 长为cm y ,腰长为cm x .⑴写出y 关于x 的函数关系式; ⑵求x 的取值范围; ⑶求y 的取值范围.17.已知一次函数()22312y a x a =-+-.求:①a 为何值时,一次函数的图象经过原点.②a 为何值时,一次函数的图象与y 轴交于点()0,9.18.已知一次函数()22312y a x a =-+-.求:①a 为何值时,一次函数的图象经过原点. ②a 为何值时,一次函数的图象与y 轴交于点()0,9.19.右图是某汽车行驶的路程()S km 与时间()min t 的函数关系图.观察图中所提供的信息,解答下列问题:⑴汽车在前9分钟内的平均速度是 ; ⑵汽车在中途停了多长时间? ; ⑶当3016t ≤≤时,求S 与t 的函数关系式.20.判断下列式子中y是否是x的函数.⑴22(35)y x=-⑵y=⑶12y x=-⑷8y x=-21.等腰三角形的周长为30,写出它的底边长y与腰长x之间的函数关系,并写出自变量的取值范围?22.甲乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的方案:甲超市累计购买商品超出300元后,超出部分按原价的8折优惠,在已超市累计购买商品超出200元后,超出部分按原价8.5折优惠.设顾客预计累计购物X元.(X>300)试比较顾客到哪家超市购物更实惠?说明理由人教版八年级下册数学《一次函数》单元测试卷答案解析一、选择题1.A2.A3.D4.A5.C6.B;由题意得:16(4)y k x-=+,将y kx=带入等式,即16(4)kx k x-=+,所以解出4k=-7.B8.C9.B10.B;【解析】了解P点的运动路线,根据已知矩形的长和宽求出当点P运动到C点时的S值为1,即当x为1时的S值为1,之后面积保持不变.二、填空题11.x为任意实数12.减小13.0x>14.16;【解析】分别将点()8m,代入两个一次函数解析式,得8m a=-+和8m b=+,联立方程得88m a m b+=-+++,所以16a b+=15.3717;【解析】如图,分别求出123y y y,,交点的坐标3322A⎛⎫⎪⎝⎭,;252599B⎛⎫⎪⎝⎭,;60371717C ⎛⎫ ⎪⎝⎭, 当32x <,1y y =;当232529x y y =,;当2560917x <,2y y = 当36017x y y =,.看图象可得到C 点最高, ∴6017x =,16037=+1=31717y ⨯最大.三 、解答题16.⑴102y x =-;⑵2.55x <<;⑶05y <<【解析】⑴由题意,得10x x y ++=,即102y x =-⑵因为x 、y 为线段,所以0x >,0y >.所以1020x ->,即05x <<;又因为x 、y 为三角形的边长,所以x x y +>,即2102x x >-,所以 2.5x >.所以2.55x << ⑶由2.55x <<,得5210x <<,所以1025x -<-<-,所以01025x <-<.因此y 的取值范围是05y <<.17.①2a =-;②a =18.①2a =-;②a =19.⑴4/min 3km ;⑵7分钟;⑶()3022016t S t =-≤≤. 20.⑴、⑶不是,⑵、⑷是.“y 有唯一值与x 对应”.21.⑴302y x =-,由三角形的三边关系可得:2x y >,0x >,0y >,可得15152x <<. 22.设在甲超市所付的购物费用为y 甲元,在乙超市所付的购物费用为y 乙元,由题意可得,y 甲=300+0.8(x-300)=60+0.8x ,y 乙=20090%200)0.920(300)x x x +⨯-=+>(当y 甲=y 乙时0.9200.860x x +=+,解得400x =; 当y 甲<y 乙,时0.9200.860x x +<+,解得400x >;当y甲>y乙,时0.9200.860x x+>+,解得400x<.所以当购买多于300元而少于400元的商品时,选择乙超市比较优惠,当购买400元的商品时,两个超市费用相同,选择哪个都可以,当购买商品大于400元时,选择甲超市比较优惠.人教版八年级下册数学《一次函数》单元测试卷(二)姓名:__________班级:__________考号:__________一 、选择题(本大题共10小题,每小题3分,共30分。
最新人教版八年级数学下册 一次函数 单元测试题

人教版八年级数学下册第十九章一次函数单元测试题一、选择题1.下列关系式中,y不是x的函数的是( )(A)y=√x-1(B)y2=2x(C)y=x(D)y=x2-22.有一天,兔子与乌龟赛跑,比赛开始后,兔子飞快地奔跑,乌龟慢慢地爬行,不一会儿,乌龟就被远远地甩在了后面,兔子想:“这比赛也太轻松了,不如先睡一会儿.”而乌龟一刻不停地继续爬行,当兔子醒来跑到终点时,发现乌龟已经到达了终点.正确反映这则寓言故事的大致图象是( )3.下列函数解析式中,y是x的正比例函数的是( )(A)y=-2x+1(B)y=3(x+2)(C)y=πx (D)y=3x4.若函数y=(1-k)x2|k|-3是正比例函数,且y随x的增大而减小,则(k-3)2 019 ()(A)-2(B)-1 (C)1(D)25.一个蓄水池有15 m3的水,以每分钟0.5 m3的速度向池中注水,蓄水池中的水量Q(m3)与注水时间t(分钟)之间的函数解析式为( ) (A)Q=0.5t (B)Q=15t(C)Q=15+0.5t(D)Q=15-0.5t6.函数y=(a-√3)x-1的函数值y随自变量x的增大而减小,下列描述中:①a<√3;②函数图象与y轴的交点为(0,-1);③函数图象经过第一象限;④点(a+√3,a2-4)在该函数图象上,正确的描述有()(A)①②④(B)①②③④(C)①②③(D)②③④7.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )x+5(A)y=34(B)y=2x+55(C)y=1x+54(D)y=4x+558.如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( )(A)x≥-1(B)x>-1(C)x≤-1(D)x<-19.已知一次函数y=kx-1,若y随x的增大而增大,则它的函数图象经过的象限是( )(A)一、二、三(B)一、二、四(C)一、三、四(D)二、三、四10.如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是()(A)-2(B)-1 (C)1(D)2二、填空题的自变量x的取值范围是11.函数y=√x+312.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.根据图中提供的信息,下列说法:①以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多②以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少③以高于80 km/h的速度行驶时,行驶相同路程,乙车比丙车省油④以80 km/h的速度行驶时,行驶100 km,甲车消耗的汽油量约为10 L正确的是(填写正确说法的序号).13.已知正比例函数y=kx 的图象经过(-2,4),则当x=1时,函数y 的值为.14.据调查,某地铁自行车存放处在某星期天的存车量为4 000辆次,其中每辆变速车存车费是0.30元/次,普通自行车存车费是每辆0.20元/次,若普通自行车存车数为x 辆,存车费总收入为y 元,则y 关于x 的函数解析式为15.在同一直角坐标系内分别作出一次函数y=12x+1和y=2x-2的图象,则①函数y=2x-2的图象与y 轴的交点是(-2,0);②方程组{2y -x =2,2x -y =2的解是{x =2,y =2;③两直线与y 轴所围成的三角形的面积为3. 其中正确的有.(填序号)三、解答题16.分别写出下列各题中的函数解析式及自变量的取值范围.(1)已知等腰三角形的面积为20,设它的底边长为x,底边上的高y 随x 的变化而变化.(2)水池中有水10 L,此后每小时漏水0.05 L,水池中的水量V随时间t 的变化而变化.17.已知y与x+2成正比例,当x=4时,y=12.(1)写出y与x之间的函数解析式;(2)求当x=5时,y的值;(3)求当y=36时,x的值.18.已知y=(m+1)x2-|m|+n+4.(1)当m,n为何值时,y是x的一次函数?(2)当m,n为何值时,y是x的正比例函数?19.甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60 km/h.(1)求甲车的速度;(2)当甲、乙两车相遇后,乙车速度变为a km/h,并保持匀速行驶,甲车速度不变,结果乙车比甲车晚38分钟到达终点,求a的值.20.已知y+2与x-2成正比例,且当x=3时,y=-3.(1)求y关于x的函数解析式;(2)若点P(a1,b1),Q(a2,b2)在该函数的图象上,且b1>b2,试判断a1与a2的大小关系;(3)点M(-1,2)与N(3,-3)是否在该函数的图象上?21.直线y=2x+3与x轴交于点A,与y轴交于点B.(1)求A,B点坐标;(2)过B点作直线BP与x轴交于点P,且OP=2OA,求△ABP的面积.22.某大剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.(1)设学生人数为x(人),付款总金额为y(元),分别建立两种方案中y与x的函数关系式;(2)请计算并确定出最节省费用的购票方案.参考答案:一、选择题1.下列关系式中,y不是x的函数的是( B )(A)y=√x-1(B)y2=2x(C)y=x(D)y=x2-22.有一天,兔子与乌龟赛跑,比赛开始后,兔子飞快地奔跑,乌龟慢慢地爬行,不一会儿,乌龟就被远远地甩在了后面,兔子想:“这比赛也太轻松了,不如先睡一会儿.”而乌龟一刻不停地继续爬行,当兔子醒来跑到终点时,发现乌龟已经到达了终点.正确反映这则寓言故事的大致图象是( D )3.下列函数解析式中,y是x的正比例函数的是( C )(A)y=-2x+1(B)y=3(x+2)(C)y=πx (D)y=3x4.若函数y=(1-k)x2|k|-3是正比例函数,且y随x的增大而减小,则(k-3)2 019 (B )(A)-2(B)-1 (C)1(D)25.一个蓄水池有15 m3的水,以每分钟0.5 m3的速度向池中注水,蓄水池中的水量Q(m3)与注水时间t(分钟)之间的函数解析式为( C ) (A)Q=0.5t (B)Q=15t(C)Q=15+0.5t(D)Q=15-0.5t6.函数y=(a-√3)x-1的函数值y随自变量x的增大而减小,下列描述中:①a<√3;②函数图象与y轴的交点为(0,-1);③函数图象经过第一象限;④点(a+√3,a2-4)在该函数图象上,正确的描述有( A )(A)①②④(B)①②③④(C)①②③(D)②③④7.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( A )(A)y=3x+54(B)y=2x+55(C)y=1x+54x+5(D)y=458.如图,直线y1=x+b与y2=kx-1相交于点P,若点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是( B )(A)x≥-1(B)x>-1(C)x≤-1(D)x<-19.已知一次函数y=kx-1,若y随x的增大而增大,则它的函数图象经过的象限是( C )(A)一、二、三(B)一、二、四(C)一、三、四(D)二、三、四10.如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是( D )(A)-2(B)-1 (C)1(D)2二、填空题的自变量x的取值范围是x>-311.函数y=√x+312.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.根据图中提供的信息,下列说法:①以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多②以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少③以高于80 km/h的速度行驶时,行驶相同路程,乙车比丙车省油④以80 km/h的速度行驶时,行驶100 km,甲车消耗的汽油量约为10 L正确的是③④(填写正确说法的序号).13.已知正比例函数y=kx 的图象经过(-2,4),则当x=1时,函数y 的值为 -2 .14.据调查,某地铁自行车存放处在某星期天的存车量为4 000辆次,其中每辆变速车存车费是0.30元/次,普通自行车存车费是每辆0.20元/次,若普通自行车存车数为x 辆,存车费总收入为y 元,则y 关于x 的函数解析式为 y=-0.10x+1 200(0≤x ≤4 000) .15.在同一直角坐标系内分别作出一次函数y=12x+1和y=2x-2的图象,则①函数y=2x-2的图象与y 轴的交点是(-2,0);②方程组{2y -x =2,2x -y =2的解是{x =2,y =2;③两直线与y 轴所围成的三角形的面积为3. 其中正确的有 ②③ .(填序号)三、解答题16.分别写出下列各题中的函数解析式及自变量的取值范围.(1)已知等腰三角形的面积为20,设它的底边长为x,底边上的高y 随x 的变化而变化.(2)水池中有水10 L,此后每小时漏水0.05 L,水池中的水量V随时间t 的变化而变化.,x>0.解:(1)y=40x(2)V=10-0.05t,0≤t≤200.17.已知y与x+2成正比例,当x=4时,y=12.(1)写出y与x之间的函数解析式;(2)求当x=5时,y的值;(3)求当y=36时,x的值.解:(1)设y=k(x+2),因为当x=4时,y=12,所以12=k(4+2),解得k=2,所以y=2(x+2)=2x+4.(2)当x=5时,y=2×5+4=14.(3)当y=36时,36=2x+4,解得x=16.18.已知y=(m+1)x2-|m|+n+4.(1)当m,n为何值时,y是x的一次函数?(2)当m,n为何值时,y是x的正比例函数? 解:(1)若y是x的一次函数,则{m+1≠0, 2−|m|=1,解得m=1,所以当m=1,n为任意实数时,y是x的一次函数.(2)若y是x的正比例函数,则{m+1≠0,2−|m|=1,n+4=0,解得{m=1,n=−4,所以当m=1,n=-4时,y是x的正比例函数.19.甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60 km/h.(1)求甲车的速度;(2)当甲、乙两车相遇后,乙车速度变为a km/h,并保持匀速行驶,甲车速度不变,结果乙车比甲车晚38分钟到达终点,求a 的值. 解:(1)由图象可得,甲车的速度为280−1202=80 km/h. (2)相遇时间为28080+60=2 h, 由题意可得,60×280+3860=80×2a ,解得,a=75, 经检验,a=75是所列分式方程的解,即a 的值是75.20.已知y+2与x-2成正比例,且当x=3时,y=-3.(1)求y 关于x 的函数解析式;(2)若点P(a 1,b 1),Q(a 2,b 2)在该函数的图象上,且b 1>b 2,试判断a 1与a 2的大小关系;(3)点M(-1,2)与N(3,-3)是否在该函数的图象上?解:(1)因为y+2与x-2成正比例,所以可设y+2=k(x-2),因为当x=3时,y=-3,所以-3+2=k(3-2),解得k=-1,所以y+2=-(x-2),即y=-x.(2)因为y=-x,所以y随x的增大而减小,因为b1>b2,所以a1<a2,(3)因为当x=-1时,y=-(-1)=1≠2,当x=3时,y=-3,所以点M(-1,2)不在该函数的图象上,N(3,-3)在该函数的图象上.21.直线y=2x+3与x轴交于点A,与y轴交于点B.(1)求A,B点坐标;(2)过B点作直线BP与x轴交于点P,且OP=2OA,求△ABP的面积.,解:(1)令x=0,则y=3,令y=0,则x=-32所以A(-32,0),B(0,3). (2)因为A(-32,0),所以AO=32, 因为OP=2OA,所以OP=3.如图,当点P 与点A 在y 轴异侧时,AP=OA+OP,即AP=32+3=92, 所以S △ABP =12AP ·OB=12×92×3=274,当点P 与点A 在y 轴同侧时,AP=OP-OA=3-32=32,所以S △ABP =12AP ·OB=12×32×3=94, 故△ABP 的面积为274或94. 22.某大剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款,某校有4名老师与若干名(不少于4人)学生听音乐会.(1)设学生人数为x(人),付款总金额为y(元),分别建立两种方案中y 与x 的函数关系式;(2)请计算并确定出最节省费用的购票方案.解:(1)按优惠方案1可得y 1=20×4+(x-4)×5=5x+60(x ≥4); 按优惠方案2可得y 2=(5x+20×4)×90%=4.5x+72(x ≥4).(2)因为y1-y2=0.5x-12(x≥4),①当y1-y2=0时,解得x=24,②当y1-y2<0时,解得x<24,③当y1-y2>0时,解得x>24,所以当购买24张票时,两种方案付款一样多. 当4≤x<24时,y1<y2,方案1付款较少.当x>24时,y1>y2,方案2付款较少.。
人教版八年级数学 下册 第十九章 一次函数 单元综合与测试题(含答案)

1 / 3第十九章 一次函数 单元复习与检测题(含答案)一、选择题 1、函数2y x =+的自变量的取值范围是( )A .x ≥-2B .x < -2C .x >-2D .x ≤ -2 2、下列函数关系中,属于正比例函数关系的是( )A.圆的面积与它的半径B.面积为常数S 时矩形的长y 与宽xC.路程是常数时,行驶的速度v 与时间tD. 三角形的底边是常数a 时它的面积S 与这条边上的高h3、若一个正比例函数的图象经过点(2,-3),则这个图象一定也经过点( ) A .(-3,2) B .(32,-1) C .(23,-1) D .(-32,1)4、下列问题中,两个变量成正比例的是( ) A .等腰三角形的面积一定,它的底边和底边上的高 B .等边三角形的面积和它的边长C .长方形的一边长确定,它的周长与另一边长D .长方形的一边长确定,它的面积与另一边长5、在直角坐标系中,既是正比例函数y=kx,又是y 的值随x 的增大而减小的图象是( )A .B .C .D .6、如图,函数y =2x 和y =ax +4的图象相交于点A(m, 2),则不等式2x <ax +4的解集为( )A. x >3B. x <1C. x >1D. x <37、如图,直线y =kx +b 交坐标轴于A (-3,0).B (0,5)两点,则不等式-kx -b <0的解集为( )A .x >-3B .x <-3C .x >3D .x <38、李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的矩形ABCD ,设BC 的边长为x 米,AB 边的长为y 米,则y 与x 之间的函数关系式是( )A.y=-2x+24(0<x <12)B. y=-21x+12(0<x <24) C. y=2x-24(0<x <12) D. y=21x-12(0<x <24) 9、某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )10、已知一次函数32y x m =+和12y x n =-+的图象都经过点A (-2,0),且与y 轴分别交于B ,C 两点,那么△ABC 的面积等于( ).A .2B .3C .4D .6二、填空题11、某物体从上午7时至下午4时的温度M (℃)是时间t(h)的函数:35100m t t =-+ (其中t=0表示中午12时,t=-1表示上午11时,t=1表示13时),则上午10时此物体的温度为 ℃12、已知直线y=(2-3m )x 经过点A (x 1,y 1)、B (x 2,y 2),当x 1<x 2时,有y 1>y 2,则m 的取值范围是 .13、如图,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm )和注水时间x(s)之间的关系满足如图2中的图象,则至少需要________s 能把小水杯注满.2 / 314、已知一次函数y =ax -b 的图象经过一.二.三象限,且与x 轴交于点(-2,0),则不等式ax >b 的解集为 .15、已知直线l 1,l 2的解析式分别为y 1=ax +b ,y 2=mx +n (0<m <a ),根据图中的图象填空:(1)方程组,y ax b y mx n=+⎧⎨=+⎩的解为__________;(2)当-1≤x ≤2时,y 2的范围是__________;(3)当-3≤y 1≤3时,自变量x 的取值范围是__________.三、解答题16、如图,在平面直角坐标系中,点A 的坐标为(0,6),将△OAB 沿x 轴向左平移得到△O'A'B',点A 的对应点A'落在直线y=-34x 上,求点B 与其对应点B'间的距离.17、一次越野跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程s (米)与时间t (秒)的关系如图,结合结合图象,求图中S 1和S 0的数值.提示:求得小刚和李明速度,再乘以相遇时间,两个路程相减即可得出两人的路程之差150.18、已知A 、B 两地相距30km ,小明以6km /h 的速度从A 步行到B 地的距离为y km ,步行的时间为x h .(1)求y 与x 之间的函数表达式,并指出y 是x 的什么函数; (2)写出该函数自变量的取值范围.19、在平面直角坐标系xoy 中,已知一次函数()10y mx m =≠与()20y kx b k =+≠相交于点()12A ,,且()20y kx b k =+≠与y 轴交于点()03B ,.(1)求一次函数1y 和2y 的解析式; (2)当120y y >>时,求出x 的取值范围.20、在社会主义新农村建设中,长春某乡镇决定对A 、B 两村之间的公路进行改造,并有甲工程队从A 村向B 村方向修筑,乙工程队从B 村向A 村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y (米)与施工时间x (天)之间的函数图象,请根据图象所提供的信息解答下列问题:(1)乙工程队每天修公路多少米?(2)分别求甲、乙工程队修公路的长度y (米)与施工时间x (天)之间的函数关系式. (3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?3 / 3参考答案:一、1、A 2、D 3、C 4、D 5、C 6、B 7、A 8、B 9、D 10、C 二、 11、102 12、m >2313、5 14、 x >-215、(1)2,3x y =⎧⎨=⎩ (2)0≤y 2≤3 (3)0≤x ≤2三、16、解析:由题意可知,点A 移动到点A'位置时,纵坐标不变,∴点A'的纵坐标为6,∵点A'落在直线y=-34x 上,∴-34x=6,解得x=-8,∴△OAB 沿x 轴向左平移到△O'A'B'位置,移动了8个单位,∴点B 与其对应点B'间的距离为8.17、解设小刚速度为xm/s ,李明速度为ym/s 由题意可得1001450160010020014503001600x yx y +=+⎧⎨+=+⎩解得31.5x y =⎧⎨=⎩所以S 0=1450+100x=1750m ,S 1=1450+200x=2050m 18、解:(1)由题意可得:y=6x , 此函数是正比例函数; (2)∵A 、B 两地相距30km , ∴0≤6x ≤30, 解得:0≤x ≤5,即该函数自变量的取值范围是:0≤x ≤5.19、∵一次函数()10y mx m =≠过点()12A ,∴2m = ∴12y x =;又∵一次函数()20y kx b k =+≠经过点()12A ,, ()03B , ∴2{3k bb=+=;解得: 1{3k b =-= ∴23y x =-+; (2)1<<3x .20、(1)由图得:720÷(9-3)=120(米) 答:乙工程队每天修公路120米.(2)设y 乙=kx+b ,则,309720k b k b +=⎧⎨+=⎩,解得120360k b =⎧⎨=-⎩,所以y 乙=120x-360,当x=6时,y 乙=360,设y 甲=k 1x ,∵y 乙与y 甲的交点是(6,360) ∴把(6,360)代入上式得: 360=6k 1,k 1=60, 所以y 甲=60x ;(3)当x=15时,y 甲=900,所以该公路总长为:720+900=1620(米), 设需x 天完成,由题意得: (120+60)x=1620,解得:x=9,答:该项工程由甲、乙两工程队一直合作施工,需9天完成.。
【3套试卷】人教版八年级下册数学基础训练题: 第十九章 一次函数(含答案)

人教版八年级下册数学基础训练题:第十九章一次函数(含答案)一、选择题1.下列哪一个点在直线y=-2x-5上()A. (2,-1)B. (3,1)C. (-2,1)D. (-1,-3)2.一次函数y=(m+1)x+5中,y的值随x的增大而减小,则m的取值范围是()A. m<-1B. m>-1C. m>0D. m<03.一次函数的图象经过点A(﹣2,﹣1),且与直线y=2x﹣3平行,则此函数的解析式为()A. y=x+1B. y=2x+3C. y=2x﹣1D. y=﹣2x﹣54.某种签字笔的单价为2元,购买这种签字笔x支的总价为y元.则y与x之间的函数关系式为()A. B. C. y=-2x D. y=2x5.某乡镇企业现在年产值是15万元,如果每增加100元投资,一年增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为( )A. y=25x+15B. y=2.5x+1.5C. y=2.5x+15D. y=25x+1.56.一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )A. x>0B. x<0C. x>2D. x<27.如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家,其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为()A. 1.1千米B. 2千米C. 15千米D. 37千米8.如图,在平面直角坐标系中,直线l1:y=x+3与直线l2:y=mx+n交于点A(﹣1,b),则关于x、y的方程组的解为()A. B. C. D.9.一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集是()A. x>﹣2B. x<﹣2C. x>﹣4D. x<﹣410.小明到离家900米的春晖超市卖水果,从家中到超市走了20分钟,在超市购物用了10分钟,然后用15分钟返回家中,下列图形中表示小明离家的时间与距离之间的关系是()A. B. C. D.11.一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为()A. 9B. 16C. 25D. 3612.一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是()A. x<2B. x<0C. x>0D. x>2二、填空题13.函数y=中,自变量x的取值范围为________ .14.已知,函数y=(k﹣1)x+k2﹣1,当k________ 时,它是一次函数.15.当x=-1时,一次函数y=kx+3的值为5,则k的值为________ .16.已知长方形的周长为30cm,一边长为ycm,另一边长为xcm,则y与x的关系式为________,其中变量是________,常量是________.17.根据如图所示的计算程序计算变量y的对应值,若输入变量x的值为- ,则输出的结果为 ________18.某书定价25元,如果一次购买20本以上,超过20本的部分打八折,试写出付款金额y (单位:元)与购书数量x(单位:本)之间的函数关系________.19.已知A地在B地的正南方3km处,甲、乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(km)与所行时间t(h)之间的函数关系如图所示,当他们行驶3h 时,他们之间的距离为________km.20.如图,已知点A和点B是直线y=x上的两点,A点坐标是(2,).若AB=5,则点B的坐标是 ________.21.一次函数y=ax+b的图象如图,则关于x的不等式ax+b≥0的解集为________.22.某水库的水位在5小时内持续上涨,初始水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y(米)与时间x(小时)(0≤x≤5)的函数关系式为________ .三、解答题23.一次函数y=kx+b经过点(-4,-2)和点(2,4),求一次函数y=kx+b的解析式。
【3套试卷】人教版八年级下册数学基础训练题: 第十九章 一次函数(含答案)

人教版八年级下册数学基础训练题:第十九章一次函数(含答案)一、选择题1.下列哪一个点在直线y=-2x-5上()A. (2,-1)B. (3,1)C. (-2,1)D. (-1,-3)2.一次函数y=(m+1)x+5中,y的值随x的增大而减小,则m的取值范围是()A. m<-1B. m>-1C. m>0D. m<03.一次函数的图象经过点A(﹣2,﹣1),且与直线y=2x﹣3平行,则此函数的解析式为()A. y=x+1B. y=2x+3C. y=2x﹣1D. y=﹣2x﹣54.某种签字笔的单价为2元,购买这种签字笔x支的总价为y元.则y与x之间的函数关系式为()A. B. C. y=-2x D. y=2x5.某乡镇企业现在年产值是15万元,如果每增加100元投资,一年增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为( )A. y=25x+15B. y=2.5x+1.5C. y=2.5x+15D. y=25x+1.56.一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是( )A. x>0B. x<0C. x>2D. x<27.如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家,其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为()A. 1.1千米B. 2千米C. 15千米D. 37千米8.如图,在平面直角坐标系中,直线l1:y=x+3与直线l2:y=mx+n交于点A(﹣1,b),则关于x、y的方程组的解为()A. B. C. D.9.一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集是()A. x>﹣2B. x<﹣2C. x>﹣4D. x<﹣410.小明到离家900米的春晖超市卖水果,从家中到超市走了20分钟,在超市购物用了10分钟,然后用15分钟返回家中,下列图形中表示小明离家的时间与距离之间的关系是()A. B. C. D.11.一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为()A. 9B. 16C. 25D. 3612.一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是()A. x<2B. x<0C. x>0D. x>2二、填空题13.函数y=中,自变量x的取值范围为________ .14.已知,函数y=(k﹣1)x+k2﹣1,当k________ 时,它是一次函数.15.当x=-1时,一次函数y=kx+3的值为5,则k的值为________ .16.已知长方形的周长为30cm,一边长为ycm,另一边长为xcm,则y与x的关系式为________,其中变量是________,常量是________.17.根据如图所示的计算程序计算变量y的对应值,若输入变量x的值为- ,则输出的结果为 ________18.某书定价25元,如果一次购买20本以上,超过20本的部分打八折,试写出付款金额y (单位:元)与购书数量x(单位:本)之间的函数关系________.19.已知A地在B地的正南方3km处,甲、乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(km)与所行时间t(h)之间的函数关系如图所示,当他们行驶3h 时,他们之间的距离为________km.20.如图,已知点A和点B是直线y=x上的两点,A点坐标是(2,).若AB=5,则点B的坐标是 ________.21.一次函数y=ax+b的图象如图,则关于x的不等式ax+b≥0的解集为________.22.某水库的水位在5小时内持续上涨,初始水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y(米)与时间x(小时)(0≤x≤5)的函数关系式为________ .三、解答题23.一次函数y=kx+b经过点(-4,-2)和点(2,4),求一次函数y=kx+b的解析式。
人教版数学八年级下册第19章一次函数单元测试卷4份含答案

人教版数学八年级下册第19章一次函数单元测试卷4份第19章单元测试(1)一、填空题1.若一次函数的图象经过点(1,3)与(2,-1),则它的解析式为___________________,函数y随x的增大而____________.2.若函数y=(m-1)x|m|-2-1是关于x的一次函数,且y随x的增大而减小,则m=_______.3.一次函数y=(m+4)x-5+2m,当m__________时,y随x增大而增大;当m_______时,图象经过原点;当m__________时,图象不经过第一象限.4.一次函数y=2x-3的图象可以看作是函数y=2x的图象向__________平移________个单位长度得到的,它的图象经过_______________象限.5.已知一次函数y=kx-1的图象不经过第二象限,则正比例函数y=(k+1)x必定经过第______________象限.6.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水x吨(x>10),应交水费y元,则y关于x 的关系式.7.小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖瓜千克数之间的关系如图所示,那么小李赚了______元.8.写出同时具备下列两个条件的一次函数表达式(写出一个即可) .(1)y随着x的增大而减小.(2)图象经过点(1,-3)9.已知一次函数y=kx+b的图象经过点P(2,-1)与点Q(-1,5),则当y 的值增加1时,x的值将_______________________.10.已知直线y=kx+b经过点(252,0)且与坐标轴所围成的三角形的面积是254,则该直线的解析式为_____________________________________.二、选择题11.一次函数y=2x+3的图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限12.已知一次函数y=(-1-m 2)x+3(m 为实数),则y 随x 的增大而 ( )A .增大B .减小C .与m 有关D .无法确定13.直线y =-x +2和直线y =x -2的交点P 的坐标是 ( )A .P (2,0)B .P (-2,0)C .P (0,2)D .P (0,-2)14.无论实数m 取什么值,直线y=x+21m 与y=-x+5的交点都不能在( )A .第一象限B .第二象限C .第三象限D .第四象限15.已知一次函数y=(m -1)x+1的图象上两点A (x 1,y 1),B (x 2,y 2),当x 1>x 2时,有y 1<y 2,那么m 的取值范围是 ( ) A .m>0 B . m<0 C .m>1 D .m<1 16.若点A(2,-3)、B(4,3)、C(5,a)在同一条直线上,则a 的值是 ( ) A .6或-6 B .6 C .-6 D .6和3 17.一次函数y=kx+b 与y=kbx ,它们在同一坐标系内的图象可能为 ( )18.已知一次函数y=ax+4与y=bx-2的图象在x 轴上相交于同一点,则ba 的值是( )A .4B .-2C .12D . 1219.某公司市场营部的营销人员的个人收入与其每月的销售业绩满足一次函数关系,其图象如图所示,由图中给出的信息可知:营销人员没有销售业绩时的收入是( )元.A .280B .290C .300D .31020.如图,点P 按A →B →C →M 的顺序在边长为1的正方形边上运动,M 是CD 边上的中点.设点P 经过的路程x 为自变量,△APM 的面积为y ,则函数y 的大致图像是 ( )21.如图中的图象(折线ABCDE )描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s (千米)和行驶时间t (小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为380千米/时;④汽车自出发后3小时至 4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有 ( )A .1个B .2个C .3个D .4个三、解答题22.已知一次函数y=(2m+4)x+(3-n).⑴当m 、n 是什么数时,y 随x 的增大而增大? ⑵当m 、n 是什么数时,函数图象经过原点?⑶若图象经过一、二、三象限,求m 、n 的取值范围.23.已知一次函数y=(3m-7)x+m-1的图象与y轴交点在x轴的上方,且y随x 的增大而减小,求整数m的值.24.作出函数y=1x42的图象,并根据图象回答问题:⑴当x取何值时,y>0?⑵当-1≤x≤2时,求y的取值范围.25.已知直线y=3x+1和x、y轴分别交于点A、B两点,以线段AB为边在第一象限内作一个等边三角形ABC,第一象限内有一点P(m,0.5),且S△ABP =S△ABC,求m值.26.某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元.小彬经常来该店租碟,若每月租碟数量为x张.(1)写出零星租碟方式应付金额y(元)与租碟数量x(张)之间的函数关系1式;(2)写出会员卡租碟方式应付金额y(元)与租碟数量x(张)之间的函数关2系式;(3)小彬选取哪种租碟方式更合算?27.某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:①求出y与x的函数关系式.(纯利润=总收入-总支出)②当y=106000时,求该厂在这个月中生产产品的件数.28.一报刊销售亭从报社订购某晚报的价格是每份0.7元,销售价是每份1元,卖不掉的报纸还可以以0.20元的价格返回报社,在一个月内(以30天计算),有20天每天可卖出100份,其余10天,每天可卖出60份,但每天报亭从报社订购的份数必须相同,若以报亭每天从报社订购报纸的份数为x,每月所获得的利润为y.(1)写出y与x之间的函数关系式,并指出自变量x的取值范围;(2)报亭应该每天从报社订购多少份报纸,才能使每月获得的利润最大?最大利润是多少?答案一、1.47y x =-+ 减小 2.-3 3.4m >- 52m =4m <- 4.下,三,一、三、四象限 5.一、三 6. 1.86y x =- 7.36 8.3y x =-等9.减小1210.22112525y x y x =-=-+或二、11.D 12.B 13.A 14.C 15.D 16.B 17.A 18.D 19.C 20.A 21.A三、22.(1)2m >- n 为任何实数 (2)23m n ≠-⎧⎨=⎩ (3)23m n >-⎧⎨<⎩23.71,23m m m <<∴=又为整数,24.(1)由图像可知,当8,0x y >>时 (2)当912,32x y -≤≤-≤≤-时25.S △ABP m ==26.(1)1(0)y x x =≥ (2)20.412(0)y x x =+≥1212123,0.412,20,0.412,20,0.412,20y y x x x y y x x x y y x x x <<+<==+=>>+>()令则 令则 令则,所以,当租碟少于20张时,选零星租碟方式合算;当租碟20张时,两种方式一样;当租碟大于20张时,选会员卡租碟合算 27.(1)198000y x =- (2)6000x =(件)28.(1)20(10.7)1060(10.7)(0.70.2)(60)10y x x =-+⨯----⨯ 480(60100)x x x =+≤≤且为整数10100580(2)k y x x y =>==∴∴最大值随增大而增大当时(元),第19章单元测试(2)一、填空题 1.已知函数1231x y x -=-,x =__________时,y 的值时0,x=______时,y 的值是1;x=_______时,函数没有意义. 2.已知253x y x+=-,当x=2时,y=_________.3.在函数3y x =-中,自变量x 的取值范围是__________.4.一次函数y =kx +b 中,k 、b 都是 ,且k ,自变量x 的取值范围是 ,当 k ,b 时它是正比例函数. 5.已知82)3(-+=mx m y 是正比例函数,则m .6.函数n m x m y n +--=+12)2(,当m= ,n= 时为正比例函数; 当m= ,n= 时为一次函数.7.当直线y=2x+b 与直线y=kx-1平行时,k________,b___________.8.直线y=2x-1与x 轴的交点坐标是____________;与y 轴的交点坐标是_____________. 9.已知点A 坐标为(-1,-2),B 点坐标为(1,-1),C 点坐标为(5,1),其中在直线y=-x+6上的点有____________.在直线y=3x-4上的点有____________.10.一个长为120米,宽为100米的矩形场地要扩建成一个正方形场地,设长增加x 米,宽增加y 米,则y 与x 的函数关系式是 ,自变量的取值范围是 ,且y 是x 的 函数.11.直线y=kx+b 与直线y=32x -平行,且与直线y=312+-x 交于y 轴上同一点,则该直线的解析式为________________________________.二、选择题:12.下列函数中自变量x 的取值范围是x ≥5的函数是 ( )A .y =B .y =C .yD .y = 13.下列函数中自变量取值范围选取错误..的是( )A .2y x x =中取全体实数B .1y=中x ≠0x-1C .1y=中x ≠-1x+1D .1y x =≥14.某小汽车的油箱可装汽油30升,原有汽油10升,现再加汽油x 升。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级一次函数 和一元二次方程练习
一、选择题 1.直线xy39与x轴交点的坐标是________,与y轴交点的坐标是_______. 2.把直线121xy向上平移21个单位,可得到函数__________________. 3.若点P1(–1,3)和P2(1,b)关于y轴对称,则b= . 4.若一次函数y=mx-(m-2)过点(0,3),则m= . 5.函数-5yx的自变量x的取值范围是 . 6.如果直线baxy经过一、二、三象限,那么ab____0 (“<”、“>”或“=”). 7.若直线12xy和直线xmy的交点在第三象限,则m的取值范围是________. 8.函数y= -x+2的图象与x轴,y轴围成的三角形面积为_________________. 9.某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过10立方米的,按每立方米m元水费收费;用水超过10立方米的,超过部分加倍收费.某职工某月缴水费16m元,则该职工这个月实际用水为___________立方米. 10.有边长为1的等边三角形卡片若干张,使用这些三角形卡片拼出边长分别是2、3、4„的等边三角形(如图).根据图形推断每个等边三角形卡片总数S与边长n的关系式 . 二、选择题 11.函数y=x-2x+2 的自变量x的取值范围是( ) A.x≥-2 B.x>-2 C.x≤-2 D.x<-2 12.一根弹簧原长12cm,它所挂的重量不超过10kg,并且挂重1kg就伸长1.5cm,
写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是( )
A.y=1.5(x+12)(0≤x≤10) B.y=1.5x+12 (0≤x≤10)
C.y=1.5x+10 (0≤x) D.y=1.5(x-12) (0≤x≤10)
13.无论m为何实数,直线mxy2与4xy的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.某兴趣小组做实验,将一个装满水的啤酒瓶倒置(如图),
并设法使瓶里的水从瓶中匀速流出.那么该倒置啤酒瓶内水面
高度h随水流出的时间t变化的图象大致是 ( )
A. B. C. D.
15.已知函数122yx,当-1<x≤1时,y 的取值范围是( )
A.5322y B.3522y C.3522y D.3522y
16.某学校组织团员举行申奥成功宣传活动,从学校骑车出
发,先上坡到达A地后,宣传8分钟;然后下坡到B地
宣传8分钟返回,行程情况如图.若返回时,上、下坡速
度仍保持不变,在A地仍要宣传8分钟,那么他们从B
地返回学校用的时间是( )
A.45.2分钟 B.48分钟 C.46分钟 D.33分钟
h t O h t O h t O h
t
O
三、解答题 17.观察图,先填空,然后回答问题: (1)由上而下第n行,白球有_______个;黑球有_______个. (2)若第n行白球与黑球的总数记作y, 则请你用含n的代数式表示y,并指出其中n的取值范围. 18.已知,直线y=2x+3与直线y=-2x-1. 求两直线与y轴交点A,B的坐标; 求两直线交点C的坐标; 求△ABC的面积. 19. 某军加油飞机接到命令,立即给另一架正在飞行 的运输飞机进行空中加油.在加油的过程中, 设运输飞机的油箱余油量为Q1吨,加油飞机的 加油油箱的余油量为Q2吨,加油时间为t分钟, Q1、Q2与t之间的函数关系如图.回答问题: (1) 加油飞机的加油油箱中装载了多少吨油? 将这些油全部加给运输飞机需要多少分钟? (2) 求加油过程中,运输飞机的余油量Q1(吨) 与时间t(分钟)的函数关系式; (3) 运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用? 请通过计算说明理由. 20.将长为30cm,宽为10cm的长方形白纸,按如图所示的方发粘合起来,粘合
部分的宽为3cm.设x张白纸粘合后的总长度为ycm,写出y与x的函数关系式,
并求出当x=20时, y的值.
一、选择
1.下列方程是关于x的一元二次方程的是( );
A、02cbxax B、2112xx
C、)1)(1(22xxxx D )1(2)1(32xx
2.、把方程(2x-1)(3x+2)= x 2 +2化成一般形式后,二次项的系数和常数项分
别是( ); A、5 、-4 B、5 、1 C、5、 4 D、1、 -4
3、方程(m²-1)x²+m x -5=0是关于x的一元二次方程,则m满足的条件
是 ( ) A m≠1 B m≠0 C ∣m∣≠1 D m=±1
4、关于x的一元二次方程x²-2x+2k=0有实数根,则k的取值范围是( );
A k< 21 B k≤ 21 C k> 21 D k≥ 21
5、已知关于x的方程x²-mx+2m-1=0的两个实数根的平方和为7,那么m的值
是( );
A . 5 B -1 C 5或-1 D -5或1
6、王刚同学在解关于x的方程x²-3x+c=0时,误将-3x看作+3x,结果解得
x
y
A
B
C
3
10
30
x1=1 x2=-4,则原方程的解为( ); (A) x1=-1 x2=-4 (B)x1=1 x2=4 (C)x1=-1 x2=4 (D)x1=2 x2=3 7、某饲料厂一月份生产饲料500吨,三月份生产饲料720吨,若二、三月份每月平均增长的百分率为x,则有( ); A 500(1+x2)=720 B 500(1+x)2=720 C 500(1+2x)=720 D 720(1+x)2=500 8、已知m是方程x2-x-1=0的一个根,则代数式m2-m的值等于( ) A、 -1 B、0 C、1 D、2 二、 填空题 9、若关于x的方程2x2-3x+c = 0的一个根是1,则另一个根是 . 10、一元二次方程 x2-3x+2 = 0的解是 . 11、如果(2a+2b+1)(2a+2b-1)=63,那么a+b的值是 . 12、关于x一元二次方程 (kx-4) 2x - 2 x +6=0没有实数根,则k的最小整数值是______。 13、已知方程x2+3x+1=0的两个根为α、β,则α+β的值为 . 14.写出一个以-1,2为根的二元二次方程:______________。 15.已知1x,2x是方程2630xx的两实数根,则2112xxxx的值为______ 16、某钢铁厂的钢产量,今年第一季度平均每月增长率为20%,若3月份钢产量为7200吨,则1月份的钢产量为______吨。 三、解方程 1. 02522)(x直接开平方法 2. 0542xx(配方法) 3 x2 -5x+6=0 (因式分解法) 4. 03722xx(公式法) 四、解答题
1、已知关于x的方程x²-2(m+1)x+m2=0
(1) 当m取什么值时,一元二次方程没有实数根?
(2)对m选取一个合适的非零整数,使原方程有两个实数根,并求这两个实
数根的差的平方。
2、 幸福村种的水稻2006年平均每公顷产7200千克,2008年平均每公顷产
8450千克,求水稻每公顷产量的年平均增长率。
3、一个直角梯形的下底比上底大2cm,高比上底小1 cm,面积等于8 cm2画出
这个梯形。
4、要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安
排15场比赛,主邀请多少个球队参加比赛?
不等式和不等式组 1.不等式组423532xx的解集是( c ) A.x<1 B.x≥2 C.无解 D.1<x≤2 2.若方程组323ayxyx的解是负数,那么a的取值范围是( ) A.-3<a<-6 B.a>6 C.a<-3 D.无解 3.若不等式组axx2的解集为a<x<2,则a的取值范围为( b ) A.a>2 B.a<2 C.0<a<2 D.不确定 4.设a>b,则不等式组bxax的解集为( c ) A.x>b B.x<a C.b<x<a D.无解 5.若一元一次不等式组bxax(a≠b)无解,则a与b的关系是( b ) A.a<b B.a>b C.a>b>0 D.a<b<0 二、填空题 6.不等式组12xx的解集是________. 7.不等式组23xx的解集是________. 8.若a<1,则不等式组1xax的解集为________. 9.不等式-3<1-2x≤5的解集为________,它的非负整数解为________.
10.代数式321x的值小于等于2且大于-1,则x的取值范围是________.
11.解下列不等式组:
(1)243213xxxx (2)23423521xxxx
12.如果关于x的方程x+2m-3=3x+7的解为不大于2的非负数,求m的范围.
13.已知方程组172652yxmyx的解x、y都是正数,求m的取值范围.
14.每年3月12日是植树节,某学校植树小组若干人植树,植树若干棵.若每人
植4棵,则余20棵没人植,若每人植8棵,则有一人比其他人植的少(但有树
植),问这个植树小组有多少人?共有多少棵树?
