双向板三角形荷载计算公式
双向板设计与计算
②荷载等效
将板上永久荷载g和活荷载q分成为对称荷载和反对称荷载两 种情况,取
对称荷载
g’=g+q/2
反对称荷载
q’=±q/2
, ③对称型荷载作用下
近似认为板的中间支座处转角为零
中间区格板可按四边固定的板来计算内力 边区格板的三个内支承边、角区格的两个 内支承边都可以看成固定边。
④反对称型荷载作用下
M max
1 8
(g
q
)
l
2 0
式中 g 、q ——作用于梯段板上的沿水平投影方向的
恒载及活载设计值; l0 — — 梯 段 板 的 计 算 跨 度 。
简支斜板(梁)在竖向均布荷载作用下的最大剪力为:
1 V max 2 ( g q ) l n
式 中 ln — — 净 跨 的 水 平 投 影 长 度 。
但 在 配 筋 计 算 时 ,考 虑 到 梯 段 板 与 平 台 梁 整 体 连 接 ,平
台梁对梯段板有一定的弹性约束作用,计算时最大弯矩可
取:
M
1 10
(g
q
)
l
2 0
○6 由于梯段板为斜向搁置的受弯构件,还将产生轴向力, 但其影响很小,设计时可不考虑。
○7 梯段斜板和一般板计算一样,可不必进行斜截面抗剪承 载力验算。
长度为≥ ln / 4 (图 7.3.12)。
(2)斜边梁 1)计算要点
○1 斜边梁两端支承在平台梁上,承受踏步传板传来的荷载
和本身自重,内力计算时与板式楼梯中梯段斜板的计算原理相
同,斜边梁的计算不考虑平台梁的弹性约束作用,按两端简支
计算,即:
M max
1 8
(g
q
)l
双向板楼等效活荷载的计算

浅谈双向板等效均布活荷载的计算摘要:本文根据《建筑结构荷载规范》(GB50009-2001)(2006版)附录B中对双向板等效荷载计算的概述,介绍了工程设计中双向板上等效均布活荷载的计算方法,为后续使用电算软件对结构整体进行受力分析提供了计算数据。
关键词:双向板等效均布活荷载计算0 前言双向楼板由于其经济、美观等优势而被广泛应用于建筑中。
本人在设计某污水处理厂脱水机房时,遇到了设备搁置于二层楼面的情况,由于脱水机房内设备较多以及工艺的要求,无法将所有设备布置于梁上,需要将布置于楼板上的设备重量进行等效均布活荷载的换算。
根据《建筑结构荷载规范》(GB50009-2001)(2006版)第4.1.3条规定,楼面板上的局部线荷载、面荷载等可按附录B的规定,换算为等效均布活荷载。
而附录B中仅对局部荷载作用下,如何计算等效均布荷载做了粗略的规定,所提供的计算公式也仅适用于单向板情况。
对于双向板的等效均布活荷载计算,本文基于对规范的规定理解提出一种计算方法。
《建筑结构荷载规范》(GB50009-2001)(2006版)第B.0.1条指出:楼面(板、次梁及主梁)的等效均布活荷载应在其设计控制部位上,根据需要按内力(如弯矩、剪力等)、变形裂缝的等值要求来确定在一般情况下,可仅按内力的等值来确定;第B.0.6条指出,双向板的等效均布荷载可按与单向板相同的原则,按四边简支板的绝对最大弯矩等值来确定。
这里通过一块楼板及其上部的设备荷载来介绍一下《建筑结构荷载规范》(GB50009-2001)第B.0.6条所述的双向板(这里所指的双向板一般指长边与短边长度之比小于或等于2.0的板,长边与短边长度之比大于2.0的板可按沿短边受力的单向板考虑)如何按四边简支的绝对最大弯矩等值确定其等效均布荷载。
而对于单向板上局部荷载的等效,《建筑结构荷载规范》(GB50009-2001)第B.0.4条、第B.0.5条已有详细说明,这里不再进行讨论。
%双向板荷载导算及计算

永久荷载标准值:由板传来(1-2α^2+α^3)×(qGk×lcy/2)=长边梁自重bx×hx×25/1000000=长边梁梁侧抹灰自重2×20×hx×20/1000000=可变荷载标准值:由板传来基本组合:由可变荷载效应控制由永久荷载效应控制标准组合:准永久组合:作6.21(kN/m)由板传来2.16(kN/m)短边梁自重0.24(kN/m)短边梁梁侧抹灰自重qxGk =8.37(kN/m)qxQk =(1-2α^2+α^3)×(qQk ×lcy/2)=0.52(kN/m).qgx1=1.2qxGk+1.4qxQk =10.76(kN/m)qgx2=1.35qxGk+1.4*0.7qxQk =11.80(kN/m)(kN/m)qgxK =qxGk+qxQk =8.88(kN/m)qgxQ =qxGk+0.5qxQk =8.62(kN/m)永久荷载标准值:(5/8)×(qGk×lcy/2)=4.69(kN/m)by×hy×25/1000000= 2.59(kN/m)2×20×hy×20/1000000=0.32(kN/m)qyGk =7.28(kN/m)可变荷载标准值:由板传来qyQk =(5/8)×(qQk ×lcy/2)=0.39(kN/m)基本组合:.由可变荷载效应控制qgy1=1.2qyGk+1.4qyQk =9.28(kN/m)由永久荷载效应控制qgy2=1.35qyGk+1.4*0.7qyQk =10.21(kN/m)qgy =max(qgy1,qgy2)=10.21(kN/m)标准组合:qgyK =qyGk+qyQk =7.67(kN/m)准永久组合:qgyQ =qyGk+0.5qyQk =7.47(kN/m)作用在短边梁上的荷载。
双向板梁板结构设计

均布荷载
泊松比=0时的数值(详见P292 附录8)。当 0时: m = m + m ;
m2 = m1 + m2
混凝土: =0.2
1
1
2
有自由边的板不能用上述公式查表计算!
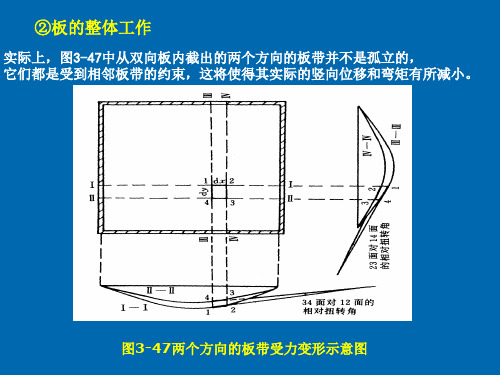
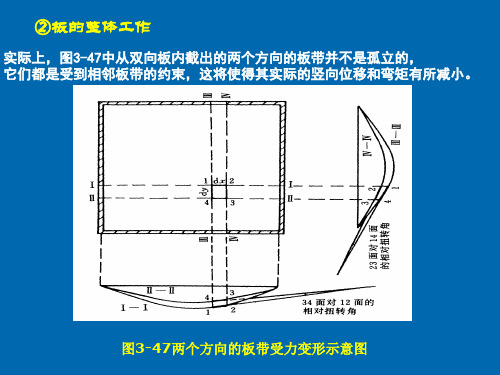
②连续双向板的内力计算(多区格双向板)
基本假定:双向板支承梁抗弯线刚度很大,其竖向 位移可忽略不计;支承梁抗扭线刚度很小,可以自 由转动,忽略梁对板的约束作用。 即:将支承梁视为双向板的不动铰支座。 适用条件:同一方向相邻跨度相对差值小于20%。 思想:确定结构的控制截面(支座、跨中截面); 确定结构控制截面产生最危险内力时的最不利荷载 组合。利用单跨板的计算表格。
发生虚位移
虚功原理求极限荷载
⑤塑性铰线法的基本方程
——(以均布荷载作用下的四边支承双向板为例)
塑性铰线
为简化计算,近似假定:斜向塑性铰线与板边的夹角为45°
塑性铰线法的基本方程
四边固定
2 qlx (3l y lx ) M x 充条件才能求解
2
I.弹性理论计算方法
双向板内力计算
①单块双向板的内力计算 四边支承的板,有六种边界条件: •四边简支; •一边固定,三边简支; •两对边固定,两对边简支; •两邻边固定,两邻边简支;
•三边固定,一边简支。
•四边固定;
短跨方向的计算跨度, 计算同单向板
2 M (表中的系数 ) pl01
单位板宽 内的弯矩
的计算跨度 —— 垂直于楼板边缘 0 方向的计算跨度
② 边区格板的跨内截面及第一内支座截面:
③ 角区格板截面弯矩值不予折减。
配筋计算 由单位宽度的截面弯矩设计值m计算受拉钢筋的截面积:
m As s h0 f y
弹性双向板计算

弹性双向板计算
在进行弹性双向板的计算时,需要使用一些基本的公式和原理。
下面是关于弹性双向板计算的一些基本原理和公式:
1.位移和应变的关系:
ε=(ΔL/L)=(y/r)
其中,ε是单位长度的应变,ΔL是位移,L是板的边长,y是位移距离,r是板的曲率半径。
2.应力和应变的关系:
σ=Eε=Ey/r
其中,σ是单位面积的应力,E是材料的弹性模量。
3.弯曲方程:
弯曲是弹性双向板最主要的变形形式。
根据弯曲理论,弹性双向板的弯曲方程可以表示为:
M=Dη/z
其中,M是弯矩,D是抵抗弯曲的几何刚度系数(弯曲刚度),η是受力方式的常数(取决于荷载类型和边界条件),z是抵抗弯曲的几何形状参数。
4.抵抗弯曲的几何刚度系数:
抵抗弯曲的几何刚度系数D可以通过以下公式计算:
D=(Eh^3/12(1-μ^2))
其中,E是材料的弹性模量,h是板的厚度,μ是材料的泊松比。
5.抵抗弯曲的几何形状参数:
抵抗弯曲的几何形状参数z可以通过以下公式计算:
z=(h^2/6)
其中,h是板的厚度。
以上是弹性双向板计算中的一些基本原理和公式。
需要根据具体的设计条件和要求,结合实际情况选取适合的公式和原理进行计算。
通过应用这些公式和原理,可以对弹性双向板进行合理的设计和计算,以满足结构的强度和稳定性要求。
双向板设计与计算
q)l
2 0
计算。当板的
一边与梁整体连接而另一边支承在墙上时(7.3.4a),板的
跨中弯矩应按
M
1 8
(g
q)l
2 0
计算。
2)构造要求 平台板与平台梁相接处及嵌固在墙内部分,考虑到支座处有负 弯矩或墙对板部分嵌固作用,在靠近支座的板面上应配置构造负钢 筋。工程中常采用分离式配筋,构造负钢筋一般为φ8@200,伸出
双向板支承梁的荷载分配
换算的等效均布荷载
(4)内力计算
三角形荷载
q5p 8
梯形荷载 q (1 2 2 3 ) p
a/l
(5)配筋计算
内力求出后,梁的截面配筋与单向板肋形楼盖中的次梁、主梁相同
2. 梁的配筋构造 双向板肋梁楼盖中梁的配筋构造同单向板中梁的配筋构造
二、现浇楼梯的计算与构造
(g
q)ln
cos
○2 斜边梁的计算截面形式与斜边梁和踏步板的相对位置
有关,当踏步板在斜边梁上部时(图 7.3.12a),若仅有一根斜 梁,可按矩形截面计算;若有两根斜梁,则按倒 L 形截面计算。 当踏步板在斜边梁的中下部时(图 7.3.12b)应按矩形截面计算。
○3 斜边梁截面高度取垂直于斜梁轴线的高度,一般取 h ≥ l0 / 20 ( l0 为斜边梁水平投影的计算跨度)。
2. 考虑泊桑比(μ≠ 0) 时的内力计算
M M ( ) M
x
x
y
M M ( ) M
y
y
x
μ——泊桑比,钢筋混凝土的μ通常取1/6;
注意:计算支座截面弯矩时,不考虑泊桑比的影响, 即可直接按式(3-20)计算内力。
梁上荷载计算

9。
3。
2梁上荷载的确定梁上荷载主要是梁自重、梁上墙体重和板传来的荷载。
1、梁自重:比如250m m ×600mm 的混凝土梁,其表面为20厚水泥砂浆打底,外加涂料抹面。
那么,梁自重标准值为:0。
25×0。
6×25+0.02×20×(0.25+0。
6×2)=4.33kN/m 但在计算梁自重时要注意,当梁和板整浇时,如果板上荷载按照轴线尺寸计算的话,梁高要减去板厚。
如图9.3。
2-1图9。
3.2—1 梁截面尺寸示意计算梁自重时,梁高为500mm 。
同时梁侧抹灰也相应改变。
梁自重标准值为:0。
25×0。
5×25+0.02×20×(0.25+0。
5×2)=3。
625kN m2、梁上墙体重量框架结构在PMCAD 输模型时也要计算梁上墙体重量,作为梁间荷载输入。
有些设计资料上给出了双面粉刷的墙体重量.比如200厚加气混凝土墙体加双面粉刷的重量是2。
08kN m ,这是按20厚混合砂浆粉面计算的。
加气混凝土的容重为7。
0~7.53kN m ,则0.2×7.0+0。
02×2×17=2。
08 kN m 。
若是内墙,直接采用此值即可.若是外墙,就要根据外墙装饰情况调整墙体。
比如,200厚加气混凝土外墙,室内装饰为20厚混合砂浆打底,涂料抹面,外墙为面砖,则墙体重量为0。
2×7.0+0.02×17+0.7=2。
44kN m 。
若外墙为大理石或外墙设有保温等,墙体重量与所给双面粉刷重量相差更大,故必须根据实际情况计算。
当墙上有门窗洞口时,可分别计算墙体重量和门窗重量,然后,简化为作用在梁上的均布荷载。
比如,开间3.6m ,层高3.0m ,梁高500mm ,窗户尺寸为1800mm ×2100mm 墙体为200厚加气混凝土墙,窗为铝合金窗,柱尺寸为500mm ×500mm 那么梁上墙体线荷载为 ()()(){}()3.60.5 3.00.5 1.8 2.10.27.00.02172 1.8 2.10.53.60.5 3.27/kN m-⨯--⨯⨯⨯+⨯⨯+⨯⨯⎡⎤⎣⎦÷-= 3、板传到梁上的荷载若某一梁是相邻两个单向板的支座,梁上线荷载为板上面荷载乘以单向板本跨跨度即可。
(一)双向板按弹性理论的计算方法

(一)双向板按弹性理论的计算方法1.单跨双向板的弯矩计算为便于应用,单跨双向板按弹性理论计算,已编制成弯矩系数表,供设计者查用。
在教材的附表中,列出了均布荷载作用下,六种不同支承情况的双向板弯矩系数表。
板的弯矩可按下列公式计算:M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m);g、p为板上恒载及活载设计值(kN/m2);l x为板的跨度(m)。
显示更多隐藏2.多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。
当求某跨跨中最大弯矩时,应在该跨布置活载,并在其前后左右每隔一区格布置活载,形成如上图(a)所示棋盘格式布置。
图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。
为了能利用单跨双向板的弯矩系数表,可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况,将图(c)与(d)叠加即为与图(b)等效的活载分布。
在对称荷载作用下,板在中间支座处的转角很小,可近似地认为转角为零,中间支座均可视为固定支座。
因此,所有中间区格均可按四边固定的单跨双向板计算;如边支座为简支,则边区格按三边固定、一边简支的单跨双向板计算;角区格按两邻边固定、两邻边简支的单跨双向板计算。
在反对称荷载作用下,板在中间支座处转角方向一致,大小相等接近于简支板的转角,所有中间支座均可视为简支支座。
因此,每个区格均可按四边简支的单跨双向板计算。
将上述两种荷载作用下求得的弯矩叠加,即为在棋盘式活载不利位置下板的跨中最大弯矩。
(2)支座弯矩支座弯矩的活载不利位置,应在该支座两侧区格内布置活载,然后再隔跨布置,考虑到隔跨活载的影响很小,可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩,即为支座的最大弯矩。
这样,所有中间支座均可视为固定支座,边支座则按实际情况考虑,因此可直接由单跨双向板的弯矩系数表查得弯矩系数,计算支座弯距。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双向板三角形荷载计算公式
【原创版】
目录
1.引言
2.双向板三角形荷载计算公式的概述
3.双向板三角形荷载计算公式的推导过程
4.双向板三角形荷载计算公式的应用实例
5.结论
正文
【引言】
在结构力学中,计算结构的荷载是至关重要的。
双向板三角形结构由于其良好的力学性能,被广泛应用于桥梁、楼板等工程结构中。
为了更好地理解和计算这种结构的荷载,本文将介绍双向板三角形荷载计算公式。
【双向板三角形荷载计算公式的概述】
双向板三角形荷载计算公式,是一种计算双向板三角形结构在给定荷载条件下的内部应力和应变的方法。
该公式通过对结构进行分析,考虑了结构的几何参数和材料性能,从而可以得到结构的内部应力和应变。
【双向板三角形荷载计算公式的推导过程】
在推导双向板三角形荷载计算公式时,我们首先需要根据结构的几何参数和材料性能,建立结构的有限元模型。
然后,通过对模型施加荷载,并求解模型的线性或非线性方程组,我们可以得到结构的内部应力和应变。
【双向板三角形荷载计算公式的应用实例】
假设我们有一个双向板三角形结构,其几何参数如下:a=10cm,b=20cm,h=30cm。
我们希望计算在均匀分布荷载 q=5kN/m作用下,结构的内部应
力和应变。
根据双向板三角形荷载计算公式,我们可以得到结构的内部应力和应变。
【结论】
双向板三角形荷载计算公式,是一种计算双向板三角形结构在给定荷载条件下的内部应力和应变的方法。
该公式通过对结构进行分析,考虑了结构的几何参数和材料性能,从而可以得到结构的内部应力和应变。
