第二章 二次函数 C中考挑战区
2020年九年级数学中考二轮复习:《二次函数综合》压轴题专题训练(含答案)

《二次函数综合》压轴题专题训练1.定义:关于x轴对称且对称轴相同的两条抛物线叫作“同轴对称抛物线”.例如:y=(x﹣1)2﹣2的“同轴对称抛物线”为y=﹣(x﹣1)2+2.(1)满足什么条件的抛物线与其“同轴对称抛物线”的顶点重合:.(2)求抛物线y=﹣x2+x+1的“同轴对称抛物线”.(3)如图,在平面直角坐标系中,点B是抛物线L:y=ax2﹣4ax+1上一点,点B的横坐标为1,过点B作x轴的垂线,交抛物线L的“同轴对称抛物线”于点C,分别作点B、C关于抛物线对称轴对称的点B′、C′,连接BC、CC′、B′C′、BB′,设四边形BB′C′C的面积为S(S>0).①当四边形BB′C′C为正方形时,求a的值.②当抛物线L与其“同轴对称抛物线”围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时,直接写出a的取值范围.2.已知抛物线C:y=ax2+bx+c向左平移1个单位长度,再向上平移4个单位长度得到抛1物线C:y=x2.2(1)直接写出抛物线C的解析式;1与x轴交于A,B两点,点A在点B的左侧,点P(,t)(2)如图1,已知抛物线C1在抛物线C上,QB⊥PB交抛物线于点Q.求点Q的坐标;1上,EM∥x轴,点E在点M的左侧,过点M的直线MD与抛(3)已知点E,M在抛物线C2物线C只有一个公共点(MD与y轴不平行),直线DE与抛物线交于另一点N.若线段2NE=DE,设点M,N的横坐标分别为m,n,直接写出m和n的数量关系(用含m的式子表示n)为.3.如图1,抛物线y=x2+bx+c过点A(4,﹣1),B(0,﹣),点C为直线AB下方抛物线上一动点,M为抛物线顶点,抛物线对称轴与直线AB交于点N.(1)求抛物线的表达式与顶点M的坐标;(2)在直线AB上是否存在点D,使得以C,D,M,N为顶点的四边形是平行四边形,若存在,请求出D点坐标;(3)在y轴上是否存在点Q,使∠AQM=45°?若存在,求点Q的坐标;若不存在,请说明理由.4.如图,已知抛物线y=ax2+bx+c与x轴的交点为A(﹣1,0),B(2,0)且与y轴交于点C,OA=OC.(1)求该抛物线的表达式;(2)点C关于x轴的对称点为C1,M是线段BC1上的一个动点(不与B、C1重合),ME⊥x轴,MF⊥y轴,垂足分别为E、F,当点M在什么位置时,矩形MFOE的面积最大?说明理由;(3)已知点P时直线y=x+1上的动点,点Q为抛物线上的动点,当以C、C1、P、Q 为顶点的四边形为平行四边形时,求出相应的点P和点Q的坐标.5.如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点(点A位于点B的左侧),与y轴相交于点C,M是抛物线的顶点,直线x=1是抛物线的对称轴,且点C的坐标为(0,3).(1)求抛物线的解析式;(2)已知P为线段MB上一个动点,过点P作PD⊥x轴于点D.若PD=m,△PCD的面积为S.①求S与m之间的函数关系式,并写出自变量m的取值范围;②当S取得最值时,求点P的坐标.(3)在(2)的条件下,在线段MB上是否存在点P,使△PCD为等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.6.如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y 轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;=3,请求出点P的坐标.(2)如图2,点P为直线BD上方抛物线上一点,若S△PBD(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.7.已知抛物线交x轴于A,B两点(A在B右边),A(3,0),B(1,0)交y轴于C点,C(0,3),连接AC;(1)求抛物线的解析式;(2)P为抛物线上的一点,作PE⊥CA于E点,且CE=3PE,求P点坐标;(3)将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,过H作直线MH,NH,当MH⊥NH时,求MN恒过的定点坐标.:y=(x﹣1)2+k(k>0)经过y轴上的点A,顶点为B.抛物线8.如图,已知抛物线l1l:y=(x﹣h)2+2﹣h(h≥2)的顶点为D,直线y=﹣x+b经过A,B,D三点,两抛物2线交于点C.(1)求b的值和点B的坐标;(2)设点C的横坐标为m,探究m与h之间的数量关系;(3)当△ABC是直角三角形时,求h的值.9.综合与探究.如图1,抛物线y=x2﹣x﹣2与x轴交于A,B两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).(1)求A,B,C三点的坐标及直线BE的解析式.(2)如图2,过点A作BE的平行线交抛物线于点D,点P是抛物线上位于线段AD下方的一个动点,连接PA,PD,求OAPD面积的最大值.(3)若(2)中的点P为抛物线上一动点,在x轴上是否存在点Q,使得以A,D,P,Q 为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.10.如图,抛物线y=ax2+bx+c与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C(0,3),抛物线的对称轴与直线BC交于点D.(1)求抛物线的表达式;(2)在抛物线的对称轴上找一点M,使|BM﹣CM|的值最大,求出点M的坐标;(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,直接写出点E的坐标.11.如图1,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC.(1)求抛物线的解析式;(2)点D是抛物线顶点,求△ACD的面积;(3)如图2,射线AE交抛物线于点E,交y轴的负半轴于点F(点F在线段AE上),点P是直线AE下方抛物线上的一点,S=,求△APE面积的最大值和此动点P的坐标.△ABE12.图①,抛物线y=﹣2x2+bx+c过A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC.(1)求该抛物线的表达式和对称轴;(2)点D是抛物线对称轴上一动点,当△BCD是以BC为直角边的直角三角形时,求所有符合条件的点D的坐标;(3)如图2,将抛物线在BC上方的图象沿BC折叠后与y轴交与点E,求点E的坐标.13.已知,抛物线y=ax2,其中a>0.(1)如图1,若点A、B是此抛物线上两点,且分属于y轴两侧,连接AB与y轴相交于点C,且∠AOB=90°.求证:CO=;(2)如图2,若点A是此抛物线上一点,过点A的直线恰好与此抛物线仅有一个交点,且与y轴交于点B,与x轴相交于点C.求证:AC=BC.14.如图,抛物线y=ax2﹣x+c与x轴交于A,B两点,与y轴交于C点,连结AC,已知B(1﹣,0),且抛物线经过点D(2,﹣2).(1)求抛物线的解析式;(2)若点E是抛物线上位于x轴下方的一点,且S△ACE =S△ABC,求E的坐标;(3)若点P是y轴上一点,以P、A、C三点为顶点的三角形是等腰三角形,求P点的坐标.15.如图,在平面直角坐标系中,直线y=﹣x+4分别与x轴、y轴相交于点B、C,经过点B、C的抛物线y=﹣+bx+c与x轴的另一个交点为A.(1)求出抛物线表达式,并求出点A坐标.(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.参考答案1.解:(1)∵“同轴对称抛物线”的顶点重合,∴顶点关于x轴对称且重合,∴顶点在x轴上,故答案为:顶点在x轴上;(2)∵y=﹣x2+x+1=﹣(x﹣1)2+,∴“同轴对称抛物线”的顶点坐标为(1,﹣),∴y=(x﹣1)2﹣;(3)①由题可知,B(1,1﹣3a),∴C(1,3a﹣1),∵抛物线y=ax2﹣4ax+1的对称轴为x=2,∴B'(3,1﹣3a),C'(3,3a﹣1),∴BB'=CC'=2,∴BC=2﹣6a或BC=6a﹣2,∴2﹣6a=2或6a﹣2=2,∴a=0(舍去)或a=;②函数的对称轴为x=2,函数L的顶点坐标为(2,1﹣4a),∵L与“同轴对称抛物线”是关于x轴对称的,所以整数点也是对称的出现,∵抛物线L与其“同轴对称抛物线”围成的封闭区域内,在x轴上的整数点可以是3个或5个,∴L与x轴围城的区域的整数点为4个或3个;当a>0时,当x=1时,﹣2≤1﹣3a<﹣1,∴<a≤1,当x=2时,1﹣4a<﹣2,∴a>,∴<a≤1;当a<0时,当x=2时,1﹣4a≤2,∴a≥﹣,当x=﹣1时,5a+1<0,∴a<﹣,∴﹣≤a<﹣;综上所述:<a≤1或﹣≤a<﹣.2.解:(1)由已知可知,抛物线C:y=x2向右平移1个单位长度,再向下平移4个单位2:y=ax2+bx+c,长度得到抛物线C1:y=(x﹣1)2﹣4,∴抛物线C1故答案为y=(x﹣1)2﹣4;(2)∵y=(x﹣1)2﹣4,令y=0,(x﹣1)2﹣4=0,解得x=3或x=﹣1,∴A(﹣1,0),B(3,0),上,∵点P(,t)在抛物线C1∴t=(﹣1)2﹣4,解得t=﹣,∴P(,﹣),设Q(t,t2﹣2t﹣3),过点P作PM⊥x轴交于点M,过点Q作QN⊥x轴交于点N,∵BQ⊥BP,∴∠QBN+∠MBP=∠QBN+∠MQN=90°,∴∠BQN=∠PBM,∴△BNQ∽△QMP,∴=,∴=,∴t=﹣或t=3,∵Q点在第二象限,∴t=﹣,∴Q(﹣,);(3)∵点M与N在y=x2上,∴M(m,m2),N(n,n2)∵EM∥x轴,∴E(﹣m,m2),设MD的解析式为y=kx+b,∴m2=km+b,∴b=m2﹣km,∴y=kx+m2﹣km,∵直线MD与抛物线y=x2只有一个交点,∴kx+m2﹣km=x2,∴△=k2﹣4(m2+km)=0,∴k=2m,∴直线MD的解析式为y=2mx﹣m2,∵NE=DE,∴D(﹣2m﹣n,2m2﹣n2),∴2m2﹣n2=2m(﹣2m﹣n)﹣m2,整理得,n2﹣2mn﹣7m2=0,∴n=(1±2)m,故答案为n=(1±2)m.3.解:(1)将点A(4,﹣1),B(0,﹣)代入抛物线y=x2+bx+c,得,解得,∴y=x2﹣x﹣,∴M点的坐标为(1,﹣4);(2)设直线AB的表达式为y=mx+n,∴,解得,∴y=x﹣;当x=1时,y=﹣3,∴N(1,﹣3),∴MN=1;①若MN为平行四边形的一边时,则有CD∥MN,且CD=MN,设C(t,t2﹣t﹣),则D(t,t﹣),∴CD=t﹣﹣(t2﹣t﹣)=1,∴t=3或t=1(舍去),∴D(3,﹣);②若MN为平行四边形的对角线,设D(t,t﹣),则C(2﹣t,﹣t﹣),将点C代入抛物线解析式得,(2﹣t)2﹣(2﹣t)﹣=﹣t﹣,∴t=﹣1或t=1(舍去),∴D(﹣1,﹣);综上所述:符合条件的D点坐标为(3,﹣)或(﹣1,﹣);(3)在对称轴上取点P(1,﹣1),∴PA=PM=3,∠APM=90°,以P为圆心,PA为半径作圆交y轴于点Q,∴∠AQM=∠APM=45°,作PE⊥y轴交于点E,∴PE=1,∵PQ=3,∴EQ==2,∴Q点坐标为(0,﹣1+2)或(0,﹣1﹣2).4.解:(1)∵点A (﹣1,0)∴OA =1,∵OA =OC =1,且点C 在y 轴负半轴,∴点C (0,﹣1)∵抛物线y =ax 2+bx +c 与x 轴的交点为A (﹣1,0),B (2,0)且与y 轴交于点C , ∴ 解得:∴抛物线的表达式为:y =x 2﹣x ﹣1;(2)∵点C 关于x 轴的对称点为C 1,∴C 1(0,1),∵点B (2,0),点C 1(0,1),∴直线BC 1的解析式为:y =﹣x +1,∴设点M 坐标为(m ,﹣m +1)∴MF =m ,ME =﹣m +1,∴矩形MFOE 的面积=MF ×ME =m ×(﹣m +1)=﹣m 2+m =﹣(m ﹣1)2+, ∴当m =1时,矩形MFOE 的最大面积为,此时点M 的坐标为(1,),即点M 为线段C 1B 中点时,S 矩形MFOE 最大;(3)由题意,C (0,﹣1),C 1(0,1),以C 、C 1、P 、Q 为顶点的四边形为平行四边形,分以下两种情况:①C 1C 为边,则C 1C ∥PQ ,C 1C =PQ ,设P (m ,m +1),Q (m ,m 2﹣m ﹣1),∴|(m 2﹣m ﹣1)﹣(m +1)|=2,解得:m 1=4,m 2=﹣2,m 3=2,m 4=0(舍),P 1(4,3),Q 1(4,5);P 2(﹣2,0),Q 2(﹣2,2);P 3(2,2),Q 3(2,0) ②C 1C 为对角线,∵C 1C 与PQ 互相平分,C 1C 的中点为(0,0),∴PQ 的中点为(0,0),设P (m ,m 2﹣m +1),则Q (﹣m ,m 2+m ﹣1) ∴(m +1)+(m 2+m ﹣1)=0,解得:m 1=0(舍去),m 2=﹣2,∴P 4(﹣2,0),Q 4(2,0);综上所述,点P 和点Q 的坐标为:P 1(4,3),Q 1(4,5)或P 2(﹣2,0),Q 2(﹣2,2)或P 3(2,2),Q 3(2,0)或P 4(﹣2,0),Q 4(2,0).5.解:(1)∵直线x =1是抛物线的对称轴,且点C 的坐标为(0,3),∴c =3,﹣=1,∴b =2,∴抛物线的解析式为:y =﹣x 2+2x +3;(2)①∵y =﹣x 2+2x +3=﹣(x ﹣1)2+4,∴点M (1,4),∵抛物线的解析式为:y =﹣x 2+2x +3与x 轴相交于A ,B 两点(点A 位于点B 的左侧), ∴0=﹣x 2+2x +3∴x 1=3,x 2=﹣1,∴点A (﹣1,0),点B (3,0),∵点M (1,4),点B (3,0)∴直线BM 解析式为y =﹣2x +6,∵点P 在直线BM 上,且PD ⊥x 轴于点D ,PD =m ,∴点P (3﹣,m ),∴S △PCD =×PD ×OD =m ×(3﹣)=﹣m 2+m ,∵点P 在线段BM 上,且点M (1,4),点B (3,0),∴0<m ≤4∴S与m之间的函数关系式为S=﹣m2+m(0<m≤4)②∵S=﹣m2+m=﹣(m﹣3)2+,∴当m=3时,S有最大值为,∴点P(,3)∵0<m≤4时,S没有最小值,综上所述:当m=3时,S有最大值为,此时点P(,3);(3)存在,若PC=PD=m时,∵PD=m,点P(3﹣,m),点C(0,3),∴(3﹣﹣0)2+(m﹣3)2=m2,∴m1=18+6(舍去),m2=18﹣6,∴点P(﹣6+3,18﹣6);若DC=PD=m时,∴(3﹣﹣0)2+(﹣3)2=m2,∴m3=﹣2﹣2(舍去),m4=﹣2+2,∴点P(4﹣,﹣2+2);若DC=PC时,∴(3﹣﹣0)2+(m﹣3)2=(3﹣﹣0)2+(﹣3)2,∴m5=0(舍去),m6=6(舍去)综上所述:当点P的坐标为:(﹣6+3,18﹣6)或(4﹣,﹣2+2)时,使△PCD为等腰三角形.6.解:(1)设抛物线的解析式为y=a(x﹣1)2+4,将点B(3,0)代入得,(3﹣1)2×a+4=0.解得:a=﹣1.∴抛物线的解析式为:y=﹣(x﹣1)2+4=﹣x2+2x+3.(2)过点P作PQ∥y轴交DB于点Q,∵抛物线的解析式为y=﹣x2+2x+3∴D(0,3).设直线BD的解析式为y=kx+b,∴,解得:,∴直线BD的解析式为y=﹣x+3.设P(m,﹣m2+2m+3),则Q(m,﹣m+3),∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.∵S△PBD =S△PQD+S△PQB,∴S△PBD=(3﹣m)=PQ=﹣m,∵S△PBD=3,∴﹣m=3.解得:m1=1,m2=2.∴点P的坐标为(1,4)或(2,3).(3)∵B(3,0),D(0,3),∴BD==3,设M(a,0),∵MN∥BD,∴△AMN∽△AMD,∴,即.∴MN=(1+a),DM==,∵△DNM∽△BMD,∴,∴DM2=BD•MN.∴9+a2=3(1+a).解得:a=或a=3(舍去).∴点M的坐标为(,0).7.解:(1)∵抛物线过A(3,0),B(1,0),∴可设抛物线的解析式为y=a(x﹣3)(x﹣1)(a≠0),把c(0,3)代入,得3a=3,∴a=1,∴抛物线的解析式是y=(x﹣3)(x﹣1)=x2﹣4x+3,即y=x2﹣4x+3;(2)过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,延长FE与PD交于点G,如图1,∵A(3,0),C(0,3),∴OA=OC=3,∴∠OAC=45°,∵FG∥OA,∴∠CEF=45°,∴CF=EF=CE,∵PE⊥CA,∴∠PEG=45°,∴PG=EG=PE,∵CE=3PE,∴EF=3FG,设EF=3m,则PG=EG=m,FG=4m,∴DG=OF=OC﹣CF=3﹣3m,PD=PG+DG=3﹣2m,∴P(4m,3﹣2m),把P(4m,3﹣2m)代入y=x2﹣4x+3中得,3﹣2m=16m2﹣16m+3,∴m=,或m=0(舍去),∴P(,);(3)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线y=x2﹣4x+3的顶点为(2,﹣1),∵将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,∴H(2,0),由题意知,点H是新抛物线的顶点,∴新抛物线的解析式为y=(x﹣2)2,设M(m,(m﹣2)2),N(n,(n﹣2)2),过M作MK⊥x轴于点K,过点N作NL⊥x轴于点L,则MK=(m﹣2)2,KH=2﹣m,HL=n﹣2,NL=(n﹣2)2,∵MH⊥NH,∴∠MHK+∠HMK=∠MHK+∠NHL=90°,∴∠HMK=∠NHL,∵∠MKH=∠HLN=90°,∴△KHM∽△LNH,∴,,∴,∴,设直线MN的解析式为:y=kx+b(k≠0),则,∴,∴直线MN的解析式为:,当x=2时,y=﹣(m2﹣4m+3)=m2﹣4m+4﹣m2+4m﹣3=1,∴MN恒过的定点(2,1).8.解:(1)∵y=(x﹣1)2+k(k>0)经过y轴上的点A,顶点为B,∴A(0,1+k),B(1,k),∵y=(x﹣h)2+2﹣h(h≥2)的顶点为D,∴D(h,2﹣h),∵直线y=﹣x+b经过A,D,∴,∴,∴b的值为2,点B的坐标为(1,1);:y=(x﹣1)2+1,(2)由(1)知,抛物线l1∵点C的横坐标为m,两抛物线交于点C.∴(m﹣1)2+1=(m﹣h)2﹣h+2,整理得2mh﹣2m=h2﹣h∵h≥2∴m==;(3)当AC⊥AB时,则直线AC解析式为:y=x+2,∴∴(舍去),,∴点C坐标为(3,5),∴3=∴h=6;当BC⊥AB时,则直线BC解析式为:y=x,∴∴(舍去),∴点C坐标为(2,2),∴2=∴h=4;9.解:(1)令y=0,则x2﹣x﹣2=0,解得x=4或x=﹣1,∴A(﹣1,0),B(4,0),令x=0,则y=﹣2,∴C(0,﹣2),设直线BE的解析式为y=kx+b,将B(4,0)、E(0,2)代入得,,解得:,∴y=﹣x+2;(2)由题意可设AD的解析式为y=﹣x+m,将A(﹣1,0)代入,得到m=﹣,∴y=﹣x﹣,联立,解得:,,∴D(3,﹣2),过点P作PF⊥x轴于点F,交AD于点N,过点D作DG⊥x轴于点G.∴S△APD =S△APN+S△DPN=PN•AF+PN•FG=PN(AF+FG)=PN•AG=×4PN=2PN,设P(a,﹣a2﹣a﹣2),则N(a,﹣a﹣),∴PN=﹣a2+a+,∴S△APD=﹣a2+2a+3=﹣(a﹣1)2+4,∵﹣1<0,﹣1<a<3,∴当a=1时,△APD的面积最大,最大值为4;(3)存在;①当PD与AQ为平行四边形的对边时,∵AQ∥PD,AQ在x轴上,∴P(0,﹣2),∴PD=3,∴AQ=3,∵A(﹣1,0),∴Q(2,0)或Q(﹣4,0);②当PD与AQ为平行四边形的对角线时,PD与AQ的中点在x轴上,∴P点的纵坐标为2,∴P(,2)或P(,2),∴PD的中点为(,0)或(,0),∵Q点与A点关于PD的中点对称,∴Q(,0)或Q(,0);综上所述:点Q的坐标为(2,0)或(﹣4,0)或(,0)或(,0).10.解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、B(3,0)、C(0,3),∴,解得,∴抛物线的表达式为y=x2﹣4x+3;(2)∵抛物线对称轴是线段AB的垂直平分线,∴AM=BM,由三角形的三边关系,|BM﹣CM|=|AM﹣CM|<AC,∴点A、C、M三点共线时,|BM﹣CM|最大,设直线AC的解析式为y=mx+n,则,解得,又∵抛物线对称轴为直线x =﹣=2,∴x =2时,y =﹣3×2+3=﹣3,故,点M 的坐标为(2,﹣3);(3))∵OB =OC =3,OB ⊥OC ,∴△BOC 是等腰直角三角形,∵EF ∥y 轴,直线BC 的解析式为y =﹣x +3,∴△DEF 只要是直角三角形即可与△BOC 相似,∵D (2,1),A (1,0),B (3,0),∴点D 垂直平分AB 且到点AB 的距离等于AB ,∴△ABD 是等腰直角三角形,∴∠ADB =90°,如图,①点F 是直角顶点时,点F 的纵坐标与点D 的纵坐标相同,是1,∴x 2﹣4x +3=1,整理得x 2﹣4x +2=0,解得x =2±, 当x =2﹣时,y =﹣(2﹣)+3=1+, 当x =2+时,y =﹣(2+)+3=1﹣, ∴点E 1(2﹣,1+)E 2(2+,1﹣), ②点D 是直角顶点时,联立, 解得,,当x =1时,y =﹣1+3=2,当x =4时,y =﹣4+3=﹣1,∴点E 3(1,2),E 4(4,﹣1),综上所述,存在点E 1(2﹣,1+)或E 2(2+,1﹣)或E 3(1,2)或E 4(4,﹣1),使以D 、E 、F 为顶点的三角形与△BCO 相似.11.解:(1)∵抛物线y =ax 2+2ax +c (a ≠0)与x 轴交于点A ,B (1,0)两点,与y 轴交于点C ,且OA =OC ,∴a +2a +c =0,点C 的坐标为(0,c ),∴点A 的坐标为(c ,0),∴ac 2+2ac +c =0, ∴, 解得,或,∵函数图象开口向上,∴a >0,∴a =1,c =﹣3,∴抛物线的解析式为y =x 2+2x ﹣3;(2)∵y =x 2+2x ﹣3=(x +1)2﹣4,抛物线与与y 轴交于点C ,顶点为D ,OA =OC ,抛物线y =ax 2+2ax +c (a ≠0)与x 轴交于点A ,B (1,0)两点,∴点D 的坐标为(﹣1,﹣4),点C 的坐标为(0,﹣3),点A 的坐标为(﹣3,0), 连接OD ,如右图1所示,由图可知:S △ACD =S △OAD +S △OCD ﹣S △OAC==3;(3)∵A(﹣3,0),点B(1,0),∴AB=4,设点E的纵坐标为t,t<0,∵S△ABE=,∴=,得t=,把y=﹣代入y=x2+2x﹣3,得﹣=x2+2x﹣3,解得,x1=,x2=,∵点E在y轴的右侧,∴点E(,﹣),设直线AE的解析式为y=mx+n(m≠0),∴,得,∴直线AE的解析式为y=﹣x﹣1,过点P作y轴的平行线交AC于点G,如图2所示,设点P的横坐标为x,则P(x,x2+2x﹣3),点G(x,﹣x﹣1),∴PG=(﹣x﹣1)﹣(x2+2x﹣3)=﹣x2﹣x+2,又∵A(﹣3,0),E(,﹣),∴S△APE =S△APG+S△PEG=(﹣x2﹣x+2)(x+3)+(﹣x2﹣x+2)(﹣x)=(﹣x2﹣x+2)(3+)=(x+)2+,∴当x=﹣时,S取得最大值,最大值是,△APE把x=﹣代入y=x2+2x﹣3,得y=(﹣)2+2×(﹣)﹣3=﹣,∴此时点P的坐标为(﹣,﹣).12.解:(1)∵抛物线y=﹣2x2+bx+c过A(﹣1,0)、B(3,0)两点,∴,得,∴y=﹣2x2+4x+6=﹣2(x﹣1)2+8,∴抛物线的对称轴是直线x=1,即该抛物线的解析式为y=﹣2x2+4x+6,对称轴是直线x=1;(2)分两种情况:设点D的坐标为(1,y)第一种情况是:∠BCD=90°时,则CD2+BC2=BD2,∵点B的坐标为(3,0),抛物线y=﹣2x2+4x+6交y轴于点C,∴点C的坐标为(0,6),∴[12+(y﹣6)2]+(32+62)=(3﹣1)2+y2,解得,y=6.5,∴点D的坐标为(1,6.5);第二种情况:当∠DBC=90°时,BD2+BC2=CD2,即[(3﹣1)2+y2]+(32+62)=12+(6﹣y)2,解得,y=﹣1,∴点D的坐标为(1,﹣1),综上所述,符合条件的点D的坐标为(1,6.5),(1,﹣1);(3)因为点C的坐标为(0,6),点B的坐标为(3,0),设直线BC的解析式为y=kx+6,则3k+6=0,得k=﹣2,即直线BC的解析式为y=﹣2x+6,如右图所示,作点E关于直线BC的对称点E′交BC于点F,过点F作FN⊥y轴于点N,设E(0,m),E′(x,y),则EE′⊥BC,∴∠CFE=∠COB=90°,∴BC==3,∵∠ECF=∠BCO,∴△ECF∽△BCO,∴,即,解得,CF=,又∵∠CNF=∠COB,∠NCF=∠OCB,∴△NCF∽△OCB,∴,即,解得,FN=,∴点F的横坐标为,把x=代入直线BC的解析式,得y=,∴点F的坐标为(,),∵EE′关于直线BC对称,∴点F为EE′的中点,∴,解得,∴E′(,),∵点E′在抛物线y=﹣2x2+4x+6上,∴=﹣2×[]2+4×+6,解得,m1=6,m2=,∴点E的坐标为(0,6)或(0,).13.证明:(1)设A(b,ab2),B(c,ac2),∵∠AOB=90°,∴AB2=AO2+BO2,∴(b﹣c)2+(ab2﹣ac2)2=b2+a2b4+c2+a2c4,﹣2bc﹣2a2b2c2=0,1+a2bc=0,∴bc=﹣,设直线AB的解析式为:y=mx+n,则,解得,∴直线AB的解析式为:y=a(b+c)x﹣abc,当x=0时,y=OC=﹣abc=﹣a•(﹣)=;(2)如图2,过A作AD⊥y轴于D,设直线AB的解析式为:y=kx+b,当y=0时,kx+b=0,∴x=﹣,∴OC=﹣,∵过点A的直线AB恰好与此抛物线仅有一个交点,∴ax2=kx+b,∴ax2﹣kx﹣b=0,△=k2+4ab=0,∴b =﹣,OC =﹣=,∴x =,∵a >0,k >0,∴AD =,∵AD ∥OC , ∴==,∴AB =2BC ,∴AC =BC .14.解:(1)把B (﹣1,0),D (2,﹣2)代入y =ax 2﹣x +c 得, 解得:.故抛物线的解析式为y =x 2﹣x ﹣2;(2)当y =0时,x 2﹣x ﹣2=0,解得x 1=﹣1,x 2=3,∴A (3,0),∴AB =4,当x =0时,y =﹣2,∴C (0,﹣2),∴OC =2,∴S △ABC =×4×2=4,设AC 的解析式为y =kx +b ,把A (3,0),C (0,﹣2)代入y =kx +b 得, 解得.∴y =x ﹣2,如图1,过点E 作x 轴的垂线交直线AC 于点F ,设点F (a ,a ﹣2),点E (a ,a 2﹣a ﹣2),其中﹣1<a <3,∴S △ACE =EF |x A ﹣x C |=|a 2﹣a |=,∵S △ACE =S △ABC ,∴a 2﹣3a =2或﹣a 2+3a =2,解得a 1=(舍去),a 2=,a 3=1,a 4=2, ∴E 1(,),E 2(1,﹣),E 3(2,﹣2);(3)在y =ax 2+bx ﹣2中,当x =0时,y =﹣2,∴C (0,﹣2),∴OC =2,如图2,设P (0,m ),则PC =m +2,OA =3,AC ==,①当PA =CA 时,则OP 1=OC =2,∴P 1(0,2);②当PC =CA =时,即m +2=,∴m =﹣2, ∴P 2(0,﹣2); ③当PC =PA 时,点P 在AC 的垂直平分线上,则△AOC ∽△P 3EC , ∴=,∴P 3C =,∴m =,∴P 3(0,),④当PC =CA =时,m =﹣2﹣,∴P 4(0,﹣2﹣).综上所述,P点的坐标(0,2)或(0,﹣2)或(0,)或(0,﹣2﹣).15.解:(1)由已知可求B(6,0),C(0,4),将点B(6,0),C(0,4)代入y=﹣+bx+c,则有,解得,∴y=﹣x2+x+4,令y=0,则﹣x2+x+4=0,解得x=﹣1或x=6,∴A(﹣1,0);(2)∵点D在抛物线上,且横坐标为3,∴D(3,8),过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;∴E(0,8),F(6,8),∴S△BCD =S梯形ECBF﹣S△CDE﹣S△BFD=(EC+BF)×OB﹣×EC×ED﹣×DF×BF=×(4+8)×6﹣×4×3﹣×3×8=36﹣6﹣12=18;(3)设P(m,﹣m2+m+4),∵PQ垂直于x轴,∴Q(m,0),且∠PQO=90°,∵∠COB=90°,∴点A、P、Q为顶点的三角形与△BOC相似有两种情况:①△PAQ∽△CBO时,==,∴=,解得m=5或m=﹣1,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=5,∴P(5,4);②△PAQ∽△BCO时,==,∴=,解得m=﹣1或m=,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=,∴P(,);综上所述:P(5,4)或P(,)时,点A、P、Q为顶点的三角形与△BOC相似.。
中考数学专题训练第9讲二次函数2(原卷版)

二次函数题型一 二次函数的相关概念1.(2021·上海市洛川学校九年级期中)下列函数中.属于二次函数的是( )A .()()242 y x x x =-++B .()()213y x x =+-C .2y ax bx c =++D .42x y x= 2.(2021·山东·济南市莱芜实验中学九年级期中)若抛物线258(3)23mm y m x x -+=-+-是关于x 的二次函数.那么m 的值是( )A .3B .2-C .2D .2或33.(2021·山东省陵城区江山实验学校九年级月考)下列函数中不属于二次函数的是( )A .(1)(2)y x x =+-B .21(1)2y x =+C .222(2)2y x x =+-D .213y x =-4.(2021·北京海淀·九年级期中)如图.在ABC 中.90C ∠=︒.5AC =.10BC =.动点M .N 分别从A .C 两点同时出发.点M 从点A 开始沿边AC 向点C 以每秒1个单位长度的速度移动.点N 从点C 开始沿CB 向点B 以每秒2个单位长度的速度移动.设运动时间为t .点M .C 之间的距离为y .MCN △的面积为S .则y 与t .S 与t 满足的函数关系分别是( )A .正比例函数关系.一次函数关系B .正比例函数关系.二次函数关系C .一次函数关系.正比例函数关系D .一次函数关系.二次函数关系5.(2021·河北赵县·九年级月考)对于y =ax 2+bx +c .有以下四种说法.其中正确的是( ) A .当b =0时.y =ax 2+c 是二次函数 B .当c =0时.y =ax 2+bx 是二次函数C .当a =0时.y =bx +c 是一次函数D .以上说法都不对6.(2021·北京·首都师范大学附属中学九年级月考)边长为5的正方形ABCD .点F 是BC 上一动点.过对角线交点E 作EG ⊥EF .交CD 于点G .设BF 的长为x .△EFG 的面积为y .则y 与x 满足的函数关系是( )A .正比例函数B .一次函数C .二次函数D .以上都不是 7.(2021·北京海淀·二模)如图.一架梯子AB 靠墙而立.梯子顶端B 到地面的距离BC 为2m .梯子中点处有一个标记.在梯子顶端B 竖直下滑的过程中.该标记到地面的距离y 与顶端下滑的距离x 满足的函数关系是( )A .正比例函数关系B .一次函数关系C .二次函数关系D .反比例函数关系8.(2021·安徽·宣城市第六中学九年级期中)若函数y =(a ﹣1)x 2+2x +a 2﹣1是二次函数.则( )A .a ≠1B .a ≠﹣1C .a =1D .a =±19.以x 为自变量的函数:①(2)(2)y x x =+-.②2(2)y x =+.③2123y x x =+-.④()21y x x x =--.是二次函数的有( )A .②③B .②③④C .①②③D .①②③④ 10.(2021·湖南炎陵·九年级期末)已知二次函数y=(m+2)23m x -.当x<0时.y 随x 的增大而增大.则m 的值为( )A .5B 5C .5±D .211.(2021·湖北嘉鱼·九年级期末)下列各点中.一定不在抛物线222y mx mx =-+上的是( )A .(1.1)B .(2.2)C .(1.2)D .(1.3)12.(2021·浙江湖州·九年级月考)在抛物线245y x x =--上的一个点的坐标为( ) A .()0,4- B .()2,0 C .()1,0 D .()1,0-题型二 二次函数的图像与性质13.(2021·北京·景山学校九年级期中)抛物线y =(x ﹣3)2+1的顶点坐标是( ) A .(3.1) B .(3.﹣1) C .(﹣3.1) D .(﹣3.﹣1) 14.(2021·北京房山·九年级期中)已知二次函数2(2)6y x =--.当14x -≤≤时.y 的最小值为( )A .3B .0C .2-D .6-15.(2021·广东·珠海市九洲中学九年级期中)顶点(﹣5.﹣1).且开口方向、形状与函数y =13x 2的图象相同的抛物线是( )A .2153y x =-B .21(5)13y x =-+ C .21(5)13y x =-- D .21(5)13y x =+- 16.(2021·浙江·杭州市文晖中学九年级期中)对于二次函数y =﹣(x ﹣1)2+4的图象.下列说法正确的是( )A .开口向上B .顶点坐标是(﹣1.4)C .图象与y 轴交点的坐标是(0.4)D .函数有最大值417.(2021·吉林磐石·九年级期中)抛物线y =﹣x 2+3的顶点在( )A .x 轴上B .y 轴上C .第一象限D .第二象限 18.(2021·湖北江汉·九年级期中)已知抛物线y =ax 2+bx +c (a .b .c 为常数且a ≠0)经过P 1(1.y 1).P 2(2.y 2).P 3(3.y 3).P 4(4.y 4)四点.若y 3<y 2<y 1.则下列说法中正确的是( ) A .抛物线开口向下B .对称轴可能为直线x =3C .y 1>y 4D .5a +b >019.(2021·上海市洛川学校九年级期中)已知抛物线()222y ax x a =++-.a 是常数.且0a <.下列选项中可能是它大致图像的是( )A .B .C .D .20.(2021·安徽·宣城市第六中学九年级期中)关于二次函数228y x x =-.下列结论中正确的是( )A .图象与x 轴有两个交点B .当2x =时.y 有最大值8-C .当1x >时.y 随x 的增大而增大D .函数图象开口朝下21.(2021·山东·日照港中学九年级月考)已知二次函数2225y x bx b b =-++-(b 为常数)的图象与x 轴有交点.且当 3.5x <时.y 随x 的增大而减小.则b 的取值范围是( ) A .5b ≤ B .5b ≥ C .3.55b ≤≤ D .3.55b ≤< 22.(2021·北京十四中九年级期中)点()10,A y .()25,B y 在二次函数241y x x =-+的图象上.1y 与2y 的大小关系是( )A .12y y >B .12y y =C .12y y <D .无法比较 23.(2021·浙江·杭州市采荷中学九年级期中)已知二次函数y =2mx 2+(4﹣m )x .它的图象可能是( )A .B .C .D .24.(2021·福建·厦门市第十一中学九年级期中)将二次函数262y x x =+-化成()2y x h k =-+的形式应为( ) A .()237y x =++B .()311y x =-+C .()2311y x =+-D .()224y x =++题型三 二次函数图像与系数的关系25.(2021·山东嘉祥·九年级期中)如图.抛物线2y ax bx c =++的对称轴是1x =.下列结论:①0abc >.②240b ac ->.③a c b +>.④80a c +<.正确的有( )A .1个B .2个C .3个D .4个26.(2021·山东惠民·九年级期中)如图是二次函数2y ax bx c =++图象的一部分.该图象过点()5,0A -.对称轴为直线2x =-.下列结论:①0abc <.②420a b c -+>.③若()13,B y -与()24,C y -是抛物线上两点.则21y y >.④50a c +=.其中正确的有( )A .1个B .2个C .3个D .4个27.(2021·天津市第七中学九年级期中)已知抛物线2(0)y ax bx c a =++>的对称轴为直线1x =-.该抛物线与x 轴的一个交点为()1,0x .且101x <<.有下列结论:①0abc >②930a b c -+>③b a <④30a c +>.其中正确结论的个数是( )A .1B .2C .3D .428.(2021·山东·临沭县第五初级中学九年级月考)关于抛物线y =x 2﹣2x +1.下列说法错误的是( )A .开口向上B .与x 轴有两个重合的交点C .对称轴是直线x =1D .当x >1时.y 随x 的增大而减小 29.(2021·广东惠阳高级中学初中部九年级期中)如图所示.已知二次函数y =ax 2+bx +c 的图象与x 轴交于A 、B 两点.与y 轴交于点C .对称轴为直线x =1.直线y =﹣x +c 与抛物线y =ax 2+bx +c 交于C 、D 两点.D 点在x 轴下方且横坐标小于3.则下列结论:①2a +b +c >0.②a ﹣b +c <0.③ax 2﹣a ≥b ﹣bx .④a <﹣1.其中正确的有( )A .4个B .3个C .2个D .1个30.(2021·广东·珠海市九洲中学九年级期中)如图.二次函数y =ax 2+bx 的图象经过点P .若点P 的横坐标为﹣1.则一次函数y =(a ﹣b )x +b 的图象大致是( )A .B .C .D .31.(2021·云南·云大附中九年级期中)已知反比例函数b y x=的图象如图所示.则一次函数y cx a =+和二次函数2y ax bx c =++在同一直角坐标系中的图象可能是( )A .B .C .D .32.(2021·山东南区·九年级期末)在同一平面直角坐标系中.二次函数y =ax 2+bx .一次函数y =ax +b 和反比例函数y ab x =的图象可能是( )A.B.C.D.33.(2021·山东·青岛大学附属中学二模)一次函数y=ax+b与反比列函数y=cx的图象如图所示.则二次函数y=ax2+bx+c的大致图象是()A.B.C .D .34.(2021·山东·青岛实验学校九年级期末)已知二次函数21y ax bx c =++和22y bx ax c =++.a b >.则下列说法正确的是( )A .当0x <时.12y y <B .当01x <<时.12y y <C .当01x <<时.12y y >D .当1x >时12y y <35.(2021·安徽淮南·九年级月考)在同一平面直角坐标系中.函数y =ax 2+b 与y =bx 2+ax 的图象可能是( )A .B .C .D . 36.(2021·广东·汕头市龙湖实验中学九年级期中)如图.抛物线2(0)y ax bx c a =++≠的顶点为(1,)n .与x 轴的一个交点(3,0)B .与y 轴的交点在(0,3)-和(0,2)-之间.下列结论中:①0ab c>.②22()0a c b +-=.③22c a n -<.则正确的个数为( )A .0B .1C .2D .3题型四 二次函数的对称性与最值37.(2021·广东·广州市南武中学九年级期中)二次函数y =ax 2+bx +c 的图象如图所示.则该二次函数的顶点坐标为( )A .(1.3)B .(0.1)C .(0.—3)D .(2.1) 38.(2021·广东·珠海市九洲中学九年级期中)已知二次函数y =ax 2+bx +c (a ≠0)图象上部分点的坐标(x .y )的对应值如表所示.则方程ax 2+bx +2.32=0的根是( ) x …… 0 5 4 …… y …… 0.32 ﹣2 0.32 ……A .0或4B .1或5C .5或4﹣5D .5或5﹣2 39.(2021·陕西·安康高新区初级中学(汉滨初中高新校区)九年级期中)已知点()11,A y -、()23,B y -、()32,C y 均在抛物线22y x x m =-+-上.则1y .2y .3y 的大小关系是( ) A .123y y y >> B .231y y y >> C .213y y y >> D .312y y y >>40.(2021·山西·九年级期中)如果三点()()1122,1,1,P y P y -和()335,P y 在抛物线25y x x c =-++的图象上.那么123,,y y y 之间的大小关系是( )A .312y y y <<B .231y y y <<C .132y y y <<D .321y y y <<41.(2021·四川·江油外国语学校九年级月考)已知抛物线和直线l 在同一直角坐标系中的图象如图所示.抛物线的对称轴为直线x =﹣1.P 1(x 1.y 1)、P 2(x 2.y 2)是抛物线上的点.P 3(x 3.y 3)是直线l 上的点.且﹣1<x 1<x 2.x 3<﹣1.则y 1、y 2、y 3的大小关系为( )A .y 1>y 2>y 3B .y 2>y 1>y 3C .y 3>y 1>y 2D .y 3>y 2>y 142.(2021·湖北武昌·九年级月考)若点(2.5).(4.5)在抛物线y =ax 2+bx +c 上.则它的对称轴是( ) A .x =0B .x =1C .x =2D .x =343.(2021·福建福州·九年级期末)二次函数y =x 2+2bx +4c 的图象与x 轴的两个交点的横坐标分别为x 1.x 2.且x 1>1.x 2-x 1=4.当1≤x ≤3时.该函数的最小值为m .则m 与b .c 的数量关系是( ) A .m =1+2b +4c B .m =4+4b +4c C .m =9+6b +4cD .m =-b 2+4c44.(2021·福建省泉州实验中学九年级期中)若二次函数2y ax bx c =++的图象经过()11,A x y 、()22,B x y 、()2,C m n -、()()1,D m n y n ≠则下列命题正确的是( )A .若0a >且1211x x ->-.则12y y <B .若0a <且12y y <.则1211x x -<-C .若1211x x ->-且12y y >.则0a <D .若()12122x x x x +=≠.则//AB CD45.(2021·浙江平阳·九年级期中)二次函数221y x x =-++.当12x -≤≤时.下列说法正确的是( )A .有最大值1.有最小值-2B .有最大值2.有最小值-2C .有最大值1.有最小值-1D .有最大值2.有最小值146.(2021·湖北十堰·九年级期中)若二次函数24y mx x m =-+有最大值-3.则m 等于( ) A .4m =B .1m =或-4C .4m =-D .1m =47.(2021·辽宁台安·九年级月考)函数21215555y x x =---的最大值是( )A .15-B .155C .5-D .155-48.(2021·江苏·南闸实验学校九年级月考)如图.矩形ABCD 中.AB =8.AD =4.E 为边BC 上一个动点.连接AE .取AE 的中点G .点G 绕点E 顺时针旋转90°得到点F .连接DF 、DE .EFD 面积的最小值是( )A .15B .16C .14D .12题型五 二次函数的解析式与图像平移49.(2021·广东海珠·九年级期中)已知二次函数的图象的顶点是(1,2)-.且经过点(0,5)-.则二次函数的解析式是( ). A .23(1)2y x =-+-B .23(1)2y x =+-C .23(1)2y x =---D .23(1)2=--y x50.(2021·安徽·合肥蜀山行知学校九年级期中)已知抛物线与二次函数y =2x 2的图象的开口大小相同.开口方向相反.且顶点坐标为(﹣1.2021).则该抛物线对应的函数表达式为( )A .y =﹣2(x ﹣1)2 +2021B .y =2(x ﹣1)2 +2021C .y =﹣2(x +1)2+2021D .y =2(x +1)2+202151.(2021·福建·龙岩市第五中学九年级月考)设函数y =a (x ﹣h )2+k (a .h .k 是实数.a ≠0).当x =1时.y =1.当x =6时.y =6.( ) A .若h =2.则a <0 B .若h =3.则a >0 C .若h =4.则a>0D .若h =5.则a >052.(2021·浙江·杭州市公益中学九年级开学考试)已知抛物线2y ax bx =+经过点(3,3)A --.且该抛物线的对称轴经过点A .则该抛物线的解析式为( )A .2123y x x =--B .2123y x x =-+C .2123yx xD .2123y x x =+53.(2021·四川巴中·中考真题)已知二次函数y =ax 2+bx +c 的自变量x 与函数y 的部分对应值见表格.则下列结论:①c =2.②b 2﹣4ac >0.③方程ax 2+bx =0的两根为x 1=﹣2.x 2=0.④7a +c <0.其中正确的有( ) x … ﹣3 ﹣2 ﹣1 1 2 … y …1.875 3m1.875…54.(2021·湖南绥宁·九年级期末)在平面直角坐标系中.如果点P 的横坐标与纵坐标相等.则称点P 为和谐点.例如:点P (1.1)、(﹣2.﹣2)、(0.5.0.5)….都是和谐点.若二次函数y =ax 2+7x +c (a ≠0)的图象上有且只有一个和谐点(﹣1.﹣1).则此二次函数的解析式为( ) A .y =3x 2+7x +3B .y =2x 2+7x +4C .y =x 2+7x +5D .y =4x 2+7x +255.(2021·湖南长沙·模拟预测)如图.是抛物线21y ax bx c =++(0a ≠)图象的一部分.抛物线的顶点坐标是A (1.3).与x 轴的一个交点B (4.0).直线2y mx n =+(0m ≠)与抛物线交于A .B 两点.下列结论:①20a b +=. ②抛物线与x 轴的另一个交点是(2-.0).③方程23ax bx c ++=有两个相等的实数根.④当时14x <<.有21y y <.⑤若221122ax bx ax bx +=+.且12x x ≠.则121x x =+.则命题正确的个数为( )A .5个B .4个C .3个D .2个56.(2021·天津津南·九年级期中)把抛物线21(2)12y x =+-向上平移2个单位长度.则平移后抛物线的解析式是( )A .2112y x =-B .21(2)2y x =+C .21(2)12y x =++ D .21(4)12y x =+-57.(2021·山东惠民·九年级期中)在平面直角坐标系中.将抛物线244y x x =--向左平移3个单位.再向上平移5个单位.得到抛物线的表达式为( ) A .()2113y x =+- B .()2513y x =-- C .()253y x =--D .()213y x =+-58.(2021·浙江·杭州市采荷中学九年级期中)将抛物线y =3x 2的图象先向右平移2个单位.再向上平移5个单位后.得到的抛物线解析式是( ) A .y =3(x ﹣2)2﹣5 B .y =3(x ﹣2)2+5 C .y =3(x +2)2﹣5D .3(x +2)2+559.(2021·广东·广州市第九十七中学九年级期中)抛物线22y x =-向左平移2个单位长度.再向下平移3个单位长度后得到的抛物线解析式为( ) A .()2223y x =-+- B .()2223y x =--- C .()2223y x =-++D .()2223y x =--+.60.(2021·辽宁连山·九年级月考)如图.在平面直角坐标系中.二次函数212y x b =-+的图象经过正方形ABOC 的顶点A .B .C .且A 点为其顶点.将该抛物线经过平移.使其顶点为C 点.则平移后抛物线的表达式为( )A .21(2)22y x =--+B .21(2)22y x =-++ C .22(2)2y x =-+- D .22(2)2y x =--+题型六 二次函数与一元二次方程61.(2021·黑龙江·鸡西市第一中学校九年级期中)如果二次函数2y ax bx c =++中.有0a b c -+=.那么二次函数图像一定经过的点是( )A .(1,0)B .(1,0)-C .(0,1)-D .(0,1)62.(2021·山东费县·九年级期中)抛物线221y x x =-+与坐标轴的交点个数为( )A .0个B .1个C .2个D .3个63.(2021·北京市大兴区第三中学九年级期中)如图.抛物线y =ax 2+bx +c (a ≠0)的对称轴为直线x =1.与x 轴的一个交点坐标为(﹣1.0).其部分图象如图所示.下列结论: ①4ac <b 2.②方程ax 2+bx +c =0的两个根是x 1=﹣1.x 2=3. ③3a +c >0④当y >0时.x 的取值范围是﹣1≤x <3.其中结论正确的个数是( )A .4个B .3个C .2个D .1个64.(2021·安徽·蒙城县第六中学九年级期中)若抛物线y =ax 2+bx +c 与x 轴两个交点之间的距离为10.且4a +b =0.则关于x 的方程ax 2+bx +c =0的根为( ) A .x 1=﹣7.x 2=3B .x 1=﹣6.x 2=4C .x 1=6.x 2=﹣4D .x 1=7.x 2=﹣365.(2021·天津市南开田家炳中学九年级月考)已知抛物线212y x x =-.它与x 轴的两个交点间的距离为( ) A .0B .1C .2D .466.(2021·安徽合肥·九年级月考)已知抛物线y=x2-x-1.与x轴的一个交点为(m.0).则代数式m2-m+2021的值为()A.2019 B.2020 C.2021 D.2022 67.(2021·河北·育华中学九年级月考)如图.点A.B的坐标分别为(1.4)和(4.4).抛物线y=a(x﹣m)2+n的顶点在线段AB上运动.与x轴交于C、D两点(C在D的左侧).点C的横坐标最小值为﹣3.则点D的横坐标最大值为()A.13 B.7 C.5 D.8 68.(2021·广东·珠海市九洲中学九年级期中)抛物线y=x2+4x﹣m2+2(m是常数)与坐标轴交点的个数为()A.0 B.1 C.3 D.2或3 69.(2021·湖北武昌·九年级月考)抛物线y=x2﹣2x+1与坐标轴的交点个数是()A.0 B.1 C.2 D.3 70.(2021·陕西·交大附中分校模拟预测)将抛物线y=x2+2mx+m2﹣1向左平移8个单位.平移后的抛物线对称轴为直线x=1.则平移后的抛物线与y轴的交点坐标为()A.(0.0) B.(0.4) C.(0.15) D.(0.16) 71.(2021·天津·南开翔宇学校九年级开学考试)如图.已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1.0).与y轴的交点B在(0.﹣2)和(0.﹣1)之间(不包含这两点).对称轴为直线x=1.在下列结论中:①abc>0.②16a+4b+c<0.③4ac﹣b2<8a.④13<a<23.⑤b<c.正结论的个数为()A.1 B.2 C.3 D.4 72.(2021·广东·佛山市华英学校九年级月考)根据表格对应值:x 1.1 1.2 1.3 1.4 ax 2+bx +c﹣0.590.842.293.76判断关于x 的方程ax 2+bx +c =3的一个解x 的范围是( ) A .1.1<x <1.2B .1.2<x <1.3C .1.3<x <1.4D .无法判定题型七 二次函数与不等式73.(2021·广东·广州市第九十七中学九年级期中)如图.直线1y x b =-+与抛物线()220y ax a =≠交于点A (-2.4).B (1.1).若12y y <.则x 的取值范围是( )A .2x <-B .21x -<<C .2x <-或1x >D .1x >74.(2021·吉林·长春市第八十七中学九年级月考)二次函数y =ax 2+bx +c (a ≠0)的部分图象如图所示.它与x 轴的一个交点坐标为(﹣3.0).当y >0时.则x 的取值范围是( )A .x <﹣3B .x >1C .﹣3<x <1D .x <﹣3或x >175.二次函数y =a x 2+bx +c 的图象如图所示.且方程a x 2+bx +c =k 有两个不相等的实数根.则k 的取值范围是( )A .k <2B .k ≤2C .k <3D .1<k <376.(2021·江苏·苏州高新区实验初级中学九年级月考)如图.反比例函数4y x=的图象和二次函数23y x x =+图象交于点()1,4A .则不等式32340x x +->的解集为( )A .1x >B .01x <<C .0x <D .1x >或0x <77.(2021·山东济南·二模)已知函数227y x ax =-+.当3x ≤时.函数值随x 增大而减小.且对任意的112x a ≤≤+和212x a ≤≤+.1x .2x 相应的函数值1y .2y 总满足129y y -≤.则实数a 的取值范围是( ) A .34a -≤≤B .35a -≤≤C .34a ≤≤D .35a ≤≤78.(2021·山东·胶州市初级实验中学模拟预测)函数2y x bx c =++与y x =的图象如图所示.下面结论:①240b c ->.②10b c ++=.③360b c ++=.④当13x <<时.()210x b x c +-+<.其中正确的是( )A .②③④B .③④C .①②③④D .①79.(2021·福建·厦门市槟榔中学九年级期中)已知二次函数y =x 2+bx +1当102x <<的范围内.都有y ≥0.则b 的取值范围是( ) A .b ≥0B .b ≥﹣2C .b ≥﹣52D .b ≥﹣380.(2021·浙江杭州·九年级期中)若二次函数2y x bx c =-++中函数y 与自变量x 之间的部分对应值如下表x … 0 1 2 3 … y…1-232…点()11,A x y 点()22,B x y 在该函数图象上.当12101,23,x x y <<<<与2y 的大小关系是( ) A .12y y <B .12y y >C .12y y ≥D .12y y ≤81.(2021·江苏建湖·二模)如图为某二次函数的部分图像.有如下四个结论:①此二次函数表达式为y =14x 2﹣x +9:②若点B (﹣1.n )在这个二次函数图像上.则n >m .③该二次函数图像与x 轴的另一个交点为(﹣4.0).④当0<x <5.5时.m <y <8.所有正确结论的序号是( )A .①③B .①④C .②③D .②④82.(2021·陕西·安康高新区初级中学(汉滨初中高新校区)九年级期中)如图.抛物线()20y ax bx c a =++≠的对称轴为直线1x =.与x 轴的一个交点坐标为(-1.0).其图象如图所示.下列结论:①0abc >.②24ac b <.③方程20ax bx c ++=的两个根是11x =-.23x =.④30a c +>.⑤当0y >时.x 的取值范围是13x .⑥()a b m am b +>+(1m ≠.m 为实数).其中结论正确的个数是( )A .4个B .3个C .2个D .1个83.(2021·浙江·杭州市余杭区维翰学校九年级月考)已知函数y 1=ax 2+bx +c 与函数y 2=kx +b 的图象大致如图所示.若y 1<y 2.则自变量x 的取值范围是( )A .﹣2<x <32B .x >2或x <﹣32C .x <﹣2或x >32D .﹣32<x <284.(2021·重庆云阳·九年级月考)如图是抛物线y 1=ax 2+bx +c (a ≠0)图象的一部分.抛物线的顶点坐标A (1.3).与x 轴的一个交点B (4.0).直线y 2=mx +n (m ≠0)与抛物线交于A .B 两点.下列结论:①2a +b =0.②abc >0.③方程ax 2+bx +c =3有两个相等的实数根.④抛物线与x 轴的另一个交点是(﹣1.0).⑤当1<x <4时.有y 2<y 1.其中正确结论的个数是( )A .5B .4C .3D .2题型八 二次函数综合85.(2021·黑龙江·鸡西市第一中学校九年级期中)已知抛物线()230y ax bx a =++≠交x轴于(1,0)A 和(3,0)B -.交y 轴于C .(1)求抛物线的解析式.(2)D 是抛物线的顶点.P 为抛物线上的一点(不与D 重合).当PAB ABD S S ∆∆=时.求P 的坐标.86.(2021·广东·广州市南武中学九年级期中)如图.已知抛物线的顶点为A (1.4).抛物线与y 轴交于点B (0.3).与x 轴交于C 、D 两点. (1)求此抛物线的解析式. (2)求△BCD 的面积.87.(2021·吉林·九年级期中)如图.在平面直角坐标系中.过原点的抛物线的顶点M 的坐标为()1,1--.点A 的坐标为()1,1.以OA 为边的菱形OABC 的顶点C 在x 轴的正半轴上.把菱形OABC 沿AB 向上翻折得到菱形EABD . (1)求抛物线对应的函数关系式.(2)若把抛物线向右平移使抛物线经过点D .求平移的距离.88.(2021·甘肃·平凉市第十中学九年级期中)如图.已知顶点是M的抛物线()230y ax bx a=+-≠与x轴交于()1,0A-.()3,0B两点.与y轴交于点C.(1)求抛物线对应的函数解析式.(2)点P是x轴上方抛物线上的一点.若PAB△的面积等于3.求点P的坐标.(3)是否在y轴存在一点Q.使得QBM为直角三角形?若存在.求出Q的坐标.若不存在.说明理由.89.(2021·吉林·长春市第八十七中学九年级月考)在平面直角坐标系中.函数y=x2﹣ax+2a﹣2(a为常数)与y轴交于点A.(1)当函数图象经过点(1.0)时.①求此函数的表达式并写出当y随x的增大而增大时.自变量x的取值范围.②此时函数有最值为.(2)已知点M(1.2)、N(3.2).连结M、N.若函数y=x2﹣ax+2a﹣2(a为常数)的图像与线段MN只有一个交点.直接写出a的取值范围.90.(2021·河南·息县教育体育局基础教育教学研究室九年级月考)已知二次函数2 13y x bx=+-的图象与直线21y x=+交于点()1,0A-和点()4,B m.(1)求1y 的表达式和m 的值.(2)当12y y 时.则自变量x 的取值范围为__________.(3)将直线AB 沿y 轴上下平移.当平移后的直线与抛物线只有一个公共点时.求平移后的直线表达式.。
中考数学二次函数a-b-c符号问题---讲解例题
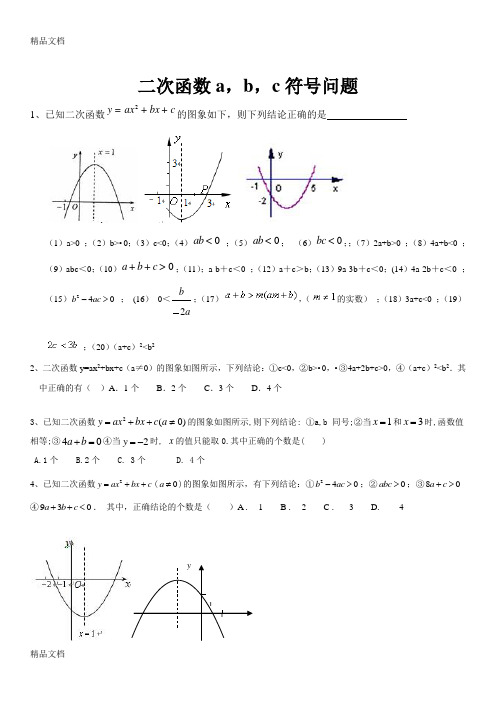
精品文档二次函数a ,b ,c 符号问题1、已知二次函数2y ax bx c =++的图象如下,则下列结论正确的是(1)a>0 ;(2)b>•0;(3)c<0;(4)0ab < ;(5)0ab <; (6)0bc <;;(7)2a+b>0 ;(8)4a+b<0 ;(9)abc <0;(10)0a b c ++>;(11);a-b +c <0 ;(12)a +c >b ;(13)9a-3b +c <0;(14)4a-2b +c <0 ;(15)240b ac -> ; (16) 0<a b 2;(17),(的实数) ;(18)3a+c<0 ;(19);(20)(a+c )2<b 22、二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,下列结论:①c<0,②b>•0,•③4a+2b+c>0,④(a+c )2<b 2.其中正确的有( )A .1个 B .2个 C .3个 D .4个3、已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( )A.1个B.2个C. 3个D. 4个4、已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列结论:①240b ac ->;②0abc >;③80a c +> ④930a b c ++<. 其中,正确结论的个数是( )A . 1 B . 2 C . 3 D . 411O y精品文档 5、已知二次函数2y ax bx c =++的图象如图所示,有以下结论:①0a b c ++<;②1a b c -+>;③0abc >;④420a b c -+<;⑤1c a ->其中所有正确结论的序号是( )A .①②B . ①③④C .①②③⑤D .①②③④⑤。
中考数学:二次函数的推理计算与证明综合问题真题+模拟(原卷版北京专用)

中考数学二次函数的推理计算与证明综合问题【方法归纳】据北京历年中考题型来推测,二次函数的压轴题目多数会以参数的形式出现的,难度之大,可想而知。
在解决含参数二次函数的题目时,通常先观察解析式,看能否求出对称轴,图像与坐标轴交点能否用参数来表示?根据设出点的坐标可求出相应的线段,然后观察题意,再考虑我们所学过的知识点(勾股,相似等)能否用上.常用的二次函数的基础知识有:1.几种特殊的二次函数的图象特征如下:2.用待定系数法求二次函数的解析式:(1)一般式:(a≠0).已知图象上三点或三对x 、y 的值,通常选择一般式.(2)顶点式:(a≠0).已知图象的顶点或对称轴,通常选择顶点式. (可以看成的图象平移后所对应的函数.)(3)交点式:已知图象与x 轴的交点坐标x 1、x 2,通常选用交点式:(a≠0).(由此得根与系数的关系:,). 3. 二次函数图象和一元二次方程的关系:【典例剖析】【例1】(2021·北京·中考真题)在平面直角坐标系xOy 中,点(1,m )和点(3,n )在抛物线y=2y ax bx c =++()2y a x h k =-+2y ax =()()12y a x x x x =--12b x x a +=-12c x x a⋅=ax2+bx(a>0)上.(1)若m=3,n=15,求该抛物线的对称轴;(2)已知点(−1,y1),(2,y2),(4,y3)在该抛物线上.若mn<0,比较y1,y2,y3的大小,并说明理由.【例2】(2022·北京·中考真题)在平面直角坐标系xOy中,点(1,m),(3,n)在抛物线y=ax2+ bx+c(a>0)上,设抛物线的对称轴为x=t.(1)当c=2,m=n时,求抛物线与y轴交点的坐标及t的值;(2)点(x0,m)(x0≠1)在抛物线上,若m<n<c,求t的取值范围及x0的取值范围.【真题再现】1.(2013·北京·中考真题)在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0))与轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标;(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;(3)若该抛物线在-2<x<-1这一段位于直线l的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式.2.(2014·北京·中考真题)在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,−2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点)CD与图象G有公共点,结合函数图像,求点D纵坐标t的取值范围.3.(2015·北京·中考真题)在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.(1)求点A,B的坐标;(2)求抛物线C1的表达式及顶点坐标;(3)若拋物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.4.(2016·北京·中考真题)在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.(1)求抛物线的顶点坐标;(2)横、纵坐标都是整数的点叫做整点.①当m=1时,求线段AB上整点的个数;②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.5.(2017·北京·中考真题)在平面直角坐标系xOy中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B的左侧),与y轴交于点C.(1)求直线BC的表达式;(2)垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC交于点N(x3,y3),若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.6.(2018·北京·中考真题)在平面直角坐标系xOy中,直线y=4x+4与x轴、y轴分别交于点A,B,抛物线y=ax2+bx−3a经过点A,将点B向右平移5个单位长度,得到点C.(1)求点C的坐标;(2)求抛物线的对称轴;(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.7.(2019·北京·中考真题)在平面直角坐标系xOy中,抛物线y=ax2+bx−1a与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示);(2)求抛物线的对称轴;(3)已知点P(12,−1a),Q(2,2).若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.8.(2020·北京·中考真题)在平面直角坐标系xOy中,M(x1,y1),N(x2,y2)为抛物线y=ax2+ bx+c(a>0)上任意两点,其中x1<x2.(1)若抛物线的对称轴为x=1,当x1,x2为何值时,y1=y2=c;(2)设抛物线的对称轴为x=t.若对于x1+x2>3,都有y1<y2,求t的取值范围.【模拟精练】一、解答题(共30题)1.(2022·北京市广渠门中学模拟预测)已知抛物线y=ax2+2ax+3a2−4(a≠0)(1)该抛物线的对称轴为_____________;(2)若该抛物线的顶点在x轴上,求a的值;(3)设点M(m,y1),N(2,y2)该抛物线上,若y1>y2,求m的取值范围.2.(2022·北京·二模)在平面直角坐标系xOy中,抛物线y=x2−2mx.(1)当抛物线过点(2,0)时,求抛物线的表达式;(2)求这个二次函数的顶点坐标(用含m的式子表示);(3)若抛物线上存在两点A(m−1,y1)和B(m+2,y2),其中m>0.当y1⋅y2>0时,求m的取值范围.3.(2022·北京昌平·二模)在平面直角坐标系xOy中,已知抛物线y=ax2+bx−1(a>0).(1)若抛物线过点(4,−1).①求抛物线的对称轴;②当−1<x<0时,图像在x轴的下方,当5<x<6时,图像在x轴的上方,在平面直角坐标系中画出符合条件的图像,求出这个抛物线的表达式;(2)若(−4,y1),(−2,y2),(1,y3)为抛物线上的三点且y3>y1>y2,设抛物线的对称轴为直线x=t,直接写出t的取值范围.4.(2022·北京房山·二模)在平面直角坐标系xOy中,点A(2,−1)在二次函数y=x2−(2m+ 1)x+m的图象上.(1)直接写出这个二次函数的解析式;(2)当n≤x≤1时,函数值的取值范围是−1≤y≤4−n,求n的值;(3)将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x−ℎ)2+k,当x<2时,y随x的增大而减小,求k的取值范围.5.(2022·北京朝阳·二模)在平面直角坐标系xOy中,已知抛物线y=x2+(a+2)x+2a.(1)求抛物线的对称轴(用含a的式子表示);(2)若点(-1,y1),(a,y2),(1,y3)在抛物线上,且y1<y2<y3,求a的取值范围.6.(2022·北京东城·二模)在平面直角坐标系xOy中,抛物线y=ax2+bx+1(a≠0)的对称轴是直线x=3.(1)直接写出抛物线与y轴的交点坐标;(2)求抛物线的顶点坐标(用含a的式子表示);(3)若抛物线与x轴相交于A,B两点,且AB≤4,求a的取值范围.7.(2022·北京平谷·二模)在平面直角坐标系xOy中,点(−1,y1)、(1,y2)、(3,y3)是抛物线y=x2+bx+1上三个点.(1)直接写出抛物线与y轴的交点坐标;(2)当y1=y3时,求b的值;(3)当y3>y1>1>y2时,求b的取值范围.8.(2022·北京四中模拟预测)在平面直角坐标系xOy中,已知抛物线y=x2−2tx+t2−t.(1)求抛物线的顶点坐标(用含t的代数式表示);(2)点P(x1,y1),Q(x2,y2)在抛物线上,其中t−1≤x1≤t+2,x2=1−t.①若y1的最小值是−2,求y1的最大值;②若对于x1,x2,都有y1<y2,直接写出t的取值范围.9.(2022·北京丰台·二模)在平面直角坐标系xOy中,已知抛物线y=x2−2ax−3.(1)求该抛物线的对称轴(用含a的式子表示)(2)A(x1,y1),B(x2,y2)为该抛物线上的两点,若x1=1−2a,x2=a+1,且y1>y2,求a的取值范围.10.(2022·北京密云·二模)已知二次函数y=ax2+bx+2的图象经过点(1,2).(1)用含a的代数式表示b;(2)若该函数的图象与x轴的一个交点为(−1,0),求二次函数的解析式;(3)当a<0时,该函数图象上的任意两点P(x1,y1)、Q(x2,y2),若满足x1=−2,y1>y2,求x2的取值范围.11.(2022·北京大兴·二模)关于x的二次函数y1=x2+mx的图象过点(−2,0).(1)求二次函数y1=x2+mx的表达式;(2)已知关于x的二次函数y2=−x2+2x,一次函数y3=kx+b(k≠0),在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≥y3≥y2均成立.①求b的值;②直接写出k的值.12.(2022·北京顺义·xOy中,已知抛物线y=x2+mx+n.(1)当m=−3时,①求抛物线的对称轴;②若点A(1,y1),B(x2,y2)都在抛物线上,且y2<y1,求x2的取值范围;(2)已知点P(−1,1),将点P向右平移3个单位长度,得到点Q.当n=2时,若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.13.(2022·北京市十一学校模拟预测)已知二次函数y=ax2−4ax−3的图象与x轴交于A、B两点(点A在点B的左侧),顶点为D.(1)直接写出函数图象的对称轴:_____;(2)若△ABD是等腰直角三角形,求a的值;(3)当−1≤x≤k(2≤k≤6)时,y的最大值m减去y的最小值n的结果不大于3,求a的取值范围.14.(2022·北京房山·二模)已知二次函数y=ax2−4ax.(1)二次函数图象的对称轴是直线x=__________;(2)当0≤x≤5时,y的最大值与最小值的差为9,求该二次函数的表达式;(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t−1≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.15.(2022·北京海淀·二模)在平面直角坐标系xOy中,点(m – 2, y1),(m, y2),(2- m, y3)在抛物线y = x2-2ax + 1上,其中m≠1且m≠2.(1)直接写出该抛物线的对称轴的表达式(用含a的式子表示);(2)当m = 0时,若y1= y3,比较y1与y2的大小关系,并说明理由;(3)若存在大于1的实数m,使y1>y2>y3,求a的取值范围.16.(2022·北京西城·二模)在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点(0,−2),(2,−2).(1)直接写出c的值和此抛物线的对称轴;(2)若此抛物线与直线y=−6没有公共点,求a的取值范围;(3)点(t,y1),(t+1,y2)在此抛物线上,且当−2≤t≤4时,都有|y2−y1|<7.直接写出a2的取值范围.17.(2022·北京东城·一模)在平面直角坐标系xOy中,抛物线y=x2−2mx+m2+1与y 轴交于点A.点B(x1,y1)是抛物线上的任意一点,且不与点A重合,直线y=kx+b(k≠0)经过A,B两点.(1)求抛物线的顶点坐标(用含m的式子表示);(2)若点C(m−2,a),D(m+2,b)在抛物线上,则a_______b(用“<”,“=”或“>”填空);(3)若对于x1<−3时,总有k<0,求m的取值范围.18.(2022·北京市十一学校二模)在平面直角坐标系xOy中,点A(t,2)(t≠0)在二次函数y=ax2+bx+2(a≠0)的图象上.(1)当t=4时,求抛物线对称轴的表达式;(2)若点B(5−t,0)也在这个二次函数的图象上.①当这个函数的最小值为0时,求t的值;②若在0≤x≤1时,y随x的增大而增大,求t的取值范围.19.(2022·北京石景山·一模)在平面直角坐标xOy中,点(4,2)在抛物线y=ax2+bx+2(a>0)上.(1)求抛物线的对称轴;(2)抛物线上两点P(x1,y1),Q(x2,y2),且t<x1<t+1,4−t<x2<5−t.①当t=3时,比较y1,y2的大小关系,并说明理由;2②若对于x1,x2,都有y1≠y2,直接写出t的取值范围.20.(2022·北京大兴·一模)在平面直角坐标系xOy中,已知关于x的二次函数y=x2−2ax+ 6.(1)若此二次函数图象的对称轴为x=1.①求此二次函数的解析式;②当x≠1时,函数值y______5(填“>”,“<”,或“≥”或“≤”);(2)若a<−2,当−2≤x≤2时,函数值都大于a,求a的取值范围.21.(2022·北京·东直门中学模拟预测)在平面直角坐标系xOy中,抛物线y=ax2−(a+ 4)x+3经过点(2,m).(1)若m=−3,①求此抛物线的对称轴;②当1<x<5时,直接写出y的取值范围;(2)已知点(x1,y1),(x2,y2)在此抛物线上,其中x1<x2.若m>0,且5x1+5x2≥14,比较y1,y2的大小,并说明理由.22.(2022·北京市燕山教研中心一模)在平面直角坐标系xOy中,抛物线y=ax2+bx+3a(a≠0)与x轴的交点为点A(1,0)和点B.(1)用含a的式子表示b;(2)求抛物线的对称轴和点B的坐标;(3)分别过点P(t,0)和点Q(t+2,0)作x轴的垂线,交抛物线于点M和点N,记抛物线在M,N之间的部分为图象G(包括M,N两点).记图形G上任意一点的纵坐标的最大值是m,最小值为n.①当a=1时,求m−n的最小值;②若存在实数t,使得m−n=1,直接写出a的取值范围.23.(2022·北京平谷·一模)在平面直角坐标系xOy中,抛物线y=x2﹣2bx.(1)当抛物线过点(2,0)时,求抛物线的表达式;(2)求这个二次函数的对称轴(用含b的式子表示);(3)若抛物线上存在两点A(b﹣1,y1)和B(b+2,y2),当y1•y2<0时,求b的取值范围.24.(2022·北京门头沟·一模)在平面直角坐标系xOy中,已知抛物线y=−x2+2mx−m2+ m−2(m是常数).(1)求该抛物线的顶点坐标(用含m代数式表示);(2)如果该抛物线上有且只有两个点到直线y=1的距离为1,直接写出m的取值范围;(3)如果点A(a,y1),B(a+2,y2)都在该抛物线上,当它的顶点在第四象限运动时,总有y1>y2,求a的取值范围.25.(2022·北京房山·一模)已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(1,0)与点C(0,-3),其顶点为P.(1)求二次函数的解析式及P点坐标;(2)当m≤x≤m+1时,y的取值范围是-4≤y≤2m,求m的值.26.(2022·北京朝阳·一模)在平面直角坐标系xOy中,点(−2,0),(−1,y1),(1,y2),(2,y3)在抛物线y=x2+bx+c上.(1)若y1=y2,求y3的值;(2)若y2<y1<y3,求y3值的取值范围.27.(2022·北京市第一六一中学分校一模)在平面直角坐标系xOy中,直线l1:y=﹣2x+6与y轴交于点A,与x轴交于点B,二次函数的图象过A,B两点,且与x轴的另一交点为点C,BC=2;(1)求点C的坐标;(2)对于该二次函数图象上的任意两点P1(x1,y1),P2(x2,y2),当x1>x2>2时,总有y1>y2.①求二次函数的表达式;②设点A在抛物线上的对称点为点D,记抛物线在C,D之间的部分为图象G(包含C,D 两点).若一次函数y=kx﹣2(k≠0)的图象与图象G有公共点,结合函数图象,求k的取值范围.28.(2022·北京顺义·一模)在平面直角坐标系xOy中,点(2,−2)在抛物线y=ax2+bx−2(a<0)上.(1)求该抛物线的对称轴;(2)已知点(n−2,y1),(n−1,y2),(n+1,y3)在抛物线y=ax2+bx−2(a<0)上.若0<n< 1,比较y1,y2,y3的大小,并说明理由.29.(2022·北京海淀·一模)在平面直角坐标系xOy中,二次函数y=ax2−2ax(a≠0)的图象经过点A(−1,3).(1)求该二次函数的解析式以及图象顶点的坐标;(2)一次函数y=2x+b的图象经过点A,点(m,y1)在一次函数y=2x+b的图象上,点(m+4,y2)在二次函数y=ax2−2ax的图象上.若y1>y2,求m的取值范围.30.(2022·北京市第七中学一模)在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在抛物线y=−x2+(2a−2)x−a2+2a上,其中x1<x2.(1)求抛物线的对称轴(用含a的式子表示);(2)①当x=a时,求y的值;②若y1=y2=0,求x1的值(用含a;(3)若对于x1+x2<−5,都有y1<y2,求a的取值范围.。
九年级数学 第二章 二次函数检测题

第二章 二次函数检测题 班级: 姓名:(试卷满分为150分,考试时间为120分钟.)一、选择题(本大题共12小题,每小题3分,共36分)1.下列各式中,y 是x 的二次函数的是 ( )A . 21xy x +=B . 220x y +-=C . 22y ax -=-D . 2210x y -+= 2.把二次函数122--=x x y 配方成顶点式为( ) A .2)1(-=x yB . 2)1(2--=x yC .1)1(2++=x yD .2)1(2-+=x y3.已知22y x =的图象是抛物线,若抛物线不动,把x 轴,y 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( ).A.22(2)2y x =-+ B.22(2)2y x =+-C.22(2)2y x =-- D.22(2)2y x =++4.若二次函数22(1)23y m x m m =++--的图象经过原点,则m 的值为 ( ) A .-1或3 B .一1 C.3 D .无法确定5.二次函数y=-x 2+bx +c 图象的最高点是(-1,-3),则b 、c 的值是( ) A .b=2,c=4 B .b=2,c=-4 C .b=-2,c=4 D .b=-2,c =-46.已知二次函数2y ax bx c =++的图象如图所示,对称轴是1x =,则下列结论中正确的是( ). A.0ac > B.0b <C.240b ac -<D.20a b +=7.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h=3.5t -4.9t 2(t 的单位:秒;h 的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )A .0.71秒 B .0.70秒 C .0.63秒 D .0.36秒 8、抛物线22n mx x y --=)0(≠mn 则图象与x 轴交点为 ( )A . 二个交点B . 一个交点C . 无交点D . 不能确定 9、已知函数222y x x =--的图象如图所示,根据其中提供的信息,可求得使1y ≥成立的x 的取值范围是( ) A.13x -≤≤ B.31x -≤≤ C.3x -≥ D.1x -≤或3x ≥ 10、二次函数2y ax bx c =++中,2b ac =,且0x =时4y =-,则( ) A .4y =-最大B .4y =-最小C . 3y =-最大D .3y =-最小11、在同一平面直角坐标系中,一次函数y ax b =+和二次函数2y ax bx =+的图象可能为( )12、一位篮球运动员站在罚球线后投篮,球入篮得分.下列图象中,可以大致反映篮球出手后到入篮框这一时间段内,篮球的高度()h 米与时间()t 秒之间变化关系的是( )二、填空题(本大题共8小题,每小题4分,共32分)13.函数.)21(122++-=k kxk y 是二次函数则k= .14. 二次函数y=21x 2+3x +25的图象是函数y=21x 2的图象先向 平移 个单位,再向 平移 个单位得到的。
专题05 二次函数函数综合的压轴真题训练(解析版)--2023 年中考数学压轴真题汇编

挑战2023年中考数学选择、填空压轴真题汇编专题05二次函数函数综合的压轴真题训练一.二次函数的图象1.(2022•株洲)已知二次函数y=ax2+bx﹣c(a≠0),其中b>0、c>0,则该函数的图象可能为()A.B.C.D.【答案】C【解答】解:∵c>0,∴﹣c<0,故A,D选项不符合题意;当a>0时,∵b>0,∴对称轴x=<0,故B选项不符合题意;当a<0时,b>0,∴对称轴x=>0,故C选项符合题意,故选:C二.二次函数的性质2.(2022•陕西)已知二次函数y=x2﹣2x﹣3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当﹣1<x1<0,1<x2<2,x3>3时,y1,y2,y3三者之间的大小关系是()A.y1<y2<y3B.y2<y3<y1C.y3<y1<y2D.y2<y1<y3【答案】D【解答】解:∵抛物线y=x2﹣2x﹣3=(x﹣1)2﹣4,∴对称轴x=1,顶点坐标为(1,﹣4),当y=0时,(x﹣1)2﹣4=0,解得x=﹣1或x=3,∴抛物线与x轴的两个交点坐标为:(﹣1,0),(3,0),∴当﹣1<x1<0,1<x2<2,x3>3时,y2<y1<y3,故选:D.3.(2022•岳阳)已知二次函数y=mx2﹣4m2x﹣3(m为常数,m≠0),点P(x p,y p)是该函数图象上一点,当0≤x p≤4时,y p≤﹣3,则m的取值范围是()A.m≥1或m<0B.m≥1C.m≤﹣1或m>0D.m≤﹣1【答案】A【解答】解:∵二次函数y=mx2﹣4m2x﹣3,∴对称轴为x=2m,抛物线与y轴的交点为(0,﹣3),∵点P(x p,y p)是该函数图象上一点,当0≤x p≤4时,y p≤﹣3,∴①当m>0时,对称轴x=2m>0,此时,当x=4时,y≤﹣3,即m•42﹣4m2•4﹣3≤﹣3,解得m≥1;②当m<0时,对称轴x=2m<0,当0≤x≤4时,y随x增大而减小,则当0≤x p≤4时,y p≤﹣3恒成立;综上,m的取值范围是:m≥1或m<0.故选:A.4.(2022•衢州)已知二次函数y=a(x﹣1)2﹣a(a≠0),当﹣1≤x≤4时,y的最小值为﹣4,则a的值为()A.或4B.或﹣C.﹣或4D.﹣或4【答案】D【解答】解:y=a(x﹣1)2﹣a的对称轴为直线x=1,顶点坐标为(1,﹣a),当a>0时,在﹣1≤x≤4,函数有最小值﹣a,∵y的最小值为﹣4,∴﹣a=﹣4,∴a=4;当a<0时,在﹣1≤x≤4,当x=4时,函数有最小值,∴9a﹣a=﹣4,解得a=﹣;综上所述:a的值为4或﹣,故选:D.5.(2022•荆门)如图,函数y=的图象由抛物线的一部分和一条射线组成,且与直线y=m(m为常数)相交于三个不同的点A(x1,y1),B(x2,y2),C(x3,y3)(x1<x2<x3).设t=,则t的取值范围是.【答案】<t<1【解答】解:由二次函数y=x2﹣2x+3(x<2)可知:图象开口向上,对称轴为x=1,∴当x=1时函数有最小值为2,x1+x2=2,由一次函数y=﹣x+(x≥2)可知当x=2时有最大值3,当y=2时x=,∵直线y=m(m为常数)相交于三个不同的点A(x1,y1),B(x2,y2),C (x3,y3)(x1<x2<x3),∴y1=y2=y3=m,2<m<3,∴2<x3<,∴t==,∴<t<1.故答案为:<t<1.三.二次函数图象与系数的关系6.(2022•南充)已知点M(x1,y1),N(x2,y2)在抛物线y=mx2﹣2m2x+n (m≠0)上,当x1+x2>4且x1<x2时,都有y1<y2,则m的取值范围为()A.0<m≤2B.﹣2≤m<0C.m>2D.m<﹣2【答案】A【解答】解:方法一:∵抛物线y=mx2﹣2m2x+n(m≠0),∴该抛物线的对称轴为直线x=﹣=m,∵当x1+x2>4且x1<x2时,都有y1<y2,∴当m>0时,0<2m≤4,解得0<m≤2;当m<0时,2m>4,此时m无解;由上可得,m的取值范围为0<m≤2,故选:A.方法二:由y1<y2可得,(mx22﹣2m2x2+n)﹣(mx12﹣2m2x1+n)>0,整理,得:m(x2﹣x1)(x2+x1﹣2m)>0,∵x1+x2>4且x1<x2,∴当m>0时,则x2+x1﹣2m>0,即2m≤4,解得m≤2,∴0<m≤2;当m<0时,则x2+x1﹣2m<0,此时无解;由上可得,0<m≤2,故选:A.7.(2022•凉山州)已知抛物线y=ax2+bx+c经过点(1,0)和点(0,﹣3),且对称轴在y轴的左侧,则下列结论错误的是()A.a>0B.a+b=3C.抛物线经过点(﹣1,0)D.关于x的一元二次方程ax2+bx+c=﹣1有两个不相等的实数根【答案】C【解答】解:由题意作图如下:由图知,a>0,故A选项说法正确,不符合题意,∵抛物线y=ax2+bx+c经过点(1,0)和点(0,﹣3),∴a+b+c=0,c=﹣3,∴a+b=3,故B选项说法正确,不符合题意,∵对称轴在y轴的左侧,∴抛物线不经过(﹣1,0),故C选项说法错误,符合题意,由图知,抛物线y=ax2+bx+c与直线y=﹣1有两个交点,故关于x的一元二次方程ax2+bx+c=﹣1有两个不相等的实数根,故D选项说法正确,不符合题意,故选:C.8.(2022•广安)已知抛物线y=ax2+bx+c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc>0;②2c﹣3b<0;③5a+b+2c=0;④若B(,y1)、C(,y2)、D(,y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有()A.1B.2C.3D.4【答案】B【解答】解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴是直线x=1,∴1=﹣,∴b=﹣2a,∴b<0,∵抛物线交y轴于负半轴,∴c<0,∴abc>0,故①正确,∵抛物线y=ax2﹣2ax+c经过(3,0),∴9a﹣6a+c=0,∴c=﹣3a,∴2c﹣3b=﹣6a+6a=0,故②错误,5a+b+2c=5a﹣2a﹣6a=﹣3a<0,故③错误,观察图象可知,y1<y2<y3,故④正确,故选:B.9.(2022•恩施州)已知抛物线y=x2﹣bx+c,当x=1时,y<0;当x=2时,y<0.下列判断:①b2>2c;②若c>1,则b>;③已知点A(m1,n1),B(m2,n2)在抛物线y=x2﹣bx+c上,当m1<m2<b时,n1>n2;④若方程x2﹣bx+c=0的两实数根为x1,x2,则x1+x2>3.其中正确的有()个.A.1B.2C.3D.4【答案】C【解答】解:∵a=>0,∴抛物线开口向上,当x=1时,y<0;当x=2时,y<0,∴抛物线与x轴有两个不同的交点,∴Δ=b2﹣4ac=b2﹣2c>0,故①正确;∵当x=1时,y<0;当x=2时,y<0,∴﹣b+c<0;∴b>+c,当c>1时,则b>,故②正确;抛物线的对称轴为直线x=b,且开口向上,当x<b时,y的值随x的增大而减小,∴当m1<m2<b时,n1>n2,故③正确;∵方程x2﹣bx+c=0的两实数根为x1,x2,∴x1+x2=2b,由②可知,当c>1时,则b>,∴x1+x2不一定大于3,故④错误;综上,正确的有①②③,共3个,故选:C.10.(2022•呼和浩特)在平面直角坐标系中,点C和点D的坐标分别为(﹣1,﹣1)和(4,﹣1),抛物线y=mx2﹣2mx+2(m≠0)与线段CD只有一个公共点,则m的取值范围是.【答案】m=3或﹣1<m≤﹣【解答】解:抛物线的对称轴为:x=﹣=1,当x=0时,y=2,∴抛物线与y轴的交点坐标为(0,2),顶点坐标为(1,2﹣m),直线CD 的表达式y=﹣1,当m>0时,且抛物线过点D(4,﹣1)时,16m﹣8m+2=﹣1,解得:m=﹣(不符合题意,舍去),当抛物线经过点(﹣1,﹣1)时,m+2m+2=﹣1,解得:m=﹣1(不符合题意,舍去),当m>0且抛物线的顶点在线段CD上时,2﹣m=﹣1,解得:m=3,当m<0时,且抛物线过点D(4,﹣1)时,16m﹣8m+2=﹣1,解得:m=﹣,当抛物线经过点(﹣1,﹣1)时,m+2m+2=﹣1,解得:m=﹣1,综上,m的取值范围为m=3或﹣1<m≤﹣,故答案为:m=3或﹣1<m≤﹣.11.(2022•遂宁)抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=a﹣b+c,则m的取值范围是.【答案】﹣4<m<0【解答】解:∵抛物线开口向上,∴a>0,∵抛物线对称轴在y轴左侧,∴﹣<0,∴b>0,∵抛物线经过(0,﹣2),∴c=﹣2,∵抛物线经过(1,0),∴a+b+c=0,∴a+b=2,b=2﹣a,∴m=a﹣b+c=a﹣(2﹣a)+(﹣2)=2a﹣4,∴y=ax2+(2﹣a)x﹣2,当x=﹣1时,y=a+a﹣2﹣2=2a﹣4,∵b=2﹣a>0,∴0<a<2,∴﹣4<2a﹣4<0,故答案为:﹣4<m<0.12.(2022•随州)如图,已知开口向下的抛物线y=ax2+bx+c与x轴交于点(﹣1,0),对称轴为直线x=1.则下列结论正确的有()①abc>0;②2a+b=0;③函数y=ax2+bx+c的最大值为﹣4a;④若关于x的方程ax2+bx+c=a+1无实数根,则﹣<a<0.A.1个B.2个C.3个D.4个【答案】C【解答】解:∵抛物线开口向下,∴a<0,∵抛物线交y轴于正半轴,∴c>0,∵﹣>0,∴abc<0,故①错误.∵抛物线的对称轴是直线x=1,∴﹣=1,∴2a+b=0,故②正确.∵抛物线交x轴于点(﹣1,0),(3,0),∴可以假设抛物线的解析式为y=a(x+1)(x﹣3),当x=1时,y的值最大,最大值为﹣4a,故③正确.∵ax2+bx+c=a+1无实数根,∴a(x+1)(x﹣3)=a+1无实数根,∴ax2﹣2ax﹣4a﹣1=0,Δ<0,∴4a2﹣4a(﹣4a﹣1)<0,∴a(5a+1)<0,∴﹣<a<0,故④正确,故选:C.13.(2022•广元)二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)abc<0;(2)4a+c>2b;(3)3b﹣2c>0;(4)若点A(﹣2,y1)、点B(﹣,y2)、点C(,y3)在该函数图象上,则y1<y3<y2;(5)4a+2b≥m(am+b)(m为常数).其中正确的结论有()A.5个B.4个C.3个D.2个【解答】解:∵抛物线的开口向下,∴a<0,∵抛物线的对称轴为直线x=﹣=2,∴b>0,∵抛物线交y轴的正半轴,∴c>0,∴abc<0,所以(1)正确;∵对称轴为直线x=2,∴﹣=2,∴b=﹣4a,∴b+4a=0,∴b=﹣4a,∵经过点(﹣1,0),∴a﹣b+c=0,∴c=b﹣a=﹣4a﹣a=﹣5a,∴4a+c﹣2b=4a﹣5a+8a=7a,∵a<0,∴4a+c﹣2b<0,∴4a+c<2b,故(2)不正确;∵3b﹣2c=﹣12a+10a=﹣2a>0,故(3)正确;∵|﹣2﹣2|=4,|﹣﹣2|=,|﹣2|=,∴y1<y2<y3,故(4)错误;当x=2时,函数有最大值4a+2b+c,∴4a+2b+c≥am2+bm+c,4a+2b≥m(am+b)(m为常数),故(5)正确;综上所述:正确的结论有(1)(3)(5),共3个,故选:C.14.(2022•巴中)函数y=|ax2+bx+c|(a>0,b2﹣4ac>0)的图象是由函数y =ax2+bx+c(a>0,b2﹣4ac>0)的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论正确的是()①2a+b=0;②c=3;③abc>0;④将图象向上平移1个单位后与直线y=5有3个交点.A.①②B.①③C.②③④D.①③④【答案】D【解答】解:∵图象经过(﹣1,0),(3,0),∴抛物线y=ax2+bx+c的对称轴为直线x=1,∴﹣=1,∴b=﹣2a,即2a+b=0,①正确.由图象可得抛物线y=ax2+bx+c与y轴交点在x轴下方,∴c<0,②错误.由抛物线y=ax2+bx+c的开口向上可得a>0,∴b=﹣2a<0,∴abc>0,③正确.设抛物线y=ax2+bx+c的解析式为y=a(x+1)(x﹣3),代入(0,3)得:3=﹣3a,解得:a=﹣1,∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点坐标为(1,4),∵点(1,4)向上平移1个单位后的坐标为(1,5),∴将图象向上平移1个单位后与直线y=5有3个交点,故④正确;故选:D.15.(2022•黄石)已知二次函数y=ax2+bx+c的部分图象如图所示,对称轴为直线x=﹣1,有以下结论:①abc<0;②若t为任意实数,则有a﹣bt≤at2+b;③当图象经过点(1,3)时,方程ax2+bx+c﹣3=0的两根为x1,x2(x1<x2),则x1+3x2=0,其中,正确结论的个数是()A.0B.1C.2D.3【答案】D【解答】解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x=﹣1,即﹣=﹣1,∴b=2a>0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc<0,所以①正确;∵x=﹣1时,y有最小值,∴a﹣b+c≤at2+bt+c(t为任意实数),即a﹣bt≤at2+b,所以②正确;∵图象经过点(1,3)时,得ax2+bx+c﹣3=0的两根为x1,x2(x1<x2),∴二次函数y=ax2+bx+c与直线y=3的一个交点为(1,3),∵抛物线的对称轴为直线x=﹣1,∴二次函数y=ax2+bx+c与直线y=3的另一个交点为(﹣3,3),即x1=﹣3,x2=1,∴x1+3x2=﹣3+3=0,所以③正确.故选:D.16.(2022•济南)抛物线y=﹣x2+2mx﹣m2+2与y轴交于点C,过点C作直线l垂直于y轴,将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G,点M(m﹣1,y1),N(m+1,y2)为图形G上两点,若y1<y2,则m的取值范围是()A.m<﹣1或m>0B.<m<C.0≤m<D.﹣1<m<1【答案】D【解答】解:在y=﹣x2+2mx﹣m2+2中,令x=m﹣1,得y=﹣(m﹣1)2+2m (m﹣1)﹣m2+2=1,令x=m+1,得y=﹣(m+1)2+2m(m+1)﹣m2+2=1,∴(m﹣1,1)和(m+1,1)是关于抛物线y=﹣x2+2mx﹣m2+2对称轴对称的两点,①若m﹣1≥0,即(m﹣1,1)和(m+1,1)在y轴右侧(包括(m﹣1,1)在y轴上),则点(m﹣1,1)经过翻折得M(m﹣1,y1),点(m+1,1)经过翻折得N (m+1,y2),如图:由对称性可知,y1=y2,∴此时不满足y1<y2;②当m+1≤0,即(m﹣1,1)和(m+1,1)在y轴左侧(包括(m+1,1)在y轴上),则点(m﹣1,1)即为M(m﹣1,y1),点(m+1,1)即为N(m+1,y2),∴y1=y2,∴此时不满足y1<y2;③当m﹣1<0<m+1,即(m﹣1,1)在y轴左侧,(m+1,1)在y轴右侧时,如图:此时M(m﹣1,1),(m+1,1)翻折后得N,满足y1<y2;由m﹣1<0<m+1得:﹣1<m<1,故选:D.17.(2022•荆门)抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=﹣2,过点(1,﹣2)和点(x0,y0),且c>0.有下列结论:①a<0;②对任意实数m都有:am2+bm≥4a﹣2b;③16a+c>4b;④若x0>﹣4,则y0>c.其中正确结论的个数为()A.1个B.2个C.3个D.4个【答案】B【解答】解:∵抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=﹣2,过点(1,﹣2),且c>0,∴抛物线开口向下,则a<0,故①正确;∵抛物线开口向下,对称轴为x=﹣2,∴函数的最大值为4a﹣2b+c,∴对任意实数m都有:am2+bm+c≤4a﹣2b+c,即am2+bm≤4a﹣2b,故②错误;∵对称轴为x=﹣2,c>0.∴当x=﹣4时的函数值大于0,即16a﹣4b+c>0,∴16a+c>4b,故③正确;∵对称轴为x=﹣2,点(0,c)的对称点为(﹣4,c),∵抛物线开口向下,∴若﹣4<x0<0,则y0>c,故④错误;故选:B.四.二次函数图象上点的坐标特征18.(2022•常德)我们发现:=3,=3,=3,…,=3,一般地,对于正整数a,b,如果满足=a时,称(a,b)为一组完美方根数对.如上面(3,6)是一组完美方根数对,则下面4个结论:①(4,12)是完美方根数对;②(9,91)是完美方根数对;③若(a,380)是完美方根数对,则a=20;④若(x,y)是完美方根数对,则点P(x,y)在抛物线y=x2﹣x上,其中正确的结论有()A.1个B.2个C.3个D.4个【答案】C【解答】解:将(4,12)代入=4,=4,=4,…,∴(4,12)是完美方根数对;故①正确;将(9,91)代入=10≠9,=,∴(9,91)不是完美方根数对,故②错误;③∵(a,380)是完美方根数对,∴将(a,380)代入公式,=a,=a,解得a=20或a=﹣19(舍去),故③正确;④若(x,y)是完美方根数对,则=x,=x,整理得y=x2﹣x,∴点P(x,y)在抛物线y=x2﹣x上,故④正确;故选:C.19.(2022•成都)如图,二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B两点,对称轴是直线x=1,下列说法正确的是()A.a>0B.当x>﹣1时,y的值随x值的增大而增大C.点B的坐标为(4,0)D.4a+2b+c>0【答案】D【解答】解:A、由图可知:抛物线开口向下,a<0,故选项A错误,不符合题意;B、∵抛物线对称轴是直线x=1,开口向下,∴当x>1时y随x的增大而减小,x<1时y随x的增大而增大,故选项B错误,不符合题意;C、由A(﹣1,0),抛物线对称轴是直线x=1可知,B坐标为(3,0),故选项C错误,不符合题意;D、抛物线y=ax2+bx+c过点(2,4a+2b+c),由B(3,0)可知:抛物线上横坐标为2的点在第一象限,∴4a+2b+c>0,故选项D正确,符合题意;故选:D.20.(2022•贵港)已知二次函数y=ax2+bx+c(a≠0)图象的一部分如图所示,该函数图象经过点(﹣2,0),对称轴为直线x=﹣.对于下列结论:①abc<0;②b2﹣4ac>0;③a+b+c=0;④am2+bm<(a﹣2b)(其中m≠﹣);⑤若A(x1,y1)和B(x2,y2)均在该函数图象上,且x1>x2>1,则y1>y2.其中正确结论的个数共有个.【答案】3【解答】解:∵抛物线的对称轴为直线x=﹣,且抛物线与x轴的一个交点坐标为(﹣2,0),∴抛物线与x轴的另一个交点坐标为(1,0),把(﹣2,0)(1,0)代入y=ax2+bx+c(a≠0),可得:,解得,∴a+b+c=a+a﹣2a=0,故③正确;∵抛物线开口方向向下,∴a<0,∴b=a<0,c=﹣2a>0,∴abc>0,故①错误;∵抛物线与x轴两个交点,∴当y=0时,方程ax2+bx+c=0有两个不相等的实数根,∴b2﹣4ac>0,故②正确;∵am2+bm=am2+am=a(m+)2﹣a,(a﹣2b)=(a﹣2a)=﹣a,∴am2+bm﹣(a﹣2b)=a(m+)2,又∵a<0,m≠﹣,∴a(m+)2<0,即am2+bm<(a﹣2b)(其中m≠﹣),故④正确;∵抛物线的对称轴为直线x=﹣,且抛物线开口朝下,∴可知二次函数,在x>﹣时,y随x的增大而减小,∵x1>x2>1>﹣,∴y1<y2,故⑤错误,正确的有②③④,共3个,故答案为:3.21.(2022•达州)二次函数y=ax2+bx+c的部分图象如图所示,与y轴交于(0,﹣1),对称轴为直线x=1.下列结论:①abc>0;②a>;③对于任意实数m,都有m(am+b)>a+b成立;④若(﹣2,y1),(,y2),(2,y3)在该函数图象上,则y3<y2<y1;⑤方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为4.其中正确结论有()个.A.2B.3C.4D.5【答案】A【解答】解:∵抛物线开口向上,∴a>0,∴抛物线与y轴交于点(0,﹣1),∴c=﹣1,∵﹣=1,∴b=﹣2a<0,∴abc>0,故①正确,∵y=ax2﹣2ax﹣1,当x=﹣1时,y>0,∴a+2a﹣1>0,∴a>,故②正确,当m=1时,m(am+b)=a+b,故③错误,∵点(﹣2,y1)到对称轴的距离大于点(2,y3)到对称轴的距离,∴y1>y3,∵点(,y2)到对称轴的距离小于点(2,y3)到对称轴的距离,∴y3>y2,∴y2<y3<y1,故④错误,∵方程|ax2+bx+c|=k(k≥0,k为常数)的解,是抛物线与直线y=±k的交点,当有3个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为3,当有4个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为4,当有2个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为2,故⑤错误,故选:A.22.(2022•徐州)若二次函数y=x2﹣2x﹣3的图象上有且只有三个点到x轴的距离等于m,则m的值为.【答案】4【解答】解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线开口向上,抛物线对称轴为直线x=1,顶点为(1,﹣4),∴顶点到x轴的距离为4,∵函数图象有三个点到x轴的距离为m,∴m=4,故答案为:4.五.二次函数的最值23.(2022•舟山)已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k ≠0)上,若ab的最大值为9,则c的值为()A.B.2C.D.1【答案】B【解答】解:∵点A(a,b),B(4,c)在直线y=kx+3上,∴,由①可得:ab=a(ak+3)=ka2+3a=k(a+)2﹣,∵ab的最大值为9,∴k<0,﹣=9,解得k=﹣,把k=﹣代入②得:4×(﹣)+3=c,∴c=2,故选:B.24.(2022•嘉兴)已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k ≠0)上,若ab的最大值为9,则c的值为()A.1B.C.2D.【答案】C【解答】解:∵点A(a,b),B(4,c)在直线y=kx+3上,∴,由①可得:ab=a(ak+3)=ka2+3a=k(a+)2﹣,∵ab的最大值为9,∴k<0,﹣=9,解得k=﹣,把k=﹣代入②得:4×(﹣)+3=c,∴c=2,故选:C六.二次函数图象与几何变换25.(2022•湘西州)已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是.【答案】﹣<b<﹣1【解答】解:如图,当y=0时,﹣x2+4x+5=0,解得x1=﹣1,x2=5,则A (﹣1,0),B(5,0),将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+1)(x﹣5),即y=x2﹣4x﹣5(﹣1≤x≤5),当直线y=﹣x+b经过点A(﹣1,0)时,1+b=0,解得b=﹣1;当直线y=﹣x+b与抛物线y=x2﹣4x﹣5(﹣1≤x≤5)有唯一公共点时,方程x2﹣4x﹣5=﹣x+b有相等的实数解,解得b=﹣,所以当直线y=﹣x+b与新图象有4个交点时,b的取值范围为﹣<b<﹣1.故答案为:﹣<b<﹣1.26.(2022•荆州)规定:两个函数y1,y2的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数y1=2x+2与y2=﹣2x+2的图象关于y轴对称,则这两个函数互为“Y函数”.若函数y=kx2+2(k﹣1)x+k﹣3(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为.【答案】y=2x﹣3或y=﹣x2+4x﹣4【解答】解:∵函数y=kx2+2(k﹣1)x+k﹣3(k为常数)的“Y函数”图象与x轴只有一个交点,∴函数y=kx2+2(k﹣1)x+k﹣3(k为常数)的图象与x轴也只有一个交点,当k=0时,函数解析式为y=﹣2x﹣3,它的“Y函数”解析式为y=2x﹣3,它们的图象与x轴只有一个交点,当k≠0时,此函数是二次函数,∵它们的图象与x轴都只有一个交点,∴它们的顶点分别在x轴上,∴=0,解得:k=﹣1,∴原函数的解析式为y=﹣x2﹣4x﹣4=﹣(x+2)2,∴它的“Y函数”解析式为y=﹣(x﹣2)2=﹣x2+4x﹣4,综上,“Y函数”的解析式为y=2x﹣3或y=﹣x2+4x﹣4,故答案为:y=2x﹣3或y=﹣x2+4x﹣4.七.抛物线与x轴的交点27.(2022•内蒙古)如图,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(﹣1,0),抛物线的对称轴为直线x=1,下列结论:①abc<0;②3a+c =0;③当y>0时,x的取值范围是﹣1≤x<3;④点(﹣2,y1),(2,y2)都在抛物线上,则有y1<0<y2.其中结论正确的个数是()A.1个B.2个C.3个D.4个【答案】C【解答】解:根据函数的对称性,抛物线与x轴的另外一个交点的坐标为(3,0);①函数对称轴在y轴右侧,则ab<0,而c已经修改>0,故abc<0,故①正确,符合题意;②∵x=﹣=1,即b=﹣2a,而x=﹣1时,y=0,即a﹣b+c=0,∴a+2a+c=0,∴3a+c=0.∴②正确,符合题意;③由图象知,当y>0时,x的取值范围是﹣1<x<3,∴③错误,不符合题意;④从图象看,当x=﹣2时,y1<0,当x=2时,y2>0,∴有y1<0<y2,故④正确,符合题意;故选:C.28.(2022•枣庄)小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图象他得出下列结论:①ab>0且c>0;②a+b+c =0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有.(填序号,多选、少选、错选都不得分)【答案】①②③【解答】解:∵抛物线对称轴在y轴的左侧,∴ab>0,∵抛物线与y轴交点在x轴上方,∴c>0,①正确;∵抛物线经过(1,0),∴a+b+c=0,②正确.∵抛物线与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,∴另一个交点为(﹣3,0),∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1,③正确;∵﹣1﹣(﹣2)<﹣1﹣(﹣4)<3﹣(﹣1),抛物线开口向下,∴y2>y1>y3,④错误.∵抛物线与x轴的一个交点坐标为(1,0),∴a+b+c=0,∵﹣=﹣1,∴b=2a,∴3a+c=0,⑤错误.故答案为:①②③.29.(2022•福建)已知抛物线y=x2+2x﹣n与x轴交于A,B两点,抛物线y=x2﹣2x﹣n与x轴交于C,D两点,其中n>0.若AD=2BC,则n的值为.【答案】8【解答】方法1、解:针对于抛物线y=x2+2x﹣n,令y=0,则x2+2x﹣n=0,∴x=﹣1±,针对于抛物线y=x2﹣2x﹣n,令y=0,则x2﹣2x﹣n=0,∴x=1±,∵抛物线y=x2+2x﹣n=(x+1)2﹣n﹣1,∴抛物线y=x2+2x﹣n的顶点坐标为(﹣1,﹣n﹣1),∵抛物线y=x2﹣2x﹣n=(x﹣1)2﹣n﹣1,∴抛物线y=x2﹣2x﹣n的顶点坐标为(1,﹣n﹣1),∴抛物线y=x2+2x﹣n与抛物线y=x2﹣2x﹣n的开口大小一样,与y轴相交于同一点,顶点到x轴的距离相等,∴AB=CD,∵AD=2BC,∴抛物线y=x2+2x﹣n与x轴的交点A在左侧,B在右侧,抛物线y=x2﹣2x ﹣n与x轴的交点C在左侧,D在右侧,∴A(﹣1﹣,0),B(﹣1+,0),C(1﹣,0),D(1+,0),∴AD=1+﹣(﹣1﹣)=2+2,BC=﹣1+﹣(1﹣)=﹣2+2,∴2+2=2(﹣2+2),∴n=8,故答案为:8.方法2、∵y=x2+2x﹣n=(x+1)2﹣n﹣1,∴抛物线y=x2+2x﹣n的对称轴为直线x=﹣1,顶点坐标为(﹣1,﹣n﹣1),∵y=x2﹣2x﹣n=(x﹣1)2﹣n﹣1,∴抛物线y=x2﹣2x﹣n的对称轴为直线x=1,顶点坐标为(1,﹣n﹣1),∴抛物线y=x2﹣2x﹣n的图象可由y=x2+2x﹣n的图象向右平移两个单位得到,∵n>0,∴﹣n﹣1<﹣1,两函数的图象如图所示:由平移得,AC=BD=2,∵AB=CD,AD=2BC,∴BC=2AC=4,∴CD=BC+BD=6,∵点C,D关于直线x=1对称,∴C(﹣2,0),∵点C在抛物线y=x2﹣2x﹣n上,∴4+4﹣n=0,∴n=8,故答案为:8.八.二次函数综合题30.(2022•丹东)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a=.其中正确的有()A.1个B.2个C.3个D.4个【答案】D【解答】解:∵抛物线开口向上,∴a>0,∵对称轴是直线x=2,∴﹣=2,∴b=﹣4a<0∵抛物线交y轴的负半轴,∴c<0,∴abc>0,故①正确,∵b=﹣4a,a>0,∴b+3a=﹣a<0,故②正确,观察图象可知,当0<x≤2时,y随x的增大而减小,故③错误,一次函数y=kx+b(k≠0)的图象经过点A,∵b<0,∴k>0,此时E(k,b)在第四象限,故④正确.∵抛物线经过(﹣1,0),(5,0),∴可以假设抛物线的解析式为y=a(x+1)(x﹣5)=a(x﹣2)2﹣9a,∴M(2,﹣9a),C(0,﹣5a),过点M作MH⊥y轴于点H,设对称轴交x轴于点K.∵AM⊥CM,∴∠AMC=∠KMH=90°,∴∠CMH=∠KMA,∵∠MHC=∠MKA=90°,∴△MHC∽△MKA,∴=,∴=,∴a2=,∵a>0,∴a=,故⑤正确,故选:D.31.(2022•自贡)已知A(﹣3,﹣2),B(1,﹣2),抛物线y=ax2+bx+c(a >0)顶点在线段AB上运动,形状保持不变,与x轴交于C,D两点(C在D的右侧),下列结论:①c≥﹣2;②当x>0时,一定有y随x的增大而增大;③若点D横坐标的最小值为﹣5,则点C横坐标的最大值为3;④当四边形ABCD为平行四边形时,a=.其中正确的是()A.①③B.②③C.①④D.①③④【答案】D【解答】解:∵点A,B的坐标分别为(﹣3,﹣2)和(1,﹣2),∴线段AB与y轴的交点坐标为(0,﹣2),又∵抛物线的顶点在线段AB上运动,抛物线与y轴的交点坐标为(0,c),∴c≥﹣2,(顶点在y轴上时取“=”),故①正确;∵抛物线的顶点在线段AB上运动,开口向上,∴当x>1时,一定有y随x的增大而增大,故②错误;若点D的横坐标最小值为﹣5,则此时对称轴为直线x=﹣3,C点的横坐标为﹣1,则CD=4,∵抛物线形状不变,当对称轴为直线x=1时,C点的横坐标为3,∴点C的横坐标最大值为3,故③正确;令y=0,则ax2+bx+c=0,CD2=(﹣)2﹣4×=,根据顶点坐标公式,=﹣2,∴=﹣8,即=8,∴CD2=×8=,∵四边形ABCD为平行四边形,∴CD=AB=1﹣(﹣3)=4,∴=42=16,解得a=,故④正确;综上所述,正确的结论有①③④.故选:D.。
中考数学热点题型专练二次函数含解析

热点09 二次函数【命题趋势】中考中对二次函数的考查除定义、识图、性质、求解析式等常规题外,还会出现与二次函数有关的贴近生活实际的应用题,阅读理解和探究题,二次函数与其他函数方程、不等式、几何知识的综合题在压轴题中出现的可能性很大. 【满分技巧】一、二次函数表达式的确定 步骤:(1)设二次函数的表达式;(2)根据已知条件,得到关于待定系数的方程组;(3)解方程组,求出待定系数的值,从而写出函数的表达式. 二、二次函数的实际应用(1)利用二次函数解决实际生活中的利润问题,应理清变量所表示的实际意义,注意隐含条件的使用,同时考虑问题要周全,此类问题一般是运用“总利润=总售价-总成本”或“总利润=每件商品所获利润×销售数量”,建立利润与价格之间的函数关系式;(2)最值:若函数的对称轴在自变量的取值范围内,顶点坐标即为其最值,若顶点坐标不是其最值,那么最值可能为自变量两端点的函数值;若函数的对称轴不在自变量的取值范围内,可根据函数的增减性求解,再结合两端点的函数值对比,从而求解出最值. 三、二次函数的图象与几何图形的关系将函数知识与几何知识有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将问题转化函数模型,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件. 【限时检测】(建议用时:30分钟) 一、选择题 1.抛物线y =﹣21(23)2x -+1的顶点坐标为 A .(3,1) B .(﹣3,1) C .(32,1) D .(﹣32,1) 【答案】C【解析】∵抛物线y =﹣21(23)2x -+1中,2x ﹣3=0时,x =32,故抛物线y =﹣21(23)2x -+1的顶点坐标为:(32,1). 故选C .2.对于函数y =–2(x –3)2,下列说法不正确的是 A .开口向下 B .对称轴是3x = C .最大值为0 D .与y 轴不相交【答案】D【解析】对于函数y =–2(x –3)2的图象,∵a =–2<0,∴开口向下,对称轴x =3,顶点坐标为(3,0),函数有最大值0, 故选项A 、B 、C 正确,选项D 错误, 故选D .3.若二次函数y =|a |x 2+bx +c 的图象经过A (m ,n )、B (0,y 1)、C (3-m ,n )、D ,y 2)、E (2,y 3),则y 1、y 2、y 3的大小关系是A .y 1<y 2<y 3B .y 1<y 3<y 2C .y 3<y 2<y 1D .y 2<y 3<y 1【答案】D【解析】∵经过A (m ,n )、C (3-m ,n ),∴二次函数的对称轴x =32,∵B (0,y 1)、D ,y 2)、E (2,y 3)与对称轴的距离B 最远,D 最近,∵|a |>0, ∴y 1>y 3>y 2,故选D .4.当x =a 和x =b (a ≠b )时,二次函数y =2x 2﹣2x +3的函数值相等、当x =a +b 时,函数y =2x 2﹣2x +3的值是 A .0 B .﹣2 C .1 D .3【答案】D【解析】∵当x =a 或x =b (a ≠b )时,二次函数y =2x 2﹣2x +3的函数值相等, ∴以a 、b 为横坐标的点关于直线x =12对称,则122a b +=,∴a +b =1, ∵x =a +b ,∴x =1,当x =1时,y =2x 2﹣2x +3=2﹣2+3=3,故选D . 5.若函数y =(m ﹣1)x 2﹣6x +32m 的图象与x 轴有且只有一个交点,则m 的值为A .﹣2或3B .﹣2或﹣3C .1或﹣2或3D .1或﹣2或﹣3【答案】C【解析】当m =1时,函数解析式为:y =﹣6x +32是一次函数,图象与x 轴有且只有一个交点, 当m ≠1时,函数为二次函数, ∵函数y =(m ﹣1)x 2﹣6x +32m 的图象与x 轴有且只有一个交点, ∴62﹣4×(m ﹣1)×32m =0, 解得,m =﹣2或3,故选C . 6.将抛物线2yx 向右平移2个单位长度,再向上平移3个单位长度,得到的抛物线的解析式为A .2(2)3y x =++B .2(2)3y x =-+C .2(2)3y x =+-D .2(2)3y x =--【答案】B【解析】抛物线y =x 2先向右平移2个单位长度,得:y =(x –2)2;再向上平移3个单位长度,得:y =(x –2)2+3.故选B .7.反比例函数k y x=的图象如图所示,则二次函数y =2kx 2﹣4x +k 2的图象大致是A .B .C.D.【答案】D【解析】∵函数kyx=的图象经过二、四象限,∴k<0,由图知当x=﹣1时,y=﹣k<1,∴k>﹣1,∴抛物线y=2kx2﹣4x+k2开口向下,对称轴为x=﹣422k-⨯=1k,﹣1<1k<0,∴对称轴在﹣1与0之间,∵当x=0时,y=k2>1.故选D.8.已知两点A(﹣5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1<y2≤y0,则x0的取值范围是A.x0>﹣1 B.x0>﹣5C.x0<﹣1 D.﹣2<x0<3【答案】A【解析】∵点C(x0,y0)是该抛物线的顶点.且y1<y2≤y0,∴a<0,x0﹣(﹣5)>|3﹣x0|,∴x0>﹣1.故选A.9.(福建省厦门市集美区2019年初中毕业班总复习练习(二模)数学试题)二次函数y=x2+bx﹣t的对称轴为x=2.若关于x的一元二次方程x2+bx﹣t=0在﹣1<x<3的范围内有实数解,则t的取值范围是A.﹣4≤t<5 B.﹣4≤t<﹣3C.t≥﹣4 D.﹣3<t<5【答案】A【解析】∵抛物线的对称轴x =2b -=2, ∴b =﹣4,则方程x 2+bx ﹣t =0,即x 2﹣4x ﹣t =0的解相当于y =x 2﹣4x 与直线y =t 的交点的横坐标, ∵方程x 2+bx ﹣t =0在﹣1<x <3的范围内有实数解, ∴当x =﹣1时,y =1+4=5, 当x =3时,y =9﹣12=﹣3, 又∵y =x 2﹣4x =(x ﹣2)2﹣4,∴当﹣4≤t <5时,在﹣1<x <3的范围内有解. ∴t 的取值范围是﹣4≤t <5, 故选A .10.已知抛物线()()1y x a x a =+--(a 为常数,0a ≠).有下列结论:①抛物线的对称轴为12x =;②方程()()11x a x a +--=有两个不相等的实数根;③抛物线上有两点P (x 0,m ),Q (1,n ),若m n <,则001x <<,其中,正确结论的个数为 A .0 B .1 C .2 D .3【答案】D【解析】∵()()1y x a x a =+--=x 2–x –a 2–a ,∴对称轴为直线x =121--⨯=12. ∴①正确,∵()()1x a x a +--=x 2–x –a 2–a =1, ∴x 2–x –a 2–a –1=0,∴∆=(–1)2–4×1×(–a 2–a –1)=1+4a 2+4a +4=(2a +1)2+4>0,∴方程(x +a )(x –a –1)=1有两个不相等的实数根; ∴②正确,∵P (x 0,m ),Q (1,n )在抛物线上,∴m =x 02–x 0–a 2–a ,n =12–1–a 2–a =–a 2–a , ∵m <n ,∴x02–x0–a2–a<–a2–a,∴x02–x0<0,∴x0(x0–1)<0∵x0>x0–1,∴x0>0且x0–1<0,即0<x0<1,∴③正确,综上所述:正确的结论有①②③,共3个,故选D.11.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示则下列结论:①4a﹣b=0;②c<0;③c>3a;④4a﹣2b>at2+bt(t为实数);⑤点(﹣72,y1),(﹣52,y2),(312y,)是该抛物线上的点,则y2<y1<y3,其中,正确结论的个数是A.1 B.2C.3 D.4【答案】C【解析】∵抛物线的对称轴为直线x=﹣2,∴4a﹣b=0,所以①正确;∵与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,∴由抛物线的对称性知,另一个交点在(﹣1,0)和(0,0)之间, ∴抛物线与y轴的交点在y轴的负半轴,即c<0,故②正确;∵由②知,x=﹣1时y>0,且b=4a,即a﹣b+c=a﹣4a+c=﹣3a+c>0,所以③正确;由函数图象知当x=﹣2时,函数取得最大值,∴4a ﹣2b +c ≥at 2+bt +c ,即4a ﹣2b ≥at 2+bt (t 为实数),故④错误; ∵抛物线的开口向下,且对称轴为直线x =﹣2, ∴抛物线上离对称轴水平距离越小,函数值越大, ∴y 2>y 1>y 3,故⑤错误,故选C . 二、填空题12.二次函数2245y x x =--+的最大值是__________.【答案】7【解析】222452(1)7y x x x =--+=-++, 即二次函数245y x x =--+的最大值是7, 故答案为:7.13.已知函数y =﹣x 2+2x ﹣2图象上两点A (2,y 1),B (a ,y 2),其中a >2,则y 1与y 2的大小关系是__________.(填“<”“>”或“=”) 【答案】>【解析】y =﹣x 2+2x ﹣2=﹣(x ﹣1)2﹣1, 对称轴x =1,∵A (2,y 1),B (a ,y 2),其中a >2, ∴点A 与B 在对称轴的右侧, ∵–1<0,∴x >2时,y 随x 的增大而减小, ∴y 1>y 2, 故答案为:>.14.已知抛物线y =ax 2+bx +c (a >0)的对称轴是直线x =2,且经过点P (3,1),则a +b +c 的值为__________.【答案】1【解析】∵抛物线y =ax 2+bx +c (a >0)的对称轴是直线x =2, ∴P (3,1)对称点坐标为(1,1), ∴当x =1时,y =1, 即a +b +c =1, 故答案为:1.15.已知关于x 的一元二次方程ax 2+bx +c =5的一个根是2,且二次函数y =ax 2+bx +c 的对称轴是直线x =2,则抛物线y =ax 2+bx +c 的顶点坐标为__________. 【答案】(2,5)【解析】∵二次函数y =ax 2+bx +c 的对称轴是直线x =2,方程ax 2+bx +c =5的一个根是2, ∴当x =2时,y =ax 2+bx +c =5, ∴抛物线的顶点坐标是(2,5). 故答案为:(2,5).16.将抛物线y =2(x ﹣1)2+3绕它的顶点旋转180°后得到的抛物线的函数表达式为__________.【答案】y =﹣2(x ﹣1)2+3【解析】抛物线y =2(x ﹣1)2+3的顶点坐标为(1,3),由于抛物线y =2(x ﹣1)2+3绕其顶点旋转180°后抛物线的顶点坐标不变,只是开口方向相反, 则所得抛物线解析式为y =﹣2(x ﹣1)2+3, 故答案为:y =﹣2(x ﹣1)2+3.17.如图,若被击打的小球飞行高度h (单位:m )与飞行时间t (单位:s )之间具有的关系为2205h t t =-,则小球从飞出到落地所用的时间为__________s .【答案】4【解析】依题意,令0h =得:∴20205t t =-, 得:(205)0t t -=,解得:0t =(舍去)或4t =, ∴即小球从飞出到落地所用的时间为4s ,故答案为:4. 三、解答题18.已知抛物线224y x x c =-+与x 轴有两个不同的交点.(1)求c 的取值范围;(2)若抛物线224y x x c =-+经过点()2,A m 和点()3,B n ,试比较m 与n 的大小,并说明理由.【解析】(1)()2244816 8b ac c c -=--=-,由题意,得240b ac ->, ∴16 80c ->,∴c 的取值范围是2c <. (2)m n <,理由如下: ∵抛物线的对称轴为直线1x =, 又∵20a =>,∴当1x ≥时,y 随x 的增大而增大, ∵23<,∴m n <.19.已知抛物线26y x x c =-++.(1)若该抛物线与x 轴有公共点,求c 的取值范围;(2)设该抛物线与直线21y x =+交于M ,N 两点,若MN =,求C 的值;(3)点P ,点Q 是抛物线上位于第一象限的不同两点,PA QB ,都垂直于x 轴,垂足分别为A ,B ,若OPA OQB △≌△,求c 的取值范围.【解析】(1)∵抛物线26y x x c =-++与x 轴有交点, ∴一元二次方程260x x c -++=有实根.240b ac ∴∆=-,即264(1)0c -⨯-⨯.解得9c -.(2)根据题意,设()()1122,21,,21M x x N x x ++由2621y x x cy x ⎧=-++⎨=+⎩,消去y ,得2410x x c -+-=①. 由2(4)4(1)1240c c ∆=---=+>,得3c >-.∴方程①的解为1222x x ==()()()()22221212122121520(3)MN x x x x x x c ∴=-++-+=-=+⎡⎤⎣⎦, 20(3)20c ∴+=,解得2c =-.(3)设点P 的坐标为(, )m n ,则点Q 的坐标为(,)n m ,且0,0,m n m n >>≠,2266m m c n n n c m⎧-++=∴⎨-++=⎩,两式相减,得227()0n m m n -+-=,即()(7)0m n m n -+-= 7m n ∴+=,即7n m =-2770m m c ∴-+-=,其中07m <<由0∆,即274(1)(7)0c -⨯-⨯-,得214c -. 当214c =-时,72m n ==,不合题意. 又70c ->,得7c <. ∴c 的取值范围是2174c -<<. 20.我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为x 元/件(x ≥6,且x 是按0.5元的倍数上涨),当天销售利润为y 元.(1)求y 与x 的函数关系式(不要求写出自变量的取值范围); (2)要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)若每件文具的利润不超过80%,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.【解析】(1)由题意,y =(x -5)(100-60.5x -×5)=-10x 2+210x -800, 故y 与x 的函数关系式为:y =-10x 2+210x -800. (2)要使当天利润不低于240元,则y ≥240, ∴y =-10x 2+210x -800=-10(x -10.5)2+302.5=240, 解得,x 1=8,x 2=13,∵-10<0,抛物线的开口向下,∴当天销售单价所在的范围为8≤x ≤13. (3)∵每件文具利润不超过80%, ∴50.8x x-≤,得x ≤9, ∴文具的销售单价为6≤x ≤9,由(1)得y =-10x 2+210x -800=-10(x -10.5)2+302.5, ∵对称轴为x =10.5,∴6≤x ≤9在对称轴的左侧,且y 随着x 的增大而增大,∴当x =9时,取得最大值,此时y =-10(9-10.5)2+302.5=280,即每件文具售价为9元时,最大利润为280元.21.如图,已知抛物线经过点A (–1,0),B (4,0),C (0,2)三点,点D 与点C 关于x 轴对称,点P 是线段AB 上的一个动点,设点P 的坐标为(m ,0),过点P 作x 轴的垂线l 交抛物线于点Q ,交直线BD 于点M .(1)求该抛物线所表示的二次函数的表达式;(2)在点P 运动过程中,是否存在点Q ,使得△BQM 是直角三角形?若存在,求出点Q 的坐标;若不存在,请说明理由;(3)连接AC ,将△AOC 绕平面内某点H 顺时针旋转90°,得到△A 1O 1C 1,点A 、O 、C 的对应点分别是点A 、O 1、C 1、若△A 1O 1C 1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“和谐点”,请直接写出“和谐点”的个数和点A 1的横坐标.【解析】(1)设抛物线解析式为y =ax 2+bx +c ,将点A (–1,0),B (4,0),C (0,2)代入解析式,∴001642a b c a b c c =-+⎧⎪=++⎨⎪=⎩,∴1232a b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴y =–212x +32x +2. (2)∵点C 与点D 关于x 轴对称,∴D (0,–2).设直线BD 的解析式为y =kx –2.∵将(4,0)代入得:4k –2=0,∴k =12. ∴直线BD 的解析式为y =12x –2.当P 点与A 点重合时,△BQM 是直角三角形,此时Q (–1,0); 当BQ ⊥BD 时,△BQM 是直角三角形,则直线BQ 的直线解析式为y =–2x +8,∴–2x +8=–21x 2+32x +2,可求x =3或x =4(舍), ∴x =3;∴Q (3,2)或Q (–1,0).(3)两个和谐点; AO =1,OC =2,设A 1(x ,y ),则C 1(x +2,y –1),O 1(x ,y –1),①当A 1、C 1在抛物线上时,∴()2213222131(2)2222y x x y x x ⎧=-++⎪⎪⎨⎪-=-++++⎪⎩, ∴13x y =⎧⎨=⎩, ∴A 1的横坐标是1;当O 1、C 1在抛物线上时,()22131222131(2)2222y x x y x x ⎧-=-++⎪⎪⎨⎪-=-++++⎪⎩, ∴12218x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴A 1的横坐标是12.。
二次函数的图象和性质备战2023年中考数学考点微专题

考向3.5 二次函数的图象和性质例1、(2021·四川德阳·中考真题)已知函数y 21213x 583x 8x ≤⎧=⎨-+≤≤⎩(<)()()的图象如图所示,若直线y =kx ﹣3与该图象有公共点,则k 的最大值与最小值的和为 _____.解:当直线经过点(1,12)时,12=k -3,解得k =15; 当直线与抛物线只有一个交点时,(x -5)2+8=kx -3, 整理得x 2-(10+k )x +36=0,∴10+k =±12,解得k =2或k =-22(舍去), ∴k 的最大值是15,最小值是2, ∴k 的最大值与最小值的和为15+2=17. 故答案为:17.1、二次函数抛物线位置与a ,b ,c 的关系:(1)a 决定抛物线的开口方向⎩⎨⎧⇔<⇔>开口向下开口向上00a a(2)c 决定抛物线与y 轴交点的位置:c>0⇔图像与y 轴交点在x 轴上方;c=0⇔图像过原点;c<0⇔图像与y 轴交点在x 轴下方; (3)a ,b 决定抛物线对称轴的位置:a ,b 同号,对称轴在y 轴左侧;b =0,对称轴是y 轴; a ,b 异号。
对称轴在y 轴右侧;1、本题考查分段函数的图象与性质,一次函数图象上点的坐标特征,结合图象求出k 的最大值和最小值是解题的关键;2、二次函数的性质是中考必考点,熟悉并运用二次函数性质解决问题是考前学生必须掌握的内容;例 2、(2021·山东泰安·中考真题)如图是抛物线2y ax bx c =++的部分图象,图象过点(3,0),对称轴为直线1x =,有下列四个结论:①0abc >;②0a b c -+=;③y 的最大值为3;④方程210ax bx c +++=有实数根.其中正确的为________(将所有正确结论的序号都填入).解:∵抛物线的开口向下,与y 轴的交点在y 轴的正半轴, ∴a <0,c >0,∵抛物线的对称轴为直线x =1, ∴﹣2ba=1,即b =﹣2a >0 ∴abc <0,故①错误;∵抛物线与x 轴的一个交点坐标为(3,0),∴根据对称性,与x 轴的另一个交点坐标为(﹣1,0), ∴a ﹣b +c =0,故②正确;根据图象,y 是有最大值,但不一定是3,故③错误; 由210ax bx c +++=得2=1ax bx c ++﹣, 根据图象,抛物线与直线y =﹣1有交点, ∴210ax bx c +++=有实数根,故④正确, 综上,正确的为②④, 故答案为:②④.理解并熟练运用二次函数的图象与性质,会利用数形结合思想解决问题是解答的关键。
