第五章 频率响应法4
5.频率响应法

1 V , = − ωT 1 + ω2T 2 U 1 ⇒U = V2 1+ 2 U ⇒ U 2 −U +V 2 = 0 1 1 ⇒ (U − ) 2 + V 2 = ( ) 2 2 2
Im
0
1 2 ω =0
1
ω = +∞
Re
ω
《自动控制原理》 自动控制原理》第五章 频率响应法
上海交通大学电子信息与电气工程学院
与虚轴负段 重合 的 直线。
G (s ) = s
G ( j ω ) = jω ∠G ( jω ) = 90° G ( jω ) = ω
Im ω =∞
G (s ) =
1 s
ω =0 0 Re
1 jω 1 G ( jω ) = ω ∠G ( jω) = −90° G ( jω ) =
Im
0
ω =∞ ω =0
l l
实验法:通过实验的方法直接测得 解析法:根据传递函数求取
l
用 s=jω代入 系统的传递函数
R(s)
G (s)
C (s)
C(s) b m s m + b m −1s m −1 + LL + b1 s + b 0 G(s) = = R(s) a n s n + a n −1s n −1 + LL + a 1s + a 0 C(jω ) b m (jω ) m + b m −1 (jω ) m −1 + LL + b1 (jω ) + b 0 ⇒ G(jω ) = = R(jω ) a n (jω ) n + a n −1 (jω ) n −1 + LL + a 1 (jω ) + a 0 = A(ω )e jϕ (ω ) = U(ω ) + jV(ω )
第五章放大器的频率响应

,
Z R // 1
jC
高频时,Z ,AV , 使频带适当展宽。
二、负反馈法
放大电路加入负反馈后,增益下降,但通 频带却加宽了,如图21所示。
2 0 l gA / d B
80 60 40 20 0
1 01 1 02 1 03 1 04 1 05 1 06 1 07
图21 负反馈对通频带的影响
图4 RC低通电路的频率特性曲线
(2) RC高通电路( 如图5所示 )
其电压放大倍数
.
Av
为:
.
.
Av
=V.o
Vi
j /L 1 j / L
jf / 1 jf
fL / fL
式中
L
1 RC
1
。
下限截止频率、模和相角分别为
图5 RC高通电路
f0
fL
1
2RC
Av
f / fL 1 ( f fL)2
非标准式
标准式
(2 如1)何其电求R压C电放低路大通倍的电数传(路传输递(函函如数数)图为 3所示幅 特 处fH)称频 性 的为特 将 误上性 以 差限2的 最0截dX大B轴V+-止,./id和频有ecY率的-轴。斜R3都d当率B是。下f采≥Cf降H用时。对,在数幅f坐频=+Vf-标H.o,
AU
Uo Ui
负反馈。
(a)
•图(b)电路,也为电流并联负反馈。
(b)
前四章小结
第一章:
1.半导体的基础知识:(本征、杂质、P型、N型、 P N结 ) 2.二极管:(构成、伏安特性、特殊二极管、应用)
第二章:
1.半导体三极管:(构成、放大原理、伏安特性、参数 ) 2.基本放大电路:(构成原理、静态分析、动态分析、三种组态的放大电路的分 析) 3.放大器的级间耦合:(耦合方式、特点、) 4.多级放大电路的参数计算:
第五章 放大电路的频率响应
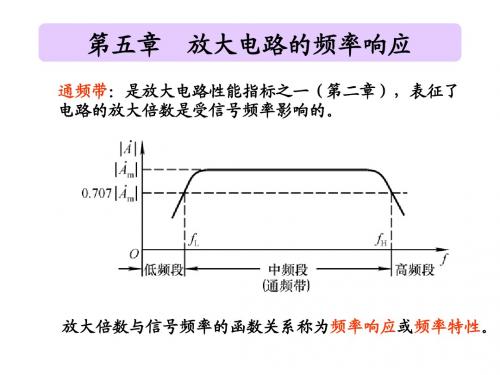
1 fH 2 RC
1 fL 2 RC
当信号频率等于上(下)限频率时,放大电路的 增益下降3dB,且产生±45°相移
近似分析时,可用折线化的波特图表示电路的频 率特性
一个电容对应的渐进线斜率为20dB/十倍频
简单 RC 电路的频率特性
Ui
•
R C
Uo
•
Ui
•
C R
Uo
•
RC 低通电路
RC 高通电路
Au
• |Au |
1 0.707
1 f 1 j fH
1 0.707
Au
1 fL 1 j f
|Au |
fL
f
•
O
fH f
f
O
O –45° –90°
90° 45° O
f
研究频率响应的方法 (1) 三个频段的划分 1) 中频区(段) 特点:Aus与f无关
与f无关
5.4 单管放大电路的频率响应
本节以单管共射电路为例,介绍频率响应的一般 分析方法。
5.4.1 单管共射放大电路的频率响应
1、画出全频段的微变等效电路
+VCC RB C1 + . Ui VT RL . Uo RC C2 + + . Ui _ RB rb′e
C1
rbb′ . gmUb'e Cπ′
C2 + RC . RL U o _
R
fL
L 1 1 下限截止频率 2 2 2 RC
Au பைடு நூலகம்
1
L 1 j
1 fL 1 jf
f j fL f 1 j fL
1、RC高通电路的频率响应
第五章 频率特性法 (4)

ω=0 Re
根的实部为负,系统稳 根的实部为负, 相角增量为90 定,相角增量为 0 。
第四节 用频率特性法分析系统稳定性
TS-1 因子的相角变化量为: 因子的相角变化量为:
ω=0→∞
∆ ∠(jωT-1)
TS-1幅相频率特性曲线 幅相频率特性曲线
Im ∞
=90o-180o=-90o 根的实部为正, 根的实部为正, 系统不稳定, 系统不稳定,相角 增量为-90 增量为 0 。
第四节 用频率特性法分析系统稳定性
例 已知系统开环传递函数试判断 闭环系统的稳定性。 闭环系统的稳定性。 K G(s)H(s)= S(TS-1) 奈氏曲线: 奈氏曲线: 系统开环频率特性为: 解: 系统开环频率特性为: ω=0+ 特殊点: 特殊点: Im K G(jω)H(jω)= jω(jωT-1) 曲线顺时针方向 ω=0+ υ =1 点的, 绕过 (-1, j0)φ(ω)=90o K A(ω)=∞ 点的, A(ω)= ω 1+(ωT)2 所以系统不稳定。 ω=∞ 所以系统不稳定。 ω= ∞ 0 Re ω=0 -1 o-tg-1 ωT φ(ω)=-90 A(ω)= 0 φ(ω)=180o -1
ω=0+ + ω=0
-1
Im Im ω=∞ ω=0 ω=∞ ω=0 Re -1 0 0 Re
曲线包围了(-1,j0)点, 曲线包围了 点 曲线没有包围(-1,j0)点, 点 曲线没有包围 系统不稳定。 系统不稳定。 系统是稳定的。 系统是稳定的。
第四节 用频率特性法分析系统稳定性
五、对数频率稳定判据
第四节 用频率特性法分析系统稳定性
已知系统的奈氏曲线,试判断系统的 例 已知系统的奈氏曲线 试判断系统的 稳定性。 稳定性。 解: 系统的 系统的G(jω)H (jω)曲线如图 曲线如图
自动控制原理

ω = +∞ (1, j 0) ω = ∞
奈氏曲线顺时针包围 (-1,j0)点2圈,即 N=-2 所以有: Z=P-N=2
仿真
即闭环系统在s右半平面有2个极点,所以系统不稳定。
5.4.3 虚轴上有开环极点时的奈氏判据
如下列图所示的奈氏曲线中,判别哪些是稳定的,哪些 是不稳定的。
Im
Im
Im
1
ω = +∞ 0
1.6 ∞
奈氏曲线顺时针包围 (-1,j0)点2圈,即 N=-2 所以有:
(1, j 0)
ω = 0+
仿真
Z=P-N=2
即闭环系统在s右半平面有2个极点,所以系统不稳定。
5.4.3 虚轴上有开环极点时的奈氏判据
对于如下形式的开环传递函数 K G(s)H(s) = s(Ts +1)(T2s +1) 1 其奈氏图与实轴交点为 此时的 ω =
5.4.3 虚轴上有开环极点时的奈氏判据
虚轴上有开环极点时的奈氏判据
jω
由于不能通过F(s)的任何零、极点,所 以当F(s)有若干个极点处于s平面虚轴 (包括原点)上时,则以这些点为圆 心,作半径ε为无穷小的半圆,按逆时 针方向从右侧绕过这些点。 F ( s ) 的极点 因此,F(s)的位于s平面右半部的零点 和极点均被新奈氏回线包围在内。而将 位于坐标原点处的开环极点划到了复平 面的左半部。 这样处理满足了奈氏判据的要求(应用 奈氏判据时必须首先明确位于s平面右 半部和左半部的开环极点的数目)。
2ω + ω + 0.5ω 2ω ω 0.5ω = 0
ω = 1.87
此时
A(ω) = 0.44
可以判断出交点在点(-1,j0) 的右侧
第五章 放大电路频率响应

ωH 2π
1 2 ππ o C o
fH为RoC’o低通电路的上限频率。 那么
Au
1 j 1 ( f
f fH )
2
1 1 j ω ωH
1 1 j f fH
(2)频率特性
fH
①幅频特性分析
Au
1 1 ( f fH )
2
当f<<fH时(即中频及以下): A u 1; 当f=fH时:
R rbe //rbb ( Rs // Rb )
Ausm Uo rbe Ri gm Rc Rs Ri rbe Us
二、单管共源放大电路及其等效电路
单管共源放大电路及其等效电路
在中频段 C 开路,C短路,中频电压放大倍数为
gs
A um
Uo
gm U
gs
( R d // R L )
gs
g m RL
Ui
U
在高频段,C短路,考虑 C gs 的影响,Rg和 C 组成 低通电路,上限频率为:
其近似波特图自行画出。
四、高频段的频率特性
1.高频段交流通路
2.电路的输出电阻Ro与管子的结电容Ccb、Cbe以及输出电 路元件分布电容Co组成低通电路
C o 为Ccb、Cbe以及Co的等效电容。考虑
它们的影响后,uce中不同频率成分在 等效电容上的分压不同。利用相量分压 法讨论分压,进而得频率特性。
和低频段下降的主要原因分别是什么。
本章讨论的问题:
1.为什么要讨论频率响应?如何讨论一个RC网络的频 率响应?如何画出频率响应曲线?
2.晶体管与场效应管的h参数等效模型在高频下还适应吗? 为什么? 3.什么是放大电路的通频带?哪些因素影响通频带?如何 确定放大电路的通频带? 4.如果放大电路的频率响应窄,应该怎么办? 5.对于放大电路,通频带愈宽愈好吗? 6.为什么集成运放的通频带很窄?有办法展宽吗?
五章节频率响应法
G (jc s)(st )G (a ) e ej jt( )aejt
频率特性:
系统对正弦输入信号的稳态响应特性。
G (j) G (j)e j G (j ) G () e j( )
其振幅比依赖于角频率的函数G()称为
系统的幅频特性;
其稳态输出信号对正弦输入信号的相移
f()称为系统的相频特性。
一、 频率特性的极坐标图
G k(s)b a 00 ssm n b a 1 1 ssm n 1 1 b am n 1 1s s a bn m
K
1 sv
h i1
1
(Tis 1)
1(nvh) 2
(Ti2
1
2
s 2iTis 1)
i1
L
1(mL) 2
( j 1)
( 2j s2 2 j js 1)
例5-2系统开环传递函数是
G(s)H(sG )=(js)(H TsK(j1))j,试(T绘Kj制其1奈) 氏图。
-KT
Im 0 Re
当 l渐 i0 近 R 当幅相m 线 G 值 角幅 相横 (e : :j值 角 坐0): :时H 标时(:j 0 G ) ( lG 9 i)0 (9 H T 0m 0 0)2 (H 9 K 4() 0 )0 T 2 0 1 K 8T
开环系统的频率特性通常是若干典型环节频率特性的乘积
n
G (j) G 1 (j)G 2 (j) G n (j) G i(nj)
极坐标形式:G (j
n
)G ( )ej()
i 1 j i()
G i( )ei1
i1
求系统的开环幅相特性: 分别求出系统各串联环节频率特性的幅值及相角, 然后算出不同频率下开环系统频率特性的幅值及 相角,从而就可绘制极坐标图。
第5章频率响应法
第 5 章频率响应法频率响应法是控制理论的重要组成部分,是分析和综合控制系统的一种工程实用方法。
它不仅适用于单变量系统,而且也可以推广至多变量系统。
它的特点是:不必求解系统的高阶微分方程,可直接根据频率特性曲线的形状及其特征量来研究系统的性能。
其突出的优点是:物理意义明确,可用实验的方法求出系统的频率特性和传递函数;而且计算量小,方法形象和直观,因而广为工程界所采用。
根据它在系统分析和综合中的应用,将频率响应法分为两部分:频率响应分析法和频率响应综合法,并分别在第 5 章和第6 章讨论。
在这一章里主要介绍:频率响应法的基本概念和控制系统频率特性曲线的绘制方法,以及它在系统分析与综合中的应用,重点在于其基本概念和应用。
5.1 频率特性频率响应法起源于通讯学科。
它的基本思想是:将控制系统的变量也看作是信号;这些信号通过傅里叶(Fourier) 分析,对于周期信号可展开为傅氏级数,对于非周期信号可进行傅氏变换,它们均可视为由不同频率成分的正弦信号所合成的;线性定常系统各个变量的运动,就是系统对各个不同频率信号响应叠加的结果。
频率响应法的优点:第一,这种方法具有鲜明的物理意义。
第二,可以用实验方法测出系统的频率特性,并获得其传递函数以及其它形式的数学模型。
第三,它是一种图解法,形象直观、计算量小。
频率响应法也存在一定的局限性:首先它只适用于线性定常系统。
其次,频率响应法的筒便和实用性是以它的工程近似性为代价的。
5.1.1 频率特性的基本概念首先考察图 5.1 一阶RC 电路图图 5.1 所示的简单系统。
该系统为一阶RC 电路。
该电路的微分方程为:(5.1)系统的传递函数为:(5.2)图 5.1 一阶 RC 电路图若外施正弦输入电压,则可得系统的输出响应为:式中等号右边的第一项为输出响应的暂态分量,第二项为输出响应的稳态分量。
当t趋于无穷大时第一项的暂态分量将趋于零,故系统的稳态输出响应为:可以看到:在正弦输入电压作用下系统的稳态输出,是与输入同频率的正弦电压,其幅值为输入幅值的倍,相角比输入的迟后arctgωT。
第五章频率响应分析法
求拉氏反变换,得系统输出
n i 1
对于稳定系统,极点实部一定为负
c(t ) ai e pi t b1e jt b2 e jt
t 时,瞬 态分量为零
c ss (t ) lim c(t ) b1e jt b2 e jt
t
系统输出的 稳态响应
7
频率特性一般形式的推导 Ar G j Ar G j b1 b2 css t 2 j s j 2 j s j s j s j
1 1 幅频特性:A( ) 1 jT 1 2T 2
1 j ( ) G( j ) A( ) e 1 jT
描述系统对不同频率的输入信号在稳 态情况下的衰减或放大特性 相频特性: () G( j) arctgT 描述系统的稳态输出对于不同频率的 正弦输入信号的相位滞后或超前特性
G( j ) A( )e j ( )
ImG( j ) ReG( j )
Ar G( j ) 2j
G j e jt G j e jt e j[t ( )] e j[t ( )] css t Ar Ar A( ) 2j 2j
1 r ( t ) j( 135o ) A sin t r ( t ) cos t , r .707e 若 (s ) , 则( j1) 0 , css (t ) ! s 1 o o )] 2 ( j ) 若系统稳定 ,则 c ( t ) [ A cos ( j 友情提醒 t 90 ss ] cssr(t ) 0.707 cos(t 135 ) 11 [
b1 G(s) Ar (s j ) s2 2
C (s)
s j
第五章 控制系统的频率响应法概要
第五章 控制系统的频率响应法例5-1 已知某单位负反馈开环频率特性如图5-1所示,试: (1) 写出开环传递函数; (2) 确定ω1,ω2及ω3数值; (3) 求出闭环系统ζ和ωn 值。
(a ) (b) 图5-1 例5-1图 解:由图5-1(b )可写出开环传递函数为)1()11()(21+=+=Ts s Ks s s G ωω可知,。
时当022135)(-=∠=ωωωj G 由图5-1(a )知,5.0212===T T,故此时ω 。
,即,故又40401021==-=-ωK KT )s .s(s G 15040)(+=∴ ,140)(23333==/ωωωj ωG ,=时又ωω 解出:ω3=8.94。
22229489481110294.8405.040)(1)()s (s .s ..s s s s G s G +⨯⨯+=++=+=Φ 其中ωn =8.94,ζ=0.111。
例5-2 已知单位负反馈系统开环传递函数为)14)(1(10)(2++=s s s s G 试分析其稳定性。
解:该系统由放大环节、积分环节、惯性环节和ζ=0的二阶振荡环节串联而成。
2221110)(⎪⎭⎫⎝⎛-+=ωωωωA2021a r c t a n a r c t a n 90)(=⎪⎭⎫ ⎝⎛----=ζωζωωωϕ图5-2 例5-2图;)0(A 0∞→=++时,当ω 随ω增加A (ω)减小;当ω→2时,幅值又增加;当ω=2时A (2) →∞; 之后ω→∞,A (∞)→0。
0000360)(,333)2(,153)2(,90)0(-=∞-=-=-=+-ϕϕϕϕ其频率特性如图5-2所示,在L (ω)>0区间内,有一次负穿越,0=p ,故 Z =0-2(-1)=2,系统不稳定。
例5-3 已知单位反馈控制系统的开环传递函数为)1)(5)(2()(1-++=s s s K s G试画出系统的极坐标频率特性曲线并确定系统稳定性条件。
