二次根式(提高-巩固练习)
沪教版八年级上册数学(全册知识点考点梳理、重点题型分类巩固练习)(提高版)(家教、补习、复习用)

沪教版初二数学上册知识点梳理重点题型(常考知识点)巩固练习二次根式的概念和性质(提高)知识讲解【学习目标】1、理解二次根式的概念,了解被开方数是非负数的理由.2、理解并掌握下列结论:,,,并利用它们进行计算和化简.3、理解并掌握同类二次根式和最简二次根式的概念,能运用二次根式的有关性质进行化简.【要点梳理】要点一、二次根式及代数式的概念1.二次根式:一般地,我们把形如 (a≥0)•的式子叫做二次根式,“”称为二次根号.要点诠释:二次根式的两个要素:①根指数为2;②被开方数为非负数.2.代数式:形如5,a,a+b,ab,,x3,这些式子,用基本的运算符号(基本运算包括加、减、乘、除、乘方、开方)把数和表示数的字母连接起来的式子,我们称这样的式子为代数式.要点二、二次根式的性质1、;2.;3..要点诠释:1.二次根式 (a≥0)的值是非负数。
一个非负数可以写成它的算术平方根的形式,即.2.与要注意区别与联系:1).的取值范围不同,中≥0,中为任意值.2).≥0时, ==; <0时,无意义, =.要点三、最简二次根式(1)被开方数不含有分母;(2)被开方数中不含能开得尽方的因数或因式.满足这两个条件的二次根式叫最简二次根式.要点诠释:二次根式化成最简二次根式主要有以下两种情况:(1) 被开放数是分数或分式;(2)含有能开方的因数或因式.要点四、同类二次根式1.定义:几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式就叫做同类二次根式.要点诠释:(1)判断几个二次根式是否是同类二次根式,必须先将二次根式化成最简二次根式,再看被开方数是否相同;(2)几个二次根式是否是同类二次根式,只与被开方数及根指数有关,而与根号外的因式无关.2.合并同类二次根式合并同类二次根式,只把系数相加减,根指数和被开方数不变(合并同类二次根式的方法与整式加减运算中的合并同类项类似).要点诠释:(1)根号外面的因式就是这个根式的系数;(2)二次根式的系数是带分数的要变成假分数的形式.【典型例题】类型一、二次根式的概念1.(2016春•天津期末)已知y=+﹣4,计算x﹣y2的值.【思路点拨】根据二次根式有意义的条件可得:,解不等式组可得x的值,进而可求出y的值,然后代入x﹣y2求值即可.【答案与解析】解:由题意得:,解得:x=,把x=代入y=+﹣4,得y=﹣4,当x=,y=﹣4时x﹣y2=﹣16=﹣14.【总结升华】此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.举一反三【变式】方程,当时,的取值范围是()A. B.≥2 C. D.≤2【答案】 C.类型二、二次根式的性质2.根据下列条件,求字母x的取值范围:(1); (2).【答案与解析】(1)(2)【总结升华】二次根式性质的运用.举一反三【变式】(2014春•铁东区校级月考)问题探究:因为,所以,因为,所以请你根据以上规律,结合你的以验化简下列各式:(1);(2).【答案】解:(1)==;(2)==.3. (2015•罗平县校级模拟)已知,1≤x≤3,化简: =_______.【思路点拨】由题意1≤x≤3,可以判断1﹣x≤0;x﹣3≤0,然后再直接开平方进行求解.【答案】2.【解析】解:∵1≤x≤3,∴1﹣x≤0,x﹣3≤0,∴=x﹣1+3﹣x=2.【总结升华】此题主要考查二次根式的性质和化简,计算时要仔细,是一道基础题.【:高清: 381279:经典例题4】4.已知为三角形的三边,则=.【答案】.【解析】为三角形的三边, ,即原式==.【总结升华】重点考查二次根式的性质:的同时,复习了三角形三边的性质.类型三、最简二次根式5.已知0<<,化简.【答案与解析】原式===.【总结升华】成立的条件是>0;若<0,则.类型四、同类二次根式6. 如果两个最简二次根式和是同类二次根式,那么、的值是( ) A. =2, =1 B. =1, =2 C. =1, =-1 D. =1, =1 【答案】 D.【解析】根据题意,得,解之,得,故选D.【总结升华】同类二次根式必须满足两个条件:(1)根指数是2;(2)被开方数相同;由此可以得到关于a、b的二元一次方程组,此类问题都可如此.举一反三【变式】若最简根式与根式是同类二次根式,求、的值.【答案】同类二次根式是指几个二次根式化成最简二次根式后,被开方数相同;•事实上,根式不是最简二次根式,因此把化简==|b|×由题意得,∴,∴=1,b=1.沪教版初二数学上册知识点梳理重点题型(常考知识点)巩固练习二次根式的概念和性质(提高)巩固练习【巩固练习】一、选择题1.(2016•贵港)式子在实数范围内有意义,则x的取值范围是()A.x<1 B.x≤1 C.x>1 D.x≥12.使式子有意义的未知数x有( )个A.0 B.1 C.2 D.无数3. 把根号外的因式移到根号内,得().A. B. C. D.4.(2015•蓬溪县校级模拟)下列四个等式:①;②(﹣)=16;③()=4;④.正确的是()A.①②B.③④C.②④D.①③5. 若,则等于()A.B. C. D.6.将中的移到根号内,结果是()A. B. C. D.二. 填空题7. 若最简二次根式与是同类二次根式,则.8. (2015•江干区一模)在,,,﹣,中,是最简二次根式的是_________.9.已知,求的值为____________.10.若,则化简的结果是__________.11. 观察下列各式:,,,……请你探究其中规律,并将第n(n≥1)个等式写出来________________.12.(2016•乐山)在数轴上表示实数a的点如图所示,化简+|a﹣2|的结果为.三. 综合题13. 已知,求的值.14. 若时,试化简.15. (2015春•武昌区期中)已知a、b、c满足+|a﹣c+1|=+,求a+b+c的平方根.【答案与解析】一、选择题1.【答案】C.【解析】依题意得:x﹣1>0,解得x>1.2.【答案】B.3.【答案】C.4.【答案】D.【解析】解:①==4,正确;②=(﹣1)2=1×4=4≠16,不正确;③=4符合二次根式的意义,正确;④==4≠﹣4,不正确.①③正确.故选:D.5.【答案】D.【解析】因为=,即.6.【答案】 A.【解析】因为≤0,所以=.二、填空题7.【答案】1;1.【解析】,所以.8.【答案】.9.【答案】.【解析】,即,,即原式=.10.【答案】3.【解析】因为原式==.11.【答案】 .12.【答案】 3.【解析】由数轴可得:a﹣5<0,a﹣2>0,则+|a﹣2|=5﹣a+a﹣2=3.三、解答题13.【解析】因为,所以2x-1≥0,1-2x≥0,即x=,y=则.14.【解析】因为,所以原式==.15.【解析】解:由题意得,b﹣c≥0且c﹣b≥0,所以,b≥c且c≥b,所以,b=c,所以,等式可变为+|a﹣b+1|=0,由非负数的性质得,,解得,所以,c=2,a+b+c=1+2+2=5,所以,a+b+c的平方根是±.沪教版初二数学上册知识点梳理重点题型(常考知识点)巩固练习二次根式的运算(提高)知识讲解【学习目标】1、理解并掌握二次根式的加减法法则,会合并同类二次根式,进行简单的二次根式加减运算;2、掌握二次根式的乘除法法则和化简二次根式的常用方法,熟练进行二次根式的乘除运算;3、会利用运算律和运算法则进行二次根式的混合运算.【要点梳理】要点一、二次根式的加减二次根式的加减实质就是合并同类二次根式,即先把各个二次根式化成最简二次根式,再把其中的同类二次根式进行合并.对于没有合并的二次根式,仍要写到结果中.要点诠释:(1)在进行二次根式的加减运算时,整式加减运算中的交换律、结合律及去括号、添括号法则仍然适用.(2)二次根式加减运算的步骤:1)将每个二次根式都化简成为最简二次根式;2)判断哪些二次根式是同类二次根式,把同类的二次根式结合为一组;要点二、二次根式的乘法及积的算术平方根1.乘法法则:(≥0,≥0),即两个二次根式相乘,根指数不变,只把被开方数相乘.要点诠释:(1).在运用二次根式的乘法法则进行运算时,一定要注意:公式中a、b都必须是非负数;(在本章中,如果没有特别说明,所有字母都表示非负数).(2).该法则可以推广到多个二次根式相乘的运算:≥0,≥0,…..≥0).(3).若二次根式相乘的结果能写成的形式,则应化简,如.2.积的算术平方根:(≥0,≥0),即积的算术平方根等于积中各因式的算术平方根的积.要点诠释:(1)在这个性质中,a、b可以是数,也可以是代数式,无论是数,还是代数式,都必须满足≥0,≥0,才能用此式进行计算或化简,如果不满足这个条件,等式右边就没有意义,等式也就不能成立了; (2)二次根式的化简关键是将被开方数分解因数,把含有形式的a移到根号外面.要点三、二次根式的除法及商的算术平方根1.除法法则:(≥0, >0),即两个二次根式相除,根指数不变,把被开方数相除.。
人教版数学八年级下册《二次根式》巩固练习

16.1二次根式巩固练习(一)一、单选题1.下列计算正确的是()A.√2+√2=2B.(a3)2=a53=−2C.(π−3.14)0=0D.√−82.式子√x−1有意义,则x的取值范围是()A.x>1B.x<1C.x≥1D.x≤1 3.若√a2+a=0,则a的取值范围是()A.a>0B.a<0C.a≥0D.a≤0 4.如果一个三角形的三边长分别为1、k、3,化简7−√4k2−36k+81+|2k−3|结果是()A.4k—5B.1C.13D.19—4k 5.计算√(−5)2的结果为()A.√5B.±5C.-5D.5 6.若|3−a|+√2+b=0,则a+b的值是()A.2B.1C.0D.−1 7.若√x−1+√x+y=0,则x2005+y2005的值为:()A.0B.1C.-1D.2 8.如果√−53−x是二次根式,那么x 应适合的条件是()A.x ≥3B.x ≤3C.x >3D.x <3 9.计算√(−11)2+|-11|- √112,正确的结果是()A.-11B.11C.22D.-22 10.已知是正整数,则实数n的最大值为()A.12B.11C.8D.3二、填空题11.若y=√x2−4+√4−x2+3,则√(x−y)2=.12.若√x−1+(y+2)2=0,则(x+y)2017= .13.观察下列各式:√1+13=2√13,√2+14=3√14,√3+15=4√15,┉┉ 请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是.14.如果(x﹣√x2−2008)(y﹣√y2−2008)=2008,求3x2﹣2y2+3x﹣3y﹣2007=.15.已知,y=√(x−3)2+4−x,当x分别取1,2,3,…,2021时,所对应的y值的总和是 .三、解答题16.已知 y =√|x|−3+√3−|x|+12x−3,求 x 2y 的值.17.若 x , y 为实数,且 x =√y 2−1+√1−y 2+y y+1,求 x −3+y 的值.18.如图,以直角三角形AOC 的直角顶点O 为原点,以 OA ,OC 所在直线为x 轴,y轴建立平面直角坐标系,点 A(0,a),C(c ,0) 满足 √a −2c +|c −4|=0 (1)则 C 点的坐标为 ; A 点的坐标为 . (2)直角三角形 AOC 的面积为 .(3)已知坐标轴上有两动点 P 、Q 同时出发, P 点从 C 点出发沿 x 轴负方向以1个单位长度每秒的速度匀速移动, Q 点从 O 点出发以2个单位长度每秒的速度沿 y 轴正方向移动,点 Q 到达 A 点整个运动随之结束. AC 的中点 D 的坐标是 (2,4) ,设运动时间为t (t >0)秒,问:是否存在这样的t 使 S △ODP =S △ODQ ?若存在,请求出 t 的值;若不存在,请说明理由.四、综合题19.比较大小,并说理:.(1)√35与6;(2)−√5+1与−√2220.先阅读下面的解题过程,然后再解答,形如√m±2√n的化简,我们只要找到两个数a,b,使a+b=m,ab=n,即(√a)2+(√b)2=m,√a⋅√b=√n,那么便有:√m±2√n=√(√a±√b)2=√a±√b(a>b>0).例如化简:√7+4√3解:首先把√7+4√3化为√7+2√12,这里m=7,n=12,由于4+3=7,4×3=12,所以(√4)2+(√3)2=7,√4×√3=√12,所以√7+4√3=√7+2√12=√(√4+√3)2=2+√3(1)根据上述方法化简:√4+2√3(2)根据上述方法化简:√13−2√42(3)根据上述方法化简:√4−√1521.如图,在平面直角坐标系中,点A,B的坐标分别为(a,0),(b,0),且a,b满足a=√b−3+√3−b−1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(1)求点C,D的坐标和四边形ABDC的面积S面积ABDC.(2)在y轴上是否存在一点P,连接PA,PB,使SΔPAB=S四边形ABDC,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①∠DCP+∠BOP ∠CPO的值不变,②∠DCP+∠CPO ∠BOP的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.22.阅读材料:材料一:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号,如: √(√1)2+(√2)2−2×√1×√2=√(√1−√2)2=|√1−√2|=√2−1材料二:配方法是初中数学思想方法中的一种重要的解题方法,配方法的最终目的就是配成完全平方式,利用完全平方式来解决问题,它的应用非常广泛,在解方程、化简根式、因式分解等方面都经常 用到.如: x 2+2√2x +3=x 2+2·√2·x +(√2)2+1=(x +√2)2+1 ∵(x +√2)2≥0 ,∴(x +√2)2+1≥1 ,即 x 2+2√2x +3≥1∴x 2+2√2x +3 的最小值为 1阅读上述材料解决下面问题:(1)√4−2√3=,√5+2√6=;(2)求x2+4√3x+11的最值;(3)已知x=√3−√13−4√3,求−14(4+2√3)x2y2+(√3+1)xy−5的最值.23.已知在平面直角坐标系中,点A(a,b)满足12√a−3+(2−b)2=0,AB⊥x轴垂足为B.(1)点A的坐标为,点B的坐标为;(2)如图1,若点M在坐标轴上,连接MA,使S△ABM=2S△ABO,求出点M的坐标;(3)如图2,P是线段AB所在直线上一动点,连接OP,N为y轴负半轴上一点,OE平分∠PON,交直线AB于点E,作OF⊥OE,当点P在直线AB上运动过程中,请探究∠OPE与∠FOP的数量关系,并证明.答案解析1.【答案】D【解析】解:A. √2+√2=2√2,故本选项错误;B. (a3)2=a3×2=a6,故本选项错误;C. (π−3.14)0=1,故本选项错误;D. √−83=−2,故本选项正确.故答案为:D.2.【答案】C【解析】根据二次根式的被开方数是非负数列出不等式x-1≥0,通过解该不等式即可求得x 的取值范围.【解答】根据题意,得x-1≥0,解得,x≥1.故选C.3.【答案】D【解析】解:已知等式变形得:√a2=|a|=﹣a,∴a≤0,故选D.4.【答案】A【解析】因为三角形三边长分别为1、k、3,所以3-1<k<3+1,即2<k<4,所以原式=7-√(2k−9)2+|2k-3|=7-(9-2k)+2k-3=4k-5,故答案为:A.5.【答案】D【解析】解:√(−5)2=5.故答案为:D.6.【答案】B【解析】解:由题意得,3﹣a=0,2+b=0,解得,a=3,b=﹣2,a+b=1.故答案为:B.7.【答案】A【解析】由√x−1+√x+y=0,得x-1=0,x+y=0,解得x=1,y=-1,所以x2005+y2005 =12005+(−1)2005=1-1=0,故选A.8.【答案】C【解析】因为原式是二次根式,所以−53−x≥0,3-xǂ0,所以3-x<0,所以x>3,故选C.9.【答案】B【解析】原式=11+11-11=11,故选B . 10.【答案】B【解析】解答:由题意是正整数所以>0,且n 为整数,所以12-n>0,所以n<12,所以n 最大取11,故选B11.【答案】1或5或1【解析】解:依题意可得 {x 2−4≥04−x 2≥0∴x=2或x=-2, 故y=3∴√(x −y)2 = √(2−3)2=1 ; 或 √(x −y)2 = √(−2−3)2=5. 故答案为:1或5.12.【答案】-1【解析】由题意得,x-1=0,y+2=0,解得x=1,y=-2,所以(x+y)2017=(1-2)2017=-1. 故答案为:-1.13.【答案】√n +1n+2=(n +1)√1n+2【解析】观察可得 √1+11+2=(1+1)√11+2 ; √2+12+2=(2+1)√12+2;√3+13+2=(3+1)√13+2 ;…由此可得规律,用含自然数n (n≥1)的等式表示出来是√n +1n+2=(n +1)√1n+2 . 14.【答案】1【解析】解:设a= √x 2−2008 ,b= √y 2−2008 ,则x 2﹣a 2=y 2﹣b 2=2008,∴(x+a )(x ﹣a )=(y+b )(y ﹣b )=2008① ∵(x ﹣a )(y ﹣b )=2008② ∴由①②得 x+a=y ﹣b ,x ﹣a=y+b ∴x=y ,a+b=0,∴√x 2−2008 + √y 2−2008 =0, ∴x 2=y 2=2008,∴3x 2﹣2y 2+3x ﹣3y ﹣2007=3×2008﹣2×2008+3(x ﹣y )﹣2007=2008+3×0﹣2007=1.故答案为:115.【答案】2027【解析】解:由二次函数的性质,则y=√(x−3)2+4−x=|x−3|+4−x,当x≤3时,y=−(x−3)+4−x=−2x+7;当x>3时,y=(x−3)+4−x=1;∴对应的y值的总和是:5+3+1+⋯+1 = 8+1×2019= 2027;故答案为:2027.16.【答案】解:∵y=√|x|−3+√3−|x|+12x−3,∴{|x|−3≥0 3−|x|≥0 x−3≠0∴|x|=3且x≠3,∴x=−3,∴y=0+0+12−3−3=−2,∴x2y=(−3)2×(−2)=−18. 17.【答案】解:由题意得,y2-1≥0且1-y2≥0,所以,y2≥1且y2≤1,所以,y2=1所以,y=±1,又∵y+1≠0,∴y≠-1,所以,y=1,所以,x=11+1=12,∴x−3+y=(12)−3+1=918.【答案】(1)∵√a−2c+|c﹣4|=0,∴c﹣4=0,a﹣2c=0,解得:c=4,a=8,∴C(4,0),A(0,8).故答案为(4,0),(0,8);(2)直角三角形AOC的面积= 12AO×OC= 12×8×4=16;(3)解:存在.由条件可知P点从C点运动到O点的时间为4秒,Q点从O点运动到A点的时间为4秒,∴当0<t≤4时,点Q在线段AO上,点P在线段OC上,由题意可得:CP=t,OP=4-t,OQ=2t,AQ=8-2t,D(2,4),SΔDOP=12OP⋅yD=12(4−t)×4=8−2t,SΔDOQ=12OQ⋅x=12×2t×2=2t.∵S┉ODP=S┉ODQ,∴8﹣2t=2t,∴解得:t=2.19.【答案】(1)解:因为6= √36,√35<√36,所以√35<6.(2)解:因为−√5+1−(−√22)= −2√5+2+√22= (−√5+2)+(−√5+√2)2<0,所以−√5+1<−√22.20.【答案】(1)解:∵√4+2√3,∴m=4,n=3,∵3+1=4,3×1=3,∴(√3)2+(√1)2=4,√3×√1=√3,∴√4+2√3=√(√3)2+(√1)2+2×√3×√1=√(√3+√1)2=√3+1;(2)解:∵√13−2√42,∴m=13,n=42,∵7+6=13,7×6=42,∴(√7)2+(√6)2=13,√7×√6=√42,∴√13−2√42√(√7)2+(√6)2−2×√7×√6=√(√7−√6)2=√7−√6.(3)解:∵√4−√15=√12(8−2√15)=√22√8−2√15,∴m=8,n=15,∵3+5=8,3×5=15,∴(√3)2+(√5)2=8,√3×√5=√15,∴√4−√15=√12((√3)2+(√5)2−2×√3×√5)=√22√(√5−√3)2=√102−√62. 21.【答案】(1)解:∵a =√b −3+√3−b −1 ∴b =3,a =−1,∴点A (−1,0),点B (3,0),∵将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,∴点C (0,2),点D (4,2);∴AB =4,OC =2∴S 面积ABDC =AB ×OC =4×2=8(2)解:存在,点P (0,4)或(0,−4);理由如下,∵点A (−1,0),点B (3,0),点C (0,2),∴AB =4,OC =2,∴四边形ABDC 的面积=2×4=8,设点P (0,y ),∵┉ABP 的面积与四边形ABDC 的面积相等,∴12×4×|y|=8, ∴y =±4,∴点P (0,4)或(0,−4);(3)解:∠DCP+∠BOP ∠CPO=1,比值不变. 理由如下:由平移的性质可得AB┉CD ,如图,过点P 作PE┉AB ,则PE┉CD ,∴┉DCP =┉CPE ,┉BOP =┉OPE ,∴┉CPO =┉CPE +┉OPE =┉DCP +┉BOP ,∴∠DCP+∠BOP ∠CPO=1,比值不变. 故①正确,②错误22.【答案】解:(1)√4−2√3=√(√3−1)2=|√3−1|=√3−1,√5+2√6=√(√3+√2)2=|√3+√2|=√3+√2;故答案为:√3−1,√3+√2;(2)∵x2+4√3x+11= x2+4√3x+12−1= (x+2√3)2−1≥-1∴x2+4√3x+11的最小值为- 1;(3)∵x=√3−√13−4√3= √3−√(2√3−1)2=√3−(2√3−1)=√4−2√3=√3−1∴−14(4+2√3)x2y2+(√3+1)xy−5= −14(4+2√3)(4−2√3)y2+(√3+1)(√3−1)y−5 = −y2+2y−5= −(y−1)2−4≤-4故−14(4+2√3)x2y2+(√3+1)xy−5的最大值为-4.23.【答案】(1)∵12√a−3+(2−b)2=0,∴√a−3=0,(2−b)2=0∴a−3=0,2−b=0,∴a=3,b=2,∴点A(3,2),∵AB⊥x轴,∴OB=3,∴B(3,0);故答案为:(3,2),(3,0);(2)解:若点M在x轴上时,设M(m,0)∵OB=3,AB=2∴S△ABM=2S△ABO=12×2|m−3|=2×12×3×2=6解得,m=9或m=−3∴M(9,0)或(−3,0)若点M在y轴上时不成立(3)解:∠OPE=2∠FOP∵OE平分∠PON∴∠POE=∠NOE∵AB∥y轴∴∠OPE+∠NOP=180°,即∠OPE=180°−2∠POE ∵OF⊥OE∴∠FOE=90°∴∠FOP=90°−∠POE ∴∠OPE=2∠FOP。
二次根式的计算200 题

1
√6
÷
3
√2
.
1
6.计算:√72 ÷ 3√2 × √2 .
7.计算:√18 × √2.
2
8.计算:√ × √12.
3
1
2
9.计算:√45 ÷ √ × √2 .
被开方数中不含能开得尽方的因数或因式)
2.合并
将同类二次根式进行合并
易错总结:
① 不是最简二次根式的要化成最简二次根式
② 去括号时括号外如果是负号括号里的符号要变号
③ 注意同类二次根式要合并
例题解析:
1
1
3
3√18 − √32 + 4√ + √−8.
8
2
1
解:原式= 3 × 3√2 − × 4√2 + 4 ×
4
3
38.计算:(√48 − 4√ ) − (3√ − 2√0.5).
39.计算:√8 + 2√3 − (√27 − √2).
2
1
1
40.计算:√125 + 3√ − √24 + 3√ .
27
5
4
\ 5 /
3
1
41.计算: √4 + 2√ − √ + 2√ .
2
2
9
1
1
1
42.计算:(√48 − 4√8) − (3√3 − 2 √8).
3
\ 4 /
1
1
32.计算:3√5 + 2√ − √20 − √32.
2
2
33.计算:√18 − √50 − √8.
1
34.计算:√ + √24 − √600.
二次根式练习题含答案

一、选择题
1.已知 =5﹣x,则x的取值范围是( )
A.为任意实数B.0≤x≤5C.x≥5D.x≤5
2.若 ,则 ( ).
A. B. C. D.
3.下列计算正确的是()
A. B.
C. D.
4.下列计算正确的是()
A. B. C. D.
5.下列算式:(1) ;(2) ;(3) = ;(4) ,其中正确的是()
请模仿小明的方法探索并解决下列问题:
(1)当 为正整数时,若 ,请用含有 的式子分别表示 ,得: , ;
(2)填空: = - ;
(3)若 ,且 为正整数,求 的值.
【答案】(1) , ;(2) ;(3) 或46.
【解析】
试题分析:
(1)把等式 右边展开,参考范例中的方法即可求得本题答案;
(2)由(1)中结论可得: ,结合 都为正整数可得:m=2,n=1,这样就可得到: ;
=-10.
【点睛】
此题主要考查了二次根式的化简,熟练掌握二次根式的性质是解答此题的关键.
25.先观察下列等式,再回答下列问题:
① ;
②
③
(1)请你根据上面三个等式提供的信息,猜想 的结果,并验证;
(2)请你按照上面各等式反映的规律,用含n的等式表示(n为正整数).
【答案】(1) (2) (n为正整数)
【详解】
=
=
= .
【点睛】
此题考查二次根式的混合运算,二次根式的化简,正确掌握二次根式的化简法则是解题的关键.
22.观察下列各式子,并回答下面问题.
第一个:
第二个:
第三个:
第四个: …
(1)试写出第 个式子(用含 的表达式表示),这个式子一定是二次根式吗?为什么?
二次根式 专题练习(含答案)

二次根式专题练习(含答案)一.选择题(共10小题)1.如果ab>0,a+b<0,那么下面各式:①=,②•=1,③÷=﹣b,其中正确的是()A.①②B.②③C.①③D.①②③2.已知:m,n是两个连续自然数(m<n),且q=mn.设,则p()A.总是奇数B.总是偶数C.有时是奇数,有时是偶数D.有时是有理数,有时是无理数3.化简二次根式的结果是()A.B. C.D.4.已知,,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于()A.﹣5 B.5 C.﹣9 D.95.若实数a满足方程,则[a]=(),其中[a]表示不超过a的最大整数.A.0 B.1 C.2 D.36.若实数x,y满足x﹣y+1=0且1<y<2,化简得()A.7 B.2x+2y﹣7 C.11 D.9﹣4y7.已知a﹣b=2+,b﹣c=2﹣,则a2+b2+c2﹣ab﹣bc﹣ac的值为()A.10B.12C.10 D.158.下列计算中正确的是()A. B.C.D.9.若实数a,b满足+=3,﹣=3k,则k的取值范围是()A.﹣3≤k≤2B.﹣3≤k≤3C.﹣1≤k≤1D.k≥﹣110.已知,,则的值为()A.3 B.4 C.5 D.6二.填空题(共8小题)11.二次根式中字母x的取值范围是.12.若y=++2,则x y=.13.若=3﹣x,则x的取值范围是.14.已知a、b为有理数,m、n分别表示的整数部分和小数部分,且amn+bn2=1,则2a+b=.15.已知xy=3,那么的值是.16.当﹣4≤x≤1时,不等式始终成立,则满足条件的最小整数m=.17.若a、b、c三个数在数轴上对应点的位置如图所示,化简:=.18.设,,,…,.设,则S=(用含n的代数式表示,其中n为正整数).三.解答题(共10小题)19.化简求值:,其中.20.已知:a=,b=.求代数式的值.21.已知:,求的值.22.阅读下面问题:;;.试求:(1)的值;(2)的值;(3)(n为正整数)的值.23.阅读下列材料,然后回答问题:在进行二次根式运算时,我们有时会碰上如、这样的式子,其实我们还可以将其进一步化简:;.以上这种化简过程叫做分母有理化.还可以用以下方法化简:.(1)请用其中一种方法化简;(2)化简:.24.已知y=+2,求+﹣2的值.25.已知x=,y=,且19x2+123xy+19y2=1985.试求正整数n.26.观察下列等式:①==﹣1②==﹣③==﹣…回答下列问题:(1)化简:=;(n为正整数)(2)利用上面所揭示的规律计算:+++…++.27.先阅读下列的解答过程,然后再解答:形如的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得+=m,=,那么便有:==±(a>b).例如:化简.解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12即+=7,×=∴===2+.由上述例题的方法化简:.28.阅读下列解题过程:;.请回答下列问题:(1)观察上面的解题过程,请直接写出式子=;(2)利用上面所提供的解法,请化简:的值.参考答案与试题解析一.选择题(共10小题)1.如果ab>0,a+b<0,那么下面各式:①=,②•=1,③÷=﹣b,其中正确的是()A.①②B.②③C.①③D.①②③【分析】由ab>0,a+b<0先求出a<0,b<0,再进行根号内的运算.【解答】解:∵ab>0,a+b<0,∴a<0,b<0①=,被开方数应≥0,a,b不能做被开方数,(故①错误),②•=1,•===1,(故②正确),③÷=﹣b,÷=÷=×=﹣b,(故③正确).故选:B.【点评】本题是考查二次根式的乘除法,解答本题的关键是明确a<0,b<0.2.已知:m,n是两个连续自然数(m<n),且q=mn.设,则p()A.总是奇数B.总是偶数C.有时是奇数,有时是偶数D.有时是有理数,有时是无理数【分析】m、n是两个连续自然数(m<n),则n=m+1,所以q=m(m+1),所以q+n=m(m+1)+m+1=(m+1)2,q﹣m=m(m+1)﹣m=m2,代入计算,再看结果的形式符合偶数还是奇数的形式.【解答】解:m、n是两个连续自然数(m<n),则n=m+1,∵q=mn,∴q=m(m+1),∴q+n=m(m+1)+m+1=(m+1)2,q﹣m=m(m+1)﹣m=m2,∴=m+1+m=2m+1,即p的值总是奇数.故选A.【点评】本题的关键是根据已知条件求出p的值,判断p的值.3.化简二次根式的结果是()A.B. C.D.【分析】根据二次根式找出隐含条件a+2≤0,即a≤﹣2,再化简.【解答】解:若二次根式有意义,则﹣≥0,﹣a﹣2≥0,解得a≤﹣2,∴原式==.故选B.【点评】本题考查了二次根式的化简,注意要化简成最简二次根式,且不改变原式符号.4.已知,,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于()A.﹣5 B.5 C.﹣9 D.9【分析】观察已知等式可知,两个括号里分别有m2﹣2m,n2﹣2n的结构,可由已知m、n的值移项,平方得出m2﹣2m,n2﹣2n的值,代入已知等式即可.【解答】解:由m=1+得m﹣1=,两边平方,得m2﹣2m+1=2即m2﹣2m=1,同理得n2﹣2n=1.又(7m2﹣14m+a)(3n2﹣6n﹣7)=8,所以(7+a)(3﹣7)=8,解得a=﹣9故选C.【点评】本题考查了二次根式的灵活运用,直接将m、n的值代入,可能使运算复杂,可以先求部分代数式的值.5.若实数a满足方程,则[a]=(),其中[a]表示不超过a的最大整数.A.0 B.1 C.2 D.3【分析】对已知条件变形整理并平方,解方程即可得到a的值,求出后直接选取答案.【解答】解:根据二次根式有意义的条件,可得a≥1.原方程可以变形为:a﹣=,两边同平方得:a2+1﹣﹣2a=a﹣,a2+1﹣2=a.a2﹣a﹣2+1=0,解得=1,∴a2﹣a=1,a=(负值舍去).a≈1.618.所以[a]=1,故选B.【点评】此题首先能够根据二次根式有意义的条件求得a的取值范围,然后通过平方的方法去掉根号.灵活运用了完全平方公式.6.若实数x,y满足x﹣y+1=0且1<y<2,化简得()A.7 B.2x+2y﹣7 C.11 D.9﹣4y【分析】求出y=x+1,根据y的范围求出x的范围是0<x<1,把y=x+1代入得出+2,推出+2,根据二次根式的性质得出|2x+1|+2|x﹣3|,根据x的范围去掉绝对值符号求出即可.【解答】解:∵x﹣y+1=0,∴y=x+1,∵1<y<2,∴1<x+1<2,∴0<x<1,∴,=+2,=+2,=+2,=|2x+1|+2|x﹣3|,=2x+1+2(3﹣x),=7,故选A.【点评】本题考查了完全平方公式,二次根式的性质,绝对值等知识点的应用,主要考查学生综合运用性质进行化简和计算的能力,题目具有一定的代表性,但是一道比较容易出错的题目,有一定的难度.7.已知a﹣b=2+,b﹣c=2﹣,则a2+b2+c2﹣ab﹣bc﹣ac的值为()A.10B.12C.10 D.15【分析】由a﹣b=2+,b﹣c=2﹣可得,a﹣c=4然后整体代入.【解答】解:∵a﹣b=2+,b﹣c=2﹣,∴a﹣c=4,∴原式====15.故选D.【点评】此题的关键是把原式转化为的形式,再整体代入.8.下列计算中正确的是()A. B.C.D.【分析】根据二次根式的性质对各选项分析判断后利用排除法求解.【解答】解:A、+不能进行运算,故本选项错误;B、==×,负数没有算术平方根,故本选项错误;C、x﹣x=(﹣)x,故本选项正确;D、不能进行运算,=a+b,故本选项错误.故选C.【点评】本题考查了二次根式的性质与混合运算,是基础题,比较简单,但容易出错.9.若实数a,b满足+=3,﹣=3k,则k的取值范围是()A.﹣3≤k≤2B.﹣3≤k≤3C.﹣1≤k≤1D.k≥﹣1【分析】依据二次根式有意义的条件即可求得k的范围.【解答】解:若实数a,b满足+=3,又有≥0,≥0,故有0≤≤3 ①,0≤≤3,则﹣3≤≤0 ②①+②可得﹣3≤﹣≤3,又有﹣=3k,即﹣3≤3k≤3,化简可得﹣1≤k≤1.故选C.【点评】主要考查了二次根式的意义和性质.概念:式子(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.10.已知,,则的值为()A.3 B.4 C.5 D.6【分析】先分母有理化求出a、b的值,再求出a2+b2的值,代入求出即可.【解答】解:∵a===+2,b==﹣2,∴a2+b2=(a﹣b)2+2ab=42+2×(5﹣4)=18,∴==5,故选C.【点评】本题考查了分母有理化,二次根式的化简,关键是求出a、b和a2+b2的值,题目比较好,难度适中.二.填空题(共8小题)11.二次根式中字母x的取值范围是x≥3.【分析】由二次根式有意义的条件得出不等式,解不等式即可.【解答】解:当x﹣3≥0时,二次根式有意义,则x≥3;故答案为:x≥3.【点评】本题考查了二次根式有意义的条件、不等式的解法;熟记二次根式有意义的条件是解决问题的关键.12.若y=++2,则x y=9.【分析】根据二次根式有意义的条件得出x﹣3≥0,3﹣x≥0,求出x,代入求出y即可.【解答】解:y=有意义,必须x﹣3≥0,3﹣x≥0,解得:x=3,代入得:y=0+0+2=2,∴x y=32=9.故答案为:9.【点评】本题主要考查对二次根式有意义的条件的理解和掌握,能求出x y的值是解此题的关键.13.若=3﹣x,则x的取值范围是x≤3.【分析】根据二次根式的性质得出3﹣x≥0,求出即可.【解答】解:∵=3﹣x,∴3﹣x≥0,解得:x≤3,故答案为:x≤3.【点评】本题考查了二次根式的性质的应用,注意:当a≥0时,=a,当a<0时,=﹣a.14.已知a、b为有理数,m、n分别表示的整数部分和小数部分,且amn+bn2=1,则2a+b= 2.5.【分析】只需首先对估算出大小,从而求出其整数部分a,其小数部分用﹣a表示.再分别代入amn+bn2=1进行计算.【解答】解:因为2<<3,所以2<5﹣<3,故m=2,n=5﹣﹣2=3﹣.把m=2,n=3﹣代入amn+bn2=1得,2(3﹣)a+(3﹣)2b=1化简得(6a+16b)﹣(2a+6b)=1,等式两边相对照,因为结果不含,所以6a+16b=1且2a+6b=0,解得a=1.5,b=﹣0.5.所以2a+b=3﹣0.5=2.5.故答案为:2.5.【点评】本题主要考查了无理数大小的估算和二次根式的混合运算.能够正确估算出一个较复杂的无理数的大小是解决此类问题的关键.15.已知xy=3,那么的值是±2.【分析】先化简,再分同正或同负两种情况作答.【解答】解:因为xy=3,所以x、y同号,于是原式=x+y=+,当x>0,y>0时,原式=+=2;当x<0,y<0时,原式=﹣+(﹣)=﹣2.故原式=±2.【点评】此题比较复杂,解答此题时要注意x,y同正或同负两种情况讨论.16.当﹣4≤x≤1时,不等式始终成立,则满足条件的最小整数m=4.【分析】根据x的取值范围确定m的取值范围,然后在其取值范围内求得最小的整数.【解答】解:∵﹣4≤x≤1,∴4+x≥0,1﹣x≥0,∴不等式两边平方得:m2>5+2∵当x=﹣1.5时,最大为2.5,∴m2>10∴满足条件的最小的整数为4.故答案为4.【点评】本题考查了二次根式有意义的条件,关键是确定m的取值范围.17.若a、b、c三个数在数轴上对应点的位置如图所示,化简:=3.【分析】先根据数轴判断出a、b、c的大小及符号,再根据有绝对值的性质及二次根式的定义解答.【解答】解:由数轴上各点的位置可知,a<b<0,c>0,|a|>|b|>c,∴=﹣a;|a﹣b|=b﹣a;|a+b|=﹣(a+b);|﹣3c|=3c;|a+c|=﹣(a+c);故原式====3.故答案是:3.【点评】解答此题的关键是根据数轴上字母的位置判断其大小,再根据绝对值的规律计算.绝对值的规律:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.18.设,,,…,.设,则S=(用含n的代数式表示,其中n为正整数).【分析】由S n=1++===,求,得出一般规律.【解答】解:∵S n=1++===,∴==1+=1+﹣,∴S=1+1﹣+1+﹣+…+1+﹣=n+1﹣==.故答案为:.【点评】本题考查了二次根式的化简求值.关键是由S n变形,得出一般规律,寻找抵消规律.三.解答题(共10小题)19.化简求值:,其中.【分析】由a=2+,b=2﹣,得到a+b=4,ab=1,且a>0,b>0,再把代数式利用因式分解的方法得到原式=+,约分后得+,接着分母有理化和通分得到原式=,然后根据整体思想进行计算.【解答】解:∵a=2+>0,b=2﹣>0,∴a+b=4,ab=1,∴原式=+=+=+=,当a+b=4,ab=1,原式=×=4.【点评】本题考查了二次根式的化简求值:先把各二次根式化为最简二次根式,再合并同类二次根式,然后把字母的值代入(或整体代入)进行计算.20.已知:a=,b=.求代数式的值.【分析】先求得a+b=10,ab=1,再把求值的式子化为a与b的和与积的形式,将整体代入求值即可.【解答】解:由已知,得a+b=10,ab=1,∴===.【点评】本题关键是先求出a+b、ab的值,再将被开方数变形,整体代值.21.已知:,求的值.【分析】首先化简a=2﹣,然后根据约分的方法和二次根式的性质进行化简,最后代入计算.【解答】解:∵a==2﹣<1,∴原式==a﹣3+=2﹣﹣3+2+=1.【点评】此题中注意:当a<1时,有=1﹣a.22.阅读下面问题:;;.试求:(1)的值;(2)的值;(3)(n为正整数)的值.【分析】观察问题中的三个式子,不难发现规律:用平方差公式完成分母有理化.【解答】解:(1)原式==;(2)原式==;(3)原式==.【点评】要将中的根号去掉,要用平方差公式()()=a﹣b.23.阅读下列材料,然后回答问题:在进行二次根式运算时,我们有时会碰上如、这样的式子,其实我们还可以将其进一步化简:;.以上这种化简过程叫做分母有理化.还可以用以下方法化简:.(1)请用其中一种方法化简;(2)化简:.【分析】(1)运用第二种方法求解,(2)先把每一个加数进行分母有理化,再找出规律后面的第二项和前面的第一项抵消,得出答案,【解答】解:(1)原式==;(2)原式=+++…=﹣1+﹣+﹣+…﹣=﹣1=3﹣1【点评】本题主要考查了分母有理化,解题的关键是找准有理化因式.24.已知y=+2,求+﹣2的值.【分析】由二次根式有意义的条件可知1﹣8x=0,从而可求得x、y的值,然后将x、y的值代入计算即可.【解答】解:由二次根式有意义的条件可知:1﹣8x=0,解得:x=.当x=,y=2时,原式==﹣2=+4﹣2=2.【点评】本题主要考查的是二次根式有意义的条件,掌握二次根式的被开方数大于等于零是解题的关键.25.已知x=,y=,且19x2+123xy+19y2=1985.试求正整数n.【分析】首先化简x与y,可得:x=()2=2n+1﹣2,y=2n+1+2,所以x+y=4n+2,xy=1;将所得结果看作整体代入方程,化简即可求得.【解答】解:化简x与y得:x=,y=,∴x+y=4n+2,xy=1,∴将xy=1代入方程,化简得:x2+y2=98,∴(x+y)2=x2+y2+2xy=98+2×1=100,∴x+y=10.∴4n+2=10,解得n=2.【点评】此题考查了二次根式的分母有理化.解题的关键是整体代入思想的应用.26.观察下列等式:①==﹣1②==﹣③==﹣…回答下列问题:(1)化简:=;(n为正整数)(2)利用上面所揭示的规律计算:+++…++.【分析】(1)根据平方差公式,进行分母有理化,即可解答;(2)根据(1)中的规律化简,即可解答.【解答】解:(1)=;故答案为:.(2)+++…++=…+=﹣1.【点评】本题考查了分母有理化,解决本题的关键是发现分母有理化的规律.27.先阅读下列的解答过程,然后再解答:形如的化简,只要我们找到两个数a、b,使a+b=m,ab=n,使得+=m,=,那么便有:==±(a>b).例如:化简.解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12即+=7,×=∴===2+.由上述例题的方法化简:.【分析】应先找到哪两个数的和为13,积为42.再判断是选择加法,还是减法.【解答】解:根据,可得m=13,n=42,∵6+7=13,6×7=42,∴==.【点评】解题关键是把根号内的式子整理为完全平方的形式.28.阅读下列解题过程:;.请回答下列问题:(1)观察上面的解题过程,请直接写出式子=;(2)利用上面所提供的解法,请化简:的值.【分析】(1)通过观察题目中的解题过程可以看出:相邻的两个数算术平方根的和的倒数等于它们算术平方根的差;(2)根据规律,先化简成二次根式的加减运算,再进行计算就可以了.【解答】解:(1)=;(2)由题意可知:==.【点评】本题考查的是分式的加减运算,同时还考查了根据题目的已知来获取信息的能力,总结规律并运用规律是近年中考的热点之一.。
二次根式练习题及答案

二次根式练习题1.如果二次根式有意义,那么x应该满足的条件是.2.若两个最简二次根式与是同类二次根式,则a =.3.已知,则x2﹣4x+1的值为.4.关于x的代数式有意义,满足条件的所有整数x的和是9,则a的取值范围.5.已知,.则(1)x2+y2=.(2)(x﹣y)2﹣xy=.6.若x=1+,则x3﹣3x2+2x﹣=.7.实数a、b满足,则a2+b2的最大值为.8.已知x=,y=,且19x2+123xy+19y2=1985,则正整数n的值为.9.计算:(1)82014×(﹣0.125)2015;(2)﹣﹣(π+2020)0.10.计算题:(1)(3+)(3﹣)﹣(﹣1)2;(2)(2﹣3).11.一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2.设a+b(其中a、b、m、n均为正整数),则有a+b =m2+2n2+2mn,∴a=m2+2n2,b=2mn.这样可以把部分a+b的式子化为平方式的方法.请你仿照上述的方法探索并解决下列问题:(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得:a=,b=.(2)利用所探索的结论,找一组正整数a、b、m、n填空:+=(+)2;(3)化简参考答案与试题解析1.如果二次根式有意义,那么x应该满足的条件是x≤,且x.【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.【解答】解:由题意得,2x+1≠0,且2﹣3x≥0,解得x≤,且x.故答案为:x≤,且x.【点评】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.2.若两个最简二次根式与是同类二次根式,则a=2.【分析】根据一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式列出方程求a即可.【解答】解:∵3a﹣1=11﹣3a,∴6a=12,∴a=2.故答案为:2.【点评】本题考查了同类二次根式,最简二次根式,掌握一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式是解题的关键.3.已知,则x2﹣4x+1的值为2.【分析】先根据分母有理化求出x值,然后利用完全平方公式对代数式变形,再代入数据求解即可.【解答】解:===,x2﹣4x+1=x2﹣4x+4﹣4+1=(x﹣2)2﹣3,把代入上式中,原式===2,故答案为:2.【点评】本题主要考查了代数式求值,二次根式的运算,分母有理化等知识点,解题的关键在于能够利用完全平方公式对代数式进行变形求解.4.关于x的代数式有意义,满足条件的所有整数x的和是9,则a的取值范围﹣1<a≤0.【分析】根据二次根式的被开方数是非负数求出x的取值范围,根据满足条件的所有整数x的和是9,得到x=4,3,2,从而1<a+2≤2,从而得出答案.【解答】解:∵4﹣x≥0,x﹣a﹣2≥0,∴a+2≤x≤4,∵满足条件的所有整数x的和是9,∴x=4,3,2,∴1<a+2≤2,∴﹣1<a≤0.故答案为:﹣1<a≤0.【点评】本题考查了二次根式有意义的条件,根据二次根式的被开方数是非负数求出x 的取值范围是解题的关键.5.已知,.则(1)x2+y2=14.(2)(x﹣y)2﹣xy=11.【分析】(1)先分母有理化求出x,再去求x﹣y和xy的值,根据完全平方公式进行变形,最后代入求出答案即可;(2)把x﹣y=﹣2,xy=1代入,即可求出答案.【解答】解:(1)∵x===2﹣,y=2+,∴x﹣y=(2﹣)﹣(2+)=﹣2,xy=(2﹣)×(2+)=4﹣3=1,∴x2+y2=(x﹣y)2+2xy=(﹣2)2+2×1=12+2=14,故答案为:14;(2)由(1)知:x﹣y=﹣2,xy=1,所以(x﹣y)2﹣xy=(﹣2)2﹣1=12﹣1=11,故答案为:11.【点评】本题考查了二次根式的化简求值,分母有理化和完全平方公式等知识点,能求出x﹣y和xy的值是解此题的关键,注意:(x﹣y)2=x2﹣2xy+y2.6.若x=1+,则x3﹣3x2+2x﹣=5.【分析】先将原式进行分组,然后进行因式分解,代入x的值,再根据二次根式混合运算顺序(先算乘方,然后算乘法,最后算加减)及计算法则进行计算.【解答】解:原式=(x3﹣3x2)+2x﹣=x2(x﹣3)+2x﹣,当x=1+时,原式=(1+)2(1+﹣3)+2(1+)﹣=(1+2+7)(﹣2)+2+2﹣=(8+2)(﹣2)+2+2﹣=8﹣16+14﹣4+2+2﹣=5.故答案为:5.【点评】本题考查二次根式的混合运算,理解二次根式的性质,掌握完全平方公式(a+b)2=a2+2ab+b2的结构是解题关键.7.实数a、b满足,则a2+b2的最大值为52.【分析】根据=|a|化简变形得:|a﹣2|+|a﹣6|+|b+4|+|b﹣2|=10,a到2和6的距离之和=4,b到﹣4和2的距离之和是6,得到2≤a≤6,﹣4≤b≤2,根据|a|最大为6,|b|最大为4即可得出答案.【解答】解:原式变形为++|b+4|+|b﹣2|=10,∴|a﹣2|+|a﹣6|+|b+4|+|b﹣2|=10,∴a到2和6的距离之和是4,b到﹣4和2的距离之和是6,∴2≤a≤6,﹣4≤b≤2,∴|a|最大为6,|b|最大为4,∴a2+b2=62+(﹣4)2=36+16=52.故答案为:52.【点评】本题考查了二次根式的性质与化简,根据绝对值的性质得到2≤a≤6,﹣4≤b ≤2是解题的关键.8.已知x=,y=,且19x2+123xy+19y2=1985,则正整数n的值为2.【分析】先将x,y分母有理化化简为含n的代数式,可得x+y=4n+2,xy=1,然后将xy =1代入19x2+123xy+19y2=1985,结果化简为x2+y2=98,进而求解.【解答】解:∵x===()2=2n+1﹣2,y=,=()2=2n+1+2,∴x+y=4n+2,xy=1,将xy=1代入19x2+123xy+19y2=1985得19x2+123+19y2=1985,化简得x2+y2=98,(x+y)2=x2+y2+2xy=98+2=100,∴x+y=10.∴4n+2=10,解得n=2.故答案为:2.【点评】本题考查二次根式的分母有理化,解题关键是利用整体思想求解.9.计算:(1)82014×(﹣0.125)2015;(2)﹣﹣(π+2020)0.【分析】(1)原式逆用积的乘方运算法则计算即可求出值;(2)原式利用二次根式性质,分母有理化,以及零指数幂法则计算即可求出值.【解答】解:(1)原式=(﹣8×0.125)2014×(﹣0.125)=(﹣1)2014×(﹣0.125)=﹣0.125;(2)原式=2﹣﹣1=﹣1.【点评】此题考查了分母有理化,幂的乘方与积的乘方,以及零指数幂,熟练掌握运算法则是解本题的关键.10.计算题:(1)(3+)(3﹣)﹣(﹣1)2;(2)(2﹣3).【分析】(1)利用平方差公式及完全平方公式进行求解较简便;(2)先化简,再算括号里的运算最后算除法即可.【解答】解:(1)(3+)(3﹣)﹣(﹣1)2=9﹣5﹣(3﹣2+1)=9﹣5﹣3+2﹣1=2;(2)(2﹣3)=(8)=﹣=.【点评】本题主要考查二次根式的混合运算,解答的关键是对相应的运算法则的掌握与运用.11.一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2.设a+b(其中a、b、m、n均为正整数),则有a+b=m2+2n2+2mn,∴a=m2+2n2,b=2mn.这样可以把部分a+b的式子化为平方式的方法.请你仿照上述的方法探索并解决下列问题:(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得:a=m2+3n2,b=2mn.(2)利用所探索的结论,找一组正整数a、b、m、n填空:21+4=(1+ 2)2;(3)化简【分析】(1)将(m+n)2用完全平方公式展开,与原等式左边比较,即可得答案;(2)设a+b=,则=m2+2mn+5n2,比较完全平方式右边的值与a+b,可将a和b用m和n表示出来,再给m和n取特殊值,即可得答案;(3)利用题中描述的方法,将要化简的双重根号,先化为一重根号,再利用分母有理化化简,再合并同类二次根式和同类项即可.【解答】解:(1)∵,=m2+2mn+3n2∴a=m2+3n2,b=2mn故答案为:m2+3n2,2mn.(2)设a+b=则=m2+2mn+5n2∴a=m2+5n2,b=2mn若令m=1,n=2,则a=21,b=4故答案为:21,4,1,2.(3)=﹣=﹣=﹣=﹣=++﹣=+【点评】本题考查了利用分母有理化和利用完全平方公式对二次根式化简,以及对这种方法的拓展应用,本题具有一定的计算难度.。
二次根式全章同步练习(含答案)

同步练习 (2)二次根式 (2)第1课时21.1二次根式(1) (2)第2课时21.1二次根式(2) (3)第3课时21.1二次根式(3) (3)第4课时21.2二次根式的乘除(1) (4)第5课时21.2二次根式的乘除(2) (6)第6课时21.2二次根式的乘除(3) (7)第7课时21.3二次根式的加减(1) (8)第8课时21.3 二次根式的加减(2) (9)第9课时21.3 二次根式的加减(3) (10)第10课时第21章二次根式单元复习(1) (12)第11课时第21章二次根式单元复习(2) (13)第12课时二次根式全章练习 (14)第13课时21.3二次根式的加减 (17)答案: (19)二次根式的乘除 (22)第1课时课堂练习 (22)第1课时课堂练习答案 (24)第2课时课堂练习 (24)第2课时课堂练习答案 (25)第3课时课堂练习 (26)第3课时课堂练习答案 (28)二次根式的加减 (29)答案 (32)同步练习二次根式第1课时21.1二次根式(1)一、选择题1.下列式子中,是二次根式的是()D.x2.下列式子中,不是二次根式的是()D.1 x3.已知一个正方形的面积是5,那么它的边长是()A.5 C.15D.以上皆不对二、填空题1.形如________的式子叫做二次根式.2.面积为a的正方形的边长为________.3.负数________平方根.三、综合提高题1.某工厂要制作一批体积为1m3的产品包装盒,其高为0.2m,按设计需要,•底面应做成正方形,试问底面边长应是多少?2.当x是多少时,x+x2在实数范围内有意义?3.4.x有()个.A.0B.1C.2D.无数5.已知a、b,求a、b的值.第2课时 21.1二次根式(2)一、选择题1.、个数是( ).A.4B.3C.2D.12.数a 没有算术平方根,则a 的取值范围是( ).A.a>0B.a ≥0C.a<0D.a=0二、填空题1.()2=________.2.x+1是一个_______数.三、综合提高题1.计算(1)2 (2)-2 (3)(12)2 (4)()2(5)2.把下列非负数写成一个数的平方的形式:(1)5 (2)3.4 (3)16(4)x (x ≥0)3.=0,求x y 的值.4.在实数范围内分解下列因式:(1)x 2-2 (2)x 4-9 3x 2-5第3课时 21.1二次根式(3)一、选择题的值是().A.0B.23C.423D.以上都不对2.a≥0比较它们的结果,下面四个选项中正确的是().二、填空题2.是一个正整数,则正整数m的最小值是________.三、综合提高题1.先化简再求值:当a=9时,求的值,甲乙两人的解答如下:甲的解答为:原式(1-a)=1;乙的解答为:原式=a+(a-1)=2a-1=17.两种解答中,_______的解答是错误的,错误的原因是__________.2.若│1995-a│=a,求a-19952的值.(提示:先由a-2000≥0,判断1995-a•的值是正数还是负数,去掉绝对值)3. 若-3≤x≤2时,试化简│x-2│。
人教版八级数学下册二次根式全章复习(知识点@习题)
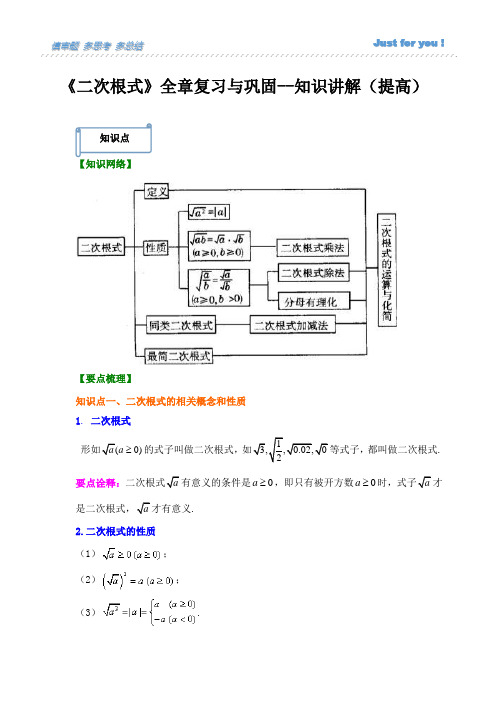
《二次根式》全章复习与巩固--知识讲解(提高)【知识网络】【要点梳理】知识点一、二次根式的相关概念和性质 1. 二次根式的式子叫做二次根式,等式子,都叫做二次根式. 要点诠释:有意义的条件是,即只有被开方数. 2.二次根式的性质 (1); (2);(3).0)a a ≥13,,0.02,02a 0a ≥0a ≥a a 知识点要点诠释:(1) 一个非负数可以写成它的算术平方根的平方的形式,即(),如().(2)的取值范围可以是任意实数,即不论. (3,再根据绝对值的意义来进行化简. (4的异同可以取任何实数,而中的必须取非负数;,=().相同点:被开方数都是非负数,当. 3. 最简二次根式1)被开方数是整数或整式;2)被开方数中不含能开方的因数或因式.满足上述两个条件的二次根式,叫做最简二次根式.简二次根式.要点诠释:最简二次根式有两个要求:(1)被开方数不含分母;(2)被开方数中每个因式的指数都小于根指数2. 4.同类二次根式几个二次根式化成最简二次根式后,被开方数相同,这几个二次根式就叫同类二次根式.要点诠释:判断是否是同类二次根式,一定要化简到最简二次根式后,看被开方数是否相同,再判断.. 知识点二、二次根式的运算 1. 乘除法 (1)乘除法法则:类型法则逆用法则a a 2a =0a ≥2221122););33x x ===0x ≥2a a a 2a 2a a 2a 2a 2a a 2a a 2a a 2a a 0a ≥a 2a 2a 222,,3,ab x a b +2882228二次根式的乘法积的算术平方根化简公式:二次根式的除法商的算术平方根化简公式:要点诠释:(1)当二次根式的前面有系数时,可类比单项式与单项式相乘(或相除)的法则,如 (2)被开方数a 、b 一定是非负数(在分母上时只能为正数).如.2.加减法将二次根式化为最简二次根式后,将同类二次根式的系数相加减,被开方数和根指数不变,即合并同类二次根式. 要点诠释:二次根式相加减时,要先将各个二次根式化成最简二次根式,再找出同类二次根式,最后合并同类二次根式. 类型一、二次根式的概念与性质例1. x 是怎样的实数时,下列各式在实数范围内有意义? (1); (2).举一反三: 【变式】已知,求的值.(0,0)a b ab a b =≥≥(0,0)ab a b a b =≥≥0,0)a aa b b b=≥>0,0)a aa b b b=≥>b c d ac bd =(4)(9)49-⨯-≠--23252(1322=+-=典型例题例2. 把1a --中根号外的因式移到根号内的结果是( ).A a -B .a -C .a -D a举一反三:【变式】已知x 为奇数,且=,求•.例3. 实数在数轴上对应的点如图:.,,a b c 22()1()a c c b a b c --+++举一反三:【变式】ABC 的三边长为a 、b 、c = .类型二、二次根式的运算 例4.计算(1)(2).∆22()()a b c a b c --+-举一反三:【变式】计算例5.已知a 、b 、c 为△ABC 的三边长,化简例6.若.0x >___________x xy xy y xy yx xy+-=+-举一反三:【变式】当.221221123a a a a a a -+-+=-+《二次根式》全章复习与巩固--巩固练习(提高)一、选择题1.是怎样的实数时,在实数范围内有意义?( ) A. B. C. D.2()21221a a -=-,那么 ( ).A .12a <B .12a ≤C .12a >D .12a ≥ 3,那么满足上述条件的整数的个数是( ).A .4 B. 5 C. 6 D. 74.若x <0,则的结果是( ).A .0B .-2C .0或-2D .2 5.的值是( ).A .-7B .-5C .3D .76.下列计算正确的是( ) A.B.=2C.()﹣1=D.(﹣1)2=27.小明的作业本上有以下四题:①;②;③;④.做错的题是( ).A .①B .②C .③D .④x 212x x --122x x >≠且122x x ≥≠±且122x x ≠≠±且122x x ≥≠且3253x <<+-x 5220,x y x y-++=-若则8. ).二. 填空题 9. 计算=___________.10. 若的整数部分是a ,小数部分是b ,则___________. 11.比较大小①______;②___.(用>或<填空)12. 已知最简根式是同类根式,则的值为___________.13.若m <0,则=___________.14.已知实数满足,则=____________. 15.已知数在数轴上的位置如图所示:=__________.16.已知x=,则x 2+x+1= .三 综合题 17. 计算: (1)(2)()2220,a a a a ≥-时,和()222a a a =-≥()222a a a >->()222a a a <-<-()222a a a >=-232a b a b -+-+-2a+b-1与b-2a b aa b +a 20102011a a a --=22010a -,,a b c 22()a a c c b b -+--()ab bab a b a ab --÷-+18. 已知:,求的值.19.若,a b都是实数,且114412b a a=--22b a b aa b a b+++-.20.某号台风的中心位于O地,台风中心以25千米/小时的速度向西北方向移动,在半径为240千米的范围内将受影响、城市A在O地正西方向与O地相距320千米处,试问A市是否会遭受此台风的影响?若受影响,将有多少小时?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次根式(提高) 撰稿: 赵炜 审稿: 杜少波
【巩固练习】
一、选择题 1.若代数式在实数范围内有意义,则x 的取值范围为( ) A .x >0 B .x ≥0 C .x ≠ 0 D .x ≥0且x ≠ 1
2.使式子有意义的未知数x 有( )个
A .0
B .1
C .2
D .无数
3.下列说法正确的是( )
A .4是一个无理数
B .函数11
y x =-的自变量x 的取值范围是x ≥1 C .8的立方根是2±
D.若点(2,)-3)P a Q
和点(b ,关于x 轴对称,则a b +的值为5. 4. 已知a,b,c 在数轴上的位置如右图所示,则代数
式( )
A. 2c a -
B.32a b --
C. c a --
D. a
5. 若
,则 等于( ) A . B . C . D .
6.将a a --中的a 移到根号内,结果是( )
A .3a -- B. 3a - C.3a - D.3a
二. 填空题
7.当x_________时,式子31
x x --没有意义。
8.若,则
____________;若,则____________. 9.已知,求的值为____________
10.若,则化简的结果是__________.
11. 观察下列各式:,,,……请你探究其中规
律,并将第 n(n ≥1)个等式写出来________________.
12.x 取何值时,函数在实数范围内有意义?y=2||12--x x ,_______________________. 三 综合题
13. 已知x x y 211221-+-+=
,求22y xy x ++的值.
14. 若
时,试化简.
15.已知一次函数(2)1y a x =-+的图象不经过第三象限,化简224496a a a a -+--+的结果是多少?
【答案与解析】
一、选择题
1.【答案】 D. 【解析】 由二次根式和分式的性质可知:被开方数要大于等于0,分母不等于0,即x ≥0,10x -≠, 所以选D.
2.【答案】 B.
3.【答案】 D.
【解析】选项A: 4=2是有理数;选项B: 11
y x =-的x 的取值范围是x>1; 选项C: 8的立方根是2;选项D:因为(2,)-3)P a Q
和点(b ,关于x 轴对称,所以3,2a b ==,及5a b +=,所以选D. 4.【答案】C.
5.【答案】D.
【解析】 因为
=22(4)a +222(4)4A a a =+=+. 6.【答案】B.
二、填空题
7.【答案】10x =或x<1.
【解析】因为x-1≥0才有意义,所以x<1时无意义;因为310x -≠,所以10x ≠,即无意义时x=10.
8.【答案】m ≤0;a ≥
13. 9.5【解析】23100x x x -+=∴≠
13,x x ∴+=即21()9x x += 22
17x x ∴+=,即原式=725-=. 10.【答案】3 【解析】因为原式=21x x -++=213x x -++=.
11.【答案】 11(1)22n n n n +
=+++ 12.【答案】 x ≥122
x ≠且 【解析】 121020, 2.2
x x x x --≠≠≥,∴≥,且.
三、解答题
13.【解析】因为1+21122y x x =-+-,所以2x-1≥0,1-2x ≥0,即x=12,y=12
, 则2234
x xy y ++=. 14.【解析】 因为,
所以原式=
=23523510x x x x x x x -+++-=-+++-=-.
15.【解析】 因为一次函数(2)1y a x =-+的图象不经过第三象限
所以20a -<,即2a <;
224496a a a a -+-+23231a a a a ---=--+=-.。
