线性代数作业2

《线性代数》上机作业(二)
课程《线性代数》上机
内容
《线性代数》综合实例成绩
姓名唐莉专业
班级
测控10级学号1007010303
教学班2204 指导
教师
李春泉
上机
日期
2011-12-18
一、上机目的
1.培养学生运用线性代数的知识解决实际
2.问题的意识、兴趣和能力;
3.掌握常用计算方法和处理问题的方法.
二、上机内容
1.求向量组的最大无关组;
2.解线性方程;
3.解决实际问题举例.
三、上机作业
1、
2、①记线性方程组的系数矩阵和其增广矩阵为A和B,则解为
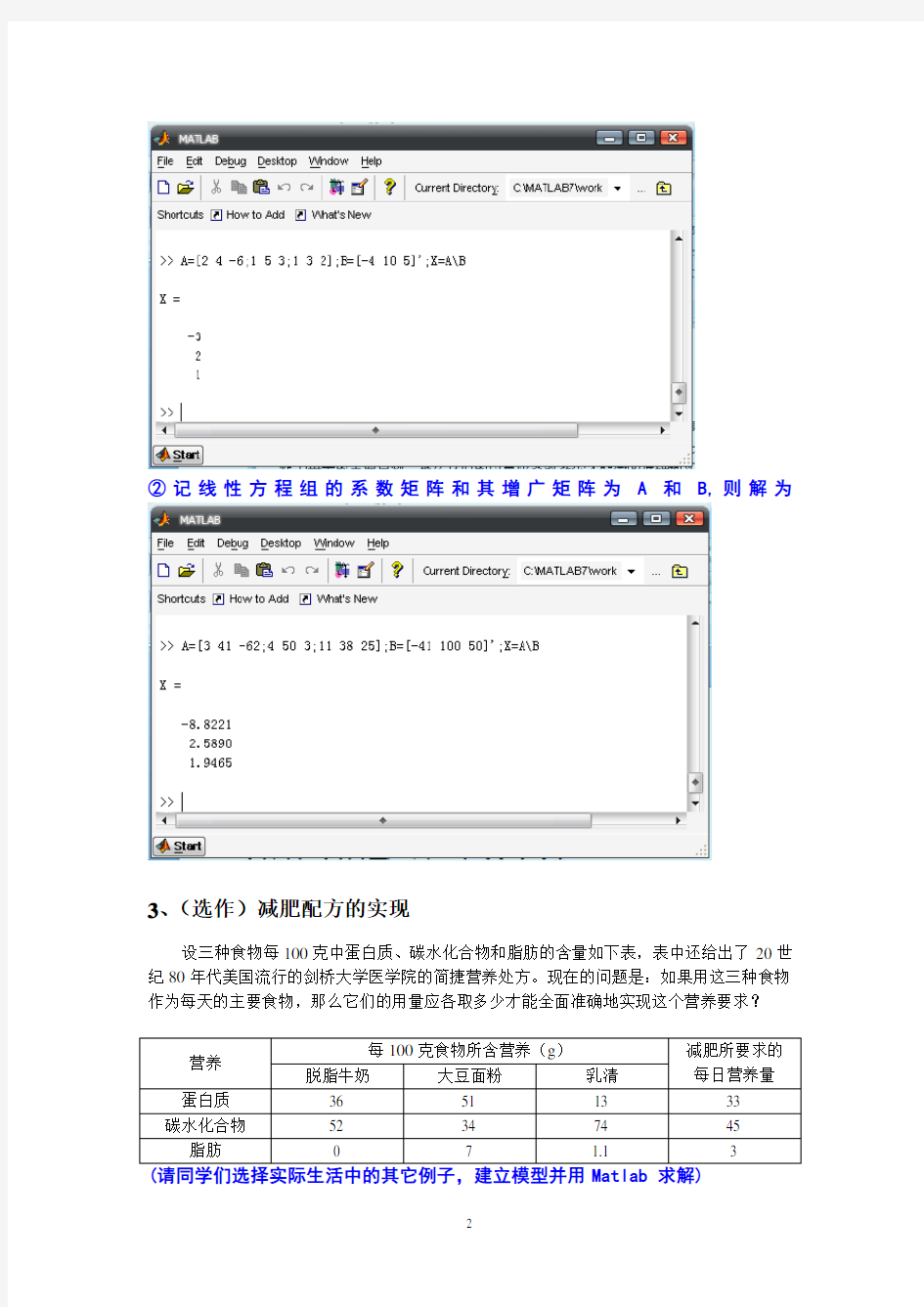
②记线性方程组的系数矩阵和其增广矩阵为A和B,则解为
3、(选作)减肥配方的实现
设三种食物每100克中蛋白质、碳水化合物和脂肪的含量如下表,表中还给出了20世纪80年代美国流行的剑桥大学医学院的简捷营养处方。现在的问题是:如果用这三种食物作为每天的主要食物,那么它们的用量应各取多少才能全面准确地实现这个营养要求?
营养
每100克食物所含营养(g)减肥所要求的
每日营养量脱脂牛奶大豆面粉乳清
蛋白质36 51 13 33 碳水化合物52 34 74 45 脂肪0 7 1.1 3
解:设脱脂牛奶.大豆面粉.乳清各取x1,x2,x3克,则有线性方程组
①36x1+51x2+13x3=33
②52x1+34x2+74x3=45
③7x2+1.1x3=3
解得
四、上机心得体会
西南大学线性代数作业答案
西南大学线性代数作业答案
第一次 行列式部分的填空题 1.在5阶行列式ij a 中,项a 13a 24a 32a 45a 51前的符 号应取 + 号。 2.排列45312的逆序数为 5 。 3.行列式2 5 1122 1 4---x 中元素x 的代数余子式是 8 . 4.行列式10 2 3 25403--中元素-2的代数余子式是 —11 。 5.行列式25 11 22 14--x 中,x 的代数余子式是 — 5 。 6.计算00000d c b a = 0 行列式部分计算题 1.计算三阶行列式 3 811411 02--- 解:原式=2×(—4)×3+0×(—1)×(—1)+1×1×8—1×(—1)× (—4)—0×1×3—2×(—1)×8=—4 2.决定i 和j ,使排列1 2 3 4 i 6 j 9 7 为奇排列. 解:i =8,j =5。
3.(7分)已知0010413≠x x x ,求x 的值. 解:原式=3x 2—x 2—4x=2 x 2—4x=2x(x —2)=0 解得:x 1=0;x 2=2 所以 x={x │x ≠0;x ≠2 x ∈R } 4.(8分)齐次线性方程组 ?? ? ??=++=++=++000z y x z y x z y x λλ 有非零解,求λ。 解:()211 1 1 010001 1 111111-=--= =λλλλλD 由D=0 得 λ=1 5.用克莱姆法则求下列方程组: ?? ? ??=+-=++=++10329253142z y x z y x z y x 解:因为 33113 210421711 7021 04 21 911 7018904 2 1 351 1321 5 421231 312≠-=?-?=-------=-------=)(r r r r r r D 所以方程组有唯一解,再计算: 81 1 11021 29 42311-=-=D 108 1 103229543112-==D 135 10 13291 5 31213=-=D 因此,根据克拉默法则,方程组的唯一解是:
线性代数(李建平)习题答案详解__复旦大学出版社
线性代数课后习题答案 习题一 1.2.3(答案略) 4. (1) ∵ (127435689)415τ=+= (奇数) ∴ (127485639)τ为偶数 故所求为127485639 (2) ∵(397281564)25119τ=+++= (奇数) ∴所求为397281564 5.(1)∵(532416)421106τ=++++= (偶数) ∴项前的符号位()6 11-=+ (正号) (2)∵325326114465112632445365a a a a a a a a a a a a = (162435)415τ=+= ∴ 项前的符号位5(1)1-=- (负号) 6. (1) (2341)(1)12n n τ-?L L 原式=(1)(1)!n n -=- (2)()((1)(2)21) 1(1)(2)21n n n n n n τ--??---??L L 原式=(1)(2) 2 (1) !n n n --=- (3)原式=((1)21) 12(1)1(1) n n n n n a a a τ-?--L L (1) 2 12(1)1(1)n n n n n a a a --=-L 7.8(答案略) 9. ∵162019(42)0D x =?-?+?--?= ∴7x = 10. (1)从第2列开始,以后各列加到第一列的对应元素之上,得 []11(1)1110 01(1)1110 (1)1 1 (1)1 1 1 x x n x x x n x x x n x x n x x +-+--==+-+--L L L L L L L L L L L L L L L L L L L L L []1(1)(1)n x n x -=+-- (2)按第一列展开: 11100000 (1)(1)0 0n n n n n y x y D x x y x y x y -++=?+-=+-L L L L L L L L
线性代数作业
普通高等教育“十五”国家级规划教材线性代数 标准化作业 山东理工大学数学中心 2011.2
学院班级姓名学号 第一章行列式作业 1、按自然数从小到大为标准次序,求下列排列的逆序数: (1)1 3…(2n-1)2 4…(2n); (2)1 3…(2n-1)(2n) (2n-2)…4 2. 2、填空题 (1)排列52341的逆序数是________,它是________排列; (2)排列54321的逆序数是________,它是________排列; (3)1~9这九数的排列1274i56j9为偶排列,则i=______ ,j=_______; (4)四阶行列式中含有因子a11a23的项为________________; (5)一个n阶行列式D中的各行元素之和为零,则D=__________. 3、计算行列式212 111 321 10 x x x x x x - 展开式中x4与x3的系数. 4、计算下列各行列式的值: (1) 2116 4150 1205 1422 D - - = -- -- ;(2) 111 1 222 111 1 222 111 1 222 111 1 222 D=;
(3) 1 12 23 3 100 110 011 0011 b b b D b b b -- = -- -- ;(4) 222 b c c a a b D a b c a b c +++ =; (5) 1111 1111 1111 1111 a a D b b + - = + - ;
(6)10 2 20030 2004D = . 5、用克拉默法则解方程组 1231231 23241,52,4 3. x x x x x x x x x +-=?? ++=??-++=? 7、已知齐次线性方程组有非零解,求λ。 1231231 23230,220,50. x x x x x x x x x λ++=?? +-=??-+=?
线性代数 李建平版本 复旦大学出版社 答案
线性代数(低分数版) 习题一 1.2.3(答案略) 4. (1) ∵ (奇数) ∴为偶数 故所求为 (2) ∵(奇数) ∴所求为397281564 5.(1)∵ (偶数) ∴项前的符号位(正号) (2)∵ ∴项前的符号位(负号) 6. (1) (2) (3)原式= 7.8(答案略) 9. ∵ ∴ 10. (1)从第2列开始,以后各列加到第一列的对应元素之上,得 (2)按第一列展开: (3) 习题二 1.2.3.4.5(答案略) 6. 设为与可交换的矩阵,则有 即 解之得 7. (1),记为 ,记为
(2)即 8(答案略) 9. 10.(1) (2) = 11. ∵ ∴ 反之若 , 则 ,即 12. (1) 设∵∴ 又∵∴ 又 当时,有 ∴ (2)设,则 ∵∴ 当时,有 故即 13.(1) ∵∴为对称矩阵 同理也为对称矩阵 (2)∵ ∴为对称矩阵 又∵ ∴为反对称矩阵 (3)∵ 由(2)知,为对称矩阵,为反对称矩阵 故可表示成一个对称矩阵与一个反对称矩阵的和。 14. (1)必要性:∵ ∴ 充分性:∵ ∴ (2) 必要性:∵ ∴ 充分性:∵ ∴ (3) 必要性:∵ ∴ 即 充分性:∵ ∴ 15(答案略) 16. ∵ ∴可逆。
且 17. ∵ ∴可逆,且 18.(答案略) 19. ∵,若可逆,则 ∴故可逆,且 20.设,∵是对称矩阵∴记,则 ,即为对称矩阵,又∵ , ∴为对称矩阵。 21.(1)设,则 (2)∵∴ 又∵ ∴ 于是即 (3)∵∴ 于是 (4) (注意加条件:可逆) ∵可逆∴ ∴ 22. ∵∴ 23. 24.(答案略) 25. ∵∴ ∴可逆,且 26. ∵∴ 又∵, , ∴ 27(答案略) 28. ∵∴ 又∵∴ 故 29. ∵∴ ∴ 30.(答案略) 31.(1) (2) 32. 33. (1) ∵ ∴ (2) ∵
线性代数课后作业答案(胡觉亮版)
第一章 1.用消元法解下列线性方程组: (1)??? ??=++=++=++. 5432,9753,432321 321321x x x x x x x x x 解 由原方程组得同解方程组 12323234,23,x x x x x ++=?? +=? 得方程组的解为13232, 2 3. x x x x =-?? =-+?令3x c =,得方程组的通解为 c x c x c x =+-=-=321,32,2,其中c 为任意常数. 2.用初等行变换将下列矩阵化成行阶梯形矩阵和行最简形矩阵: (2)???? ? ??--324423211123. 解 1102 232111232551232041050124442300000000r r ? ?- ?-???? ? ? ? ? -??→--??→- ? ? ? ? ?- ????? ? ?? ? ,得 行阶梯形:????? ? ?---0000510402321(不唯一);行最简形:???? ??? ? ? ? - -00004525 10212 01 3.用初等行变换解下列线性方程组: (1)?? ? ??=+-=+-=++.3,1142,53332321321x x x x x x x x
解 2100313357214110109011320019r B ? ? ??? ? ? ?=-??→- ? ? ?- ??? ? ?? ?M M M M M M , 得方程组的解为 9 20 ,97,32321=-==x x x . (2)??? ??=+++=+++=++-. 2222,2562, 1344321 43214321x x x x x x x x x x x x 解 114311143121652032101222200001r B --???? ? ? =?? →-- ? ? ? ????? M M M M M M , 得方程组无解. 第二章 1.(2) 2 2 x y x y . 解 原式()xy y x =-. (2)01000 020 00010 n n -L L L L L L L L L . 2.解 原式1 100 020 (1) 001 n n n +=-=-L L M M M L !)1(1n n +-
线性代数上机作业题答案
线性代数机算与应用作业题 学号: 姓名: 成绩: 一、机算题 1.利用函数rand 和函数round 构造一个5×5的随机正整数矩阵A 和B 。 (1)计算A +B ,A -B 和6A (2)计算()T AB ,T T B A 和()100 AB (3)计算行列式A ,B 和AB (4)若矩阵A 和B 可逆,计算1 A -和1 B - (5)计算矩阵A 和矩阵B 的秩。 解 输入: A=round(rand(5)*10) B=round(rand(5)*10) 结果为: A = 2 4 1 6 3 2 2 3 7 4 4 9 4 2 5 3 10 6 1 1 9 4 3 3 3 B = 8 6 5 4 9 0 2 2 4 8 9 5 5 10 1 7 10 6 0 3 5 5 7 9 3 (1)输入: A+B 结果为:
ans= 10 10 6 10 12 2 4 5 11 12 13 14 9 12 6 10 20 12 1 4 14 9 10 12 6 输入: A-B 结果为: ans = -6 -2 -4 2 -6 2 0 1 3 -4 -5 4 -1 -8 4 -4 0 0 1 -2 4 -1 -4 -6 0 输入: 6*A 结果为: ans = 12 24 6 36 18 12 12 18 42 24 24 54 24 12 30 18 60 36 6 6 54 24 18 18 18 (2)输入: (A*B)' 结果为: ans = 82 112 107 90 135 100 121 107 83 122
80 99 105 78 107 61 82 137 121 109 78 70 133 119 134 输入: B'*A' 结果为: ans = 82 112 107 90 135 100 121 107 83 122 80 99 105 78 107 61 82 137 121 109 78 70 133 119 134 输入: (A*B)^100 结果为: ans = 1.0e+270 * 1.6293 1.6526 1.4494 1.5620 1.6399 1.9374 1.9651 1.7234 1.8573 1.9499 2.4156 2.4501 2.1488 2.3158 2.4313 2.0137 2.0425 1.7913 1.9305 2.0268 2.4655 2.5008 2.1932 2.3636 2.4815 (3)输入: D=det(A) 结果为: D = 5121 输入: D=det(B) 结果为:
线性代数(复旦大学出版社周勇)课后习题集规范标准答案
第一章课后答案 一、 1. 5)1(122211 2=-?-?=-; 2. 1)1)(1(1 1123222 2 --=-++-=++-x x x x x x x x x x ; 3. b a ab b a b a 222 2 -= 4.5361582732559841 31 11=---++= 5.比例)第一行与第三行对应成(,00 000 0=d c b a 6.1866627811 32213 3 21=---++=。 二.求逆序数 1. 55 1243 1 2 2 =↓↓↓↓↓ τ即 2. 52 134 2 3 =↓↓↓↓τ即 3. 2 ) 1(12)2()1(1 2)1(0 1 ) 2() 1(-= +++-+-=-↓↓-↓-↓n n n n n n n n ΛΛ τ即 4. 2 )1(* 2]12)2()1[()]1(21[2 4)22()2()12(310 1 2 1 1 1 -=+++-+-+-+++=--↓↓-↓-↓-↓↓↓n n n n n n n n n n n ΛΛΛ Λ τ 三.四阶行列式中含有2311a a 的项为4234231144322311a a a a a a a a +- 四.计算行列式值
1. 071 108517002 02145 9001577 1 1 202150202142701047 110 0251020214214 43412321=++------r r r r r r r r 2. 310 0100001 0111130 11110111101111130 1131013110311130 1111011110111104 321-=---?=? =+++c c c c 3.abcdef adfbce ef cf bf de cd bd ae ac ab 4111 111 1 11=---=--- 4. d c d c b a d c b a 10 10 1110 11 110 1 10011001--------按第一行展开 ad cd ab d c d a d c ab +++=-+ ---=)1)(1(11 1111 5. b a c c b c a b a a c b a c c b c a b a a b b a c c c b c a b b a a a b a c c c b c a b b a a c b a --------------=------202022202022222222222222 其中
线性代数(本)习题册行列式-习题详解(修改)(加批注)
||班级: 姓名: 学号: 成绩: 批改日期: || 第 1 页 共 18 页 行列式的概念 一、选择题 1. 下列选项中错误的是( ) (A) b a d c d c b a - = ; (B) a c b d d c b a = ; (C) d c b a d c d b c a = ++33; (D) d c b a d c b a ----- =. 答案:D 2.行列式n D 不为零,利用行列式的性质对n D 进行变换后,行列式的值( ). (A)保持不变; (B)可以变成任何值; (C)保持不为零; (D)保持相同的正负号. 答案:C 二、填空题 1. a b b a log 1 1 log = . 解析: 0111log log log 1 1log =-=-=a b a b b a b a . 2. 6 cos 3sin 6sin 3 cos π π ππ = . 解析: 02cos 6sin 3sin 6cos 3cos 6 cos 3 sin 6sin 3 cos ==-=πππππππ π π 3.函数x x x x x f 1213 1 2)(-=中,3x 的系数为 ; x x x x x x g 2 1 1 12)(---=中,3x 的系数为 . 答案:-2;-2.
||班级: 姓名: 学号: 成绩: 批改日期: || 第 2 页 共 18 页 阶行列式n D 中的n 最小值是 . 答案:1. 5. 三阶行列式11342 3 2 1-中第2行第1列元素的代数余子式 等于 . 答案:5. 6.若 02 1 8 2=x ,则x = . 答案:2. 7.在 n 阶行列式ij a D =中,当i 第一章 行列式 §1 行列式的概念 1. 填空 (1) 排列6427531的逆序数为 ,该排列为 排列。 (2) i = ,j = 时, 排列1274i 56j 9为偶排列。 (3) n 阶行列式由 项的代数和组成,其中每一项为行列式中位于不同行不同列的 n 个元素的乘积,若将每一项的各元素所在行标按自然顺序排列,那么列标构 成一个n 元排列。若该排列为奇排列,则该项的符号为 号;若为偶排列,该项的符号为 号。 (4) 在6阶行列式中, 含152332445166a a a a a a 的项的符号为 ,含 324314516625a a a a a a 的项的符号为 。 2. 用行列式的定义计算下列行列式的值 (1) 11 222332 33 000 a a a a a 解: 该行列式的3!项展开式中,有 项不为零,它们分别为 ,所以行列式的值为 。 (2) 12,121,21,11,12 ,100000 0n n n n n n n n n n n n nn a a a a a a a a a a ------L L M M M M L L 解:该行列式展开式中唯一不可能为0的项是 ,而它的逆序数是 ,故行列式值为 。 3. 证明:在全部n 元排列中,奇排列数与偶排列数相等。 证明:n 元排列共有!n 个,设其中奇排列数有1n 个,偶排列数为2n 个。对于任意奇排 列,交换其任意两个元的位置,就变成偶排列,故一个奇排列与许多偶排列对应,所以有1n 2n ,同理得2n 1n ,所以1n 2n 。 4. 若一个n 阶行列式中等于0的元素个数比n n -2 多,则此行列式为0,为什么? 5. n 阶行列式中,若负项的个数为偶数,则n 至少为多少? (提示:利用3题的结果) 6. 利用对角线法则计算下列三阶行列式 (1)2 011 411 8 3 --- (2)2 2 2 1 11a b c a b c 线性代数课后习题答案-复旦大学出版社-熊维玲 第一章 3.如果排列n x x x 2 1是奇排列,则排列1 1 x x x n n 的奇偶 性如何? 解:排列 1 1x x x n n 可以通过对排列 n x x x 21经过 (1)(1)(2)212 n n n n L 次邻换得到,每一次邻换都 改变排列的奇偶性,故当2)1( n n 为偶数时,排列 1 1x x x n n 为奇排列,当2)1( n n 为奇数时,排列1 1 x x x n n 为 偶排列。 4. 写出4阶行列式的展开式中含元素13 a 且带负 号的项. 解:含元素13a 的乘积项共有13223144 (1)t a a a a ,13223441 (1)t a a a a , 13213244 (1)t a a a a ,13213442 (1)t a a a a ,13243241 (1)t a a a a ,13243142 (1)t a a a a 六项, 各项列标排列的逆序数分别为(3214)3t , (3241)4t , (3124)2 t , (3142)3 t , (3421)5t ,(3412)4 t , 故所求为13223144 1a a a a , 132134421a a a a , 13243241 1a a a a 。 5.按照行列式的定义,求行列式 n n 0 000100200100 的 值. 解:根据行列式的定义,非零的乘积项只有 1,12,21,1(1)t n n n nn a a a a L , 其中(1)(2) [(1)(2)21]2 n n t n n n L ,故行列式的值等于: (1)(2) 2 (1) ! n n n 6. 根据行列式定义,分别写出行列式x x x x x 1 11 1231112 1 2 的 展开式中含4 x 的项和含3 x 的项. 解:展开式含4 x 的乘积项为 4 11223344 (1)(1)22t a a a a x x x x x 含3 x 的乘积项为13 12213344 (1)(1)1t a a a a x x x x 8. 利用行列式的性质计算下列行列式: 解 : (1) 41 131123421 1234 1111 1 1 1 1 410234123410121 10310 ()341234120121 2412341230321 r r r r r r r r r r r 第三章 线性方程组 一、温习巩固 1. 求解齐次线性方程组??? ??=-++=--+=-++0 51050363024321 43214321x x x x x x x x x x x x 解: 化系数矩阵为行最简式 ???? ? ????→?????? ??----=000001001-0215110531631121行变换A 因此原方程同解于? ? ?=+-=0234 21x x x x 令2412,k x k x ==,可求得原方程的解为 ???? ?? ? ??+??????? ??-=1001001221k k x ,其中21,k k 为任意常数。 2. 求解非齐次线性方程组?? ? ??=+=+-=-+8 31110232 2421321321x x x x x x x x 解:把增广矩阵),(b A 化为阶梯形 ?? ? ? ? ????→?????? ??---??→?????? ??--=-6-000341110-08-3-318031110213833180311102132124),(21行变换r r b A 因此3),(2)(=<=b A R A R ,所以原方程组无解。 3. 设)1,2,1,3(),1,1,2,3(--=--=βα。求向量γ,使βγα=+32。 解:??? ? ? --=-= 31,0,35,3)2(31αβγ 4. 求向量组123(1,1,2,4),(0,3,1,2),(3,0,7,14),T T T ααα=-==4(1,1,2,0),T α=- T )6,5,1,2(5=α的秩和一个极大线性无关组。 解:将51,ααΛ作为列向量构成矩阵,做初等行变换 第一部分 专项同步练习 第一章 行列式 一、单项选择题 1.下列排列是5阶偶排列的是 ( ). (A) 24315 (B) 14325 (C) 41523 (D)24351 2.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C) k n -2 ! (D)k n n --2)1( 3. n 阶行列式的展开式中含1211a a 的项共有( )项. (A) 0 (B)2-n (C) )!2(-n (D) )!1(-n 4. =0 00100100 1001 000( ). (A) 0 (B)1- (C) 1 (D) 2 5. =0 00110000 0100 100( ). (A) 0 (B)1- (C) 1 (D) 2 6.在函数1 3232 111 12)(x x x x x f ----= 中3x 项的系数是( ). (A) 0 (B)1- (C) 1 (D) 2 7. 若2 1 33 32 31 232221 131211==a a a a a a a a a D ,则=---=32 3133 31 2221232112 111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若 a a a a a =22 2112 11,则 =21 11 2212ka a ka a ( ). (A)ka (B)ka - (C)a k 2 (D)a k 2- 9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为 x ,1,5,2-, 则=x ( ). (A) 0 (B)3- (C) 3 (D) 2 10. 若5 7341111 1 326 3 478 ----= D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)0 11. 若2 23 5 001 01 11 10 403 --= D ,则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)0 12. k 等于下列选项中哪个值时,齐次线性方程组??? ??=++=++=++0 00321 321321x x kx x kx x kx x x 有非零解. ( ) (A)1- (B)2- (C)3- (D)0 二、填空题 华北水利水电学院 行列式的计算方法 课程名称:线性代数 专业班级:电子信息工程 2012154班 成员组成: 联系方式: 2013年10月27日 摘要: 行列式是线性代数的一个重要研究对象,是线性代数中的一个最基本`最常用的工具.本质上,行列式描述的是在n维空间中,一个线性变换所形成的平行多面体的体积,它被广泛应用于解线性方程组,矩阵运算,计算微积分等.尤其在讨论方程组的解,矩阵的秩,向量组的线性相关性,方阵的特征向量等问题时发挥着至关重要的作用,所以掌握行列式的计算方法显得尤其重要。 关键词: 行列式,范德蒙行列式,矩阵,特征值,拉普拉斯定理,克拉默法则。 The calculation method of determinant Abstract: Determinant is an important research object of linear algebra, is one of the most basic of linear algebra ` the most commonly used tools. In essence, the determinant is described in n dimensional space, a parallel polyhedron volume which is formed by the linear transformation, it is widely used in solving linear equations, the matrix, the calculation of calculus, etc. Especially in the discussion of solving systems of nonlinear equations, matrix rank, vector linear correlation, the problem such as characteristic vector of play a crucial role, so to master the calculation method of determinant is especially important Key words: Determinant vandermonde determinant, matrix, eigenvalue, the Laplace's theorem, kramer rule. 线性代数习题及答案(复旦版)[] 线性代数习题及答案 习题一 1. 求下列各排列的逆序数. (1) 341782659;(2) 987654321; (3) n(n?1)…321;(4) 13…(2n?1)(2n)(2n?2)…2. 【解】 (1) τ(341782659)=11; (2) τ(987654321)=36; (3) τ(n(n?1)…32221)= 0+1+2 +…+(n?1)=; (4) τ(13…(2n?1)(2n)(2n?2)…2)=0+1+…+(n?1)+(n?1)+(n?2)+…+1+0=n(n?1). 2. 略.见教材习题参考答案. 3. 略.见教材习题参考答案. 4. 本行列式的展开式中包含和的项. 解:设,其中分别为不同列中对应元素的行下标,则展开式中含项有 展开式中含项有 . 5. 用定义计算下列各行列式. (1);(2). 【解】(1) D=(?1)τ(2314)4!=24; (2) D=12. 6. 计算下列各行列式. (1);(2) ; (3);(4) . 【解】(1) ; (2) ; 7. 证明下列各式. (1) ; (2) ; (3) (4) ; (5) . 【证明】(1) (2) (3) 首先考虑4阶范德蒙行列式: 从上面的4阶范德蒙行列式知,多项式f(x)的x的系数为 但对(*)式右端行列式按第一行展开知x的系数为两者应相等,故 (4) 对D2n按第一行展开,得 据此递推下去,可得 (5) 对行列式的阶数n用数学归纳法. 当n=2时,可直接验算结论成立,假定对这样的n?1阶行列式结论成立,进而证明阶数为n时结论也成立. 按Dn的最后一列,把Dn拆成两个n阶行列式相加: 但由归纳假设 从而有 8. 计算下列n阶行列式. (1) (2) ; (3). (4)其中; (5). 【解】(1) 各行都加到第一行,再从第一行提出x+(n?1),得 将第一行乘(?1)后分别加到其余各行,得 (2) 按第二行展开 (3) 行列式按第一列展开后,得 (4)由题意,知 . (5) . 即有 由得 . 9. 计算n阶行列式. 【解】各列都加到第一列,再从第一列提出,得 将第一行乘(?1)后加到其余各行,得 《线性代数》作业 第一章 1、求排列(2n)(2n-1)…(n+1)1 2…(n -1)n 的逆序数。 解:后面是正常顺序,逆序出现在前n 个数与后n 个数之间,2n 的逆序数是2n-1,2n-1的逆序数是2n-2,……,n+1的逆序数是n ,所以整个排列的逆序数是(2n-1)+(2n-2)+……+n =n(3n-1)/2 2、求排列246......(2n)135……(2n-1)的逆序数。 解析:后一项比前一项的算逆序一次,246......(2n)无逆序,所以从1开始,有246......(2n)共N 个,3开始有46......(2n)有N-1个,.......,.2n-1有一个,所以,加一起得,逆序数为1+2+......+N=N (N+1)/2 N=n+(n-1)+......+2+1=n(n+1)/2 3、试判断655642312314a a a a a a ,662551144332a a a a a a -,662552144332a a a a a a -是否都是六阶行列式中的项。 解a 14a 23a 31a 42a 56a 65 下标的逆序数为 t (431265)=0+1+2+2+0+1=6 所以655642312314a a a a a a 是六阶行列式中的项。 662551144332a a a a a a -下标的逆序数为 t (452316)=8所以662551144332a a a a a a -不是六阶行列式中的项。 662552144332a a a a a a -下标的逆序数为t(452316)=8所以662552144332a a a a a a -不是六阶行列式中的项。 4、已知4阶行列式D 中的第3列上的元素分别是3,-4,4,2,第1列上元素的余子式依次为8,2,-10,X ,求X 。 解:X=20 5、设15234312a a a a a j i 是5阶行列式的一项,若该项的符号为负,则 i= 5 ,j= 4 。 6、要使3972i15j4成为偶排列,则 i= 6 ,j= 8 。 7、设D 为一个三阶行列式,并且D=4,现对D 进行下列变换:先交换第1和第2行,然后用2乘以行列式的每个元素,再用-3乘以第2列加到第3列,则行列式最后结果为 32 。 8、设对五阶行列式(其值为m )依次进行下面变换,求其结果:交换一行与第五行,再转置,用2乘所有元素,现用-3乘以第二列加到第四列,最后用4除第二行各元素。 解析:交换一行与第五行 行列式的值变号 转置 行列式的值不变 用2乘所有元素 行列式的值乘以2^5 现用-3乘以第二列加到第四列 行列式的值不变 最后用4除以第二行各元素(应该是用4“除”第二行各元素吧?) 行列式的值乘以1/4 ______________________________________________________________________________________________________________ 第一部分 专项同步练习 第一章 行列式 一、单项选择题 1.下列排列是5阶偶排列的是 ( ). (A) 24315 (B) 14325 (C) 41523 (D)24351 2.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C) k n -2 ! (D)k n n --2)1( 3. n 阶行列式的展开式中含1211a a 的项共有( )项. (A) 0 (B)2-n (C) )!2(-n (D) )!1(-n 4. =0 0010 0100 1001 000( ). (A) 0 (B)1- (C) 1 (D) 2 5. =0 0011 0000 0100 100( ). (A) 0 (B)1- (C) 1 (D) 2 6.在函数1 3232 111 12)(x x x x x f ----= 中3x 项的系数是( ). (A) 0 (B)1- (C) 1 (D) 2 7. 若2 1 33 32 31 232221 131211 ==a a a a a a a a a D ,则=---=32 3133 31 2221232112 111311 122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若 a a a a a =22 2112 11,则 =21 11 2212ka a ka a ( ). (A)ka (B)ka - (C)a k 2 (D)a k 2- 9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为 x ,1,5,2-, 则=x ( ). (A) 0 (B)3- (C) 3 (D) 2 10. 若5 7 3 4 11111 3263 478 ----= D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)0 11. 若2 23 5 101 1110 40 3 --= D ,则D 中第四行元的余子式的和为( ). 线性代数期中练习 一、单项选择题。 1. 12 021 k k -≠-的充分必要条件是( )。 (A) 1k ≠- (B) 3k ≠ (C) 1k ≠- 且3k ≠ (D) 1k ≠-或3k ≠ 2.若AB =AC ,当( )时,有B =C 。 (A) A 为n 阶方阵 (B) A 为可逆矩阵 (C) A 为任意矩阵 (D) A 为对称矩阵 3.若三阶行列式M a a a a a a a a a =3332 31 232221 13 1211 ,则=---------33 32 312322 2113 1211222222222a a a a a a a a a ( ) 。 (A) -6M (B) 6M (C) 8M (D) -8M 4.齐次线性方程组123123123 000ax x x x ax x x x x ++=?? ++=??++=?有非零解,则a 应满足( )。 (A) 0a ≠; (B) 0a =; (C) 1a ≠; (D) 1a =. 5.设12,ββ是Ax b =的两个不同的解,12,αα是0=Ax 的基础解系,则Ax b = 的通解是( )。 (A) 11212121()()2c c αααββ+-+ + (B) 11212121 ()()2 c c αααββ+++- (C) 11212121()()2c c αββββ+++- (D) 11212121 ()()2 c c αββββ+-++ 二.填空题。 6.A = (1, 2, 3, 4),B = (1, -1, 3, 5),则A ·B T = 。 7.已知A 、B 为4阶方阵,且A =-2,B =3,则| 5AB | = 。 | ( AB )-1 |= 。 8. 在分块矩阵A=B O O C ?? ??? 中,已知1-B 、1 -C 存在,而O 是零矩阵,则 =-1A 。 线性代数复旦大学出版社练习题答案习题一 1.2.3 4. ∵ ∴ 为偶数 故所求为 ∵ ∴所求为397281564 5.∵ ∴项前的符号位 ∵ ∴ 项前的符号位 6. 原式= 7.8 9. ∵ ∴ 10. 从第2列开始,以后各列加到第一列的对应元素之上,得 按第一列展开: 习题二 1.2.3.4.5 6. 设为与可交换的矩阵,则有 即 解之得 7. ,记为 ,记为 即 8 9. 10. = 11. ∵ ∴ 反之若 , 则 ,即 12. 设∵∴ 又∵∴ 又 当时,有 ∴ 设,则 ∵∴ 当时,有 故即 13. ∵∴为对称矩阵 同理也为对称矩阵 ∵ ∴为对称矩阵 又∵ ∴ 为反对称矩阵 ∵ 由知,为对称矩阵,为反对称矩阵 故可表示成一个对称矩阵与一个反对称矩阵的和。 14. 必要性:∵ ∴ 充分性:∵ ∴ 必要性:∵ ∴ 充分性:∵ ∴ 必要性:∵ ∴ 即 充分性:∵ ∴ 15 16. ∵ ∴ 可逆。 且 17. ∵ ∴ 可逆,且 18. 19. ∵,若可逆,则 ∴故可逆,且 20.设,∵是对称矩阵∴ 记,则 ,即为对称矩阵,又∵ , ∴ 为对称矩阵。 21.设,则 ∵ ∴ 又∵ ∴ 于是即 ∵ ∴ 于是 ∵ 可逆∴ ∴ 22. ∵∴ 23.4. 25. ∵ ∴ ∴ 可逆,且 26. ∵ ∴ 又∵, , ∴ 27 28. ∵ ∴ 又∵∴ 故 29. ∵∴ ∴ 30. 31. 32. 33. ∵ ∴ ∵ ∴ 习题三 1.2.3.4 5. ∵ 不能由线性表示 ∴线性方程组无解 不妨假设能由线性表示,则存在一组数,使 从而 此式与方程组无解矛盾。 故不能由的任何部分组线性表示 6. 依题意 所以 即 7. ∵ ∴ 令∵ ∴可逆,于是 即 8. 9.当即当或时,线性相关 否则线性无关。 10 .设 则 线性代数标准化作业答案 第一章:行列式 基础必做题:(一) 一、填空题: 1、3,n (n-1); 2、1222+++c b a ; 3、70,-14; 4、-3M ; 5、1 二、选择题: 1、C 2、D 3、D 4、A 5、C 三、计算题: 1、解:原式 11 110 01)1()1(1 11 11C 1 21 11++++=--?-?-+--?-++cd ad ab abcd d c d c b a ()(展开按2、解:原式 3 1 323 121) c b a () c b a (0 00) c b a (0 111 )c b a (2cr r 2br r b a c 2c 2c 2b a c b 2b 111 )c b a (2222++=++-++-++------++----++++++++提公因子b a c c c b a c b b c b a c b a c b a r r r r 四、解: ) )()()((0 000001) (1 111 ) ()(c x b x a x c b a x c x b c a b b x a b a x c b a c b a x x c b c x b c b x c b a c b a x x f ---+++=------+++=+++= 因,0)(=x f 故,,,c b a x =或)(c b a ++-。 基础必做题(二) 一、填空题: 1、6,8; 2、0; 3、0,0; 4、4; 5、24 二、选择题: 1、D ; 2、C ; 3、A ; 4、A ; 5、A,B,D 三、1、解:原式 第一次 行列式部分的填空题 1.在5阶行列式ij a 中,项a 13a 24a 32a 45a 51前的符号应取 + 号。 2.排列45312的逆序数为 5 。 3.行列式251122 14 ---x 中元素x 的代数余子式是 8 . 4.行列式1 02325 4 03 --中元素-2的代数余子式是 —11 。 5.行列式2 5 1 122 1 4 --x 中,x 的代数余子式是 —5 。 6.计算0 00 0d c b a = 0 行列式部分计算题 1.计算三阶行列式 3 8 1 141 102 --- 解:原式=2×(—4)×3+0×(—1)×(—1)+1×1×8—1×(—1)×(—4)—0×1×3—2×(—1)×8=—4 2.决定i 和j ,使排列1 2 3 4 i 6 j 9 7 为奇排列. 解:i =8,j =5。 3.(7分)已知00 1 04 13 ≠x x x ,求x 的值. 解:原式=3x 2—x 2—4x=2 x 2—4x=2x(x —2)=0 解得:x 1=0;x 2=2 所以 x={x │x ≠0;x ≠2 x ∈R } 4.(8分)齐次线性方程组 ?? ? ??=++=++=++000z y x z y x z y x λλ 有非零解,求λ。 解:()2 11 1 1 0100 011 1 1 11 11 -=--==λλλλλ D 由D=0 得 λ=1 5.用克莱姆法则求下列方程组: ?? ? ??=+-=++=++10329253142z y x z y x z y x 解:因为 033113 2104 21 711 7 2104 21 911 7 18904 213511 3 215 421231 312≠-=?-?=-------=-------=)(r r r r r r D 所以方程组有唯一解,再计算: 811 1 10 2129 4 2311-=-=D 1081 10 3 22954 311 2-==D 13510 1 3 2915 31213=-=D 因此,根据克拉默法则,方程组的唯一解是: x=27,y=36,z=—45 第二次 线性方程组部分填空题 1.设齐次线性方程组A x =0的系数阵A 的秩为r ,当r= n 时,则A x =0 只有零解;当A x =0有无穷多解时,其基础解系含有解向量的个数为 n-r .线性代数习题参考答案
线性代数课后习题答案-复旦大学出版社-熊维玲
修订版-线性代数习题三答案
线性代数习题集(带答案)
线性代数实践课作业
线性代数习题及答案复旦版
《线性代数》作业
线性代数习题集(带答案)
线性代数练习题及答案
线性代数复旦大学出版社练习题答案
线性代数标准化作业答案
西南大学线性代数作业答案
