三面角是立体几何的基本概念之一汇总

第三讲 三面角

三面角是立体几何的基本概念之一，是组成多面体的重要元素。与平面几何中有关三角形的正、余弦定理类似，有关三面角的正、余弦定理是解三面角的重要依据。熟练掌握解三面角的方法，可以较大地提高立体几何的解题能力。

一、三面角和补三面角

有公共端点且不共面的三条射线以及相邻两射线间的平

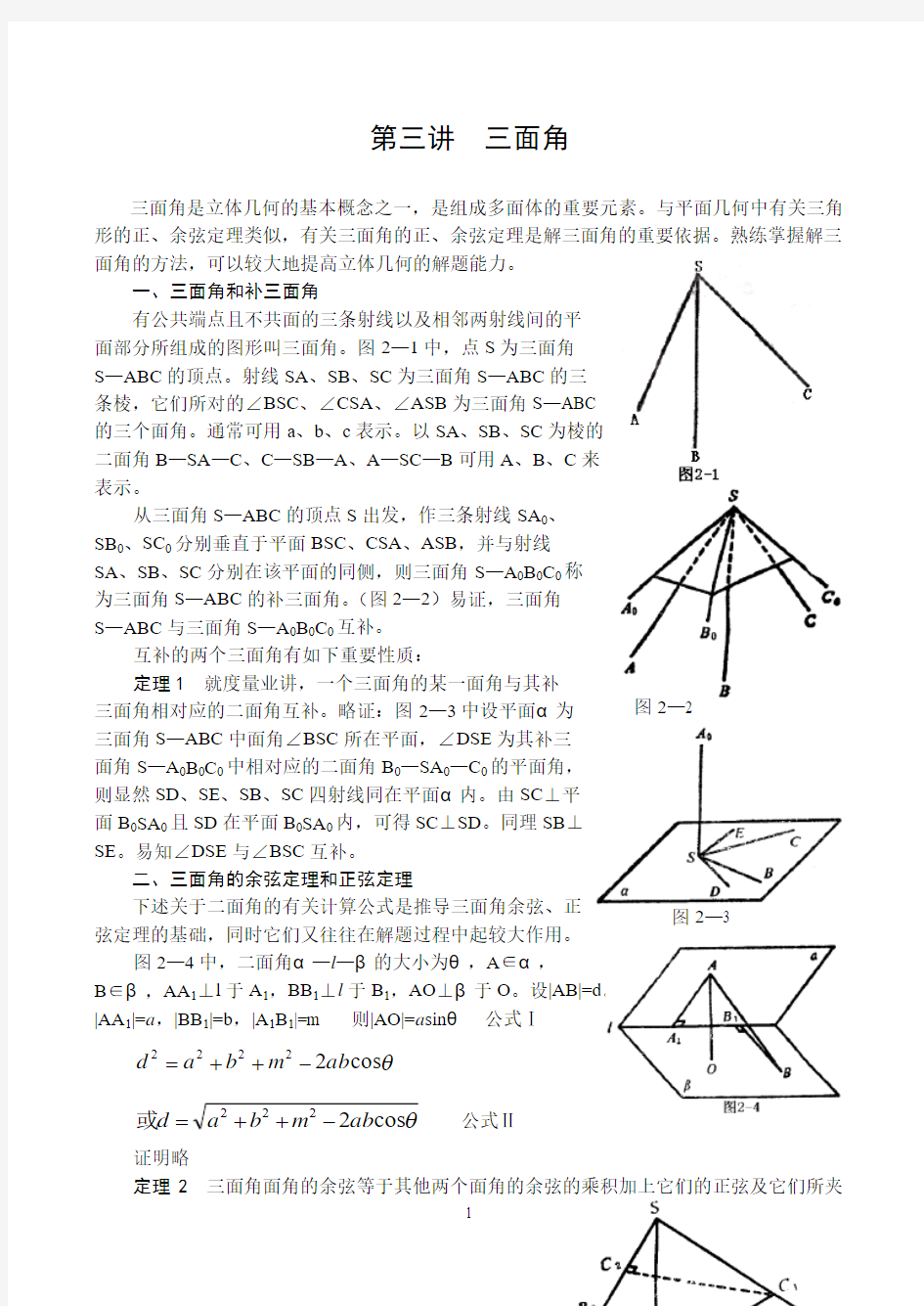
面部分所组成的图形叫三面角。图2—1中，点S 为三面角

S —ABC 的顶点。射线SA 、SB 、SC 为三面角S —ABC 的三

条棱，它们所对的∠BSC 、∠CSA 、∠ASB 为三面角S —ABC

的三个面角。通常可用a 、b 、c 表示。以SA 、SB 、SC 为棱的

二面角B —SA —C 、C —SB —A 、A —SC —B 可用A 、B 、C 来

表示。

从三面角S —ABC 的顶点S 出发，作三条射线SA 0、

SB 0、SC 0分别垂直于平面BSC 、CSA 、ASB ，并与射线

SA 、SB 、SC 分别在该平面的同侧，则三面角S —A 0B 0C 0称

为三面角S —ABC 的补三面角。（图2—2）易证，三面角

S —ABC 与三面角S —A 0B 0C 0互补。

互补的两个三面角有如下重要性质：

定理1 就度量业讲，一个三面角的某一面角与其补 三面角相对应的二面角互补。略证：图2—3中设平面α为

三面角S —ABC 中面角∠BSC 所在平面，∠DSE 为其补三

面角S —A 0B 0C 0中相对应的二面角B 0—SA 0—C 0的平面角，

则显然SD 、SE 、SB 、SC 四射线同在平面α内。由SC ⊥平

面B 0SA 0且SD 在平面B 0SA 0内，可得SC ⊥SD 。同理SB ⊥

SE 。易知∠DSE 与∠BSC 互补。

二、三面角的余弦定理和正弦定理

下述关于二面角的有关计算公式是推导三面角余弦、正 弦定理的基础，同时它们又往往在解题过程中起较大作用。

图2—4中，二面角α—l —β的大小为θ，A ∈α，

B ∈β，AA 1⊥l 于A 1，BB 1⊥l 于B 1，AO ⊥β于O 。设|AB|=d 。

|AA 1|=a ，|BB 1|=b ，|A 1B 1|=m 则|AO|=a sin θ 公式Ⅰ

θcos 22222ab m b a d -++=

θcos 2222ab m b a d -++=或 公式Ⅱ 证明略

定理2

三面角面角的余弦等于其他两个面角的余弦的乘积加上它们的正弦及它们所夹 图2— 3 图2— 2

二面角的连乘积。

分析 不失一般性，对三面角S —ABC ，

只须证明A c b c b a cos sin sin cos cos cos ?+=

证明时利用上述公式Ⅱ及三角形的余弦定理即可。

证明 图2—5中，设三面角S —ABC 的面角

b 及

c 均为锐角。在SB 、SC 上分别取|SB 1|=|SC 1|=1。

作B 1B 2⊥SA 于B 2，C 1C 2⊥SA 于C 2，则|B 1B 2|=sinC ，

|C 1C 2|=sinb 二面角B —SA —C 中，

|B 1C 1|2=|B 1B 2|2+|C 1C 2|2+|B 2C 2|2－2|B 1B 2|·|C 1C 2|·

cosA=A b c b c B C cos sin sin 2)cos (cos sin sin 222--++

△B 1SC 1中，A SC SB SC SB C B cos 22cos ||||2||||||112121211-=??-+=α

因此A A b c b c B C cos 22cos sin sin 2)cos (cos sin sin 222-=--++

经整理即得 A c b c b a cos sin sin cos cos cos +=

至于b 、c 大小的其他情况，请读者自证。

定理3 三面角中任一二面角的余弦等于其余两个二面角的余弦乘积的相反数加上此两个二面角的正弦及其所夹面角的余弦的连乘积。

已知 三面角S —ABC

求证 a C B C B A c o s s i n s i n c o s c o s

c o s +-= 证明 取三面角S —ABC 的补三面角S —A 0B 0C 0，由定理2可知

000000cos sin sin cos cos cos A c b c b a +=

由定理1，a A C C B b A a -?=-?=-?=-?=180180,180,1800000

因此，)180cos()180sin()180sin()180cos()180cos()180cos(a C B C B A -?-?-?+-?-?=-?

经整理可得 a C B C B A c o s s i n s i n c o s c o s

c o s +-= 定理4 三面角中面角的正弦的比等于所对二面角的正弦的比。

分析 定理4的证法很多，这里可用利用公式Ⅰ来证明。

证明 设三面角S —ABC ，在SB 上任取一点B 1，作B 1D ⊥SA

于D ，B 1E ⊥SC 于E ，见图2—6。令B 1到平面ASC 的距离为d ，

由公式Ⅰ.在二面角B —SA —C 中,d=|B 1D|·sinA=|SB 1|·sinC ·sinA

在二面角B —SC —A 中,C a SB C E B d sin sin ||sin ||11??=?= 因此C a SB A c SB sin sin ||sin sin ||11?=? 即

C

c A a sin sin sin sin = 同理B b A a sin sin sin sin = 因此C c B b A a sin sin sin sin sin sin == 定理2和定理3分别称为三面角第一余弦定理和第二余弦定理，定理4称为三面角正弦

定理。

与平面几何中解三角形的各种基本情况类似，恰当运用三面角的正、余弦定理，可以解有关三面角的各种情况。如果我们把三面角的面角称为“边”，二面角称为“解”，那末就可以用三角形的语言来叙述三面角的各种情况。如三面角有三条边及三个角共六个基本元素，有关解三面角的基本情况也可以归纳为诸如“两角夹一边”、“两边夹一角”、“三边”，“三角”……等，这里不一一列举。另外，结合有关三角函数公式，可以推出很多有关三面角各基本元素之间的关系式。

例1 求证：三面角S —ABC 中 A b c b c B a cos sin cos cos sin cos sin -=

证明 由三面角第一余弦定理可得c

b c b a A sin sin cos cos cos cos -= c a c a b B s i n s i n c o s c o s c o s c o s -= 因此C

c a b B a sin cos cos cos cos sin -= （1） C

c b a c b c A b c b sin )cos cos (cos cos cos sin cos sin cos cos sin --=- C

c a c c b C b c c a b sin cos cos )cos (sin cos sin cos cos cos cos cos sin 2222-+=+-= C

c a b sin cos cos cos -=

（2） 由（1）及（2）即证A b c b c B a cos sin cos cos sin cos sin -= 本式中适当换字母，即可得到另外五个公式。

例2 求证三面角S —ABC 中。

a C B C B c A cos sin cos cos sin cos sin +=

分析 取三面角S —ABC 的补三面角S —A 0B 0C 0将例1中的公式应用于三面角S —A 0B 0C 0，再应用定理1即可。

证明 取三面角S —ABC 的补三面角S —A 0B 0C 0

则由0000000cos sin cos cos sin cos sin A c b c b C a -=

得)180cos()180sin()180cos(

)180sin(C B c A -?-?=-?-? )180cos()180sin()180cos(a C B -?-?-?-

)cos (sin c A -)cos (sin )cos ()cos (sin a C B C B -?---=

因此a C B C B c A cos sin cos cos sin cos sin +=

例3 求证三面角S —ABC 中 A c A c t g B c c t g b c o s c o s s i n s

i n += 分析 利用正弦定理及例1的公式

证明 由例1 A b c b c B a cos sin cos cos sin cos sin -=

两边同除b sin 得

A c b

b c B b a c o s c o s s i n c o s s i n c o s s i n s i n -?= 由正弦定理知 ,sin sin sin sin B A b a =代入得A C ctgb c B B A cos cos sin cos sin sin -?=? 因此A c c ctgb ctgB A cos cos sin sin -=? 即A c A ctgB c ctgb cos cos sin sin += 例4 已知，三面角S —ABC 中。.cos ,60,90,45C C b a 求?=?=?=

分析 本题为已知“边、角、边”解三面角型，可采用第一余弦定理。

解 由C b a b a c cos sin sin cos cos cos +=

得 4

260cos 90sin 45sin 90cos 45cos cos =?????+??=C 注意 三面角的三个面角之和不一定等于180°，因此不能误用解平面几何中三角形时三内角之和为180°来求第三个面角，本题中的面角C 显然大于45°。由此可知，尽管三面角与三角形有许多类似之处，但它们之间又有许多完全不同的性质。例如正弦定理，三角形的正弦定理中边与其对应角的正弦的比值除相等外，还等于常量——此三角形外接圆直径。而三面角中面角正弦与其对应二面角正弦之比只是相等，但不等于常量。至于余弦定理，三面角的余弦定理有两类更是有别于三角形的。