求解系统的状态方程

求解系统的状态方程

一、实验设备

PC计算机，MATLAB软件，控制理论实验台

二、实验目的

(1)掌握状态转移矩阵的概念。学会用MATLAB求解状态转移矩阵

(2)学习系统齐次、非齐次状态方程求解的方法，计算矩阵指数，求状态响应；

(3)通过编程、上机调试，掌握求解系统状态方程的方法，学会绘制输出响应和状态响应曲线；

(4)掌握利用MATLAB导出连续状态空间模型的离散化模型的方法。

三、实验原理及相关基础

(1)参考教材P99~101“3.8利用MATLAB求解系统的状态方程”

(2)MATLAB现代控制理论仿真实验基础

（3）控制理论实验台使用指导

四、实验内容

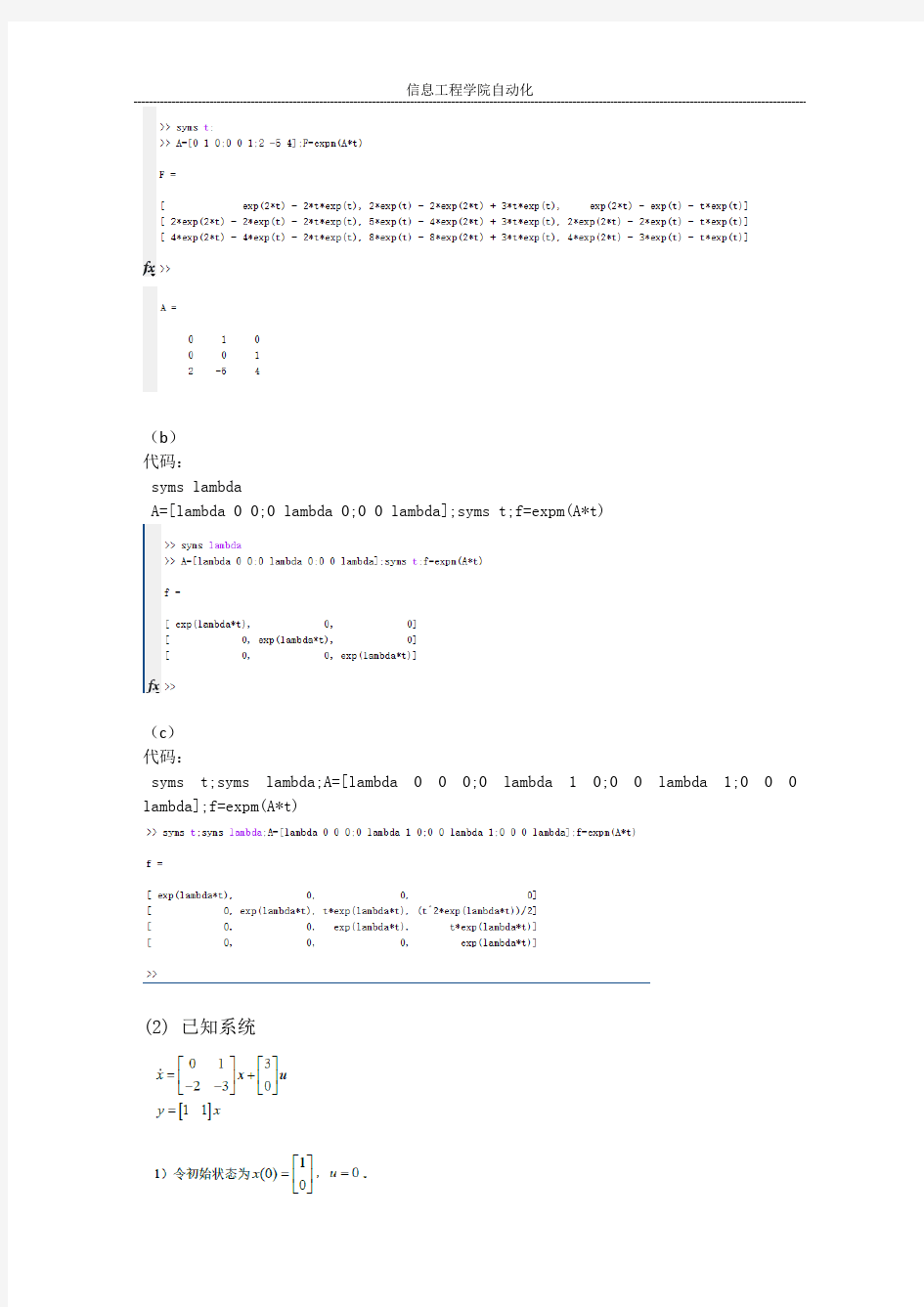
(1)求下列系统矩阵A对应的状态转移矩阵

（a）

（b）

代码：

syms lambda

A=[lambda 0 0;0 lambda 0;0 0 lambda];syms t;f=expm(A*t)

（c）

代码：

syms t;syms lambda;A=[lambda 0 0 0;0 lambda 1 0;0 0 lambda 1;0 0 0 lambda];f=expm(A*t)

(2) 已知系统

a) 用MATLAB求状态方程的解析解。选择时间向量t，绘制系统的状态响应曲线。观察并记录这些曲线。

（1）

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

u=1;

syms t;

f=expm(A*t);%状态转移矩阵

x0=0;

s1=f*B*u;

s2=int(s1,t,0,t)%状态方程解析解

状态曲线：

（2）A=[0 1;-2 -3];

syms t;

f=expm(A*t);

X0=[1;0];

t=[0:0.5:10];

for i=1:length(t);

g(i)=double(subs(f(1),t(i)));

end

plot(t,g)

（3）状态转移矩阵

syms lambda

A=[lambda 0 0;0 lambda 0;0 0 lambda];

syms t

f=expm(A*t)

b) 计算系统在初始状态作用下状态响应和输出响应的数值解(用函数

initial( )), 绘制系统的状态响应曲线和输出响应曲线。观察并记录这些响应曲线，然后将这一状态响应曲线与a)中状态响应曲线进行比较。

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

G=ss(A,B,C,D);

t=[0:0.5:10];

x0=[1;0]

[y0,t,x0]=initial(G,x0,t);

plot(t,x0,'-',t,y0,'-')

c) 根据b)中所得的状态响应的数值解，绘制系统的状态轨迹(用命令plot(x(:,1), x(:,2)))。记录系统状态转移的过程，结合a)和b)中的状态响应曲线分析这一过程。

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

t=[0:0.01:10];

x0=[1;0];

G=ss(A,B,C,D)

[y,t,x]=initial(G,x0,t);

plot(x(:,1),x(:,2))

2) 令初始状态为零，输入为u(t)=1(t).

a)用MATLAB求状态方程的解析解。选择时间向量t，绘制系统的状态响应曲线。观察并

记录这些曲线。

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

G=ss(A,B,C,D);

[y,t,x]=step(G);

plot(t,x)

b)计算系统在初始状态作用下状态响应和输出响应的数值解, 绘制系统的状态

响应曲线和输出响应曲线。观察并记录这些响应曲线，然后将这一状态响应曲线与a).中状态响应曲线进行比较。

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

G=ss(A,B,C,D);

G=ss(A,B,C,D);

t=[0:0.5:10];

x0=[1;-1];

[y0,t,x0]=initial(G,x0,t);

plot(t,x0,'-',t,y0,'-')

c) 根据b)中所得的状态响应的数值解，绘制系统的状态轨迹。记录系统状态转移的过程，结合a)和b)中的状态响应曲线分析这一过程。

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

t=[0:0.5:10];

G=ss(A,B,C,D);

x0=[0 0];

[y0,t,x0]=initial(G,x0,t);

plot(t,x0,'-',t,y0,'-')

绘制系统的状态响应曲线、输出响应曲线和状态轨迹。观察和分析这些响应曲线和状态轨迹是否是（1）和（2）中的响应曲线和状态轨迹的叠加。

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

t=[0:0.01:10];

x0=[1 -1];

G=ss(A,B,C,D);

[y,t,x]=initial(G,x0,t);

plot(t,x)

4）令初始状态为零，输入为u(t)=3sin(5t)。计算状态响应和输出响应的数值解(用函数lsim( ))，并绘制系统的状态响应曲线、输出响应曲线和状态轨迹。

代码：

A=[0 1; -2 -3];

B=[3;0];

C=[1 1];

D=[0];

t=[0:0.01:10];

u=3*sin(5*t);

G=ss(A,B,C,D);

[y,t,x]=lsim(G,u,t);

plot(t,x)

（3）已知系统

1）当输入为u(t)=(t)时，用函数initial( )和 impulse( )求解系统的状态响应和输出响应的

数值解，并绘制系统的状态响应曲线、输出响应曲线和状态轨迹。

状态响应：

A=[0,1,0;0,0,1;-6,-11,-6];

B=[0;0;1];

C=[6,0,0];

D=0;

t=[0:0.5:10];

G=ss(A,B,C,D);

x0=[1,0,-1];

[y,t,x]=initial(G,x0,t);

u=ones(size(t));

plot(t,x,t,y)

输出响应：

A=[0,1,0;0,0,1;-6,-11,-6]; B=[0;0;1];

C=[6,0,0];

D=0;

t=[0:0.01:10];

u=ones(size(t));

G=ss(A,B,C,D);

[y,t,x]=lsim(G,u,t);

plot(t,x)