圆中有关定理

切线长定理、弦切角定理、切割线定理、相交弦定理

以及与圆有关的比例线段

1.切线长概念

切线长是在经过圆外一点的圆的切线上，这点和切点之间的线段的长度，“切线长”是切线上一条线段的长，具有数量的特征，而“切线”是一条直线，它不可以度量长度。

2.切线长定理

如图1对于切线长定理，应明确（1）若已知圆的两条切线相交，则切线长相等；（2）若已知两条切线平行，则圆上两个切点的连线为直径；（3）经过圆外一点引圆的两条切线，连结两个切点可得到一个等腰三角形；（4）经过圆外一点引圆的两条切线，切线的夹角与过切点的两个半径的夹角互补；（5）圆外一点与圆心的连线，平分过这点向圆引的两条切线所夹的角。

3.弦切角（如图2）：顶点在圆上，一边和圆相交，另一边和圆相切的角。

直线AB切⊙O于P，PC、PD为弦，图中几个弦切角呢？（四个）∠APC,∠APD,∠BPD,∠BPC

4.弦切角定理：弦切角等于其所夹的弧所对的圆周角。即如上图中∠APC=∠CDP等

证明：如图2，连接CD、OC、OP，因为∠CPO=∠PCO,所以∠COP=180?-2∠CPO而∠CPO=90?-∠APC,故∠COP=2∠APC,即∠CDP=∠APC。

5.弄清和圆有关的角：圆周角，圆心角，弦切角，圆内角，圆外角。

6.遇到圆的切线，可联想“角”弦切角，“线”切线的性质定理及切线长定理。

7.与圆有关的比例线段

定理图形已知结论证法

相交

弦定

理

⊙O中，

AB、CD

为弦，交

于P. PA·PB＝PC·PD

连结AC、BD，∠C=∠B,∠A=∠D,

所以△APC∽△DPB

相交

弦定

理的

推论

⊙O中，

AB为直

径，

CD⊥AB

于P.

PC2＝PA·PB

用相交弦定理.

切割

线定

理

⊙O中，

PT切⊙O

于T，割

线PB交

⊙O于A

PT2＝PA·PB

连结TA、TB，则∠PTA=∠B（弦

切角等于同弧圆周角）所以

△PTA∽△PBT，所以

PT2＝PA·PB

图1 图2

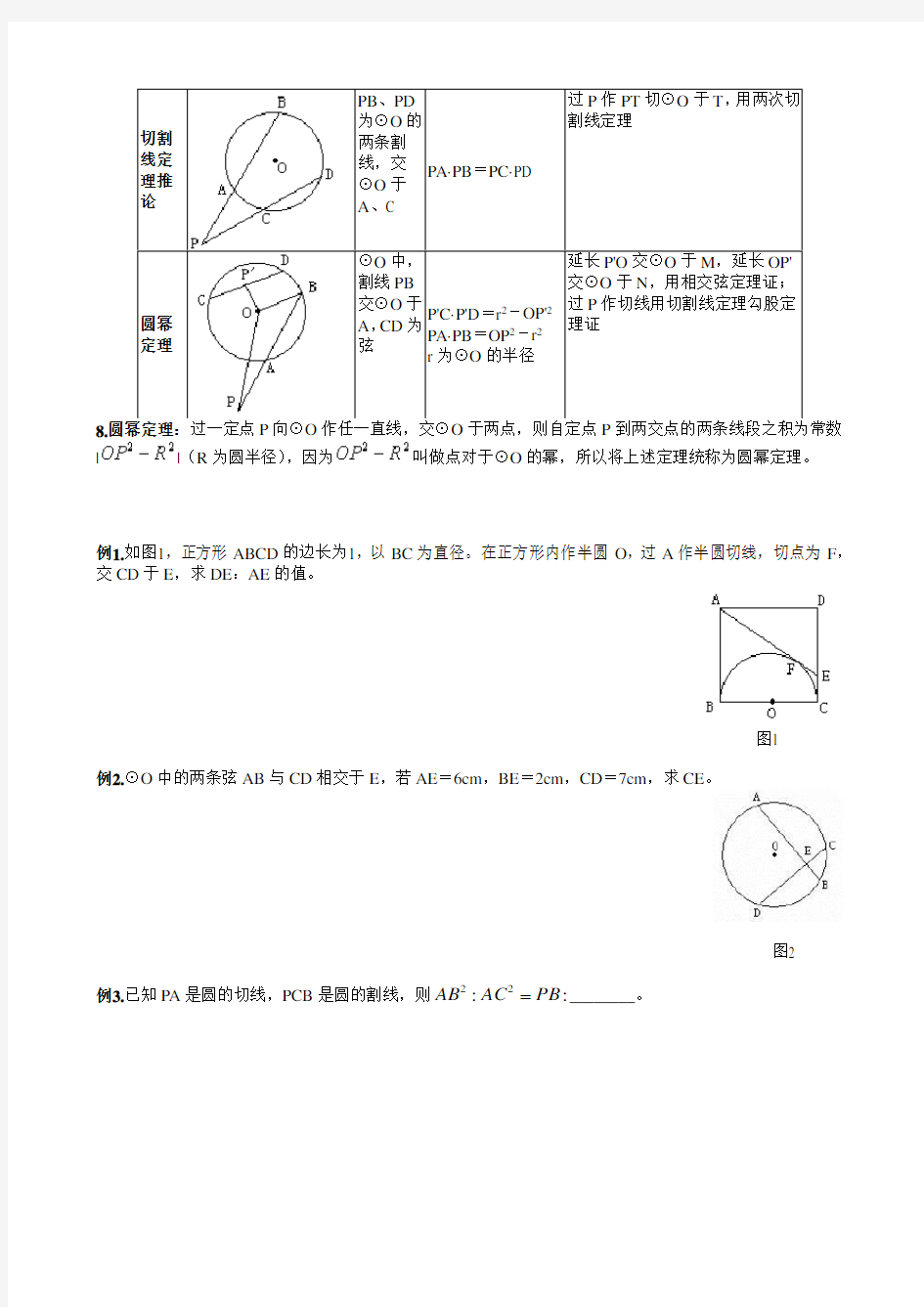
切割线定理推论

PB 、PD 为⊙O 的两条割

线，交⊙O 于A 、C

PA·PB ＝PC·PD 过P 作PT 切⊙O 于T ，用两次切割线定理

圆幂定理

⊙O 中，割线PB 交⊙O 于

A ，CD 为

弦

P'C·P'D ＝r 2－OP'2

PA·PB ＝OP 2－r 2

r 为⊙O 的半径

延长P'O 交⊙O 于M ，延长OP'交⊙O 于N ，用相交弦定理证；过P 作切线用切割线定理勾股定理证

8.圆幂定理：过一定点P 向⊙O 作任一直线，交⊙O 于两点，则自定点P 到两交点的两条线段之积为常数||（R 为圆半径），因为叫做点对于⊙O 的幂，所以将上述定理统称为圆幂定理。

例1.如图1，正方形ABCD 的边长为1，以BC 为直径。在正方形内作半圆O ，过A 作半圆切线，切点为F ，交CD 于E ，求DE ：AE 的值。

图1

例2.⊙O 中的两条弦AB 与CD 相交于E ，若AE ＝6cm ，BE ＝2cm ，CD ＝7cm ，求CE 。

图2

例3.已知PA 是圆的切线，PCB 是圆的割线，则::2

2PB AC AB ________。

例4.如图3，P 是⊙O 外一点，PC 切⊙O 于点C ，PAB 是⊙O 的割线，交⊙O 于A 、B 两点，如果PA ：PB ＝1：4，PC ＝12cm ，⊙O 的半径为10cm ，则圆心O 到AB 的距离是___________cm 。

图3

例5.如图4，AB 为⊙O 的直径，过B 点作⊙O 的切线BC ，OC 交⊙O 于点E ，AE 的延长线交BC 于点D ，求证：（1）CB CD CE ?=2

；（2）若AB ＝BC ＝2厘米，求CE 、CD 的长。

图4

例6.如图5，AB 为⊙O 的直径，弦CD ∥AB ，AE 切⊙O 于A ，交CD 的延长线于E 。求证：DE AB BC ?=2

图5

例7.如图6，PA 、PC 切⊙O 于A 、C ，PDB 为割线。求证：AD·BC ＝CD·AB

图6

例8.如图7，在直角三角形ABC 中，∠A ＝90°，以AB 边为直径作⊙O ，交斜边BC 于点D ，过D 点作⊙O 的切线交AC 于E 。求证：BC ＝2OE 。

图7

例9.如图8，在正方形ABCD 中，AB ＝1，?

AC 是以点B 为圆心，AB 长为半径的圆的一段弧。点E 是边AD 上的任意一点（点E 与点A 、D 不重合），过E 作?

AC 所在圆的切线，交边DC 于点F ，G 为切点。 当∠DEF ＝45°时，求证:点G 为线段EF 的中点；

图8

【模拟试题】（答题时间：40分钟）

一、选择题

1.已知：PA 、PB 切⊙O 于点A 、B ，连结AB ，若AB ＝8，弦AB 的弦心距3，则PA ＝（ ） A.20/3 B.25/3 C. 5 D. 8

2.下列图形一定有内切圆的是（ ）

A.平行四边形

B.矩形

C.菱形

D.梯形

3.已知：如图1直线MN 与⊙O 相切于C ，AB 为直径，∠CAB ＝40°，则∠MCA 的度数（ ）

图1

A. 50°

B. 40°

C. 60°

D. 55°

4.圆内两弦相交，一弦长8cm 且被交点平分，另一弦被交点分为1：4，则另一弦长为（ ） A. 8cm B. 10cm C. 12cm D. 16cm

5.在△ABC 中，D 是BC 边上的点，AD=22cm ，BD ＝3cm ，DC ＝4cm ，如果E 是AD 的延长线与△ABC 的外接圆的交点，那么DE 长等于（ ）

A. 32cm

B. 23cm

C. 22cm

D. 33cm 6. PT 切⊙O 于T ，CT 为直径，D 为OC 上一点，直线PD 交⊙O 于B 和A ，B 在线段PD 上，若CD ＝2，AD ＝3，BD ＝4，则PB 等于（ ）

A. 20

B. 10

C. 5

D.

二、填空题 7. AB 、CD 是⊙O 切线，AB ∥CD ，EF 是⊙O 的切线，它和AB 、CD 分别交于E 、F ，则∠EOF ＝_____________度。

8.已知：⊙O 和不在⊙O 上的一点P ，过P 的直线交⊙O 于A 、B 两点，若PA·PB ＝24，OP ＝5，则⊙O 的半径长为_____________。

9.若PA 为⊙O 的切线，A 为切点，PBC 割线交⊙O 于B 、C ，若BC ＝20，PA=310，则PC 的长为_____________。

10.正△ABC 内接于⊙O ，M 、N 分别为AB 、AC 中点，延长MN 交⊙O 于点D ，连结BD 交AC 于P ，则

PA

PC

=_____________。 三、解答题

11.如图2，△ABC 中，AC ＝2cm ，周长为8cm ，F 、K 、N 是△ABC 与内切圆的切点，DE 切⊙O 于点M ，且DE ∥AC ，求DE 的长。

图2

12.如图3，已知P 为⊙O 的直径AB 延长线上一点，PC 切⊙O 于C ，CD ⊥AB 于D ，求证：CB 平分∠DCP 。

图3

13.如图4，已知AD 为⊙O 的直径，AB 是⊙O 的切线，过B 的割线BMN 交AD 的延长线于C ，且BM ＝MN ＝NC ，若AB=22cm ，求⊙O 的半径。

图4

圆的有关定理例题答案

例1解：由切线长定理知：AF ＝AB ＝1，EF ＝CE 设CE 为x ，在Rt △ADE 中，由勾股定理

∴

，

，

例2解：由相交弦定理，得 AE·BE ＝CE·DE ∵AE ＝6cm ，BE ＝2cm ，CD ＝7cm ，

， ∴

，

即

∴CE ＝3cm 或CE ＝4cm 。 故应填3或4。

点拨：相交弦定理是较重要定理，结果要注意两种情况的取舍。

例3 解：∵∠P ＝∠P ∠PAC ＝∠B ， ∴△PAC ∽△PBA ，

∴， ∴。

又∵PA 是圆的切线，PCB 是圆的割线，由切割线定理，得

∴

，

即 ， 故应填PC 。 点拨：利用相似得出比例关系式后要注意变形，推出所需结论。 例4 解：∵PC 是⊙O 的切线，PAB 是⊙O 的割线，且PA ：PB ＝1：4 ∴PB ＝4PA 又∵PC ＝12cm 由切割线定理，得

∴

∴

，

∴

∴PB ＝4×6＝24（cm ） ∴AB ＝24－6＝18（cm ）

设圆心O 到AB 距离为d cm ， 由勾股定理，得

故应填

。

例5 证明：（1）连结BE

（2）

。

又∵

，

∴厘米。

点拨：有切线，并需寻找角的关系时常添辅助线，为利用弦切角定理创造条件。 例6 证明：连结BD ，∵AE 切⊙O 于A ，

∴∠EAD ＝∠ABD ∵AE ⊥AB ，又AB ∥CD ， ∴AE ⊥CD ∵AB 为⊙O 的直径 ∴∠ADB ＝90°

∴∠E ＝∠ADB ＝90° ∴△ADE ∽△BAD ∴ ∴

∵CD ∥AB

∴AD ＝BC ，∴

例7 点悟：由结论AD·

BC ＝CD·AB 得，显然要证△PAD ∽△PBA 和△PCD ∽△PBC

证明：∵PA 切⊙O 于A ， ∴∠PAD ＝∠PBA 又∠APD ＝∠BPA ， ∴△PAD ∽△PBA ∴ 同理可证△PCD ∽△PBC ∴

∵PA 、PC 分别切⊙O 于A 、C

∴PA ＝PC ∴

∴AD·BC ＝DC·AB

例8 点悟：由要证结论易想到应证OE是△ABC

的中位线。而OA＝OB，只须证AE＝CE。

证明：连结OD。∵AC⊥AB，AB为直径

∴AC为⊙O的切线，又DE切⊙O于D

∴EA＝ED，OD⊥DE ∵OB＝OD，∴∠B＝

∠ODB

在Rt△ABC中，∠C＝90°－∠B ∵∠ODE＝90°

∴

∴∠C＝∠EDC ∴ED＝EC∴AE＝EC

∴OE是△ABC的中位线∴BC＝2OE

例9 解：由∠DEF＝45°，得

，

∴∠DFE＝∠DEF ∴DE＝DF

又∵AD＝DC ∴AE＝FC

因为AB是圆B的半径，AD⊥AB，所以AD切圆

B于点A；同理，CD切圆B于点C。

又因为EF切圆B于点G，所以AE＝EG，FC＝

FG。

因此EG＝FG，即点G为线段EF的中点。

模拟测试答案

一、选择题：ACABBA

7. 90 8. 1 9. 30 10.

13.设BM＝MN＝NC＝xcm

又∵

∴

又∵OA是过切点A的半径，∴OA⊥AB即

AC⊥AB

在Rt△ABC中，由勾股定理，得，

由割线定理：，又

∵

∴

∴半径为。

11.由切线长定理得△BDE周长为4，由

△BDE∽△BAC，得DE＝1cm

12.证明：连结AC，则AC⊥CB

∵CD⊥AB，∴△ACB∽△CDB，∴∠A＝∠1

∵PC为⊙O的切线，∴∠A＝∠2，又∠1＝

∠2，

∴BC平分∠DCP