(完整版)考研三角函数公式

三角公式表
倒数关系:
商的关系:
平方关系:tanα ·cotα=1
sinα ·cscα=1
cosα ·secα=1
sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα
sin2α+cos2α=1
1+tan2α=sec2α
1+cot2α=csc2α
诱导公式(口诀:奇变偶不变,符号看象限。)
sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
(其中k∈Z)
两角和与差的三角函数公式万能公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tanα+tanβ
tan(α+β)=——————
1-tanα ·tanβ
tanα-tanβ
tan(α-β)=——————
1+tanα ·tanβ
2tan(α/2)
s inα=——————
1+tan2(α/2)
1-tan2(α/2)
cosα=——————
1+tan2(α/2)
2tan(α/2)
tanα=——————
1-tan2(α/2)
半角的正弦、余弦和正切公式三角函数的降幂公式
二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式
sin2α=2sinαcosαsin3α=3sinα-4sin3α
cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α
2tanα
tan2α=—————
1-tan2α
cos3α=4cos3α-3cosα
3tanα-tan3α
tan3α=——————
1-3tan2α
三角函数的和差化积公式三角函数的积化和差公式
α+βα-β
sinα+sinβ=2sin———·cos———
2 2
α+βα-β
sinα-sinβ=2cos———·sin———
2 2
α+βα-β
cosα+cosβ=2cos———·cos———
2 2
α+βα-β
cosα-c osβ=-2sin———·sin———
2 2
1
sinα ·cosβ=-[sin(α+β)+sin(α-β)]
2
1
cosα ·sinβ=-[sin(α+β)-sin(α-β)]
2
1
cosα ·cosβ=-[cos(α+β)+cos(α-β)]
2
1
sinα ·sinβ=— -[cos(α+β)-cos(α-β)]
2
反三角函数
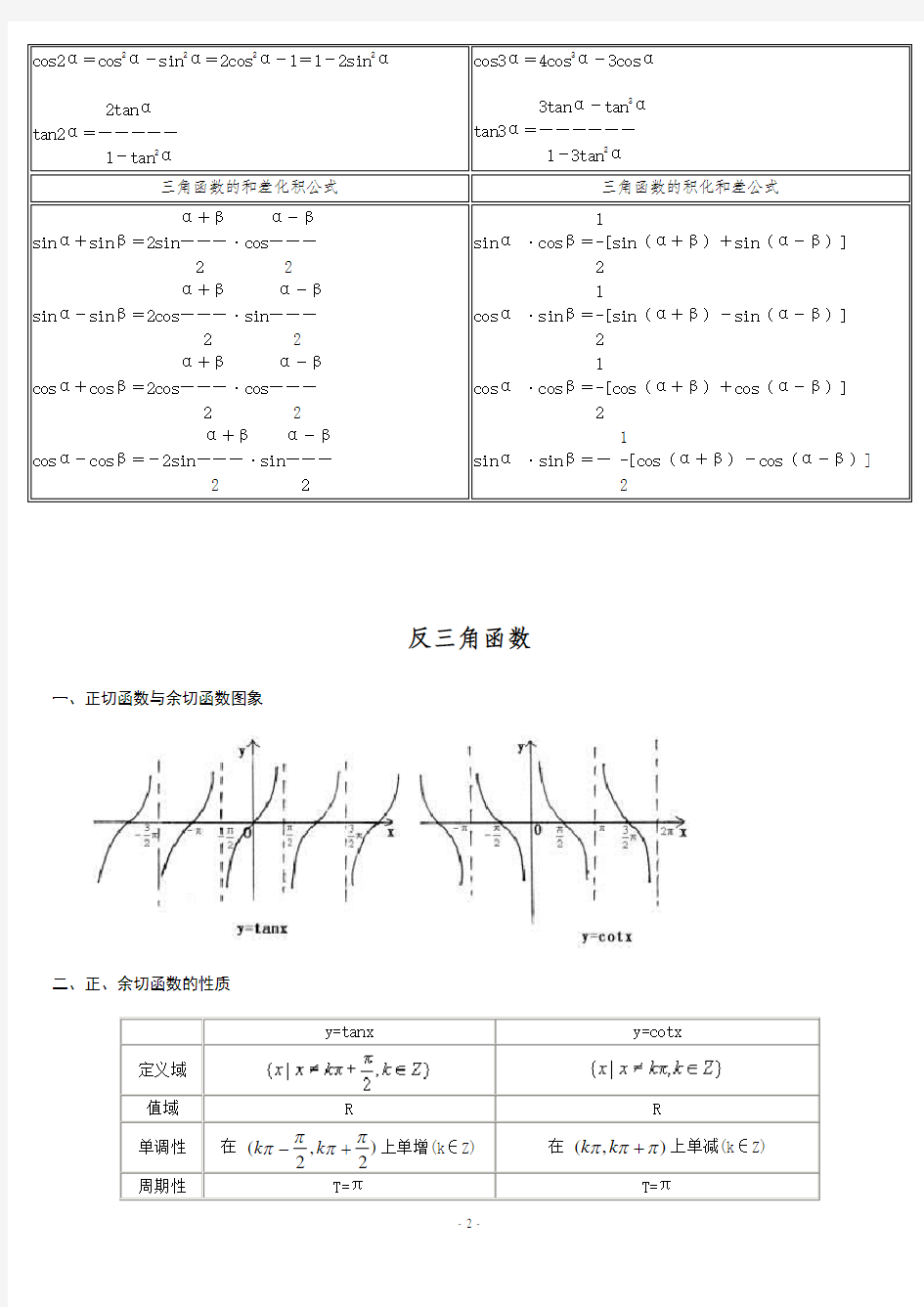
一、正切函数与余切函数图象
二、正、余切函数的性质
y=tanx y=cotx
定义域
值域R R
单调性在)
2
,
2
(
π
π
π
π+
-k
k上单增(k∈Z)在)
,
(π
π
π+
k
k上单减(k∈Z)
周期性T=πT=π
对称性
10
对称中心
)0,
(πk,奇函数(k∈Z)
20对称轴;无
10对称中心)0,
2
(
π
,奇函数(k∈Z)
20对称轴;无
注: 1、由定义域知,y=tanx与y=cotx图象都存在无数多个间断点(不连续点).
2、每个单元区间一定是连续的.
3、由单调性可解决比较大小问题,但要务必使两个自变量在同一单调区间内.
三、反三角函数的概念和图象
四种三角函数都是由x到y的多值对应,要使其有反函数,必须缩小自变量x的范围,使之成为由x到y的对应.从方便的角度而言,这个x的范围应该(1)离原点较近;(2)包含所有的锐角;(3)能取到所有的函数值;(4)最好是连续区间.从这个原则出发,我们给出如下定义:
1.y=sinx, x∈]
2
,
2
[
π
π
-的反函数记作y=arcsinx, x∈[-1,1],称为反正弦函数.
y=cosx, x∈]
,0[π的反函数记作y=arccosx, x∈[-1,1],称为反余弦函数.
y=tanx,x∈]
2
,
2
[
π
π
-的反函数记作y=arctanx, x∈R,称为反正切函数.
y=cotx,x∈]
,0[π的反函数记作y=arccotx, x∈R,称为反余切函数.
2.反三角函数的图象
由互为反函数的两个函数图象间的关系,可作出其图象.
注:(1)y=arcsinx, x ∈[-1,1]图象的两个端点是)1,2
()2
,
1(--
π
π
和
(2)y=arccosx, x ∈[-1,1]图象的两个端点是(1,0)和(-1,π).
(3)y=arctanx, x ∈R 图象的两条渐近线是2
π
=
y 和2
π
-
=y .
(4)y=arccotx, x ∈R 图象的两条渐近线是y=0和y=π.
四、反三角函数的性质由图象
y=arcsinx y=arccosx y=arctanx
y=arccotx
定义域 [-1,1]
[-1,1] R
R 值域 ]2
,2[π
π-
[0, π]
]2
,2[π
π-
(0, π) 单调性
在[-1,1]上单增 在[-1,1]上单减
在R 上单增
在R 上单减
对称性
10
对称中心 (0,0)奇函数 20
对称轴;无
10
对称中心 )
2
,
0(π
非奇非偶 20
对称轴;无
10
对称中心
(0,0)奇函数
20
对称轴;无 10
对称中心 )2
,0(π
非奇非偶 20
对称轴;无
周期性 无 无 无 无
另外:
1.三角的反三角运算
arcsin(sinx)=x(x ∈ ]2
,2[ππ-) arccos(cosx)=x (x ∈[0, π]) arctan(tanx)=x(x ∈ ]2
,2[π
π-
) arccot(cotx)=x(x ∈(0, π)) 2.反三角的三角运算
sin(arcsinx)=x (x ∈[-1,1]) cos(arccosx)=x (x ∈[-1,1]) tan(arctanx)=x (x ∈R) cot(arccotx)=x (x ∈R)
3.x 与-x 的反三角函数值关系 arcsin(-x)=-arcsinx(x ∈[-1,1]) arccos(-x)=π-arccosx (x ∈[-1,1]) arctan(-x)=-arctanx (x ∈R)
arccot(-x)=π-arccotx(x ∈R) 4.])1,1[(2
arccos arcsin -∈=+x x x π
,)(2
cot arctan R x x arc x ∈=
+π
五、已知三角函数值求角
1. 若sinx=a (|a|≤1),则x=k π+(-1)k
arcsina(k ∈Z) 2. 若cosx=a (|a|≤1),则x=2k π+arccosa(k ∈Z) 3. 若tanx=a (a ∈R), 则x=k π+arctana (k ∈Z)
4. 若cotx=a (a ∈R), 则x=k π+arccota(k ∈Z)
