《解方程》典型例题

例1 解方程：89210+-=+-x x

例2 解方程：)2(3)3(2+=-x x

例3 解方程：7722121-=--

x x

例4 解方程：

6233)5(54--+=--+x x x x

例5 解方程：

5303.02.05.05.01.24.0=--+x x

例6 下面解题过程正确吗？如果正确，请指出每一步的依据；如果不正确，请指出错在哪里，并给出正确的解答．

（1）解方程4

13x x += 两边都乘以12，得 134=-x x ∴1=x （2）解方程83243212

x x --+= 去分母，得 x x 326220--+=

移项，得 202623--=-x x

合并同类项，得 16-=x

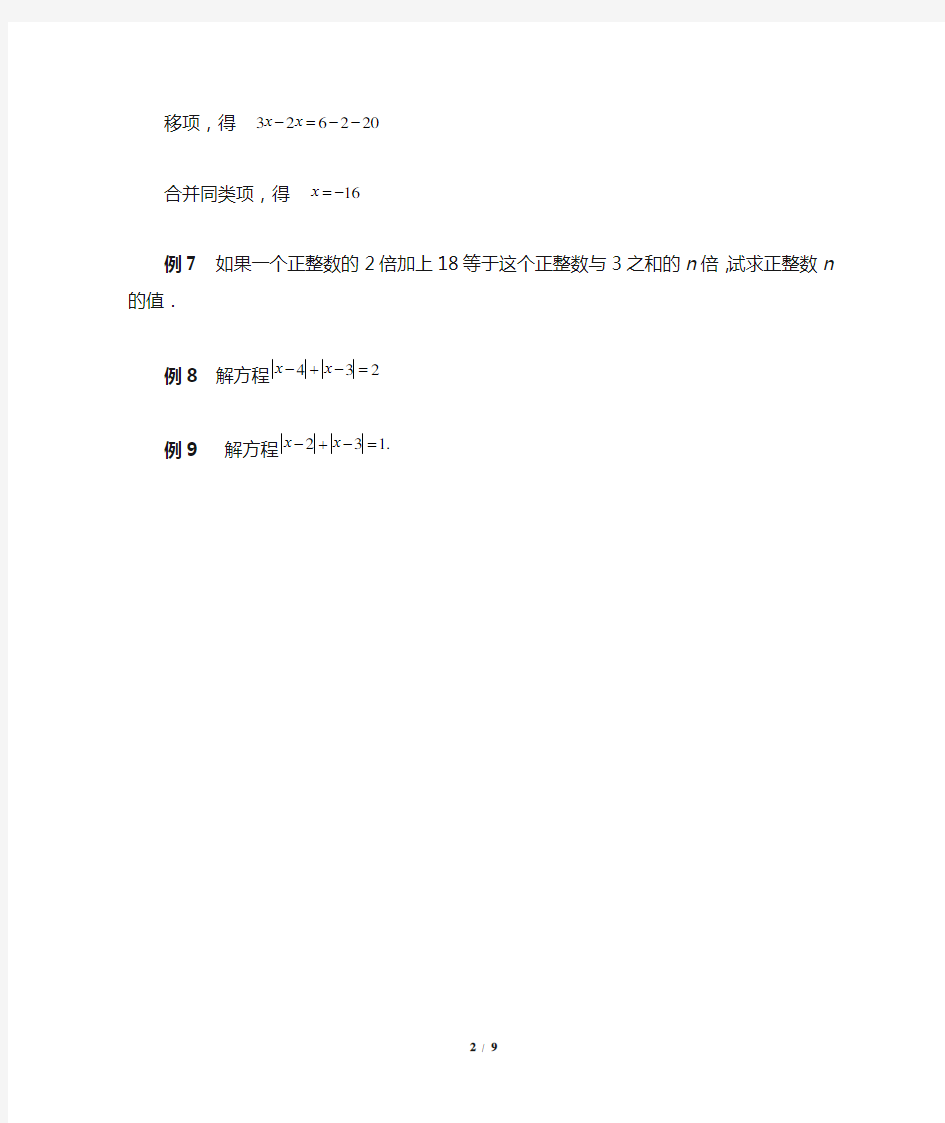
例7 如果一个正整数的2倍加上18等于这个正整数与3之和的n 倍，试求正整数n 的值．

例8 解方程234=-+-x x

例9 解方程.132=-+-x x

参考答案

例1 分析这个方程可以先移项，再合并同类项．

解移项，得.28910-=+-x x

合并同类项，得6=-x

把系数化为1，得6-=x

说明：初学解方程者应该进行检验，就是把求得的方程的解代入原方程中，看方程的左右两边是否相等，如果相等则是方程的解，否则就不是方程的解．则说明我们的解题过程有误．当熟练之后可以不进行检验，以后我们会知道一元二次方程不会产生增根．

例2 分析这个方程含有括号，我们应先去掉括号，然后再进行合并同类项等．

解去括号，得.6362+=-x x

移项，得6632+=-x x

合并同类项，得12=-x

把系数化为1，得.12-=x

说明：在去括号时要注意符号的变化，同时还应该注意要用括号前的数去乘括号内的每一项，避免出现漏乘的现象．

例3 分析该方程中含有分母，一般我们是要先去掉分母，然后再按其他步骤进行．

解去分母，得217)2(3)2(21?-?=--x x

去括号，得1476221-=+-x x

移项，得2211476---=--x x

合并同类项，得1707-=-x

把系数化为1，得.7

224=x 说明：初学者在去括号时，如果分子是两项的，应该用括号把分子括上以避免出现符号的错误．

例4 分析在这个方程中既有括号又有分母，先做哪一步这应因题而定．

解去分母，得)2(5)3(10)5(30)4(6--+=--+x x x x

去括号，得105301015030246+-+=+-+x x x x

移项，得150241*********--+=+--x x x x

合并同类项，得13429-=-x

把系数化为1，得.29

184=x 说明：要灵活应用解方程的步骤，在熟练之后这些解方程的步骤可以省略不写．

例5 分析在这个方程中既有小数又有分数，一般是先把分子分母中的小数都化成整数再进行计算．

解原方程可化为：5

3320505214=--+x x 去分母，得9)2050(5)214(3=--+x x

去括号，得91002506312=+-+x x

移项并合并同类项，得196112=x

把系数化为1，得4

31=x 说明：在解方程时解方程的步骤可以灵活使用，如在去括号后发现项比较多时，并有同类项可以合并，也可以先合并一次同类项然后再移项．

例6 分析第（1）小题方程中有两项有分母，另一项没有分母，在去分母时应注意不要漏

乘没有分母的项．

第（2）小题的各项，尤其是右边两项比较复杂，去分母时必须小心谨慎，防止出错．

解（1）错，错在去分母时漏乘了方程中间的“1”，正确解答如下：去分母，得 x x 3124+=

移项 12 1234==-x x x

（2）错，错在将方程的两边乘以8后，8

32x --这一项应化为)32(x --而不

是x 32--，正确解答如下：

去分母，得 )32()3(220x x --+=

去括号，得 x x 326220+-+=

移项，得 5

16 165=-=-x x 说明对于比较复杂的方程，求出解后要检验一下看是不是原方程的解，这样有利于减少解方程的错误．

在解方程的过程中，认真、细致是解题的关键．

例7 解设已知的正整数为a ，依题意得

)3(182+=+a n a ，

即n a n 318)2(-=-， ∴.2

)6(3--=n n a 因为a 和n 都是正整数，所以.62<

当3=n 时，9=a ，

36)39(31892=+?=+?；

当4=n 时，3=a ，

24)33(41832=+?=+?；

当5=n 时，1=a ，

.20)31(51812=+?=+?

答：3=n ，或4=n ，或.5=n

说明：本例的解法用到了分类讨论．

例8 分析对于4-x 来说，当4>x 时，44-=-x x ，当4x 时与在3

注意到以上情况，是因为我们感到只有把题目中的绝对值符号去掉，才能解

出方程．因此，对本题，可以分为434≤≤>x x 、

和3

解当4>x 时，原方程可化为2)3()4(=-+-x x ，解得.2

9=x 当43≤≤x 时，原方程可化为2)3()4(=-+-x x ，

这个方程无解．

当3

5=x 所以，原方程的解是29=x ，或.2

5=x 说明：①从上面解题过程可以看出，带绝对值符号的方程，可以转化为不带绝对值符号的方程来解，而分类思想是实现这样的转化的法宝．

②上面解题过程有读者不易察觉的一步，这就是检验．本题检验的具体做法

是：在以4>x 为前提，求得29=

x 之后，要看一看2

9是否与4>x 相符．在以3

例9 分析对这类方程的常规解法，用分类讨论去绝对值．从绝对值的几何意义出发，2-x 和3-x 分别表示数轴上表示x 的点到表示2的点与表示3的点之间的距离．

如图所示，设数轴上表示2的点为A ，表示3的点为B ，那么示x 的点不会在点A 的左边或点B 的右边．

解方程132=-+-x x 的几何意义是数轴上表示x 的点到表示2的点的距离与表示3的点的距离之和为1．

设数轴上表示2的点为A，表示3的点为B，则线段AB上的点都符合要求，线段AB之外的点均不符合要求．

所以，这个方程的解是3

≤x．

2≤

说明：从解方程来说，上面解法并不很重要，但从体会数学中的数形结合思想来说，则值得同学们拍案叫绝．这也是解不定方程的实例．

8列方程解应用题1

课时八:列方程解应用题1 教学内容：数学书P60例3、及61页的做一做，练习十一的第8题。教学目标： 1、初步学会如何利用方程来解答问题的基本方法和解题步骤，能够正确地列方程解答比较容易的问题。 2、进一步提高学生分析数量关系的能力。教学重点：掌握列方程解决问题的一般步骤。教学难点：找题中的等量关系，并根据等量关系列出方程。教学过程：一、复习导入 1、先列出方程，再解方程：比x多5.7的数是10 x减3.4的差是7.6 2、看图列方程，并求出方程的解 X 20 60 100千克 23.5千克 X千克学习方程的目的是为了利用方程解决生活中的问题，这节课就来学习如何用方程来解决问题。板书：解决问题。二、新知学习。 1、教学例3. （1）出示题目。（课件）出示洪泽湖的图片，介绍到：洪泽湖是我国五大淡水湖之一，位于江苏西部淮河下游，风景优美，物产丰富。但每当上游的洪水来临时，湖水猛涨，给湖泊周围的人民的生命财产带来了危险。因此，密切注视水位的变化情况，保证大坝的安全十分重要，如果湖水到了警戒水位的高度，就要引起高度警惕，超出警戒水位越多，大坝的危险就越大。下面，我们来就来看一则有关大坝水位的新闻。谁来

当主持人，为大家播报一下。 “今天上午8时，洪泽湖蒋坝水位达14.14m，超过警戒水位0.64m.” （2）分析，解题。根据刚才所了解的信息，这个问题中有哪几个关键的数量呢？警戒水位、今日水位、超出部分。它们之间有哪些数量关系呢？（板）警戒水位+超出部分=今日水位① 今日水位—警戒水位=超出部分② 今日水位—超出部分=警戒水位③ 同学们能解决这个问题吗？学生独立用算术方法解决问题。（3）学习（如何用方程来解决本题。）师:这题我们还可以用方程的方法来解决，由于警戒水位是未知数，可以设它为比X米，再列出方程解答。学生尝试独立列方程。学生展示，学生列出的方程可能有：① x+0.64=14.14②14.14﹣x= 0.64 ③14.14﹣0.64= x 每一种方法，都需要学生说出是根据什么列出的方程。比较交流各种方程的利弊。师生共同解决问题，板书解：设警戒水位为x米，得： x+0.64=14.14 x=14.14－0.64 x=13.5 答:警戒水位为13.5米. 小结:在解决问题中，我们是怎样来列方程的？将未知数设为x，再根据题中的等量关系列出方程。列方程解应用题的基本步骤, 1、弄清题意，找出未知数，并用x表示； 2、找出题目中数量之间的相等关系，列出方程； 3、解方程； 4、检验，写出答。

高考数学-指数函数图像和性质及经典例题

高考数学-指数函数图像和性质及经典例题【基础知识回顾】一、指数公式部分有理指数幂的运算性质（1）r a ·s r r a a += ),,0(Q s r a ∈>；（2）rs s r a a =)( ),,0(Q s r a ∈>；（3）s r r a a a b =)( ),0,0(Q r b a ∈>>．正数的分数指数幂的意义 )1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(1 1*>∈>= = - n N n m a a a a n m n m n m 二、指数函数 1.指数函数的概念:一般地，函数)1a ,0a (a y x ≠>=且叫做指数函数，其中x 是自变量，函数的定义域为R ． 2.指数函数的图象和性质 1．在同一坐标系中画出下列函数的图象：（1）x )31(y = （2）x )2 1 (y = （3）x 2y = （4）x 3y = （5）x 5y =

【指数函数性质应用经典例题】例1．设a 是实数， 2 ()()21 x f x a x R =- ∈+，试证明：对于任意,()a f x 在R 上为增函数．证明：设1212,,x x R x x ∈<，则 12()()f x f x -12 22()()2121 x x a a =- --++ 21222121 x x = - ++ 121 22(22)(21)(21) x x x x -=++，由于指数函数2x y =在R 上是增函数，且12x x <，所以1222x x < 即1 2220x x -<，又由20x >，得1 1 20x +>，2120x +>， ∴12()()0f x f x -< 即12()()f x f x <，所以，对于任意,()a f x 在R 上为增函数．例2.已知函数2 ()1 x x f x a x -=+ +(1)a >，求证：（1）函数()f x 在(1,)-+∞上为增函数；（2）方程()0f x =没有负数根．

六年级解方程练习题1

六年级解方程练习题1 加数＋加数＝和一个加数＝和－另一个加数因数×因数＝积一个因数＝积÷另一个因数被减数－减数＝差被减数＝差＋减数减数＝被减数－差被除数÷除数＝商被除数＝商×除数除数＝被除数÷商类型一： 4.1236.20=+x x －52＝10 3 练习一： 1、解方程 250100=+x 42.1=+x 9.67.2=+x 3.27.2=-x 5.175.33=-x 153.12=+x 83＋x ＝5 2 6324=-x 4.28.1=-x 类型二： 4.83=x 3.07=÷x 107x ＝25 14 例2、一个数x 的13倍是364，求这个数？练习二： 1、解方程 1266=x 3.65.0=x 188.1=÷x x ×53=20×41 x ÷ 356=4526×25 13 7.234=÷x 4.66.1=x 9 5x ＝10 31.1=÷x 类型三： 3x +5=50 4x -27=29 5x ÷2＝10 4x －3 ×9 = 29 例3：一个长方形的周长是10.8厘米，长是4厘米，这个长方形的宽是多少厘米？练习3： 1、解方程 5147=÷x 4202=-x 42318=+x 4.539=÷x 2x + 25 = 35

25% + 10x = 54 78414=+x 32x ÷4 1＝12 4x －3 ×9 = 29 （1）红光小学有女教师57人，比男教师的3倍还多9人。红光小学有男教师多少人？类型四： 554=+x x 6 x －x ＝20 70%x + 20%x = 3.6 2x －32x ＝4 3 练习四： 1、解方程 x － 27 x =43 270615=-x x 169619=-x x 54x ＋52x ＝2 1 x ＋87x =43 25.36.3=-x x 2.164.04.9=-x x 2.94389=-x x x －52x ＝10 3 2、用方程解应用题（1）果园里有桃树和梨树一共180棵，梨树的棵树是桃树的3倍。桃树和梨树各有多少棵？（2）小明的爸爸比小明大26岁，当爸爸的年龄是小明年龄的4.25倍时，小明是多少岁？类型五：416=÷x 416=-x 8)6.2(2=-x 6(46)14x x +-= 453(2)3x x ---= 练习五： 1、解方程 5.72.34=-x 54)3(87=--x 57572=-x 4(55)14x x ++= 7(43)6x x -+= 510=÷x 8568=÷x 126.037.0=+÷x 138(103)34x x -+-= 55%(0.250.6)0.6x x -+= 350%(30)35x x +-= 5121() 6.46256x x --= 42(20)60x x +-= 13(25)172x x -+-=

一次函数经典例题大全

一.定义型例1. 已知函数是一次函数，求其解析式。解：由一次函数定义知，，故一次函数的解析式为y=-6x+3。注意：利用定义求一次函数y=kx+b解析式时，要保证k≠0。如本例中应保证m-3≠0。二. 点斜型例2. 已知一次函数y=kx-3的图像过点(2, -1)，求这个函数的解析式。解：一次函数的图像过点(2, -1)，，即k=1。故这个一次函数的解析式为y=x-3。变式问法：已知一次函数y=kx-3 ，当x=2时，y=-1，求这个函数的解析式。三. 两点型例3.已知某个一次函数的图像与x轴、y轴的交点坐标分别是(-2, 0)、(0, 4)，则这个函数的解析式为_____。解：设一次函数解析式为y=kx+b，由题意得，故这个一次函数的解析式为y=2x+4 四. 图像型例4. 已知某个一次函数的图像如图所示，则该函数的解析式为__________。解：设一次函数解析式为y=kx+b由图可知一次函数的图像过点(1, 0)、(0, 2) 有故这个一次函数的解析式为y=-2x+2 五. 斜截型例5. 已知直线y=kx+b与直线y=-2x平行，且在y轴上的截距为2，则直线的解析式为___________。解析：两条直线；。当k1=k2，b1≠b2时，

直线y=kx+b与直线y=-2x平行，。又直线y=kx+b在y轴上的截距为2，故直线的解析式为y=-2x+2 六. 平移型例6. 把直线y=2x+1向下平移2个单位得到的图像解析式为___________。解析：设函数解析式为 y=kx+b，直线y=2x+1向下平移2个单位得到的直线y=kx+b与直线y=2x+1平行直线y=kx+b在y轴上的截距为 b=1-2=-1，故图像解析式为七. 实际应用型例7. 某油箱中存油20升，油从管道中匀速流出，流速为0.2升/分钟，则油箱中剩油量Q（升）与流出时间t（分钟）的函数关系式为___________。解：由题意得Q=20-0.2t ，即Q=-0.2t+20 故所求函数的解析式为 Q=-0.2t+20（）注意：求实际应用型问题的函数关系式要写出自变量的取值范围。八. 面积型例8. 已知直线y=kx-4与两坐标轴所围成的三角形面积等于4，则直线解析式为__________。解：易求得直线与x轴交点为，所以，所以|k|=2 ，即故直线解析式为y=2x-4或y=-2x-4 九. 对称型若直线与直线y=kx+b关于（1）x轴对称，则直线的解析式为y=-kx-b （2）y轴对称，则直线的解析式为y=-kx+b （3）直线y=x对称，则直线的解析式为（4）直线y=-x对称，则直线的解析式为（5）原点对称，则直线的解析式为y=kx-b 例9. 若直线l与直线y=2x-1关于y轴对称，则直线l的解析式为____________。解：由（2）得直线l的解析式为y=-2x-1 十. 开放型例10. 已知函数的图像过点A(1, 4)，B(2, 2)两点，请写出满足上述条件的两个不同的函数解析式，并简要说明解答过程。解：（1）若经过A、B两点的函数图像是直线，由两点式易得y=-2x+6 （2）由于A、B两点的横、纵坐标的积都等于4，所以经过A、B两点的函数图像还可以是双曲线，解析式为（3）其它（略）

指数函数经典例题和课后习题

指数函数及其基本性质指数函数的定义一般地，函数()10≠>=a a a y x 且叫做指数函数，其中x 是自变量，函数的定义域是R . 问题：指数函数定义中，为什么规定“10≠>a a 且”如果不这样规定会出现什么情况？ (1)若a<0会有什么问题？（如2 1 ,2= -=x a 则在实数范围内相应的函数值不存在） (2)若a=0会有什么问题？（对于0≤x ,x a 无意义） (3)若 a=1又会怎么样？（1x 无论x 取何值,它总是1,对它没有研究的必要.）师：为了避免上述各种情况的发生,所以规定0>a 且 1≠a . 指数函数的图像及性质函数值的分布情况如下：

指数函数平移问题（引导学生作图理解）用计算机作出的图像，并在同一坐标系下作出下列函数的图象，并指出它们与指数函数y =x 2的图象的关系（作图略）， ⑴y =1 2+x 与y =2 2+x . ⑵y =12 -x 与y =2 2 -x . f (x )的图象向左平移a 个单位得到f (x ＋a )的图象; 向右平移a 个单位得到f (x －a )的图象; 向上平移a 个单位得到f (x )＋a 的图象; 向下平移a 个单位得到f (x )－a 的图象.

指数函数·经典例题解析 (重在解题方法) 【例1】求下列函数的定义域与值域： (1)y 3 (2)y (3)y 12x ＝＝＝-+---213321x x 解 (1)定义域为x ∈R 且x ≠2．值域y ＞0且y ≠1． (2)由2x+2－1≥0，得定义域{x|x ≥－2}，值域为y ≥0． (3)由3－3x-1≥0，得定义域是{x|x ≤2}，∵0≤3－3x －1＜3， ∴值域是≤＜．0y 3 及时演练求下列函数的定义域与值域（1）4 12-=x y ；（2）|| 2()3 x y =；（3）1241++=+x x y ；【例2】指数函数y ＝a x ，y ＝b x ，y ＝c x ，y ＝d x 的图像如图2．6－2所示，则a 、b 、c 、d 、1之间的大小关系是 [ ] A ．a ＜b ＜1＜c ＜d B ．a ＜b ＜1＜d ＜c C ． b ＜a ＜1＜d ＜c D ．c ＜d ＜1＜a ＜b 解选(c)，在x 轴上任取一点(x ，0)，则得b ＜a ＜1＜d ＜c ．及时演练

解方程练习题

第一类、解简易方程（并检验） X + 32 = 76 X - 20 = 0 7X = 49 3X + 6 = 18 X ÷ 6 = 12 16 + 8X = 40 4X - 4×5 = 0 65X - 5×6 = 100

2（X + 3）= 10 15（X - 5）= 45 12（X - 1）= 24 42X + 28X = 140 19X + X = 40 2X + 8X + X = 11

80 ÷ 5X = 100 25 - 5X = 15 2 6x-3.6=8x 20×0.04+3.6x=1.52 2（X÷4）＝0.8 3x+6=18 7.8x－2.4x =1.86

4x －3×9=29 （X－3）÷2＝7.5 2x-0.24=1.2 3.6x+ 4.5x =56.7 4.5×6 +4x=41 13（X+5）＝ 169 （二）先写出数量关系式再列方程解应用题

1、小明去买商店衣服，优惠了38元，现价是75元，原价多少钱？等量关系式：解：设列式： 2、明明有34张邮票，比亮亮的少3张，亮亮有多少张邮票？等量关系式：解：设列式： 3、每平方米阔叶林每天能制造75克氧气，是每平方米草地每天制造氧气的5倍，每平方米草地每天制造氧气多少克？等量关系式：解：设列式：

《简易方程》练习题一、1、爸爸比小红大3岁，小红a岁时爸爸的年龄是___________岁。 2、在月球上，人能举起物体的质量是地面上的6倍。一位同学在地球上能举起a千克的物体，在月球上他能举起___________的物体。 3叔叔每天投报a份，阿姨每天投报b份。（1）他们每天共投报几份，30天共投报__份。（2）当a=60，b=75时，用第（1）天题中的式子，计算他们30天的总数。（）4、（1）一天早晨的温度是b摄氏度，中午比早晨高8摄氏度。b+8表示____________________。（2）某班共有50名学生，女生有50-c，这里的c表示____________________。 5、小林的玻璃球是小明的2倍，要是小林给小明3颗，他们俩就一样多了，小林有( )颗玻璃球，小明有（）颗玻璃球。二、解方程并检验 2（5x－9）=1.8 8.4－0.32x=1.6

函数概念典型例题

函数概念及其表示---典例分析例1．下列各组函数中，表示同一函数的是（ C ）. 选题理由：函数三要素。 A. 1,x y y x == B. 11,y x y = += C. ,y x y == D. 2||,y x y == 点评：有利于理解函数概念，强化函数的三要素。变式： 1．函数f (x )= 2(1)x x x ??+? ,0,0x x ≥< ，则(2)f -=（）. A. 1 B .2 C. 3 D. 4 例2．集合{}22M x x =-≤≤，{}02N y y =≤≤，给出下列四个图形，其中能表示以M 为定义域，N 为值域的函数关系的是（ B ）. 选题理由：更好的帮助学生理解函数概念，同时也体现函数的重要表示法图像法，图形法是数形结合思想应用的前提。变式： 1．下列四个图象中，不是函数图象的是（B ）. 2．设集合A ＝｛x ｜0≤x ≤6｝，B ＝｛y ｜0≤y ≤2｝，从A 到B 的对应法则f 不是映射的是（）. A. f ：x →y ＝ 1 2x B. f ：x →y ＝ 1 3x C. f ：x →y ＝1 4x D. f ：x →y ＝1 6 x A. B. C. D.

函数的表达式及定义域—典例分析【例1】求下列函数的定义域：（1）1 21 y x = +-；（2 ）y = . 选题理由：考查函数三要素，定义域是函数的灵魂。解：（1）由210x +-≠，解得1x ≠-且3x ≠-，所以原函数定义域为(,3)(3,1)(1,)-∞----+∞. （2 ）由30 20 x -≥??≠，解得3x ≥且9x ≠，所以原函数定义域为[3,9)(9,)+∞. 选题理由：函数的重要表示法，解析式法。变式： 1 ．函数y =的定义域为（）. A. (,1]-∞ B. (,2]-∞ C. 11(,)(,1]22-∞-- D. 1 1(,) (,1]2 2 -∞-- 2．已知函数()f x 的定义域为[1,2)-，则(1)f x -的定义域为（）. A ．[1,2)- B ．[0,2)- C ．[0,3)- D ．[2,1)- 【例2】已知函数1( )1x f x x -=+. 求：（1）(2)f 的值；（2）()f x 的表达式解：（1）由121x x -=+，解得13x =-，所以1 (2)3f =-. （2）设11x t x -=+，解得11t x t -= +，所以1()1t f t t -=+，即1()1x f x x -=+. 点评：此题解法中突出了换元法的思想. 这类问题的函数式没有直接给出，称为抽象函数的研究，常常需要结合换元法、特值代入、方程思想等. 变式： 1．已知()f x ＝2x ＋x ＋1，则f ＝______；f ［(2)f ］＝______． 2．已知2(21)2f x x x +=-，则(3)f = . 【例 2】已知f (x )=33x x -+?? (,1) (1,)x x ∈-∞∈+∞，求f [f (0)]的值. 选题理由：分段函数生活重要函数，是考察重点。解：∵ 0(,1)∈-∞ ， ∴ f 又 ∵ >1， ∴ f )3)-3=2+ 12=52，即f [f (0)]=5 2 . 点评：体现了分类讨论思想。 2．某同学从家里到学校，为了不迟到，先跑，跑累了再走余下的路，设在途中花的时间为 t ，离开家里的路程为d ，下面图形中，能反映该同学的行程的是（）.

列方程解应用题1-五

列方程解应用题 ①弄清题意，找出已知条件和所求问题； ②依题意确定等量关系，设未知数x；③根据等量关系列出方程； ⑤检验，写出答案。 2支铅笔和3本练习本，一共用了3.9元钱,每支铅笔0.6元, 每本练习本多少元? 【例2】两数相除,商4余8,被除数、除数、商、余数之和等于415,则被除数是多少? 【例3】王师傅一天生产的零件比他的徒弟一天生产的零件多128个，且是徒弟的3倍。师徒二人一天各生产多少个零件？【例4】小军和他爸爸今年的年龄之和是42岁，年龄之差是26岁。小军与他爸爸今年各多少岁？【例5】某小卖部有啤酒200瓶,汽水132瓶,每天卖出去啤酒和汽水各14瓶,几天后剩下的啤酒是汽水的3倍? 【例6】甲班51人,乙班49人,某次考试两个班全体同学的平均成绩是81分,乙班的平均成绩要比甲班的平均成绩高7分,那么乙班的平均成绩是多少分? 【例7】一批小朋友去买东西，若每人出10元则多8元；若每人出7元则少4元。问：有多少个小朋友？东西的价格是多少？【例8】松鼠采松籽,晴天每天采20个,雨天每天只能采12个,它一连几天共采了112个松籽,平均每天采14个,那么这几天中共有几天是雨天? 【例9】A、B两村相距2800米,小明从A村出发步行5分钟后,小军骑车从B村出发,又经过10分钟两人相遇。已知小军骑车比小明每分钟多行160米,小明步行速度是每分钟多少米?

筐正好装完。现在每筐装多少千克? 2、甲、乙两数的和是41.36,如果甲数的小数点向右移动一位就等于乙数,则乙数是多少? 3、小明买了两本书，故事书的页数比科技书的页数多36页，且故事书的页数是科技书的3倍多4页，故事书和科技书各有多少页？ 4、三年级一班有学生49人，其中女生比男生少5人。这个班男、女生各多少人？ 5、甲仓存粮32吨，乙仓存粮57吨，甲仓每天存入4吨，乙仓每天存入9吨，多少天后乙仓存粮是甲仓的2倍。7、王老师去买儿童小提琴，若买7把，则所带的钱差110元，若买5把，则所带的钱还差30元。问：儿童小提琴多少钱一把？王老师带了多少钱？ 8、学校数学竞赛，共10道题，每做对一道得10分，每做错一题倒扣2分，小明得了64分，他做错了几道题？ 9、客货两列火车同时从甲、乙两地相对开出，5小时后相遇，两地相距770千米，已知客车速度是货车速度的1.2倍,那么客车速度是多少千米?货车速度是多少千米?

指数函数典型例题详细解析汇报

实用标准指数函数·例题解析第一课时【例1】（基础题）求下列函数的定义域与值域： (1)y 3 (2)y (3)y 1 2x ＝＝＝-+---213321x x 解 (1)定义域为{x|x ∈R 且x ≠2}．值域{y|y ＞0且y ≠1}． (2)由2x+2－1≥0，得定义域{x|x ≥－2}，值域为{|y|y ≥0}． (3)由3－3x-1≥0，得定义域是{x|x ≤2}，∵0≤3－3x －1＜3， ∴值域是≤＜．0y 3 1.指数函数Y=ax （a>0且a ≠1）的定义域是R ，值域是（0，+∞） 2. 求定义域的几个原则：①含根式（被开方数不为负）②含分式，分母不为０③形如a0,(a ≠ 0) 3. 求函数的值域:①利用函数Y=ax 单调性②函数的有界性(x2≥0;ax>0)③换元法.如:y=4x+6×2x-8(1≤x ≤2) 先换元,再利用二次函数图象与性质(注意新元的范围)

【例2】（基础题）指数函数y＝a x，y＝b x，y＝c x，y＝d x的图像如图2．6－2所示，则a、b、c、d、1之间的大小关系是 [ ] A．a＜b＜1＜c＜d B．a＜b＜1＜d＜c C．b＜a＜1＜d＜c D．c＜d＜1＜a＜b 解选(c)，在x轴上任取一点(x，0)，则得b＜a＜1＜d＜c．

【例3】（基础题）比较大小： (1)2(2)0.6 、、、、的大小关系是：． 2481632 35894 5 12--() (3)4.54.1________3.73.6 解(1)y 221()x ∵，，，，，函数＝，＞，该函数在－∞，＋∞上是增函数，又＜＜＜＜，∴＜＜＜＜．22224282162133825491 2 28416212313525838949 3859=====

解比例及解方程练习题

人教版六年级解方程及解比例练习题解比例: x:10=41:31 0.4:x=1.2:2 4.212=x 3 21:51=41:x 0.8:4=x:8 4 3 :x=3:12 1.25:0.25=x:1.6 92=x 8 x 36=3 54 x: 32=6: 2524 x 5.4=2 .26 45:x=18:26 2.8:4.2=x:9.6 101:x=81:4 1 2.8:4.2=x:9.6 x:24= 43:31 8:x=54:43 85:61=x: 12 1 0．6∶4＝2.4∶x 6∶x ＝15∶13 0.612＝1.5x 34∶12＝x ∶45 1112∶45＝2536∶x x ∶114＝0.7∶1 2 10∶50＝x ∶40 1.3∶x ＝5.2∶20 x ∶3.6＝6∶18 13∶120＝169∶ x 4.60.2＝8x 38＝x 64 解方程 X － 27 X=4 3 2X + 25 = 35 70%X + 20%X = 3.6 X ×53=20×41 25% + 10X = 54 X - 15%X = 68 X ＋83X ＝121 5X －3×215＝75 32X ÷4 1 ＝12 6X ＋5 =13.4 834143=+X 3X=83 X ÷7 2 = 167 X ＋87X=43 4X －6×3 2 =2 125 ÷X=310 53 X = 7225 98 X = 61×5116 X ÷ 356=4526×2513 4x －3 ×9 = 29 21x + 6 1 x = 4

103X －21×32=4 204 1 =+x x 8)6.2(2=-x 6X ＋5 =13.4 25 X-13 X=3 10 4χ－6＝38 5X= 1915 218X=154 X ÷54=2815 32X ÷41=12 53X=7225 98X=61×51 16 X ÷356=4526÷2513 X-0.25=41 4 X =30% 4+0.7X=102 32X+21X=42 X+4 1 X=105 X-83X=400 X-0.125X=8 X 36 = 4 3 X+37 X=18 X ×( 16 + 38 )=1312 x －0.375x=65 x ×3 2+2 1=4×8 3 X －7 3X ＝12 5 X －2.4×5＝8 0.36×5- 34 x = 35 23 (x- 4.5) = 7 1 2 x- 25%x = 10 x- 0.8x = 16+6 20 x – 8.5= 1.5 x- 4 5 x -4= 21 X ＋25%X=90 X －37 X= 89 X － 27 X=43 2X + 25 = 35 70%X + 20%X = 3.6 X ×53 =20 ×41 25% + 10X = 54 X - 15%X = 68 X ＋83 X ＝121 5X －3×215＝75 32X ÷41 ＝12 6X ＋5 =13.4 83 4143=+X 3X=83 X ÷72=167 X ＋87X=43 4X －6×3 2 =2 125 ÷

列方程解应用题练习题及答案

列方程解应用题训练 1.某商店出售甲、乙两种成衣，其中甲种成衣卖价120元盈利20% ，乙种成衣卖价也是 120元但亏损20% ，问该商店在本次销售中实际上是盈还是亏，盈或亏多少钱 2．甲、乙两人分别在相距50km的地方同向出发，乙在甲的前面，甲每小时走16km，乙每小时走18km，如果乙先走1小时，问甲走多少时间后，两个人相距70km 3．某中学组织七年级学生春游，如果租用45座的客车，则有15个人没有座位，如果租用同样数量的60座的客车，则除多出一辆外，其余车恰好坐满。已知租用45座的客车每日租金为每辆车250元，60座的车每日租金每辆300元，问租用哪种客车更合算租几辆车 4．某商店的冰箱先按原价提高40% ，然后在广告中写上大酬宾八折优惠，结果每台冰箱反而多赚了270元，试问冰箱的原标价是多少元现售价是多少元 5．某种商品的进价为100元，若要使利润率达20% ，则该商品的销售价格应为多少元此时每件商品可获利润多少元 6．某商品的进价是1000元，标价为1500元，商店要求以利润率不低于5% 的售价打折出售，售票员最低可以打几折出售此商品 7．某车间有60名工人，生产某种由一个螺栓与两个螺母为一套的配套产品，每人每天平均生产螺栓14个或螺母20个，问应分配多少人生产螺母，多少人生产螺栓，才能使每天生产出的螺栓与螺母恰好配套 8．A、B两地相距60km，甲乙两人分别从A、B两地骑车出发，相向而行，甲比乙迟出发20min,每小时比乙多行3km ,在甲出发后1h40min ,两人相遇，问甲乙两人每小时各行多少km 9.要加工200个零件，甲先单独加工了5小时，然后又与乙一起加工了4小时，完成了任务已知甲每小时比乙多加工2个零件，求甲、乙两人每小时各加工多少个零件 10．一件工作，甲单独完成需小时, 乙单独完成需5小时，先由甲、乙两人合做1小时，再由乙单独完成剩余任务，共需多少小时完成任务

指数函数经典例题(标准答案)

指数函数 1．指数函数的定义：函数)1 (≠ > =a a a y x且叫做指数函数，其中x是自变量，函数定义域是R 2.指数函数的图象和性质：在同一坐标系中分别作出函数y=x2，y= x ? ? ? ? ? 2 1 ，y=x 10，y= x ? ? ? ? ? 10 1 的图象. 我们观察y=x2，y= x ? ? ? ? ? 2 1 ，y=x 10，y= x ? ? ? ? ? 10 1 图象特征，就可以得到)1 (≠ > =a a a y x且的图象和性质。 a>10

()x f c 的大小关系是_____．分析：先求b c ，的值再比较大小，要注意x x b c ，的取值是否在同一单调区间内．解：∵(1)(1)f x f x +=-， ∴函数()f x 的对称轴是1x =．故2b =，又(0)3f =，∴3c =． ∴函数()f x 在(]1-， ∞上递减，在[)1+，∞上递增．若0x ≥，则321x x ≥≥，∴(3)(2)x x f f ≥；若0x <，则321x x <<，∴(3)(2)x x f f >．综上可得(3)(2)x x f f ≥，即()()x x f c f b ≥．评注：①比较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论． 2．求解有关指数不等式例2 已知2321(25)(25)x x a a a a -++>++，则x 的取值范围是___________．分析：利用指数函数的单调性求解，注意底数的取值范围．解：∵2225(1)441a a a ++=++>≥， ∴函数2(25)x y a a =++在()-+，∞∞上是增函数， ∴31x x >-，解得1 4x >．∴x 的取值范围是14 ??+ ??? ， ∞．评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论． 3．求定义域及值域问题例3 求函数y = 解：由题意可得2160x --≥，即261x -≤， ∴20x -≤，故2x ≤． ∴函数()f x 的定义域是(]2-， ∞．令26x t -=，则y =，又∵2x ≤，∴20x -≤． ∴2061x -<≤，即01t <≤． ∴011t -<≤，即01y <≤．

(完整版)解方程练习题

五年级解方程练习题方程：含有未知数的等式叫做方程。方程的解：使方程成立的未知数的值叫做方程的解。解方程：求方程的解的过程叫做解方程。解方程的依据：1. 等式性质（等式两边同时加上或减去同一个数，等式仍然成立；等式两边同时乘以或除以同一个数，等式仍然成立。） 2. 加减乘除法的变形。加法：加数1+加数2=和加数1=和–加数2 加数2=和–加数1 减法：被减数–减数=差被减数=差+减数减数=被减数–差乘法：乘数1×乘数2 =积乘数1=积÷乘数2 乘数2=积÷乘数1 除法：被除数÷除数= 商被除数=商×除数

除数=被除数÷商一、解方程： 20x-50=50 28+6 x =88 32-22 x =10 24-3 x =3 10 x ×（5+1）=60 99 x =100- x 36÷x=18 x÷6=12 56-2 x =20 4y+2=6 x+32=76 3x+6=18 16+8x=40 2x-8=8 4x-3×9=29 二、解方程： 8x-3x=105 x-6×5=42+2x 2x+5=7 ÷ 3 2（x+3）=10 12x-9x=9 6x+18=48

56x-50x=30 5x=15（x-5）78-5x=28 32y-29y=3 5（x+5）=15 89 – 9x =80 100-20x=20+30x 55x-25x=60 76y÷ 75=1 23y÷23=23 4x-20=0 80y+20=100-20y 53x-90=16 2x+9x=11 12（y-1）=24 80÷5x=100 7x÷8=6 65x+35=100 19y+y=40 25-5x=15

函数·典型例题精析

2．2 函数2例题解析【例1】判断下列各式，哪个能确定y 是x 的函数？为什么？ (1)x 2＋y ＝1 (2)x ＋y 2＝1 (3)y ＝11 --x x 解 (1)由x 2＋y ＝1得y ＝1－x 2，它能确定y 是x 的函数． (2)x y 1y y x 2由＋＝得＝±．它不能确定是的函数，因为对1-x 于任意的x ∈{x|x ≤1}，其函数值不是唯一的． (3)y y x ＝的定义域是，所以它不能确定是的函数．11 --?x x 【例2】下列各组式是否表示同一个函数，为什么？ (1)f(x)|x|(t)(2)f(x)g(x)(x)2＝，＝＝，＝?t x 2 2 (3)f(x)g(x)(4)f(x)g(x)＝2，＝＝2，＝x x x x x x +--+--111 11122 解 (1)中两式的定义域部是R ，对应法则相同，故两式为相同函数． (2)、(3)中两式子的定义域不同，故两式表示的是不同函数． (4)中两式的定义域都是－1≤x ≤1，对应法则也相同，故两式子是相同函数．【例3】求下列函数的定义域： (1)f(x)2 (2)f(x)(3)f(x)＝＋＋＝＝x x x x x x x --+----145 3210215 2||

(4)f(x)(4x 5)(1)x 10 4x 0 1x 4{x|1x 4}(2)3x 20x {x|x }＝＋－由－≥－≥得≤≤．∴定义域是≤≤由－＞，得＞，∴定义域是＞812323|| x -???解 (3)10x x 210 |x|503x 7x 5{x|3x 7x 5} 2由－－≥－≠得≤≤且≠，∴定义域是≤≤，且≠??? (4)10 |x|0 4x 508x 00x x 8[80)(0)()由－≥≠－≠解得－≤＜或＜＜或＜≤∴定义域是－，∪，∪，854545454 8||x ?????? ??? 【例4】已知函数f(x)的定义域是[0，1]，求下列函数的定义域： (1)y f (2)y f(2x)f (3)y f ＝＝＋＝()()()123 2x x x a + 解(1)01x 1x 1f(){x|x 1x 1}由＜≤，得≤－或≥，∴的定义域是≤－或≥1 122x x

列方程解应用题练习题

一、列方程解应用题和倍问题例1 图书馆买回来60本文艺书和科普书，其中文艺书的本数是科普书的3倍，文艺书有多少本？例2 一个果园有荔枝、龙眼和芒果这三种果树108棵，其中荔枝的棵树是龙眼的3倍，芒果的棵树是龙眼的2倍，这三种果树各有多少棵？例3一个水池装有甲、乙两排水管，甲管每小时的排水量是乙管的3倍。水池里有16吨水，打开两管5小时能把水排完，甲管每小时排水量多少吨？例4 某粮店全天卖出大米、面粉和玉米面11520千克，卖出大米的千克数是面粉的6倍，面粉的千克数是玉米免的5倍，卖出的大米比玉米面多多少千克？较复杂的和倍问题例1甲粮仓有510吨大米，乙粮仓有1170吨大米，每天从乙粮仓调30吨大米到甲粮仓，多少天以后甲粮仓大米的吨数是乙粮仓的6倍？例2 图书馆买回来故事书、科普书和连环画236本，如果故事书增加10本，就是科普书本数的2倍，科普书减少12本，就是连环画本数的一半，买回来的故事书有多少本？例3 甲数与乙数的和是30，甲数的8倍与乙数的3倍的和是160.甲数、乙数各是多少？

例4 甲站和乙站相距299千米，一辆大客车从甲站开往乙站，1.5小时后一辆小轿车从乙站开往甲站，行驶速度是客车的3倍，小轿车行驶2.5小时遇见大客车，小轿车每小时行多少千米？差倍问题一个问题的已知条件是有关数量的差与数量之间的倍的关系，这种问题就是差倍问题。列方程解差倍问题，可以吧问题中的一个未知数量用x表示，再根据问题中的“差”或“倍”的关系，把其他未知数量用含有x 的式子表示，再找出数量之间的等量关系列方程。在设未知数x时，通常把倍的关系中作为1的数量设为x较好。例1一张办公桌的价钱是一把椅子的4倍，办公桌的定价比椅子贵138元，一张办公桌的价钱是多少钱？例2 一个书柜下层放的书的本数是上层的3倍，如果从下层取43本数放到上层，两层的书的本数相同，这个书柜一共方有多少本书？例3 水果店购进的一批西瓜，分三天售完，其中第一天售出的千克数是第二天的2倍，第二天售出的千克数是第三天的1.5倍，第三天售出的比第一天少88千克，这批西瓜共有多少千克？例4 有对黑棋子和白棋子，其中黑棋子的个数是白棋子的3倍，每次取走相同的个数的黑棋子和白棋子，取了若干次后，白棋子还剩8个，黑棋子还剩94个，原来这堆棋子中多少个黑棋子? 较复杂的差倍问题例1 有两根同样长的绳子，第一根绳子剪去10米，第二根绳子剪去28米，第一根绳子剩下的长度是第二根的4倍。原来两根绳子一共有多少米？

高一数学指数函数经典例题

高一数学指数函数平移问题 ⑴y =12+x 与y =22+x . ⑵y =12-x 与y =22-x . f (x )的图象向左平移a 个单位得到f (x ＋a )的图象;向右平移a 个单位得到f (x －a )的图象; 向上平移a 个单位得到f (x )＋a 的图象;向下平移a 个单位得到f (x )－a 的图象. 指数函数·经典例题解析 (重在解题方法) 【例1】求下列函数的定义域与值域： (1)y 3 (2)y (3)y 12x ＝＝＝-+---213321x x 解 (1)定义域为x ∈R 且x ≠2．值域y ＞0且y ≠1． (2)由2x+2－1≥0，得定义域{x|x ≥－2}，值域为y ≥0． (3)由3－3x-1≥0，得定义域是{x|x ≤2}，∵0≤3－3x －1＜3，∴值域是≤＜．0y 3 及时演练求下列函数的定义域与值域（1）4 12 -=x y ；（2）|| 2()3 x y =；（3）12 41 ++=+x x y ；【例2】指数函数y ＝a x ，y ＝b x ，y ＝c x ，y ＝d x 的图像如图2．6－2所示，则a 、b 、c 、d 、1之间的大小关系是 [ ] A ．a ＜b ＜1＜c ＜d B ．a ＜b ＜1＜d ＜c C ． b ＜a ＜1＜d ＜c D ．c ＜d ＜1＜a ＜b 解选(c)，在x 轴上任取一点(x ，0)，则得b ＜a ＜1＜d ＜c ．及时演练指数函数① ② 满足不等式 ,则它们的图象是 ( ). 【例3】比较大小： (1)2(2)0.6 、、、、的大小关系是：． 2481632 358945 12--()

高中数学函数知识点总结与经典例题与解析

函数知识点总结知识点一、平面直角坐标系 1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴，就组成了平面直角坐标系。其中，水平的数轴叫做x 轴或横轴，取向右为正方向；铅直的数轴叫做y 轴或纵轴，取向上为正方向；两轴的交点O （即公共的原点）叫做直角坐标系的原点；建立了直角坐标系的平面，叫做坐标平面。为了便于描述坐标平面内点的位置，把坐标平面被x 轴和y 轴分割而成的四个部分，分别叫做第一象限、第二象限、第三象限、第四象限。注意：x 轴和y 轴上的点，不属于任何象限。 2、点的坐标的概念点的坐标用（a ，b ）表示，其顺序是横坐标在前，纵坐标在后，中间有“，”分开，横、纵坐标的位置不能颠倒。平面内点的坐标是有序实数对，当b a ≠时，（a ，b ）和（b ，a ）是两个不同点的坐标。知识点二、不同位置的点的坐标的特征 1、各象限内点的坐标的特征点P(x,y)在第一象限0,0>>?y x 点P(x,y)在第二象限0,0>?y x 2、坐标轴上的点的特征点P(x,y)在x 轴上0=?y ，x 为任意实数点P(x,y)在y 轴上0=?x ，y 为任意实数点P(x,y)既在x 轴上，又在y 轴上?x ，y 同时为零，即点P 坐标为（0，0） 3、两条坐标轴夹角平分线上点的坐标的特征点P(x,y)在第一、三象限夹角平分线上?x 与y 相等点P(x,y)在第二、四象限夹角平分线上?x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征位于平行于x 轴的直线上的各点的纵坐标相同。位于平行于y 轴的直线上的各点的横坐标相同。5、关于x 轴、y 轴或远点对称的点的坐标的特征点P 与点p ’关于x 轴对称?横坐标相等，纵坐标互为相反数点P 与点p ’关于y 轴对称?纵坐标相等，横坐标互为相反数

列方程解应用题带答案

列方程解应用题 1、有一个三位数，其各位数字之和是 16，十位数字是个位数字与百位数字之和，若把百位数字与个位数字对调，那么新数比原数大 594，求原数？ 2、一个两位数，个位上的数字与十位上的数字和为 10，如果把十位的数字与个位上数字对调，新数就比原数少 36，求原来的两位数？ 4、学校组织新年联欢会，用于奖品的铅笔、圆珠笔、钢笔共 232支，价值 100元，其中铅笔的数量是圆珠笔的 4倍，已知每支铅笔0.2元，每支圆珠笔 0.9元，每支钢笔2.1元。三种笔各值多少元？ 5、蜘蛛有8只脚，晴蜓有6只脚和2双翅膀，蝉有6只脚和一对翅膀，现在有这三种小虫共16只，共有110条腿，14对翅膀，问每只小虫各有多少只？ 6、有大、中、小卡车共42辆，每次共运货315箱，已知每辆大卡车每次能运 10箱，中卡车每辆每次运8箱，小卡车每辆每次可运5箱，又知中卡车的辆数和小卡车同样多，求大卡车有多少辆？ 3、一个两位数，个位数是十位上的数的数对调，那么所得的两位数比原来的大 3倍，若把这个十位上的数与个位上的 54，求原两位数。

7、甲、乙两人分别从AB两地同时出发，如果两人同向而行，经过13分钟，甲赶上乙。如两人相向而行，经过3分钟两人相遇。已知乙每分钟行25千米, 问AB 两地相距多少米？ & 一架飞机飞行于两城之间顺风需要6小时30分，逆风时需要7小时，已知风速是每小时26千米，求两城之间的距离是多少千米？ 9、学校组织暑假旅游，一共用了10辆车，大客车每辆坐100人，小客车每辆坐60人，大客车比小客车一共多坐了520人，问大小客车各几辆？ 10、五年一班有52人做手工，男生每人做3件，女生每人做2件，已知男生比女生多做36件，求五年一班男女生各有多少人？