编码器零点

编码器零点

旋转编码器是一种光电式旋转测量装置，它将被测的角位移直接转换成数字信号（高速脉冲信号），主要应用于机床、电梯、伺服电机配套、纺织机械、包装机械、印刷机械、起重机械等行业。

旋转编码器按照工作原理编码器可分为增量式和绝对式两类。

A增量式编码器是将位移转换成周期性的电信号，再把这个电信号转变成计数脉冲，用脉冲的个数表示位移的大小；

B绝对式编码器的每一个位置对应一个确定的数字码，因此它的示值只与测量的起始和终止位置有关，而与测量的中间过程无关。

二者区别:

增量型的位置从零位标记开始计算的脉冲数量确定的；

而绝对型的位置是由输出代码的读数确定的。在一圈里，每个位置的输出代码的读数是唯一的；因此，当电源断开时，绝对型编码器并不与实际的位置分离。如果电源再次接通，那么位置读数仍是当前的，有效的；不像增量编码器那样，必须去寻找零位标记。

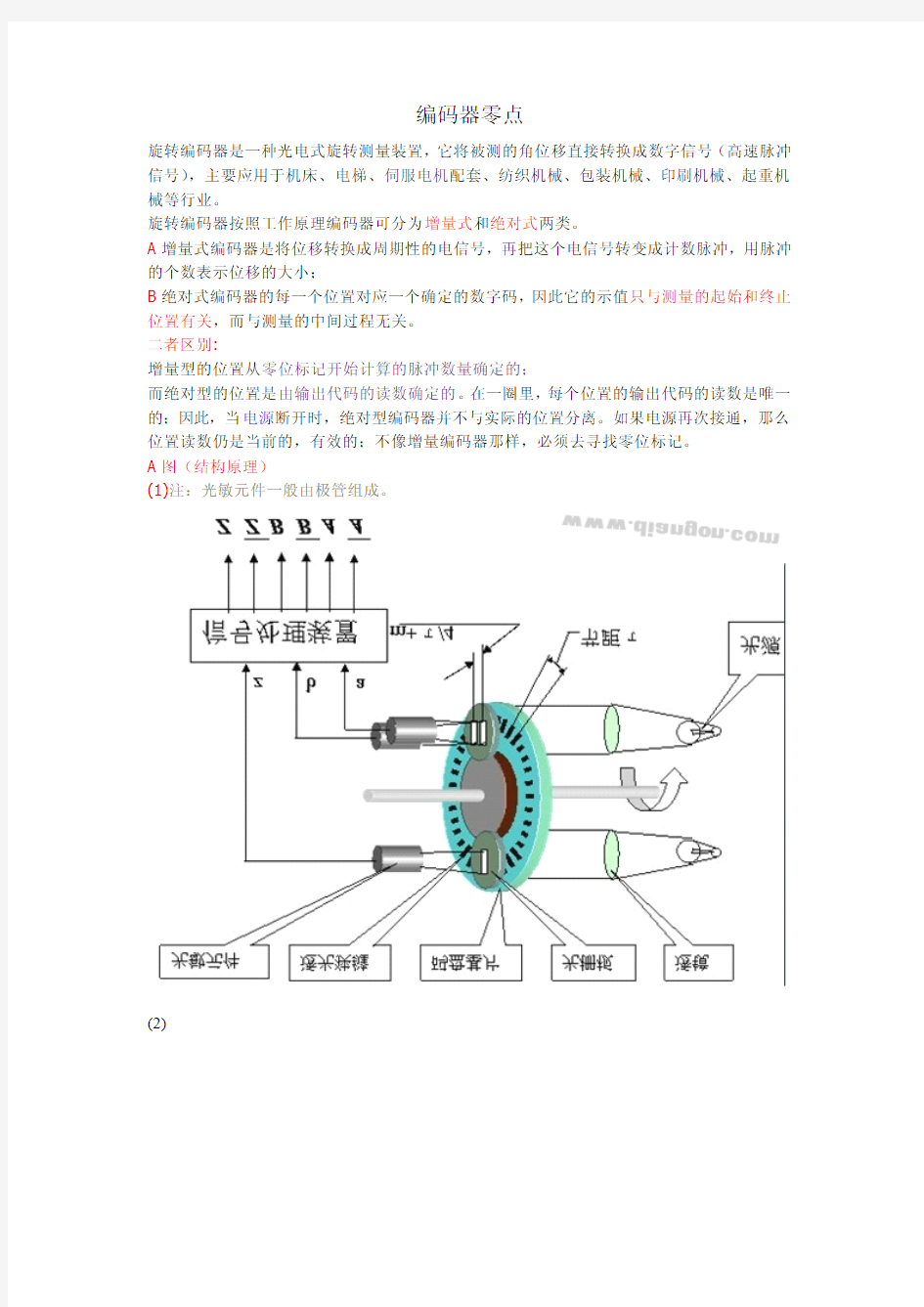
A图（结构原理）

(1)注：光敏元件一般由极管组成。

(2)

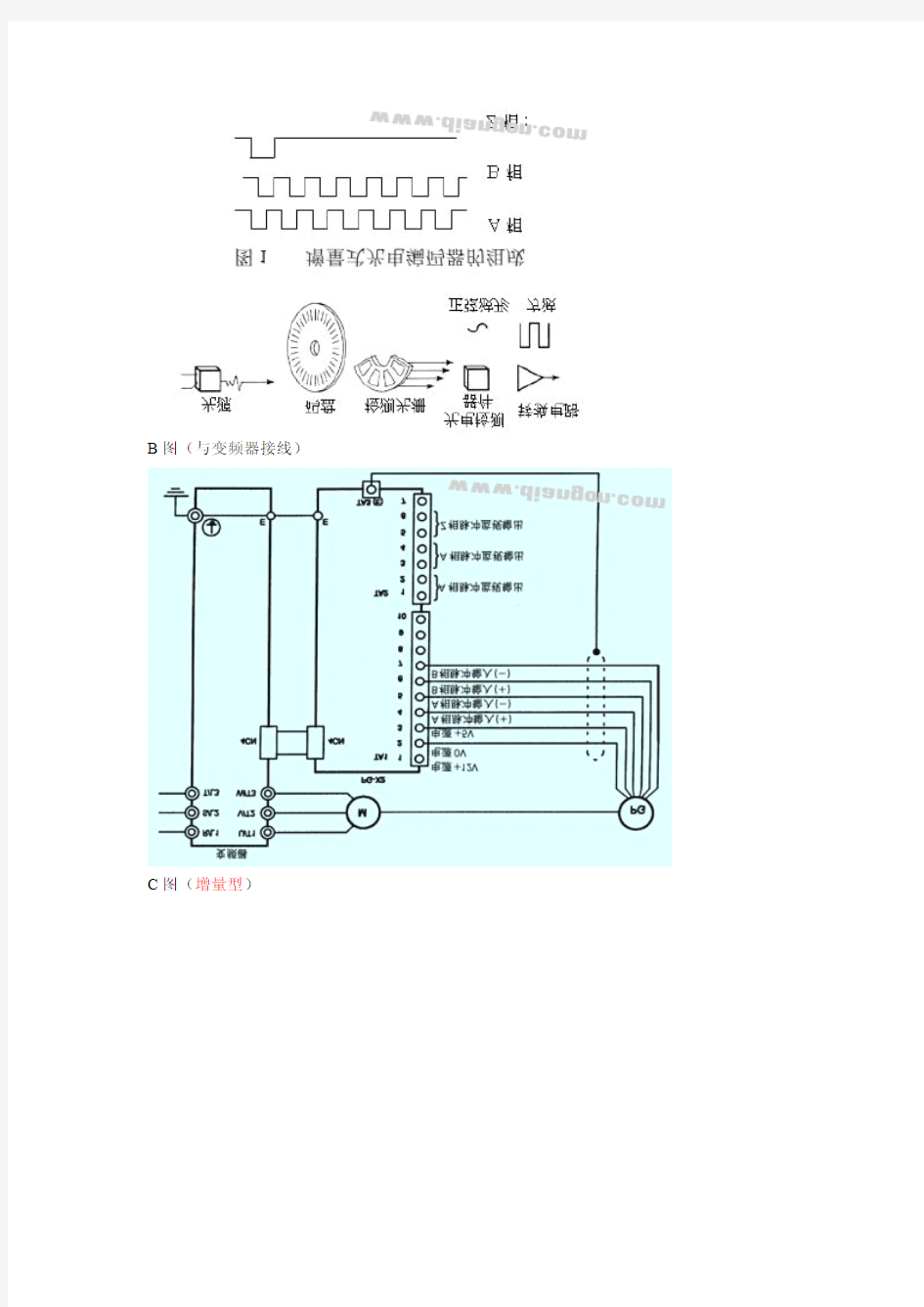
B图（与变频器接线）

C图（增量型）

D图（绝对型）

我们通常用的是增量型编码器，可将旋转编码器的输出脉冲信号直接输入给PLC，利用PLC 的高速计数器对其脉冲信号进行计数，以获得测量结果。

这里所讲的确定零位指的是增量型。

1、编码器轴转动找零，编码器在安装时，旋转转轴对应零位，一般增量值与单圈绝对值会用这种方法，而轴套型的编码器也用这种方法。缺点，零点不太好找，精度较低。

2、与上面方法相当，只是编码器外壳旋转找零，这主要是对于一些紧凑型安装的同步法兰（也有叫伺服法兰）外壳所用。

3、通电移动安装机械对零，通电将安装的机械移动到对应的编码器零位对应位置安装。

4、偏置计算，机械和编码器都不需要找零，根据编码器读数与实际位置的偏差计算，获得偏置量，以后编码器读数后减去这个偏置量。例如编码器的读数为100，而实际位置是90，计算下在实际位置0位时，编码器的读数应该是10，而这个“10”就是偏置量，以后编码器读到的数，减去这个偏置量就是位置值。可重复多次，修正偏置量。对于增量值编码器，是读取原始机械零位到第一个Z点的读数，作为偏置量。精度较高的编码器，或者量程较大的绝对值多圈编码器，多用这种方法。

5、智能化外部置零，有些带智能化功能的编码器，可提供外部置位功能，例如通过编码器附带的按键，或外带的软件设置功能置零。

6、需要说明的是，绝对值编码器的零位再往下就是编码的循环最大值，无论是单圈绝对值，还是多圈绝对值，如果置零位，那么再往下（下滑、移动，惯性过冲等），就可能数据一下子跳到最大了，对于高位数的绝对值多圈，可能数据会溢出原来的设定范围。另外，绝对值编码器还有一个旋转方向的问题，置零后，如果方向不对，是从0跳到最大，然后由大变小的。一些进口的编码器尽管带有外部置零功能，但建议还是不要用此功能。（我们碰到很多用进口绝对值编码器会碰到这样的困惑，不要就迷信进口的）。

7、最好的置位方法，预置一个非零位（留下下滑、过冲的余量）并预置旋转方向+偏置计算的方法。另外一种方法是置“中”，偏置量就是中点值，置位线与电源正相触后，编码器输出的就是中点位置，这样的行程是+/-半全程，在这样的行程范围内，无论旋转方向，确保不会经过零点跳变。

1、按码盘的刻孔方式不同分类：

（1）增量型：就是每转过单位的角度就发出一个脉冲信号(也有发正余弦信号，然后对其进行细分，斩波出频率更高的脉冲)，通常为A相、B相、Z相输出，A相、B相为相互延迟1/4周期的脉冲输出，根据延迟关系可以区别正反转，而且通过取A相、B相的上升和下降沿可以进行2或4倍频；Z相为单圈脉冲，即每圈发出一个脉冲。

（2）绝对值型：就是对应一圈，每个基准的角度发出一个唯一与该角度对应二进制的数值，通过外部记圈器件可以进行多个位置的记录和测量。

编码器-----------PLC

A-----------------X0

B-----------------X1

Z------------------X2

+24V------------+24V

COM-------------24V-----------COM[1]

注：可以是DC-5V或DC-24V。

常见故障：

1、编码器本身故障：是指编码器本身元器件出现故障，导致其不能产生和输出正确的波形。这种情况下需更换编码器或维修其内部器件。

2、编码器连接电缆故障：这种故障出现的几率最高，维修中经常遇到，应是优先考虑的因素。通常为编码器电缆断路、短路或接触不良，这时需更换电缆或接头。还应特别注意是否是由于电缆固定不紧，造成松动引起开焊或断路，这时需卡紧电缆。

3、编码器+5V电源下降：是指+5V电源过低，通常不能低于4.75V，造成过低的原因是供电电源故障或电源传送电缆阻值偏大而引起损耗，这时需检修电源或更换电缆。

4、编码器安装松动：这种故障会影响位置控制精度，造成停止和移动中位置偏差量超差，甚至刚一开机即产生伺服系统过载报警，请特别注意。

一般地，旋转编码器也能得到一个速度信号，这个信号要反馈给变频器，从而调节变频器的输出数据。

故障现象：1、旋转编码器坏（无输出）时，变频器不能正常工作，变得运行速度很慢，而且一会儿变频器保护，显示“PG断开”（PG可以理解为变频器检测电路模块）联合动作才能起作用。要使电信号上升到较高电平，并产生没有任何干扰的方波脉冲，这就必须用电子电路来处理。编码器pg接线与参数矢量变频器与编码器pg之间的连接方式，必须与编码器

pg的型号相对应。一般而言，编码器pg型号分差动输出、集电极开路输出和推挽输出三种，其信号的传递方式必须考虑到变频器pg卡的接口，因此选择合适的pg卡型号或者设置合理。

总结：

1它主要是以高精度计量光栅为检测元件，通过光电转换；

2将轴的机械角位移信息以LED光源为介质通过光栅码盘转换成相应的数字代码，用它可以实现角位移、角速度、和角加速度及其他物理量的精确测量；

3.工作原理(如下图)

1：光源（LED）2：透镜（Lens）3：指示光栅4：码盘（Disk）5：接受器（ASIC）

点光源（LED）发出的光经过透镜（Lens）的折射变成准直的平行光，通过光栅和码盘，照射到光电接受器上，如果码盘发生转动，光线就会把码盘转动的情况反应到接受器上。接受器会把这些光信号转换成电信号输出，从而以电脉冲的形式反应出物理的运动量（位移、角速度、加速度）。