导数中的构造函数
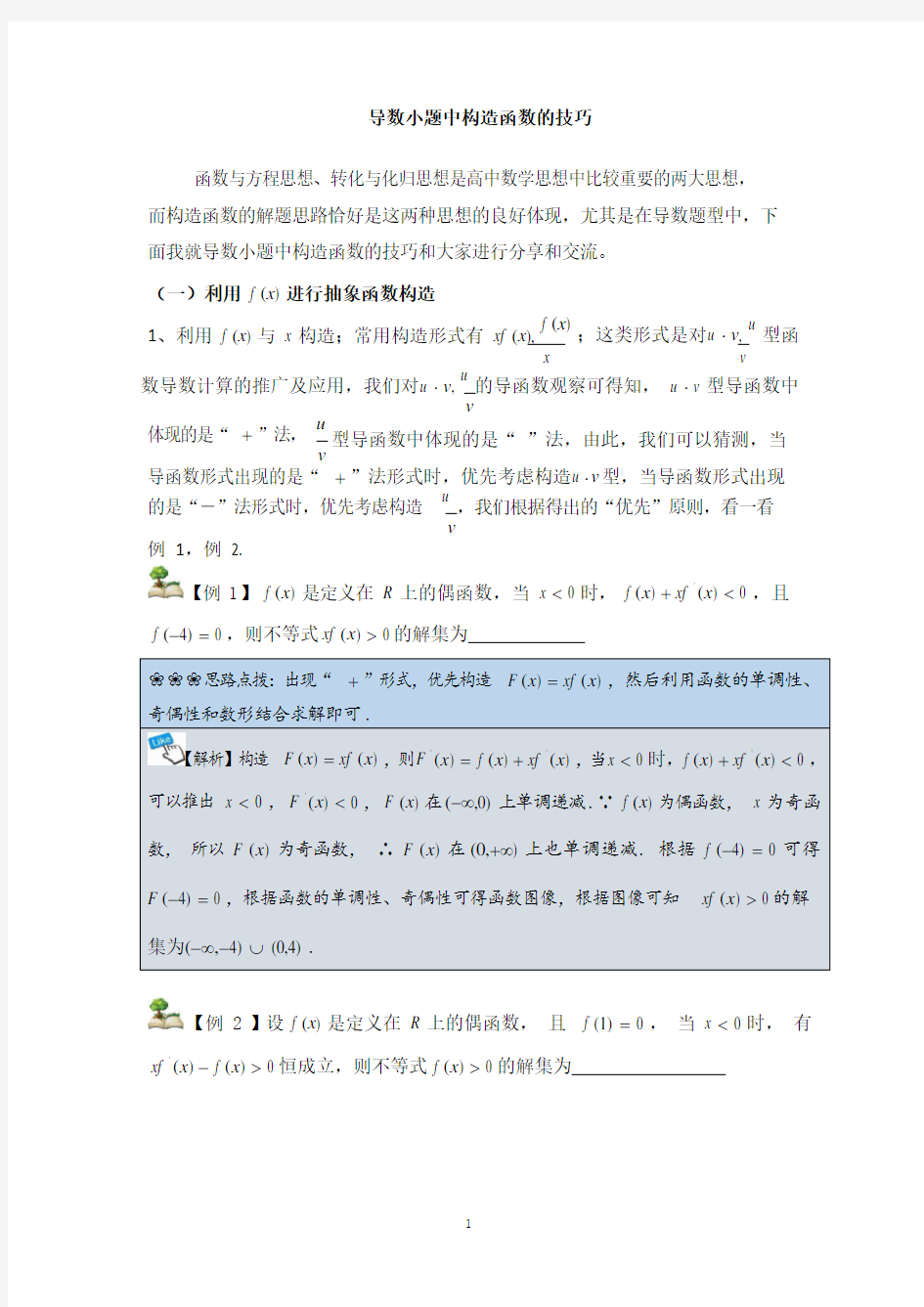

【解析】构造 F (x ) = xf (x ) ,则 F ' (x ) = f (x ) + xf ' (x ) ,当 x < 0 时,f (x ) + xf ' (x ) < 0 , 可以推出 x < 0 , F ' (x ) < 0 , F (x ) 在(-∞,0) 上单调递减.∵ f (x ) 为偶函数, x 为奇函数, 所以 F (x ) 为奇函数, ∴ F (x ) 在 (0,+∞) 上也单调递减. 根据 f (-4) = 0 可得F (-4) = 0 ,根据函数的单调性、奇偶性可得函数图像,根据图像可知 xf (x ) > 0 的解 集为(-∞,-4) ? (0,4) .
???思路点拨:出现“ + ”形式,优先构造 F (x ) = xf (x ) ,然后利用函数的单调性、奇偶性和数形结合求解即可.
导数小题中构造函数的技巧
函数与方程思想、转化与化归思想是高中数学思想中比较重要的两大思想, 而构造函数的解题思路恰好是这两种思想的良好体现,尤其是在导数题型中,下面我就导数小题中构造函数的技巧和大家进行分享和交流。 (一)利用 f (x ) 进行抽象函数构造
1、利用 f (x ) 与 x 构造;常用构造形式有 xf (x ), f (x ) ;这类形式是对u ? v , u
型函
x v
数导数计算的推广及应用,我们对u ? v , u
的导函数观察可得知, u ? v 型导函数中
v
体现的是“ + ”法, u
v
型导函数中体现的是“ ”法,由此,我们可以猜测,当
导函数形式出现的是“ + ”法形式时,优先考虑构造u ? v 型,当导函数形式出现
的是“-”法形式时,优先考虑构造 u
,我们根据得出的“优先”原则,看一看
v
例 1,例 2.
【例 1】 f (x ) 是定义在 R 上的偶函数,当 x < 0 时, f (x ) + xf '
(x ) < 0 ,且
f (-4) = 0 ,则不等式 xf (x ) > 0 的解集为
【例 2 】设 f (x ) 是定义在 R 上的偶函数, 且 f (1) = 0 , 当 x < 0 时, 有
xf ' (x ) - f (x ) > 0 恒成立,则不等式 f (x ) > 0 的解集为
x
n 出现 xf ' (x ) - nf (x ) 形式,构造函数 F (x ) =
f (x )
. 结论:
出现nf (x ) + xf ' (x ) 形式,构造函数 F (x ) = x n f (x ) ; ; xf ' (x ) - nf (x ) x n +1 f ' (x ) ? x n - nx n -1 f (x ) = x 2n '
,
F (x ) = f (x ) x n F (x ) = F (x ) = x n f (x ) , F ' (x ) = nx n -1 f (x ) + x n f (x ) = x n -1[nf (x ) + f ' (x )] ; x n
然 后 利 用
F (x ) = f (x ) ???思路点拨:满足“ xf ' (x ) - nf (x ) ”形式,优先构造 函数的单调性、奇偶性和数形结合求解即可.
xf (x ), f (x )
是比较简单常见的 f (x ) 与 x 之间的函数关系式,如果碰见复杂的,
x
不易想的我们该如何处理,由此我们可以思考形如此类函数的一般形式.
我们根据得出的结论去解决例 3 题
【例 3】已知偶函数 f (x )(x ≠ 0) 的导函数为 f ' (x ) ,且满足 f (-1) = 0 ,当 x > 0 时, 2 f (x ) > xf ' (x ) ,则使得 f (x ) > 0 成立的 x 的取值范围是
xf ' (x ) - f (x ) > 0 ,可以推出 x < 0 , F ' (x ) > 0 , F (x ) 在(-∞,0) 上单调递增.∵ f (x ) 为偶函数, x 为奇函数,所以 F (x ) 为奇函数,∴ F (x ) 在(0,+∞) 上也单调递减.根据f (1) = 0 可得 F (1) = 0 ,根据函数的单调性、奇偶性可得函数图像,根据图像可知 f (x ) > 0 的解集为(-∞,-1) ?(1,+∞) .
f '
(x ) ? x - f (x ) , 当 x < 0 时 , x 2
'
, 则 F (x ) = f (x ) x 【 解 析 】 构 造 F (x ) = 然后利用函数的单调
F (x ) = f (x ) x
???思路点拨:出现“ ”形式,优先构造 性、奇偶性和数形结合求解即可.
【 解 析 】 构 造 F (x ) = xf (2x ) , 则 F ' (x ) = 2xf ' (x ) + f (2x ) , 当 x < 0 时 , F ' (x ) = 2xf ' (x ) + f (2x ) < 0 ,可以推出 x < 0 , F ' (x ) < 0 , F (x ) 在(-∞,0) 上单调递减.
∵ f (x ) 为奇函数, x 为奇函数,所以 F (x ) 为偶函数,∴ F (x ) 在(0,+∞) 上单调递增. 根据 f (-2) = 0 可得 F (-1) = 0 ,根据函数的单调性、奇偶性可得函数图像,根据图像可知 xf (2x ) < 0 的解集为(-1,0) ? (0,1) .
???思路点拨:满足“ xf ' (x ) + nf (x ) ”形式,优先构造 F (x ) = xf (2x ) ,然后利用函数的单调性、奇偶性和数形结合求解即可.注意 f (-2) = 0 和 F (x ) 的转化.
【变式提升】设函数 f (x ) 满足 x 3
f '
(x ) + 3x 2
f (x ) = 1+ ln x ,且 f (
则 x > 0 时, f (x ) ( ) A 、有极大值,无极小值 B 、有极小值,无极大值 C 、既有极大值又有极小值
D 、既无极大值也无极小值
e ) = 1
, 2e
且 f (-2) = 0 ,则不等式 xf (2x ) < 0 的解集为
.
【例 4】设 f (x ) 是定义在 R 上的奇函数,在(-∞,0) 上有2xf ' (2x ) + f (2x ) < 0 , 然后利用积分、函数的性质求解即可. x n ???思路点拨:满足“ xf ' (x ) + nf (x ) ”形式,为n = 3 时情况,优先构造 F (x ) = f (x ) ,
xf ' (x ) - 2 f (x ) < 0 ,可以推出 x > 0 ,F ' (x ) < 0 ,F (x ) 在(0,+∞) 上单调递减.∵ f (x ) 为偶函数, x 2 为偶函数,所以 F (x ) 为偶函数,∴ F (x ) 在(-∞,0) 上单调递增.根据f (-1) = 0 可得 F (-1) = 0 ,根据函数的单调性、奇偶性可得函数图像,根据图像可知 f (x ) > 0 的解集为(-1,0)?(0,1) .
f '
(x ) ? x - 2 f (x ) , 当 x > 0 时 , x 3
'
, 则 F (x ) =
f (x ) x 2 【 解 析 】 构 造 F (x ) =
函数 f ' (x ) 满足 f ' (x ) < f (x ) ,则 F ' (x ) < 0 , F (x ) 在 R 上单调递减,根据单调性可知 选 D.
,导 f ' (x ) - f (x ) e x
e x
f ' (x ) - e x f (x ) = e 2 x '
形式,则 F (x ) = f (x ) e x 【解析】构造 F (x ) = (2) 利用 f (x ) 与e x
构造;
f (x ) 与 e x
构造, 一方面是对 u ? v , u v
函数形式的考察, 另外一方面是对 (e x ) = e x 的考察.所以对于 f (x ) ± f ' (x ) 类型,我们可以等同
xf (x ), f (x ) 的类型处 x
理,“ + ”法优先考虑构造 F (x ) = f (x ) ? e x ,“ ”法优先考虑构造 F (x ) = f (x )
e
x .
【例 5】已知 f (x ) 是定义在(-∞,+∞) 上的函数,导函数 f ' (x ) 满足 f ' (x ) < f (x ) 对于 x ∈ R 恒成立,则( ) A 、 f (2) > e 2 f (0), f (2014) > e 2014 f (0)
B 、 f (2) < e 2 f (0), f (2014) > e 2014 f (0)
C 、 f (2) > e 2 f (0), f (2014) < e 2014 f (0)
D 、 f (2) < e 2 f (0), f (2014) < e 2014 f (0)
???思路点拨:满足“ f '
(x ) - f (x ) < 0 ”形式,优先构造 F (x ) = 函数的单调性和数形结合求解即可.注意选项的转化.
f (x ) ,然后利用
e
x
同样e x f (x ), f (x )
是比较简单常见的 f (x ) 与e x 之间的函数关系式,如果碰
e x
见复杂的,我们是否也能找出此类函数的一般形式呢?
我们根据得出的结论去解决例 6 题.
e
nx 2、出现 f ' (x ) - nf (x ) 形式,构造函数 F (x ) =
f (x )
. 结论:1、出现 f ' (x ) + nf (x ) 形式,构造函数 F (x ) = e nx f (x ) ;
; f ' (x )e nx - ne nx f (x ) = [ f ' (x ) - nf (x )] e 2nx
e nx , '
F (x ) = f (x ) e nx F (x ) = F (x ) = e nx f (x ) , F ' (x ) = n ? e nx f (x ) + e nx f ' (x ) = e nx [ f ' (x ) + nf (x )] ;
e
2 x f (0) = 1,则 F (0) = 1 , f (x ) > e 2 x ?
f (x )
> 1 ? F (x ) > F (0) ,根据单调性得 x > 0 . 导函数 f ' (x ) 满足 f ' (x ) - 2 f (x ) > 0 , 则 F ' (x ) > 0 , F (x ) 在 R 上单调递增. 又∵ , f ' (x ) - 2 f (x ) e 2 x
e 2 x
f ' (x ) - 2e 2 x f (x ) = e 4 x '
形式,则 F (x ) =
f (x ) e 2 x 【解析】构造 F (x ) =
【例 7】已知函数 f ( x ) 在 R 上可导,其导函数为 f '( x ) ,若 f ( x ) 满足: e 2 x
e
2 x
???思路点拨:利用通式构造函数时考虑- 4 如何转化.构造函数 F (x ) = f (x ) - 2
函数 f ' (x ) 满足(x -1)[ f ' (x ) - f (x )] > 0 ,则 x ≥ 1时 F ' (x ) ≥ 0 , F (x ) 在[1,+∞) 上单调递增 . 当 x < 1 时 F ' (x ) < 0 , F (x ) 在 (-∞,1] 上 单 调 递 减 . 又 由 f (2 - x ) = f (x )e 2-2 x ? F (2 - x ) = F (x ) ? F (x ) 关于 x = 1 对称,根据单调性和图像, 可知选 C.
,导 f ' (x ) - f (x ) e x
e x
f ' (x ) - e x f (x ) = e 2 x '
形式,则 F (x ) =
f (x ) e x 【解析】构造 F (x ) = 【例 6】若定义在 R 上的函数 f (x ) 满足 f ' (x ) - 2 f (x ) > 0, f (0) = 1 ,则不等式 f (x ) > e 2 x 的解集为
???思路点拨:满足“ f '
(x ) - 2 f (x ) < 0 ”形式,优先构造 F (x ) = 函数的单调性和数形结合求解即可.注意选项的转化.
f (x ) ,然后利用
e
2 x
【变式提升】若定义在 R 上的函数 f (x ) 满足 f ' (x ) - 2 f (x ) - 4 > 0, f (0) = -1,
则不等式 f (x ) > e 2 x - 2 的解集为
(x -1)[ f '( x ) - f (x )] > 0 , f (2 - x ) = f (x )e 2-2 x ,则下列判断一定正确的是(
)
(A ) f (1) < f (0)
(B ) f (2) > e 2 f (0)
(C ) f (3) > e 3 f (0) (D ) f (4) < e 4 f (0)
???思路点拨:满足“ f '
(x ) - f (x ) ”形式,优先构造 F (x ) = 的单调性和数形结合求解即可.注意选项的转化.
f (x ) ,然后利用函数
e
x
. f ' (x ) cos x + f (x ) s in x cos 2 x ' , F (x ) = f (x ) cos x F (x ) = F (x ) = f (x ) cos x , F ' (x ) = f ' (x ) cos x - f (x ) s in x ; ; f ' (x ) sin x - f (x ) cos x sin 2 x '
, F (x ) = f (x ) sin x F (x ) = F (x ) = f (x ) s in x , F ' (x ) = f ' (x ) sin x + f (x ) cos x ; , )
(3) 利用 f (x ) 与sin x , cos x 构造.
sin x , cos x 因为导函数存在一定的特殊性,所以也是重点考察的范畴,我们一起看看常考的几种形式.
根据得出的关系式,我们来看一下例 8
【 例 8 】 已 知 函 数 y = f (
x )
对 于 任 意 的 x ∈(- π π
满 足 2 2
f '( x ) c os x + f (x )sin x > 0 (其中 f '( x ) 是函数 f ( x ) 的导函数),则下列不等式 不成立的是( )
A 、 π π
π
π
f ( ) < f ( ) 3 4
B 、
f (- ) < f (- )
3 4 C 、 f (0) < π
2 f ( )
4
D 、 f (0) < π
2 f ( )
3
【变式提升】定义在(0,
π
) 上的函数,函数 f 2
' (x ) 是它的导函数,且恒有
化后可知选 B. 2 2
π π '
( )
( ) 满足 f ' x cos x + f x sin x > 0 ,则 F (x ) > 0 ,F (x ) 在(- , ) 上单调递增.把选项转 '
,导函数 f (x ) f ' (x ) cos x + f (x ) s in x cos 2
x ' 形式,则 F (x ) = f (x ) cos x
【解析】构造 F (x ) = 然后利用函数的单调性和数形结合求解即可.注意选项的转化.
cos x
???思路点拨:满足“ f '( x ) c os x + f (x )sin x > 0 ”形式,优先构造 F (x ) = f (x )
2 2
3 2 3
f (x ) < f ' (x ) tan x 成立,则( )
π π π
A 、 f ( ) > 4
f ( ) 3 B 、 f (1) < 2 f ( ) sin1
6 π π π π
C 、 f ( ) > 6 f ( ) 4
D 、 f ( ) < 6
f ( )
3
(二)构造具体函数关系式构造
这类题型需要根据题意构造具体的函数关系式,通过具体的关系式去解决不等式及求值问题.
【例 9】α,β∈[- π π
,且αsin α- βsin β> 0 ,则下列结论正确的是( )
, ] 2 2
A 、α> β
B 、α2 > β2
C 、α< β
D 、α+ β> 0
【变式提升】定义在 R 上的函数 f (x ) 满足 f (1) = 1 且对?x ∈ R , f ' (x ) < 则
不等式 f (log 2
, 2 x ) > log 2 x +1 的解集为 . 2
则 f ' (0) = ( )
A 、26
B 、29
C 、212
D 、215
【例10】等比数列{a n }中,a 1 = 2 ,a 8 = 4 ,函数 f (x ) = x (x - a 1 )(x - a 2 )...(x - a 8 ) , ,利用单调性求解集,然后解对数不等式即可
.
2
2 t +1 2 f (t ) > ???思路点拨:构造函数 F (x ) = f (x ) - 1 x 2 ,令t = log x ,然后原不等式等价于 2 f ' (x ) ≥ 0 , f (x ) 单调递增;x ∈[- π
,0) 时导函数 f ' (x ) < 0 , f (x ) 单调递减.有∵ f (x )
2
为偶函数,根据单调性和图像可知选 B. π
' 【解析】构造 f (x ) = x sin x 形式,则 f (x ) = sin x + x cos x , x ∈[0, ] 时导函数
???思路点拨:构造函数 f (x ) = x sin x ,然后利用函数的单调性和数形结合求解即可.
???思路点拨:满足“ f ' (x ) sin x - f (x ) cos x ”形式,优先构造 F (x ) = f (x )
,然后
sin x
利用函数的单调性和数形结合求解即可.注意选项的转化.
2
? = 8
?
1+1 ? | 0 - 2 - 2 ?2
为(0,-2) ,所以(a - c )2
+ (b - d )2
的最小值为 ? d -1
1- c = 1 ? d = 2 - c ? g (x ) = 2 - x ;由 f ' (x ) = 1- 2e x = -1,得 x = 0 ,所以切点坐标
x a 1 ? b = a - 2e 进 而 ? f (x ) = x - 2e ; 又 由
b a - 2e a =
【 解 析 】 由 ???思路点拨:把(a - c )2 + (b - d )2 看成两点距离的平方,然后利用数形结合以及点到直线的距离即可.
???思路点拨:构造函数 f (x ) = 2x 2 - 5 ln x , g (x ) = -x ,然后利用两点之间的距离公式和数形结合思想求解即可.
) )
【例 11】已知实数a , b , c 满足
a - 2e a b
= 1- c
d -1 = 1 ,其中
e 是自然对数的底数,
那么(a - c )2 + (b - d )2 的最小值为( )
A 、8
B 、10
C 、12
D 、18
【变式提升】已知实数a , b 满足2a 2 - 5 l n a - b = 0 ,c ∈ R ,则的最小值为
【课后作业】设函数 f (x ) 在 R 上的导函数 f ' (x ) , 在(0,+∞) 上
f ' (x ) < sin 2x ,且?x ∈ R ,有 f (-x ) + f (x ) = 2 sin 2 x ,则以下大小关系一定
正确的是( )
f (5π 4π π
A 、 ) < f ( ) 6 3
B 、 f ( ) < 4
f (π)
C 、 f (- 5π
< 6
f (- 4π 3 D 、 f (- π
> 4
f (-π)
8 1 2 f ' (x ) = g (x ) + xg ' (x ) ,∴ f ' (0) = g (0) = a ? a ?...? a = (2 ? 4)4 = 212
,故选 C.
【 解 析 】 令 g (x ) = (x - a 1 )(x - a 2 )...(x - a 8 ) 形 式 , 则 f (x ) = xg (x ) ,
???思路点拨:构造函数 f (x ) = xg (x ) ,然后利用整体代换思想和数列的性质求解即可.
(a - c )2 + (b + c )2 )
构造函数,作为一种做题技巧的体现,考察了学生的思考能力和动手能力,是一种非常实用的做题技巧,希望我的总结分享能够给大家带来帮助。
专题6.1 导数中的构造函数 高考数学选填题压轴题突破讲义(解析版)
【方法综述】 函数与方程思想、转化与化归思想是高中数学思想中比较重要的两大思想,而构造函数的解题思路恰好是这两种思想的良好体现,尤其是在导数题型中.在导数小题中构造函数的常见结论:出现()()nf x xf x '+形式,构造函数()()F n x x f x =;出现()()xf x nf x '-形式,构造函数()() F n f x x x = ;出现()()f x nf x '+形式,构造函数()()F nx x e f x =;出现()()f x nf x '-形式,构造函数()() F nx f x x e = . 【解答策略】 类型一、利用()f x 进行抽象函数构造 1.利用()f x 与x (n x )构造 常用构造形式有()xf x , ()f x x ;这类形式是对u v ?,u v 型函数导数计算的推广及应用,我们对u v ?,u v 的导函数观察可得知,u v ?型导函数中体现的是“+”法,u v 型导函数中体现的是“-”法,由此,我们可以猜测,当导函数形式出现的是“+”法形式时,优先考虑构造u v ?型,当导函数形式出现的是“-”法形式时,优先考虑构造 u v . 例1.【2019届高三第二次全国大联考】设 是定义在上的可导偶函数,若当 时, ,则函数 的零点个数为 A .0 B .1 C .2 D .0或2 【答案】A 【解析】 设 ,因为函数 为偶函数,所以 也是上的偶函数,所以 .由已知, 时, ,可得当 时, , 故函数在上单调递减,由偶函数的性质可得函数在 上单调递增.所以
,所以方程,即无解,所以函数没有零点.故选A. 【指点迷津】设,当时,,可得当时,,故函数 在上单调递减,从而求出函数的零点的个数. 【举一反三】【新疆乌鲁木齐2019届高三第二次质量检测】的定义域是,其导函数为,若,且(其中是自然对数的底数),则 A.B. C.当时,取得极大值D.当时, 【答案】C 【解析】 设,则 则 又得 即,所以 即 , 由得,得,此时函数为增函数 由得,得,此时函数为减函数 则,即,则,故错误 ,即,则,故错误 当时,取得极小值 即当,,即,即,故错误 当时,取得极小值 此时,则取得极大值
导数运算中构造函数解决抽象函数问题
导数运算中构造函数解决抽象函数问题 【模型总结】 关系式为“加”型 (1)'()()0f x f x +≥ 构造[()]'['()()]x x e f x e f x f x =+ (2)'()()0xf x f x +≥ 构造[()]''()()xf x xf x f x =+ (3)'()()0xf x nf x +≥ 构造11[()]''()()['()()]n n n n x f x x f x nx f x x xf x nf x --=+=+ (注意对x 的符号进行讨论) 关系式为“减”型 (1)'()()0f x f x -≥ 构造2()'()()'()()[]'()x x x x x f x f x e f x e f x f x e e e --== (2)'()()0xf x f x -≥ 构造2()'()()[ ]'f x xf x f x x x -= ! (3)'()()0xf x nf x -≥ 构造121 ()'()()'()()[]'()n n n n n f x x f x nx f x xf x nf x x x x -+--== (注意对x 的符号进行讨论) 小结:1.加减形式积商定 2.系数不同幂来补 3.符号讨论不能忘 典型例题: 例1.设()()f x g x 、是R 上的可导函数,'()()()'()0f x g x f x g x +<,(3)0g -=,求不等式()()0f x g x <的解集 变式:设()()f x g x 、分别是定义在R 上的奇函数、偶函数,当0x <时,'()()()'()0f x g x f x g x +>,(3)0g -=,求不等式()()0f x g x <的解集. 例 2.已知定义在R 上的函数()()f x g x 、满足()() x f x a g x =,且'()()()'()f x g x f x g x <,(1)(1)5(1)(1)2f f g g -+=-,若有穷数列*()()()f n n N g n ??∈???? 的前n 项和等于3132,则n 等于 . 变式:已知定义在R 上的函数()()f x g x 、满足()() x f x a g x =,且'()()()'()f x g x f x g x <,
【高考数学】构造函数法证明导数不等式的八种方法
第 1 页 共 6 页 构造函数法证明不等式的八种方法 1、利用导数研究函数的单调性极值和最值,再由单调性来证明不等式是函数、导数、不等式综合中的一个难点,也是近几年高考的热点。 2、解题技巧是构造辅助函数,把不等式的证明转化为利用导数研究函数的单调性或求最值,从而证得不等式,而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键。 以下介绍构造函数法证明不等式的八种方法: 一、移项法构造函数 【例1】 已知函数x x x f -+=)1ln()(,求证:当1->x 时,恒有 x x x ≤+≤+-)1ln(1 11 分析:本题是双边不等式,其右边直接从已知函数证明,左边构造函数 11 1)1ln()(-++ +=x x x g ,从其导数入手即可证明。 【解】1111)(+-=-+='x x x x f ∴当01<<-x 时,0)(>'x f ,即)(x f 在)0,1(-∈x 上为增函数 当0>x 时,0)(<'x f ,即)(x f 在),0(+∞∈x 上为减函数 故函数()f x 的单调递增区间为)0,1(-,单调递减区间),0(+∞ 于是函数()f x 在),1(+∞-上的最大值为0)0()(max ==f x f ,因此,当1->x 时,0)0()(=≤f x f ,即0)1ln(≤-+x x ∴x x ≤+)1ln( (右面得证), 现证左面,令111)1ln()(-+++=x x x g , 22) 1()1(111)(+=+-+='x x x x x g 则 当0)(,),0(;0)(,)0,1(>'+∞∈<'-∈x g x x g x 时当时 , 即)(x g 在)0,1(-∈x 上为减函数,在),0(+∞∈x 上为增函数, 故函数)(x g 在),1(+∞-上的最小值为0)0()(min ==g x g , ∴当1->x 时,0)0()(=≥g x g ,即011 1)1ln(≥-++ +x x ∴111)1ln(+-≥+x x ,综上可知,当x x x x ≤+≤-+->)1ln(11 1,1有时 【警示启迪】如果()f a 是函数()f x 在区间上的最大(小)值,则有()f x ≤()f a (或()f x ≥()f a ), 那么要证不等式,只要求函数的最大值不超过0就可得证. 2、作差法构造函数证明 【例2】已知函数.ln 21)(2x x x f += 求证:在区间),1(∞+上,函数)(x f 的图象在函数33 2)(x x g =的图象的下方;
构造函数法证明导数不等式的八种方法Word版
构造函数法证明不等式的八种方法 1、利用导数研究函数的单调性极值和最值,再由单调性来证明不等式是函数、导数、不等式综合中的一个难点,也是近几年高考的热点。 2、解题技巧是构造辅助函数,把不等式的证明转化为利用导数研究函数的单调性或求最值,从而证得不等式,而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键。 以下介绍构造函数法证明不等式的八种方法: 一、移项法构造函数 【例1】 已知函数x x x f -+=)1ln()(,求证:当1->x 时,恒有x x x ≤+≤+-)1ln(1 11 分析:本题是双边不等式,其右边直接从已知函数证明,左边构造函数 11 1)1ln()(-++ +=x x x g ,从其导数入手即可证明。 【解】1111)(+-=-+='x x x x f ∴当01<< -x 时,0)(>'x f ,即)(x f 在)0,1(-∈x 上为增函数 当0>x 时,0)(<'x f ,即)(x f 在),0(+∞∈x 上为减函数 故函数()f x 的单调递增区间为)0,1(-,单调递减区间),0(+∞ 于是函数()f x 在),1(+∞-上的最大值为0)0()(max ==f x f ,因此,当1->x 时,0)0()(=≤f x f , 即0)1ln(≤-+x x ∴x x ≤+)1ln( (右面得证), 现证左面,令111)1ln()(-++ +=x x x g , 22)1()1(111)(+=+-+='x x x x x g 则 当0)(,),0(;0)(,)0,1(>'+∞∈<'-∈x g x x g x 时当时 , 即)(x g 在)0,1(-∈x 上为减函数,在),0(+∞∈x 上为增函数, 故函数)(x g 在),1(+∞-上的最小值为0)0()(min ==g x g , ∴当1->x 时,0)0()(=≥g x g ,即0111)1ln(≥-++ +x x ∴111) 1ln(+-≥+x x ,综上可知,当x x x x ≤+≤-+->)1ln(11 1,1有时 【警示启迪】如果()f a 是函数()f x 在区间上的最大(小)值,则有()f x ≤()f a (或()f x ≥()f a ),那么要 证不等式,只要求函数的最大值不超过0就可得证. 2、作差法构造函数证明 【例2】已知函数.ln 2 1)(2x x x f += 求证:在区间),1(∞+上,函数)(x f 的图象在函数332)(x x g =的图象的下方; 分析:函数)(x f 的图象在函数)(x g 的图象的下方)()(x g x f =F
高考数学(文)专题07+导数有关的构造函数方法(教师版)
专题07 导数有关的构造函数方法 一.知识点 基本初等函数的导数公式 (1)常用函数的导数 ①(C )′=________(C 为常数); ②(x )′=________; ③(x 2)′=________; ④???? 1x ′=________; ⑤(x )′=________. (2)初等函数的导数公式 ①(x n )′=________; ②(sin x )′=__________; ③(cos x )′=________; ④(e x )′=________; ⑤(a x )′=___________; ⑥(ln x )′=________; ⑦(log a x )′=__________. 5.导数的运算法则 (1)[f (x )±g (x )]′=________________________; (2)[f (x )·g (x )]′=_________________________; (3)???? ??f (x )g (x )′=____________________________. 6.复合函数的导数 (1)对于两个函数y =f (u )和u =g (x ),如果通过变量u ,y 可以表示成x 的函数,那么称这两个函数(函数y =f (u )和u =g (x ))的复合函数为y =f (g (x )). (2)复合函数y =f (g (x ))的导数和函数y =f (u ),u =g (x )的导数间的关系为___________________,即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积. 二.题型分析 1.构造多项式函数 2.构造三角函数型 3.构造x e 形式的函数 4.构造成积的形式 5.与ln x 有关的构造 6.构造成商的形式
构造函数解决导数问题
16. 已知)(x f 的导函数为)(x f ',当x >0时,)(2x f >)(x f x ',且1)1(=f 。若存 在x ∈+ R 使 )(x f =2x ,求x 的值。
构造函数解决导数问题 变式:已知)(x f 、)(x g 都是定义在R 上的函数,且满足以下条件① a x g a x f x ).(()(=>0,)0≠a 。 ② 0)(≠x g 。③ )()(x g x f '>)()(x g x f '。若25 )1()1()1()1(= --+g f g f 。 求:关于x 的不等式 x a log >1的解集。
导数的常见构造 1.对于()()x g x f ''>,构造()()()x g x f x h -= 遇到()()0'≠>a a x f ,即导函数大于某种非零常数(若a =0,则无需构造),则可构()()ax x f x h -= 2.对于()()0''>+x g x f ,构造()()()x g x f x h += 3.对于()()0'>+x f x f ,构造()()x f e x h x = 4.对于()()x f x f >'[或()()0'>-x f x f ],构造()()x e x f x h = 5.对于()()0'>+x f x xf ,构造()()x xf x h = 6.对于()()0'>-x f x xf ,构造()()x x f x h = 7.对于 ()() 0'>x f x f ,分类讨论:(1)若()0>x f ,则构造()()x f x h ln =; (2)若()0 导数选择题之构造函数法解不等式的一类题 一、单选题 1.定义在上的函数的导函数为,若对任意实数,有,且为奇函数,则不等式的解集为 A. B. C. D. 2.设函数是奇函数的导函数,,当时,,则使得 成立的的取值范围是() A. B. C. D. 3.定义在上的偶函数的导函数,若对任意的正实数,都有恒成立,则使成立的实数的取值范围为() A. B. C. D. 4.已知函数定义在数集上的偶函数,当时恒有,且,则不等式的解集为( ) A. B. C. D. 5.定义在上的函数满足,,则不等式的解集为() A. B. C. D. 6.设定义在上的函数满足任意都有,且时,有,则的大小关系是() A. B. C. D. 7.已知偶函数满足,且,则的解集为 A. B. C. D. 8.定义在R上的函数满足:是的导函数,则不等式(其中e为自然对数的底数)的解集为( ) A. B. C. D. 9.已知定义在上的函数的导函数为,满足,且,则不等式 的解集为() A. B. C. D. 10.定义在上的函数f(x)满足,则不等式的解集为A. B. C. D. 11.已知定义在上的函数满足,其中是函数的导函数.若 ,则实数的取值范围为() A. B. C. D. 12.已知函数f(x)是定义在R上的可导函数,且对于?x∈R,均有f(x)>f′(x),则有() A. e2017f(-2017) 【解析】构造 F (x ) = xf (x ) ,则 F ' (x ) = f (x ) + xf ' (x ) ,当 x < 0 时,f (x ) + xf ' (x ) < 0 , 可以推出 x < 0 , F ' (x ) < 0 , F (x ) 在(-∞,0) 上单调递减.∵ f (x ) 为偶函数, x 为奇函数, 所以 F (x ) 为奇函数, ∴ F (x ) 在 (0,+∞) 上也单调递减. 根据 f (-4) = 0 可得F (-4) = 0 ,根据函数的单调性、奇偶性可得函数图像,根据图像可知 xf (x ) > 0 的解 集为(-∞,-4) ? (0,4) . ???思路点拨:出现“ + ”形式,优先构造 F (x ) = xf (x ) ,然后利用函数的单调性、奇偶性和数形结合求解即可. 导数小题中构造函数的技巧 函数与方程思想、转化与化归思想是高中数学思想中比较重要的两大思想, 而构造函数的解题思路恰好是这两种思想的良好体现,尤其是在导数题型中,下面我就导数小题中构造函数的技巧和大家进行分享和交流。 (一)利用 f (x ) 进行抽象函数构造 1、利用 f (x ) 与 x 构造;常用构造形式有 xf (x ), f (x ) ;这类形式是对u ? v , u 型函 x v 数导数计算的推广及应用,我们对u ? v , u 的导函数观察可得知, u ? v 型导函数中 v 体现的是“ + ”法, u v 型导函数中体现的是“ ”法,由此,我们可以猜测,当 导函数形式出现的是“ + ”法形式时,优先考虑构造u ? v 型,当导函数形式出现 的是“-”法形式时,优先考虑构造 u ,我们根据得出的“优先”原则,看一看 v 例 1,例 2. 【例 1】 f (x ) 是定义在 R 上的偶函数,当 x < 0 时, f (x ) + xf ' (x ) < 0 ,且 f (-4) = 0 ,则不等式 xf (x ) > 0 的解集为 【例 2 】设 f (x ) 是定义在 R 上的偶函数, 且 f (1) = 0 , 当 x < 0 时, 有 xf ' (x ) - f (x ) > 0 恒成立,则不等式 f (x ) > 0 的解集为 构造函数解决不等式问题 例:[2011·卷]函数f (x )的定义域为R ,f (-1)=2,对任意x ∈R ,f ′(x )>2, 则f (x )>2x +4的解集为( ) A .(-1,1) B .(-1,+∞) C .(-∞,-1) D .(-∞,+∞) 【解析】构造函数G (x )=f (x )-2x -4,所以G ′(x )=f ′(x )-2,由于对任意x ∈R ,f ’(x )>2, 所以G ′(x )=f ′(x )-2>0恒成立,所以G (x )=f (x )-2x -4是R 上的增函数, 又由于G (-1)=f (-1)-2×(-1)-4=0,所以G (x )=f (x )-2x -4>0, 即f (x )>2x +4的解集为(-1,+∞),故选B. 训练: 1.已知函数()y f x =的图象关于y 轴对称,且当(,0),()'()0x f x xf x ∈-∞+<成 立0.2 0.22 (2)a f =,log 3(log 3)b f ππ=,33log 9(log 9)c f =,则a,b,c 的大小关系是 ( ) A. b a c >> B.c a b >> C.c b a >> D.a c b >> 解:因为函数()y f x =关于y 轴对称,所以函数()y xf x =为奇函数.因为 [()]'()'()xf x f x xf x =+,所以当(,0)x ∈-∞时,[()]'()'()0xf x f x xf x =+<,函数()y xf x =单调递减,当(0,)x ∈+∞时,函数()y xf x =单调递减.因为 0.2122<<,0131og π<<,3192og =,所以0.23013219og og π<<<,所以b a c >>,选A. 2. 已知()f x 为R 上的可导函数,且x R ?∈,均有()()f x f x '>,则有 A .2013 (2013)(0)e f f -<,2013(2013)(0)f e f > B .2013 (2013)(0)e f f -<,2013(2013)(0)f e f < C .2013 (2013)(0)e f f ->,2013(2013)(0)f e f > D .2013 (2013)(0)e f f ->,2013(2013)(0)f e f < 解:构造函数() (),x f x g x e =则2()()()()()()()x x x x f x e e f x f x f x g x e e '''--'==, 因为,x ?∈R 均有()()f x f x '>,并且0x e >,所以()0g x '<,故函数() ()x f x g x e =在R 上单调递减,所以(2013)(0)(2013)(0)g g g g -><,,即 20132013 (2013)(2013) (0)(0)f f f f e e --><,, 也就是20132013(2013)(0)(2013)(0)e f f f e f -><,,故选D . 6. 已知函数))((R x x f ∈满足1)1(=f ,且)(x f 的导函数21)('< x f ,则2 1 2)(+ 导数小题中构造函数的技巧 函数与方程思想、转化与化归思想是高中数学思想中比较重要的两大思想,而构造函数的解题思路恰好是这两种思想的良好体现,尤其是在导数题型中,下面我就导数小题中构造函数的技巧和大家进行分享和交流。 (一)利用)(x f 进行抽象函数构造 1、利用)(x f 与x 构造;常用构造形式有x x f x xf )(), (;这类形式是对v u v u ,?型函数导数计算的推广及应用,我们对v u v u ,?的导函数观察可得知,v u ?导函数中 体现的是“+”法,v u 型导函数中体现的是“-”法,由此,我们可以猜测,当导函数形式出现的是“+”法形式时,优先考虑构造v u ?型,当导函数形式出现的是“-”法形式时,优先考虑构造v u ,我们根据得出的“优先”原则,看一看例1,例2. 【例1】)(x f 是定义在R 上的函数,当0 ???思路点拨:出现“-”形式,优先构造然后利用函数的单调性、奇偶性和数形结合求解即可.x x f x F )()(= x x f x xf )(),(是比较简单常见的)(x f 与x 之间的函数关系式,如果碰见复杂的,不易想的我们该如何处理,由此我们可以思考形如此类函数的一般形式.)()(x f x x F n =,)]()([)()()('11'x f x nf x x f x x f nx x F n n n +=+=--; n x x f x F )()(=,1'21'')()()()()(+--=-?=n n n n x x nf x xf x x f nx x x f x F ;结论: 出现)()('x xf x nf +形式,构造函数)()(x f x x F n =; 出现)()('x nf x xf -形式,构造函数n x x f x F )()(=.我们根据得出的结论去解决例3题 【例3】已知偶函数)0)((≠x x f 的导函数为)('x f ,且满足0)1(=-f ,当0>x 时,)()(2'x xf x f >,则使得0)(>x f 成立的x 的取值范围是___________???思路点拨:满足“)()('x nf x xf -”形式,优先构造然后利用函数的单调性、奇偶性和数形结合求解即可. n x x f x F )()(= 导数运算中的构造函数 1. 若()()0f x f x '+>,则可构造函数()()x F x e f x =?; 2. 若()()0f x f x '->,则可构造函数() ()x f x F x e = ; 3. ①若()2()0f x f x '+>,则可构造函数12()()x F x e f x =?; ②若()()0f x nf x '+>,则可构造函数1()()x n F x e f x =?,(*n N ∈). 4. ①若()2()0f x f x '->,则可构造函数12 ()()x f x F x e = ; ②若()()0f x nf x '->,则可构造函数1()()x n f x F x e = ,(*n N ∈). 5. ①若2()()0f x f x '+>,则可构造函数2()()x F x f x e =?; ②若()()0nf x f x '+>,则可构造函数()()nx F x f x e =?,(*n N ∈). 6. ①若2()()0f x f x '->,则可构造函数2() ()x f x F x e = ; ②若()()0nf x f x '->,则可构造函数() ()nx f x F x e =,(*n N ∈). 7. 若()()0f x x f x '+?>,则可构造函数()()F x x f x =?; 8. 若()()0f x x f x '-?>,则可构造函数() (),(0)f x F x x x = ≠; 9.①若2 2()()0x f x x f x '?+?>,则可构造函数2 ()()F x x f x =?; ②若2()()0f x x f x '?+?>,则可构造函数2 ()()F x x f x =?(注意x 的正负); ③若()()0n f x x f x '?+?>,则可构造函数()()n F x x f x =?(注意x 的正负,n 的奇偶); 10. 若()()0n f x x f x '?-?>,则可构造函数() ()n f x F x x = (注意x 的正负,n 的奇偶); 11. ① 若()cos ()sin 0f x x f x x '+>,则可构造函数()sin ()F x x f x =?; ②若()()tan 0f x f x x '+>,则可构造函数()sin ()F x x f x =?(注意x 的取值范围); 12. ①若()cos ()sin 0f x x f x x '->,则可构造函数() ()sin f x F x x =; ②若()()tan 0f x f x x '->,则可构造函数() ()sin f x F x x = (注意x 的取值范围); 13. ①若 () ln ()0f x x f x x '+?>,则可构造函数()ln ()F x x f x =?; ②若()ln ()0f x x x f x '+??>,则可构造函数()ln ()F x x f x =?; 2 合理构造函数解导数问题 从近几年的高考命题分析,高考对导数的考查常以函数为依托的小综合题, 考查函数、导数的基础知识和基本方法.近年的高考命题中的解答题将导数容和 传统容中有关不等式和函数的单调性、 方程根的分布、解析几何中的切线问题等 有机的结合在一起,设计综合试题。在容上日趋综合化,在解题方法上日趋多样 化?解决这类有关的问题,有时需要借助构造函数,以导数为工具构造函数是解导 数问题的基本方法,但是有时简单的构造函数对问题求解带来很大麻烦甚至是解 决不了问题的,那么怎样合理的构造函数就是问题的关键, 这里我们来一起探讨 一下这方面问题。 (3)方法一、变量分离直接构造函数 例 1:( 2009 年市高三第三次模拟试卷 22题) 已知函数 f x In ax 1 x 3 x 2 ax . f x 的极值点,数a 的值; 在1, 上增函数,数a 的取值围; 若a 1时, 方程f1 x 1 x 3 b 有实根,数b 的取值围。 x 解: (1)因为X 2 —是函数的一个极值点,所以 3 2 f ( ) 0,进而解得:a 0,经检验是 3 符合的,所以a 0. (2)显然f 成立,所以a 0且 a 2 3x 2 2x a,结合定义域知道 ax 1 0在x 1, 上恒 ax 1 a ax 1 0。同时3x 2 2x a 此函数是x -时递减,x 1时递增, 3 3 故此我们只需要保证f 1話 2 a 0,解得: 解:由于x 0,所以:b x lnx x2xl nx x2 2 2 g x In x 1 2x 3x g x - 2 6x x 6x 2 2x 1 x 1 7 时, x 0,所以g x 在0 1 7 x 亍上递增 1 .7」 1 . 7 当x 时,g x 0,所以g x 在x 上递减 6 6 1 <7 又g 1 0, g X 0 0, 0 X 0 6 当 0 x X 0 时,g x 0,所以g x 在0 x X 0上递减; 当 X 。 x 1 时,g x 0,所以x 。 x 1上递增; 当x 1 时,g x 0,所以g x 在x 1上递减; 又当 x 时,g x 7 . 2 3 2 , 1 g x xln x x x x In x x x x In x - 4 当x 0 时,In x - 0,则 g x 0,且 g 1 ,0. b 的取值围为 一阶导数草图 构造函数法在抽象不等式中的 巧妙应用 构造函数是解决抽象不等式的基本方法,根据题设的条件,并借助初等函数的导数公式和导数的基本运算法则,相应地构造出辅助函数. 通过进一步研究辅助函数的有关性质,给予巧妙的解答. 本文从一到高考试题出发,追根溯源,研究并揭示高考试题的本质. 1 小荷才露尖尖角 真题 设函数()f x '是奇函数()()f x x R ∈的导函数,(1)0f -=,当0x >时,()()0xf x f x '-<,则使得()0f x >成立的x 取值范围( ). A. (,1)(0,1)-∞- B. (1,0)(1,)-+∞ C. (,1)(1,0)-∞-- D. (0,1)(1,)+∞ 解析:设() ()f x F x x =, 则2 ()() '()xf x f x F x x '-= . 因为0x >时,()()0xf x f x '-<,所以'()0F x <, 即当0x >时,()F x 单调递减. 又因为()f x 为奇函数,且(1)0f -=,所以 () ()f x F x x =为偶函数,且(1)(1)0F F -==, 则当0x <时,()F x 单调递增. 当(,1)x ∈-∞-时,()0F x <,()0f x >. 当(0,1)x ∈时,()0F x <,()0f x >. 所以()0f x >成立的x 取值范围 (,1)(0,1)-∞- ,即答案为A.. 上述题为2015年课标全国Ⅱ选择题第12题,创新有难度,丰富有内涵. 此其题表面看上,不知道如何入手,解决问题. 因为这是一道没有具体函数表达式的不等式试题,且不等式中含有()f x '和 ()f x ,更是难上加难. 从试题的解析可以看出,巧 妙地构造出了函数()F x ,通过分析()F x 的单调性和奇偶性,解答问题. 解题突破口不易寻找,给人一种“旧时茅店社林边,路转溪桥忽见”的感觉. 对题的解析过程进行回顾,本题是如何构造出 () ()f x F x x = ,从而给出极其巧妙的解答. 为了寻求问题的本质,这里对以下例题进行分析. 2 千树万树梨花开 例 1 已知函数()f x 的图像关于y 轴对称,且当 (,0)x ∈-∞时,()()0f x x f x '+<成 立,若0.20.22(2)a f =?,log 3(log 3)b f ππ=?,33log 9(log 9)b f =?, 则,,a b c 的大小关系( ) A. b a c >> B. c a b >> C. c b a >> D. a b c >> 解析:设()()F x xf x =,则'( )()()F x f x x f x '=+. 因为0x <时,()()0f x xf x '+<,所以'()0F x <,则当0x <时,()F x 单调递减. 又因为函数()f x 的图像关于y 轴对称,所以()f x 为奇函数,当0x >时,()F x 单调递减. 又因为0.2 122<<,0log 31π<<,3log 92=, 则b a c >>,即答案为A. 例 2已知函数()f x 满足:()2()0f x f x '+>,那么系列不等式成立的是( ) A. (1)f > B. (0) (2)f f e < C. (1)(2)f > D. 2 (0)(4)f e f > 解析:设12 ()2()x F x e f x =, 则111 22 21'()2[()()][()2()]2 x x x F x e f x e f x e f x f x ''=+=+. 因为()2()0f x f x '+>,所以'()0F x >,则() F x 在定义域上单调递增,所以(1)(0)F F >, 则(1)f > ,即答案为A. 例 3 已知()f x 为定义在(,)-∞+∞上的可导函数,且()()f x f x '<对于x R ∈恒成立且e 为自然 对数的底,则( ) A. 2012 (1)(0),(2012)(0)f e f f e f >?>? B. 2012 (1)(0),(2012)(0)f e f f e f ? C. 2012 (1)(0),(2012)(0)f e f f e f >? 专题07 导数有关的构造函数方法 二.题型分析 1.构造多项式函数 2.构造三角函数型 3.构造x e 形式的函数 4.构造成积的形式 5.与ln x 有关的构造 6.构造成商的形式 7.对称问题 (一)构造多项式函数 例1.已知函数满足(1)1f =,且的导函数,则的解集为( ) A. B. C. D. 【答案】D 考点:函数的单调性与导数的关系. 【方法点晴】本题主要考查了函数的单调性与函数的导数之间的关系,其中解答中涉及到利用导数研究函数的单调性,利用导数研究函数的极值与最值等知识点的综合考查,着重考查了学生分析问题和解答问题的能力,以及转化与化归思想的应用,本题的解答中根据题设条件,构造新函数,利用新函数的性质是解答问题的关键,属于中档试题. 练习 1.设函数在上存在导函数,对于任意的实数,都有2 ()4()f x x f x =--,当 时,1 ()42 f x x + <'. 若(1)()42f m f m m +≤-++,则实数m 的取值范围是( ) A . B . C . D . 【答案】A ()()f x x R ∈()f x ()1'2f x <()1 22 x f x <+{}|x 1x <-{}|1x x >()F x ()f x R '()f x x (,0)x ∈-∞1[,)2-+∞3[,)2 -+∞[1,)-+∞[2,)-+∞ 【解析】∵22()2()20f x x f x x -+--=,设2 ()()2g x f x x =-,则()()0g x g x +-=,∴为奇函数,又1 ()()42 g x f x x '='-<- ,∴在上是减函数,从而在上是减函数, 又(1)()42f m f m m +≤-++等价于2 2 (1)2(1)()2()f m m f m m +-+≤---, 即(1)()g m g m +≤-,∴,解得. 考点:导数在函数单调性中的应用. 【思路点睛】因为 ,设 ,则 ,可得为奇函数,又 ,得在上是减函数,从而在上是减函数,在根据函 数的奇偶性和单调性可得 ,由此即可求出结果. 练习2. 设奇函数()f x 在R 上存在导数()f x ',且在()0,+∞上2 ()f x x '<,若 33 1(1)()(1)3f m f m m m ??--≥--? ?,则实数m 的取值范围为( ) A . B . C . D . 【答案】B 【方法点晴】本题主要考查了函数的奇偶性及其应用,其中解答中涉及到利用导数求函数的单调性、利用导数研究函数的极值、以及函数的奇偶性的判定等知识点的综合考查,着重考查了转化与化归的思想方法,以及学生的推理与运算能力,属于中档试题,解答中得出函数的奇函数和函数的单调性是解答的关键. 练习3. 设函数()f x 在R 上存在导数()f x ',,对任意,都有2 ()()f x f x x +-=,且()g x ()g x (,0)-∞R 1m m +≥-1 2 m ≥-() g x ()g x (,0)-∞R x R ∈(0,) x ∈+∞ 数学高考题型专题讲解28 ---导数中的构造函数 【方法综述】 函数与方程思想、转化与化归思想是高中数学思想中比较重要的两大思想,而构造函数的解题思路恰好是这两种思想的良好体现,尤其是在导数题型中.在导数小题中构造函数的常见结论:出现()()nf x xf x '+形式,构造函数()()F n x x f x =;出现()()xf x nf x '-形式,构造函数()() F n f x x x = ;出现()()f x nf x '+形式,构造函数()()F nx x e f x =;出现()()f x nf x '-形式,构造函数()() F nx f x x e = . 【解答策略】 类型一、利用()f x 进行抽象函数构造 1.利用()f x 与x (n x )构造 常用构造形式有()xf x , ()f x x ;这类形式是对u v ?,u v 型函数导数计算的推广及应用,我们对u v ?,u v 的导函数观察可得知,u v ?型导函数中体现的是“+”法,u v 型导函数中体现的是“-”法,由此,我们可以猜测,当导函数形式出现的是“+”法形式时,优先考虑构造u v ?型,当导函数形式出现的是“-”法形式时,优先考虑构造 u v . 例1.【2019届高三第二次全国大联考】设 是定义在上的可导偶函数,若当 时, ,则函数 的零点个数为 A .0 B .1 C .2 D .0或2 【答案】A 【解析】 设,因为函数为偶函数,所以也是上的偶函数,所以 .由已知,时,,可得当时,,故函数在上单调递减,由偶函数的性质可得函数在上单调递增.所以 ,所以方程,即无解,所以函数没有零点.故选A. 【指点迷津】设,当时,,可得当时,,故函数 在上单调递减,从而求出函数的零点的个数. 【举一反三】【新疆乌鲁木齐2019届高三第二次质量检测】的定义域是,其导函数为,若,且(其中是自然对数的底数),则 A.B. C.当时,取得极大值D.当时, 【答案】C 【解析】 设,则 则 又得 即,所以 即 , 由得,得,此时函数为增函数 由得,得,此时函数为减函数 则,即,则,故错误 ,即,则,故错误 当时,取得极小值 导数中的构造函数方法 一、 构造函数比较大小 例1. 对任意R x ∈,函数)(x f 的导数存在,若)()('x f x f >且0>a ,,则 )0()(f e a f a 与的大小关系为 解析: 令x e x f x g )()(=,则0)()()()()('2''>-=-=x x x x e x f x f e e x f e x f x g , 所以x e x f x g )()(=在R上为增函数, 因为0>a ,所以)0()(g a g >。 故)0()(f e a f a > 点评:此类问题,通常需要根据已知条件提供的与)(' x f 有关的不等式,结合需比较大小的两个表达式的特征构造函数,利用所构造函数的单调性进行大小比较。 二、 构造函数证明不等式 例2:设函数x b ax x g x x f + ==)(,ln )(,它们的图象在x 轴上的公共点处有公切线. 求证:当)()(,1x g x f x <>时 解析:因为x x f ln )(=与x 轴的公共点为(1,0),)()(x g x f 与的图象在x 轴上的公共点处有公切线.所以1,0)1(=-=b a g 即.故可得x x x g b a 2121)(,21,21-=-==所以 令x x x x g x f x h 2121ln )()()(+-=-=, 由02)1(21211)(12 2 2'<--=--=>x x x x x h x 知由 所以0)1()(,),1()(=<+∞h x h x h 即上是减函数在,所以)()(x g x f < 点评:在证明不等式时,通常根据要证明结论的特点合理的构造函数(不一定要把不等式右边的项全移到左边),将问题转化为证明新函数的最大值非正或最小值非负的问题来解决。 三、 构造函数求参数值 例3:已知函数x x x g x x x f 14)(,ln 8)(22+-=-=若方程m x g x f +=)()( 有唯一解,试求实数x 的值。 解析:原方程等价于.14ln 822 m x x x =--令,14ln 82)(2x x x x h --= 则原方程,)(m x h =因为0>x 且原方程有唯一解, I 导数小题中构造函数技巧 一、利用()f x 与x 进行抽象函数构造 (1)构造形式()x f x ?,()f x x 例1. ()f x 是定义在R 上的偶函数,当0x <时,()()0f x x f x '+?<,且(4)0f -=,则不等式()0xf x >的解集为 . 例2. ()f x 是定义在R 上的偶函数,且(1)0f =,当0x <时,()()0x f x f x '?->恒成立,则不等式()0f x >的解集为 . n x f x , () n f x x (2)构造形式() 例3. ()f x 是定义在R 上的偶函数,且满足(1)0f -=,当0x >时,2()()f x x f x '>?,则不等式()0f x >的解集为 . 例4.设()f x 是定义在R 上的奇函数,(2)0f -=,当0x <时,2(2)+(2)0x f x f x '?<,则不等式(2)0xf x <的解集为 . 二、利用()f x 与x e 进行抽象函数构造 构造形式()x f x e ?,()x f x e ,()nx f x e ?,()nx f x e 例5. ()f x 是定义在R 上函数,()()f x f x '<恒成立,则 A .22014(2)(0),(2014)(0)f e f f e f >> B. 22014(2)(0),(2014)(0)f e f f e f <> C. 22014(2)(0),(2014)(0)f e f f e f >< D. 22014(2)(0),(2014)(0)f e f f e f << 例6. 设()f x 是定义在R 上的函数,(0)1f =,()2()0f x f x '->,则不等式2()x f x e >的解集为 .导数选择题之构造函数法解不等式的一类题
导数中的构造函数
构造函数利用导数解决函数问题
导数中的构造函数(最全精编)学生版
导数运算中的构造函数
合理构造函数解导数问题
构造函数法在导数中的巧妙应用
导数有关的构造函数方法
数学高考题型专题讲解28---导数中的构造函数
导数中的构造函数方法
导数小题中构造函数技巧
