38、线面垂直判断与性质(教师版)

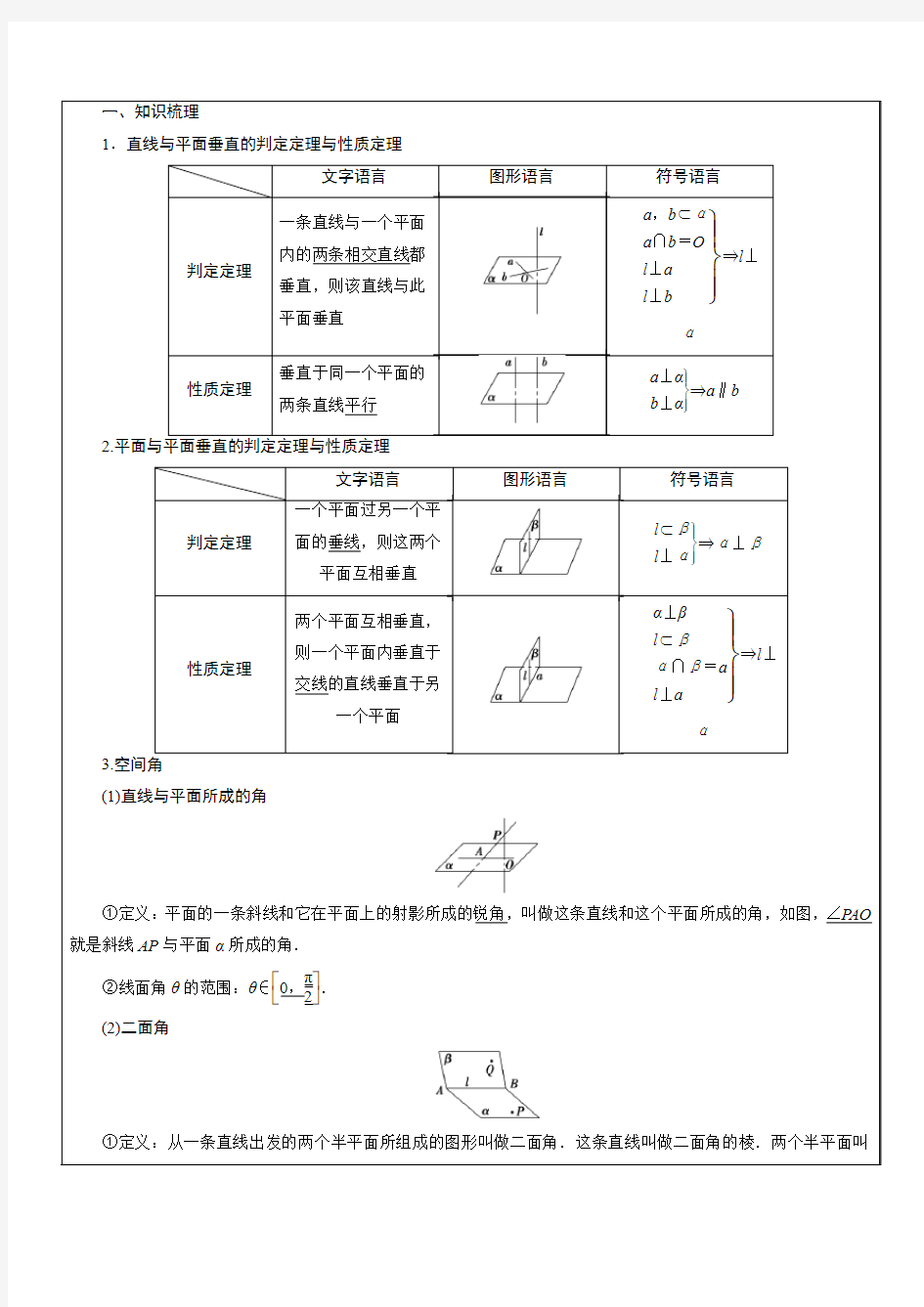
**教育ISO讲义直线、平面垂直的判定及性质思考：如何一条直线与一个平面不相交，该直线可能与平面垂直吗？如果一个平面与另一个平面不相交，这两个平面可能垂直吗？一、知识梳理1．直线与平面垂直的判定定理与性质定理文字语言 图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直⎭⎪⎬⎪⎫a ，b ⊂αa ∩b ＝Ol ⊥a l ⊥b⇒l ⊥α性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒a ∥b 2.平面与平面垂直的判定定理与性质定理文字语言 图形语言符号语言判定定理一个平面过另一个平面的垂线，则这两个平面互相垂直⎭⎪⎬⎪⎫l ⊂βl ⊥α⇒α⊥β性质定理两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl ⊂βα∩β＝al ⊥a⇒l ⊥α3.空间角(1)直线与平面所成的角①定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角，如图，∠P AO 就是斜线AP 与平面α所成的角．②线面角θ的范围：θ∈⎣⎡⎦⎤0，π2． (2)二面角①定义：从一条直线出发的两个半平面所组成的图形叫做二面角．这条直线叫做二面角的棱．两个半平面叫做二面角的面．如图的二面角，可记作：二面角α­l ­β或二面角P ­AB ­Q ．②二面角的平面角如图，过二面角α­l ­β的棱l 上一点O 在两个半平面内分别作BO ⊥l ，AO ⊥l ，则∠AOB 就叫做二面角α­l ­β的平面角．③二面角的范围设二面角的平面角为θ，则θ∈[0，π]． ④当θ＝π2时，二面角叫做直二面角．常用结论1．线线、线面、面面垂直间的转化2．两个重要定理 (1)三垂线定理在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直． (2)三垂线定理的逆定理在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直． 3．重要结论(1)若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．(2)若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法)． (3)垂直于同一条直线的两个平面平行．(4)一条直线垂直于两平行平面中的一个，则这一条直线与另一个平面也垂直．考点1 线面垂直的判定与性质(多维探究)【例1】如图所示，在四棱锥P ­ABCD 中，AB ⊥平面P AD ，AB ∥CD ，PD ＝AD ，E 是PB 的中点，F 是DC 上的点，且DF ＝12AB ，PH 为△P AD 中AD 边上的高．求证：(1)PH ⊥平面ABCD ； (2)EF ⊥平面P AB .【解析】(1)因为AB ⊥平面P AD ，PH ⊂平面P AD ，所以PH ⊥AB . 因为PH 为△P AD 中AD 边上的高，所以PH ⊥AD .因为AB ∩AD ＝A ，AB ⊂平面ABCD ，AD ⊂平面ABCD ，所以PH ⊥平面ABCD .(2)如图，取P A 的中点M ，连接MD ，ME .因为E 是PB 的中点，所以ME 綊12AB .又因为DF 綊12AB .所以ME 綊DF ，所以四边形MEFD 是平行四边形， 所以EF ∥MD .因为PD ＝AD ，所以MD ⊥P A . 因为AB ⊥平面P AD ，所以MD ⊥AB . 因为P A ∩AB ＝A ，所以MD ⊥平面P AB ， 所以EF ⊥平面P AB .【例2】如图，在三棱锥A ­BCD 中，AB ⊥AD ，BC ⊥BD ，平面ABD ⊥平面BCD ，点E ，F (E 与A ，D 不重合)分别在棱AD ，BD 上，且EF ⊥AD .求证：(1)EF ∥平面ABC ； (2)AD ⊥AC .【解析】(1)在平面ABD内，因为AB⊥AD，EF⊥AD，所以EF∥AB.又因为EF⊄平面ABC，AB⊂平面ABC，所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，BC⊂平面BCD，BC⊥BD，所以BC⊥平面ABD.因为AD⊂平面ABD，所以BC⊥AD.又AB⊥AD，BC∩AB＝B，AB⊂平面ABC，BC⊂平面ABC，所以AD⊥平面ABC.又因为AC⊂平面ABC，所以AD⊥AC.(1)判定线面垂直的四种方法(2)判定线线垂直的四种方法【变式一】如图所示，在四棱锥P ­ABCD 中，P A ⊥底面ABCD ，AB ⊥AD ，AC ⊥CD ，∠ABC ＝60°，P A ＝AB ＝BC ，E 是PC 的中点．证明：(1)CD ⊥AE ； (2)PD ⊥平面ABE .【解析】(1)在四棱锥P ­ABCD 中， 因为P A ⊥底面ABCD ，CD ⊂平面ABCD ， 所以P A ⊥CD .因为AC ⊥CD ，P A ∩AC ＝A ， 所以CD ⊥平面P AC .而AE ⊂平面P AC ，所以CD ⊥AE .(2)由P A ＝AB ＝BC ，∠ABC ＝60°，可得AC ＝P A . 因为E 是PC 的中点，所以AE ⊥PC . 由(1)知AE ⊥CD ，且PC ∩CD ＝C ， 所以AE ⊥平面PCD . 而PD ⊂平面PCD ， 所以AE ⊥PD .因为P A ⊥底面ABCD ，所以P A ⊥AB . 又因为AB ⊥AD 且P A ∩AD ＝A ， 所以AB ⊥平面P AD ，而PD ⊂平面P AD ， 所以AB ⊥PD .又因为AB ∩AE ＝A ， 所以PD ⊥平面ABE .【变式二】如图，在三棱锥P ­ABC 中，平面PAB ⊥平面ABC ，AB ＝6，BC ＝23，AC ＝26，D 为线段AB 上的点，且AD ＝2DB ，PD ⊥AC .(1)求证：PD ⊥平面ABC ；(2)若∠PAB ＝π4，求点B 到平面PAC 的距离．【解析】：(1)连接CD，据题知AD＝4，BD＝2，AC2＋BC2＝AB2，∴∠ACB＝90°，∴cos∠ABC＝236＝33，∴CD2＝22＋(23)2－2×2×23cos∠ABC＝8，∴CD＝22，∴CD2＋AD2＝AC2，则CD⊥AB.∵平面PAB⊥平面ABC，∴CD⊥平面PAB，∴CD⊥PD，∵PD⊥AC，AC∩CD＝C，∴PD⊥平面ABC.(2)由(1)得PD⊥AB，∵∠PAB＝π4，∴PD＝AD＝4，PA＝42，在Rt△PCD中，PC＝PD2＋CD2＝26，∴△PAC是等腰三角形，∴可求得S△PAC＝8 2. 设点B到平面PAC的距离为d，由V B­PAC＝V P­ABC，得13S△PAC×d＝13S△ABC×PD，∴d＝S△ABC×PDS△PAC＝3.故点B到平面PAC的距离为3.考点2 面面垂直的判定与性质【例1】如图，四棱锥P ­ABCD 中，AB ⊥AC ，AB ⊥P A ，AB ∥CD ，AB ＝2CD ，E ，F ，G ，M ，N 分别为PB ，AB ，BC ，PD ，PC 的中点．(1)求证：CE ∥平面P AD ； (2)求证：平面EFG ⊥平面EMN .【解析】(1)法一：取P A 的中点H ，连接EH ，DH .又E 为PB 的中点， 所以EH 綊12AB .又CD 綊12AB ，所以EH 綊CD .所以四边形DCEH 是平行四边形， 所以CE ∥DH .又DH ⊂平面P AD ，CE ⊄平面P AD . 所以CE ∥平面P AD .法二：连接CF .因为F 为AB 的中点，所以AF ＝12AB .又CD ＝12AB ，所以AF ＝CD .又AF∥CD，所以四边形AFCD为平行四边形．因此CF∥AD.又CF⊄平面P AD，AD⊂平面P AD，所以CF∥平面P AD.因为E，F分别为PB，AB的中点，所以EF∥P A.又EF⊄平面P AD，P A⊂平面P AD，所以EF∥平面P AD.又因为CF∩EF＝F.故平面CEF∥平面P AD.又因为CE⊂平面CEF，所以CE∥平面P AD.(2)因为E，F分别为PB，AB的中点，所以EF∥P A，又AB⊥P A，所以AB⊥EF.同理可得AB⊥FG.又EF∩FG＝F，EF⊂平面EFG，FG⊂平面EFG，因此AB⊥平面EFG.又M，N分别为PD，PC的中点，所以MN∥CD.又AB∥CD，所以MN∥AB，所以MN⊥平面EFG.又MN⊂平面EMN，所以平面EFG⊥平面EMN.【例2】如图，在四棱锥E­ABCD中，△EAD为等边三角形，底面ABCD为等腰梯形，满足AB∥CD，AD＝DC＝12AB，且AE⊥BD.(1)证明：平面EBD⊥平面EAD；(2)若△EAD的面积为3，求点C到平面EBD的距离．【解析】(1)证明：如图，取AB的中点M，连接DM，则由题意可知四边形BCDM为平行四边形，∴DM＝CB＝AD＝12AB，即点D在以线段AB为直径的圆上，∴BD⊥AD，又AE⊥BD，且AE∩AD＝A，∴BD⊥平面EAD.∵BD ⊂平面EBD ，∴平面EBD ⊥平面EAD. (2)∵BD ⊥平面EAD ，且BD ⊂平面ABCD ， ∴平面ABCD ⊥平面EAD. ∵等边△EAD 的面积为3， ∴AD ＝AE ＝ED ＝2，取AD 的中点O ，连接EO ，则EO ⊥AD ，EO ＝3， ∵平面EAD ⊥平面ABCD ，平面EAD ∩平面ABCD ＝AD ， ∴EO ⊥平面ABCD.由(1)知△ABD ，△EBD 都是直角三角形， ∴BD ＝AB 2－AD 2＝23， S △EBD ＝12ED ·BD ＝23，设点C 到平面EBD 的距离为h ，由V C ­EBD ＝V E ­BCD ，得13S △EBD ·h ＝13S △BCD ·EO ，又S △BCD ＝12BC ·CDsin 120°＝3，∴h ＝32.∴点C 到平面EBD 的距离为32.【变式一】如图，在四棱锥P ­ABCD 中，底面ABCD 为矩形，平面P AD ⊥平面ABCD ，P A ⊥PD ，P A ＝PD ，E ，F 分别为AD ，PB 的中点．(1)求证：PE ⊥BC ；(2)求证：平面P AB ⊥平面PCD ； (3)求证：EF ∥平面PCD .【解析】：(1)因为P A ＝PD ，E 为AD 的中点， 所以PE ⊥AD .因为底面ABCD 为矩形，所以BC ∥AD . 所以PE ⊥BC .(2)因为底面ABCD 为矩形，所以AB ⊥AD .又因为平面P AD ⊥平面ABCD ，所以AB ⊥平面P AD .所以AB ⊥PD .又因为P A ⊥PD ，所以PD ⊥平面P AB .所以平面P AB ⊥平面PCD .(3)取PC 的中点G ，连接FG ，DG .因为F ，G 分别为PB ，PC 的中点， 所以FG ∥BC ，FG ＝12BC .因为四边形ABCD 为矩形，且E 为AD 的中点， 所以DE ∥BC ，DE ＝12BC .所以DE ∥FG ，DE ＝FG .所以四边形DEFG 为平行四边形． 所以EF ∥DG .又因为EF ⊄平面PCD ，DG ⊂平面PCD ， 所以EF ∥平面PCD .【变式二】在如图所示的几何体中，四边形ABCD 是正方形，MA ⊥平面ABCD ，PD ∥MA ，E ，G ，F 分别为MB ，PB ，PC 的中点．(1)求证：平面EFG ∥平面PMA ； (2)求证：平面EFG ⊥平面PDC .【解析】 (1)∵E ，G ，F 分别为MB ，PB ，PC 的中点， ∴EG ∥PM ，GF ∥BC . 又∵四边形ABCD 是正方形， ∴BC ∥AD ，∴GF ∥AD .∵EG ，GF 在平面PMA 外，PM ，AD 在平面PMA 内， ∴EG ∥平面PMA ，GF ∥平面PMA . 又∵EG ，GF 都在平面EFG 内且相交， ∴平面EFG ∥平面PMA .(2)由已知MA ⊥平面ABCD ，PD ∥MA ， ∴PD ⊥平面ABCD .又BC ⊂平面ABCD ，∴PD ⊥BC .∵四边形ABCD为正方形，∴BC⊥DC.又PD∩DC＝D，∴BC⊥平面PDC.由(1)知GF∥BC，∴GF⊥平面PDC.又GF⊂平面EFG，∴平面EFG⊥平面PDC.考点3 垂直关系中的探索性问题【例1】如图，在三棱柱ABC­A1B1C1中，侧棱AA1⊥底面ABC，M为棱AC的中点．AB＝BC，AC＝2，AA1＝ 2.(1)求证：B1C∥平面A1BM；(2)求证：AC1⊥平面A1BM；(3)在棱BB1上是否存在点N，使得平面AC1N⊥平面AA1C1C？如果存在，求此时BNBB1的值；如果不存在，请说明理由．【解析】：证明（1）连接AB1与A1B，两线交于点O，连接OM.在△B1AC中，因为M，O分别为AC，AB1的中点，所以OM∥B1C，又因为OM⊂平面A1BM，B1C⊄平面A1BM，所以B1C∥平面A1BM.(2)证明：因为侧棱AA1⊥底面ABC，BM⊂平面ABC，所以AA1⊥BM，又因为M为棱AC的中点，AB＝BC，所以BM⊥AC.因为AA1∩AC＝A，AA1，AC⊂平面ACC1A1，所以BM⊥平面ACC1A1，所以BM⊥AC1.因为AC＝2，所以AM＝1.又因为AA1＝2，所以在Rt△ACC1和Rt△A1AM中，tan ∠AC 1C ＝tan ∠A 1MA ＝2， 所以∠AC 1C ＝∠A 1MA ，即∠AC 1C ＋∠C 1AC ＝∠A 1MA ＋∠C 1AC ＝90°， 所以A 1M ⊥AC 1.因为BM ∩A 1M ＝M ，BM ，A 1M ⊂平面A 1BM ， 所以AC 1⊥平面A 1BM . (3)当点N 为BB 1的中点，即BN BB 1＝12时， 平面AC 1N ⊥平面AA 1C 1C . 证明如下：设AC 1的中点为D ，连接DM ，DN .因为D ，M 分别为AC 1，AC 的中点， 所以DM ∥CC 1，且DM ＝12CC 1.又因为N 为BB 1的中点，所以DM ∥BN ，且DM ＝BN ， 所以四边形BNDM 为平行四边形， 所以BM ∥DN ，因为BM ⊥平面ACC 1A 1，所以DN ⊥平面AA 1C 1C . 又因为DN ⊂平面AC 1N ， 所以平面AC 1N ⊥平面AA 1C 1C .[例2] 如图，在四棱锥P ­ABCD 中，PC ⊥平面ABCD ，AB ∥DC ，DC ⊥AC .(1)求证：DC ⊥平面P AC . (2)求证：平面P AB ⊥平面P AC .(3)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得P A ∥平面CEF ？说明理由． 【解析】 (1)证明：因为PC ⊥平面ABCD ，所以PC ⊥DC . 又因为DC ⊥AC ，且PC ∩AC ＝C ， 所以DC ⊥平面P AC .(2)证明：因为AB ∥DC ，DC ⊥AC ，所以AB ⊥AC . 因为PC ⊥平面ABCD ，所以PC ⊥AB . 又因为PC ∩AC ＝C ，所以AB ⊥平面P AC . 又AB ⊂平面P AB ，所以平面P AB ⊥平面P AC .(3)棱PB上存在点F，使得P A∥平面CEF.理由如下：取PB的中点F，连接EF，CE，CF.因为E为AB的中点，所以EF∥P A.又因为P A⊄平面CEF，且EF⊂平面CEF，所以P A∥平面CEF.(1)对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论则否定假设．(2)对于探索性问题用向量法比较容易入手．一般先假设存在，设出空间点的坐标，转化为代数方程是否有解的问题，若有解且满足题意则存在，若有解但不满足题意或无解则不存在．【变式一】如图所示，平面ABCD⊥平面BCE，四边形ABCD为矩形，BC＝CE，点F为CE的中点．(1)证明：AE∥平面BDF；(2)点M为CD上任意一点，在线段AE上是否存在点P，使得PM⊥BE?若存在，确定点P的位置，并加以证明；若不存在，请说明理由．【解析】(1)证明：连接AC交BD于点O，连接OF.因为四边形ABCD是矩形，所以O为AC的中点．又F为EC的中点，所以OF∥AE.又OF⊂平面BDF，AE⊄平面BDF，所以AE∥平面BDF.(2)当点P为AE的中点时，有PM⊥BE，证明如下：取BE的中点H，连接DP，PH，CH.因为P为AE的中点，H为BE的中点，所以PH∥AB.又AB∥CD，所以PH∥CD，所以P，H，C，D四点共面．因为平面ABCD⊥平面BCE，且平面ABCD∩平面BCE＝BC，CD⊥BC，CD⊂平面ABCD，所以CD⊥平面BCE.又BE⊂平面BCE，所以CD⊥BE，因为BC＝CE，且H为BE的中点，所以CH⊥BE.又CH∩CD＝C，且CH，CD⊂平面DPHC，所以BE⊥平面DPHC.又PM⊂平面DPHC，所以PM⊥BE.考点4 平行与垂直关系中的翻折问题【例1】如图①，在等腰直角三角形ABC中，∠A＝90°，BC＝6，D，E分别是AC，AB上的点，CD＝BE ＝2，O为BC的中点．将△ADE沿DE折起，得到如图②所示的四棱锥A′－BCDE，其中A′O＝ 3.(1)证明：A′O⊥平面BCDE；(2)求二面角A′－CD－B的平面角的余弦值．【解析】(1)证明：在题图①中，易得OC＝3，AC＝32，AD＝2 2.连接OD，OE，在△OCD中，由余弦定理可得OD＝OC2＋CD2－2OC·CD cos 45 °＝ 5.由翻折不变性可知A′D＝22，所以A′O2＋OD2＝A′D2，所以A′O⊥OD，同理可证A′O⊥OE，又OD∩OE＝O，所以A′O⊥平面BCDE.(2)过O 作OH ⊥CD 交CD 的延长线于H ，连接A ′H ，因为A ′O ⊥平面BCDE ，所以A ′H ⊥CD ，所以∠A ′HO 为二面角A ′－CD －B 的平面角．结合题图①可知，H 为AC 的中点，故OH ＝322，从而A ′H ＝OH 2＋OA ′2＝302，所以cos ∠A ′HO ＝OHA ′H ＝155，所以二面角A ′－CD －B 的平面角的余弦值为155.折叠问题的关键有二：①画好两个图——折叠前的平面图和折叠后的立体图；②分析好两个关系——折叠前后哪些位置关系和数量关系发生了变化，哪些没有改变．一般地，在同一半平面内的几何元素之间的关系是不变的．涉及两个半平面内的几何元素之间的关系是要变化的．分别位于两个半平面内但垂直于折叠棱的直线翻折后仍然垂直于折叠棱．[例2] 如图，高为1的等腰梯形ABCD 中，AM ＝CD ＝13AB ＝1，M 为AB 的三等分点．现将△AMD 沿MD折起，使平面AMD ⊥平面MBCD ，连接AB ，AC .(1)在AB 边上是否存在点P ，使AD ∥平面MPC?(2)当点P 为AB 边的中点时，求点B 到平面MPC 的距离．【解析】 (1)当AP ＝13AB 时，有AD ∥平面MPC .理由如下：连接BD 交MC 于点N ，连接NP .在梯形MBCD 中，DC ∥MB ，DN NB ＝DC MB ＝12，∵△ADB 中，AP PB ＝12，∴AD ∥PN .∵AD ⊄平面MPC ，PN ⊂平面MPC ，∴AD ∥平面MPC .(2)∵平面AMD ⊥平面MBCD ，平面AMD ∩平面MBCD ＝DM ， 平面AMD 中AM ⊥DM ，∴AM ⊥平面MBCD . ∴V P ­MBC ＝13×S △MBC ×AM 2＝13×12×2×1×12＝16.在△MPC 中，MP ＝12AB ＝52，MC ＝2，又PC ＝⎝⎛⎭⎫122＋12＝52，∴S △MPC ＝12×2×⎝⎛⎭⎫522－⎝⎛⎭⎫222＝64.∴点B 到平面MPC 的距离为d ＝3V P ­MBC S △MPC ＝3×1664＝63.【变式一】如图所示，在矩形ABCD 中，AB ＝3，BC ＝4，E ，F 分别在线段BC ，AD 上，EF ∥AB ，将矩形ABEF 沿EF 折起，记折起后的矩形为MNEF ，且平面MNEF ⊥平面ECDF .(1)求证：NC ∥平面MFD ； (2)若EC ＝3，求证：ND ⊥FC ； (3)求四面体N ­EFD 体积的最大值．【解析】：(1)证明：∵平行四边形MNEF 和EFDC 都是矩形，∴MN ∥EF ，EF ∥CD ，MN ＝EF ＝CD ，∴MN ∥CD .∴四边形MNCD 是平行四边形．∴NC ∥MD . ∵NC ⊄平面MFD ，MD ⊂平面MFD ， ∴NC ∥平面MFD .(2)证明：连接ED ，交FC 于点O ，如图所示．∵平面MNEF ⊥平面ECDF ，且NE ⊥EF ，平面MNEF ∩平面ECDF ＝EF ，NE ⊂平面MNEF ，∴NE ⊥平面ECDF .∵FC ⊂平面ECDF ，∴FC ⊥NE .∵EC ＝CD ，∴四边形ECDF 为正方形，∴FC ⊥ED . 又∵ED ∩NE ＝E ，ED ，NE ⊂平面NED ，∴FC ⊥平面NED . ∵ND ⊂平面NED ，∴ND ⊥FC .(3)设NE ＝x ，则FD ＝EC ＝4－x ，其中0<x <4，由(2)得NE ⊥平面FEC ，∴四面体N ­EFD 的体积为V N ­FED ＝13S △EFD ·NE ＝12x (4－x )．∴V N ­FED ≤12⎣⎡⎦⎤x ＋(4－x )22＝2， 当且仅当x ＝4－x ，即x ＝2时，四面体N ­EFD 的体积最大，最大值为2.【变式二】如图，平面五边形ABCDE 中，AB ∥CE ，且AE ＝2，∠AEC ＝60°，CD ＝ED ＝7，cos ∠EDC ＝57.将△CDE 沿CE 折起，使点D 到P 的位置，且AP ＝3，得到四棱锥P ­ABCE . (1)求证：AP ⊥平面ABCE ；(2)记平面P AB 与平面PCE 相交于直线l ，求证：AB ∥l .【解析】：(1)在△CDE 中，∵CD ＝ED ＝7，cos ∠EDC ＝57，由余弦定理得CE ＝2.连接AC (图略)，∵AE ＝2，∠AEC ＝60°，∴AC ＝2.又AP ＝3，∴在△P AE 中，P A 2＋AE 2＝PE 2，即AP ⊥AE .同理，AP ⊥AC .而AC ⊂平面ABCE ，AE ⊂平面ABCE ，AC ∩AE ＝A ，故AP ⊥平面ABCE .(2)∵AB ∥CE ，且CE ⊂平面PCE ，AB ⊄平面PCE ，∴AB ∥平面PCE .又平面P AB ∩平面PCE ＝l ，∴AB ∥l .[基础题组练]1．(2020·辽宁大连模拟)已知直线l 和平面α，β，且l ⊂α，则“l ⊥β”是“α⊥β”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】选A.【解析】：由面面垂直的判定定理可得，若l ⊂α，l ⊥β，则α⊥β，充分性成立；若l ⊂α，α⊥β，则l 与β平行或相交或垂直，必要性不成立．所以若l ⊂α，则“l ⊥β”是“α⊥β”的充分不必要条件，故选A.2．(2020·河北唐山模拟)如图，在以下四个正方体中，直线AB 与平面CDE 垂直的是( )A ．①②B ．②④C ．①③D ．②③【答案】选B.【解析】：对于①，易证AB与CE所成角为45°，则直线AB与平面CDE不垂直；对于②，易证AB⊥CE，AB⊥ED，且CE∩ED＝E，则AB⊥平面CDE；对于③，易证AB与CE所成角为60°，则直线AB与平面CDE 不垂直；对于④，易证ED⊥平面ABC，则ED⊥AB，同理EC⊥AB，可得AB⊥平面CDE.故选B.3.(2020·黑龙江鹤岗模拟)如图，在三棱锥V－ABC中，VO⊥平面ABC，O∈CD，VA＝VB，AD＝BD，则下列结论中不一定成立的是()A．AC＝BCB．AB⊥VCC．VC⊥VDD．S△VCD·AB＝S△ABC·VO【答案】选C.【解析】：因为VO⊥平面ABC，AB⊂平面ABC，所以VO⊥AB.因为VA＝VB，AD＝BD，所以VD⊥AB.又因为VO∩VD＝V，所以AB⊥平面VCD.又因为CD⊂平面VCD，所以AB⊥CD.又因为AD＝BD，所以AC＝BC，故A正确．又因为VC⊂平面VCD，所以AB⊥VC，故B正确；因为S△VCD＝12VO·CD，S△ABC＝12AB·CD，所以S△VCD·AB＝S△ABC·VO，故D正确．由题中条件无法判断VC⊥VD.故选C.4.如图，在斜三棱柱ABC­A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在()A．直线AB上B．直线BC上C．直线AC上D．△ABC内部【答案】选A.【解析】：由AC⊥AB，AC⊥BC1，得AC⊥平面ABC1.因为AC⊂平面ABC，所以平面ABC1⊥平面ABC.所以C1在平面ABC上的射影H必在两平面的交线AB上．5.如图，在正四面体P­ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论不成立的是()A．BC∥平面PDFB．DF⊥平面P AEC．平面PDF⊥平面P AED．平面PDE⊥平面ABC【答案】选D.【解析】：因为BC∥DF，DF⊂平面PDF，BC⊄平面PDF，所以BC∥平面PDF，故选项A正确；在正四面体中，AE⊥BC，PE⊥BC，AE∩PE＝E，且AE，PE⊂平面P AE，所以BC⊥平面P AE，因为DF∥BC，所以DF⊥平面P AE，又DF⊂平面PDF，从而平面PDF⊥平面P AE.因此选项B，C均正确．6.如图，在△ABC中，∠ACB＝90°，AB＝8，∠ABC＝60°，PC⊥平面ABC，PC＝4，M是边AB上的一个动点，则PM的最小值为________．【答案】27【解析】：作CH⊥AB于H，连接PH.因为PC⊥平面ABC，所以PH⊥AB，PH为PM的最小值，等于27.7.如图所示，在四棱锥P­ABCD中，P A⊥底面ABCD，且底面各边都相等，M是边PC上的一动点，当点M 满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)【答案】DM⊥PC(或BM⊥PC)【解析】：连接AC，BD，则AC⊥BD，因为P A⊥底面ABCD，所以P A⊥BD.又P A∩AC＝A，所以BD⊥平面P AC，所以BD⊥PC.所以当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD.而PC⊂平面PCD，所以平面MBD⊥平面PCD.8.如图，P A⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC，其中正确结论的序号是________．【答案】①②④【解析】：①AE⊂平面P AC，BC⊥AC，BC⊥P A⇒AE⊥BC，故①正确；②AE⊥PC，AE⊥BC，PB⊂平面PBC ⇒AE⊥PB，AF⊥PB，EF⊂平面AEF⇒EF⊥PB，故②正确；③若AF⊥BC⇒AF⊥平面PBC，则AF∥AE与已知矛盾，故③错误；由①可知④正确．9.如图，在多面体ABCDPE中，四边形ABCD和CDPE都是直角梯形，AB∥DC，PE∥DC，AD⊥DC，PD ⊥平面ABCD，AB＝PD＝DA＝2PE，CD＝3PE，F是CE的中点．(1)求证：BF∥平面ADP；(2)已知O是BD的中点，求证：BD⊥平面AOF.【解析】：(1)如图，取PD 的中点为G ，连接FG ，AG ，因为F 是CE 的中点，所以FG 是梯形CDPE 的中位线， 因为CD ＝3PE ，所以FG ＝2PE ， FG ∥CD ，因为CD ∥AB ，AB ＝2PE ， 所以AB ∥FG ，AB ＝FG ， 即四边形ABFG 是平行四边形， 所以BF ∥AG ，又BF ⊄平面ADP ，AG ⊂平面ADP ， 所以BF ∥平面ADP .(2)延长AO 交CD 于点M ，连接BM ，FM ，因为BA ⊥AD ，CD ⊥DA ，AB ＝AD ，O 为BD 的中点， 所以ABMD 是正方形，则BD ⊥AM ，MD ＝2PE . 所以FM ∥PD ，因为PD ⊥平面ABCD ， 所以FM ⊥平面ABCD ，所以FM ⊥BD ， 因为AM ∩FM ＝M ，所以BD ⊥平面AMF ， 所以BD ⊥平面AOF .10．(一题多解)如图1，在等腰梯形PDCB 中，PB ∥DC ，PB ＝3，DC ＝1，∠DPB ＝45°，DA ⊥PB 于点A ，将△P AD 沿AD 折起，构成如图2所示的四棱锥P ­ABCD ，点M 在棱PB 上，且PM ＝12MB .(1)求证：PD ∥平面MAC ；(2)若平面P AD ⊥平面ABCD ，求点A 到平面PBC 的距离．【解析】：(1)证明：在四棱锥P ­ABCD 中，连接BD 交AC 于点N ，连接MN ，依题意知AB ∥CD ，所以△ABN ∽△CDN ， 所以BN ND ＝BACD ＝2，因为PM ＝12MB ，所以BN ND ＝BMMP＝2，所以在△BPD 中，MN ∥PD ， 又PD ⊄平面MAC ，MN ⊂平面MAC . 所以PD ∥平面MAC .(2)法一：因为平面P AD ⊥平面ABCD ，且两平面相交于AD ，P A ⊥AD ，P A ⊂平面P AD ， 所以P A ⊥平面ABCD ，所以V P ­ABC ＝13S △ABC ·P A ＝13×⎝⎛⎭⎫12×2×1×1＝13. 因为AB ＝2，AC ＝AD 2＋CD 2＝2，所以PB ＝P A 2＋AB 2＝5，PC ＝P A 2＋AC 2＝3，BC ＝AD 2＋（AB －CD ）2＝2， 所以PB 2＝PC 2＋BC 2，故∠PCB ＝90°， 记点A 到平面PBC 的距离为h ，所以V A ­PBC ＝13S △PBC ·h ＝13×⎝⎛⎭⎫12×3×2h ＝66h . 因为V P ­ABC ＝V A ­PBC ， 所以13＝66h ，解得h ＝63.故点A 到平面PBC 的距离为63. 法二：因为平面P AD ⊥平面ABCD ，且两平面相交于AD ，P A ⊥AD ，P A ⊂平面P AD ， 所以P A ⊥平面ABCD ， 因为BC ⊂平面ABCD ， 所以P A ⊥BC ，因为AB ＝2，AC ＝AD 2＋CD 2＝2， BC ＝AD 2＋（AB －CD ）2＝2，所以∠ACB ＝90°，即BC ⊥AC ， 又P A ∩AC ＝A ，P A ，AC ⊂平面P AC ， 所以BC ⊥平面P AC ，过点A 作AE ⊥PC 于点E ，则BC ⊥AE ， 因为PC ∩BC ＝C ，PC ，BC ⊂平面PBC ， 所以AE ⊥平面PBC ，所以点A 到平面PBC 的距离为AE ＝P A ·AC PC ＝1×23＝63.[综合题组练]1.如图，边长为a 的等边三角形ABC 的中线AF 与中位线DE 交于点G ，已知△A ′DE 是△ADE 绕DE 旋转过程中的一个图形，则下列命题中正确的是( )①动点A ′在平面ABC 上的射影在线段AF 上； ②BC ∥平面A ′DE ；③三棱锥A ′­FED 的体积有最大值． A ．① B ．①② C ．①②③ D ．②③【答案】选C.【解析】：①中由已知可得平面A ′FG ⊥平面ABC ， 所以点A ′在平面ABC 上的射影在线段AF 上．②BC ∥DE ，根据线面平行的判定定理可得BC ∥平面A ′DE .③当平面A ′DE ⊥平面ABC 时，三棱锥A ′­FED 的体积达到最大，故选C.2.如图，梯形ABCD 中，AD ∥BC ，∠ABC ＝90°，AD ∶BC ∶AB ＝2∶3∶4，E ，F 分别是AB ，CD 的中点，将四边形ADFE 沿直线EF 进行翻折，给出下列四个结论：①DF ⊥BC ；②BD ⊥FC ；③平面BDF ⊥平面BCF ；④平面DCF ⊥平面BCF ，则上述结论可能正确的是( )A ．①③B ．②③C ．②④D ．③④【答案】选B.【解析】：对于①，因为BC ∥AD ，AD 与DF 相交但不垂直，所以BC 与DF 不垂直，则①不成立；对于②，设点D 在平面BCF 上的射影为点P ，当BP ⊥CF 时就有BD ⊥FC ，而AD ∶BC ∶AB ＝2∶3∶4可使条件满足，所以②正确；对于③，当点D 在平面BCF 上的射影P 落在BF 上时，DP ⊂平面BDF ，从而平面BDF ⊥平面BCF ，所以③正确；对于④，因为点D 在平面BCF 上的射影不可能在FC 上，所以④不成立．3．在矩形ABCD 中，AB ＜BC ，现将△ABD 沿矩形的对角线BD 所在的直线进行翻折，在翻折的过程中，给出下列结论：①存在某个位置，使得直线AC 与直线BD 垂直； ②存在某个位置，使得直线AB 与直线CD 垂直； ③存在某个位置，使得直线AD 与直线BC 垂直．其中正确结论的序号是________．(写出所有正确结论的序号) 【答案】②【解析】：①假设AC 与BD 垂直，过点A 作AE ⊥BD 于点E ，连接CE .则⎭⎪⎬⎪⎫AE ⊥BD BD ⊥AC ⇒BD ⊥平面AEC ⇒BD ⊥CE ，而在平面BCD 中，EC 与BD 不垂直，故假设不成立，①错．②假设AB ⊥CD ，因为AB ⊥AD ，所以AB ⊥平面ACD ，所以AB ⊥AC ，由AB ＜BC 可知，存在这样的等腰直角三角形，使AB ⊥CD ，故假设成立，②正确．③假设AD ⊥BC ，因为DC ⊥BC ，所以BC ⊥平面ADC ，所以BC ⊥AC ，即△ABC 为直角三角形，且AB 为斜边，而AB ＜BC ，故矛盾，假设不成立，③错．综上，填②.4．如图，直三棱柱ABC ­A 1B 1C 1中，侧棱长为2，AC ＝BC ＝1，∠ACB ＝90°，D 是A 1B 1的中点，F 是BB 1上的动点，AB 1，DF 交于点E .要使AB 1⊥平面C 1DF ，则线段B 1F 的长为________．【答案】12【解析】：设B 1F ＝x ，因为AB 1⊥平面C 1DF ，DF ⊂平面C 1DF ，所以AB 1⊥DF . 由已知可以得A 1B 1＝2，设Rt △AA 1B 1斜边AB 1上的高为h ，则DE ＝12h ，又2×2＝h ×22＋（2）2， 所以h ＝233，DE ＝33.在Rt △DB 1E 中，B 1E ＝（22）2－（33）2＝66. 由面积相等得66× x 2＋（22）2＝22x ，得x ＝12.即线段B 1F 的长为12. 5．(2020·河南郑州第二次质量预测)如图，四棱锥P －ABCD 中，底面ABCD 是边长为2的菱形，∠BAD ＝π3，△P AD 是等边三角形，F 为AD 的中点，PD ⊥BF .(1)求证：AD ⊥PB ；(2)若E 在线段BC 上，且EC ＝14BC ，能否在棱PC 上找到一点G ，使平面DEG ⊥平面ABCD ？若存在，求出三棱锥D －CEG 的体积；若不存在，请说明理由．【解析】：(1)证明：连接PF ，因为△P AD 是等边三角形，F 是AD 的中点，所以PF ⊥AD . 因为底面ABCD 是菱形，∠BAD ＝π3，所以BF ⊥AD .又PF ∩BF ＝F ，所以AD ⊥平面BFP ，又PB ⊂平面BFP ， 所以AD ⊥PB .(2)能在棱PC 上找到一点G ，使平面DEG ⊥平面ABCD .由(1)知AD ⊥BF ，因为PD ⊥BF ，AD ∩PD ＝D ，所以BF ⊥平面P AD . 又BF ⊂平面ABCD ，所以平面ABCD ⊥平面P AD ，又平面ABCD ∩平面P AD ＝AD ，且PF ⊥AD ，所以PF ⊥平面ABCD .连接CF 交DE 于点H ，过H 作HG ∥PF 交PC 于点G ，所以GH ⊥平面ABCD . 又GH ⊂平面DEG ，所以平面DEG ⊥平面ABCD . 因为AD ∥BC ，所以△DFH ∽△ECH ，所以CH HF ＝CE DF ＝12，所以CG GP ＝CH HF ＝12，所以GH ＝13PF ＝33，所以V D －CEG ＝V G －CDE ＝13S △CDE ·GH ＝13×12DC ·CE ·sin π3·GH ＝112.6．如图(1)，在Rt △ABC 中，∠ABC ＝90°，D 为AC 的中点，AE ⊥BD 于点E (不同于点D )，延长AE 交BC于点F，将△ABD沿BD折起，得到三棱锥A1­BCD，如图(2)所示．(1)若M是FC的中点，求证：直线DM∥平面A1EF；(2)求证：BD⊥A1F；(3)若平面A1BD⊥平面BCD，试判断直线A1B与直线CD能否垂直？并说明理由．【解析】：(1)证明：因为D，M分别为AC，FC的中点，所以DM∥EF，又EF⊂平面A1EF，DM⊄平面A1EF，所以DM∥平面A1EF.(2)证明：因为A1E⊥BD，EF⊥BD且A1E∩EF＝E，所以BD⊥平面A1EF.又A1F⊂平面A1EF，所以BD⊥A1F.(3)直线A1B与直线CD不能垂直．理由如下：因为平面A1BD⊥平面BCD，平面A1BD∩平面BCD＝BD，EF⊥BD，EF⊂平面BCD，所以EF⊥平面A1BD.因为A1B⊂平面A1BD，所以A1B⊥EF，又因为EF∥DM，所以A1B⊥DM.假设A1B⊥CD，因为CD∩DM＝D，所以A1B⊥平面BCD，所以A1B⊥BD，这与∠A1BD为锐角矛盾，所以直线A1B与直线CD不能垂直．一、线面垂直的判定及性质？。