矩阵的求导运算

dF
dF
^x f2
ar 3F
如
^X 2Z dF
dF
Sn
dF ]
dfi2
dx tj
dx t j
dF
..,dp
■其中产二
%
<■
■
■1
:
dF
%
仏T1
目
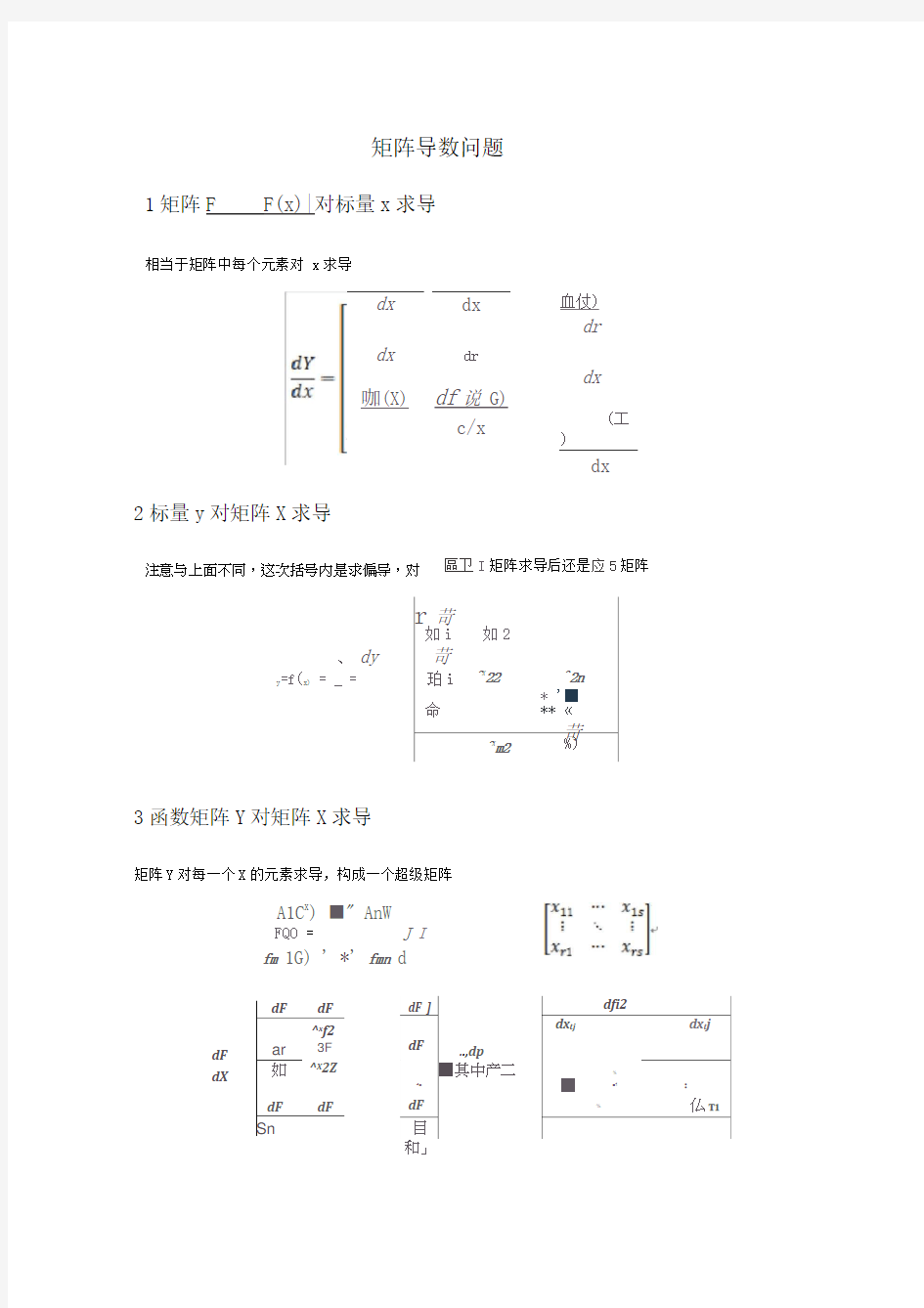
矩阵导数问题
1矩阵F
F(x)|对标量x 求导
相当于矩阵中每个元素对 x 求导
dx dx
咖(X) dx
dr
df 说 G)
c/x
血仗)
dr dx
(工)
dx
2标量y 对矩阵X 求导
3函数矩阵Y 对矩阵X 求导
矩阵Y 对每一个X 的元素求导,构成一个超级矩阵
A1C X
) ■" AnW
FQO =
J I
fm 1G) ' *' fmn d
r 苛
如i
如2
、 dy
苛
y =f(x) = _ =
珀i ^X 22
^2n
* '■
命
** ?
苛
^X
m2
%)
區卫I 矩阵求导后还是应5矩阵
注意与上面不同,这次括号内是求偏导,对
dF dX
3.1重要结论:假设—是一个向量:
A
l,驚"f 和
dx r
dx
4向量积对列向量上求导运算法则
注意与标量有点不同.假设丘0都是列向童
4.1重要结论:
dx dx
dx
d($T Ax) d(x T )
土
d(x r A T )-
才
=- Ax +' ■ x = (yl + ax dx ax
重要结论;*■'
d^X T Xu) dX
d[(_Xu - v)T
(Xu - v)]
dX
葺中空也―
dx
d{ki fl
u+ J
z a
Ji + ■■ +T i a
iz + Y :a
3J +
■ - 4
-
■■- ^a iti + J 3a
2n + —
佃祖U 幻1屯+ *” + 工」电 a+ 丫皿让壬 + T ;a i;Y : + -*+l h tt n ,X 1- ■ - ■?■『2/%+r 诃3九 4 “?+Th%丿」眉&
2^!!^! + a 21x 2 t ■"+ a nl x n + \ a 13x 3 -1 …+ y 功窃
a>i^i ++ 2a 22x 2 + a 32x 2 + …+ ◎曲心 + Q 22JC 2 + a 22x 2 + …+ a 2n x n &nl 场r + ^n2^2 牛…+ °nE-Q*n-1 +
+ 血2n 丫2 + "*" + 2。讯“芯i
dx
dx
dX
Hi 7
-(A 十 A r )x^
矩阵求导的一些公式
在网上看到有人贴了如下求导公式: Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 于是把以前学过的矩阵求导部分整理一下: 1. 矩阵Y对标量x求导: 相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了 Y = [y(ij)] --> dY/dx = [dy(ji)/dx] 2. 标量y对列向量X求导: 注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量 y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)' 3. 行向量Y'对列向量X求导: 注意1×M向量对N×1向量求导后是N×M矩阵。 将Y的每一列对X求偏导,将各列构成一个矩阵。 重要结论: dX'/dX = I d(AX)'/dX = A' 4. 列向量Y对行向量X’求导: 转化为行向量Y’对列向量X的导数,然后转置。 注意M×1向量对1×N向量求导结果为M×N矩阵。 dY/dX' = (dY'/dX)' 5. 向量积对列向量X求导运算法则: 注意与标量求导有点不同。 d(UV')/dX = (dU/dX)V' + U(dV'/dX) d(U'V)/dX = (dU'/dX)V + (dV'/dX)U' 重要结论: d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A
d(AX)/dX' = (d(X'A')/dX)' = (A')' = A d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X 6. 矩阵Y对列向量X求导: 将Y对X的每一个分量求偏导,构成一个超向量。 注意该向量的每一个元素都是一个矩阵。 7. 矩阵积对列向量求导法则: d(uV)/dX = (du/dX)V + u(dV/dX) d(UV)/dX = (dU/dX)V + U(dV/dX) 重要结论: d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A 8. 标量y对矩阵X的导数: 类似标量y对列向量X的导数, 把y对每个X的元素求偏导,不用转置。 dy/dX = [ Dy/Dx(ij) ] 重要结论: y = U'XV = ΣΣu(i)x(ij)v(j) 于是dy/dX = = UV' y = U'X'XU 则dy/dX = 2XUU' y = (XU-V)'(XU-V) 则dy/dX = d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' + 0 = 2(XU-V)U' 9. 矩阵Y对矩阵X的导数: 将Y的每个元素对X求导,然后排在一起形成超级矩阵。
矩阵求导
矩阵求导 在网上看到有人贴了如下求导公式: Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 于是把以前学过的矩阵求导部分整理一下: 1. 矩阵Y对标量x求导: 相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了 Y = [y(ij)] --> dY/dx = [dy(ji)/dx] 2. 标量y对列向量X求导: 注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)' 3. 行向量Y'对列向量X求导: 注意1×M向量对N×1向量求导后是N×M矩阵。 将Y的每一列对X求偏导,将各列构成一个矩阵。 重要结论: dX'/dX = I d(AX)'/dX = A' 4. 列向量Y对行向量X’求导: 转化为行向量Y’对列向量X的导数,然后转置。 注意M×1向量对1×N向量求导结果为M×N矩阵。 dY/dX' = (dY'/dX)' 5. 向量积对列向量X求导运算法则:
注意与标量求导有点不同。 d(UV')/dX = (dU/dX)V' + U(dV'/dX) d(U'V)/dX = (dU'/dX)V + (dV'/dX)U' 重要结论: d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A d(AX)/dX' = (d(X'A')/dX)' = (A')' = A d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X 6. 矩阵Y对列向量X求导: 将Y对X的每一个分量求偏导,构成一个超向量。注意该向量的每一个元素都是一个矩阵。 7. 矩阵积对列向量求导法则: d(uV)/dX = (du/dX)V + u(dV/dX) d(UV)/dX = (dU/dX)V + U(dV/dX) 重要结论: d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A 8. 标量y对矩阵X的导数: 类似标量y对列向量X的导数, 把y对每个X的元素求偏导,不用转置。 dy/dX = [ Dy/Dx(ij) ] 重要结论: y = U'XV = ΣΣu(i)x(ij)v(j) 于是dy/dX = [u(i)v(j)] = UV' y = U'X'XU 则dy/dX = 2XUU'
矩阵求导
1. 矩阵Y对标量x求导: 相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了 Y = [y(ij)] --> dY/dx = [dy(ji)/dx] 2. 标量y对列向量X求导: 注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量 y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)T 3. 行向量Y T对列向量X求导: 注意1×M向量对N×1向量求导后是N×M矩阵。 将Y的每一列对X求偏导,将各列构成一个矩阵。 重要结论: dX T/dX = I d(AX)T/dX = A T 4. 列向量Y对行向量X T求导: 转化为行向量Y T对列向量X的导数,然后转置。 注意M×1向量对1×N向量求导结果为M×N矩阵。 dY/dX T = (dY T/dX)T 5. 向量积对列向量X求导运算法则: 注意与标量求导有点不同。 d(UV T)/dX = (dU/dX)V T + U(dV T/dX) d(U T V)/dX = (dU T/dX)V + (dV T/dX)U 重要结论: d(X T A)/dX = (dX T/dX)A + (dA/dX)X T = IA + 0X T = A d(AX)/dX T = (d(X T A T)/dX)T = (A T)T = A d(X T AX)/dX = (dX T/dX)AX + (d(AX)T/dX)X = AX + A T X 6. 矩阵Y对列向量X求导: 将Y对X的每一个分量求偏导,构成一个超向量。 注意该向量的每一个元素都是一个矩阵。 7. 矩阵积对列向量求导法则: d(uV)/dX = (du/dX)V + u(dV/dX) d(UV)/dX = (dU/dX)V + U(dV/dX) 重要结论:
矩阵求导
矩阵函数求导 首先要区分两个概念:矩阵函数和函数矩阵 (1) 函数矩阵,简单地说就是多个一般函数的阵列,包括单变量和多变量函数。 函数矩阵的求导和积分是作用在各个矩阵元素上,没有更多的规则。 单变量函数矩阵的微分与积分 考虑实变量t 的实函数矩阵 ()()()ij m n X t x t ×=,所有分量函数()ij x t 定义域相同。 定义函数矩阵的微分与积分 0()(),()().t t ij ij t t d d X t x t X d x d dx dx ττττ?????????==????????????∫∫ 函数矩阵的微分有以下性质: (1) ()()()()()d d d X t Y t X t t dt dt dt +=+; (2) ()()()()()()()d dX t dY t X t Y t t X t dt dt dt =+; 特殊情形 (a ) 若K 是常数矩阵,则()()()d d KX t K X t dt dt =; (b ) 若()X t 是方阵,则2()()()()()d dX t dX t X t X t X t dt dt dt =+; (3) () 111()()()()d dX t X t X t X t dt dt =----; (4) 对任意的方阵A 和时变量t ,恒有At At At d e Ae e A dt ==; (5) 若AB BA =,则A B B A A B e e e e e +==。如果,A B 可交换,则许多三角不等 式可以推广到矩阵上。如sin(),sin(2)A b A +等。 参考文献:余鄂西,矩阵论,高等教育出版社。
常用求导公式矩阵公式数学建模
基本求导公式、矩阵公式、数学建模 1.基本求导公式 ⑴ 0)(='C (C 为常数)⑵ 1 )(-='n n nx x ;一般地,1 )(-='αααx x 。 特别地:1)(='x ,x x 2)(2 =',2 1 )1(x x - =',x x 21)(='。 ⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a x x 。 ⑷ x x 1)(ln = ';一般地,)1,0( ln 1)(log ≠>='a a a x x a 。 2.求导法则 ⑴ 四则运算法则 设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,) ()()()()())()(( 2 ≠'-'='x g x g x g x f x g x f x g x f ,特别21() ()()()g x g x g x ''=-。 3.微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''== 4、 常用的不定积分公式 (1) ?????+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 4 3,2,),1( 114 3 32 21αααα ; (2) C x dx x +=?||ln 1; C e dx e x x +=?; )1,0( ln ≠>+=?a a C a a dx a x x ; (3)? ?=dx x f k dx x kf )()((k 为常数) 5、定积分 ()()|()()b b a a f x dx F x F b F a ==-? ⑴ ??? +=+b a b a b a dx x g k dx x f k dx x g k x f k )()()]()([2121 ⑵ 分部积分法 设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则
常用的基本求导公式
1.基本求导公式 ⑴ 0)(='C (C 为常数)⑵ 1 )(-='n n nx x ;一般地,1 )(-='αααx x 。 特别地:1)(='x ,x x 2)(2 =',21 )1(x x - =',x x 21)(='。 ⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a x x 。 ⑷ x x 1)(ln = ';一般地,)1,0( ln 1 )(log ≠>='a a a x x a 。 2.求导法则 ⑴ 四则运算法则 设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,) ()()()()())()(( 2≠'-'='x g x g x g x f x g x f x g x f ,特别21() ()()()g x g x g x ''=-。 3.微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''== 4、 常用的不定积分公式 (1) ?????+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 4 3,2,),1( 114 3 32 21αααα ; (2) C x dx x +=?||ln 1; C e dx e x x +=?; )1,0( ln ≠>+=?a a C a a dx a x x ; (3)? ?=dx x f k dx x kf )()((k 为常数) 5、定积分 ()()|()()b b a a f x dx F x F b F a ==-? ⑴ ???+=+b a b a b a dx x g k dx x f k dx x g k x f k )()()]()([2121 ⑵ 分部积分法 设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则 ??-=b a b a b a x du x v x v x u x dv x u )()() ()()()( 6、线性代数
矩阵函数求导
矩阵函数求导 符号说明 ?d/dx (y) 是一个向量,其第(i) 个元素是dy(i)/dx ?d/d x (y) 是一个向量,其第(i) 个元素是dy/dx(i) ?d/d x (y T) 是一个矩阵,其第(i,j) 个元素是dy(j)/dx(i) ?d/dx (Y) 是一个矩阵,其第(i,j) 个元素是dy(i,j)/dx ?d/d X (y) 是一个矩阵,其第(i,j) 个元素是dy/dx(i,j) 注意 Hermitian 转置不能应用,因为复共轭不可解析,x,y 是向量,X,Y 是矩阵,x,y 是标量。 在下面的表达中 A, B, C 是不依赖于 X 的矩阵,a,b 是不依赖于x 的向量,线性积 ?d/dx (AYB) =A * d/dx (Y) * B o d/dx (Ay) =A * d/dx (y) ?d/d x (x T A) =A o d/d x (x T) =I o d/d x (x T a) = d/d x (a T x) = a ?d/d X (a T Xb) = ab T o d/d X (a T Xa) = d/d X (a T X T a) = aa T ?d/d X (a T X T b) = ba T ?d/dx (YZ) =Y * d/dx (Z) + d/dx (Y) * Z 二次积 ?d/d x (Ax+b)T C(D x+e) = A T C(Dx+e) + D T C T(Ax+b)
o d/d x (x T Cx) = (C+C T)x [C: symmetric]: d/d x (x T Cx) = 2Cx d/d x (x T x) = 2x o d/d x (Ax+b)T (D x+e) = A T (Dx+e) + D T (Ax+b) d/d x (Ax+b)T (A x+b) = 2A T (Ax+b) o [C: symmetric]: d/d x (Ax+b)T C(A x+b) = 2A T C(Ax+b) ?d/d X (a T X T Xb) = X(ab T + ba T) o d/d X (a T X T Xa) = 2Xaa T ?d/d X (a T X T CXb) = C T Xab T + CXba T o d/d X (a T X T CXa) = (C + C T)Xaa T o [C:Symmetric] d/d X (a T X T CXa) = 2CXaa T ?d/d X ((Xa+b)T C(Xa+b)) = (C+C T)(Xa+b)a T 三次积 ?d/d x (x T Axx T) = (A+A T)xx T+x T AxI 逆 ?d/dx (Y-1) = -Y-1d/dx (Y)Y-1 迹 Note: matrix dimensions must result in an n*n argument for tr(). ?d/d X (tr(X)) = I ?d/d X (tr(X k)) =k(X k-1)T ?d/d X (tr(AX k)) = SUM r=0:k-1(X r AX k-r-1)T ?d/d X (tr(AX-1B)) = -(X-1BAX-1)T o d/d X (tr(AX-1)) =d/d X (tr(X-1A)) = -X-T A T X-T ?d/d X (tr(A T XB T)) = d/d X (tr(BX T A)) = AB
矩阵求导公式
转载]矩阵求导公式【转】 (2011-11-15 11:03:34) 转载▼ 标签: 转载 原文地址:矩阵求导公式【转】作者:三寅 今天推导公式,发现居然有对矩阵的求导,狂汗--完全不会。不过还好网上有人总结了。吼吼,赶紧搬过来收藏备份。 基本公式: Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 1. 矩阵Y对标量x求导: 相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了 Y = [y(ij)] --> dY/dx = [dy(ji)/dx] 2. 标量y对列向量X求导: 注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量 y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)' 3. 行向量Y'对列向量X求导: 注意1×M向量对N×1向量求导后是N×M矩阵。 将Y的每一列对X求偏导,将各列构成一个矩阵。 重要结论: dX'/dX = I d(AX)'/dX = A' 4. 列向量Y对行向量X’求导: 转化为行向量Y’对列向量X的导数,然后转置。 注意M×1向量对1×N向量求导结果为M×N矩阵。 dY/dX' = (dY'/dX)' 5. 向量积对列向量X求导运算法则: 注意与标量求导有点不同。 d(UV')/dX = (dU/dX)V' + U(dV'/dX)
d(U'V)/dX = (dU'/dX)V + (dV'/dX)U' 重要结论: d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A d(AX)/dX' = (d(X'A')/dX)' = (A')' = A d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X 6. 矩阵Y对列向量X求导: 将Y对X的每一个分量求偏导,构成一个超向量。 注意该向量的每一个元素都是一个矩阵。 7. 矩阵积对列向量求导法则: d(uV)/dX = (du/dX)V + u(dV/dX) d(UV)/dX = (dU/dX)V + U(dV/dX) 重要结论: d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A 8. 标量y对矩阵X的导数: 类似标量y对列向量X的导数, 把y对每个X的元素求偏导,不用转置。 dy/dX = [ Dy/Dx(ij) ] 重要结论: y = U'XV = ΣΣu(i)x(ij)v(j) 于是dy/dX = [u(i)v(j)] = UV' y = U'X'XU 则dy/dX = 2XUU' y = (XU-V)'(XU-V) 则dy/dX = d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' + 0 = 2(XU-V)U' 9. 矩阵Y对矩阵X的导数: 将Y的每个元素对X求导,然后排在一起形成超级矩阵。 10.乘积的导数 d(f*g)/dx=(df'/dx)g+(dg/dx)f' 结论 d(x'Ax)=(d(x'')/dx)Ax+(d(Ax)/dx)(x'')=Ax+A'x (注意:''是表示两次转置)
基本函数求导公式
基本初等函数求导公式 (1) 0)(='C (2) 1 )(-='μμμx x (3) x x cos )(sin =' (4) x x sin )(cos -=' (5) x x 2 sec )(tan =' (6) x x 2csc )(cot -=' (7) x x x tan sec )(sec =' (8) x x x cot csc )(csc -=' (9) a a a x x ln )(=' (10) (e )e x x '= (11) a x x a ln 1 )(log = ' (12) x x 1)(ln = ', (13) 211)(arcsin x x -= ' (14) 211)(arccos x x -- =' (15) 21(arctan )1x x '= + (16) 21(arccot )1x x '=- + 函数的和、差、积、商的求导法则 设)(x u u =,)(x v v =都可导,则 (1) v u v u '±'='±)( (2) u C Cu '=')((C 是常数) (3) v u v u uv '+'=')( (4) 2v v u v u v u '-'=' ??? ?? 反函数求导法则 若函数)(y x ?=在某区间y I 可导、单调且0)(≠'y ?,则它的反函数)(x f y =在对应区 间 x I 也可导,且 )(1)(y x f ?'= ' 或 dy dx dx dy 1= 复合函数求导法则
设)(u f y =,而)(x u ?=且)(u f 及)(x ?都可导,则复合函数)]([x f y ?=的导数为 dy dy du dx du dx = 或()()y f u x ?'''= 2. 双曲函数与反双曲函数的导数. 双曲函数与反双曲函数都是初等函数,它们的导数都可以用前面的求导公式和求导法则求出. 可以推出下表列出的公式: 在第二章第六节中我们已经提出了隐函数的概念,并且指出了不经过显化直接由方程 ),(y x f =0 (1) 求它所确定的隐函数的方法。现在介绍隐函数存在定理,并根据多元复合函数的求导法来导出隐函数的导数公式. 隐函数存在定理 1 设函数),(y x F 在点 ),(00y x P 的某一邻域具有连续的偏导数,且 0),(00=y x F ,, 0),(00≠y x F y ,则方程),(y x F =0在点),(00y x 的某一邻域恒能唯一确定一个单值连续且具有连续导数的函数)(x f y =,它满足条件)(00 x f y =,并有 y x F F dx dy -= (2) 公式(2)就是隐函数的求导公式 这个定理我们不证。现仅就公式(2)作如下推导。 将方程(1)所确定的函数)(x f y =代入,得恒等式
矩阵导数
矩阵导数 1. 矩阵Y=F(x )对标量x 求导 相当于每个元素求导数 11112221221 2()()()()() ()() ()()n n m m m n d f x d f x d f x d x d x d x d f x d f x d f x d d x d x d x d x d f x d f x d f x d x d x d x ?? ? ?? ? ?? ??=? ?? ? ?? ? ?? ? Y 2. 标量y 对列向量x 求导 注意与上面不同,这次括号内是求偏导,对m×1向量求导后还是m×1向量 1 2 ()m f x f d y x y f d f x ??? ????????? ??=→=?????????????? x x 3. 行向量y T 对列向量x 求导 注意1×n 向量对m×1向量求导后是m×n 矩阵。 将y 的每一列对x 求偏导,将各列构成一个矩阵。 12111 1222212()()()()()()()()()n n T n m m m f x f x f x x x x f x f x f x d x x x d f x f x f x x x x ????? ? ????? ? ????? ? ????=????? ? ??????????? ? y x 重要结论: ()T T T d d d d ==x I x A x A x
4. 列向量y 对行向量x T 求导 转化为行向量y T 对列向量x 的导数,然后转置。 注意m×1向量对1×n 向量求导结果为m×n 矩阵。 12111 1222212()() ()()()()()()()T m T m T T m n n n f x f x f x x x x f x f x f x d d x x x d d f x f x f x x x x ????? ? ????? ? ????? ?? ? ????== ????? ??? ? ??????????? ? y y x x 重要结论: ()T T d d d d ==x I x A x A x 5. 向量积对列向量x 求导运算法则 注意与标量求导有点不同。 ()()()T T T d d d d d d = ?+ ?u v u v v u x x x 重要结论: ()()()2() ()() ()T T T T T T T T d d d d d d d d d d d d = ?+ ?== ?+ ?=+x x x x x x x x x x x A x x x A A x x A A x x x x 6. 矩阵Y 对列向量x 求导 将Y 对x 的每一个分量求偏导,构成一个超向量。 注意该向量的每一个元素都是一个矩阵。
矩阵的求导运算
dF dF ^x f2 ar 3F 如 ^X 2Z dF dF Sn dF ] dfi2 dx tj dx t j dF ..,dp ■其中产二 % <■ ■ ■1 : dF % 仏T1 目 矩阵导数问题 1矩阵F F(x)|对标量x 求导 相当于矩阵中每个元素对 x 求导 dx dx 咖(X) dx dr df 说 G) c/x 血仗) dr dx (工) dx 2标量y 对矩阵X 求导 3函数矩阵Y 对矩阵X 求导 矩阵Y 对每一个X 的元素求导,构成一个超级矩阵 A1C X ) ■" AnW FQO = J I fm 1G) ' *' fmn d r 苛 如i 如2 、 dy 苛 y =f(x) = _ = 珀i ^X 22 ^2n * '■ 命 ** ? 苛 ^X m2 %) 區卫I 矩阵求导后还是应5矩阵 注意与上面不同,这次括号内是求偏导,对 dF dX
3.1重要结论:假设—是一个向量: A l,驚"f 和 dx r dx 4向量积对列向量上求导运算法则 注意与标量有点不同.假设丘0都是列向童 4.1重要结论: dx dx dx d($T Ax) d(x T ) 土 d(x r A T )- 才 =- Ax +' ■ x = (yl + ax dx ax 重要结论;*■' d^X T Xu) dX d[(_Xu - v)T (Xu - v)] dX 葺中空也― dx d{ki fl u+ J z a Ji + ■■ +T i a iz + Y :a 3J + ■ - 4 - ■■- ^a iti + J 3a 2n + — 佃祖U 幻1屯+ *” + 工」电 a+ 丫皿让壬 + T ;a i;Y : + -*+l h tt n ,X 1- ■ - ■?■『2/%+r 诃3九 4 “?+Th%丿」眉& 2^!!^! + a 21x 2 t ■"+ a nl x n + \ a 13x 3 -1 …+ y 功窃 a>i^i ++ 2a 22x 2 + a 32x 2 + …+ ◎曲心 + Q 22JC 2 + a 22x 2 + …+ a 2n x n &nl 场r + ^n2^2 牛…+ °nE-Q*n-1 + + 血2n 丫2 + "*" + 2。讯“芯i dx dx dX Hi 7 -(A 十 A r )x^
常用的求导积分公式及解法
常用的求导积分公式及解法 1.基本求导公式 ⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。 特别地:1)(='x ,x x 2)(2=',2 1)1(x x - =',x x 21 )(='。 ⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a x x 。 ⑷ x x 1)(ln = ';一般地,)1,0( ln 1 )(log ≠>= 'a a a x x a 。 2.求导法则 ⑴ 四则运算法则 设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,) ()()()()())()(( 2 ≠'-'='x g x g x g x f x g x f x g x f ,特别21() ()()()g x g x g x ''=-。 3.微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''== 4、 常用的不定积分公式 (1) ?????+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 4 3,2,),1( 1143 32 21αααα ; (2) C x dx x +=?||ln 1; C e dx e x x +=?; )1,0( ln ≠>+= ?a a C a a dx a x x ; (3)? ?=dx x f k dx x kf )()((k 为常数) 5、定积分 ()()|()()b b a a f x dx F x F b F a ==-? ⑴ ??? +=+b a b a b a dx x g k dx x f k dx x g k x f k )()()]()([2121 ⑵ 分部积分法 设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则
常用求导公式、矩阵公式、MATLAB软件
常用求导公式、矩阵公式、MATLAB 软件 1.基本求导公式 ⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。 特别地:1)(='x ,x x 2)(2=',2 1)1(x x - =',x x 21 )(='。 ⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a x x 。 ⑷ x x 1)(ln = ';一般地,)1,0( ln 1 )(log ≠>= 'a a a x x a 。 2.求导法则 ⑴ 四则运算法则 设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,) ()()()()())()(( 2 ≠'-'='x g x g x g x f x g x f x g x f ,特别21() ()()()g x g x g x ''=-。 3.微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''== 4、 常用的不定积分公式 (1) ?????+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 4 3,2,),1( 1143 32 21αααα ; (2) C x dx x +=?||ln 1; C e dx e x x +=?; )1,0( ln ≠>+= ?a a C a a dx a x x ; (3)? ?=dx x f k dx x kf )()((k 为常数) 5、定积分 ()()|()()b b a a f x dx F x F b F a ==-? ⑴ ??? +=+b a b a b a dx x g k dx x f k dx x g k x f k )()()]()([2121 ⑵ 分部积分法 设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则
矩阵求导的一些公式讲解学习
精品文档 在网上看到有人贴了如下求导公式: Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 于是把以前学过的矩阵求导部分整理一下: 1. 矩阵Y 对标量x 求导: 相当于每个元素求导数后转置一下,注意M k N矩阵求导后变成NXM 了 Y = [y(ij)] --> dY/dx = [dy(ji)/dx] 2. 标量y 对列向量X 求导: N k 1 向注意与上面不同,这次括号内是求偏导,不转置,对N k1 向量求导后还是 量 y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)' 3. 行向量Y'对列向量X求导: 注意1k M 向量对N k1 向量求导后是N k M 矩阵。 将Y 的每一列对X 求偏导,将各列构成一个矩阵。 重要结论: dX'/dX = I d(AX)'/dX = A' 4. 列向量Y对行向量X'求导: 转化为行向量Y'对列向量X的导数,然后转置。 注意M k 1 向量对1k N 向量求导结果为M k N 矩阵。 dY/dX' = (dY'/dX)' 5. 向量积对列向量X求导运算法则: 注意与标量求导有点不同。 d(UV')/dX = (dU/dX)V' + U(dV'/dX) d(U'V)/dX = (dU'/dX)V + (dV'/dX)U 重要结论: 精品文档
d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A d(AX)/dX' = (d(X'A')/dX)' = (A')' = A d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X 6. 矩阵Y 对列向量X 求导: 将Y 对X 的每一个分量求偏导,构成一个超向量。注意该向量的每一个元素都 是一个矩阵。 7. 矩阵积对列向量求导法则: d(uV)/dX = (du/dX)V + u(dV/dX) d(UV)/dX = (dU/dX)V + U(dV/dX) 重要结论: d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A 8. 标量y 对矩阵X 的导数: 类似标量y 对列向量X 的导数,把y 对每个X 的元素求偏导,不用转置。 dy/dX = [ Dy/Dx(ij) ] 重要结论: y = U'XV = 2 2 u(i)x(ij)v(j于是dy/dX = = UV' y = U'X'XU 则dy/dX = 2XUU' y = (XU-V)'(XU-V) 则dy/dX = d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' + 0 = 2(XU-V)U' 精品文档 9. 矩阵Y 对矩阵X 的导数: 将Y 的每个元素对X 求导,然后排在一起形成超级矩阵。
一般常用求导公式
四、基本求导法则与导数公式 1. 基本初等函数的导数公式和求导法则 基本初等函数的求导公式和上述求导法则,在初等函数的基本运算中起着重要的作用,我们必须熟练的掌握它,为了便于查阅,我们把这些导数公式和求导法则归纳如下: 基本初等函数求导公式 (1) 0)(=' C (2) 1 )(-='μμμx x (3) x x cos )(sin =' (4) x x sin )(cos -=' (5) x x 2 sec )(tan =' (6) x x 2 csc )(cot -=' (7) x x x tan sec )(sec =' (8) x x x cot csc )(csc -=' (9) a a a x x ln )(=' (10) (e )e x x '= (11) a x x a ln 1 )(log = ' (12) x x 1)(ln = ', (13) 2 11)(arcsin x x -= ' (14) 2 11)(arccos x x -- =' (15) 2 1(arctan )1x x '= + (16) 2 1(arc cot )1x x '=- + 函数的和、差、积、商的求导法则 设 )(x u u =,)(x v v =都可导,则 (1) v u v u ' ±'='±)( (2) u C Cu ' =')((C 是常数) (3) v u v u uv ' +'=')( (4) 2 v v u v u v u '-'=' ??? ?? 反函数求导法则 若函数)(y x ?=在某区间 y I 内可导、单调且 0)(≠'y ?,则它的反函数 )(x f y =在对应区间 x I 内也可导,且
矩阵求导的一些公式[指南]
矩阵求导的一些公式[指南] 在网上看到有人贴了如下求导公式: Y = A * X --> DY/DX = A' Y = X * A --> DY/DX = A Y = A' * X * B --> DY/DX = A * B' Y = A' * X' * B --> DY/DX = B * A' 于是把以前学过的矩阵求导部分整理一下: 1. 矩阵Y对标量x求导: 相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了 Y = [y(ij)] --> dY/dx = [dy(ji)/dx] 2. 标量y对列向量X求导: 注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是 N×1向 量 y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)' 3. 行向量Y'对列向量X求导: 注意1×M向量对N×1向量求导后是N×M矩阵。 将Y的每一列对X求偏导,将各列构成一个矩阵。 重要结论: dX'/dX = I d(AX)'/dX = A' 4. 列向量Y对行向量X’求导: 转化为行向量Y’对列向量X的导数,然后转置。 注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' = (dY'/dX)' 5. 向量积对列向量X求导运算法则: 注意与标量求导有点不同。 d(UV')/dX = (dU/dX)V' + U(dV'/dX) d(U'V)/dX = (dU'/dX)V + (dV'/dX)U' 重要结论: d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A d(AX)/dX' = (d(X'A')/dX)' = (A')' = A d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X 6. 矩阵Y对列向量X 求导: 将Y对X的每一个分量求偏导,构成一个超向量。 注意该向量的每一个元素都是一个矩阵。 7. 矩阵积对列向量求导法则: d(uV)/dX = (du/dX)V + u(dV/dX) d(UV)/dX = (dU/dX)V + U(dV/dX) 重要结论: d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A 8. 标量y对矩阵X的导数: 类似标量y对列向量X的导数, 把y对每个X的元素求偏导,不用转置。 dy/dX = [ Dy/Dx(ij) ] 重要结论: y = U'XV = ΣΣu(i)x(ij)v(j) 于是 dy/dX = = UV' y = U'X'XU 则 dy/dX = 2XUU'
向量矩阵求导
矩阵Y对标量x求导: 相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M 了 Y = [y(ij)] --> dY/dx = [dy(ji)/dx] 2. 标量y对列向量X求导: 注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量 y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)' 3. 行向量Y'对列向量X求导: 注意1×M向量对N×1向量求导后是N×M矩阵。 将Y的每一列对X求偏导,将各列构成一个矩阵。 重要结论: dX'/dX = I d(AX)'/dX = A' 4. 列向量Y对行向量X’求导: 转化为行向量Y’对列向量X的导数,然后转置。 注意M×1向量对1×N向量求导结果为M×N矩阵。 dY/dX' = (dY'/dX)'
5. 向量积对列向量X求导运算法则: 注意与标量求导有点不同。 d(UV')/dX = (dU/dX)V' + U(dV'/dX) d(U'V)/dX = (dU'/dX)V + (dV'/dX)U' 重要结论: d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A d(AX)/dX' = (d(X'A')/dX)' = (A')' = A d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X 6. 矩阵Y对列向量X求导: 将Y对X的每一个分量求偏导,构成一个超向量。 注意该向量的每一个元素都是一个矩阵。 7. 矩阵积对列向量求导法则: d(uV)/dX = (du/dX)V + u(dV/dX) d(UV)/dX = (dU/dX)V + U(dV/dX) 重要结论: d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A 8. 标量y对矩阵X的导数:
常用求导与定积分公式(完美)
常用求导与定积分公式 (完美) -CAL-FENGHAI.-(YICAI)-Company One1
2 一.基本初等函数求导公式 (1) 0)(='C (2) 1 )(-='μμμx x (3) x x cos )(sin =' (4) x x sin )(cos -=' (5) x x 2 sec )(tan =' (6) x x 2csc )(cot -=' (7) x x x tan sec )(sec =' (8) x x x cot csc )(csc -=' (9) a a a x x ln )(=' (10) (e )e x x '= (11) a x x a ln 1 )(log = ' (12) x x 1 )(ln = ', (13) 211 )(arcsin x x -= ' (14) 211 )(arccos x x -- =' (15) 21 (arctan )1x x '= + (16) 21 (arccot )1x x '=- + 函数的和、差、积、商的求导法则 设)(x u u =,)(x v v =都可导,则 (1) v u v u '±'='±)( (2) u C Cu '=')((C 是常数) (3) v u v u uv '+'=')( (4) 2v v u v u v u '-'=' ??? ?? 反函数求导法则 若函数)(y x ?=在某区间y I 内可导、单调且0)(≠'y ?,则它的反函数 )(x f y =在对应区间x I 内也可导,且 )(1)(y x f ?'= ' 或 dy dx dx dy 1= 复合函数求导法则
