计算方法用二分法求方程的实根

1 求下列方程的所有实根。
534221.204508967.8701231924.7590738320.6246081017.082712590x x x x x +--+-=
1.1二分法计算该题
1.1.1 确定区间[a,b].
(1)用excel 进行计算出区间:
最终确定区间范围是[1,2]
(2)作图法
画出函数y=f(x)的大概图象,观察曲线y=f(x)与x 轴交点的大致位置,从而确定隔根区间。上图是大概的图形,由此确定区间为[1,2]经计算f(a)和f(b)得f(a)*f(b)<0,所以确定方程的根在[1,2]之间。
1.1.2算法过程
设函数f (x )在区间[1,2]上连续,且f(1)·f(2)<0根据连续函数的性质可知f(x)=0在[1,2]内一定有实根,并称[1,2]为方程f(x)=0的有根区间。
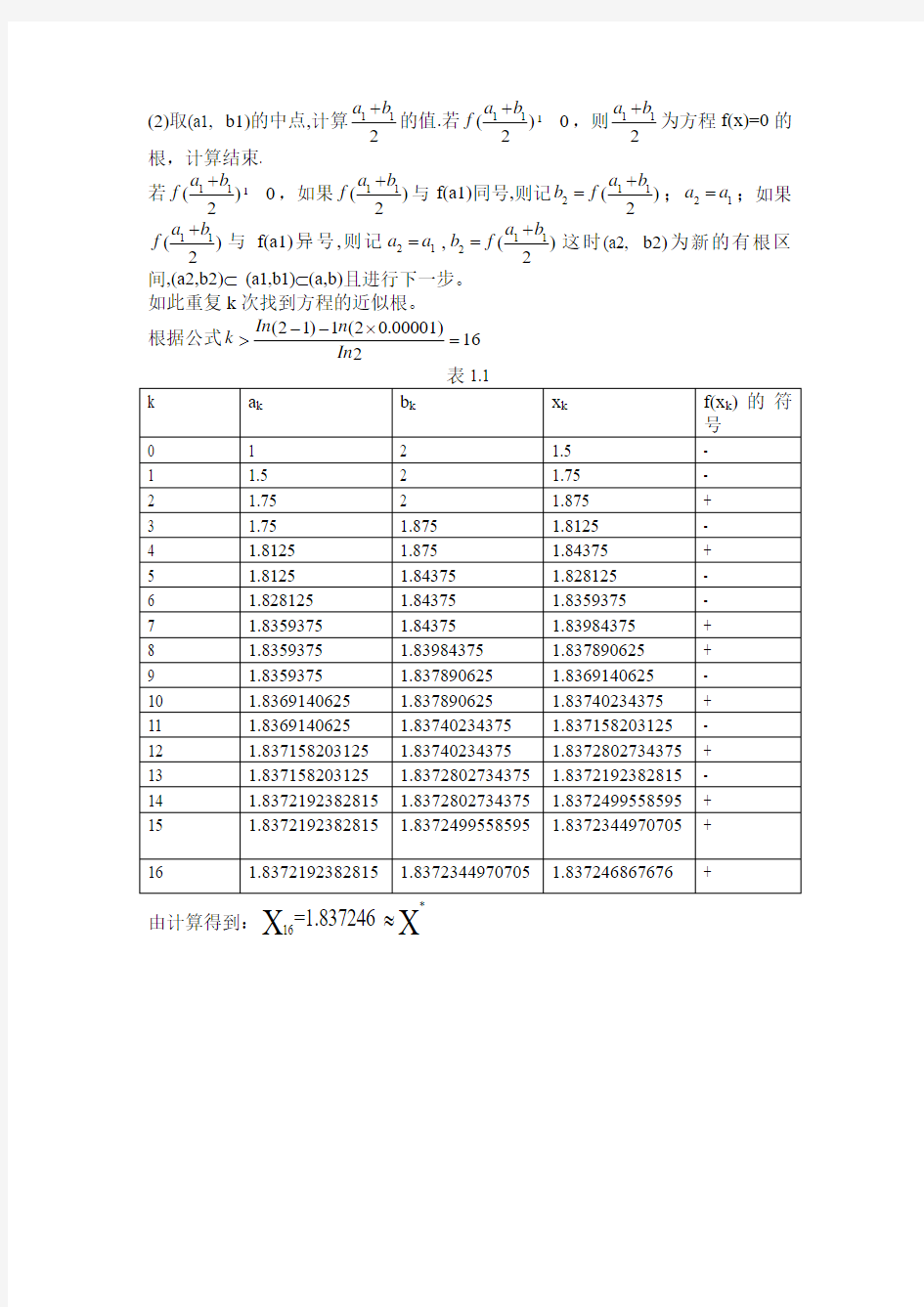
(1)取(a, b)的()k f x 中点,计算11()02a b f +=的值.若()02a b f +<,则2
a b +为方程f(x)的根,计算结束.若()02a b f +1,如果()2
a b f +与f(a)同号,则记21b b =,1b b =如果11()2a b f +与f(a)异号,则记1a a =, 12
a b b +=;(a1, b1)为新的有根区间, (a1,b1) (a,b)且进行下一步。
(2)取(a1, b1)的中点,计算112a b +的值.若11()02a b f +1,则112a b +为方程f(x)=0的根,计算结束. 若11()02a b f +1,如果11()2a b f +与f(a1)同号,则记112()2
a b b f +=;21a a =;如果11()2a b f +与f(a1)异号,则记21a a =,112()2
a b b f +=这时(a2, b2)为新的有根区间,(a2,b2)? (a1,b1)?(a,b)且进行下一步。
如此重复k 次找到方程的近似根。 根据公式(21)1(20.00001)162
In n k In --?>=
由计算得到:
*16=1.837246 X X ≈
用区间二分法求方程的根
用区间二分法求方程的根 一、前言 1.了解区间二分法求解方程基本方法。 2.学习掌握区间二分法求解方程根的过程。 3.学习掌握MATLAB软件有关的命令。 二、参数说明 function root=HalfInterval(f,a,b,eps) 方程表达式:f 区间左端点:a 区间右端点:b 根的精度:eps 求得的根:root 三、算法设计和运行结果 1.算法设计 ①计算函数f(x)在区间[a,b]中点的函数值f((a+b)/2),并做下面的判断:如果f(a)f((a+b)/2)<0,转到②; 如果f(a)f((a+b)/2)>0,令a=(a+b)/2,转到①; 如果f(a)f((a+b)/2)=0,则x=(a+b)/2为一个根。 ②如果|a-(a+b)/2| if (f1==0) root=a; end if (f2==0) root=b; end if (f1*f2>0) disp('两端点函数值乘积大于0!'); return; else root=FindRoots(f,a,b,eps); %调用求解子程序end function r=FindRoots(f,a,b,eps) f_1=subs(sym(f),findsym(sym(f)),a); f_2=subs(sym(f),findsym(sym(f)),b); mf=subs(sym(f),findsym(sym(f)),(a+b)/2); %中点函数值 if (f_1*mf>0) t=(a+b)/2; r=FindRoots(f,t,b,eps); %右递归 else if (f_1*mf==0) r=(a+b)/2; else if (abs(b-a)<=eps) r=(b+3*a)/4; %输出根 else s=(a+b)/2; r=FindRoots(f,a,s,eps); %左递归 end end end 抛物型方程有限差分法 1. 简单差分法 考虑一维模型热传导方程 (1.1) )(22x f x u a t u +??=??,T t ≤<0 其中a 为常数。)(x f 是给定的连续函数。(1.1)的定解问题分两类: 第一,初值问题(Cauchy 问题):求足够光滑的函数()t x u ,,满足方程(1.1)和初始条件: (1.2) ()()x x u ?=0,, ∞<<∞-x 第二,初边值问题(也称混合问题):求足够光滑的函数()t x u ,,满足方程(1.1)和初始条件: ()13.1 ()()x x u ?=0,, l x l <<- 及边值条件 ()23.1 ()()0,,0==t l u t u , T t ≤≤0 假定()x f 和()x ?在相应的区域光滑,并且于()0,0,()0,l 两点满足相容条件,则上述问题有唯一的充分光滑的解。 现在考虑边值问题(1.1),(1.3)的差分逼近 取 N l h = 为空间步长,M T = τ为时间步长,其中N ,M 是 自然数, jh x x j ==, ()N j ,,1,0Λ=; τ k y y k ==, ()M k ,,1,0Λ= 将矩形域G {}T t l x ≤≤≤≤=0;0分割成矩形网格。其中 ()j i y x ,表 示网格节点; h G 表示网格内点(位于开矩形G 中的网格节点)的集合; h G 表示位于闭矩形G 中的网格节点的集合; h Γ表示h G -h G 网格边界点的集合。 k j u 表示定义在网点()k i t x ,处的待求近似解,N j ≤≤0,M k ≤≤0。 注意到在节点()k i t x ,处的微商和差商之间的下列关系 ((,)k j k j u u x t t t ????≡ ? ????): ()() ()ττ O t u t x u t x u k j k j k j +??? ????=-+,,1 ()() ()2112,,ττ O t u t x u t x u k j k j k j +??? ????=--+ ()()()h O x u h t x u t x u k j k j k j +??? ????=-+,,1 ()() ()h O x u h t x u t x u k j k j k j +??? ????=--,,1 ()() ()2112,,h O x u h t x u t x u k j k j k j +??? ????=--+ ()()() ()2 222 11,,2,h O x u h t x u t x u t x u k j k j k j k j +???? ????=+--+ 可得到以下几种最简差分格式 二分法及迭代法求解非线性方程根 班级:姓名:方学号:日期: 一、实验目的 1、熟悉二分法及迭代法求解非线性方程根的数值算法; 2、用matlab软件实现二分法及迭代法,掌握迭代法的收敛性和收敛速度问 题及其加速方法; 二、基本理论及背景 1、牛顿迭代法具有平方收敛的速度,所以在迭代过程中只要迭代几次就会得到很精确的解。这是牛顿迭代法比简单迭代法优越的地方,但是选定的初值要接近方程的解,否则有可能得不到收敛的结果,再者,牛顿迭代法计算量比较大。因每次迭代除计算函数值外还要计算微商值。 2、牛顿迭代理论推导:设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0)+f'(x0)(x-x0),求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0),称x1为r的一次近似值。过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f'(x1),称x2为r的二次近似值。重复以上过程,得r的近似值序列,其中x(n+1)=x(n)- f(x(n))/f'(x(n)),称为r的n+1次近似值; 3、参考《二分法求非线性方程根》,实现二分算法,完成下面的题目: 求方程○1的根,精度至少达到10-6; 比较迭代下列迭代法求解○1中方程根的收敛性: ○2,; 用牛顿法设计迭代函数求解○1中方程的根(精度至少达到10-6),并与○2中收敛的迭代法比较收敛的速度。。 三、算法设计及实现 1、设计:方程○1function f=fun1(x) f=exp(x)-x-3;; ○2function y=Exp2(x) y=exp(x)-3; function y=Exp3(x) y=log(x+3); 牛顿迭代: A-1 用二分法求非线性方程实根 本实验用二分法求方程f (x) = x3 ?2x ?5 =0 在区间[2,3]内的根。 源程序: #include } else printf("\ not root! afresh input\n"); /*表示[a,b] 区间无根,重新选择有根区间*/ getch(); teturn(x); } 计算结果: please input data a = 2 please input data b = 3 please input data eps= 0.00001 the root of f(x)=0 is x= 2.094555 4.5.2用二分法求方程的近似解 1.二分法的概念 对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法. 2.用二分法求函数零点近似值的步骤 给定精确度ε,用二分法求函数y=f(x)零点x0的近似值的一般步骤如下: (1)确定零点x0的初始区间[a,b],验证f(a)f(b)<0. (2)求区间(a,b)的中点__c__. (3)计算f(c),并进一步确定零点所在的区间: ①若f(c)=0(此时x0=c),则__c__就是函数的零点; ②若f(a)f(c)<0(此时x0∈(a,c)),则令b=c; ③若f(c)f(b)<0(此时零点x0∈(c,b)),则令a=c. (4)判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤(2)~(4). 以上步骤可借助口诀记忆:定区间,找中点,中值计算两边看;同号去,异号算,零点落在异号间;周而复始怎么办?精确度上来判断. 1.已知函数f(x)的图象如图,其中零点的个数与可以用二分法求解的零点的个数分别为() A.4,4 B.3,4 C.5,4 D.4,3 D解析:图象与x轴有4个交点,所以零点的个数为4;左右函数值异号的零点有3个,所以可以用二分法求解的零点个数为3,故选D. 2.若函数f(x)在(1,2)内有1个零点,要使零点的近似值满足精确度为0.01,则对区间 (1,2)至少二等分( ) A .5次 B .6次 C .7次 D .8次 C 解析:设对区间(1,2)至少二等分n 次,初始区间长为1. 第1次二等分后区间长为1 2; 第2次二等分后区间长为1 22; 第3次二等分后区间长为1 23; … 第n 次二等分后区间长为1 2n . 根据题意,得1 2n <0.01, ∴n >log 2100. ∵6<log 2100<7, ∴n ≥7. 故对区间(1,2)至少二等分7次. 【例1】下面关于二分法的叙述中,正确的是( ) A .用二分法可求所有函数零点的近似值 B .用二分法求方程的近似解时,可以精确到小数点后的任一位 C .二分法无规律可循,无法在计算机上完成 D .只能用二分法求函数的零点 B 解析:用二分法求函数零点的近似值,需要有端点函数值符号相反的区间,故选项A 错误;二分法是一种程序化的运算,可以在计算机上完成,故选项 C 错误;求函数的零点的方法还有方程法、函数图象法等,故选项 D 错误.故选B. 分类号:O241.82 本科生毕业论文(设计) 题目:一类抛物型方程的计算方法 作者单位数学与信息科学学院 作者姓名 专业班级2011级数学与应用数学创新2班 指导教师 论文完成时间二〇一五年四月 一类抛物型方程的数值计算方法 (数学与信息科学学院数学与应用数学专业2011级创新2班) 指导教师 摘要: 抛物型方程数值求解常用方法有差分方法、有限元方法等。差分方法是一种对方程直接进行离散化后得到的差分计算格式,有限元方法是基于抛物型方程的变分形式给出的数值计算格式.本文首先给出抛物型方程的差分计算方法,并分析了相应差分格式的收敛性、稳定性等基本理论问题.然后,给出抛物型方程的有限元计算方法及理论分析. 关键词:差分方法,有限元方法,收敛性,稳定性 Numerical computation methods for a parabolic equation Yan qian (Class 2, Grade 2011, College of Mathematics and Information Science) Advisor: Nie hua Abstract: The common methods to solve parabolic equations include differential method, finite element method etc. The main idea of differential method is to construct differential schemes by discretizing differential equations directly. Finite element scheme is based on the variational method of parabolic equations. In this article, we give some differential schemes for a parabolic equation and analyze their convergence and stability. Moreover, the finite element method and the corresponding theoretical analysis for parabolic equation are established. Key words: differential method, finite element method, convergence, stability 【例5.21】二分法求方程的根。求方程x3+4x2+x+1=0在[-5,5]之间的近似根,误差为10-4。 若函数有实根,则函数的曲线应和x轴有交点,在根附近的左右区间内,函数的值的符号应当相反。利用这一原理,逐步缩小区间的范围,保持在区间的两个端点处函数值的符号相反,就可以逐步逼近函数的根。 设f (x)在[a, b]上连续,且f (a) f (b)<0, 找使f (x)=0的点。如图5-7-2所示。 图5-7-2 二分法示意图 二分法的步骤如下: ①取区间[a, b]中点x=(a+b)/2。 ②若f (x)=0, 即(a+b)/2为方程的根。 ③否则,若f (x)与f (a)同号,则变区间为[x,b];异号,则变区间为[a,x]。 ④重复①~③各步,直到取到近似根为止。 #include "stdio.h" #include "math.h" main() { float a,b,x; float fa,fb,fx; a=-5; b=5; fa=a*a*a+4*a*a+a+1; fb=b*b*b+4*b*b+b+1; do { x=(a+b)/2; fx=x*x*x+4*x*x+x+1; if(fa*fx<0) { b=x; fb=b*b*b+4*b*b+b+1; } else { a=x; fa=a*a*a+4*a*a+a+1; } }while(fabs(fa-fb)>1e-4); printf("x=%f\n",(a+b)/2); printf("f(%f)=%f",(a+b)/2,fa); } 运行结果: x=-3.806303 f(-3.806303)=-0.000059 经过多次迭代,当x= -3.806 303时,f(x)的结果为-0.000 059已经接近0,误差小于10- 4数量级。读者可进行简单的改写,输出每一次的迭代结果。 吉林化工学院 专业: 班级: 学号: 姓名: 有关二分法计算线性方程根的问题 1、二分法求解的提出及其背景 由于实际问题的需要,我们经常需要寻求函数的零点(即的根),对于为一次或二次函数,我们有熟知的公式解法(二次时,称为求根公式).我国古代数学家已比较系统地解决了部分方程求解的问题,在《九章算术》,北宋数学家贾宪的《黄帝九章算法细草》,南宋数学家秦九韶的《数书九章》中均有记载.在十六世纪,已找到了三次和四次函数的求根公式,人们曾经希望得到一般的五次以上代数方程的根式解,但经过长期的努力仍无结果.1824年,挪威年轻数学家阿贝尔(N. H. Abel,1802-1829)成功地证明了五次以上一般方程没有根式解.1828年,法国天才数学家伽罗瓦(E.Galois,1811-1832)巧妙而简洁地证明了存在不能用开方运算求解的具体方程.人们认识到高于4次的代数方程不存在求根公式,因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法,这是一个在计算数学中十分重要的课题。 求解非线性方程的数值解有二分法、迭代法、牛顿—雷扶生方法、正割法和抛物线法。下面我们就来讨论二分法求解非线性方程数值解的问题。 2、在求解过程中需要用到的定理: 1、(1)设f(x)于[a,b]上连续; (2)且f(a)?f(b)<0; 则存在有x*∈(a,b),使f(x*)于(a,b)内存在实的零点。 2、给定方程f(x)=0,设f(x)于[a,b]上连续,且f(a)?f(b)<0,则由二分法产生的序列{x k }收敛于方程f(x)=0的根x*,且具有性质 |x k-x*|≦(b-a)/2k(k=1,2,3,…) 3、二分法的描述: 设有非线性方程f(x=0),其中,f(x)为[a,b]上的连续函数且设f(a)?f(b)<0(不妨设该方程在[a,b]内仅有一个实根)。二分法具体方法如下: 运用上述定理2,设ε>0为给定精度要求,则由|xk-x*|≦(b-a)/2k<ε得半分次数k>[㏑(b-a)-㏑ε]/㏑2. 记a1=a,b1=b; 第一步:k=1,计算x1=(a1+b1)/2及f(x1),如果f(a1)·f(x1)<0则根一定在[ a1,x1]≡[a2,b2]内,否则根一定在区间[x1,b1] ≡[a2,b2]内(若f(x)=0,则x1=x*)。于是到长度缩小一半的含根区间[a2,b2],即f(a2)·f(b2)<0,且b2-a2=1/2(b1-a1) 第k步分半计算:重复上述计算过程,设已完成第1步,…,第k-1步分半计算得到含根区间[a1, b1] ?[a2,b2] ?…?[a k,b k]且满足: (1) f(a k )·f(a k)<0,即x*∈[a k,b k]; (2) b k-a k=1/(2k-1); 现进行第k步分部计算: (3) 计算x k=( a k+ b k)/且有|x k-x*|≦(b-a)/2=1/2k(b-a) (4) 确定新的含根区间[a k+1,b k+1],即如果f(a k)·f(b k)<0,则根一定在 例1:利用计算器,求方程0122=--x x 的一个近似解(精确到0.1). 【解】设2()21f x x x =--, 先画出函数图象的简图. (如右图所示) 因为 (2)10,(3)20f f =-<=>, 所以在区间(2,3)内,方程2210x x --=有一解,记为1x .取2与3的平均数2.5,因为 (2.5)0.250f =>, 所以 12 2.5x <<. 再取2与2.5的平均数2.25,因为(2.25)0.43750f =-<, 所以 12.25 2.5x <<. 如此继续下去,得 1(2)0,(3)0(2,3) f f x <>?∈1(2)0,(2.5)0(2,2.5) f f x <>?∈1(2.25)0,(2.5)0(2.25,2.5) f f x <>?∈1(2.375)0,(2.5)0(2.375,2.5) f f x <>?∈1(2.375)0,(2.4375)0(2.375,f f x <>?∈ 2.4375),因为2.375与2.4375精确到0.1的 近似值都为2.4,所以此方程的近似解为 1 2.4x ≈. 利用同样的方法,还可以求出方程的另一个近似解. 点评:①第一步确定零点所在的大致区间),(b a ,可利用函数性质,也可借助计算机或计算器,但尽量取端点为整数的区间,尽量缩短区间长度,通常可确定一个长度为1的区间; 如此列表的优势:计算步数明确,区间长度小于精度时,即为计算的最后一步. 例2:利用计算器,求方程x x -=3lg 的近似解(精确到0.1). 分析:分别画函数lg y x =和3y x =- 的图象,在两个函数图象的交点处,函数值相等.因此,这个程x x -=3lg 的解.由函数lg y x =与 点的横坐标就是方 22 10,01,01(,0),01(0,),(1,),01 (,)x t t x t u u x t t x u x e x u t e u t e t u x t e ++??-=<<<≤??=≤≤==<≤= 运行:前向euler 法 [xx,tt,uh]=equationepaowu2('myfun','myfun1','myfun1','myfun2',1,[0,1],[0,1],[1/10,1/200]); function [xx,tt,uh]=equationepaowu2(myfun,myfun1,myfun2,myfun3,a,xxx,ttt,step) %利用差分方法求抛物型方程数值解; %myfun--方程右端f(x,t); %myfun1--u(x,0); %myfun2--u(t1,t); %myfun3--u(t2,t); %[x1,x2]--x 的取值范围; %[t1,t2]--t 的取值范围; %a-正常数 %h,tao-分别是x,t 方向的步长。 %—————————————————————— %激活函数 f=fcnchk(myfun); f1=fcnchk(myfun1); f2=fcnchk(myfun2); f3=fcnchk(myfun3); x1=xxx(1);x2=xxx(2); t1=ttt(1);t2=ttt(2); h=step(1);tao=step(2); %__________________________________ %划分网格,x1-nt+1行,nx+1列。 x=linspace(x1,x2,round((x2-x1)/h)+1); t=linspace(t1,t2,round((t2-t1)/tao)+1); nx=size(x,2); nt=size(t,2); [xx,tt]=meshgrid(x,t); %________________________________________ %赋初值及边值 size(x1) size(x) U0=zeros(size(xx)); 专业代码:080101 楚雄师范学院 (Chxiong Normal University) 数学系2008级数学与应用数学专业教育实习 教育教学研究论文 实习生姓名茶本卫 学号20081021112 专业数学与应用数学 年级08级 实习单位紫系中学 实习时间2011年10月---11月 楚雄师范学院数学系编制 二0一一年九月二十八日 目录 浅谈二分法求方程的近似解的思路与技巧 摘要:在二分法中,由于不断取中点,区间不断缩小,区间的中点逐渐逼近方程根(或函数零点)的精确值,所以二分法体现了无限逼近的极限思想;二分法本质上又是一种区间迭代的数值算法,渗透了算法思想;二分法还体现了非此即彼的哲学思想,它综合了函数、方程、不等式、数列、极限等多种知识,主要有以下四方面的应用。 关键词:二分法;零点存在定理;精确度 Talking about the dichotomy of ideas and techniques for finding approximate solutions to equations Abstract:Dichotomy, given the access point , shrinking intervals , gradually approaching the midpoint of the interval root of equation ( or function zeros) The exact values , approximation of dichotomy reflects the infinite limit thought ; Dichotomy is essentially an interval iterative numerical algorithms , infiltrated algorithm,Dichotomy is reflected either/or philosophy , which combines functions, equations,inequalities , series, limits, and other knowledge , there are four main areas of application. Keywords:Dchotomy,zero point existence theorem, accuracy. 前言 抛物型方程解的估计及其应用 1前言 数学物理方程主要指从物理学及其它各门自然科学、技术科学中所产生的偏微分方程(有时也包括积分方程、微分方程等),它们反映了有关的未知变量关于时间的导数和关于空间变量的导数之间的制约关系.连续介质力学、电磁学、量子力学等等方面的基本方程属于数学物理方程的范围.它以具有物理背景的偏微分方程(组)作为研究的主要对象.它与其他数学分支及物理、化学等自然科学和工程技术的很多领域都有着广泛的联系,因此,无论在历史上还是在今天的现实生活中,它对于推动数学理论的发展,加强理论与实际的联系,帮助人们认识世界和改造世界都起着重要大的作用. 微积分产生以后,人们就开始把力学中的一些问题,归结为偏微分方程进行研究.早在18世纪初,人们已经将弦线振动问题归结为弦振动方程,并探讨了它的解法.随后,人们又陆续了解了流体的运动、弹性体的平衡和振动、热传导、电磁相互作用、原子核和电子的相互作用、化学反应过程等等自然现象的基本规律,把它们写成偏微分方程的形式,并且求出了典型问题的解答,从而能通过实践,验证这些基本规律的正确性,显示了数学物理方程对于认识自然界基本规律的重要性.有了基本规律,人们还要利用这些基本规律来研究复杂的自然现象和解决复杂的工程技术问题,这就需要求出数学物理方程中许多特定问题的解答,随着计算机的出现及计算技术的发展,即使是相当复杂的问题,也可以计算出足够精确的数值来,这对于预测自然现象的变化(如气象预报)和进行各种工程设计(如机械强度的计算)都有着很重要的作用. 在研究数学物理方程的同时,人们对偏微分方程的性质也了解得越来越多、越来越深入,形成数学中的一门重要分支——偏微分方程理论.它既有悠久的历史,又不断地更新着它的对象、内容和方法.它直接联系着众多自然现象和实际问题,不断地提出或产生需要解决的新课题和新方法.它所面临的数学问题多样而复杂,不断地促进着许多相关数学分支(如泛函分析、复变函数、微分几何、计算数学等)的发展,并从它们之间引进许多有力的解决问题的工具.因此,数学物理方程又是纯粹数学的 有限差分法求解抛物型方程 偏微分方程只是在一些特殊情况下,才能求得定解问题解的解析式,对比较复杂的问题要找到解的解析表达式是困难的,因此需采用数值方法来求解.有限差分法是一种发展较早且比较成熟的数值求解方法,只适用于几何形状规则的结构化网格.它在微分方程中用差商代替偏导数,得到相应的差分方程,通过解差分方程得到微分方程解的近似值.本章主要介绍有限差分法的基本思想,并给出一些具体的数值实例. §1 差分方法的基本思想 有限差分法把偏微分方程的求解区域划分为有限个网格节点组成的网格,主要采用Taylor 级数展开等方法,在每个网格节点上用有限差分近似公式代替方程中的导数,从而建立以网格节点上的函数值为未知数的代数方程组. 有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式.从差分的空间形式来考虑,可分为中心格式和逆风格式.考虑时间因子的影响,差分格式还可以分为显格式、隐格式和显隐交替格式等.目前常见的差分格式,主要是上述几种格式的组合,不同的组合构成不同的差分格式. 泰勒级数展开法对有限差分格式的分类和公式的建立起着十分重要的作用.下面采用泰勒展开式导出一个自变量系统的若干有限差分表达式. 首先考虑单变量函数()u x ,如图1把区域x 离散为一批结点,记 0()(), =0,1,2,i i u x u x ih u i =+= 图1 单变量函数离散化 函数()u x 在点i x 处的泰勒展开式为 23 ()()()()()2!3! i i i i i u x u x u x h u x u x h h h ''''''+=++ ++ (1) 或 23 ()()()()()2!3! i i i i i u x u x u x h u x u x h h h ''''''-=-+ -+ (2) 式(1)和(2)重新整理可得 2()()()()()2!3! i i i i i u x h u x u x u x u x h h h '''''+-'= --- (3) 用二分法求方程的近似解(1) 【教学目标】1.使学生理解利用二分法求方程的近似解的思想方法,会用二分法求某些方程的近似解 2.通过本节内容的学习,让学生体会到在现实世界中,等是相对的,而不等是绝对的,这样可以加深对数学的理解. 【学习指导】我们已经学过一元一次方程、一元二次方程等方程的解法,并掌握了一些方程的求根公式.实际上,大部分方程没有求根公式,那么,这些方程怎么解?学完这一课,你就会知道利用方程的根与函数的零点的关系求方程的实数解(近似解)了. 本节的重点就是利用二分法求方程的近似解,所谓二分法就是:对于在区间[a,b]上连续不断、且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而和到零点近似值的方法. 【例题精析】 例1.借助计算机或计算器,用二分法求函数f(x)= x3-5x2-4x+2的一个零点,精确到0.05. 【分析】先用大范围法寻找零点所在的区间,然后不断使用二分法,逐步缩小区间,直至达到精度的要求. 【解法】先作出x与f(x)的对应值表,并试图找出一个根所在的区间: 通过举值,发现函数在(0,1)与(5,6)内都至少有一个零点,现不妨求(0,1)内的一个零点. 令x1=0.5,f(0.5)= -1.125.因为f(0)·f(0.5)<0,所以零点x0∈(0,0.5).令x2=0.25,f(0.25)≈0.7.因为f(0.25)·f(0.5)<0,所以零点x0∈(0.25,0.5). 令x3=0.375,f(0.375)≈-0.15.因为f(0.375)·f(0.25)<0,所以零点x0∈(0.25,0.375). 令x4=0.3125,f(0.3125)≈0.29.因为f(0.375)·f(0. 3125)<0,所以零点x0∈(0.3125,0.375). 令x5=0.359375,f(0.359375)≈-0.04.因为f(0.359375)·f(0.3125)<0,所以零点x0∈(0.3125,0.359375). 由于|0.359375-0.3125|=0.047<0.05, 此时区间(0.3125,0.359375)的两个端点精确到0.05的近似值都是0.336,所以函数的一个零点为0.336. 【评注】①选好初定区间是使用二分法求近似解的关键.选取初定区间的方法有多种,常用方法有试验估计法,数形结合法,函数单调性法,函数增长速度差异法等等.②本题还有两个零点,你能把它独立求解出来吗?(答案为-1,5.646.) 例2.(师生共同探究)概括用二分法求方程的近似解的基本程序. 【分析】通过对例1的研究,希望能够对解决问题的方法进行提炼,而这一点切不可以由老师包办代替,要通过师生的合作探究解决问题.【解法】(1)在同一坐标系中分别作出两个简单函数的图象,注意两个图象与x轴的交点坐标; (2)估算出第一个解的区间(x1,x2),(x1<x2); VBA程序:二分法求方程的根 对于一般超越方程与高次代数方程求根的问题,可选用方法简单实用有效的不求导数的二分法,即在给定的寻根区间内,利用步步查找,二分缩小区间的方法,求出全部实根。 二分法求根程序框图见后附件。 主要标识符含义: A,B—方程求根区间的左、右端点[a,b] H—查根间距、跨步长度h EPS—计算精度值,ε= - x A,y A—变化过程中的左端点点值及函数值 x B,Y B—变化过程中的右端点点值及函数值 x C,y C—变化过程中的中点点值及函数值 算例 已知方程式f(x)=x3-6x2+11x-6=0,求方程的根。 给定条件x∈[,],ε=,h=。 迭代求解后,可得到方程的三个实根: x1=1 ? x2=2 x3=3 VBA程序代码 '声明方程求解给定的条件 Dim a As Double, b As Double, h As Double, eps As Double '声明数组,用来放置根 Dim dblRoot() As Double '统计根的个数 , Dim lCount As Long Sub Main() Dim Xa As Double, Ya As Double, Xb As Double, Yb As Double '赋初值 a = b = ( h = eps = Xa = a Xb = a Ya = dblFx(Xa) Xb = Xb + h If Xb > b Then Exit Sub [ Yb = dblFx(Xb) Call Root(Xa, Ya, Xb, Yb) End Sub Sub Root(Xa1 As Double, Ya1 As Double, Xb1 As Double, Yb1 As Double) If qqqRoot(Ya1, Yb1) Then % Call qRoot(Xa1, Ya1, Xb1, Yb1) Else Xa1 = Xb1 Ya1 = Yb1 Xb1 = Xb1 + h If Xb1 > b Then Exit Sub Yb1 = dblFx(Xb1) '符合求根条件则求根计算,否则继续调整求根区间 " If qqqRoot(Ya1, Yb1) Then Call qRoot(Xa1, Ya1, Xb1, Yb1) Else Call Root(Xa1, Ya1, Xb1, Yb1) End If End If End Sub , '判断是否符合求根条件 Function qqqRoot(dblYa2 As Double, dblYb2 As Double) As Boolean If dblYa2 * dblYb2 <= 0 Then qqqRoot = True Else qqqRoot = False End If End Function : Sub qRoot(dblXa As Double, dblYa As Double, dblXb As Double, dblYb As Double) Dim dblXc As Double, dblYc As Double, dblXd As Double '是否满足条件,不满足继续缩小求根区间 If Abs(dblYa - dblYb) > eps And Abs(dblXa - dblXb) > eps Then 用二分法求方程的近似解-经典例题及答案 例1:利用计算器,求方程X 2 2x 1 0的一个近似解(精确到0.1) 【解】设f (x) x 2 2x 1, 先画出函数图象的简图.'i (如右 图所示) 丨 因为 ; f(2) 1 0, f (3) 2 0, 所以在区间(2,3)内,方程x 2.5,因为 f (2.5) 0.25 0, 所以 2人 2.5. 再取2与2.5的平均数2.25,因为f(2.25) 0.4375 0, 所以2.25 治 2.5. 如此继续下去,得 f(2) 0, f(3) 人(2,3) f(2) 0, f(2.5) 0 捲(2,2.5) f(2.25) 0, f (2.5) 0 x 1 (2.25, 2.5) f (2.375) 0, f (2.5) 0 x 1 (2.375,2.5) f (2.375) 0, f (2.4375) 0 为(2.375, 2.4375),因为 2.375与 2.4375精确到 0.1的近似值都为2.4,所以此方程的近似解为 洛 2.4 . 利用同样的方法,还可以求出方程的另一个近似解 . 点评:①第一步确定零点所在的大致区间(a,b),可利用函数性质,也可借助计算 机或计算器,但尽量取端点为整数的区间,尽量缩短区间长度,通常可确定一 个长度为1的区间; ②建议列表样式如下: 零点所在 区 间 区间中点函数 值 区间长 度 [2,3] f(2.5) 0 1 [2,2.5] f (2.25) 0 0.5 [2.25,2.5] f (2.375) 0 0.25 [2.375,2.5] f (2.4375) 0.125 如此列表的优势:计算步数明确,区间长度小于精度时,即为计算的最后一 步. 1 0有一解,记为x 1.取2与3的平均数 例 2:利用计算器,求方程lgx 3 x 的近似解(精确到0.1) 1-- 3 4 I I 斗- 3-' 分析:分别画函数y lg x 和y 3 x 问题 二分法解决方程求解问题 利用二分法,求方程063422 3=-+-x x x 的实根,精确到两位小数。 分析 二分法是一种典型的迭代问题,前面已经介绍了二分法定义,这里为了便于计算 函数值)(x f 编制函数float function(float x)。在主函数中首先给出了有根区间 ],[b a ,在程序中用[x1,x2]表示。由于不确定函数需要执行的次数,因此使用do-while 循环,循环条件为区间中点的函数值小于6100.1-?,当函数值小于6100.1-?时,近似认为当前的值为方程根。 数据要求 问题中的常量: 1e – 6; 问题的输入: 无 问题的输出: 输出方程的根 设计 初始算法 1 初始化数据 2 使用二分法解方程。 算法细化 步骤2可以进一步细化, 将区间],[b a 分半,取中点2b a +,求)2(b a f +,若δ<+)2 (b a f ,则取2 b a +≈ α,否则作下一步。 计算)2()(b a f b f +?,若0)2()(>+?b a f b f ,取2 ,11b a b a a +==;否则取b b b a a =+=11,2,形成新的含根区间],[11b a ,且211a b a b -=-。 对于新的含根区间重复上述步骤,直到ε<-n n a b ,取 2 ~n n b a +=α 作为α的近似值。此时的计算误差为 12 2~+-=-<-n n n a b a b αα 流程图 实现 #include "stdio.h" #include "math.h" float function(float x) { float f; f= x*((2*x-4)*x+3)-6; return f; } void main() { float x1,x2,x0,fx1,fx2,fx0; x1=10;x2=-10; fx1=function(x1); fx2=function(x2); do { x0=(x1+x2)/2.0;/*计算中点*/ fx0=function(x0);/*计算中点处的函数值*/ if(fx0*fx1<0)/*计算新的区间*/ {/*区间中点的函数值与x1的函数值正负号相反*/ /*区间中点的y坐标与x1点的y坐标在不同y半轴上*/ x2=x0;/*新区间为[x1,x0]*/ fx2=fx0; } else {/*区间中点的y坐标与x1点的y坐标在相同y半轴上*/ x1=x0;/*新区间为[x0,x2]*/ fx1=fx0; } }while(fabs(fx0)>=1e-6); printf("The root is %f",x0); } 测试 该程序没有输入,输出结果为方程的根,此处略。 用二分法求方程的近似解 一、教学内容分析 本节选自新人教A版必修1第三章第一节的第二课时,是利用前一节课中的函数的零点和方程的根的关系来才解方程的根,而如何求得函数的零点,就是本节课的主要内容。这里要求学生懂得二分法的求解的过程,理解二分法求解的原理,更重要的是,有了计算机这种高科技产品,使得复杂的计算变成了简单,使得这种近似的计算方法有了更广泛的应用空间。为必修3算法提供了技术支持。同时让学生对函数与方程的思想,数形结合思想以及逼近的数学思想有了进一步的认识。 二、学生学习情况分析 同学们有了第一节课的基础,对函数的零点具备基本的认识;而通过生活中的案例来接触二分的思想,使二分法不要变化抽象,能够激发学生的学习兴趣,使学生明白数学就在我身边,数学无处不在的。学生也能够很容易理解这种方法。对于高次方程和超越方程对应函数零点的寻求会有困难. 三、教学目标 通过具体实例理解二分法的概念,掌握运用二分法求简单方程近似解的方法,从中体会函数的零点与方程根之间的联系及其在实际问题中的应用;能借助计算器用二分法求方程的近似解,让学生能够初步了解逼近思想;体会数学逼近过程,感受精确与近似的相对统一;通过具体实例的探究,归纳概括所发现的结论或规律,体会从具体到一般的认知过程. 四、教学重点和难点 1.教学重点:用“二分法”求方程的近似解,使学生体会函数零点与方程根之间的联系,初步形成用函数观点处理问题的意识. 2.教学难点:方程近似解所在起始区间的确定,近似解与精确度的关系。 五、教学过程设计 (一)创设情境,提出问题 体会一分为二的“逼近”思想 问题1:在班级举办的新年晚会上,有一支有100个小彩灯组成的串联彩灯电路突然不亮了,知道只有一个灯泡烧毁,如何迅速找出烧掉的灯炮并换掉,让欢乐的气氛得以继续? 这个问题会让学生有身临其境的感觉,确实,这个欢快的场面,出现了这个大杀风景的事,是有点不爽,越快找出烧毁的灯炮越好。 [学情预设] 学生独立思考,可能出现的以下解决方法:(完整版)大连理工大学高等数值分析抛物型方程有限差分法
二分法及迭代法求解非线性方程根
用二分法求非线性方程实根
用二分法求方程的近似解(带练习)
抛物型方程的计算方法
二分法求方程的根
有关二分法计算线性方程根的问题
用二分法求方程的近似解-经典例题及答案
抛物型方程求解
浅谈二分法求方程的近似解的思路与技巧
抛物型方程
有限差分法求解抛物型方程说明
用二分法求方程的近似解
VBA程序:二分法求方程的根
用二分法求方程的近似解-经典例题及答案上课讲义
二分法方程求解
用二分法求方程的近似解教案(人教A版必修)
