相似三角形添加辅助线的方法举例(有答案)

相似三角形添加辅助线的方法举例
例1: 已知:如图,△ABC 中,AB =AC ,BD ⊥AC 于D . 求证: BC 2=2CD ·AC .
例2.已知梯形ABCD 中,BC AD //,AD BC 3=,E 是腰AB 上的一点,连结CE
(1)如果AB CE ⊥,CD AB =,AE BE 3=,求B ∠的度数;
(2)设BCE ?和四边形AECD 的面积分别为1S 和2S ,且2132S S =,试求AE
BE
的值
例3.如图4-1,已知平行四边ABCD 中,E 是AB 的中点,
AD AF 31=
,连E 、F
B
C
D
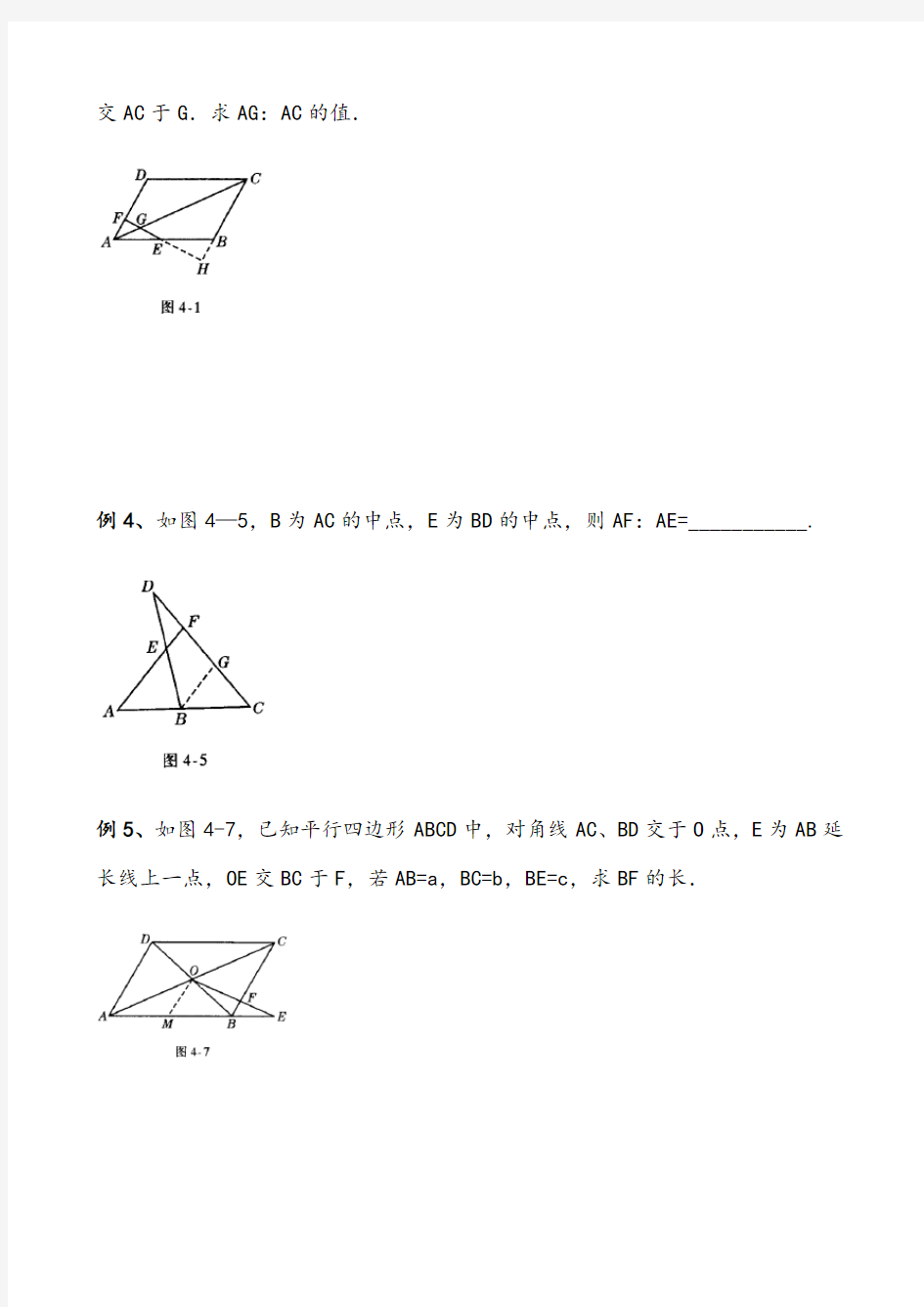
交AC于G.求AG:AC的值.
例4、如图4—5,B为AC的中点,E为BD的中点,则AF:AE=___________.
例5、如图4-7,已知平行四边形ABCD中,对角线AC、BD交于O点,E为AB延长线上一点,OE交BC于F,若AB=a,BC=b,BE=c,求BF的长.
例6、已知在△ABC 中,AD 是∠BAC 的平分线.求证:
CD BD
AC AB =
.
相似三角形添加辅助线的方法举例答案
例1: 已知:如图,△ABC 中,AB =AC ,BD ⊥AC 于D .
求证: BC 2=2CD ·AC .
分析:欲证 BC 2=2CD ·AC ,只需证
BC
AC
CD BC =
2.但因为结论中有“2”,无法直接找到它们所在的相似三角形,因此需要结合图形特点及结论形式,通过添加辅助线,对其中某一线段进行倍、分变形,构造出单一线段后,再证明三角形相似.由“2”所放的位置不同,证法也不同.
证法一(构造2CD ):如图,在AC 截取DE =DC , ∵BD ⊥AC 于D ,
B
C
D
E
B
C
D
∴BD 是线段CE 的垂直平分线, ∴BC=BE ,∴∠C=∠BEC , 又∵ AB =AC , ∴∠C=∠ABC . ∴ △BCE ∽△ACB . ∴
BC AC CE BC =, ∴BC
AC
CD BC =
2 ∴BC 2=2CD ·AC .
证法二(构造2AC ):如图,在CA 的延长线上截取AE =AC ,
连结BE ,
∵ AB =AC , ∴ AB =AC=AE . ∴∠EBC=90°, 又∵BD ⊥AC .
∴∠EBC=∠BDC=∠EDB=90°, ∴∠E=∠DBC , ∴△EBC ∽△BDC
E
∴
BC CE CD BC =即BC
AC
CD BC 2=
∴BC 2=2CD ·AC .
证法三(构造BC 2
1) :如图,取BC 的中点E ,连结AE ,则EC=BC 2
1.
又∵AB=AC ,
∴AE ⊥BC ,∠ACE=∠C ∴∠AEC=∠BDC=90° ∴△ACE ∽△BCD .
∴BC AC CD CE =即BC
AC CD BC
=21
. ∴BC 2=2CD ·AC .
证法四(构造BC 21
):如图,取BC 中点E ,连结DE ,则
∵BD ⊥AC ,∴BE=EC=EB , ∴∠EDC=∠C
又∵AB=AC ,∴∠ABC=∠C , ∴△ABC ∽△EDC . ∴
EC AC CD BC =J 即BC AC
CD BC 2
1
=. B
C
B
∴BC 2=2CD ·AC .
说明:此题充分展示了添加辅助线,构造相似形的方法和技巧.在解题中方法要灵活,思路要开阔.
例2.已知梯形ABCD 中,BC AD //,AD BC 3=,E 是腰AB 上的一点,连结CE
(1)如果AB CE ⊥,CD AB =,AE BE 3=,求B ∠的度数;
(2)设BCE ?和四边形AECD 的面积分别为1S 和2S ,且2132S S =,试求AE
BE
的值
(1)设k AE =,则k BE 3=
解法1 如图,延长BA 、CD 交于点F
BC AD //,AD BC 3=, ∴AF BF 3= ∴k AF 2=,E 为BF 的中点
又BF CE ⊥ CF BC =,又BF CF = ∴BCF ?为等边三角形 故?=∠60B 解法2 如图
作AB DF //分别交CE 、CB 于点G 、F 则DF CE ⊥,得平行四边形ABFD 同解法1可证得CDF ?为等边三角形 故?=∠=∠601B 解法3 如图
作EC AF //交CD 于G ,交BC 的延长线于F 作AB GI //,分别交CE 、BC 于点H 、I 则GI CE ⊥,得矩形AEHG
CE AF // ∴
3==AE
BE
CF BC , 又AD BC 3= ∴AD CF =,故G 为CD 、AF 的中点 以下同解法1可得CGI ?是等边三角形 故?=∠=∠601B
解法4 如图,
作CD AF //,交BC 于F ,作CE FG //,交AB 于G ,得平行四边形AFCD ,且
AB FG ⊥
读者可自行证得ABF ?是等边三角形,故?=∠60B 解法5 如图
延长CE 、DA 交于点F ,作CD AG //,分别交BC 、CE 于点G 、H ,得平行四边形AGCD
可证得A 为FD 的中点,则k AH 2=,故?=∠601 得ABG ?为等边三角形,故?=∠60B 解法6 如图(补形法),
读者可自行证明CDF ?是等边三角形,
得?=∠=∠60F B
(注:此外可用三角形相似、等腰三角形三线合和一、等积法等) (2)设S S BCE 3=?,则S S AECD 2=四边形 解法1(补形法)如图
补成平行四边形ABCF ,连结AC ,则AD DF 2= 设x S ACD =?,则x S S ACE -=?2,x S CDF 2=? 由ACF ABC S S ??=得, x x x s s 223+=-+,∴s x 4
5=
∴s x s S ACE 432=
-= ∴44
33===??s s S S AE BE ACE
BCE
解法2 (补形法)如图,延长BA 、CD 交于点F ,
9
1
=??ABC FAD S S
∴
s
S
S S FAD ABCD FAD 581??==梯形
∴s S FAD 85=
?,s s s S FEC 8
21
285=+=?,又s S EBC 3=? ∴
8
7==??BEC FBC S S BE EF 设m 8=BE ,则m 7=EF ,m 15=BF ,m 5=AF
∴m 2=AE ,∴4==
AE
BE
解法3(补形法)如图
连结AC ,作AC DF //交BA 延长线于点F 连结FC
则FAD ?∽ABC ?,故AF AB 3=(1)
ACF ACD S S ??=,FEC AECD S S ?=四边形
∴
2
3
===???AECD BCE FEC BEC S S S S EF BE 四边形 故AF AE AF AE EF BE 33)(332+=+==(2) 由(1)、(2)两式得AE BE 4= 即4=AE
BE
解法4(割补法)如图
连结A 与CD 的中点F 并延长交BC 延长线于点G ,如图,过E 、A 分别作高1h 、
2h ,则AD CG =且AECG AECD S S 四边形四边形=,∴s S S ABCD ABG 5==?梯形
∴21
2
121
5
3h BG h BC
S S ABG
EBC ????=
=
??,又43=BG BC ∴
5421=h h ,∴54=AB BE ,故4=AE
BE 说明 本题综合考查了等腰三角形的性质,相似三角形的判定和性质,解题关键是作辅助线,构造相似三角形.
例3.如图4-1,已知平行四边ABCD 中,E 是AB 的中点,AD AF 31
=
,连E 、F
交AC 于G .求AG :AC 的值.
解法1: 延长FE 交CB 的延长线于H ,
∵ 四边形ABCD 是平行四边形,∴ BC AD //,∴ ∠H=∠AFE ,∠DAB=∠HBE 又AE=EB ,∴ △AEF ≌△BEH ,即AF=BH ,
∵
AD
AF
3
1
=
,∴
BC
AF
3
1
=
,即
CH
AF
4
1
=
.
∵ AD∥CH,∠AGF=∠CGH,∠AFG=∠BHE,∴△AFG∽△CGH.∴ AG:GC=AF:CH,
∴ AG:GC=1:4,∴ AG:AC=1:5.
解法2:如图4—2,延长EF与CD的延长线交于M,由平行四边形ABCD可知,DC
AB//,即AB∥MC,
∴ AF:FD=AE:MD,AG:GC=AE:MC.∵
AD
AF
3
1
=
,∴ AF:FD=1:2,
∴ AE:MD=1:2.
∵
DC
AB
AE
2
1
2
1
=
=
.∴ AE:MC=1:4,即AG:GC=1:4,
∴ AG:AC=1:5
例4、如图4—5,B为AC的中点,E为BD的中点,则AF:AE=___________.
解析:取CF的中点G,连接BG.∵ B为AC的中点,
∴ BG:AF=1:2,且BG∥AF,又E为BD的中点,
∴ F为DG的中点.
∴ EF:BG=1:2.
故EF:AF=1:4,∴ AF:AE=4:3.
例5、如图4-7,已知平行四边形ABCD中,对角线AC、BD交于O点,E为AB延长线上一点,OE交BC于F,若AB=a,BC=b,BE=c,求BF的长.
解法1:过O点作OM∥CB交AB于M,
∵ O是AC中点,OM∥CB,
∴ M是AB的中点,即
a MB
2
1
,
∴ OM是△ABC的中位线,
b
BC
OM
2
1
2
1
=
=
,
且OM∥BC,∠EFB=∠EOM,∠EBF=∠EMO.
∴△BEF∽△MOE,∴EM
BE
OM
BF
=
,
即
c
a
c
b
BF
+
=
2
2
1
,∴c
a
bc
BF
2
+
=
.
解法2:如图4-8,延长EO与AD交于点G,则可得△AOG≌△COF,
∴ AG=FC=b-BF,∵ BF∥AG,∴AE
BE
AG
BF
=
.即c
a
c
BF
b
BF
+
=
-,
∵c
a
c
b
BF
2
+
=
∴c
a
bc
BF
2
+
=
.
解法3:延长EO与CD的延长线相交于N,则△BEF与△CNF的对应边成比例,即CN
BE
CF
BF
=
.
解得c
a
bc
BF
2
+
=
.
例6、已知在△ABC中,AD是∠BAC的平分线.求证:CD
BD
AC
AB
=
.
分析1 比例线段常由平行线而产生,因而研究比例线段问题,常应注意平行线的作用,在没有平行线时,可以添加平行线而促成比例线段的产生.此题中AD 为△ABC 内角A 的平分线,这里不存在平行线,于是可考虑过定点作某定直线的平行线,添加了这样的辅助线后,就可以利用平行关系找出相应的比例线段,再比较所证的比例式与这个比例式的关系,去探求问题的解决. 证法1: 如图4—9,过C 点作CE ∥AD ,交BA 的延长线于E .
在△BCE 中,∵ DA ∥CE ,∴
AE BA
DC BD = ① 又∵ CE ∥AD ,∴ ∠1=∠3,∠2=∠4,且AD 平分∠BAC , ∵ ∠1=∠2,于是∠3=∠4,
∴ AC=AE .代入②式得
AC AB DC BD =. 分析2 由于BD 、CD 是点D 分BC 而得,故可过分点D 作平行线. 证法2: 如图4—10,过D 作DE ∥AC 交AB 于E ,则∠2=∠3.
∵ ∠1=∠2,∴ ∠1=∠3. 于是EA=ED .
又∵DC BD EA BE =,∴ EA BE ED BE AC AB ==,∴ CD BD
AC AB =
.
分析3 欲证式子左边为AB :AC ,而AB 、AC 不在同一直线上,又不平行,故考虑将AB 转移到与AC 平行的位置.
证法3: 如图4—11,过B 作BE ∥AC ,交AD 的延长线于E ,则∠2=∠E .
∵ ∠1=∠2,∴ ∠1=∠E ,AB=BE .
又∵AC BE DC BD =,∴
CD BD
AC AB =. 分析4 由于AD 是∠BAC 的平分线,故可过D 分别作AB 、AC 的平行线,构造相
似三角形求证.
证法4 如图4—12,过D 点作DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F .
易证四边形AEDF 是菱形.则 DE=DF .
由△BDE ∽△DFC ,得DE BE
DF BE DC BD =
=.
又∵ AC AB DE BE =,∴ DC BD
AC AB =
.
相似三角形添加辅助线的方法举例有答案新
相似三角形添加辅助线的方法举例 例1: 已知:如图,△ABC 中,AB =AC ,BD ⊥AC 于D . 求证: BC 2 =2CD ·AC . 例2.已知梯形ABCD 中,BC AD //,AD BC 3=,E 是腰AB 上的一点,连结CE (1)如果AB CE ⊥ ,CD AB =,AE BE 3=,求B ∠的度数; (2)设BC E ?和四边形AECD 的面积分别为1S 和2S ,且2132S S =,试求 AE BE 的值 例3.如图4-1,已知平行四边ABCD 中,E 是AB 的中点, AD AF 31= ,连E 、F 交AC 于G .求AG :AC 的值. 例4、如图4—5,B 为AC 的中点,E 为BD 的中点,则AF :AE=___________. 例5、如图4-7,已知平行四边形ABCD 中,对角线AC 、BD 交于O 点,E 为AB 延长线上一点,OE 交BC 于F ,若AB=a ,BC=b ,BE=c ,求BF 的长. 例6、已知在△ABC 中,AD 是∠BAC 的平分线.求证:CD BD AC AB = . 相似三角形添加辅助线的方法举例答案 例1: 已知:如图,△ABC 中,AB =AC ,BD ⊥AC 于D . 求证: BC 2 =2CD ·AC . 分析:欲证 BC 2=2CD ·AC ,只需证 BC AC CD BC = 2.但因为结论中有“2”,无法直接找到它们所在的相似三角形,因此需要结合图形特点及结论形式,通过添加辅助线,对其中某一线段进行倍、分变形,构造出单一线段后,再证明三角形相似.由“2”所放的位置不同,证法也不同. 证法一(构造2CD ):如图,在AC 截取DE =DC , ∵BD ⊥AC 于D , ∴BD 是线段CE 的垂直平分线, ∴BC=BE ,∴∠C=∠BEC , 又∵ AB =AC , ∴∠C=∠ABC . ∴ △BCE ∽△ACB . ∴ BC AC CE BC =, ∴BC AC CD BC =2 ∴BC 2 =2CD ·AC . 证法二(构造2AC ):如图,在CA 的延长线上截取AE =AC ,连结BE , ∵ AB =AC , ∴ AB =AC=AE . ∴∠EBC=90°, 又∵BD ⊥AC . ∴∠EBC=∠BDC=∠EDB=90°, B C B C E B C
相似三角形之常用辅助线
相似三角形之常用辅助线 在与相似有关得几何证明、计算得过程中 ,常常需要通过相似三角形,研究两条线段之间得比例关系,或者转移线段或角。而有些时候,这样得相似三角形在问题中,并不就是十分明显、因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需得结论。 专题一、添加平行线构造“A"“X”型 定理:平行于三角形一边得直线与其它两边(或两边延长线)相交,所构成得三角形与原三角形相似。 定理得基本图形: 例1、平行四边形ABCD中,E为AB中点,AF:FD=1:2,求AG:GC 变式练习: 已知在△ABC中,AD就是∠BAC得平分线.求证:、(本题有多种解法,多想想) 例2、如图,直线交△ABC得BC,AB两边于D,E,与CA延长线交于F,若==2,求BE:EA得比值、 变式练习:如图,直线交△ABC得BC,AB两边于D,E,与CA延长线交于F,若错误!= 错误!=2,求BE:E A得比值。 例3、BE=AD,求证:EF·BC=AC·DF 变式1、如图,△ABC中,AB 相似三角形中几种常见的辅助线作法 在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种: 一、添加平行线构造“A ”“X ”型 例1:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,求:BE :EF 的值. 解法一:过点D 作CA 的平行线交BF 于点P ,则 ∴PE=EF BP=2PF=4EF 所以BE=5EF ∴BE :EF=5:1. 解法二:过点D 作BF 的平行线交AC 于点Q , ∴BE :EF=5:1. 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T , ∵BD=2DC ∴ ∴BE :EF=5:1. 变式:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点, 连结BE 并延 长交AC 于F, 求AF :CF 的值. 解法一:过点D 作CA 的平行线交BF 于点P , 解法二:过点D 作BF 的平行线交AC 于点Q , 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T , , 1==AE DE FE PE ,2==DC BD PF BP ,则2==EA DA EF DQ ,3==DC BC DQ BF , EF EF EF EF DQ EF BF BE 563=-=-=-=,则DC CT DT 2 1 ==;TC BT EF BE =, DC BT 2 5= 例2:如图,在△ABC的AB边和AC边上各取一点D和E,且使AD=AE, DE延长线与BC延长线相交于F ,求证: (证明:过点C作CG//FD交AB于G) 例3:如图,△ABC中,AB 相似三角形之常用辅助线 在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。而有些时候,这样的相似三角形在问题中,并不是十分明显。因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。 专题一、添加平行线构造“A ”“X ”型 定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似. 定理的基本图形: 例1、平行四边形ABCD 中,E 为AB 中点,AF :FD =1:2,求AG :GC 变式练习: 已知在△ABC 中,AD 是∠BAC 的平分线.求证:. (本题有多种解法,多想想) G F E D C B A G F E D C B A CD BD AC AB 例2、如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若 DC BD =FA FC =2,求BE:EA 的比值. 变式练习:如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若BD DC = FE ED =2,求BE:EA 的比 值. 例3、BE =AD ,求证:EF ·BC =AC ·DF 变式1、如图,△ABC 中,AB 例4、已知:如图,在△ABC 中,AD 为中线,E 在AB 上,AE=AC ,CE 交AD 于F ,EF ∶FC=3∶5,EB=8cm, 求AB 、AC 的长. 变式:如图,21==DE AE CD BD ,求BF AF 。(试用多种方法解) 说明:此题充分展示了添加辅助线,构造相似形的方法和技巧.在解题中方法要灵活,思路要开阔. 总结: (1)遇燕尾,作平行,构造 字一般行。 (2)引平行线应注意以下几点: 1)选点:一般选已知(或求证)中线段的比的前项或后项,在同一直线的线段的端点作为引平行线的点。 2)引平行线时尽量使较多已知线段、求证线段成比例。 第2讲相似三角形中的辅助线及动点 在解相似三角形问题时,常需要作辅助线来沟通已知条件和未知条件, 在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或得 出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种: 、作平行线 例1.如图,.VABC 的AB 边和AC 边上各取一点 ” BF BD 求证: CF CE 例2.如图,△ ABC 中,AB 例4.如图从—ABCD 顶点C向AB和AD的延长线引垂线CE和CF,垂足分别为E、F,求证: 2 AB AE AD AF =AC2。 三、作延长线例5.如图,在梯形ABCD中,AD // BC,若/ BCD的平分线CH丄AB于点H , BH=3AH,且四边形AHCD的面积为21,求厶HBC的面积。 例6?如图,https://www.360docs.net/doc/ae2824436.html,BC中,CD为斜边AB上的高,E为CD的中点,AE的延长线交BC 于F, FG _ AB于G, 求证:FG2=CF *BF 四、作中线 例 7 如图,. :ABC 中,AB 丄AC , AE 丄 BC 于 E , D 在 AC 边上,若 BD=DC=EC=1,求 AC 。 2、如图,正方形 ABCD 勺边长为2, AE = EB MN= 1,线段MN 的两端在CB CD 上滑动,当CM 为 何值时,△ AED 与以M 、N 、C 为顶点的三角形相似? 动点题型 1、如图正方形ABCD 的边长为2, AE=EB ,线段MN 的两端点分别在 MN=1,当CM 为何值时厶AED 与以M 、N 、C 为顶点的三角形相似? CB 、CD 上滑动,且 u c D N C 中考相似三角形之常 用辅助线 Revised on November 25, 2020 相似三角形之常用辅助线 在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。而有些时候,这样的相似三角形在问题中,并不是十分明显。因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。 专题一、添加平行线构造“A ”“X ”型 定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似. 定理的基本图形: 例1、平行四边形ABCD 中,E 为AB 中点,AF :FD =1:2,求AG :GC 变式练习: 已知在△ABC 中,AD 是∠BAC 的平分线.求证:. (本题有多种解法,多想想) 例2、如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若 DC BD =FA FC =2,求BE:EA 的比值. 变式练习:如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若BD DC = FE ED =2,求BE:EA 的 比值. 例3、BE =AD ,求证:EF ·BC =AC ·DF 变式1、如图,△ABC 中,AB .\ 相似三角形添加辅助线的方法举例 例1:已知:如图,△ ABC 中, AB= AC, BD⊥ AC 于 D. 求证: BC2= 2CD· AC. A D B C 例 2.已知梯形ABCD 中, AD // BC , BC 3AD , E 是腰 AB 上的一点,连结CE ( 1)如果CE AB , AB CD , BE 3AE ,求 B 的度数; ( 2)设BCE 和四边形 AECD 的面积分别为S1和 S2,且 2S13S2,试求BE 的值AE 例 3.如图 4-1,已知平行四边 AF 1 AD ABCD中, E 是 AB 的中点,3,连E、F交AC于G.求AG:AC 的值. .\例4、如图 4—5, B 为 AC 的中点, E 为 BD 的中点,则 AF:AE=___________. 例 5、如图 4-7,已知平行四边形ABCD 中,对角线AC、 BD 交于 O 点, E 为 AB 延长线上一点,OE 交 BC 于F,若 AB=a, BC=b, BE=c,求 BF 的长. AB BD 例 6、已知在△ ABC 中, AD 是∠ BAC的平分线.求证:AC CD . 相似三角形添加辅助线的方法举例答案 例 1: 已知:如图,△ ABC 中, AB = AC , BD ⊥ AC 于 D . 求证: BC 2= 2CD · AC . 分析: 欲证 BC 2 = 2CD ·AC ,只需证 BC AC .但因为结论中有“ 2”,无法 2CD BC 直接找到它们所在的相似三角形,因此需要结合图形特点及结论形式,通过添加辅 助线,对其中某一线段进行倍、 分变形, 构造出单一线段后, 再证明三角形相似. 由 “ 2”所放的位置不同,证法也不同. 证法一 (构造 2CD ):如图,在 AC 截取 DE = DC , ∵ BD ⊥ AC 于 D , ∴ BD 是线段 CE 的垂直平分线, ∴ BC=BE ,∴∠ C=∠ BEC , 又∵ AB = AC , ∴∠ C=∠ ABC . ∴ △BCE ∽△ ACB . ∴ BC AC , ∴ BC AC B CE BC 2CD BC ∴ BC 2= 2CD · AC . 证法二 (构造 2AC ):如图,在 CA 的延长线上截取 AE = AC ,连结 BE , ∵ AB = AC , ∴ AB = AC=AE . ∴∠ EBC=90°,又∵ BD ⊥ AC . ∴∠ EBC=∠ BDC=∠ EDB=90°, ∴∠ E=∠ DBC , ∴△ EBC ∽△ BDC ∴ BC CE 即 BC 2 AC CD BC CD BC ∴ BC 2= 2CD · AC . 1 BC ) :如图,取 1 BC . 证法三 (构造 BC 的中点 E ,连结 AE ,则 EC= 2 2 又∵ AB=AC , ∴ AE ⊥BC ,∠ ACE=∠ C ∴∠ AEC=∠ BDC=90° ∴△ ACE ∽△ BCD . .\ A D B C A E D C E A D B C A ∴ CE 1 BC AC . D AC 即 2 B E C CD BC CD BC ∴ BC 2=2CD · AC . A 证法四 (构造 1 1 BC . BC ):如图,取 BC 中点 E ,连结 DE ,则 CE= 2 2 ∵ BD ⊥ AC ,∴ BE=EC=EB , ∴∠ EDC=∠ C 又∵ AB=AC ,∴∠ ABC=∠ C , ∴△ ABC ∽△ EDC . D B E C 一、添辅助线有二种情况: 1、按定义添辅助线: 如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。 2、按基本图形添辅助线: 每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”!这样可防止乱添线,添辅助线也有规律可循。举例如下:(1)平行线是个基本图形: 当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线 (2)等腰三角形是个简单的基本图形: 当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。 (3)等腰三角形中的重要线段是个重要的基本图形: 出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。 (4)直角三角形斜边上中线基本图形 出现直角三角形斜边上的中点往往添斜边上的中线。出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。 (5)三角形中位线基本图形 几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。 (6)全等三角形: 全等三角形有轴对称形,中心对称形,旋转形与平移形等;如果出现两条相等线段或两个档相等角关于某一直线成轴对称就可以添加轴对称形全等三角形:或添对称轴,或将三角形沿对称轴翻转。当几何问题中出现一组或两组相等线段位于一组对顶角两边且成一直线时可添加中心对称形全等三角形加以证明,添加方法是将四个端点两两连结或过二端点添平行线 (7)相似三角形: 相似三角形有平行线型(带平行线的相似三角形),相交线型,旋转型;当出现相比线段重叠在一直线上时(中点可看成比为1)可添加平行线得平行线型相似 相似三角形中添加辅助线问题培优(张老师) (一)遇燕尾,作平行,构造 字一般行。 1、BE =AD ,求证:EF ·BC =AC ·DF (二)遇梯形,延长腰,构成A 字瞧一瞧。 1题图 2、梯形ABCD 中,AD ∥BC ,CH 平分∠BCD ,BH =3AH ,四边形AHCD 的面积为21,求△HBC 的面积。 2题图 (三)遇平分,作等腰,三线合一要记牢。 3、AC ⊥BC ,AE ⊥DE ,2∠ADE =∠B ,AC :BC =3:1,求AE :DG 3题图 (四)直角多,垂线作,再难题目你能做。 4、平行四边形ABCD 中,CE ⊥AE ,CF ⊥AF ,求证:AB ·AE +AD ·AF =AC 2 4题图 四、巩固练习:(做题目,看情况,灵活运用最恰当。) 1、BD :DC =2:1,E 为AD 中点,求①BE :EF ②AF :FC 1题图 2题图 2、平行四边形ABCD 中,E 为AB 中点,AF :FD =1:2,求AG :GC H D C B A G E D C B A A B C D E F F E D C B A G F E D C B A E D C B A 3、D 为BC 中点,求证:AF :BF =AE :EC 3题图 4、AC ⊥BC ,CD ⊥AB ,FG ⊥AB ,E 为CD 中点,求证:FG 2 =CF ·BF 4题图 5题图 5、AB =AC ,AD 为中线,CF ∥AB ,求证:BP 2 =PE ·PF 6、AD 平分∠BAC ,EF 垂直平分AD ,求证:ED 2 =EB ·EC 6题图 7、矩形ABCD 中,E 为AD 中点,EF ⊥EC ,求证:△AEF ∽△ECF 7题图 8题图 8、AB =AC ,AB ⊥BC ,AD 为中线,BE ⊥AD ,求证:①AE =2EC ②∠AEB =∠CED 9、∠BAC =90°,AE ⊥BC ,BD =DC =EC =1,求AC 的长 9题图 A B C D E F P A B C D E F A B C D E F A B C D E F P A B C D E P A B C D E A B C D E F G 相似三角形中的辅助线 在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或得出等角,等边,从而为证明三角形相似或实行相关的计算找到等量关系。主要的辅助线有以下几种: 一、作平行线 例1. 如图,的AB边和AC边上各取一点D和E,且使AD=AE,DE延长 线与BC延长线相交于F,求证: B D A C E F 证明:过点C作CG//FD交AB于G F 小结:本题关键在于AD=AE这个条件怎样使用。由这道题还能够增加一种证明线段相等的方法:相似、成比例。 例2. 如图,△ABC中,AB 分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。 不相似,因而要通过两组三角形相似,使用中间比代换得到,为构造相似三 角形,需添加平行线。 方法一:过E作EM//AB,交BC于点M,则△EMC∽△ABC(两角对应相等,两三角形相似)。 方法二:如图,过D作DN//EC交BC于N 二、作垂线 3. 如图从 ABCD 顶点C 向AB 和AD 的延长线引垂线CE 和CF ,垂足分别为E 、F ,求证:2 AC AF AD AE AB =?+?。 又 BCM ADN ??? ∴ AN=CM ∴ 2 )(AC CM AM AC AF AD AE AB =+=?+? 三、作延长线 例5. 如图,在梯形ABCD 中,AD ∥BC ,若∠BCD 的平分线CH ⊥AB 于点H ,BH=3AH ,且四边形AHCD 的面积为21,求△HBC 的面积。 分析:因为问题涉及四边形AHCD ,所以可构造相似三角形。把问题转化为相似三角形的面积比而加以解决。 解:延长BA 、CD 交于点P ∵CH ⊥AB ,CD 平分∠BCD ∴CB=CP ,且BH=PH ∵BH=3AH ∴PA :AB=1:2 ∴PA :PB=1:3 ∵AD ∥BC ∴△PAD ∽△PBC 第2讲 相似三角形中的辅助线及动点 在解相似三角形问题时,常需要作辅助线来沟通已知条件和未知条件, 在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或得出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种: 一、作平行线 例1. 如图,?A B C 的AB 边和AC 边上各取一点D 和E ,且使AD =AE ,DE 延长线与BC 延长线相交于F ,求证:BF CF BD CE = 例2. 如图,△ABC 中,AB 相似三角形中的辅助线 在解相似三角形问题时,常需要作辅助线来沟通已知条件和未知条件, 在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或得出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种: 一、作平行线 例1. 如图,?ABC 的AB 边和AC 边上各取一点D 和E ,且使AD =AE ,DE 延长线与BC 延长线相交于F ,求证:BF CF BD CE = B D A C F E 证明:过点C 作CG//FD 交AB 于G F ∴=AD AG AE AC 又 AD AE =,∴=AG AC ∴=DG CE GC DF //,∴ =BD DG BF CF ∴=BD CE BF CF 小结:本题关键在于AD =AE 这个条件怎样使用。由这道题还可以增加一种证明线段相等的方法:相似、成比例。 例2. 如图,△ABC 中,AB 分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。欲证,需证,而这四条线段所在的两个三角形显然AB DF AC EF AB AC EF DF ?=?=不相似,因而要通过两组三角形相似,运用中间比代换得到,为构造相似三角形,需添加平行线。 方法一:过E 作EM//AB ,交BC 于点M ,则△EMC ∽△ABC (两角对应相等,两三角形相似)。 ∴ =?=?EM AB EC AC EM AC AB EC 即, ∴=AB AC EM EC 同理可得??EMF DBF ~ ∴=EF DF EM BD , 又, BD EC EM EC EM BD =∴ = (为中间比),EM BD ∴=AB AC EF DF , ∴?=?AB D F AC EF 方法二:如图,过D 作DN//EC 交BC 于N 相似三角形添加辅助线的方法举例 例1:已知:如图,△ABC中,AB=AC,BD⊥AC于D. 求证:BC2=2CD·AC. 例2.已知梯形ABCD中,BC AD//,AD BC3 =,E是腰AB上的一点,连结CE (1)如果AB CE⊥,CD AB=,AE BE3 =,求B ∠的度数; (2)设BCE ?和四边形AECD的面积分别为 1 S和 2 S,且 2 1 3 2S S=,试求 AE BE 的值 例3.如图4-1,已知平行四边ABCD中,E是AB的中点, AD AF 3 1 = ,连E、F交AC于G.求AG:AC 的值. B C D 例4、如图4—5,B 为AC 的中点,E 为BD 的中点,则AF :AE=___________. 例5、如图4-7,已知平行四边形ABCD 中,对角线AC 、BD 交于O 点,E 为AB 延长线上一点,OE 交BC 于F ,若AB=a ,BC=b ,BE=c ,求BF 的长. 例6、已知在△ABC 中,AD 是∠BAC 的平分线.求证:CD BD AC AB . 相似三角形添加辅助线的方法举例答案 例1: 已知:如图,△ABC 中,AB =AC ,BD ⊥AC 于D . 求证: BC 2=2CD ·AC . 分析:欲证 BC 2=2CD ·AC ,只需证 BC AC CD BC = 2.但因为结论中有“2”,无法直接找到它们所在的相似三角形,因此需要结合图形特点及结论形式,通过添加辅助线,对其中某一线段进行倍、分变形,构造出单一线段后,再证明三角形相似.由“2”所放的位置不同,证法也不同. 证法一(构造2CD ):如图,在AC 截取DE =DC , ∵BD ⊥AC 于D , ∴BD 是线段CE 的垂直平分线, ∴BC=BE ,∴∠C=∠BEC , 又∵ AB =AC , ∴∠C=∠ABC . ∴ △BCE ∽△ACB . ∴ BC AC CE BC =, ∴BC AC CD BC = 2 ∴BC 2=2CD ·AC . 证法二(构造2AC ):如图,在CA 的延长线上截取AE =AC ,连结BE , ∵ AB =AC , ∴ AB =AC=AE . ∴∠EBC=90°, 又∵BD ⊥AC . ∴∠EBC=∠BDC=∠EDB=90°, ∴∠E=∠DBC , ∴△EBC ∽△BDC ∴BC CE CD BC =即BC AC CD BC 2= ∴BC 2=2CD ·AC . 证法三(构造 BC 21) :如图,取BC 的中点E ,连结AE ,则EC=BC 2 1 . 又∵AB=AC , ∴AE ⊥BC ,∠ACE=∠C ∴∠AEC=∠BDC=90° ∴△ACE ∽△BCD . ∴BC AC CD CE =即BC AC CD BC =21. ∴BC 2=2CD ·AC . 证法四(构造 BC 21):如图,取BC 中点E ,连结DE ,则CE=BC 2 1 . ∵BD ⊥AC ,∴BE=EC=EB , ∴∠EDC=∠C 又∵AB=AC ,∴∠ABC=∠C , ∴△ABC ∽△EDC . B C E B C B B C 相似三角形中几种常见的辅助线作法有辅助线 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】 相似三角形中几种常见的辅助线作法 在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种: 一、添加平行线构造“A ”“X ”型 例1:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,求:BE :EF 的值. 解法一:过点D 作CA 的平行线交BF 于点P ,则 ∴PE=EF BP=2PF=4EF 所以BE=5EF ∴BE :EF=5:1. 解法二:过点D 作BF 的平行线交AC 于点Q , ∴BE :EF=5:1. 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T , ∵BD=2DC ∴ ∴BE :EF=5:1. , 1==AE DE FE PE ,2==DC BD PF BP , 则 2==EA DA EF DQ , 3==DC BC DQ BF ,EF EF EF EF DQ EF BF BE 563=-=-=-=, 则DC CT DT 21 ==;TC BT EF BE =,DC BT 2 5 = 变式:如图,D是△ABC的BC边上的点,BD: DC=2:1,E是AD的中点, 连结BE并延长交AC 于F, 求AF:CF的值. 解法一:过点D作CA的平行线交BF于点P, 解法二:过点D作BF的平行线交AC于点Q, 解法三:过点E作BC的平行线交AC于点S, 解法四:过点E作AC的平行线交BC于点T, 例2:如图,在△ABC的AB边和AC边上各取一点D和E,且使 AD=AE, DE延长线与BC延长线相交于F,求证: (证明:过点C作CG 分析:证明等积式问题常常化为比例式,再通过相似三角 形对应边成比例来证明。不相似,因而要通过两组三角形相似,运用中间比代换得到,为构造相似三角形,需添加平行线。. CE BD CF BF(完整版)相似三角形中几种常见的辅助线作法(有辅助线)
相似三角形常用辅助线
相似三角形中的辅助线及动点问题(经典题型)
中考相似三角形之常用辅助线
相似三角形添加辅助线的方法举例(有规范标准答案).docx
中考数学压轴题常见辅助线整理
相似三角形中添加辅助线问题
相似三角形中的辅助线
相似三角形中的辅助线及动点问题(经典题型)
相似三角形中的辅助线
相似三角形添加辅助线的方法举例 有答案
相似三角形中几种常见的辅助线作法有辅助线
